Multi-Motor Cooperative Control Strategy for Speed Synchronous Control of Construction Platform
Abstract
:1. Introduction
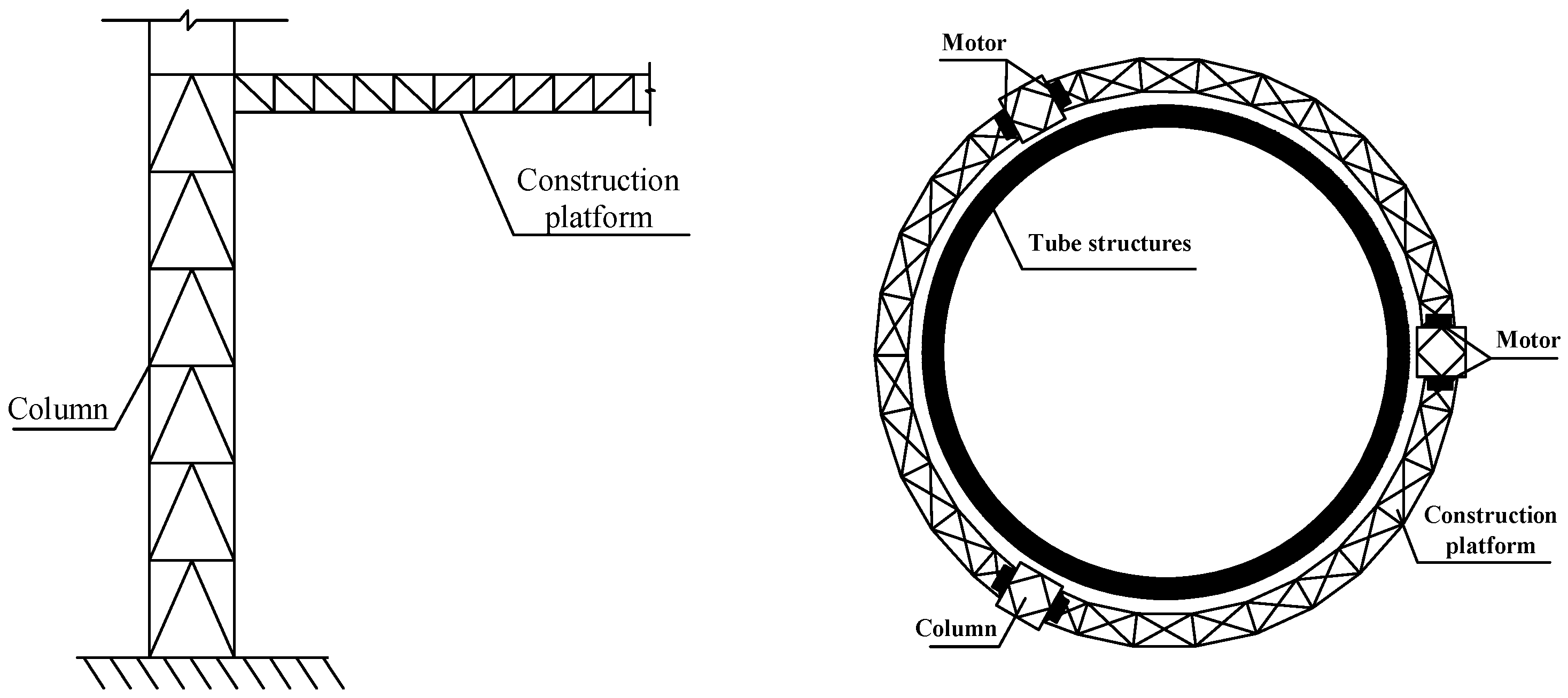
1.1. Technical Concepts
1.2. Main Contribution
1.3. Organization
2. Related Work
3. Working Principle of Single Motor
3.1. Mathematical Model
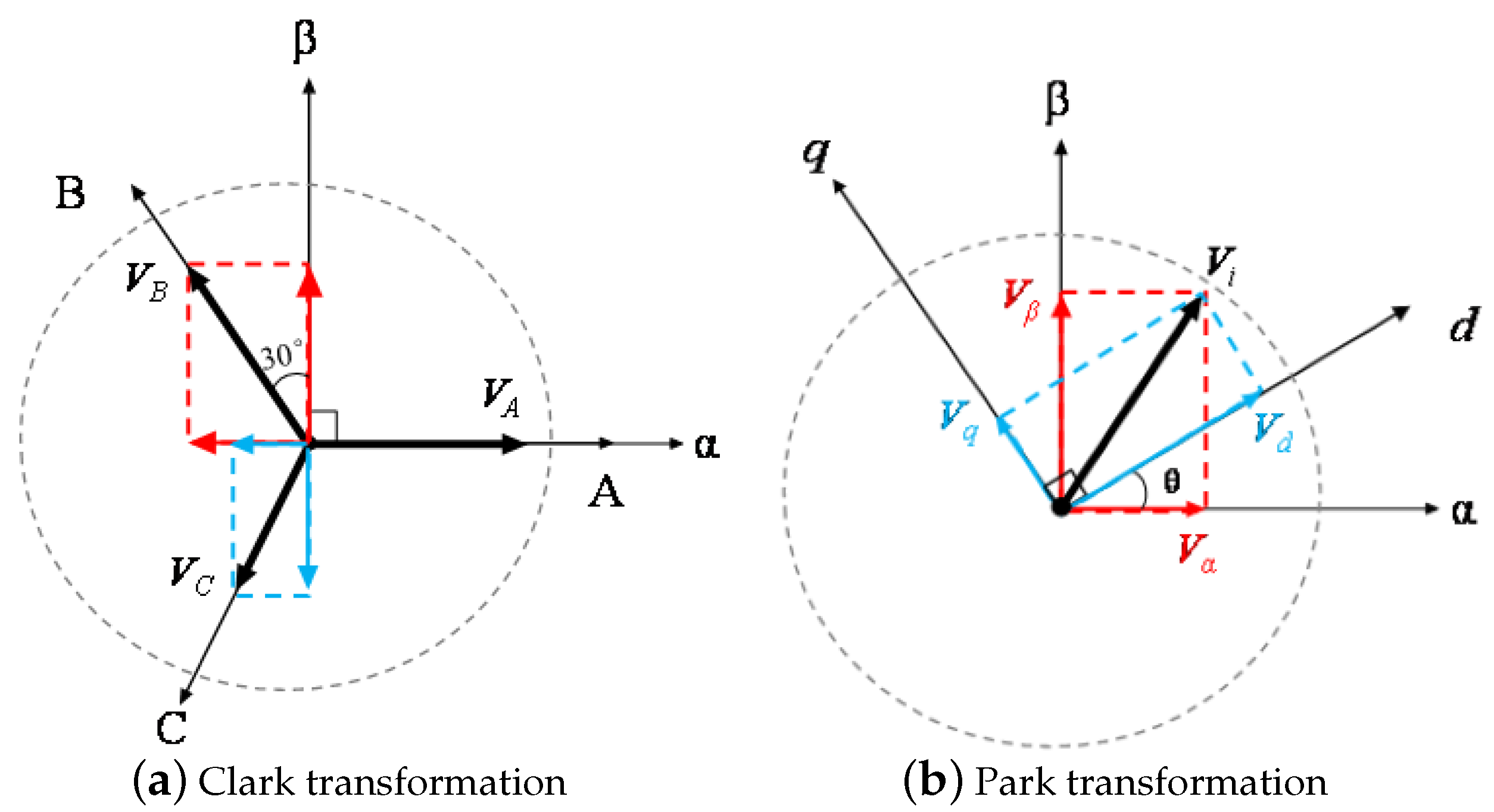
3.2. Vector Control System
4. Multi-Motor Speed Synchronous Control Structure
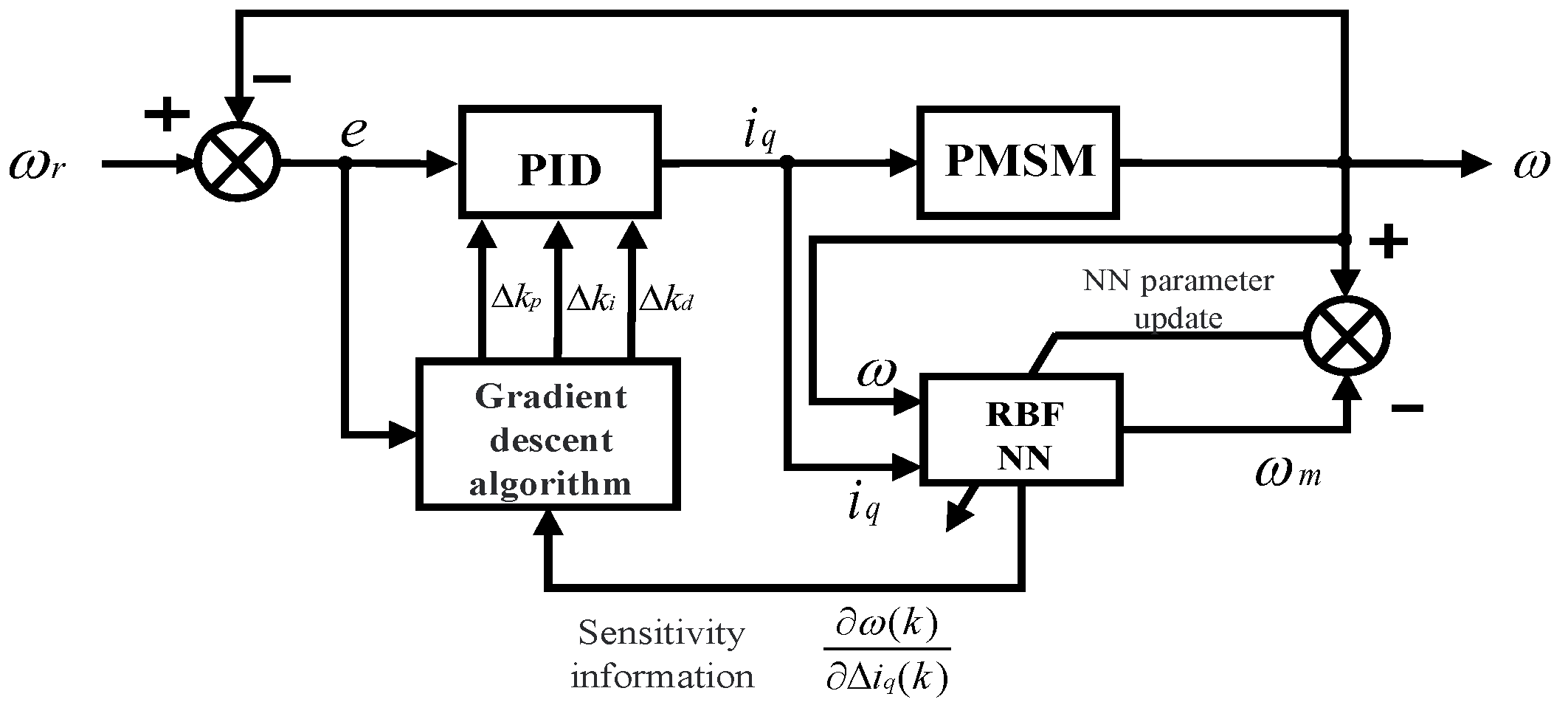
5. Improving PID Controller via RBF Neural Network
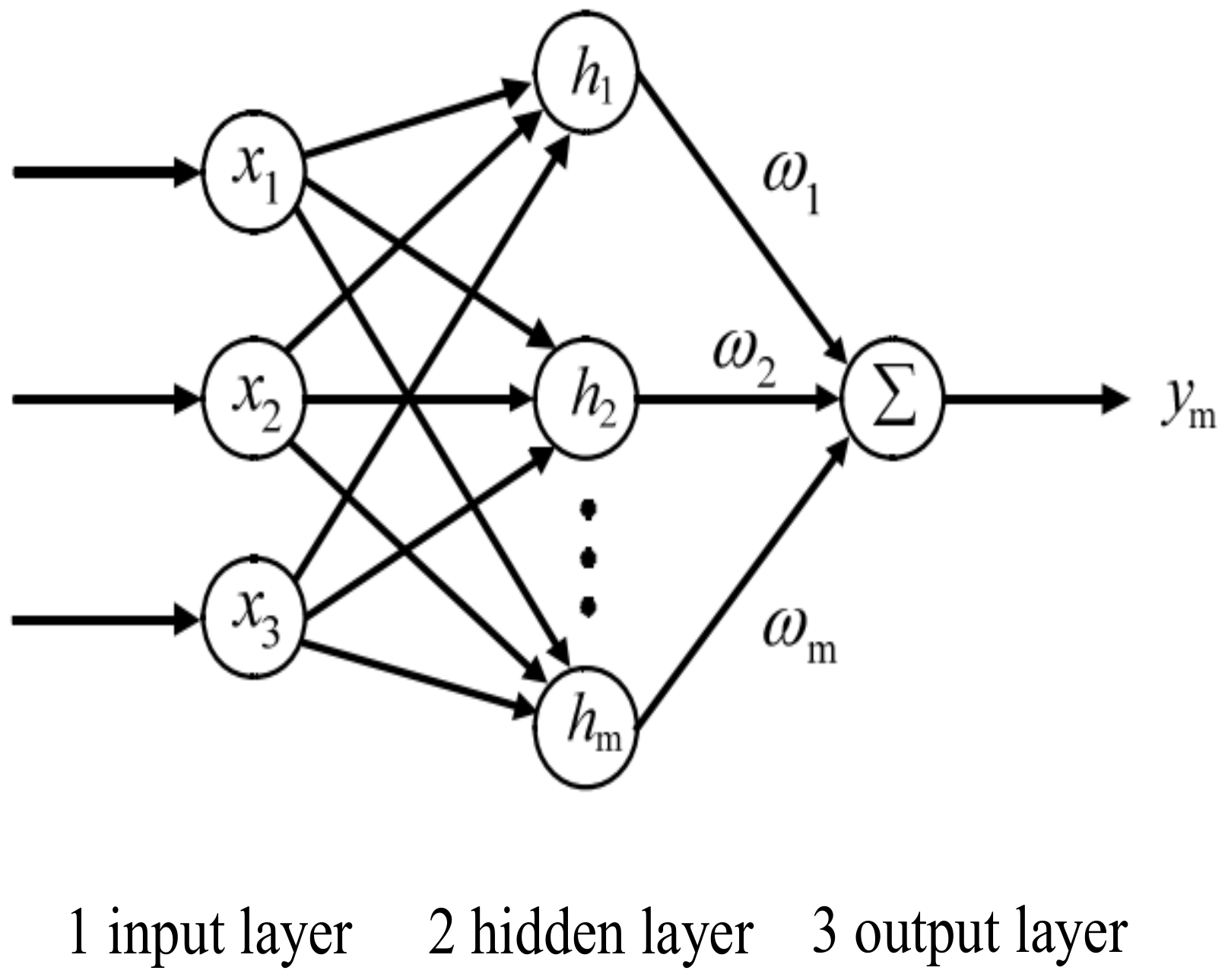
5.1. RBF Neural Network Model
5.2. Pid Tuning Principle
5.3. Improvement of the Integral Term Based on Variable Speed Integration
6. Performance Evaluation
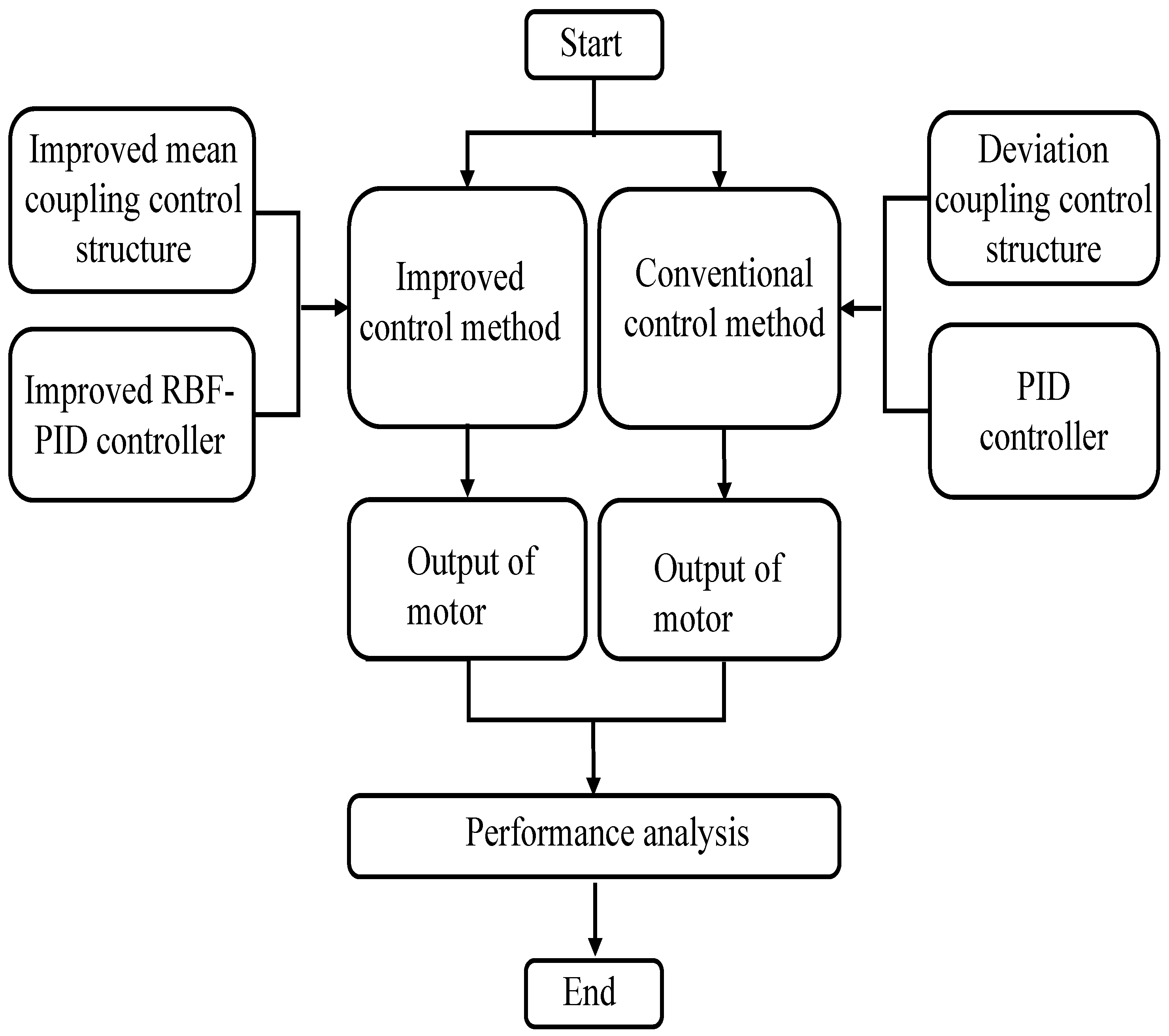
6.1. Experimental Method
6.2. Simulation and Numerical Analysis
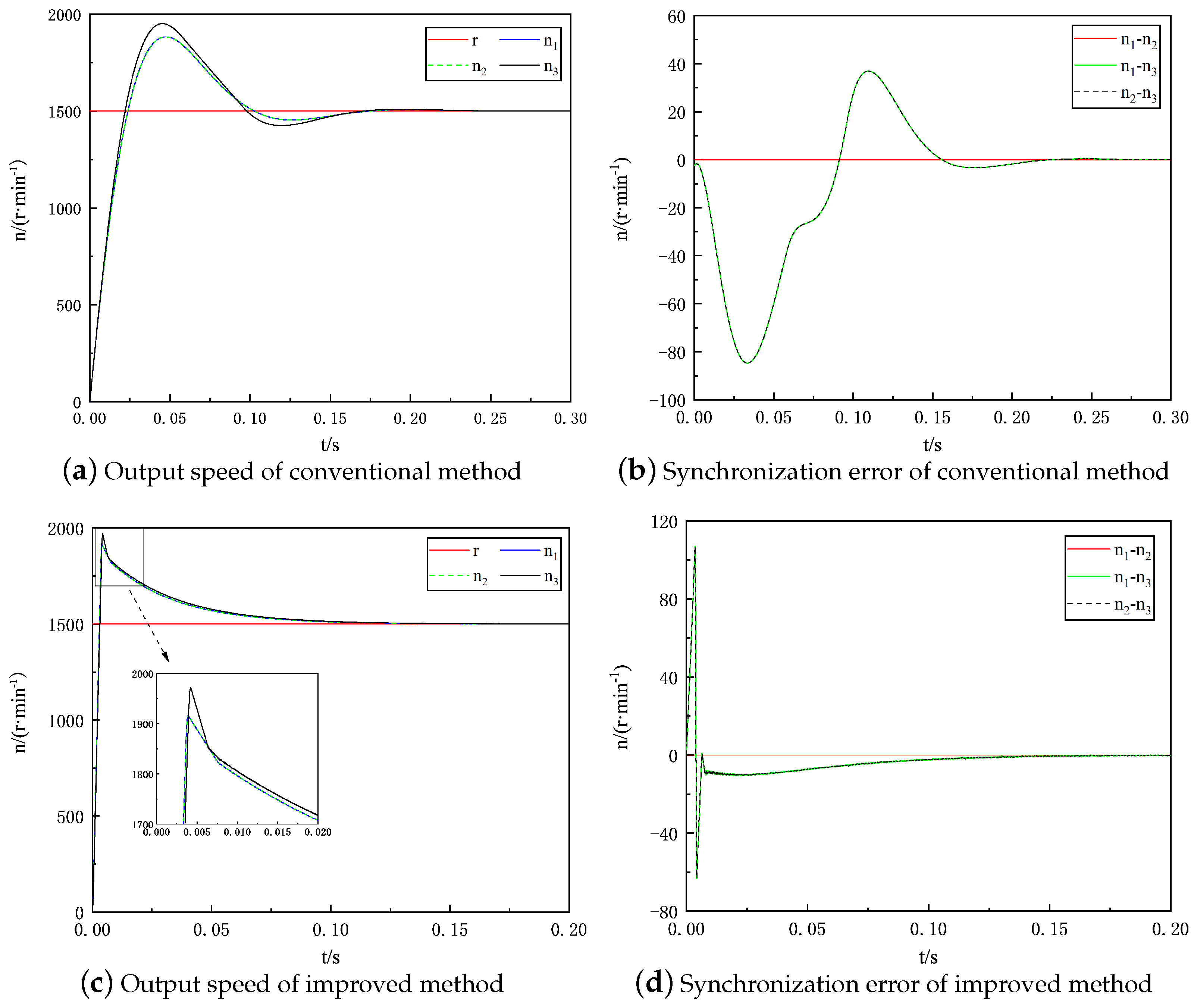
6.2.1. Comparison of Motor Starting Performance with Loading
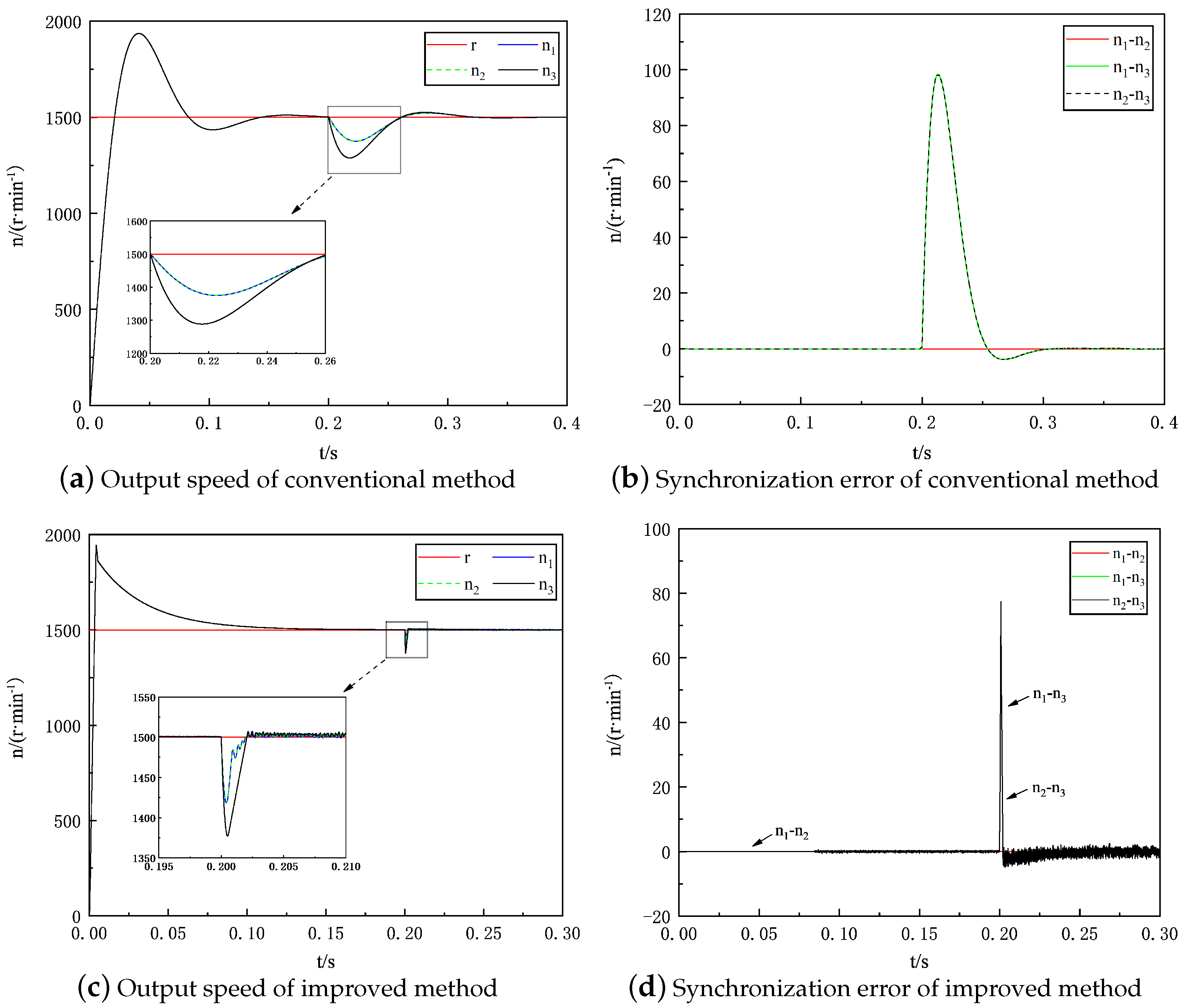
6.2.2. Performance Comparison under the Load Mutation at Steady State
7. Conclusions
- The new RBF-PID control algorithm designed can effectively track and control the motor speed and current, thus enhancing the control effect.
- By constructing the mean-coupled structure and the improved PID controller, the global compensation control of the error of the multi-motor system ensures synchronous convergence, and at the same time, reduces the computational cost.
- The multi-motor cooperative control scheme designed in this paper has strong dynamic response and regulation capability, anti-interference capability and robustness. The improved control method outperforms the conventional control method in terms of motor overshoot, motor regulation time, maximum synchronization error and the regulation time of the synchronization error.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| PID | Proportion Integration Differentiation |
| RBF | Radial Basis Function |
| NN | Neural Network |
| PMSM | Permanent Magnet Synchronous Motor |
| SVPWM | Space Vector Pulse Width Modulation |
| CNC | Computer Numerical Control |
| DC | Direct Current |
| R-Park | Reverse-Park transformation |
References
- Yang, J.; Chen, L. Safety analysis of slipform system for large silo construction. J. Wuhan Univ. (Eng. Ed.) 2020, 53, 288–292. [Google Scholar]
- Synthesis. Focus on the collapse of Jiangxi Fengcheng power plant accident that killed 74 people and injured 2 others. Saf. Health 2017, 1, 6–9. [Google Scholar]
- Yan, L. Application of silo slipform operation platform instead of formwork support system technology. Constr. Technol. 2020, 49, 73–75. [Google Scholar]
- Gao, J.; Chen, L. Exploration of key technology of sliding mode construction of variable section high pier. Highway 2017, 62, 125–127. [Google Scholar]
- Lv, Y.-Y. Dynamic Analysis of Scaffolding under the Walking Load of Construction Personnel; Beijing Jiaotong University: Beijing, China, 2017. [Google Scholar]
- Kim, H.; Son, J.; Lee, J. A High-Speed Sliding-Mode Observer for the Sensorless Speed Control of a PMSM. IEEE Trans. Ind. Electron. 2011, 58, 4069–4077. [Google Scholar]
- Vinod, J.; Sarkar, B.K. Francis turbine electrohydraulic inlet guide vane control by artificial neural network 2 degree-of-freedom PID controller with actuator fault. Proc. Inst. Mech. Eng. Part I J. Syst. Control Eng. 2021, 235, 1494–1509. [Google Scholar]
- Mohamed, I.; Salem, M.F. LFC based adaptive PID controller using ANN and ANFIS techniques. J. Electr. Syst. Inf. Technol. 2014, 1, 212–222. [Google Scholar]
- Ge, Y. Research on Multi-Motor Cooperative Control Strategy and Application; Lanzhou University of Technology: Lanzhou, China, 2020. [Google Scholar]
- Liu, P. Research on the Control Strategy of Multi-Motor Speed Synchronization Control System; Liaoning University of Engineering and Technology: Fuxin, China, 2017. [Google Scholar]
- Qi, D. Research on Multi-Motor Precise Synchronous Control System; Shenyang University of Technology: Shenyang, China, 2018. [Google Scholar]
- Yao, W. Research on Multi-Motor Synchronous Control Strategy; Xiangtan University: Xiangtan, China, 2013. [Google Scholar]
- Geng, Q.; Wang, S.; Zhou, Z. Improved deviation-coupled multi-motor speed synchronization control. J. Electr. Eng. Technol. 2019, 34, 474–482. [Google Scholar]
- Sun, M. Optimization of Multi-Motor Synchronous Control Based on Fuzzy Adaptive Strategy; Lanzhou University of Technology: Lanzhou, China, 2021. [Google Scholar]
- Xu, D.; Jiang, J.; Liu, A. Research on multi-motor synchronous control strategy of flexographic printing machine. Inf. Technol. Informatiz. 2020, 06, 129–133. [Google Scholar]
- Long, A. Application and Research of Hydraulic Slipform Technology in the Construction of Cast-in-Place Concrete Silo Structure; Anhui University of Construction: Hefei, China, 2018. [Google Scholar]
- Xu, Q. Research on the Design and Construction Key Technology of Modular Rigid Sliding Platform of Silo; Hebei Engineering University: Handan, China, 2020. [Google Scholar]
- Shao, W.Q. RBF Neural Network-Based Control System for Permanent Magnet Synchronous Motor; Harbin Institute of Technology: Harbin, China, 2019. [Google Scholar]
- Nie, Q.P.; Tang, M.X. Research on the application of RBF rectified PID in permanent magnet synchronous motor control. Autom. Instrum. 2019, 40, 1–5+10. [Google Scholar]
- Ding, W.; Du, Q.; Song, C. Mean-coupled multi-motor sliding mode speed synchronization control. J. Xi’an Jiaotong Univ. 2022, 56, 159–170. [Google Scholar]
- Feng, X.; Zhuo, Q.; Liu, X.; Qian, Y.; Li, Y. Development of multi-motor synchronous control system based on network-on-chip. Proc. Inst. Mech. Eng. Part I J. Syst. Control Eng. 2020, 234, 1000–1010. [Google Scholar] [CrossRef]
- Shao, W.Q.; Kang, E.R.L. PID control of permanent magnet synchronous motor based on RBF neural network. Micro Spec. Mot. 2018, 46, 75–78. [Google Scholar]
- Zhou, C.; Meng, J.; Zhang, W. Research on fractional order sliding mode control of permanent magnet synchronous motor based on vector control. China Equip. Eng. 2021, 11, 91–93. [Google Scholar]




| Network Structure | Function of Cost | Hidden Layer Node Function | Network Input | Learning Rate | Momentum Factor |
|---|---|---|---|---|---|
| 3-6-1 | Mean square error function | Gaussian function | 0.2 | 0.2 |
| Rise Time | Maximum Deviation | Overshoot | Setting Time | Maximum Synchronization Error | Synchronous Error Adjustment Time | |
|---|---|---|---|---|---|---|
| Conventional control method | 0.02 s | 475 r/min | 32% | 0.15 s | 85 r/min | 0.2 s |
| Improved control method | 0.005 s | 445 r/min | 29% | 0.1 s | 100 r/min | 0.05 s |
| Optimized effect | 75% | 6% | 10% | 33% | −17% | 75% |
| Maximum Tracking Error | Setting Time | Maximum Synchronization Error | Synchronous Error Adjustment Time | |
|---|---|---|---|---|
| Conventional control method | 200 r/min | 0.06 s | 100 r/min | 0.07 s |
| Improved control method | 120 r/min | 0.005 s | 80 r/min | 0.02 s |
| Optimized effect | 35% | 90% | 20% | 70% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, M.; Wang, Q.; Wang, Y.; Dong, Q. Multi-Motor Cooperative Control Strategy for Speed Synchronous Control of Construction Platform. Electronics 2022, 11, 4162. https://doi.org/10.3390/electronics11244162
Zhao M, Wang Q, Wang Y, Dong Q. Multi-Motor Cooperative Control Strategy for Speed Synchronous Control of Construction Platform. Electronics. 2022; 11(24):4162. https://doi.org/10.3390/electronics11244162
Chicago/Turabian StyleZhao, Mingchuang, Qunwei Wang, Yongwei Wang, and Qinxi Dong. 2022. "Multi-Motor Cooperative Control Strategy for Speed Synchronous Control of Construction Platform" Electronics 11, no. 24: 4162. https://doi.org/10.3390/electronics11244162
APA StyleZhao, M., Wang, Q., Wang, Y., & Dong, Q. (2022). Multi-Motor Cooperative Control Strategy for Speed Synchronous Control of Construction Platform. Electronics, 11(24), 4162. https://doi.org/10.3390/electronics11244162






