3-D Metamaterials: Trends on Applied Designs, Computational Methods and Fabrication Techniques
Abstract
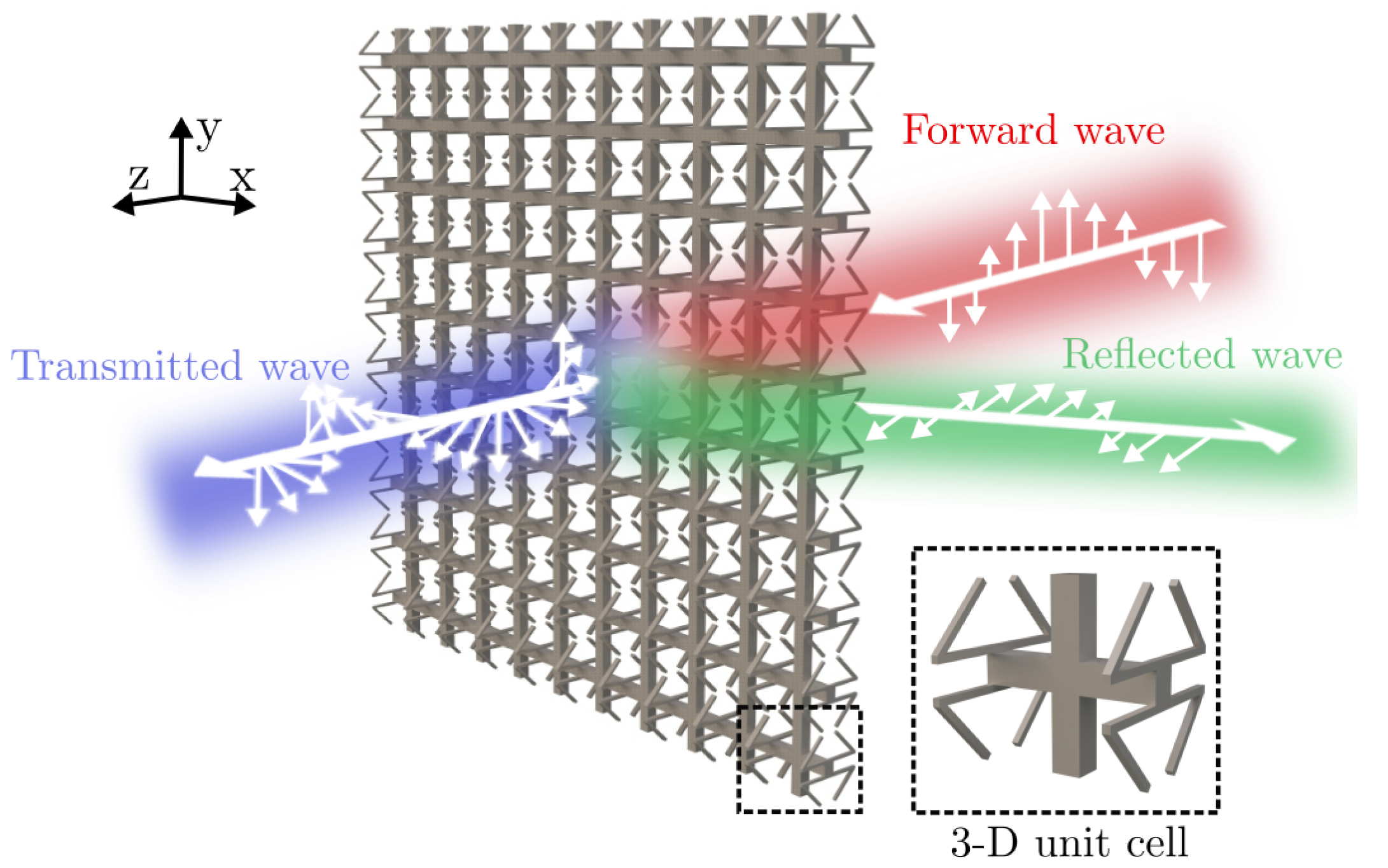
:1. Introduction
2. Computational Methods
2.1. Differential-Form Methods
2.2. Integral-Equation Methods
2.3. Modal Analysis
2.4. Circuit Models
2.5. Other Methods
2.6. Commercial Solvers
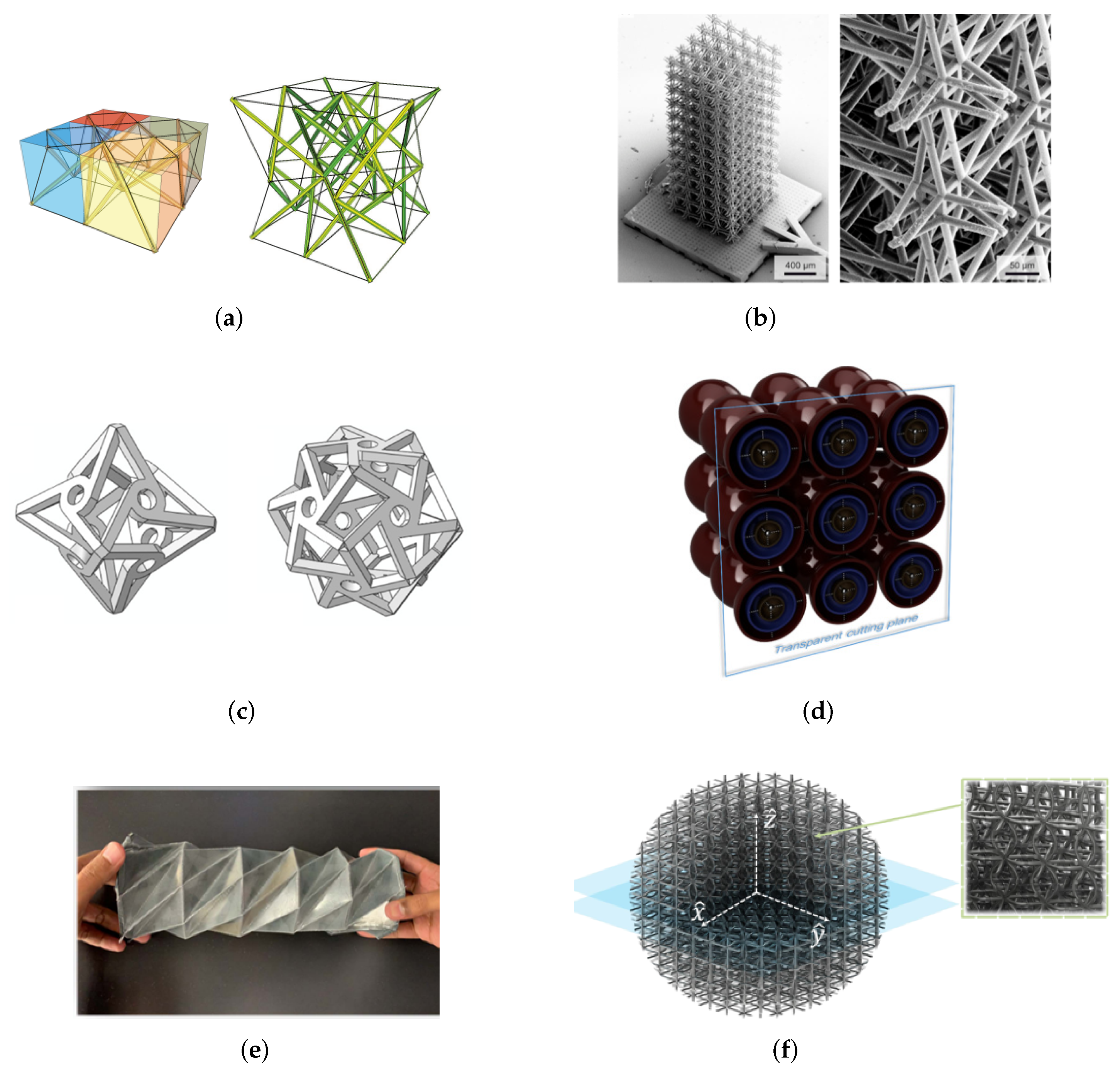
3. Designs

4. Fabrication Techniques
4.1. Conventional Manufacturing Techniques and 3-D Assembly
4.2. 3-D Printing
4.3. Alternative Techniques for 3-D Prototyping
5. Future Trends
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Smith, D.R.; Pendry, J.B.; Wiltshire, M.C.K. Metamaterials and Negative Refractive Index. Science 2004, 305, 788–792. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Engheta, N.; Ziolkowski, R.W. Metamaterials: Physics and Engineering Explorations; Wiley-IEEE Press: Hoboken, NJ, USA, 2006. [Google Scholar]
- Liu, Y.; Zhang, X. Metamaterials: A new frontier of science and technology. Chem. Soc. Rev. 2011, 40, 2494–2507. [Google Scholar] [CrossRef] [PubMed]
- Chen, H.T.; Taylor, A.J.; Yu, N. A review of metasurfaces: Physics and applications. Rep. Prog. Phys. 2016, 79, 076401. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Quevedo-Teruel, O.; Chen, H.; Díaz-Rubio, A.; Gok, G.; Grbic, A.; Minatti, G.; Martini, E.; Maci, S.; Eleftheriades, G.V.; Chen, M.; et al. Roadmap on metasurfaces. J. Opt. 2019, 21, 073002. [Google Scholar] [CrossRef]
- Kadic, M.; Milton, G.; van Hecke, M.; Wegener, M. 3D Metamaterials. Nat. Rev. Phys. 2019, 1, 198–210. [Google Scholar] [CrossRef]
- Gabriele, G.; Di Renzo, M.; Diaz-Rubio, A.; Tretyakov, S.; Caloz, C.; Peng, Z.; Alu, A.; Lerosey, G.; Fink, M.; Galdi, V.; et al. Smart Radio Environments. arXiv 2021, arXiv:2111.08676. [Google Scholar]
- Molero, C.; Palomares-Caballero, Á.; Alex-Amor, A.; Parellada-Serrano, I.; Gamiz, F.; Padilla, P.; Valenzuela-Valdés, J.F. Metamaterial-Based Reconfigurable Intelligent Surface: 3D Meta-Atoms Controlled by Graphene Structures. IEEE Commun. Mag. 2021, 59, 42–48. [Google Scholar] [CrossRef]
- Molero Jimenez, C.; Menargues, E.; García-Vigueras, M. All-Metal 3-D Frequency-Selective Surface With Versatile Dual-Band Polarization Conversion. IEEE Trans. Antennas Propag. 2020, 68, 5431–5441. [Google Scholar] [CrossRef]
- Al Sabouni-Zawadzka, A.; Gilewski, W. Soft and Stiff Simplex Tensegrity Lattices as Extreme Smart Metamaterials. Materials 2019, 12, 187. [Google Scholar] [CrossRef] [Green Version]
- Reinbold, J.; Frenzel, T.; Münchinger, A.; Wegener, M. The Rise of (Chiral) 3D Mechanical Metamaterials. Materials 2019, 12, 3527. [Google Scholar] [CrossRef] [Green Version]
- Wu, W.; Hu, W.; Qian, G.; Liao, H.; Xu, X.; Berto, F. Mechanical design and multifunctional applications of chiral mechanical metamaterials: A review. Mater. Des. 2019, 180, 107950. [Google Scholar] [CrossRef]
- Gorshkov, V.; Sareh, P.; Navadeh, N.; Tereshchuk, V.; Fallah, A.S. Multi-resonator metamaterials as multi-band metastructures. Mater. Des. 2021, 202, 109522. [Google Scholar] [CrossRef]
- Georgakopoulos, S.V.; Zekios, C.L.; Sattar-Kaddour, A.; Hamza, M.; Biswas, A.; Clark, B.; Ynchausti, C.; Howell, L.L.; Magleby, S.P.; Lang, R.J. Origami Antennas. IEEE Open J. Antennas Propag. 2021, 2, 1020–1043. [Google Scholar] [CrossRef]
- Wang, H.; Chen, Q.; Zetterstrom, O.; Quevedo-Teruel, O. Three-Dimensional Broadband and Isotropic Double-Mesh Twin-Wire Media for Meta-Lenses. Appl. Sci. 2021, 11, 7153. [Google Scholar] [CrossRef]
- Chen, Z.; Wang, C.-F.; Hoefer, W.J.R. A Unified View of Computational Electromagnetics. IEEE Trans. Microw. Theory Tech. 2022. [Google Scholar] [CrossRef]
- Jones, D.S. Methods in Electromagnetic Wave Propagation; Clarendon Press: Fairlawn, NJ, USA; Oxford University Press: New York, NY, USA, 1979. [Google Scholar]
- Tan, E.L. Unconditionally Stable LOD–FDTD Method for 3-D Maxwell’s Equations. IEEE Microw. Wirel. Compon. Lett. 2007, 17, 85–87. [Google Scholar] [CrossRef]
- Elsherbeni, A.Z.; Demir, V. The Finite-Difference Time-Domain Method for Electromagnetics with MATLAB; SciTech Publishing, Inc.: Raleigh, NC, USA, 2015. [Google Scholar]
- Yee, K. Numerical solution of initial boundary value problems involving maxwell’s equations in isotropic media. IEEE Trans. Antennas Propag. 1966, 14, 302–307. [Google Scholar] [CrossRef] [Green Version]
- Shin, W. 3D Finite-Difference Frequency-Domain Method for Plasmonics and Nanophotonics. Ph.D. Thesis, Stanford University, Stanford, CA, USA, 2013. [Google Scholar]
- Aoki, K.; Guimard, D.; Nishioka, M.; Nomura, M.; Iwamoto, S.; Arakawa, Y. Coupling of quantum-dot light emission with a three-dimensional photonic-crystal nanocavity. Nat. Photonics 2008, 2, 688–692. [Google Scholar] [CrossRef]
- Ho, Y.L.D.; Ivanov, P.S.; Engin, E.; Nicol, M.F.J.; Taverne, M.P.C.; Hu, C.; Cryan, M.J.; Craddock, I.J.; Railton, C.J.; Rarity, J.G. FDTD Simulation of Inverse 3-D Face-Centered Cubic Photonic Crystal Cavities. IEEE J. Quantum Electron. 2011, 47, 1480–1492. [Google Scholar] [CrossRef]
- Zheng, X.; Taverne, M.P.C.; Ho, Y.L.D.; Rarity, J.G. Cavity Design in Woodpile Based 3D Photonic Crystals. Appl. Sci. 2018, 8, 1087. [Google Scholar] [CrossRef] [Green Version]
- Rumpf, R. Simple implementation of arbitrarily shaped total-field/scattered-field regions in finite-difference frequency-domain. Prog. Electromagn. Res. B 2011, 36, 221–248. [Google Scholar] [CrossRef] [Green Version]
- Rumpf, R.; Garcia, C.; Berry, E.; Barton, J. Finite-Difference Frequency-Domain Algorithm for Modeling Electromagnetic Scattering From General Anisotropic Objects. Prog. Electromagn. Res. B 2014, 61, 55–67. [Google Scholar] [CrossRef] [Green Version]
- Ivinskaya, A.M.; Lavrinenko, A.V.; Shyroki, D.M. Modeling of Nanophotonic Resonators with the Finite-Difference Frequency-Domain Method. IEEE Trans. Antennas Propag. 2011, 59, 4155–4161. [Google Scholar] [CrossRef]
- Silvester, P.P.; Ferrari, R.L. Finite Elements for Electrical Engineers, 3rd ed.; Cambridge University Press: Cambridge, UK, 1996. [Google Scholar] [CrossRef]
- Zhai, Y.B.; Ping, X.W.; Jiang, W.X.; Cui, T.J. Finite-Element Analysis of Three-Dimensional Axisymmetrical Invisibility Cloaks and Other Metamaterial Devices. Commun. Comput. Phys. 2010, 8, 823–834. [Google Scholar] [CrossRef]
- Burger, S.; Klose, R.; Schaedle, A.; Schmidt, F.; Zschiedrich, L. FEM modeling of 3D photonic crystals and photonic crystal waveguides. Proc. SPIE—Int. Soc. Opt. Eng. 2005, 5728, 164–173. [Google Scholar] [CrossRef] [Green Version]
- Frenzel, T.; Hahn, V.; Ziemke, P.; Schneider, J.; Chen, Y.; Kiefer, P.; Gumbsch, P.; Wegener, M. Large characteristic lengths in 3D chiral elastic metamaterials. Commun. Mater. 2021, 2, 4. [Google Scholar] [CrossRef]
- COMSOL AB. COMSOL Multiphysics. Available online: https://www.comsol.com/comsol-multiphysics (accessed on 25 January 2022).
- Adrian, S.B.; Dély, A.; Consoli, D.; Merlini, A.; Andriulli, F.P. Electromagnetic Integral Equations: Insights in Conditioning and Preconditioning. IEEE Open J. Antennas Propag. 2021, 2, 1143–1174. [Google Scholar] [CrossRef]
- Burton, A.J.; Miller, G.F.; Wilkinson, J.H. The application of integral equation methods to the numerical solution of some exterior boundary-value problems. Proc. R. Soc. Lond. A Math. Phys. Sci. 1971, 323, 201–210. [Google Scholar]
- Volakis, J.L.; Sertel, K. Integral Equation Methods for Electromagnetics; Scitech Publishing Inc.: Raleigh, NJ, USA, 2012. [Google Scholar]
- Gibson, W.C. The Method of Moments in Electromagnetics, 3rd ed.; Chapman and Hall/CRC: Boca Raton, FL, USA, 2021. [Google Scholar]
- Paez-Rueda, C.-I. Fajardo, A. Pérez, M.; Perilla, G. Closed-Form Expressions for Numerical Evaluation of Self-Impedance Terms Involved on Wire Antenna Analysis by the Method of Moments. Electronics 2021, 10, 1316. [Google Scholar] [CrossRef]
- González-Ovejero, D.; Maci, S. Gaussian Ring Basis Functions for the Analysis of Modulated Metasurface Antennas. IEEE Trans. Antennas Propag. 2015, 63, 3982–3993. [Google Scholar] [CrossRef]
- Florencio, R.; Boix, R.R.; Encinar, J.A. Efficient Spectral Domain MoM for the Design of Circularly Polarized Reflectarray Antennas Made of Split Rings. IEEE Trans. Antennas Propag. 2019, 67, 1760–1771. [Google Scholar] [CrossRef]
- Florencio, R.; Boix, R.R.; Encinar, J.A. Enhanced MoM Analysis of the Scattering by Periodic Strip Gratings in Multilayered Substrates. IEEE Trans. Antennas Propag. 2013, 61, 5088–5099. [Google Scholar] [CrossRef]
- Florencio, R.; Somolinos, Á.; González, I.; Cátedra, F.; Lozano, L. Comparison between Specialized Quadrature Rules for Method of Moments with NURBS Modelling Applied to Periodic Multilayer Structures. Electronics 2020, 9, 2043. [Google Scholar] [CrossRef]
- Florencio, R.; Somolinos, Á.; González, I.; Cátedra, F. Fast Preconditioner Computation for BICGSTAB-FFT Method of Moments with NURBS in Large Multilayer Structures. Electronics 2020, 9, 1938. [Google Scholar] [CrossRef]
- Córcoles, J.; Boix, R.R. Spectral MoM NUFFT-Based Formulation for the Efficient Analysis of High-Order Bandpass FSSs with Tightly Packed Nonresonant Elements in Skewed Grid. IEEE Trans. Antennas Propag. 2021, 69, 6099–6104. [Google Scholar] [CrossRef]
- Silveirinha, M.; Fernandes, C. A hybrid method for the efficient calculation of the band structure of 3-D metallic crystals. IEEE Trans. Microw. Theory Tech. 2004, 52, 889–902. [Google Scholar] [CrossRef]
- Tihon, D.; Sozio, V.; Ozdemir, N.A.; Albani, M.; Craeye, C. Numerically Stable Eigenmode Extraction in 3-D Periodic Metamaterials. IEEE Trans. Antennas Propag. 2016, 64, 3068–3079. [Google Scholar] [CrossRef] [Green Version]
- Tong, M.S.; Chew, W.C. The Nystrom Method in Electromagnetics; Wiley-IEEE Press: Hoboken, NJ, USA, 2020. [Google Scholar]
- Tong, M.S.; Qian, Z.G.; Chew, W.C. Nyström Method Solution of Volume Integral Equations for Electromagnetic Scattering by 3D Penetrable Objects. IEEE Trans. Antennas Propag. 2010, 58, 1645–1652. [Google Scholar] [CrossRef]
- Chen, D.; Cho, M.H.; Cai, W. Accurate and Efficient Nyström Volume Integral Equation Method for Electromagnetic Scattering of 3-D Metamaterials in Layered Media. SIAM J. Sci. Comput. 2018, 40, B259–B282. [Google Scholar] [CrossRef] [Green Version]
- Engheta, N.; Murphy, W.D.; Rokhlin, V.; Vassiliou, M.S. The Fast Multipole Method (FMM) for Electromagnetic Scattering Problems. IEEE Trans. Antennas Propag. 1992, 40, 634–641. [Google Scholar] [CrossRef] [Green Version]
- Darve, E. The Fast Multipole Method: Numerical Implementation. J. Comput. Phys. 2000, 160, 195–240. [Google Scholar] [CrossRef] [Green Version]
- Fall, M.; Boutami, S.; Glière, A.; Stout, B.; Hazart, J. Multilevel fast multipole method based on a potential formulation for 3D electromagnetic scattering problems. J. Opt. Soc. Am. A 2013, 30, 1273–1280. [Google Scholar] [CrossRef] [PubMed]
- Daniele, V.; Zich, R. The Wiener-Hopf Method in Electromagnetics; Scitech Publishing: Edison, NJ, USA, 2014. [Google Scholar]
- Albani, M.; Capolino, F. Wave dynamics by a plane wave on a half-space metamaterial made of plasmonic nanospheres: A discrete Wiener–Hopf formulation. J. Opt. Soc. Am. B 2011, 28, 2174–2185. [Google Scholar] [CrossRef] [Green Version]
- Camacho, M.; Hibbins, A.P.; Capolino, F.; Albani, M. Diffraction by a truncated planar array of dipoles: A Wiener–Hopf approach. Wave Motion 2019, 89, 28–42. [Google Scholar] [CrossRef]
- Arens, T.; Sandfort, K.; Schmitt, S.; Lechleiter, A. Analysing Ewald’s method for the evaluation of Green’s functions for periodic media. IMA J. Appl. Math. 2011, 78, 405–431. [Google Scholar] [CrossRef] [Green Version]
- Campione, S.; Capolino, F. Ewald method for 3D periodic dyadic Green’s functions and complex modes in composite materials made of spherical particles under the dual dipole approximation. Radio Sci. 2012, 47, RS0N06. [Google Scholar] [CrossRef]
- Campione, S.; Capolino, F. Electromagnetic coupling and array packing induce exchange of dominance on complex modes in 3D periodic arrays of spheres with large permittivity. J. Opt. Soc. Am. B 2016, 33, 261–270. [Google Scholar] [CrossRef]
- Stevanoviæ, I.; Mosig, J.R. Periodic Green’s function for skewed 3-D lattices using the Ewald transformation. Microw. Opt. Technol. Lett. 2007, 49, 1353–1357. [Google Scholar] [CrossRef] [Green Version]
- Wexler, A. Solution of Waveguide Discontinuities by Modal Analysis. IEEE Trans. Microw. Theory Tech. 1967, 15, 508–517. [Google Scholar] [CrossRef]
- Collin, R.E. Field Theory of Guided Waves, 2nd ed.; IEEE-Press: New York, NY, USA, 1991. [Google Scholar]
- Ruiz-Cruz, J.A.; Montejo-Garai, J.R.; Rebollar, J.M. Computer Aided Design of Waveguide Devices by Mode-Matching Methods. In Passive Microwave Components and Antennas; Zhurbenko, V., Ed.; IntechOpen: Rijeka, Croatia, 2010; Chapter 6. [Google Scholar]
- Swartz, K.E.; White, D.A.; Tortorelli, D.A.; James, K.A. Topology optimization of 3D photonic crystals with complete bandgaps. Opt. Express 2021, 29, 22170–22191. [Google Scholar] [CrossRef]
- Ghadarghadr, S.; Mosallaei, H. Dispersion Diagram Characteristics of Periodic Array of Dielectric and Magnetic Materials Based Spheres. IEEE Trans. Antennas Propag. 2009, 57, 149–160. [Google Scholar] [CrossRef]
- Campione, S.; Steshenko, S.; Albani, M.; Capolino, F. Complex modes and effective refractive index in 3D periodic arrays of plasmonic nanospheres. Opt. Express 2011, 19, 26027–26043. [Google Scholar] [CrossRef] [PubMed]
- Varela, J.E.; Esteban, J. Characterization of Waveguides With a Combination of Conductor and Periodic Boundary Contours: Application to the Analysis of Bi-Periodic Structures. IEEE Trans. Microw. Theory Tech. 2012, 60, 419–430. [Google Scholar] [CrossRef]
- Dai, Q.I.; Lo, Y.H.; Chew, W.C.; Liu, Y.G.; Jiang, L.J. Generalized Modal Expansion and Reduced Modal Representation of 3-D Electromagnetic Fields. IEEE Trans. Antennas Propag. 2014, 62, 783–793. [Google Scholar]
- Rabinovich, O.; Epstein, A. Dual-Polarized All-Metallic Metagratings for Perfect Anomalous Reflection. Phys. Rev. Appl. 2020, 14, 064028. [Google Scholar] [CrossRef]
- Kari, N.; Seetharamdoo, D.; Laheurte, J.M.; Sarrazin, F. Modal Analysis of Chiral Metamaterial Using Characteristic Mode Analysis and Eigenmode Expansion Method. IEEE J. Multiscale Multiphys. Comput. Tech. 2020, 5, 37–43. [Google Scholar] [CrossRef]
- Alex-Amor, A.; Ghasemifard, F.; Valerio, G.; Ebrahimpouri, M.; Padilla, P.; González, J.M.F.; Quevedo-Teruel, O. Glide-Symmetric Metallic Structures with Elliptical Holes for Lens Compression. IEEE Trans. Microw. Theory Tech. 2020, 68, 4236–4248. [Google Scholar] [CrossRef]
- Alex-Amor, A.; Valerio, G.; Ghasemifard, F.; Mesa, F.; Padilla, P.; Fernández-González, J.M.; Quevedo-Teruel, O. Wave Propagation in Periodic Metallic Structures with Equilateral Triangular Holes. Appl. Sci. 2020, 10, 1600. [Google Scholar] [CrossRef] [Green Version]
- Zetterstrom, O.; Valerio, G.; Mesa, F.; Ghasemifard, F.; Norgren, M.; Quevedo-Teruel, O. Dispersion Analysis of Periodically Loaded Transmission Lines with Twist Symmetry Using the Mode-Matching Technique. Appl. Sci. 2020, 10, 5990. [Google Scholar] [CrossRef]
- Sipus, Z.; Bosiljevac, M. Modeling of Glide-Symmetric Dielectric Structures. Symmetry 2019, 11, 805. [Google Scholar] [CrossRef] [Green Version]
- Marcuvitz, N. Waveguide Handbook; Electromagnetic Waves; Institution of Engineering and Technology: New York, NY, USA, 1986. [Google Scholar]
- Mesa, F.; Rodriguez-Berral, R.; Medina, F. Unlocking Complexity Using the ECA: The Equivalent Circuit Model as An Efficient and Physically Insightful Tool for Microwave Engineering. IEEE Microw. Mag. 2018, 19, 44–65. [Google Scholar] [CrossRef]
- Costa, F.; Monorchio, A.; Manara, G. An Overview of Equivalent Circuit Modeling Techniques of Frequency Selective Surfaces and Metasurfaces. Appl. Comput. Electromagn. Soc. J. 2014, 29, 960–976. [Google Scholar]
- Kafesaki, M.; Tsiapa, I.; Katsarakis, N.; Koschny, T.; Soukoulis, C.M.; Economou, E.N. Left-handed metamaterials: The fishnet structure and its variations. Phys. Rev. B 2007, 75, 235114. [Google Scholar] [CrossRef] [Green Version]
- Carbonell, J.; Croënne, C.; Garet, F.; Lheurette, E.; Coutaz, J.L.; Lippens, D. Lumped elements circuit of terahertz fishnet-like arrays with composite dispersion. J. Appl. Phys. 2010, 108, 014907. [Google Scholar] [CrossRef]
- Perez-Palomino, G.; Page, J.E. Bimode Foster’s Equivalent Circuit of Arbitrary Planar Periodic Structures and Its Application to Design Polarization Controller Devices. IEEE Trans. Antennas Propag. 2020, 68, 5308–5321. [Google Scholar] [CrossRef]
- Borgese, M.; Costa, F. A Simple Equivalent Circuit Approach for Anisotropic Frequency-Selective Surfaces and Metasurfaces. IEEE Trans. Antennas Propag. 2020, 68, 7088–7098. [Google Scholar] [CrossRef]
- Hernández-Escobar, A.; Abdo-Sánchez, E.; Esteban, J.; Martín-Guerrero, T.M.; Camacho-Peñalosa, C. Equivalent-Circuit Modeling of Lossless and Lossy Bi-Periodic Scatterers by an Eigenstate Approach. 2021. Available online: https://www.techrxiv.org/articles/preprint/Equivalent-Circuit_Modeling_of_Lossless_and_Lossy_Bi-Periodic_Scatterers_by_an_Eigenstate_Approach/16811092 (accessed on 25 January 2022).
- Rodríguez-Berral, R.; Mesa, F.; Medina, F. Analytical Multimodal Network Approach for 2-D Arrays of Planar Patches/Apertures Embedded in a Layered Medium. IEEE Trans. Antennas Propag. 2015, 63, 1969–1984. [Google Scholar] [CrossRef]
- Astorino, M.D.; Frezza, F.; Tedeschi, N. Equivalent-circuit model for stacked slot-based 2D periodic arrays of arbitrary geometry for broadband analysis. J. Appl. Phys. 2018, 123, 103106. [Google Scholar] [CrossRef]
- Hum, S.V.; Du, B. Equivalent Circuit Modeling for Reflectarrays Using Floquet Modal Expansion. IEEE Trans. Antennas Propag. 2017, 65, 1131–1140. [Google Scholar] [CrossRef]
- Omar, S.; Jiao, D. A New Volume Integral Formulation for Broadband 3-D Circuit Extraction in Inhomogeneous Materials with and Without External Electromagnetic Fields. IEEE Trans. Microw. Theory Tech. 2013, 61, 4302–4312. [Google Scholar] [CrossRef]
- Omar, S.; Jiao, D. A Linear Complexity Direct Volume Integral Equation Solver for Full-Wave 3-D Circuit Extraction in Inhomogeneous Materials. IEEE Trans. Microw. Theory Tech. 2015, 63, 897–912. [Google Scholar] [CrossRef]
- Molero, C.; Alex-Amor, A.; Mesa, F.; Palomares-Caballero, A.; Padilla, P. Cross-Polarization Control in FSSs by Means of an Equivalent Circuit Approach. IEEE Access 2021, 9, 99513–99525. [Google Scholar] [CrossRef]
- Alex-Amor, A.; Mesa, F.; Palomares-Caballero, Á.; Molero, C.; Padilla, P. Exploring the Potential of the Multi-Modal Equivalent Circuit Approach for Stacks of 2-D Aperture Arrays. IEEE Trans. Antennas Propag. 2021, 69, 6453–6467. [Google Scholar] [CrossRef]
- Grbic, A.; Eleftheriades, G.V. An isotropic three-dimensional negative-refractive-index transmission-line metamaterial. J. Appl. Phys. 2005, 98, 043106. [Google Scholar] [CrossRef]
- Zedler, M.; Caloz, C.; Russer, P. A 3-D Isotropic Left-Handed Metamaterial Based on the Rotated Transmission-Line Matrix (TLM) Scheme. IEEE Trans. Microw. Theory Tech. 2007, 55, 2930–2941. [Google Scholar] [CrossRef]
- Zedler, M.; Russer, P. Investigation on the Dispersion Relation of a 3D LC-based Metamaterial with an Omnidirectional Left-Handed Frequency Band. In Proceedings of the 2006 IEEE MTT-S International Microwave Symposium Digest, San Francisco, CA, USA, 11–16 June 2006; pp. 1477–1479. [Google Scholar]
- Johns, P.B. A Symmetrical Condensed Node for the TLM Method. IEEE Trans. Microw. Theory Tech. 1987, 35, 370–377. [Google Scholar] [CrossRef]
- Molero, C.; García-Vigueras, M. Circuit Modeling of 3-D Cells to Design Versatile Full-Metal Polarizers. IEEE Trans. Microw. Theory Tech. 2019, 67, 1357–1369. [Google Scholar] [CrossRef] [Green Version]
- Balmaseda-Marquez, M.; Moreno, S.; Zapata, P.H.; Molero, C. Phase-resonance Exploitation in Full-Metal 3D Periodic Structures for Single- and Multi- Wideband Applications. Techrxiv 2021. [Google Scholar] [CrossRef]
- Molero, C.; Legay, H.; Pierre, T.; Garcia-Vigueras, M. Broadband 3D-Printed Polarizer based on Metallic Transverse Electro-Magnetic Unit-Cells. IEEE Trans. Antennas Propag. 2022. [Google Scholar] [CrossRef]
- Blanchard, J.; Newman, E.; Peters, M. Integral equation analysis of artificial media. IEEE Trans. Antennas Propag. 1994, 42, 727–731. [Google Scholar] [CrossRef]
- Silveirinha, M.; Fernandes, C. Homogenization of 3-D-connected and nonconnected wire metamaterials. IEEE Trans. Microw. Theory Tech. 2005, 53, 1418–1430. [Google Scholar] [CrossRef]
- Silveirinha, M. Additional boundary condition for the wire medium. IEEE Trans. Antennas Propag. 2006, 54, 1766–1780. [Google Scholar] [CrossRef]
- Lannebère, S.; Morgado, T.A.; Silveirinha, M.G. First principles homogenization of periodic metamaterials and application to wire media. C. R. Physique 2020, 21, 367–388. [Google Scholar] [CrossRef]
- Silveirinha, M.; Engheta, N. Design of matched zero-index metamaterials using nonmagnetic inclusions in epsilon-near-zero media. Phys. Rev. B 2007, 75, 075119. [Google Scholar] [CrossRef] [Green Version]
- Karamanos, T.D.; Assimonis, S.D.; Dimitriadis, A.I.; Kantartzis, N.V. Effective parameter extraction of 3D metamaterial arrays via first-principles homogenization theory. Photonics-Nanostruct.—Fundam. Appl. 2014, 12, 291–297. [Google Scholar] [CrossRef]
- Silveirinha, M.G. Metamaterial homogenization approach with application to the characterization of microstructured composites with negative parameters. Phys. Rev. B 2007, 75, 115104. [Google Scholar] [CrossRef] [Green Version]
- Fischer, B.; Valerio, G. Ultra-Wideband Homogenization of Glide-Symmetric Holey Parallel-Plate Waveguides. IEEE Trans. Antennas Propag. 2021, in press. [Google Scholar]
- Deschamps, G. Ray techniques in electromagnetics. Proc. IEEE 1972, 60, 1022–1035. [Google Scholar] [CrossRef] [Green Version]
- Xu, S.; Yang, F. Reflectarray Antennas. In Handbook of Antenna Technologies; Springer: Singapore, 2015. [Google Scholar]
- Liao, Q.; Fonseca, N.J.G.; Quevedo-Teruel, O. Compact Multibeam Fully Metallic Geodesic Luneburg Lens Antenna Based on Non-Euclidean Transformation Optics. IEEE Trans. Antennas Propag. 2018, 66, 7383–7388. [Google Scholar] [CrossRef]
- Fonseca, N.J.G.; Liao, Q.; Quevedo-Teruel, O. Equivalent Planar Lens Ray-Tracing Model to Design Modulated Geodesic Lenses Using Non-Euclidean Transformation Optics. IEEE Trans. Antennas Propag. 2020, 68, 3410–3422. [Google Scholar] [CrossRef]
- Hossain, F.; Geok, T.K.; Rahman, T.A.; Hindia, M.N.; Dimyati, K.; Ahmed, S.; Tso, C.P.; Abd Rahman, N.Z. An Efficient 3-D Ray Tracing Method: Prediction of Indoor Radio Propagation at 28 GHz in 5G Network. Electronics 2019, 8, 286. [Google Scholar] [CrossRef] [Green Version]
- Solomitckii, D. Evaluation of mmWave 5G Performance by Advanced Ray Tracing Techniques. Academic Dissertation, Tampere University, Faculty of Information Technology and Communication Sciences Finland, Tampere, Finland, 2019. [Google Scholar]
- Mesa, F.; Valerio, G.; Rodríguez-Berral, R.; Quevedo-Teruel, O. Simulation-Assisted Efficient Computation of the Dispersion Diagram of Periodic Structures: A comprehensive overview with applications to filters, leaky-wave antennas and metasurfaces. IEEE Antennas Propag. Mag. 2021, 63, 33–45. [Google Scholar] [CrossRef]
- Alex-Amor, A.; Palomares-Caballero, A.; Mesa, F.; Quevedo-Teruel, O.; Padilla, P. Dispersion Analysis of Periodic Structures in Anisotropic Media: Application to Liquid Crystals. IEEE Trans. Antennas Propag. 2021. [Google Scholar] [CrossRef]
- Weitsch, Y.; Eibert, T.F. Modal Series Expansion of Eigensolutions for Closed and Open Periodic Waveguides. IEEE Trans. Antennas Propag. 2012, 60, 5881–5889. [Google Scholar] [CrossRef]
- Giusti, F.; Mesa, F.; Chen, Q.; Valerio, G.; Quevedo-Teruel, O. Multimodal Transfer Matrix Method Applied to 3-D Periodic Structures. In Proceedings of the 2021 International Symposium on Antennas and Propagation (ISAP), Taipei, China, 25–28 January 2021; pp. 1–2. [Google Scholar]
- Li, Z.Y.; Lin, L.L. Photonic band structures solved by a plane-wave-based transfer-matrix method. Phys. Rev. E 2003, 67, 046607. [Google Scholar] [CrossRef] [PubMed]
- Dassault Systèmes. CST Microwave Studio. Available online: https://www.3ds.com/products-services/simulia/products/cst-studio-suite/solvers/ (accessed on 25 January 2022).
- Ansys. Ansys HFSS. Available online: https://www.ansys.com/products/electronics/ansys-hfss (accessed on 25 January 2022).
- Pendry, J.; Holden, A.; Robbins, D.; Stewart, W. Magnetism from conductors and enhanced nonlinear phenomena. IEEE Trans. Microw. Theory Tech. 1999, 47, 2075–2084. [Google Scholar] [CrossRef] [Green Version]
- Freire, M.J.; Marques, R.; Jelinek, L. Experimental demonstration of a μ = −1 metamaterial lens for magnetic resonance imaging. Appl. Phys. Lett. 2008, 93, 231108. [Google Scholar] [CrossRef] [Green Version]
- Algarín, J.M.; Freire, M.J.; Lapine, M. Ab initio experimental analysis of realistic resonant ring metamaterial lenses. In Proceedings of the 2010 IEEE Antennas and Propagation Society International Symposium, Toronto, ON, Canada, 11–17 July 2010; pp. 1–4. [Google Scholar] [CrossRef]
- Baena, J.D.; Jelinek, L.; Marqués, R.; Silveirinha, M. Unified homogenization theory for magnetoinductive and electromagnetic waves in split-ring metamaterials. Phys. Rev. A 2008, 78, 013842. [Google Scholar] [CrossRef] [Green Version]
- Silveirinha, M.G. Artificial plasma formed by connected metallic wires at infrared frequencies. Phys. Rev. B 2009, 79, 035118. [Google Scholar] [CrossRef]
- Sievenpiper, D.F.; Sickmiller, M.E.; Yablonovitch, E. 3D Wire Mesh Photonic Crystals. Phys. Rev. Lett. 1996, 76, 2480–2483. [Google Scholar] [CrossRef] [Green Version]
- Fietz, C.; Urzhumov, Y.; Shvets, G. Complex k band diagrams of 3D metamaterial/photonic crystals. Opt. Express 2011, 19, 19027–19041. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Belov, P.A.; Marqués, R.; Maslovski, S.I.; Nefedov, I.S.; Silveirinha, M.; Simovski, C.R.; Tretyakov, S.A. Strong spatial dispersion in wire media in the very large wavelength limit. Phys. Rev. B 2003, 67, 113103. [Google Scholar] [CrossRef]
- Sakhno, D.; Koreshin, E.; Belov, P.A. Longitudinal electromagnetic waves with extremely short wavelength. Phys. Rev. B 2021, 104, L100304. [Google Scholar] [CrossRef]
- Powell, A.W.; Mitchell-Thomas, R.C.; Zhang, S.; Cadman, D.A.; Hibbins, A.P.; Sambles, J.R. Dark Mode Excitation in Three-Dimensional Interlaced Metallic Meshes. ACS Photonics 2021, 8, 841–846. [Google Scholar] [CrossRef] [PubMed]
- Liang, B.; Bai, M. Subwavelength three-dimensional frequency selective surface based on surface wave tunneling. Opt. Express 2016, 24, 14697–14702. [Google Scholar] [CrossRef]
- Simovski, C.R.; Belov, P.A.; Atrashchenko, A.V.; Kivshar, Y.S. Wire Metamaterials: Physics and Applications. Adv. Mater. 2012, 24, 4229–4248. [Google Scholar] [CrossRef]
- Kushiyama, Y.; Arima, T.; Uno, T. Experimental verification of spoof surface plasmons in wire metamaterials. Opt. Express 2012, 20, 18238–18247. [Google Scholar] [CrossRef]
- Gansel, J.K.; Thiel, M.; Rill, M.S.; Decker, M.; Bade, K.; Saile, V.; von Freymann, G.; Linden, S.; Wegener, M. Gold Helix Photonic Metamaterial as Broadband Circular Polarizer. Science 2009, 325, 1513–1515. [Google Scholar] [CrossRef]
- Faniayeu, I.; Asadchy, V.; Fanyaev, I. Polarization Control with Helical Metasurfaces. Crystals 2020, 10, 726. [Google Scholar] [CrossRef]
- Wu, S.; Xu, S.; Zinenko, T.L.; Yachin, V.V.; Prosvirnin, S.L.; Tuz, V.R. 3D-printed chiral metasurface as a dichroic dual-band polarization converter. Opt. Lett. 2019, 44, 1056–1059. [Google Scholar] [CrossRef] [Green Version]
- Wu, S.; Yachin, V.V.; Shcherbinin, V.I.; Tuz, V.R. Chiral metasurfaces formed by 3D-printed square helices: A flexible tool to manipulate wave polarization. J. Appl. Phys. 2019, 126, 103101. [Google Scholar] [CrossRef]
- Fernandez-Corbaton, I.; Rockstuhl, C.; Ziemke, P.; Gumbsch, P.; Albiez, A.; Schwaiger, R.; Frenzel, T.; Kadic, M.; Wegener, M. New Twists of 3D Chiral Metamaterials. Adv. Mater. 2019, 31, 1807742. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ehrenberg, I.M.; Sarma, S.E.; Wu, B.I. A three-dimensional self-supporting low loss microwave lens with a negative refractive index. J. Appl. Phys. 2012, 112, 073114. [Google Scholar] [CrossRef]
- Sanz-Izquierdo, B.; Parker, E.A. 3-D Printing of Elements in Frequency Selective Arrays. IEEE Trans. Antennas Propag. 2014, 62, 6060–6066. [Google Scholar] [CrossRef]
- Zhu, D.Z.; Gregory, M.D.; Werner, P.L.; Werner, D.H. Fabrication and Characterization of Multiband Polarization Independent 3-D-Printed Frequency Selective Structures With UltraWide Fields of View. IEEE Trans. Antennas Propag. 2018, 66, 6096–6105. [Google Scholar] [CrossRef]
- Mittra, R.; Pelletti, C.; Arya, R.K.; Dong, T.; Bianconi, G. A general-purpose simulator for metamaterials with three-dimensional elements. In Proceedings of the 2013 International Symposium on Electromagnetic Theory, Hiroshima, Japan, 20–24 May 2013; pp. 78–80. [Google Scholar]
- Pelletti, C.; Bianconi, G.; Mittra, R.; Shen, Z. Frequency selective surface with wideband quasi-elliptic bandpass response. Electron. Lett. 2013, 49, 1052–1053. [Google Scholar] [CrossRef]
- Pelletti, C.; Mittra, R.; Bianconi, G. Three-dimensional FSS elements with wide frequency and angular response. In Proceedings of the 2013 International Symposium on Electromagnetic Theory, Hiroshima, Japan, 20–24 May 2013; pp. 698–700. [Google Scholar]
- Rashid, A.K.; Li, B.; Shen, Z. An overview of three-dimensional frequency-selective structures. IEEE Antennas Propag. Mag. 2014, 56, 43–67. [Google Scholar] [CrossRef]
- Omar, A.A.; Shen, Z. Multiband High-Order Bandstop 3-D Frequency-Selective Structures. IEEE Trans. Antennas Propag. 2016, 64, 2217–2226. [Google Scholar] [CrossRef]
- Omar, A.A.; Shen, Z.; Huang, H. Absorptive Frequency-Selective Reflection and Transmission Structures. IEEE Trans. Antennas Propag. 2017, 65, 6173–6178. [Google Scholar] [CrossRef]
- Wang, W.; Cao, Q.; Zheng, Y. Bandstop Frequency-Selective Structures Based on Stepped-Impedance Loop Resonators: Design, Analysis, and Measurement. IEEE Trans. Antennas Propag. 2019, 67, 1053–1064. [Google Scholar] [CrossRef]
- Omar, A.A.; Shen, Z. Thin 3-D Bandpass Frequency-Selective Structure Based on Folded Substrate for Conformal Radome Applications. IEEE Trans. Antennas Propag. 2019, 67, 282–290. [Google Scholar] [CrossRef]
- Li, H.; Li, B.; Zhu, L. Wideband Bandpass Frequency-Selective Structures on Stacked Slotline Resonators: Proposal and Synthetic Design. IEEE Trans. Antennas Propag. 2020, 68, 7068–7078. [Google Scholar] [CrossRef]
- Li, H.; Li, B.; Zhu, L. Wideband Linear-to-Circular Polarizer Based on Orthogonally Inserted Slot-Line Structures. IEEE Antennas Wirel. Propag. Lett. 2019, 18, 1169–1173. [Google Scholar] [CrossRef]
- Luo, G.Q.; Yu, W.; Yu, Y.; Zhang, X.H.; Shen, Z. A Three-Dimensional Design of Ultra-Wideband Microwave Absorbers. IEEE Trans. Microw. Theory Tech. 2020, 68, 4206–4215. [Google Scholar] [CrossRef]
- Omar, A.A.; Shen, Z. Double-Sided Parallel-Strip Line Resonator for Dual-Polarized 3-D Frequency-Selective Structure and Absorber. IEEE Trans. Microw. Theory Tech. 2017, 65, 3744–3752. [Google Scholar] [CrossRef]
- Zhou, L.; Shen, Z. 3-D Absorptive Energy-Selective Structures. IEEE Trans. Antennas Propag. 2021, 69, 5664–5672. [Google Scholar] [CrossRef]
- Omar, A.A.; Shen, Z. Tunable Absorptive Frequency-Selective Transmission Structure. In Proceedings of the 2018 IEEE International Symposium on Antennas and Propagation USNC/URSI National Radio Science Meeting, Boston, MA, USA, 8–13 July 2018; pp. 2063–2064. [Google Scholar] [CrossRef]
- Omar, A.A.; Kim, J.; Hong, W. A 3-D Lumped-Components-Free Absorptive Frequency-Selective Transmission Structure Featuring Very Wide Two-Sided Absorption Bandwidths. IEEE Antennas Wirel. Propag. Lett. 2020, 19, 761–765. [Google Scholar] [CrossRef]
- Yu, Y.; Luo, G.Q.; Liu, Q.; Yu, W.; Jin, H.; Liao, Z.; Shen, Z. 3D Band-Absorptive Frequency Selective Rasorber: Concept and Analysis. IEEE Access 2019, 7, 2520–2528. [Google Scholar] [CrossRef]
- Yu, W.; Luo, G.Q.; Yu, Y.; Liao, Z.; Jin, H.; Shen, Z. Broadband Band-Absorptive Frequency-Selective Rasorber with a Hybrid 2-D and 3-D Structure. IEEE Antennas Wirel. Propag. Lett. 2019, 18, 1701–1705. [Google Scholar] [CrossRef]
- Yu, Y.; Shen, Z.; Deng, T.; Luo, G. 3-D Frequency-Selective Rasorber With Wide Upper Absorption Band. IEEE Trans. Antennas Propag. 2017, 65, 4363–4367. [Google Scholar] [CrossRef]
- Deng, T.; Yu, Y.; Chen, Z.N. A broadband 3D frequency selective rasorber by using magnetic materials. In Proceedings of the 2017 International Conference on Electromagnetics in Advanced Applications (ICEAA), Verona, Italy, 11–15 September 2017; pp. 1731–1734. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, M.; Shen, Z.; Wu, W. 3-D Single- and Dual-Polarized Frequency-Selective Rasorbers With Wide Absorption Bands Based on Stepped Impedance Resonator. IEEE Access 2021, 9, 22317–22327. [Google Scholar] [CrossRef]
- Huang, H.; Shen, Z.; Hua, C. Ultra-Broadband 3-D Absorptive Frequency-Selective Transmission Structure Using Commercial Absorber. In Proceedings of the 2020 IEEE International Symposium on Antennas and Propagation and North American Radio Science Meeting, Montreal, QC, Canada, 5–10 July 2020; pp. 751–752. [Google Scholar] [CrossRef]
- Wang, Y.; Qi, S.S.; Shen, Z.; Wu, W. Ultrathin 3-D Frequency Selective Rasorber with Wide Absorption Bands. IEEE Trans. Antennas Propag. 2020, 68, 4697–4705. [Google Scholar] [CrossRef]
- Li, B.; Shen, Z. Wideband 3D Frequency Selective Rasorber. IEEE Trans. Antennas Propag. 2014, 62, 6536–6541. [Google Scholar] [CrossRef]
- Ge, J.; Zhu, J.; Zhang, H.; Zhuang, W.; Tang, W. 3-D square coaxial waveguide FSS and equivalent circuit model. In Proceedings of the 2016 Progress in Electromagnetic Research Symposium (PIERS), Shanghai, China, 8–11 August 2016; pp. 1110–1114. [Google Scholar] [CrossRef]
- Tang, W.; Zhu, J.; Wang, C.; Ge, J.; Yu, Z.; Zhuang, W. Waveguide 3-D FSSs by 3-D printing technique. In Proceedings of the 2016 International Conference on Electromagnetics in Advanced Applications (ICEAA), Cairns, QLD, Australia, 19–23 September 2016; pp. 675–678. [Google Scholar] [CrossRef]
- Zhu, J.; Ge, J.; Yao, J.; Hao, Z.; Tang, W. Dual-Band 3D Frequency Selective Surface Based on Square Coaxial Waveguide. In Proceedings of the 2018 International Conference on Microwave and Millimeter Wave Technology (ICMMT), Chengdu, China, 7–11 May 2018; pp. 1–3. [Google Scholar] [CrossRef]
- Zhu, J.; Hao, Z.; Wang, C.; Yu, Z.; Huang, C.; Tang, W. Dual-Band 3-D Frequency Selective Surface with Multiple Transmission Zeros. IEEE Antennas Wirel. Propag. Lett. 2019, 18, 596–600. [Google Scholar] [CrossRef]
- Velasco, J.; Parellada-Serrano, I.; Molero, C. Fully Metallic Reflectarray for the Ku-Band Based on a 3D Architecture. Electronics 2021, 10, 2648. [Google Scholar] [CrossRef]
- Sun, Y.X.; Wu, D.; Ren, J. Millimeter-Wave Dual-Polarized Dielectric Resonator Reflectarray Fabricated by 3D Printing with High Relative Permittivity Material. IEEE Access 2021, 9, 103795–103803. [Google Scholar] [CrossRef]
- Bukhari, S.S.; Vardaxoglou, J.; Whittow, W. A Metasurfaces Review: Definitions and Applications. Appl. Sci. 2019, 9, 2727. [Google Scholar] [CrossRef] [Green Version]
- Mei, P.; Zhang, S.; Pedersen, G.F. A Low-Cost, High-Efficiency and Full-Metal Reflectarray Antenna with Mechanically 2-D Beam-Steerable Capabilities for 5G Applications. IEEE Trans. Antennas Propag. 2020, 68, 6997–7006. [Google Scholar] [CrossRef]
- Wang, X.; Cheng, Y.; Dong, Y. Millimeter-Wave Dual-Polarized Metal Transmitarray Antenna with Wide Gain Bandwidth. IEEE Antennas Wirel. Propag. Lett. 2022. [Google Scholar] [CrossRef]
- Li, B.; Mei, C.Y.; Zhou, Y.; Lv, X. A 3-D-Printed Wideband Circularly Polarized Dielectric Reflectarray of Cross-Shaped Element. IEEE Antennas Wirel. Propag. Lett. 2020, 19, 1734–1738. [Google Scholar] [CrossRef]
- Yang, Y.; Wang, W.; Moitra, P.; Kravchenko, I.I.; Briggs, D.P.; Valentine, J. Dielectric Meta-Reflectarray for Broadband Linear Polarization Conversion and Optical Vortex Generation. Nano Lett. 2014, 14, 1394–1399. [Google Scholar] [CrossRef] [PubMed]
- Mei, P.; Zhang, S.; Pedersen, G.F. A Wideband 3-D Printed Reflectarray Antenna with Mechanically Reconfigurable Polarization. IEEE Antennas Wirel. Propag. Lett. 2020, 19, 1798–1802. [Google Scholar] [CrossRef]
- Cui, Y.; Nauroze, S.A.; Bahr, R.; Tentzeris, E.M. 3D Printed One-shot Deployable Flexible “Kirigami” Dielectric Reflectarray Antenna for mm-Wave Applications. In Proceedings of the 2020 IEEE/MTT-S International Microwave Symposium (IMS), Los Angeles, CA, USA, 4–6 August 2020; pp. 1164–1167. [Google Scholar] [CrossRef]
- Liang, M.; Ng, W.R.; Chang, K.; Gbele, K.; Gehm, M.E.; Xin, H. A 3-D Luneburg Lens Antenna Fabricated by Polymer Jetting Rapid Prototyping. IEEE Trans. Antennas Propag. 2014, 62, 1799–1807. [Google Scholar] [CrossRef]
- Wu, G.B.; Zeng, Y.S.; Chan, K.; Qu, S.W.; Chan, C. 3-D Printed Circularly Polarized Modified Fresnel Lens Operating at Terahertz Frequencies. IEEE Trans. Antennas Propag. 2019, 67, 4429–4437. [Google Scholar] [CrossRef]
- Ishikawa, A.; Kato, T.; Takeyasu, N.; Fujimori, K.; Tsuruta, K. Selective electroless plating of 3D-printed plastic structures for three-dimensional microwave metamaterials. Appl. Phys. Lett. 2017, 111, 183102. [Google Scholar] [CrossRef]
- Sadeqi, A.; Rezaei Nejad, H.; Owyeung, R.; Sonkusale, S. Three dimensional printing of metamaterial embedded geometrical optics (MEGO). Microsyst. Nanoeng. 2019, 5, 16. [Google Scholar] [CrossRef] [PubMed]
- Kien, N.; Hong, I.P. Application of Metaheuristic Optimization Algorithm and 3D Printing Technique in 3D Bandpass Frequency Selective Structure. J. Electr. Eng. Technol. 2020, 15, 795–801. [Google Scholar] [CrossRef]
- Fernández Álvarez, H.; Cadman, D.; Goulas, A.; Gómez, M.; Engstrom, D.; Vardaxoglou, J.; Zhang, S. 3D conformal bandpass millimeter-wave frequency selective surface with improved fields of view. Sci. Rep. 2021, 11, 12846. [Google Scholar] [CrossRef]
- Zhang, K.P.; Liao, Y.F.; Qiu, B.; Zheng, Y.K.; Yu, L.K.; He, G.H.; Chen, Q.N.; Sun, D.H. 3D Printed Embedded Metamaterials. Small 2021, 17, 2103262. [Google Scholar] [CrossRef]
- Vásquez-Peralvo, J.A.; Tamayo-Domínguez, A.; Pérez-Palomino, G.; Fernández-González, J.M.; Wong, T. 3D Inductive Frequency Selective Structures Using Additive Manufacturing and Low-Cost Metallization. Sensors 2022, 22, 552. [Google Scholar] [CrossRef]
- Harnois, M.; Himdi, M.; Yong, W.; abdul rahim, S.; Tekkouk, K.; Cheval, N. An Improved Fabrication Technique for the 3-D Frequency Selective Surface based on Water Transfer Printing Technology. Sci. Rep. 2020, 10, 1714. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Nauroze, S.A.; Novelino, L.S.; Tentzeris, M.M.; Paulino, G.H. Continuous-range tunable multilayer frequency-selective surfaces using origami and inkjet printing. Proc. Natl. Acad. Sci. USA 2018, 115, 13210–13215. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Cho, S.-S.; Yoon, S.-H.; Hong, I.-P. Design of Three-Dimensional Frequency Selective Structure with Replaceable Unit Structures Using a 3-D Printing Technique. IEEE Antennas Wirel. Propag. Lett. 2018, 17, 2041–2045. [Google Scholar] [CrossRef]
- Burckel, D.B.; Wendt, J.R.; Ten Eyck, G.A.; Ellis, A.R.; Brener, I.; Sinclair, M.B. Fabrication of 3D Metamaterial Resonators Using Self-Aligned Membrane Projection Lithography. Adv. Mater. 2010, 22, 3171–3175. [Google Scholar] [CrossRef] [PubMed]
- Xiong, X.; Xue, Z.H.; Meng, C.; Jiang, S.C.; Hu, Y.H.; Peng, R.W.; Wang, M. Polarization-dependent perfect absorbers/reflectors based on a three-dimensional metamaterial. Phys. Rev. B 2013, 88, 115105. [Google Scholar] [CrossRef]
- Pan, R.; Liu, Z.; Zhu, W.; Du, S.; Gu, C.; Li, J. Asymmetrical Chirality in 3D Bended Metasurface. Adv. Funct. Mater. 2021, 31, 2100689. [Google Scholar] [CrossRef]
- Taravati, S.; Eleftheriades, G.V. Generalized Space-Time-Periodic Diffraction Gratings: Theory and Applications. Phys. Rev. Appl. 2019, 12, 024026. [Google Scholar] [CrossRef] [Green Version]
- Tiukuvaara, V.; Smy, T.J.; Gupta, S. Floquet Analysis of Space-Time Modulated Metasurfaces with Lorentz Dispersion. IEEE Trans. Antennas Propag. 2021, 69, 7667–7678. [Google Scholar] [CrossRef]
- Huidobro, P.; Silveirinha, M.; Galiffi, E.; Pendry, J. Homogenization Theory of Space-Time Metamaterials. Phys. Rev. Appl. 2021, 16, 014044. [Google Scholar] [CrossRef]
- Caloz, C.; Deck-Léger, Z.L. Spacetime Metamaterials—Part I: General Concepts. IEEE Trans. Antennas Propag. 2020, 68, 1569–1582. [Google Scholar] [CrossRef]
- Caloz, C.; Deck-Léger, Z.L. Spacetime Metamaterials—Part II: Theory and Applications. IEEE Trans. Antennas Propag. 2020, 68, 1583–1598. [Google Scholar] [CrossRef]
- Taravati, S.; Eleftheriades, G.V. Microwave Space-Time-Modulated Metasurfaces. ACS Photonics 2022. [Google Scholar] [CrossRef]
- Massa, A.; Marcantonio, D.; Chen, X.; Li, M.; Salucci, M. DNNs as Applied to Electromagnetics, Antennas, and Propagation—A Review. IEEE Antennas Wirel. Propag. Lett. 2019, 18, 2225–2229. [Google Scholar] [CrossRef]
- Fang, Z.; Zhan, J. Deep Physical Informed Neural Networks for Metamaterial Design. IEEE Access 2020, 8, 24506–24513. [Google Scholar] [CrossRef]
- Sagar, M.D.S.I.; Ouassal, H.; Omi, A.I.; Wisniewska, A.; Jalajamony, H.M.; Fernandez, R.E.; Sekhar, P.K. Application of Machine Learning in Electromagnetics: Mini-Review. Electronics 2021, 10, 2752. [Google Scholar] [CrossRef]
- Ramírez-Arroyo, A.; García, L.; Alex-Amor, A.; Valenzuela-Valdés, J.F. Artificial Intelligence and Dimensionality Reduction: Tools for approaching future communications. arXiv 2021, arXiv:2112.10431. [Google Scholar]
- Li, L.; Ruan, H.; Liu, C.; Li, Y.; Shuang, Y.; Alù, A.; Qiu, C.; Cui, T.J. Machine-learning reprogrammable metasurface imager. Nat. Commun. 2019, 10, 1082. [Google Scholar] [CrossRef] [PubMed]
- Chahat, N.; Cook, B.; Estabrook, P. All-metal Dual Frequency RHCP High Gain Antenna for the Extreme Environments of a Potential Europa Lander. In Proceedings of the 2018 IEEE Indian Conference on Antennas and Propogation (InCAP), Krakow, Poland, 31 March–5 April 2018; pp. 1–3. [Google Scholar] [CrossRef]
- Matthaiou, M.; Yurduseven, O.; Ngo, H.Q.; Morales-Jimenez, D.; Cotton, S.L.; Fusco, V.F. The Road to 6G: Ten Physical Layer Challenges for Communications Engineers. IEEE Commun. Mag. 2021, 59, 64–69. [Google Scholar] [CrossRef]
- Chen, R.; Long, W.X.; Wang, X.; Jiandong, L. Multi-Mode OAM Radio Waves: Generation, Angle of Arrival Estimation and Reception With UCAs. IEEE Trans. Wirel. Commun. 2020, 19, 6932–6947. [Google Scholar] [CrossRef]
- Zhang, B.; Zhan, Z.; Cao, Y.; Gulan, H.; Linnér, P.; Sun, J.; Zwick, T.; Zirath, H. Metallic 3-D Printed Antennas for Millimeter- and Submillimeter Wave Applications. IEEE Trans. Terahertz Sci. Technol. 2016, 6, 592–600. [Google Scholar] [CrossRef]

| Methods | Generality, Robustness | Mathematical Complexity | Computational Complexity | Accuracy | Physical Insight |
|---|---|---|---|---|---|
| Finite Differences | M-H | M | M-H | M-H | L |
| Finite Elements | H | H | H | H | L |
| Integral Equations | M-H | M-H | M-H | M-H | M |
| Modal Analysis | M | M-H | M | M-H | M-H |
| Circuits | L-M | L-M | L | L-M | H |
| Ray Optics | L-M | L-M | L-M | L-M | M-H |
| Homogenization | L-M | L-H | L-M | L-M | M-H |
| Transfer Matrix | M | L-M | M | M | M |
| Works | Fabrication Technique | 3-D Assembly | Required Metallization |
|---|---|---|---|
| [138,141,142,143,146,147,156,163] | PCB fabrication | Yes | No * |
| [9] | EDM | No | No |
| [175,178] | FDM 3-D printing | No | Yes |
| [134,135,136] | MJ 3-D printing | No | Yes |
| [126,161,164,176,179,180] | SLA 3-D printing | No | Yes |
| [125,177] | SLS 3-D printing | No | Yes |
| [94,131] | SLM 3-D printing | No | No |
| [181] | Inkjet printing and WPT | No | No |
| [182] | Inkjet printing on origami structures | No | No |
| [183] | Inkjet printing and FDM | No | No |
| [184,185,186] | Lithography | No | Yes |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alex-Amor, A.; Palomares-Caballero, Á.; Molero, C. 3-D Metamaterials: Trends on Applied Designs, Computational Methods and Fabrication Techniques. Electronics 2022, 11, 410. https://doi.org/10.3390/electronics11030410
Alex-Amor A, Palomares-Caballero Á, Molero C. 3-D Metamaterials: Trends on Applied Designs, Computational Methods and Fabrication Techniques. Electronics. 2022; 11(3):410. https://doi.org/10.3390/electronics11030410
Chicago/Turabian StyleAlex-Amor, Antonio, Ángel Palomares-Caballero, and Carlos Molero. 2022. "3-D Metamaterials: Trends on Applied Designs, Computational Methods and Fabrication Techniques" Electronics 11, no. 3: 410. https://doi.org/10.3390/electronics11030410
APA StyleAlex-Amor, A., Palomares-Caballero, Á., & Molero, C. (2022). 3-D Metamaterials: Trends on Applied Designs, Computational Methods and Fabrication Techniques. Electronics, 11(3), 410. https://doi.org/10.3390/electronics11030410








