Design and Implementation of Scalable and Parametrizable Analog-to-Digital Converter on FPGA
Abstract
:1. Introduction
2. State of the Art
3. SAR-Based ADC
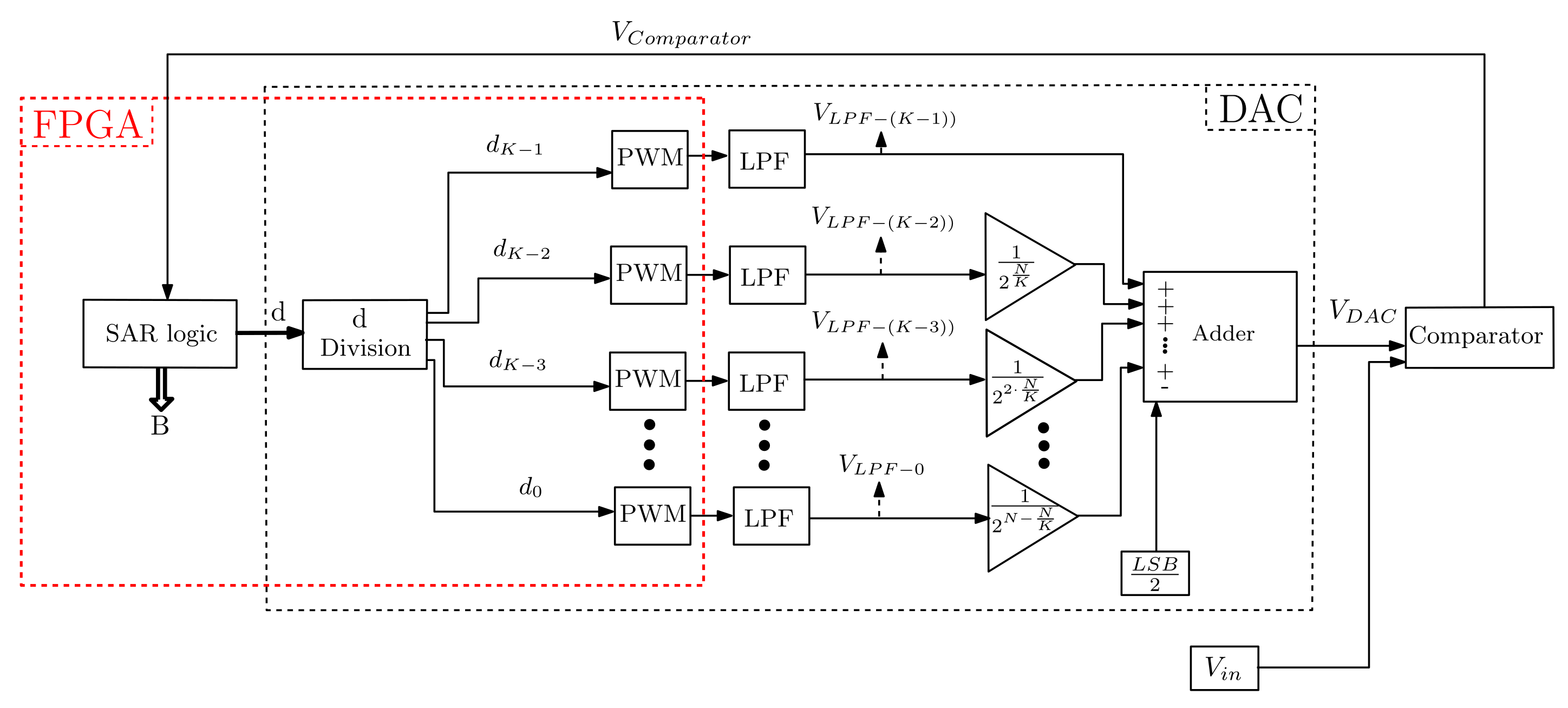
3.1. DAC Implementation with PWM and LPF
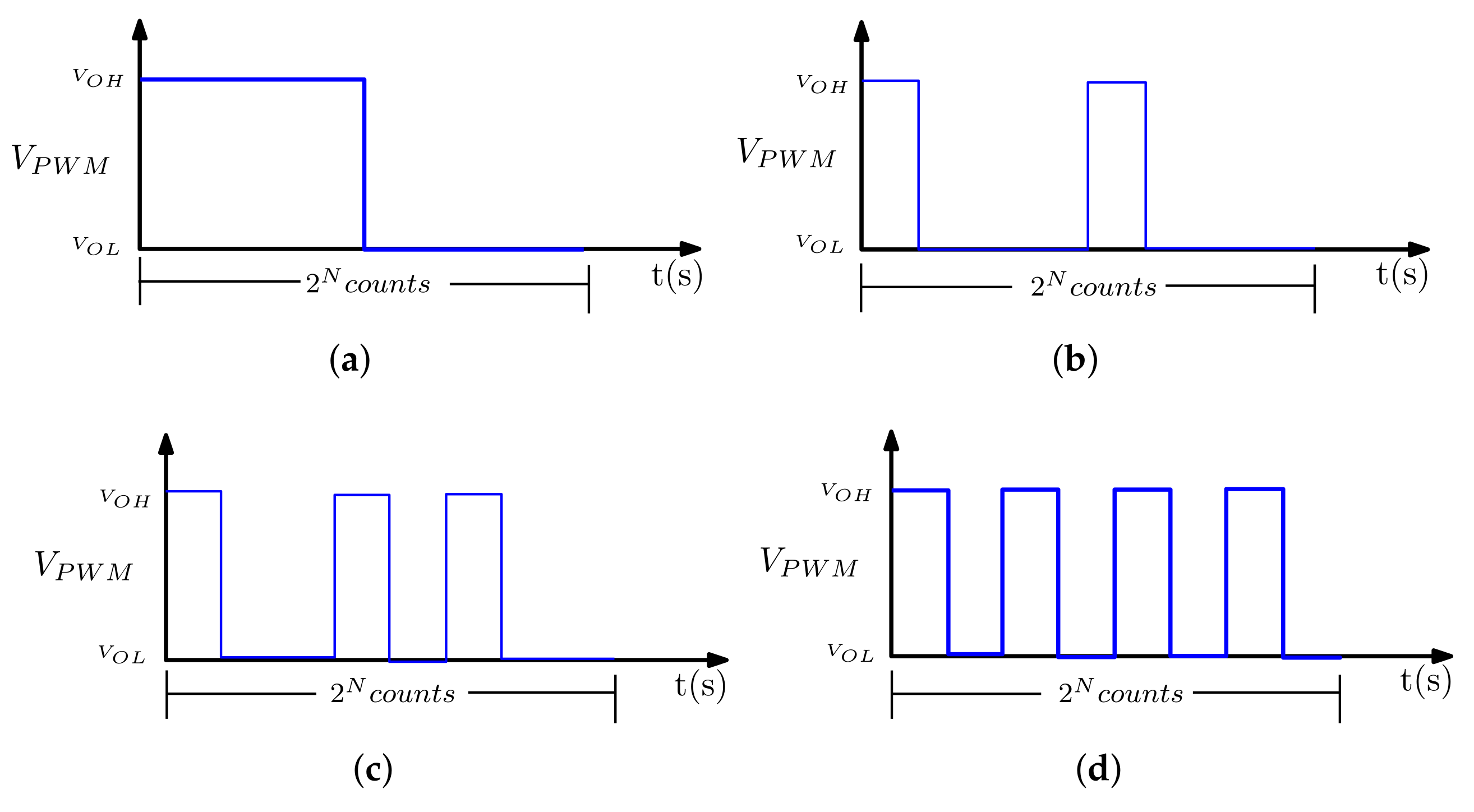
3.1.1. PWM Module
3.1.2. Low-Pass Filter (LPF)
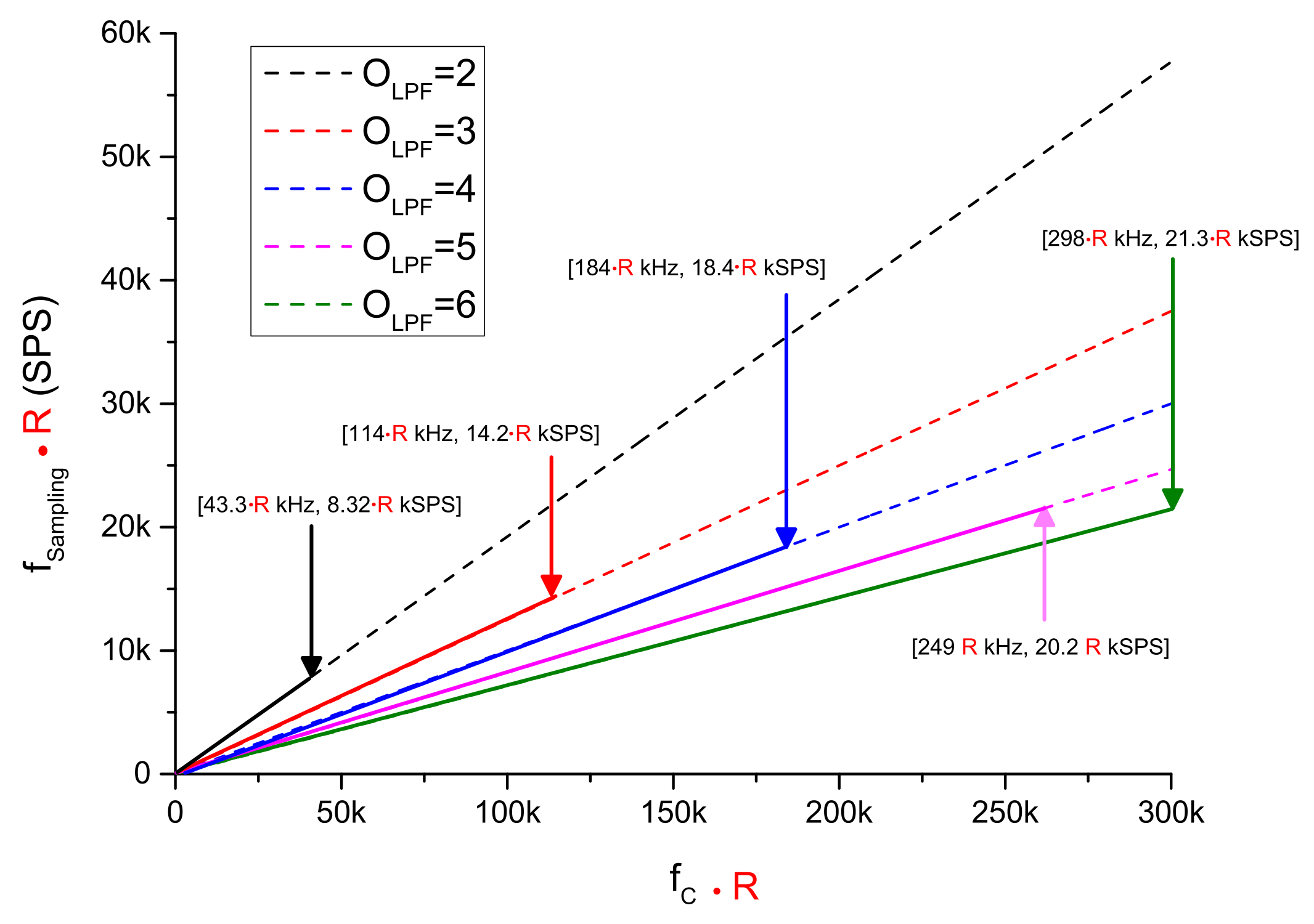
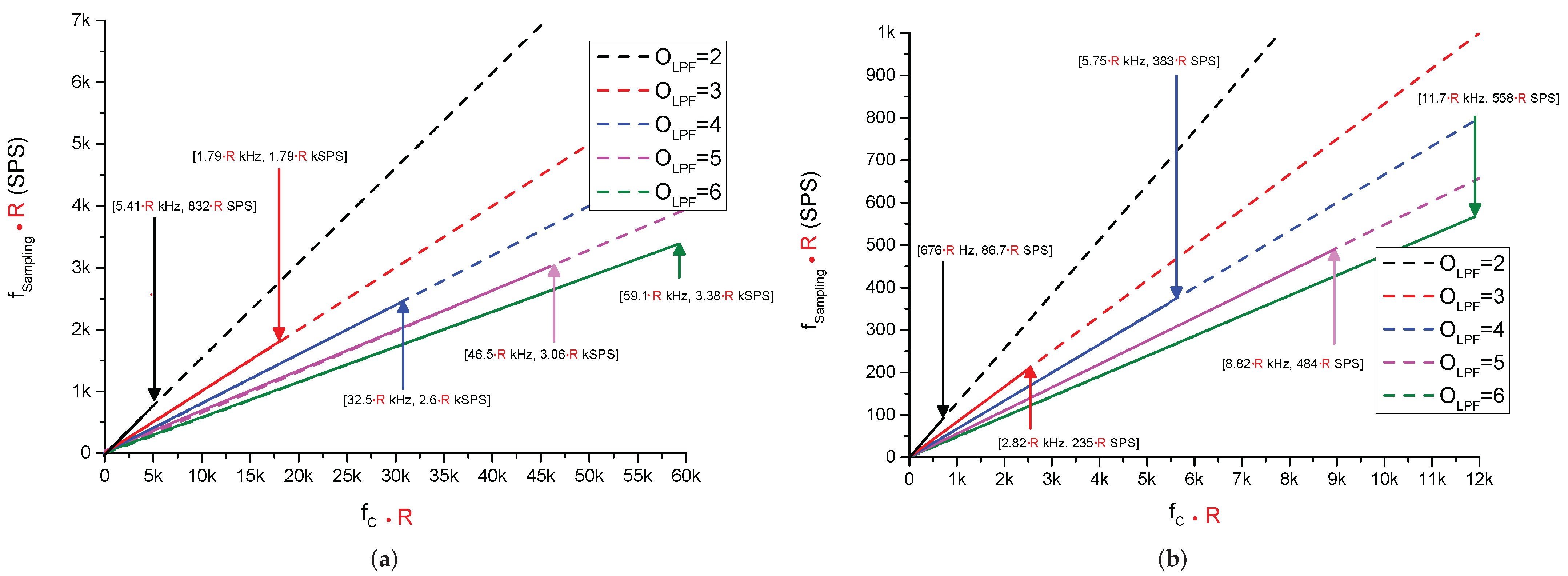
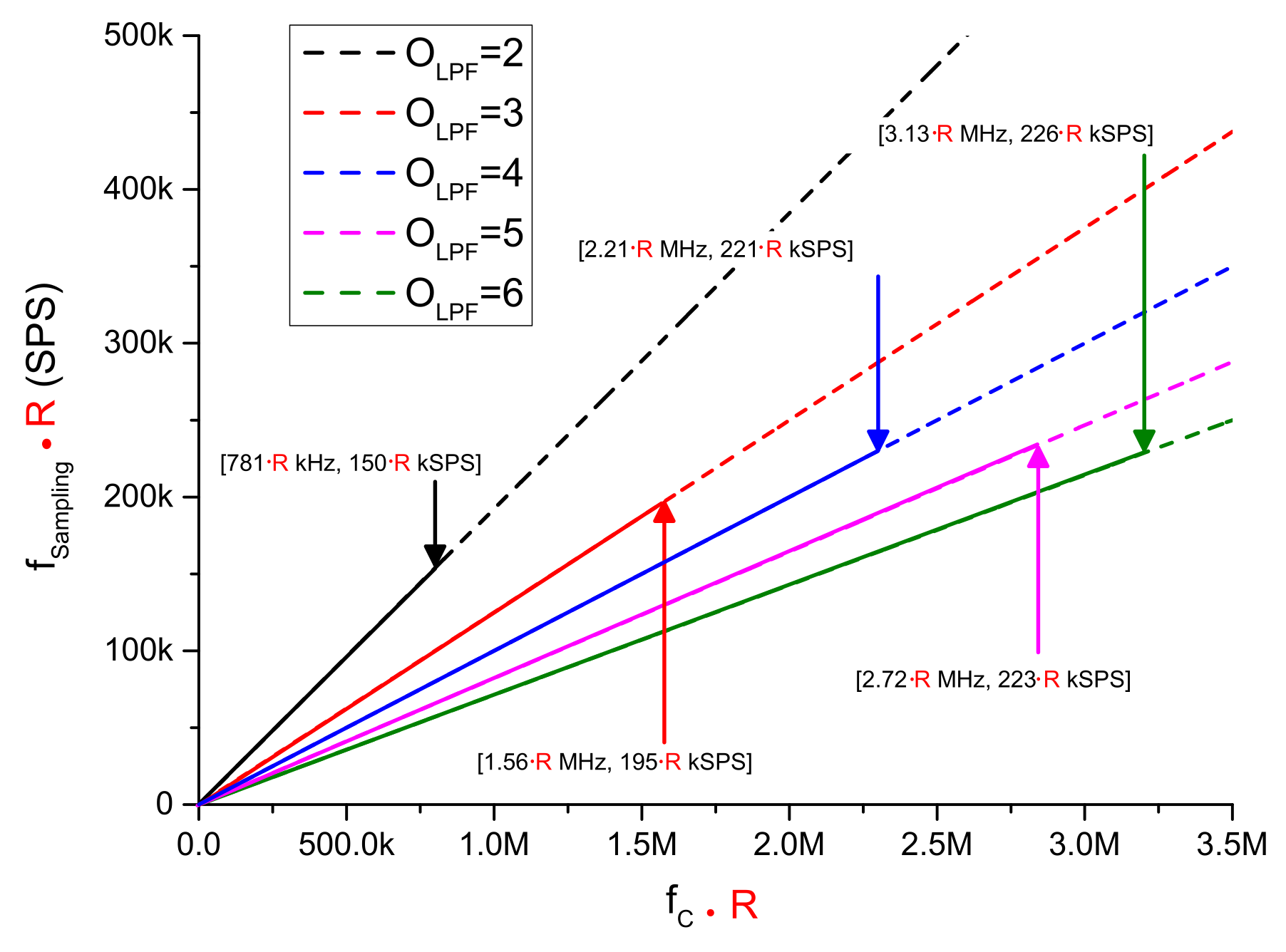
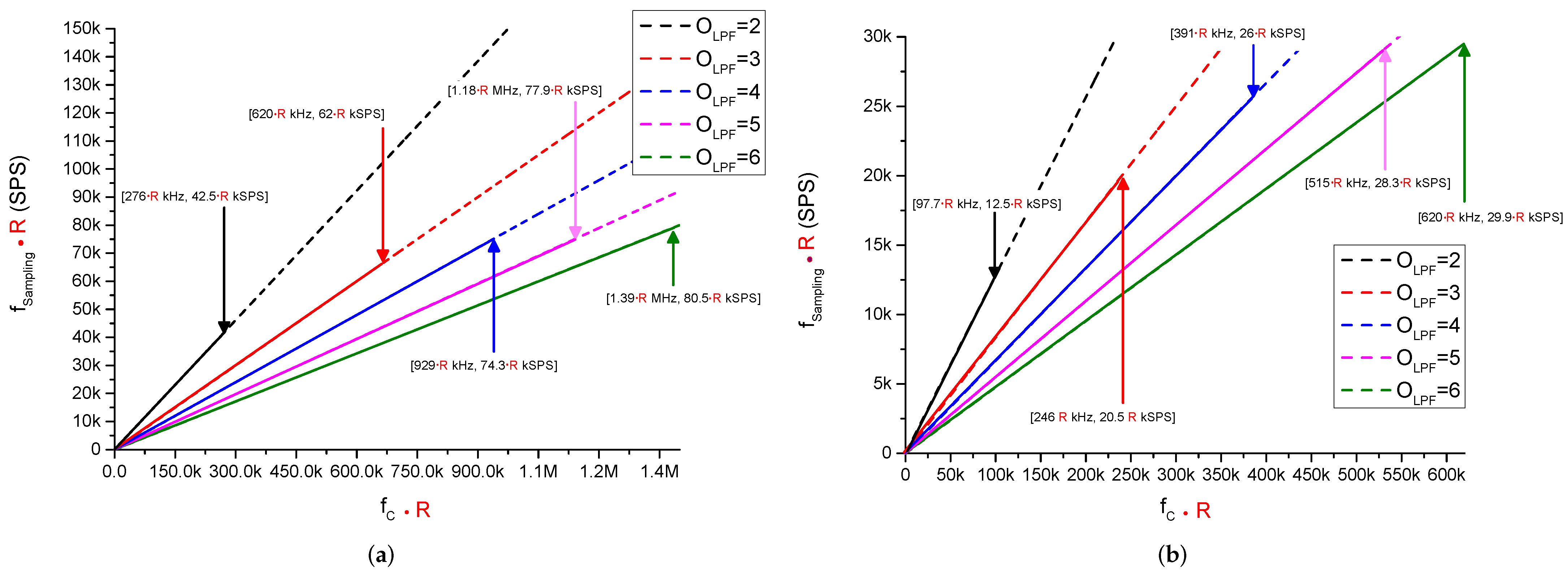
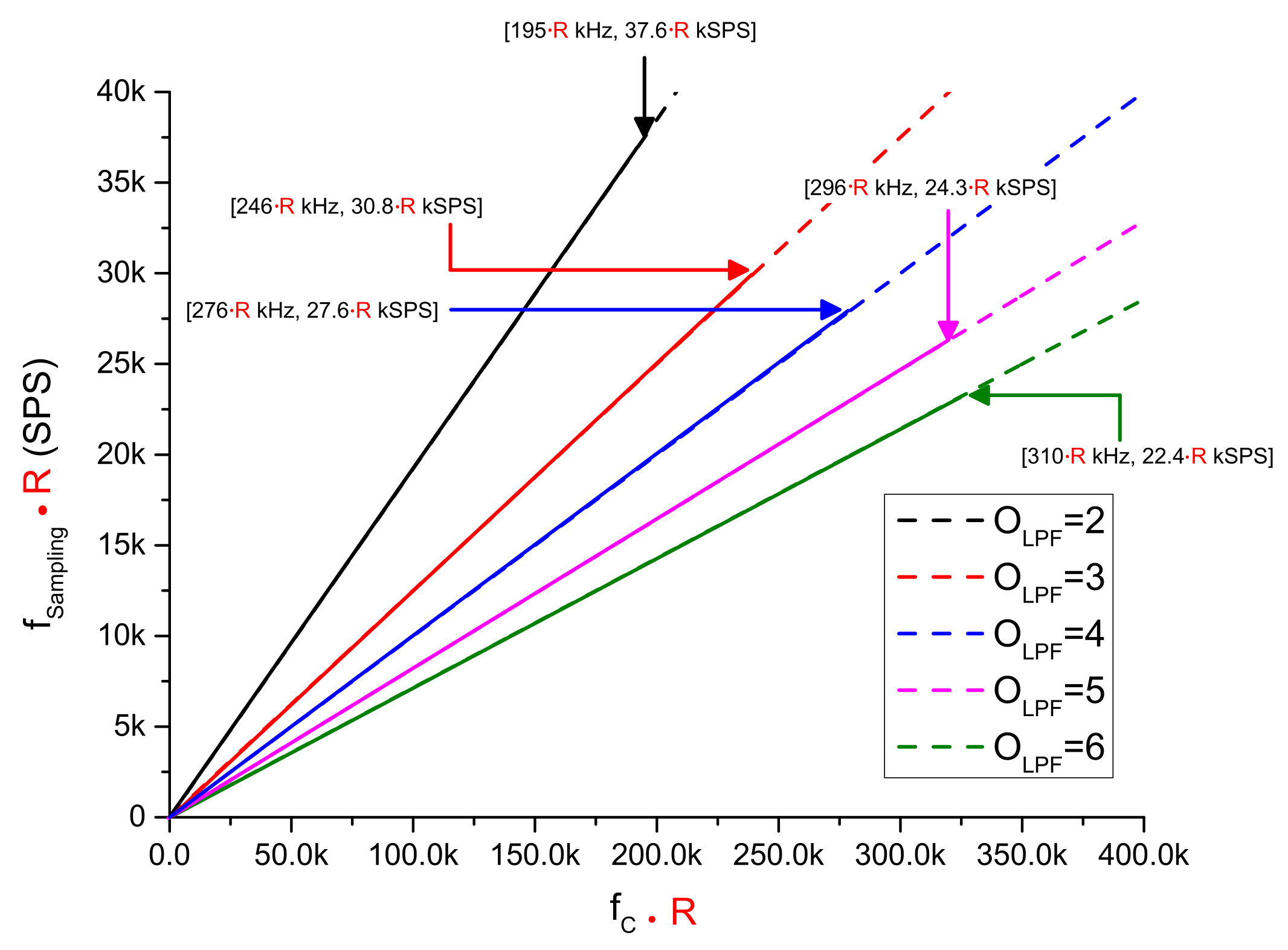
3.1.3. LPF Parameters for a N-Bit SAR-Based ADC
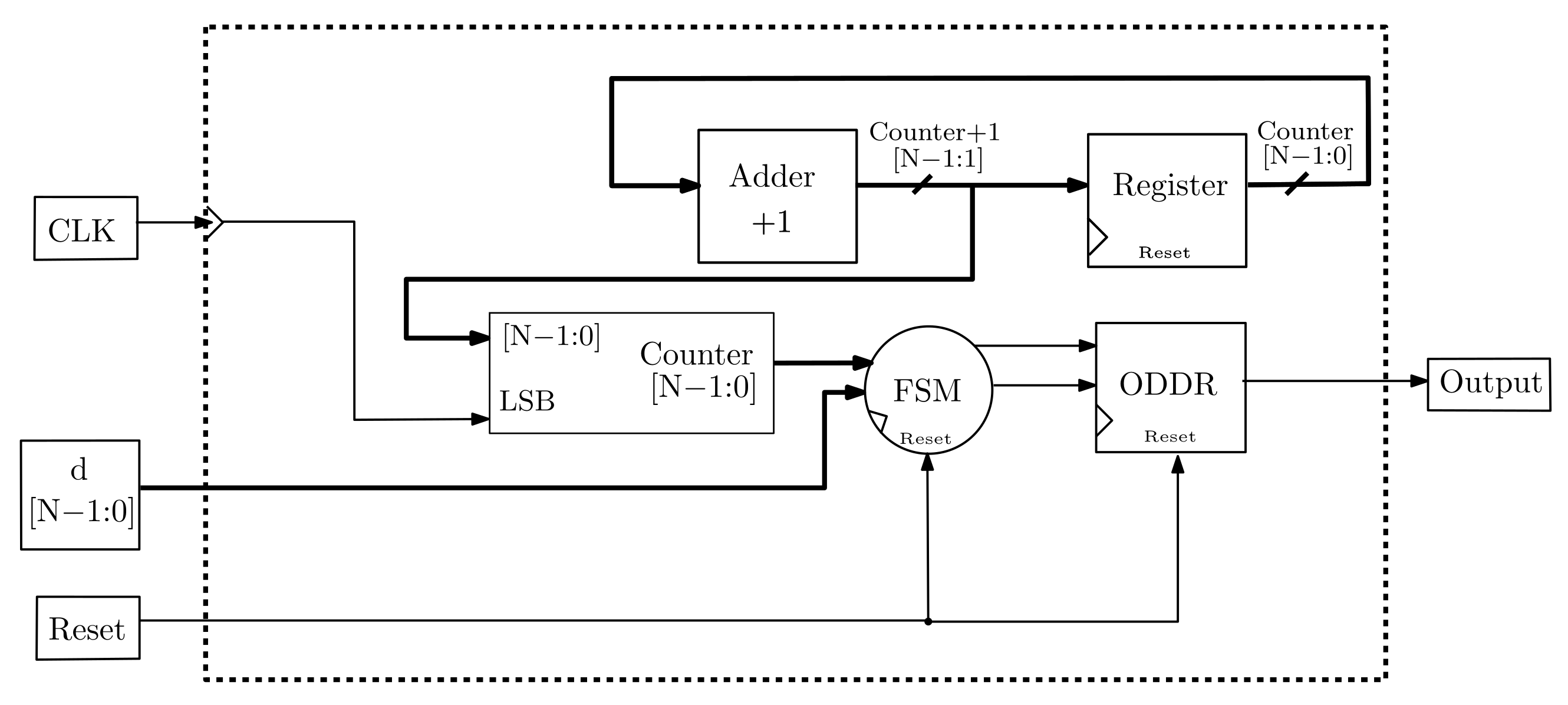
3.1.4. FPGA Implementation of an 8-Bit SAR-Based ADC
4. Double Data Rate PWM
5. Paralleled PWM
6. Distributed Duty-Cycle PWM
7. Paralleled DDR and DDC PWM
8. Experimental Results
8.1. Implementation of an 8-Bit ADC with 8-Bit DDR-PWM and LPF
8.2. Implementation of an 8-Bit ADC with 2 4-Bit DDC-PWM and DDR-PWM
8.3. Implementation of an 8-Bit ADC with 4 2-Bit DDC-PWM and DDR-PWM
9. Discussion
10. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| N | Bit resolution |
| ADC | Analog-to-digital converter |
| DAC | Digital-to-analog converter |
| LPF | Low pass filter |
| PWM | Pulse width modulation |
| Cutoff frequency | |
| LPF order | |
| SAR | successive approximation register |
| ADC sampling frequency. | |
| Clock frequency | |
| LSB | Less significant bit |
| DDR | Double data rate |
| DDC | Distributed duty cycle |
References
- Sakanushi, T.; Yamada, K.; Matsuura, S.; Hagiwara, T.; Aando, Y.; Murakami, I. A design method for two-degree-of-freedom simple repetitive control systems for multiple-input/multiple-output plants. In Proceedings of the 2010 World Automation Congress, Kobe, Japan, 19–23 September 2010; pp. 1–6. [Google Scholar]
- Ang, G.J.; Lim, W.Z.; Lim, C.M. A proposed two-input two-output self-tuning control scheme. In Proceedings of the 2018 IEEE Symposium on Computer Applications Industrial Electronics (ISCAIE), Penang, Malaysia, 28–29 April 2018; pp. 102–107. [Google Scholar]
- Zhang, J.; Kuai, Y.; Zhou, S.; Hou, G.; Ren, M. Improved minimum entropy control for two-input and two-output networked control systems. In Proceedings of the 2016 UKACC 11th International Conference on Control, Belfast, UK, 31 August–2 September 2016; pp. 1–5. [Google Scholar]
- Ren, M.; Zhang, J.; Jiang, M.; Yu, M.; Xu, J. Minimum (h,ϕ)—Entropy Control for Non-Gaussian Stochastic Networked Control Systems and Its Application to a Networked DC Motor Control System. IEEE Trans. Control Syst. Technol. 2014, 23, 406–411. [Google Scholar] [CrossRef]
- Cruz-Miguel, E.E.; García-Martínez, J.R.; Rodríguez-Reséndiz, J.; Carrillo-Serrano, R.V. A New Methodology for a Retrofitted Self-tuned Controller with Open-Source FPGA. Sensors 2020, 20, 6155. [Google Scholar] [CrossRef] [PubMed]
- Sudharsan, R.R. Synthesis of FIR Filter using ADC-DAC: A FPGA Implementation. In Proceedings of the 2019 IEEE International Conference on Clean Energy and Energy Efficient Electronics Circuit for Sustainable Development (INCCES), Krishnankoil, India, 18–20 December 2019; pp. 1–3. [Google Scholar] [CrossRef]
- Yau, Y.-T.; Hwu, K.-I.; Shieh, J.-J. Applying FPGA Control with ADC-Free Sampling to Multi-Output Forward Converter. Electronics 2021, 10, 1010. [Google Scholar] [CrossRef]
- Rodríguez-Reséndiz, J.; Mendoza-Mondragón, F.; Gómez-Loenzo, R.A.; Martínez-Hernández, M.A.; Mucino, V.H. An approach to motion control applications based on advanced programmable devices. Int. J. Electr. Eng. Educ. 2012, 49, 243–259. [Google Scholar] [CrossRef]
- Cruz-Miguel, E.E.; Rodríguez-Reséndiz, J.; García-Martínez, J.R.; Camarillo-Gómez, K.A.; Pérez-Soto, G.I. Field-programmable gate array-based laboratory oriented to control theory courses. Comput. Appl. Eng. Educ. 2019, 27, 1253–1266. [Google Scholar] [CrossRef] [Green Version]
- Sahu, N.; Londhe, N.D.; Kshirsagar, G.B. FPGA applications in inverter and converter circuits: A review on technology, benefits and challenges. In Proceedings of the 2017 International Conference on Innovations in Information, Embedded and Communication Systems (ICIIECS), Coimbatore, India, 17–18 March 2017. [Google Scholar]
- Dhede, O.S.; Shah, S.K. A review: Hardware Implementation of AES using minimal resources on FPGA. In Proceedings of the 2015 International Conference on Pervasive Computing (ICPC), Pune, India, 8–10 January 2015; pp. 1–3. [Google Scholar]
- Ni, M.; Wang, X.; Li, F.; Rhee, W.; Wang, Z. A 13-Bit 2-GS/s Time-Interleaved ADC with Improved Correlation-Based Timing Skew Calibration Strategy. IEEE Trans. Circuits Syst. I Regul. Pap. 2021, 69, 481–494. [Google Scholar] [CrossRef]
- Nam, J.; Hassanpourghadi, M.; Zhang, A.; Chen, M.S. A 12-Bit 1.6, 3.2, and 6.4 GS/s 4-b/Cycle Time-Interleaved SAR ADC with Dual Reference Shifting and Interpolation. IEEE J. -Solid-State Circuits 2018, 53, 1765–1779. [Google Scholar] [CrossRef]
- Devarajan, S.; Singer, L.; Kelly, D.; Pan, T.; Silva, J.; Brunsilius, J.; Rey-Losada, D.; Murden, F.; Speir, C.; Bray, J.; et al. A 12-b 10-GS/s Interleaved Pipeline ADC in 28-nm CMOS Technology. J. -Solid-State Circuits 2017, 52, 3204–3218. [Google Scholar] [CrossRef]
- Zhou, Y.; Xu, B.; Chiu, Y. A 12-b 1-GS/s 31.5-mW Time-Interleaved SAR ADC with Analog HPF-Assisted Skew Calibration and Randomly Sampling Reference ADC. IEEE J. -Solid-State Circ. 2019, 54, 2207–2218. [Google Scholar] [CrossRef]
- Monteiro, V.; Ferreira, J.C.; Melendez, A.A.N.; Afonso, J.A.; Couto, C.; Afonso, J.L. Experimental Validation of a Bidirectional Three-Level dc-dc Converter for On-Board or off-Board EV Battery Chargers. In Proceedings of the IECON 2019—45th Annual Conference of the IEEE Industrial Electronics Society, Lisbon, Portugal, 14–17 October 2019. [Google Scholar]
- Kim, B.; Kim, H.; Choi, S. Three-phase on-board charger with three modules of single-stage interleaved soft-switching AC-DC converter. In Proceedings of the 2018 IEEE Applied Power Electronics Conference and Exposition (APEC), San Antonio, TX, USA, 4–8 March 2018; pp. 3405–3410. [Google Scholar]
- Kamble, A.S.; Swami, P.S. On-Board Integreted Charger for Electric Vehicle Based on Split Three Phase Insuction Motor. In Proceedings of the 2018 International Conference on Emerging Trends and Innovations In Engineering and Technological Research (ICETIETR), Ernakulam, India, 1–13 July 2018; pp. 1–5. [Google Scholar]
- Mooney, J.; Halton, M.; Mahdi, A.E. Specialized Digital Signal Processor for control of multi-rail/multi-phase high switching frequency power converters. In Proceedings of the 2010 Twenty-Fifth Annual IEEE Applied Power Electronics Conference and Exposition (APEC), Palm Springs, CA, USA, 21–25 February 2010; pp. 2207–2211. [Google Scholar]
- Mooney, J.; Effler, S.; Halton, M.; Mahdi, A.E. DSP-based control of multi-rail DC-DC converter systems with non-integer switching frequency ratios. In Proceedings of the 2010 1st International Conference on Energy, Power and Control (EPC-IQ), Basrah, Iraq, 30 November–2 December 2010; pp. 203–207. [Google Scholar]
- Rahimi, A.A.; Carreira, L.B.; Gupta, S. Synchronous multi-signal acquisition for WBSNs using gold-code based joint-compressive sensing. In Proceedings of the 2016 IEEE Biomedical Circuits and Systems Conference (BioCAS), Shanghai, China, 17–19 October 2016; pp. 236–239. [Google Scholar]
- Man, X.; Wu, L.; Zhang, X.; Ma, T.; Jia, W. A High Precision Multi-Cell Battery Voltage Detecting Circuit for Battery Management Systems. In Proceedings of the 2016 IEEE 83rd Vehicular Technology Conference (VTC Spring), Nanjing, China, 15–18 May 2016; pp. 1–5. [Google Scholar]
- Amitkumar, K.S.; Narayanan, G. Simplified implementation of space vector PWM strategies for a three level inverter. In Proceedings of the 2012 IEEE 7th International Conference on Industrial and Information Systems (ICIIS), Chennai, India, 6–9 August 2012; pp. 1–6. [Google Scholar]
- Lopatkin, N.N. Voltage source multilevel inverter voltage quality comparison under multicarrier sinusoidal PWM and space vector PWM of two delta voltages. In Proceedings of the 2017 International Multi-Conference on Engineering, Computer and Information Sciences (SIBIRCON), Novosibirsk, Russia, 18–22 September 2017; pp. 439–444. [Google Scholar]
- Devi, V.S.K.; Srivani, S.G. Modified phase shifted PWM for cascaded H bridge multilevel inverter. In Proceedings of the 2017 Third International Conference on Advances in Electrical, Electronics, Information, Communication and Bio-Informatics (AEEICB), Chennai, India, 27–28 February 2017; pp. 89–94. [Google Scholar]
- Jeon, M.-K.; Yoo, W.-J.; Kim, C.-G.; Yoo, C. A Stochastic Flash Analog-to-Digital Converter Linearized by Reference Swapping. IEEE Access 2017, 5, 23046–23051. [Google Scholar] [CrossRef]
- Fahmy, A.; Liu, J.; Kim, T.; Maghari, N. An All-Digital Scalable and Reconfigurable Wide-Input Range Stochastic ADC Using Only Standard Cells. IEEE Trans. Circuits Syst. II Express Briefs 2015, 62, 731–735. [Google Scholar] [CrossRef]
- Weaver, S.; Hershberg, B.; Moon, U. Digitally Synthesized Stochastic Flash ADC Using Only Standard Digital Cells. IEEE Trans. Circuits Syst. I Regul. Pap. 2014, 61, 84–91. [Google Scholar] [CrossRef]
- Unnikrishnan, V.; Pathapati, S.R.; Vesterbacka, M. A fully synthesized all-digital VCO-based analog-to-digital converter. In Proceedings of the 2015 Nordic Circuits and Systems Conference (NORCAS): NORCHIP & International Symposium on System-on-Chip (SoC), Oslo, Norway, 26–28 October 2015; pp. 1–4. [Google Scholar] [CrossRef]
- Unnikrishnan, V.; Vesterbacka, M. A NAND gate based standard cell VCO for use in synthesizable ADCs. In Proceedings of the 2015 Nordic Circuits and Systems Conference (NORCAS): NORCHIP & International Symposium on System-on-Chip (SoC), Oslo, Norway, 26–28 October 2015; pp. 1–4. [Google Scholar] [CrossRef]
- Ghozzy, S.; Ragai, H.F.; El-Nozahi, M. A Two-Step VCO-Based ADC with PWM Pre-coded Coarse Quantizer. In Proceedings of the 2020 IEEE 3rd International Conference on Electronics Technology (ICET), Chengdu, China, 8–12 May 2020; pp. 262–265. [Google Scholar] [CrossRef]
- Vardhini, P.A.H. Analysis of integrator for continuous time Digital sigma Delta ADC on Xilinx FPGA. In Proceedings of the 2016 International Conference on Electrical, Electronics, and Optimization Techniques (ICEEOT), Chennai, India, 3–5 March 2016; pp. 2689–2693. [Google Scholar] [CrossRef]
- Rajesh, G.P.; Deepthy, C.K.; Jermila, M.M.; Raghunath, K.P.; Aparna, V.N. Force Rebalance with Multi-bit Sigma-Delta implemented with FPGA for Precision Rate Sensor. In Proceedings of the TENCON 2019—2019 IEEE Region 10 Conference (TENCON), Kochi, India, 17–20 October 2019; pp. 654–657. [Google Scholar] [CrossRef]
- Kumar, P.S.; Narayana, D.L.; Tejesvi, V.R.; Chandrasen, M.K. FPGA based Sigma-Delta analog to digital converter for power sensing. In Proceedings of the 2016 International Conference on Electrical, Electronics, and Optimization Techniques (ICEEOT), Chennai, India, 3–5 March 2016; pp. 4912–4914. [Google Scholar] [CrossRef]
- Homulle, H.; Regazzoni, F.; Charbon, E. 200 MS/s ADC implemented in a FPGA employing TDCs. In Proceedings of the 2015 ACM/SIGDA International Symposium on Field-Programmable Gate Arrays, New York, NY, USA, 22–24 February 2015; pp. 228–235. [Google Scholar] [CrossRef]
- Homulle, H.; Visser, S.; Charbon, E. A Cryogenic 1 GSa/s, Soft-Core FPGA ADC for Quantum Computing Applications. IEEE Trans. Circuits Syst. I Regul. Pap. 2016, 63, 1854–1865. [Google Scholar] [CrossRef] [Green Version]
- Xiang, Z.; Wang, T.; Geng, T.; Xiang, T.; Jin, X.; Herbordt, M. Soft-Core. Multiple-Lane, FPGA-based ADCs for a Liquid Helium Environment. In Proceedings of the 2018 IEEE High Performance Extreme Computing Conference (HPEC), Waltham, MA, USA, 25–27 September 2018; pp. 1–6. [Google Scholar] [CrossRef]
- Leuenberger, L.; Amiet, D.; Wei, T.; Zbinden, P. An FPGA-based 7-ENOB 600 MSample/s ADC without any External Components. In Proceedings of the The 2021 ACM/SIGDA International Symposium on Field-Programmable Gate Arrays, New York, NY, USA, 28 February–2 March 2021; pp. 240–250. [Google Scholar] [CrossRef]
- Crovetti, P.S. All-Digital High Resolution D/A Conversion by Dyadic Digital Pulse Modulation. IEEE Trans. Circuits Syst. I Regul. Pap. 2017, 64, 573–584. [Google Scholar] [CrossRef] [Green Version]
- Aiello, O.; Crovetti, P.; Alioto, M. Fully Synthesizable Low-Area Analogue-to-Digital Converters with Minimal Design Effort Based on the Dyadic Digital Pulse Modulation. IEEE Access 2020, 8, 70890–70899. [Google Scholar] [CrossRef]
- Aiello, O.; Crovetti, P.S.; Alioto, M. Fully Synthesizable Low-Area Digital-to-Analog Converter with Graceful Degradation and Dynamic Power-Resolution Scaling. IEEE Trans. Circuits Syst. I Regul. Pap. 2019, 66, 2865–2875. [Google Scholar] [CrossRef]
- Aiello, O.; Crovetti, P.S.; Alioto, M. Standard Cell-Based Ultra-Compact DACs in 40-nm CMOS. IEEE Access 2019, 7, 126479–126488. [Google Scholar] [CrossRef]
- Xu, Z.; Ojima, N.; Li, S.; Iizuka, T. An All-Standard-Cell-Based Synthesizable SAR ADC with Nonlinearity-Compensated RDAC. IEEE Trans. Very Large Scale Integr. (Vlsi) Syst. 2021, 29, 2153–2162. [Google Scholar] [CrossRef]
- Wang, G.; Chiu, Y. Fast FPGA emulation of background-calibrated SAR ADC with internal redundancy dithering. In Proceedings of the IEEE 2013 Custom Integrated Circuits Conference, San Jose, CA, USA, 22–25 September 2013; pp. 1–4. [Google Scholar]
- Chen, M.; Zhou, C.; He, W.; Ye, F.; Junyan, R. A Split-Based Neural Network Calibrator for SAR-Pipelined ADC on FPGA. In Proceedings of the 2020 IEEE 15th International Conference on Solid-State Integrated Circuit Technology (ICSICT), Kunming, China, 3–6 November 2020; pp. 1–3. [Google Scholar]
- Hooi, L.Y.; Hiung, L.H.; Drieberg, M.; Sebastian, P. Configurable 2 bits per cycle successive approximation register for analog to digital converter on FPGA. In Proceedings of the 2016 6th International Conference on Intelligent and Advanced Systems (ICIAS), Kuala Lumpur, Malaysia, 15–17 August 2016; pp. 1–5. [Google Scholar]
- Colletta, G.; Ferreira, D.; Crepaldi, P. A Successive Approximation A/D Converter Using a PWM Modulator DAC. In Proceedings of the 2012 IEEE Ninth Electronics, Robotics and Automotive Mechanics Conference, Cuernavaca, Mexico, 19–23 November 2012; pp. 333–337. [Google Scholar]
- David, M.A. Using PWM Output as a Digital-to-Analog Converter on a TMS320F280x Digital Signal Controller; Texas Instrument: Dallas, TX, USA, 2008; Available online: https://www.ti.com/lit/pdf/spraa88 (accessed on 30 November 2021).
- Nisarga, B. PWM DAC Using MSP430 High-Resolution Timer; Texas Instrument: Dallas, TX, USA, 2013; Available online: https://www.ti.com/lit/pdf/slaa497 (accessed on 30 November 2021).
- Lukic, Z.; Rahman, N.; Prodie, A. Multibit Σ–Δ PWM Digital Controller IC for DC-DC Converters Operating at Switching Frequencies Beyond 10 MHz. IEEE Trans. Power Electron. 2007, 5, 1693–1707. [Google Scholar] [CrossRef]
- Mitchell, M. Using PWM Timer B as a DAC; Texas Instrument: Dallas, TX, USA, 2008; Available online: https://www.ti.com/lit/pdf/slaa497 (accessed on 30 November 2021).
- Malvino, A. Principios de Electronica; McGraw-Hill: New York, NY, USA, 2007; Available online: https://books.google.es/books?id=UaxhQQfLMY8C (accessed on 30 November 2021).
- Mehta, R.; Jasani, H. FPGA realization of novel techniques for DDR based data acquisition system. In Proceedings of the 2016 2nd International Conference on Next Generation Computing Technologies (NGCT), Dehradun, India, 14–16 October 2016. [Google Scholar]
- Hamil, H.; Azzaz, M.S.; Sakhi, S.; Maali, A.; Zidelmal, Z.; Abdeslam, D.O. Design and FPGA real-time implementation of PWM and PPM modulation for Ultra Wide Band applications. In Proceedings of the 2019 6th International Conference on Image and Signal Processing and their Applications (ISPA), Mostaganem, Algeria, 24–25 November 2019; pp. 1–5. [Google Scholar]
- Tiwari, A. A low power high speed dual data rate acquisition system using FPGA. In Proceedings of the 2012 International Conference on Communication, Information Computing Technology (ICCICT), Mumbai, India, 19–20 October 2012; pp. 1–4. [Google Scholar]
- Reddy, N.U.; Babu, R.; Chaitanyakumar, M.V. A 4 bit 5GHz R-2R Digital to Analog Converter using hetrojunction HEMT. In Proceedings of the 2013 International Conference on Emerging Trends in Communication, Control, Signal Processing and Computing Applications (C2SPCA), Bangalore, India, 10–11 October 2013; pp. 1–6. [Google Scholar]
- Chen, C.C.; Lu, N.K. Nonlinearity analysis of R-2R ladder-based current-steering digital to analog converte. In Proceedings of the 2013 IEEE International Symposium on Circuits and Systems (ISCAS), Beijing, China, 9–23 May 2013; pp. 833–836. [Google Scholar]
- Radhika, V.; Baskaran, K. FPGA based DPWM/DPFM architecture for digitally controlled dc-dc converters. In Proceedings of the 2016 IEEE Uttar Pradesh Section International Conference on Electrical, Computer and Electronics Engineering (UPCON), Varanasi, India, 9–11 December 2016; pp. 78–82. [Google Scholar]
- Debnath, S.; Qin, J.; Saeedifard, M. A distributed PWM strategy for modular multilevel converter. In Proceedings of the IECON 2014—40th Annual Conference of the IEEE Industrial Electronics Society, Dallas, TX, USA, 29 October–1 November 2014. [Google Scholar]
- Hernandez, L.; Prefasi, E. Analog to digital conversion using a Pulse Width Modulator and an irregular sampling decoder. In Proceedings of the 2006 13th IEEE International Conference on Electronics, Circuits and Systems, Nice, France, 10–13 December 2006. [Google Scholar]
- Radhika, V.; Baskaran, K. Hybrid digital pulse width modulator architecture using FPGA. In Proceedings of the 2016 IEEE International Conference on Recent Trends in Electronics, Information Communication Technology (RTEICT), Bangalore, India, 20–21 May 2016. [Google Scholar]
- Sabarinath, V.; Sivanandam, K. Design and implementation of FPGA based high resolution digital pulse width modulator. In Proceedings of the 2013 International Conference on Communication and Signal Processing, Melmaruvathur, India, 3–5 April 2013. [Google Scholar]
- Shimazoe, K.; Takahashi, H.; Shi, B.; Furumiya, T.; Ooi, J.; Kumazawa, Y.; Murayama, H. Novel Front-End Pulse Processing Scheme for PET System Based on Pulse Width Modulation and Pulse Train Method. IEEE Trans. Nucl. Sci. 2010, 57, 782–786. [Google Scholar] [CrossRef]
- Zrilic, D.G. Alternative Approach to Use of Pulse Width Modulation. In Proceedings of the 2006 World Automation Congress, Budapest, Hungary, 24–26 July 2006. [Google Scholar]
- Lin, H.; Chen, R.; Li, R.; Zhu, L.; Yan, H.; Shu, Z. A Flexible and Fast Space Vector Pulse Width Modulation Technique for Multilevel Converters. In Proceedings of the 2019 22nd International Conference on Electrical Machines and Systems (ICEMS), Harbin, China, 11–14 August 2019; pp. 1–4. [Google Scholar]
- Salomon, L.; Moreno, R.; Pimenta, T. Implementation of a 17 bits Pulse Width Modulation circuit using FPGA. In Proceedings of the 2015 27th International Conference on Microelectronics (ICM), Casablanca, Morocco, 20–23 December 2015. [Google Scholar]
- Lee, Y.; Lee, J.; Kim, J. GaN FET-based synchronous buck converter with 10-bit 4-MHz digital pulse width modulator. In Proceedings of the 2015 9th International Conference on Power Electronics and ECCE Asia (ICPE-ECCE Asia), Seoul, Korea, 1–5 June 2015. [Google Scholar]
- LT1364 Dual and Quad 70 MHz, 1000V/µs Op Amps. LT1364 Datasheet LINEAR TECHNOLOGY CORPORATION. 2013. Available online: https://www.analog.com/media/en/technical-documentation/data-sheets/13645fa.pdf (accessed on 30 November 2021).


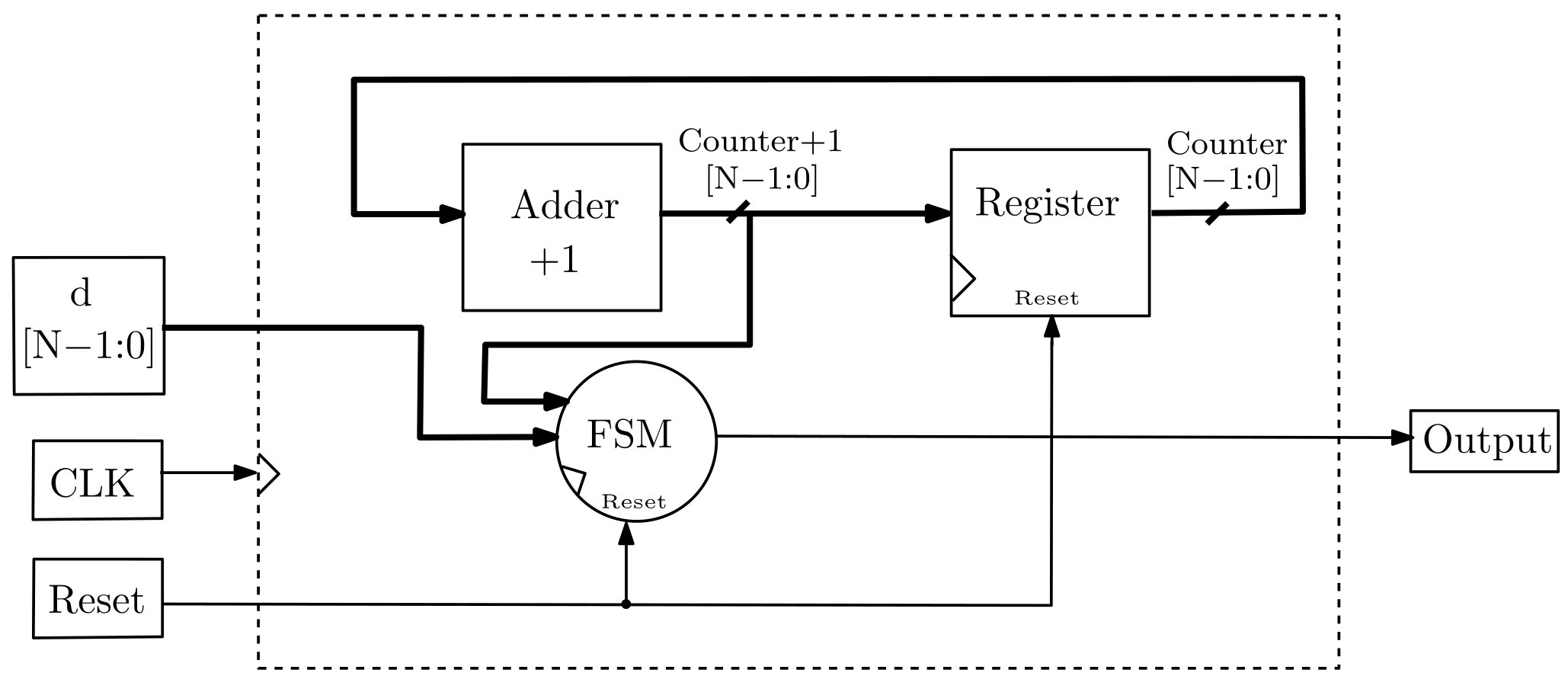
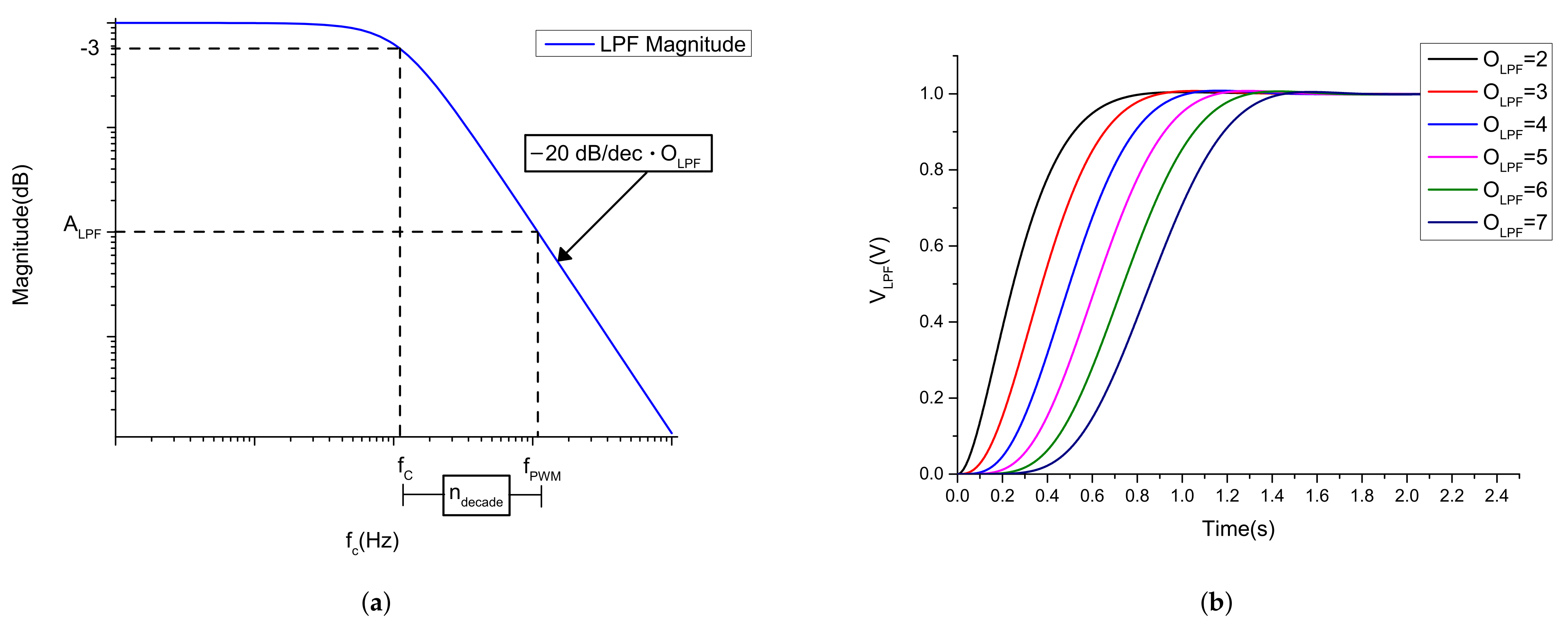

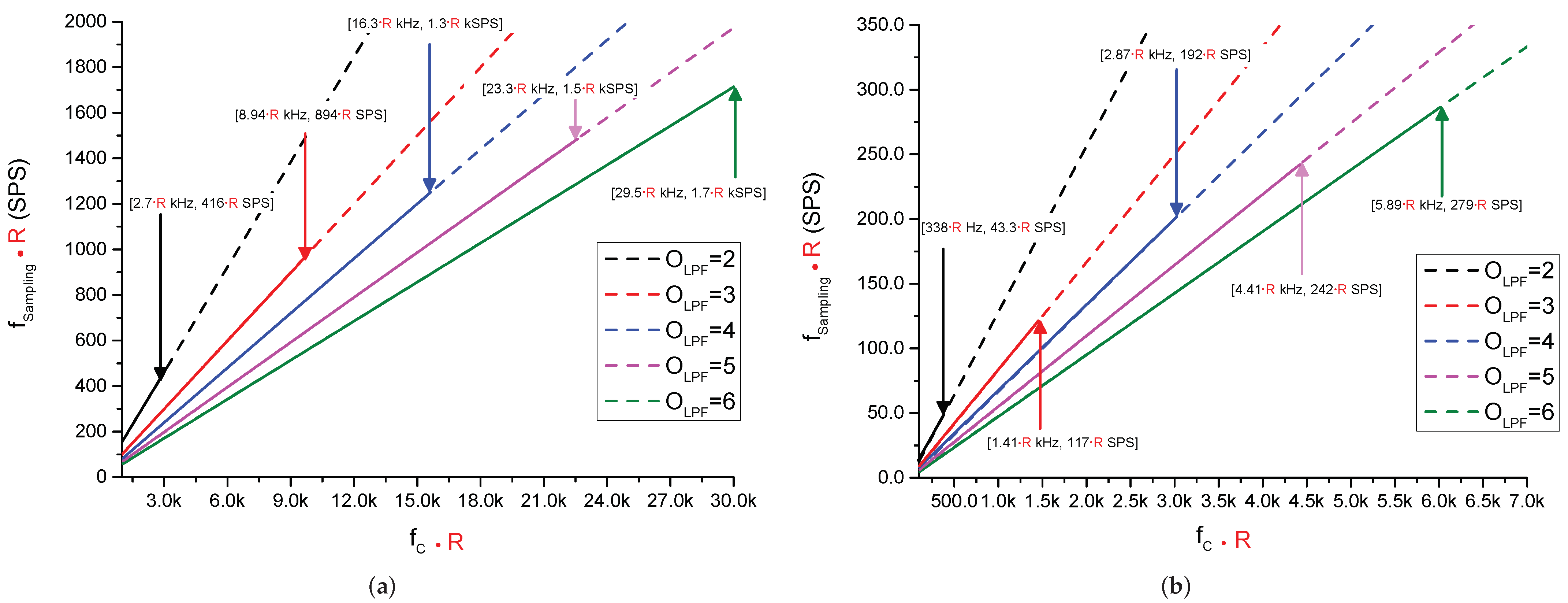


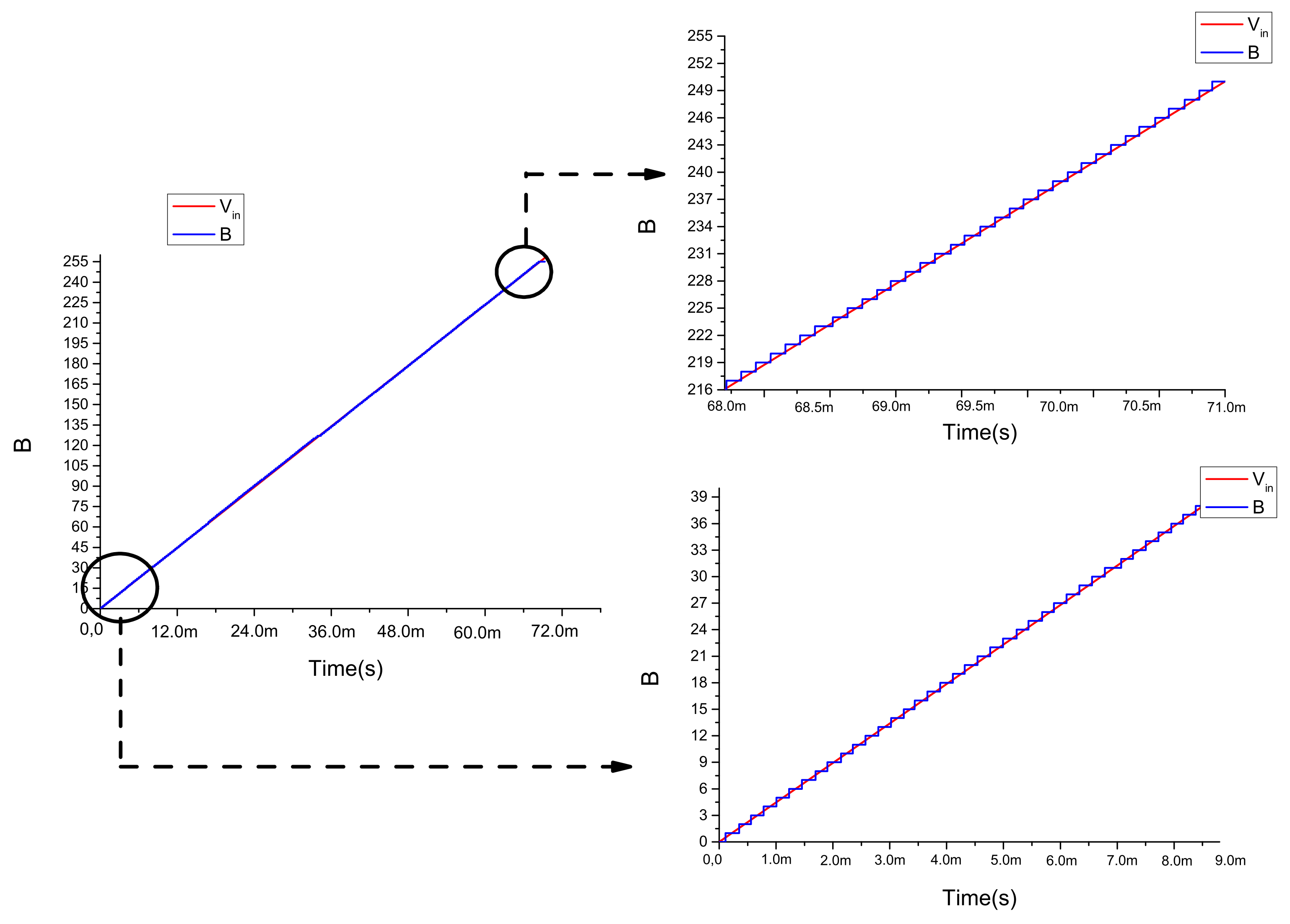


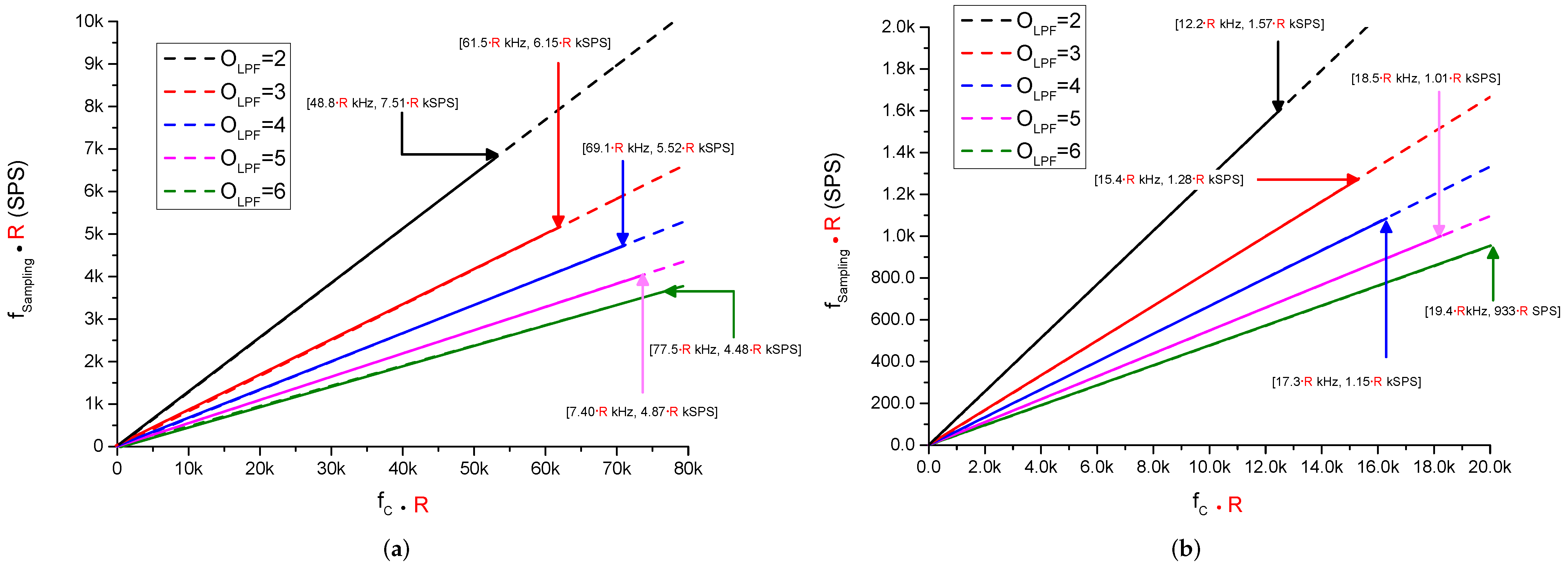


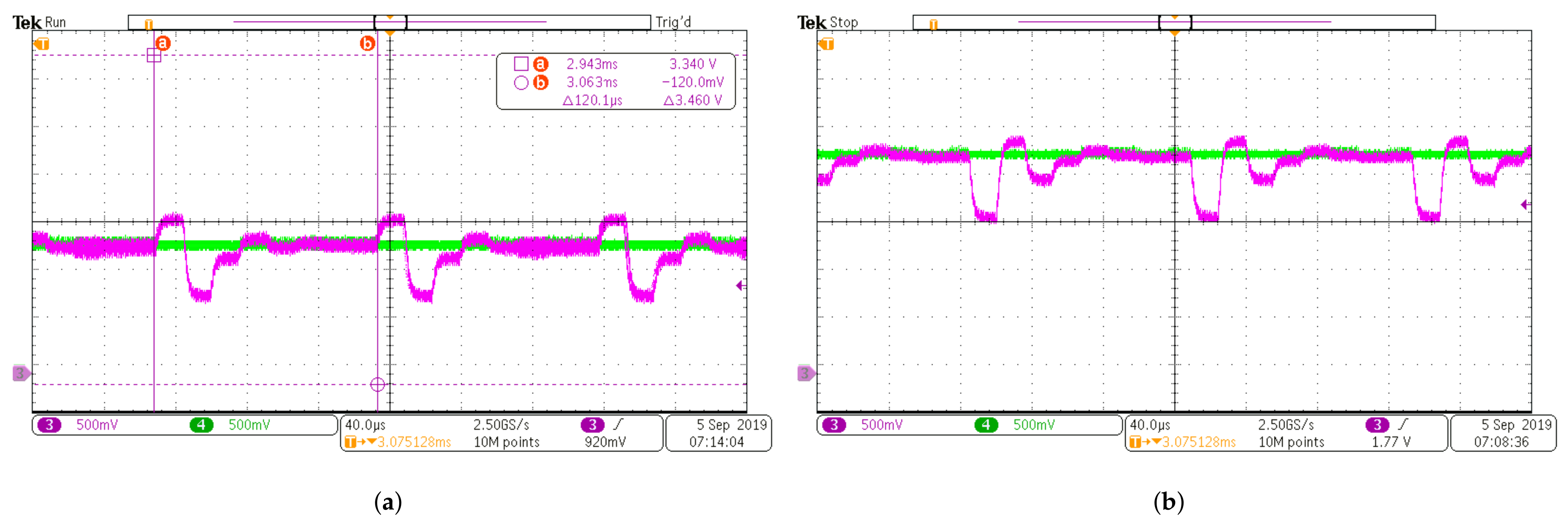
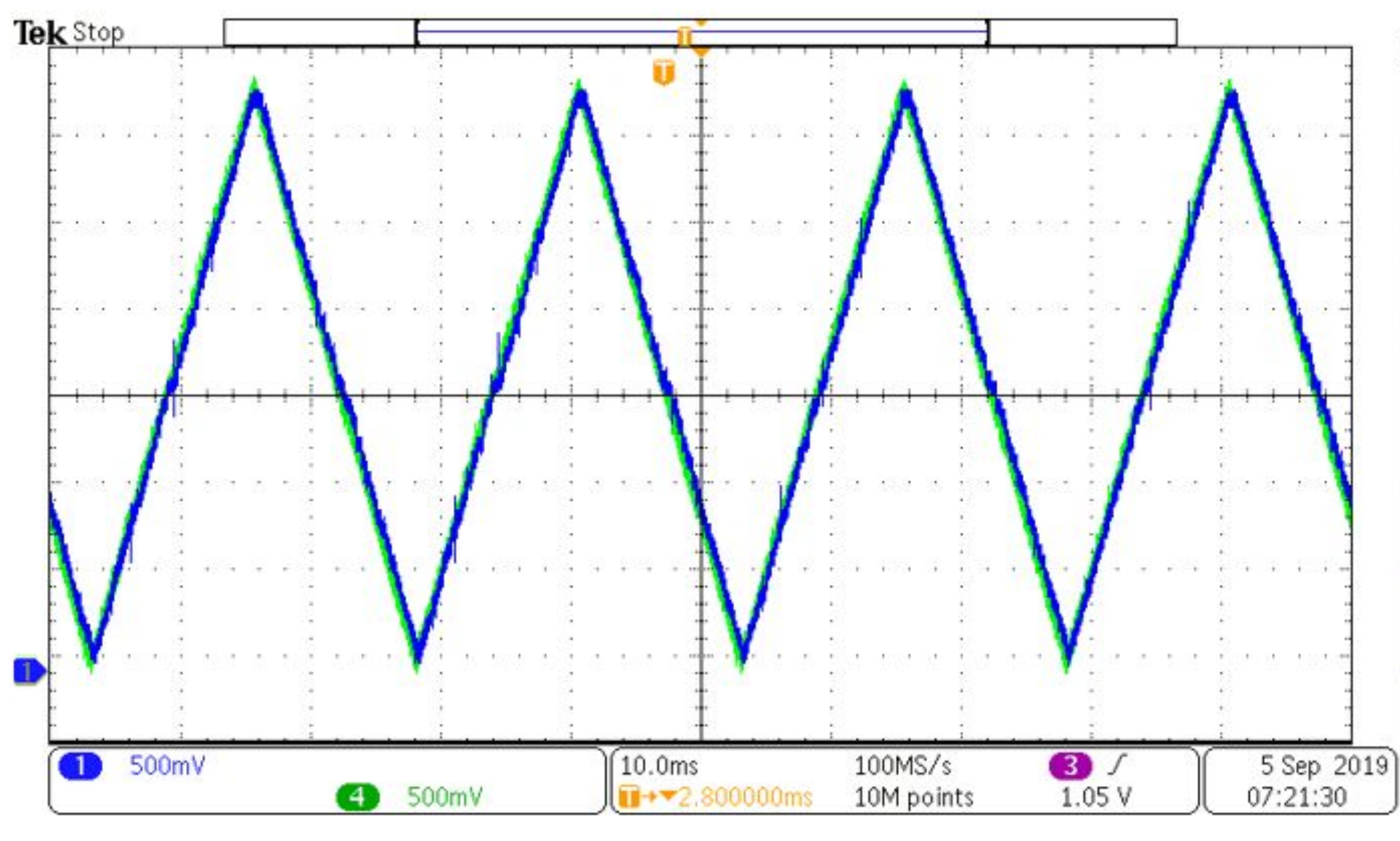

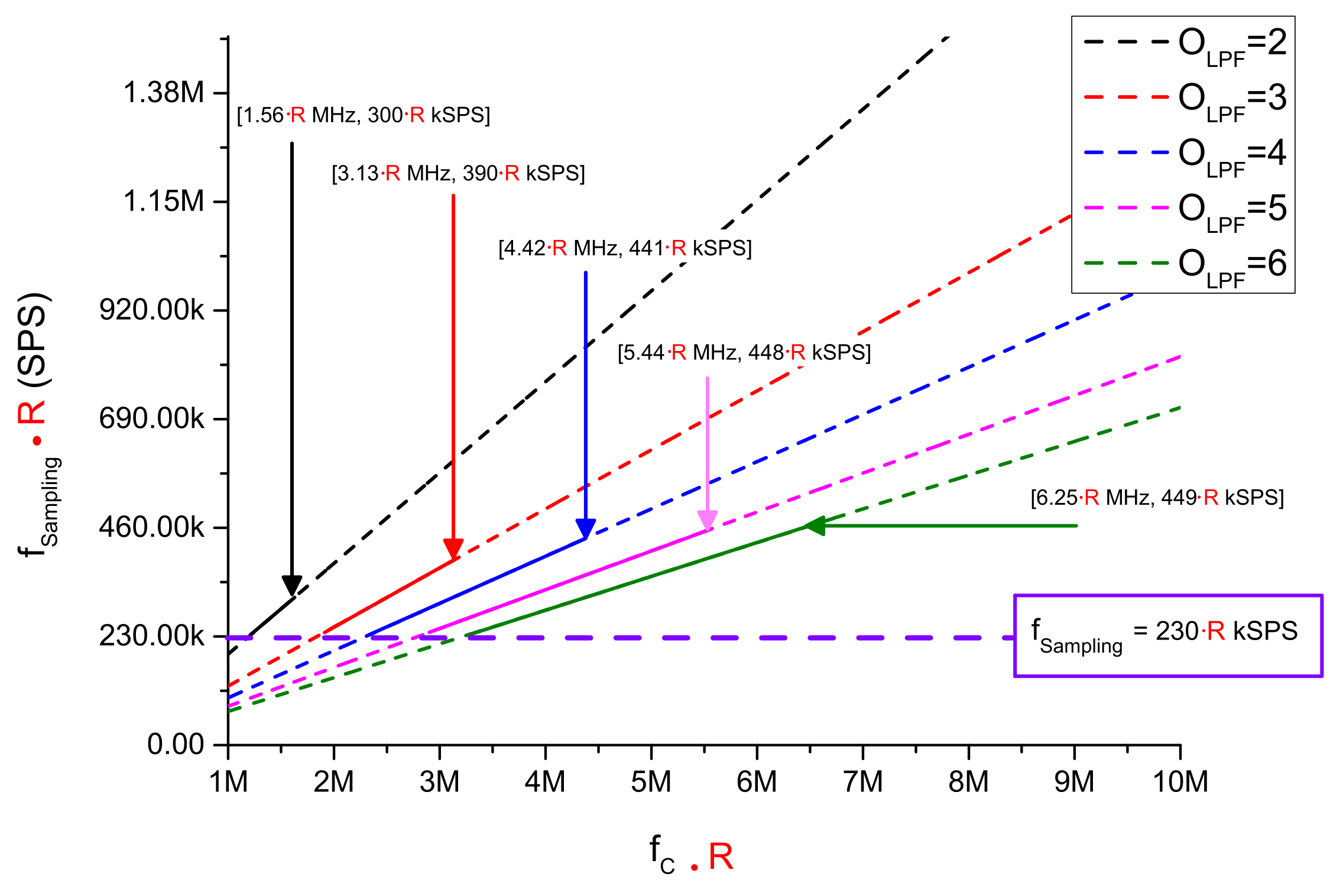

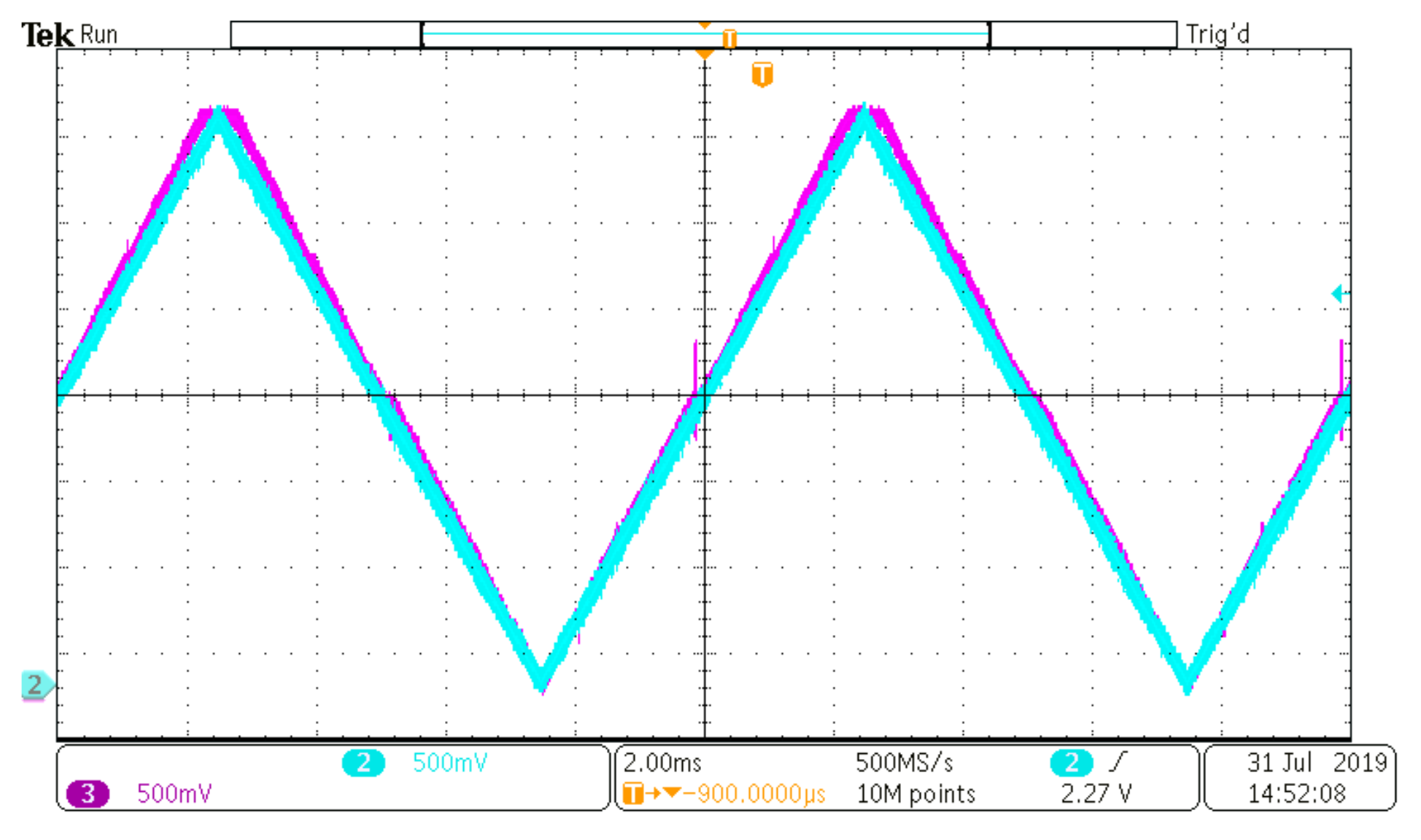

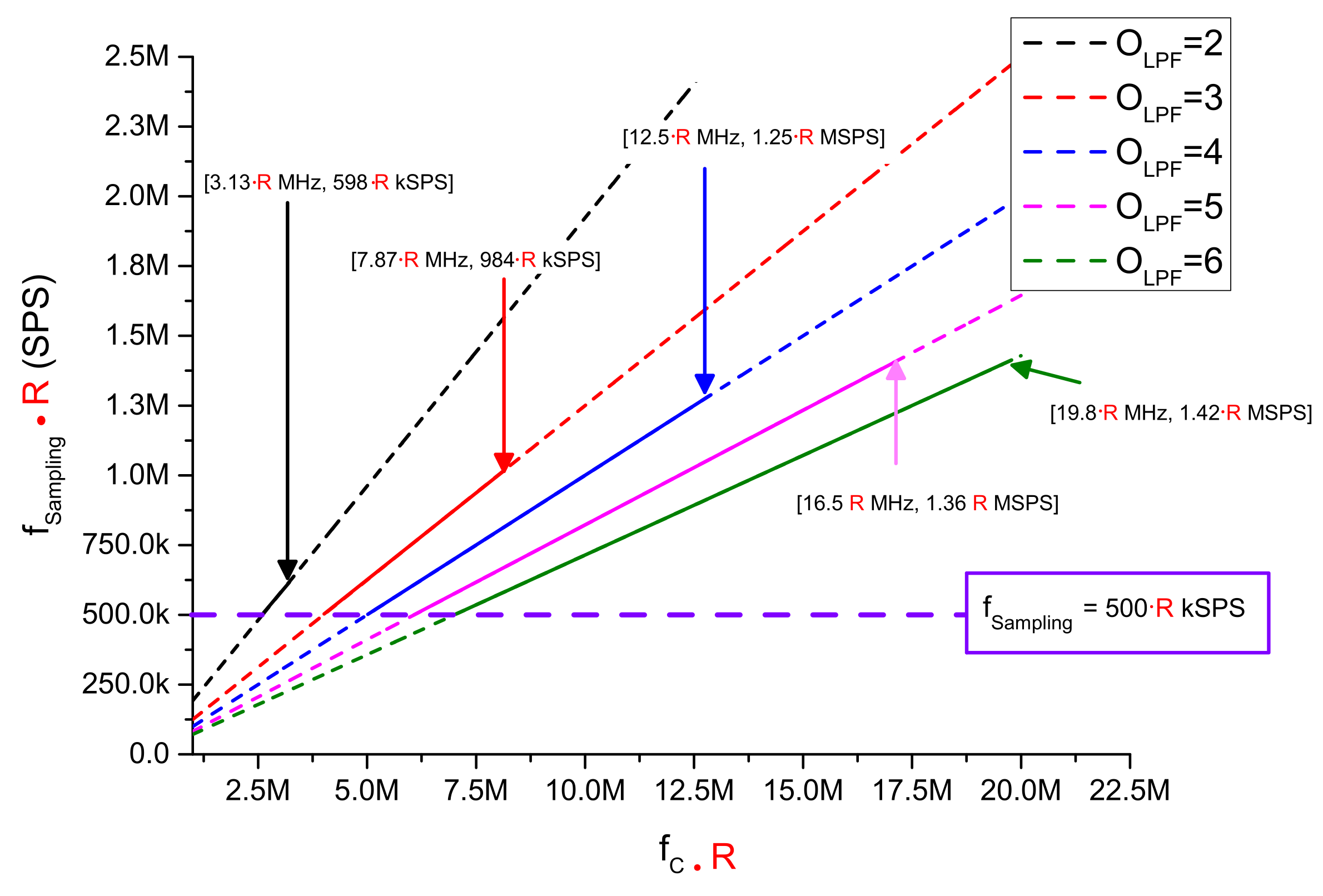
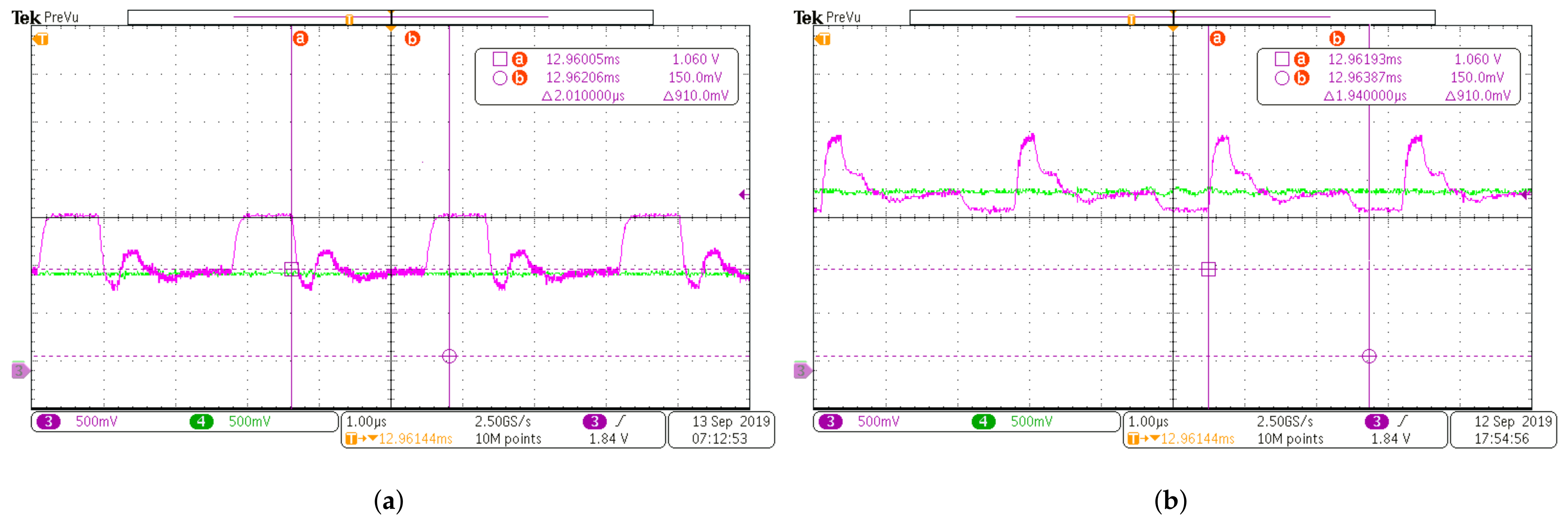

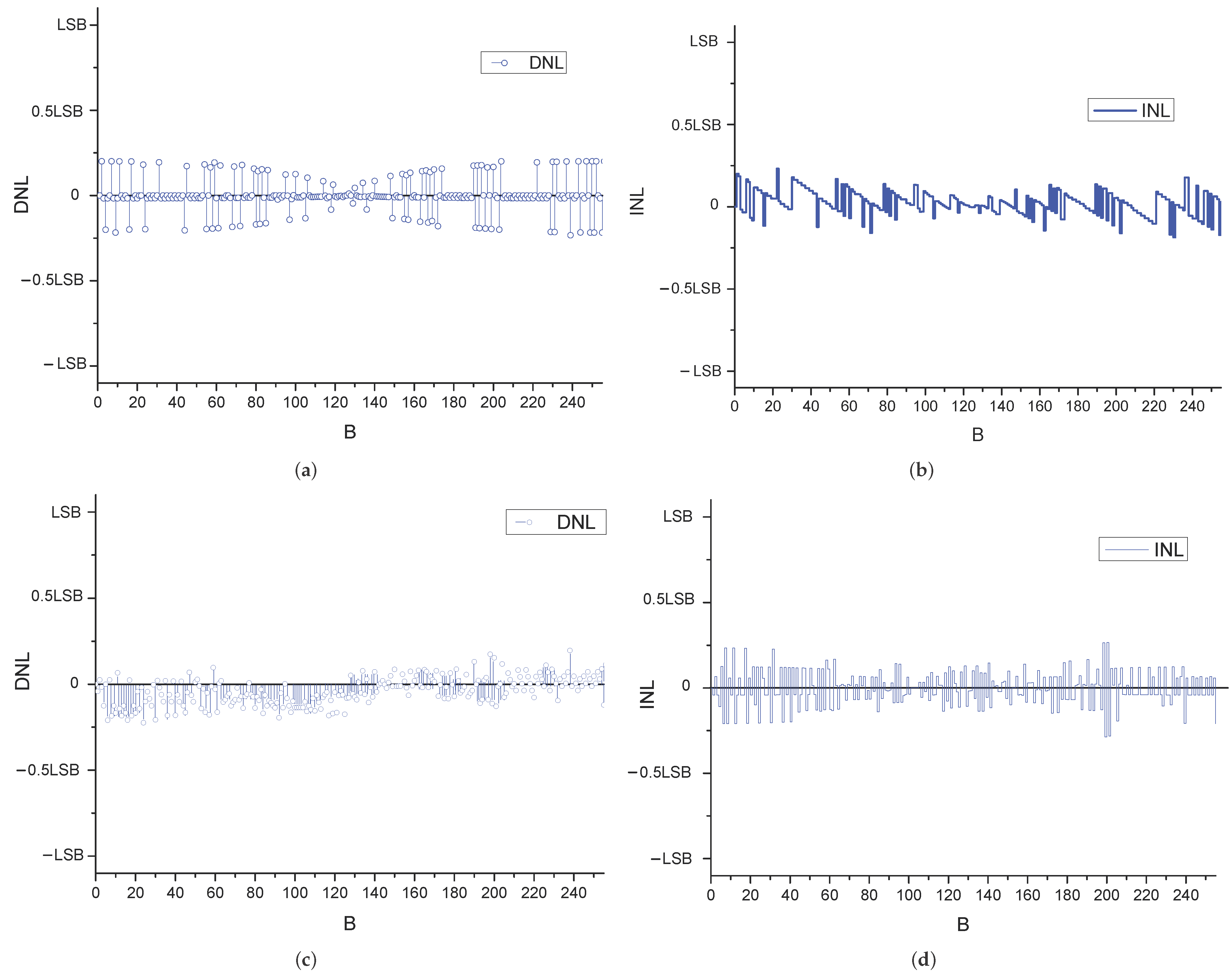
| Parameters | Value |
|---|---|
| N | 8 |
| 100 MHZ | |
| 390.625 kHz |
| LPF | LPF | ADC | ADC | |
|---|---|---|---|---|
| 2 | 21.64 kHz | 30.04 s | 240.3 s | 4.16 kSPS |
| 3 | 56.76 kHz | 17.62 s | 140.9 s | 7.10 kSPS |
| 4 | 91.93 kHz | 13.60 s | 108.8 s | 9.19 kSPS |
| 5 | 122.8 KHz | 12.38 s | 99.04 s | 10.1 kSPS |
| 6 | 148.9 kHz | 11.75 s | 94.02 s | 10.6 kSPS |
| ADC = 8-Bit | DDC-PWM DDR-PWM | |||||
|---|---|---|---|---|---|---|
| K | 1 | 2 | 4 | 1 | 2 | 4 |
| 3 | 5 | |||||
| (kSPS) | 61.5 | 390.6 | 984.3 | 48.3 | 447 | 1360 |
| FPGA in/out | 2 | 3 | 4 | 2 | 3 | 4 |
| R | 7 | 11 | 15 | 9 | 15 | 21 |
| C | 3 | 6 | 9 | 5 | 10 | 15 |
| OA | 2 | 3 | 4 | 3 | 5 | 7 |
| Comparators | 1 | 1 | ||||
| ADC = 8-bit | DDR-PWM |
|---|---|
| 43.3 kHz | |
| 15 s | |
| 2 | |
| 8 kSPS | |
| FPGA in/out | 2 |
| R | 6 |
| C | 2 |
| OA | 2 |
| Comparators | 1 |
| ADC = 8-Bit | DDR-PWM DDC-PWM |
|---|---|
| 1.20 MHz | |
| 543 ns | |
| 2 | |
| 230 kSPS | |
| FPGA in/out | 3 |
| R | 9 |
| C | 4 |
| OA | 3 |
| Comparators | 1 |
| [38] | [40] | K = 2 DDC-PWM DDR-PWM | K = 4 DDC-PWM DDR-PWM | ||
|---|---|---|---|---|---|
| Resolution (bit) | 7.2 | 9.3 | 8 | 8 | 8 |
| Signal input | Voltage | Voltage | Voltage/current | Voltage | Voltage |
| Voltage range (V) | 0–2.5 | 0.15–0.45 | 0–1 | 0–3.3 | 0–3.3 |
| Architecture | TDC | TDC | SAR | SAR | SAR |
| 200 MSPS | 600 MSPS | 2.8 kSPS/2.2 kSPS | 450 kSPS | 1.42 MSPS | |
| DNL (LSB) | −0.9 to 1.4 | ±0.9 | ±1.9 | ±0.28 | ±0.28 |
| INL (LSB) | −1.1 to 1.6 | −1.1 to 0.9 | ±1.5 | ±0.25 | ±0.32 |
| ENOB | 6 | 7 | 6.4/6.7 | 7.22 | 7.24 |
| Calibration | Yes | Yes | No | No | No |
| Easily portable | No | No | No | Yes | Yes |
| External elements | No | No | No | Yes | Yes |
| Technology | FPGA Spartan 6 families | FPGA UltraScale+ | CMOS standard cells | FPGA | FPGA |
| K = 2 DDC-PWM DDR-PWM | K = 5 DDC-PWM DDR-PWM | K = 2 DDC-PWM DDR-PWM | K = 6 DDC-PWM DDR-PWM | |
|---|---|---|---|---|
| Resolution (bit) | 10 | 10 | 12 | 12 |
| Signal input | Voltage | Voltage | Voltage | Voltage |
| Voltage range (V) | 0–3.3 | 0–3.3 | 0–3.3 | 0–3.3 |
| Architecture | SAR | SAR | SAR | SAR |
| 160 kSPS | 910 kSPS | 59.7 kSPS | 602 kSPS | |
| DNL (LSB) | ±0.42 | ±0.46 | ±0.51 | ±0.49 |
| INL (LSB) | ±0.38 | ±0.4 | ±0.47 | ±0.46 |
| ENOB | 9.3 | 9.3 | 11.1 | 11.1 |
| Calibration | No | No | No | No |
| Easily portable | Yes | Yes | Yes | Yes |
| External elements | Yes | Yes | Yes | Yes |
| Technology | FPGA | FPGA | FPGA | FPGA |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Espitia Castillo, J.D.; Cantó Navarro, E.; Vidal-Idiarte, E. Design and Implementation of Scalable and Parametrizable Analog-to-Digital Converter on FPGA. Electronics 2022, 11, 447. https://doi.org/10.3390/electronics11030447
Espitia Castillo JD, Cantó Navarro E, Vidal-Idiarte E. Design and Implementation of Scalable and Parametrizable Analog-to-Digital Converter on FPGA. Electronics. 2022; 11(3):447. https://doi.org/10.3390/electronics11030447
Chicago/Turabian StyleEspitia Castillo, Juan David, Enrique Cantó Navarro, and Enric Vidal-Idiarte. 2022. "Design and Implementation of Scalable and Parametrizable Analog-to-Digital Converter on FPGA" Electronics 11, no. 3: 447. https://doi.org/10.3390/electronics11030447
APA StyleEspitia Castillo, J. D., Cantó Navarro, E., & Vidal-Idiarte, E. (2022). Design and Implementation of Scalable and Parametrizable Analog-to-Digital Converter on FPGA. Electronics, 11(3), 447. https://doi.org/10.3390/electronics11030447








