Edge Intelligence Empowered Dynamic Offloading and Resource Management of MEC for Smart City Internet of Things

Abstract

Internet of Things (IoT) has emerged as an enabling platform for smart cities. In this paper, the IoT devices’ offloading decisions, CPU frequencies and transmit powers joint optimization problem is investigated for a multi-mobile edge computing (MEC) server and multi-IoT device cellular network. An optimization problem is formulated to minimize the weighted sum of the computing pressure on the primary MEC server (PMS), the sum of energy consumption of the network, and the task dropping cost. The formulated problem is a mixed integer nonlinear program (MINLP) problem, which is difficult to solve since it contains strongly coupled constraints and discrete integer variables. Taking the dynamic of the environment into account, a deep reinforcement learning (DRL)-based optimization algorithm is developed to solve the nonconvex problem. The simulation results demonstrate the correctness and the effectiveness of the proposed algorithm.

1. Introduction

Smart city is a promising city paradigm, which improves the quality of experience (QoE) of citizens through advanced information and communication technologies (ICTs) infrastructure and enormous Internet of Things (IoT) devices [1,2,3]. A practical problem is that the IoT devices are usually low cost with limited computing powers and storage capacities. Therefore, it is hard to complete compute-intensive and latency-sensitive tasks independently by the IoT devices. An intuitive method to alleviate this problem is to adopt the cloud computing technology for remote task computation. However, most of the clouding computing servers are deployed far away from the IoT devices, in which offloading the tasks of the IoT devices will cause severe transmission delay. Hence, traditional cloud computing technology is difficult to satisfy the latency requirements of applications in smart cities. To solve the issue mentioned above, researchers have proposed the concept of mobile edge computing (MEC).

In MEC systems, MEC servers are deployed at the edge of network to provide cloud-like computing services for the IoT devices [4,5]. IoT devices offload their compute-intensive tasks to the MEC servers for task execution. Since MEC servers are deployed around the IoT devices, the latency for task offloading is significantly reduced compared with the cloud computing. Hence, MEC has been considered as a promising solution to provide ultra-latency computation service for smart cities [1,2,3].

There have been a lot of works focused on the researches of the resource allocation and caching problems in MEC systems in IoT or IoT related areas. A multi-user MEC network consisting of a MEC server and multiple wireless devices was considered in [6]. The weighted sum computation rate of all the wireless devices maximization problem was studied. The computing mode and the system resource allocation were jointly optimized by a proposed alternating direction method of multipliers decomposition technique-based algorithm. In [7], a MEC system with a multiple antenna access point (AP) and K single antenna users was studied. The beamforming vector of the AP, the CPU frequencies, the numbers of offloaded bits and the time allocation of the users were jointly optimized to minimize the energy consumption of the AP. A device-to-device (D2D)-MEC system including one MEC server and multiple user devices was considered in [8]. The goal of this paper was to maximize the number of devices serviced by the system under the communication and computation resources constraints. Unlike the cloud computing, the MEC server has limited computing power. Hence, in single base station (BS) or MEC server scenarios, the IoT devices may have the problem of long service response time and even failure during periods of peak demand. The authors in [9] studied a heterogeneous network consisting of a multi-antenna macro-cell BS and multiple small-cells BSs. The offloading decision, offloading and computation resources allocation were optimized to minimize the total energy consumption of the devices within the coverage of the BSs. In [10], a dense small-cell network was concerned, which had multiple MEC servers. The spatial demand coupling, service heterogeneity, and decentralized coordination problems were solved by a proposed collaborative service placement algorithm. In [11], the weighted sum of the difference of the observed delay and its corresponding delay requirement at each slice was minimized through optimizing the offloading decisions of the users and the communication and computing resource allocation in a multi-cell MEC server network.

The above works focused on the MEC problems in static environment, which is a particular case of dynamic environment. In dynamic environment, the MEC system state changes randomly and unpredictable, which is more approximate to the practical scenarios. In static environment, the MEC systems mainly concern about the short-term utility, while in dynamic environment, the long-term utility are concerned. Edge intelligence empowered by artificial intelligence (AI) is promising way to optimize the system performance in the field of the smart city IoT [12,13,14]. In [15], the power control and computing resource allocation optimization problem in Industrial Internet of Things MEC network was studied, a deep reinforcement learning (DRL)-based dynamic resource management algorithm was proposed to minimize the long-term average delay of the tasks. In [16], a content caching problem was investigated, and an actor-critic DRL-based algorithm was studied to maximize the cache bit rate. In [17], the task migration problem was studied in multi-MEC server and multi-user network, a multi-agent DRL task migration algorithm was proposed to solve the formulated problem. In [18], a multi-user end-edge-cloud orchestrated network was proposed and a DRL-based computation offloading and resource allocation strategy was designed to minimize the energy consumption of the system.

In practical scenarios, there are many metrics to measure the performance of a MEC system, hence, the system requirements are always multifaceted. The works mentioned above mainly considered single-objective optimization scenarios, which may be not generalized and universal for some practical MEC systems. Motivated by these facts, we propose a multi-MEC server and multi-IoT device cellular network structure and investigate a weighted sum of multiple objectives minimization optimization problem in this paper. The weighted sum of multiple objectives optimization problems in dynamic MEC systems were also studied in [19,20,21], but the optimization objectives and system models are different to ours. The key differences between the relevant works and our work are shown in Table 1. The main contributions of this paper are summarized as follows:

Table 1. Comparison of relevant works.

Work	Objective	Method	Environments
Our work	Weighted sum of computing pressure on the PMS, energy consumption, and task dropping cost	DRL	Dynamic
[6]	Computation rate of the wireless devices	Convex optimization	Static
[7]	Energy consumption of the AP	Convex optimization	Static
[8]	Number of serviced devices	Convex optimization	Static
[9]	Total energy consumption of the devices	Convex optimization	Static
[10]	System utility	Game theory	Static
[11]	Latency	Convex optimization	Static
[15]	Long-term average delay of the tasks	DRL	Dynamic
[16]	Cache bit rate	DRL	Dynamic
[17]	Average completion time of tasks	DRL	Dynamic
[18]	Energy consumption of the system	DRL	Dynamic

(1)

A multi-MEC server and multi-IoT device cellular network structure is proposed. A high-cost and high-performance primary MEC server (PMS) with relative strong computing power is deployed in the BS, and multiple low-cost secondary MEC servers (SMSs) with relative weak computing powers are deployed within the coverage area of the BS.

(2)

An optimization problem is formulated. The problem considers the weighted sum of multiple optimization objectives, including the minimization of the weighted sum of the computing pressure on the PMS, the sum of energy consumption of the network, and the task dropping cost. The formulated problem is a nonconvex mixed integer nonlinear program (MINLP) problem, which is solved by our proposed DRL-based optimization algorithm.

(3)

Simulation results are presented to evaluate the performance of the proposed algorithm. The correctness and effectiveness of the proposed algorithm are demonstrated by the simulation results.

The remainder of this paper is organized as follows. Section 2 presents the system model and formulates the optimization problem. The proposed DRL-based optimization algorithm is described in Section 3. The complexity and convergence analysis is given in Section 4. Simulation results are provided in Section 5. Finally, Section 6 concludes this paper.

2. System Model

In this section, we first introduce the proposed multi-MEC server and multi-IoT device cellular network, the channel model, and the computation model, respectively. Then, based on these we establish the optimization problem of our paper.

2.1. Network and Channel Model

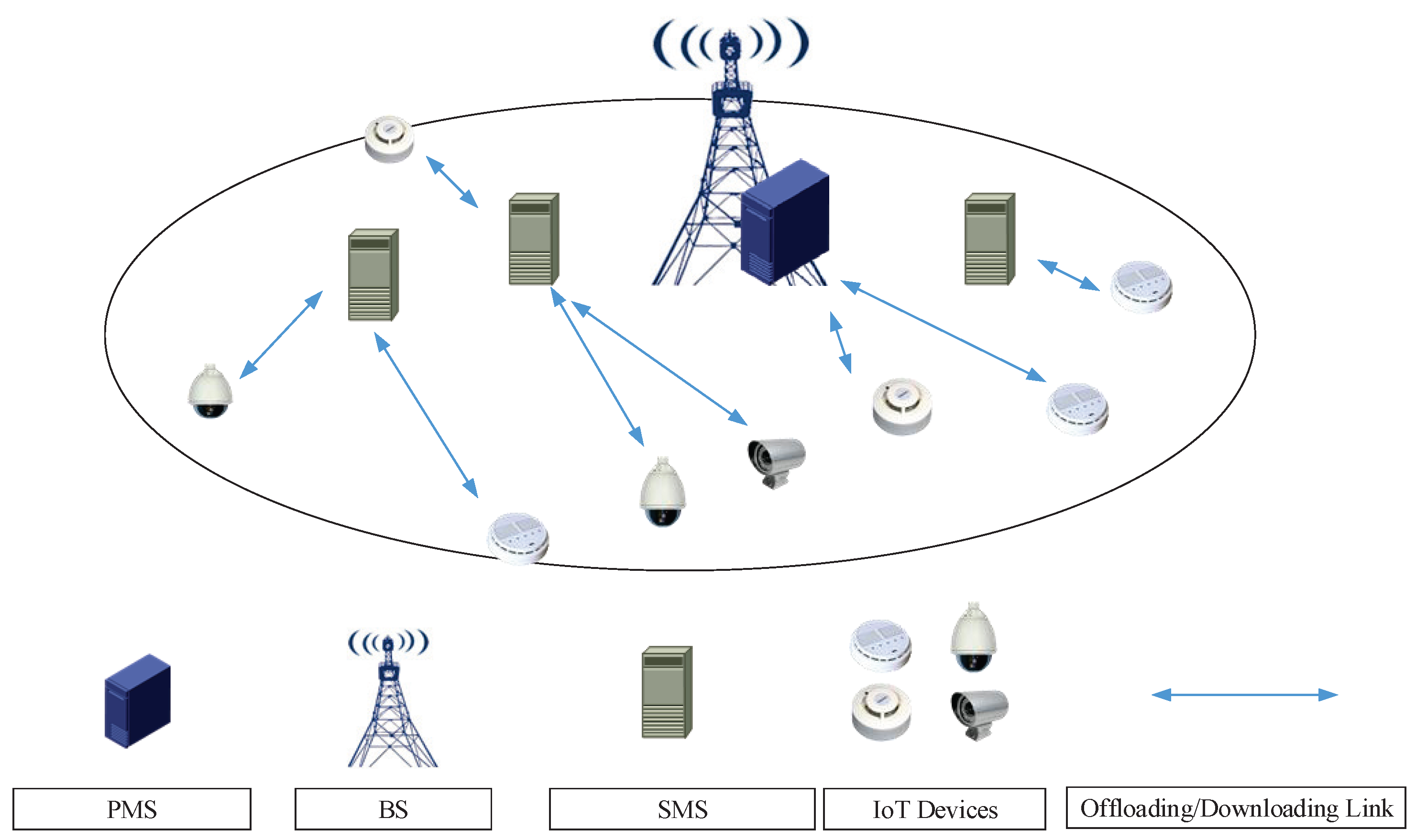
As shown in Figure 1, a multi-MEC server and multi-IoT device cellular network is considered, which consists of a high-performance PMS, M SMSs with relative weak computing powers, and K IoT devices. The computing power of the PMS is much stronger than the SMSs. The PMS is deployed at the BS, and the SMSs are deployed in the APs, which are distributed in different locations within the coverage area of the BS. A specific scenario of this network is a UAV-assisted MEC system, in which the PMS is the BS and the SMSs can be the UAVs equipped with limited computing power MEC servers. To avoid repetition, the notations used below do not distinguish between PMS and BS, the SMS and the AP. We assume each SMS’s cost is low and can be easily deployed and removed according to the requirements of the MEC system. Let $\mathcal{M}=\left\{0,1,2,\dots ,M\right\}$ denote the set of the MEC servers, where 0 denotes the PMS and others denote the SMSs. Let $\mathcal{K}=\left\{1,2,\dots ,K\right\}$ denote the set of the IoT devices. We assume that all of the IoT devices and MEC servers are equipped with one single antenna. By adopting multi-antenna technologies, our work can be extended to multi-antenna scenarios [7,9,22,23].

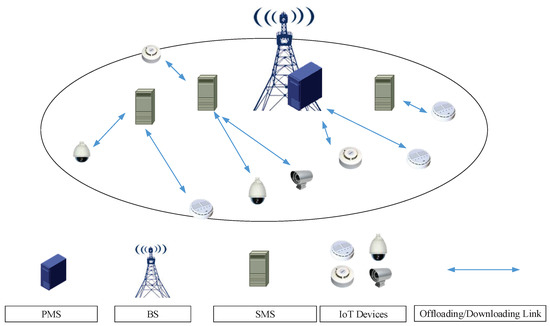
Figure 1. The illustration of the multi-MEC server cellular network.

It is assumed that the system is operated in a time-slotted manner with time-slot length $\Delta$. In this paper, we concern about the long-term return during T consecutive time-slots. The set of the time-slots is denoted as $\mathcal{T}=\left\{1,2,\dots ,T\right\}$. Let $h_{k,m,t}$ denote the channel power gain between the IoT device k and the MEC server m at time-slot t. Similar to [7,24], we assume that the wireless channels between the IoT devices and the MEC servers remain unchanged at each time-slot and vary at different time-slots. Motivated by the works in [25,26], we adopt a $Z_k$-element channel power gain state set to capture the time-varying characteristics of the $h_{k,m,t}$, denoted as ${\mathcal{H}}_{k,m}=\left\{h_{1,m}^{\left(k\right)},h_{2,m}^{\left(k\right)},\dots ,h_{Z_k,m}^{\left(k\right)}\right\}$, i.e., $h_{k,m,t}\in H_{k,m}$.

2.2. Computation Task Model

At time-slot t, the computation task of the IoT device k is denoted as ${\beta }_{k,t}$, which is defined by a tuple $\left(l_{k,t},c_{k,t},{\tau }_{k,t}\right)$, where $l{}_{k,t}$ denotes the size (in bits) of the task ${\beta }_{k,t}$, $c_{k,t}$ denotes the number of required CPU cycles for computing 1-bit of the task ${\beta }_{k,t}$ (i.e. the computational complexity), and ${\tau }_{k,t}$ is the latency requirement of the task ${\beta }_{k,t}$. Similar to the assumption in [27], we assume that at the beginning of each time-slot t, each IoT device k has a new task arrival, $l{}_{k,t}$ is randomly generated from the set ${\mathcal{L}}_k=\left\{L_1^{\left(k\right)},L_2^{\left(k\right)},\dots ,L_{N_k}^{\left(k\right)}\right\}$, and the corresponding computational complexity $c_{k,t}$ belongs the set of complexity ${\mathcal{C}}_k=\left\{C_1^{\left(k\right)},C_2^{\left(k\right)},\dots ,C_{N_k}^{\left(k\right)}\right\}$. For simplicity, the latency requirement for each task is set to ${\tau }_{k,t}=\Delta ,\forall k\in \mathcal{K},t\in \mathcal{T}$.

To facilitate the resource management, a virtual system operator (VSO) is deployed at the BS, which is responsible for collecting the network information (e.g., the channel state information, size of the each IoT device’s task, each IoT device’s task computational complexity, etc.) and allocating computation resources for the IoT devices. As the computing powers of the IoT devices are always weak, we assume that the tasks of each IoT device must be entirely offloaded to a certain MEC server for computation through wireless link. The task offloading decision variable of the IoT device k is denoted as ${\mu }_{k,m,t}\in \left\{0,1\right\}$, where ${\mu }_{k,m,t}=1$ denotes the IoT device k’s computation task is offloaded to the MEC server m for execution at time-slot t.

Let ${\tau }_{k,m,t}$ denote the time duration of task offloading from the IoT device k to the MEC server m at time-slot t. The offloaded task is processed by the MEC server m in remaining time duration $\Delta -{\tau }_{k,m,t}$. The rate of task data offloaded by the IoT device k to the MEC server m at time-slot t can be expressed as

$$\begin{array}{c}\hfill R_{k,m}\left[t\right]=B_{k,m}{log}_2\left(1+\frac{h_{k,m,t}{p}_{k,m,t}}{{\sigma }_m^2}\right),k\in \mathcal{K},m\in \mathcal{M},t\in \mathcal{T}\end{array}$$

(1)

where $B_{k,m}$ denotes the available channel bandwidth between the IoT device k and the MEC server m; $p_{k,m,t}$ denotes the transmit power of the IoT device k at the time-slot t, ${\sigma }_m^2$ is the noise power at the MEC server m. The energy consumption of the IoT device k at time-slot t for task offloading is expressed as

$$\begin{array}{c}\hfill E_{m,k}^o\left[t\right]=p_{k,m,t}{\tau }_{k,m,t},k\in \mathcal{K},m\in \mathcal{M},t\in \mathcal{T}\end{array}$$

(2)

The corresponding computation energy consumption of the MEC server m can be expressed as

$$\begin{array}{c}\hfill E_{m,k}^c\left[t\right]={\rho }_m{f}_{m,k,t}^3\left(\Delta -{\tau }_{k,m,t}\right),k\in \mathcal{K},m\in \mathcal{M},t\in \mathcal{T}\end{array}$$

(3)

where $f_{m,k,t}$ denotes the CPU frequency of the MEC server m allocated to the IoT device k’s task at time-slot t; ${\rho }_m$ is the effective capacitance coefficient of the MEC server m at time-slot t, which is determined by the chip architecture [6,7].

2.3. Problem Formulation

If the computing pressure of the PMS is too high, i.e., if the VSO allocates too many tasks to the PMS, the PMS may have higher probability for crashing. As the PMS has much stronger computing power than the SMSs, the crashing of the PMS has serious impact on the reliability of the MEC system. Meanwhile, the energy consumption and the task completion rate are also very important to the MEC system. Therefore, in this paper, we aim to minimize the weighted sum of the computing pressure of the PMS, the sum energy consumption of the MEC servers and the IoT devices, and the task dropping cost. The corresponding optimization problem is formulated as

$$\begin{array}{c}{\mathrm{P}}_1:\underset{\left\{{\mu }_{k,m,t}\right\},\left\{{\tau }_{k,m,t}\right\},\left\{f_{m,k,t}\right\},\left\{p_{k,m,t}\right\}}{min}E\left[\sum _{t=1}^T{\gamma }^{t-1}\left\{{\omega }_0{\psi }_0\sum _{k=1}^K{\mu }_{k,0,t}\right.\right.\hfill \\ \left.\left.+{\omega }_1\left[{\psi }_1\sum _{m=0}^M\sum _{k=1}^K{\mu }_{k,m,t}\left(E_{m,k}^0\left[t\right]+E_{m,k}^c\left[t\right]\right)+{\psi }_2\sum _{\mathrm{m}=0}^M\sum _{k=1}^K{\mu }_{k,m,t}{\Gamma }_{k,t}{I}_{k,t}\left({\beta }_{k,t}\right)\right]\right\}\right]\hfill \end{array}$$

(4a)

$$\begin{array}{cc}\hfill & s.t.\sum _{m=1}^M{\mu }_{k,m,t}=1,{\mu }_{k,m,t}\in \left\{0,1\right\},k\in \mathcal{K},m\in \mathcal{M},t\in \mathcal{T},\hfill \end{array}$$

(4b)

$$\begin{array}{cc}\hfill & {\tau }_{k,m,t}{R}_{k,m}\left[t\right]\ge {\mu }_{k,m,t}{l}_{k,t},k\in \mathcal{K},m\in \mathcal{M},t\in \mathcal{T},\hfill \end{array}$$

(4c)

$$\begin{array}{cc}\hfill & \frac{{\mu }_{k,m,t}{l}_{k,t}{c}_{k,t}}{f_{m,k,t}}\le \Delta -{\tau }_{k,m,t},k\in \mathcal{K},m\in \mathcal{M},t\in \mathcal{T},\hfill \end{array}$$

(4d)

$$\begin{array}{cc}\hfill & p_{k,m,t}\ge 0,p_{k,m,t}\le p_{k,max},k\in \mathcal{K},m\in \mathcal{M},t\in \mathcal{T},\hfill \end{array}$$

(4e)

$$\begin{array}{cc}\hfill & f_{m,k,t}\ge 0,f_{m,k,t}\le \frac{f_{m,max}}{{\displaystyle \sum _{k=1}^K}{\mu }_{k,m,t}},k\in \mathcal{K},m\in \mathcal{M},t\in \mathcal{T}\hfill \end{array}$$

(4f)

$$\begin{array}{cc}\hfill & 0\le {\tau }_{k,m,t}\le \Delta ,k\in \mathcal{K},m\in \mathcal{M},t\in \mathcal{T},\hfill \end{array}$$

(4g)

$$\begin{array}{cc}\hfill & {\omega }_i\in \left\{0,1\right\},i=0,1,k\in \mathcal{K},m\in \mathcal{M},t\in \mathcal{T},\hfill \end{array}$$

(4h)

where the first term of the objective function represents the computing pressure of the PMS, the second term represents the sum of energy consumption of the network and the task dropping cost; ${\omega }_0$ and ${\omega }_1$ are the weights of the two terms above, respectively; ${\omega }_i=0,i=0,1$ means the corresponding objective is not considered; ${\omega }_i=1,i=0,1$ means the corresponding objective is considered; ${\psi }_i>0,i=0,1,2$ is the normalization factors to normalize each term. $\gamma \in \left[0,1\right]$ is the discount factor, which denotes the difference on importance between the future rewards and the present reward [28]; $p_{k,max}$ and $f_{m,max}$ denote the maximal transmit power of the IoT device k and the maximal available CPU frequency of the MEC server m, respectively. ${\Gamma }_{k,t}>0$ is task dropping cost of the IoT device k at time-slot t. $I_{k,t}$ is the indicator function, which is given as

$$\begin{array}{c}\hfill I_{k,t}=\left\{\begin{array}{c}0,{\beta }_{k,t}\mathrm{is}\mathrm{completed}\hfill \\ 1,{\beta }_{k,t}\mathrm{is}\mathrm{dropped}.\hfill \end{array}\right.\end{array}$$

(5)

(4b) is the offloading decision variable constraint, which guarantees each IoT device’s task has been allocated to a MEC server. (4c) and (4d) are the IoT devices’ computation tasks constraints to make sure that each IoT device’s task can be offloaded and completed. (4e) is the transmit power constraint of the IoT devices. (4f) is the CPU frequency constraint, we assume that IoT devices equally share the CPU at the MEC server m, $m\in \mathcal{M}$. (4g) and (4h) are the constraints of task offloading time and weights, respectively.

Due to the binary variable ${\mu }_{k,m,t}$ and high coupling constraints, problem ${\mathrm{P}}_1$ is a non-convex MINLP problem. Furthermore, the computation tasks of the IoT devices and the channel gains are randomly varying during T consecutive time-slots. Hence, it is impossible to solve the problem at the beginning of the T consecutive time-slots. Thus, traditional optimization-based methods are not suitable to solve the problem ${\mathrm{P}}_1$.

3. Proposed DRL-Based Optimization Algorithm

In order to address the above issue, we propose a DRL-based optimization algorithm in this section. Specifically, we utilize the importance sampling based parameterized policy gradient approach (PPGA) DRL algorithm [28]. In order to apply the DRL-based algorithm, we first give the system state, action, reward, and the policy of the MEC system as follows:

(1) System state $\mathbf{S}\left(t\right)$: The system state at time-slot t is characterized by the channel power gain, the size (in bits) of computation task data, and the corresponding task complexity, i.e., $\mathbf{S}\left(t\right)=\left\{\left(h_{k,m,t},l_{k,t},c_{k,t}\right),k\in \mathcal{K},m\in \mathcal{M},t\in \mathcal{T}\right\}$.

(2) Action $\mathbf{A}\left(t\right)$:$\mathbf{A}\left(t\right)$ is the set of the offloading decisions of the IoT devices, i.e., $\mathbf{A}\left(t\right)=\left\{{\mu }_{k,m,t},k\in \mathcal{K},m\in \mathcal{M},t\in \mathcal{T}\right\}$.

(3) Reward $R\left(t\right)$: After executing an action $\mathbf{A}\left(t\right)$ under system state $\mathbf{S}\left(t\right)$ at time-slot t, the VSO will receive a reward $R\left(t\right)$. The reward of a DRL model is direct related with the optimization objective of the system. Therefore, the reward of our DRL model is determined by the objective function value of the problem ${\mathrm{P}}_1$ at time-slot t. With given $\left\{{\mu }_{k,m,t},k\in \mathcal{K},m\in \mathcal{M},t\in \mathcal{T}\right\}$ ($\mathbf{A}\left(t\right)$), the optimization problem for reward $R\left(t\right)$ are given as

$$\begin{array}{cc}\hfill & {\mathrm{P}}_2:-R\left(t\right)=\hfill \\ & \underset{\left\{{\tau }_{k,m,t}\right\},\left\{f_{m,k,t}\right\},\left\{p_{k,m,t}\right\}}{min}{\gamma }^{t-1}\left\{{\omega }_0{\psi }_0\sum _{k=1}^K{\mu }_{k,0,t}\right.\hfill \\ & \left.+{\omega }_1\left[{\psi }_1\sum _{m=0}^M\sum _{k=1}^K{\mu }_{k,m,t}\left(E_{m,k}^0\left[t\right]+E_{m,k}^c\left[t\right]\right)+{\psi }_2\sum _{\mathrm{m}=0}^M\sum _{k=1}^K{\mu }_{k,m,t}{\Gamma }_{k,t}{I}_{k,t}\left({\beta }_{k,t}\right)\right]\right\}\hfill \end{array}$$

(6a)

$$\begin{array}{cc}\hfill & s.t.\left(4\mathrm{b}\right)-\left(4\mathrm{h}\right).\hfill \end{array}$$

(6b)

The standard form of the DRL-based optimization problem is to maximize the accumulated reward, hence, we add a minus sign before the $R\left(t\right)$. Obviously, when $\left\{{\mu }_{k,m,t},k\in \mathcal{K},m\in \mathcal{M},t\in \mathcal{T}\right\}$ are determined, the computing pressure of the PMS is determined too. Therefore, solving the problem ${\mathrm{P}}_2$ is equal to solve the problem ${\mathrm{P}}_3$ below

$$\begin{array}{cc}\hfill {\mathrm{P}}_3:& \underset{\left\{{\tau }_{k,m,t}\right\},\left\{f_{m,k,t}\right\},\left\{p_{k,m,t}\right\}}{min}\hfill \end{array}$$

$$\begin{array}{cc}& {\omega }_1\left[{\psi }_1\sum _{m=0}^M\sum _{k=1}^K{\mu }_{k,m,t}\left(E_{m,k}^0\left[t\right]+E_{m,k}^c\left[t\right]\right)+{\psi }_2\sum _{\mathrm{m}=0}^M\sum _{k=1}^K{\mu }_{k,m,t}{\Gamma }_{k,t}{I}_{k,t}\left({\beta }_{k,t}\right)\right.\hfill \end{array}$$

(7a)

$$\begin{array}{cc}\hfill & s.t.\left(4\mathrm{c}\right)-\left(4\mathrm{g}\right).\hfill \end{array}$$

(7b)

Based on the primal decomposition theory [29], the problem ${\mathrm{P}}_3$ can be decomposed into K sub-optimization problems. Specifically, for the IoT device k and the MEC server m, $k,m\in \left\{\left.k,m\right|{\mu }_{k,m,t}=1\right\}$, the corresponding sub-optimization problem can be expressed as

$$\begin{array}{cc}\hfill & {\mathrm{P}}_{3,km}:\underset{\left\{{\tau }_{k,m,t}\right\},\left\{f_{m,k,t}\right\},\left\{p_{k,m,t}\right\}}{min}{\psi }_1\left[E_{m,k}^0\left[t\right]+E_{m,k}^c\left[t\right]\right]+{\psi }_2{\Gamma }_{k,t}{I}_{k,t}\left({\beta }_{k,t}\right)\hfill \end{array}$$

(8a)

$$\begin{array}{cc}\hfill & s.t.\left(4\mathrm{c}\right)-\left(4\mathrm{g}\right).\hfill \end{array}$$

(8b)

If the problem ${\mathrm{P}}_{3,km}$ is solvable, i.e., there exist feasible solutions of ${\tau }_{k,m,t}$, $f_{m,k,t}$, and $p_{k,m,t}$ to meet the constraints (4c)–(4g). The optimal value of ${\mathrm{P}}_{3,km}$ is equal to the optimal objective value of ${\psi }_1\left[E_{m,k}^0\left[t\right]+E_{m,k}^c\left[t\right]\right]$. On the other hand, if there exist no feasible solutions of ${\tau }_{k,m,t}$, $f_{m,k,t}$, and $p_{k,m,t}$, we let the objective value of ${\mathrm{P}}_{3,km}$ be equal to ${\Gamma }_{k,t}$. It is worth noting that, if not all the IoT devices’ tasks can be completed, our work can not be applied to minimize the sum of energy consumption of the system. According to ${\mathrm{P}}_{3,km}$, if we set ${\psi }_2=0$, the optimal solutions for ${\mu }_{k,m,t}$ is to set ${\mu }_{k,m,t}=0,k\in K,m\in M,t\in T$, which are pointless solutions. Hence, the conditions ${\psi }_1>0$ and ${\psi }_2>0$ must be satisfied simultaneously when ${\omega }_1=1$. If the problem ${\mathrm{P}}_{3,km}$ has feasible solutions, the problem ${\mathrm{P}}_{3,km}$ is transformed into ${\mathrm{P}}_{4,km}$, which is given as

$$\begin{array}{cc}\hfill & {\mathrm{P}}_{4,km}:\underset{\left\{{\tau }_{k,m,t}\right\},\left\{f_{m,k,t}\right\},\left\{p_{k,m,t}\right\}}{min}\left[E_{m,k}^0\left[t\right]+E_{m,k}^c\left[t\right]\right]\hfill \end{array}$$

(9a)

$$\begin{array}{cc}\hfill & s.t.\left(4\mathrm{c}\right)-\left(4\mathrm{g}\right).\hfill \end{array}$$

(9b)

Problem ${\mathrm{P}}_{4,km}$ is still non-convex and intractable due to the complex coupling among the variables ${\tau }_{k,m,t}$, $f_{m,k,t}$, and $p_{k,m,t}$. To address this issue, we adopt block coordinate descending (BCD) algorithm to optimize ${\tau }_{k,m,t}$, $f_{k,m,t}$, and $p_{k,m,t}$ alternately. For any given feasible ${\tau }_{k,m,t}$, the optimization problem ${\mathrm{P}}_{4,km}$ is transformed into ${\mathrm{P}}_{5,km}$, which is given as

$$\begin{array}{cc}\hfill & {\mathrm{P}}_{5,km}:\underset{f_{m,k,t},p_{k,m,t}}{min}{p}_{k,m,t}{\tau }_{k,m,t}+{\rho }_m{f}_{m,k,t}^3\left(\Delta -{\tau }_{k,m,t}\right)\hfill \end{array}$$

(10a)

$$\begin{array}{cc}\hfill & s.t.\left(4\mathrm{c}\right)-\left(4\mathrm{f}\right).\hfill \end{array}$$

(10b)

The above optimization problem can be further decomposed into the following two manageable sub-problems, namely,

$$\begin{array}{cc}\hfill & {\mathrm{P}}_{5,km,1}:\underset{p_{k,m,t}}{min}{p}_{k,m,t}{\tau }_{k,m,t}\hfill \end{array}$$

(11a)

$$\begin{array}{cc}\hfill & s.t.\left(4\mathrm{c}\right),\left(4\mathrm{e}\right).\hfill \end{array}$$

(11b)

$$\begin{array}{cc}\hfill & {\mathrm{P}}_{5,km,2}:\underset{f_{m,k,t}}{min}{\rho }_m{f}_{m,k,t}^3\left(\Delta -{\tau }_{k,m,t}\right)\hfill \end{array}$$

(12a)

$$\begin{array}{cc}\hfill & s.t.\left(4\mathrm{d}\right),\left(4\mathrm{f}\right),\hfill \end{array}$$

(12b)

Theorem 1.

For a given ${\tau }_{k,m,t}$, the optimal $p_{k,m,t}$ and $f_{k,m,t}$ can be given as

$$\begin{array}{cc}\hfill & f_{m,k,t}^{*}=\frac{{\mu }_{k,m,t}{l}_{k,t}{c}_{k,t}}{\Delta -{\tau }_{k,m,t}},\hfill \end{array}$$

(13a)

$$\begin{array}{cc}\hfill & p_{k,m,t}^{*}=\frac{{\sigma }_m^2}{h_{k,m,t}}{2}^{\frac{{\mu }_{k,m,t}{l}_{k,t}}{{\tau }_{k,m,t}{B}_{k,m}}}-\frac{{\sigma }_m^2}{h_{k,m,t}},\hfill \end{array}$$

(13b)

respectively.

Proof. 

It is easy to prove that problem ${\mathrm{P}}_{5,km,1}$ and ${\mathrm{P}}_{5,km,2}$ are both convex optimization problem and can be efficiently solved by using the Karush-Kuhn-Tucker (KKT) conditions [30]. □

Substituting the above results into ${\mathrm{P}}_{5,km}$, we have

$$\begin{array}{cc}\hfill & {\mathrm{P}}_{6,km}:\underset{{\tau }_{m.k,t}}{min}\frac{{\sigma }_m^2}{h_{k,m,t}}{\tau }_{k,m,t}{2}^{\frac{{\mu }_{k,m,t}{l}_{k,t}}{{\tau }_{k,m,t}{B}_{k,m}}}+{\rho }_m\frac{{\left({\mu }_{k,m}{l}_{k,t}{c}_{k,t}\right)}^3}{{\left(\Delta -{\tau }_{k,m,t}\right)}^2}-\frac{{\sigma }_m^2}{h_{k,m}}{\tau }_{k,m,t}\hfill \end{array}$$

(14a)

$$\begin{array}{cc}\hfill & s.t.{\tau }_{k,m,t}^{min}\le {\tau }_{k,m,t}\le {\tau }_{k,m,t}^{max},\hfill \end{array}$$

(14b)

where

$$\begin{array}{cc}\hfill & {\tau }_{k,m,t}^{min}=\frac{{\mu }_{k,m,t}{l}_{k,t}}{B_{k,m}{log}_2\left(1+\frac{h_{k,m,t}{p}_{k,max}}{{\sigma }^2}\right)},\hfill \end{array}$$

(15a)

$$\begin{array}{cc}\hfill & {\tau }_{k,m,t}^{max}=\Delta -{\mu }_{k,m,t}{l}_{k,t}{c}_{k,t}\frac{{\displaystyle \sum _{k=1}^M}{\mu }_{k,m,t}}{f_{m,max}}.\hfill \end{array}$$

(15b)

According to Theorem 1, the optimal solution of the problem ${\mathrm{P}}_{5,km}$ have closed-form optimal solutions, which are determined by the value of ${\tau }_{m.k,t}$. Therefore, if ${\tau }_{k,m,t}^{min}\le {\tau }_{k,m,t}^{max}$, solving the problem ${\mathrm{P}}_{4,km}$ is equivalent to solving the problem ${\mathrm{P}}_{6,km}$, which has one optimization variable ${\tau }_{m.k,t}$. If ${\tau }_{k,m,t}^{min}>{\tau }_{k,m,t}^{max}$, the problem ${\mathrm{P}}_{6,km}$ is unsolvable.

Theorem 2.

The optimization problem ${\mathrm{P}}_{6,km}$ is convex.

Proof. 

See Appendix A. □

Based on the convexity illustrated in Theorem 2, we can adopt the bisection method to solve the problem ${\mathrm{P}}_{6,km}$. The bisection based optimization algorithm for solving problem ${\mathrm{P}}_{6,km}$ is summarized in Algorithm 1, where $g\left({\tau }_{k,m,t}\right)$ denote the objective function of ${\mathrm{P}}_{6,km}$.

(4) Policy ${\pi }_{\mathit{\theta }}\left[\mathbf{A}\left(t\right)\left|\mathbf{S}\left(t\right)\right.\right]$: The policy ${\pi }_{\mathit{\theta }}\left[\mathbf{A}\left(t\right)\left|\mathbf{S}\left(t\right)\right.\right]$ denotes the mapping from the state $\mathbf{S}\left(t\right)$ to the action $\mathbf{A}\left(t\right)$ of the MEC system, i.e., ${\pi }_{\mathit{\theta }}\left[\mathbf{A}\left(t\right)\left|\mathbf{S}\left(t\right)\right.\right]:\mathbf{S}\left(t\right)\to \mathbf{A}\left(t\right)$, where $\mathit{\theta }$ is the parameter of the policy.

The parameter of the policy ${\pi }_{\mathit{\theta }}\left[\mathbf{A}\left(t\right)\left|\mathbf{S}\left(t\right)\right.\right]$ is obtained through gradient based method. The performance measure $Y\left(\mathit{\theta }\right)$ of the PPGA is defined as [28]

$$\begin{array}{c}\hfill Y\left(\mathit{\theta }\right)=V_{{\pi }_{\mathit{\theta }}\left[\mathbf{A}\left(t\right)\left|\mathbf{S}\left(t\right)\right.\right]}\left[\mathbf{S}\left(0\right)\right]\end{array}$$

(16)

where $V_{{\pi }_{\mathit{\theta }}}\left[\mathbf{S}\left(0\right)\right]$ is the value function for policy ${\pi }_{\mathit{\theta }}$ starting from initial state $\mathbf{S}\left(0\right)$ and $\mathit{\theta }$ is the parameter of the policy. An analytic expression for the gradient of $Y\left(\mathit{\theta }\right)$ is provided by policy gradient theorem [28], which is given as

$$\begin{array}{cc}\hfill \nabla Y\left(\mathit{\theta }\right)& \propto \sum _{\mathbf{S}\left(t\right)}\mu \left[\mathbf{S}\left(t\right)\right]\sum _{\mathbf{A}\left(t\right)}{q}_{{\pi }_{\mathit{\theta }}\left[\mathbf{A}\left(t\right)\left|\mathbf{S}\left(t\right)\right.\right]}\left[\mathbf{S}\left(t\right),\mathbf{A}\left(t\right)\right]\nabla {\pi }_{\mathit{\theta }}\left[\mathbf{A}\left(t\right)\left|\mathbf{S}\left(t\right)\right.\right]\hfill \end{array}$$

(17)

where $\mu \left[\mathbf{S}\left(t\right)\right]$ is the on-policy distribution over states, $q_{{\pi }_{\mathit{\theta }}\left[\mathbf{A}\left(t\right)\left|\mathbf{S}\left(t\right)\right.\right]}\left[\mathbf{S}\left(t\right),\mathbf{A}\left(t\right)\right]$ is the value of taking action $\mathbf{A}\left(t\right)$ in state $\mathbf{S}\left(t\right)$ under policy ${\pi }_{\mathit{\theta }}\left[\mathbf{A}\left(t\right)\left|\mathbf{S}\left(t\right)\right.\right]$.

$\mathbf{Algorithm}\mathbf{1}$: A Bisection Algorithm for Solving ${\mathrm{P}}_{6,km}$

1: Initialization:

2:  The bisection algorithm iteration index $i=1$, maximum number

of iterations $I_{max}$, $\left[{\tau }_{k,m,t}^{min},{\tau }_{k,m,t}^{max}\right]$, $\forall k\in \mathcal{K},m\in \mathcal{M}$, the tolerance errors $\xi$.

3: for: $i=1$ : $I_{max}$

4:  Update $c=\frac{{\tau }_{k,m,t}^{min}+{\tau }_{k,m,t}^{max}}{2}$.

5:  if $g^{\prime }\left(c\right)=0$ then

6:   The optimal value of ${\tau }_{k,m,t}$ is ${\tau }_{k,m,t}^{\mathrm{opt}}=c$;

7:   break;

8:  end if

9:  if $g^{\prime }\left({\tau }_{k,m,t}^{min}\right)g^{\prime }\left(c\right)<0$ then

10:   Update ${\tau }_{k,m,t}^{max}=c$;

11: end if

12: if $g^{\prime }\left(c\right)g^{\prime }\left({\tau }_{k,m,t}^{max}\right)<0$ then

13:  Update ${\tau }_{k,m,t}^{min}=c$;

14: end if

15: if $\left|{\tau }_{k,m,t}^{max}-{\tau }_{k,m,t}^{min}\right|<\xi$ or $i==I_{max}$ then

16:   The optimal value of ${\tau }_{k,m,t}$ is ${\tau }_{k,m,t}^{\mathrm{opt}}=c$;

17: end if

18: end for

An action-independent baseline $b\left[\mathbf{S}\left(t\right)\right]$ is always introduced to decrease the variance in the training process. Then, the analytic expression for the policy gradient with baseline is denoted as

$$\begin{array}{cc}\hfill & \nabla Y\left(\mathit{\theta }\right)\propto \sum _{\mathbf{S}\left(t\right)}\mu \left[\mathbf{S}\left(t\right)\right]\sum _{\mathbf{A}\left(t\right)}\left[q_{{\pi }_{\mathit{\theta }}\left[\mathbf{A}\left(t\right)\left|\mathbf{S}\left(t\right)\right.\right]}\left[\mathbf{S}\left(t\right),\mathbf{A}\left(t\right)\right]-b\left[\mathbf{S}\left(t\right)\right]\right]\nabla {\pi }_{\mathit{\theta }}\left[\mathbf{A}\left(t\right)\left|\mathbf{S}\left(t\right)\right.\right].\hfill \end{array}$$

(18)

Off-policy method adopts an exploratory behavior policy $\psi \left[\mathbf{A}\left(t\right)\left|\mathbf{S}\left(t\right)\right.\right]$ to generate behavior, while the target policy ${\pi }_{\mathit{\theta }}\left[\mathbf{A}\left(t\right)\left|\mathbf{S}\left(t\right)\right.\right]$ learns about the behavior and finally become the optimal policy. Importance sampling technique is widely used by off-policy methods, which weights the returns by importance-sampling ratio [28]. The parameter $\mathit{\theta }$ is updated as

$$\begin{array}{c}\hfill {\mathit{\theta }}_{t+1}={\mathit{\theta }}_t+\alpha {\gamma }^t\frac{1}{\psi \left[\mathbf{A}\left(t\right)\left|\mathbf{S}\left(t\right)\right.\right]}\left(G-b\left[\mathbf{S}\left(t\right)\right]\right)\frac{\nabla {\pi }_{{\mathit{\theta }}_t}\left[\mathbf{A}\left(t\right)\left|\mathbf{S}\left(t\right)\right.\right]}{{\pi }_{{\mathit{\theta }}_t}\left[\mathbf{A}\left(t\right)\left|\mathbf{S}\left(t\right)\right.\right]}\end{array}$$

(19)

where $\alpha$ is the learning rate, G is the return following time-slot t, ${\mathit{\theta }}_t$ is the estimate of $\mathit{\theta }$ at time-slot t. We adopt the estimate of the state value $v\left[\mathbf{S}\left(t\right);\mathbf{w}\right]$ as the baseline, where $\mathbf{w}$ is the weight vector of the state value function. Then, the DRL-based algorithm is summarized in Algorithm 2.

$\mathbf{Algorithm}\mathbf{2}$: The proposed DRL-based algorithm.

1: Initialization:

2: $\mathit{\theta }$, $\mathbf{w}$, target policy ${\pi }_{\mathit{\theta }}\left[\mathbf{A}\left(t\right)\left|\mathbf{S}\left(t\right)\right.\right]$, behavior policy $\psi \left[\mathbf{A}\left(t\right)\left|\mathbf{S}\left(t\right)\right.\right]$

maximal number of iterations $K_{max}$, discount factor $\gamma$, the learning

rate of policy ${\alpha }_p>0$, the learning rate of the baseline ${\alpha }_b>0$;

3: for $k=1:K_{max}$:

4: Using $\psi \left[\mathbf{A}\left(t\right)\left|\mathbf{S}\left(t\right)\right.\right]$ and Algorithm 1 to generate trajectory

$\mathbf{S}\left(0\right),\mathbf{A}\left(0\right),R\left(1\right),\mathbf{S}\left(1\right)\dots \mathbf{S}\left(T-1\right),\mathbf{A}\left(T-1\right),R\left(T\right)$,

$\mathbf{S}\left(T\right)$ by action policy $\psi$;

5: for $t=T-1,T-2,\dots ,0$:

6:  Update G: $G\leftarrow \gamma G+R_{t+1}$;

7:  Update $\mathbf{w}$: $\mathbf{w}\leftarrow \mathbf{w}+{\alpha }_b\left[G-v\left[S\left(t\right);\mathbf{w}\right]\right]\nabla v\left[\mathbf{S}\left(t\right);\mathbf{w}\right]$;

8:  Update $\mathit{\theta }$ by (18) with $\alpha ={\alpha }_b$;

9: end for

10: end for

4. Complexity and Convergence Analysis

According to [31], the computation complexity of a training step for a full-connection deep neural network (DNN) is $O\left({\displaystyle \sum _{j=1}^J}N{r}_{j-1}N{r}_j\right)$, where J is number of the layers, $N{r}_j$ is the number of the neural in j-th layer. Considering Algorithm 1 and Algorithm 2, the total complexity of our proposed algorithm is $O\left(2TU{\displaystyle \sum _{j=1}^J}N{r}_{j-1}N{r}_j{I}_{max}\right)$, where U is total training episodes.

The convergence guarantee of the DRL algorithm is still an open issue [27], which are influenced by many factors, such as the setting of the hyperparameters and the initial value of the DNN parameters. The convergence performance of our proposed algorithm is shown in Section 5.

5. Simulation Results

In this section, simulation results are provided to evaluate the performance of the proposed DRL-based algorithm. We conduct the simulations through python 3.8 and Tensorflow 2.5.0. Fully-connected hidden layer with 10 neurons in both the baseline and policy networks are employed. The learning rates ${\alpha }_b$ and ${\alpha }_p$ are set as $8e^{-3}$ and $2e^{-3}$, respectively. The channel bandwidth between each IoT device and each MEC server is 200 KHz. The maximum CPU frequency of the SMS and the PMS are set as 1 GHz and 5 GHz, respectively. The length of time-slot $\Delta$ is set as 100 ms. ${\mathcal{H}}_{k,m}$ is set as $\left\{2\times {10}^{-6},4\times {10}^{-6},6\times {10}^{-6},8\times {10}^{-6}\right\},k\in \mathcal{K},m\in \mathcal{M}$. Without loss of generality, $c_{k,t},k\in \mathcal{K},m\in \mathcal{M},t\in \mathcal{T}$ are all set as 1000. ${\rho }_m$ is set as $1\times {10}^{-27}$. ${\mathcal{L}}_k$ is set as $\left\{1.5\times {10}^4,3\times {10}^4,4.5\times {10}^4,6\times {10}^4\right\}$ bits, $k\in \mathcal{K}$. T is set as 40.

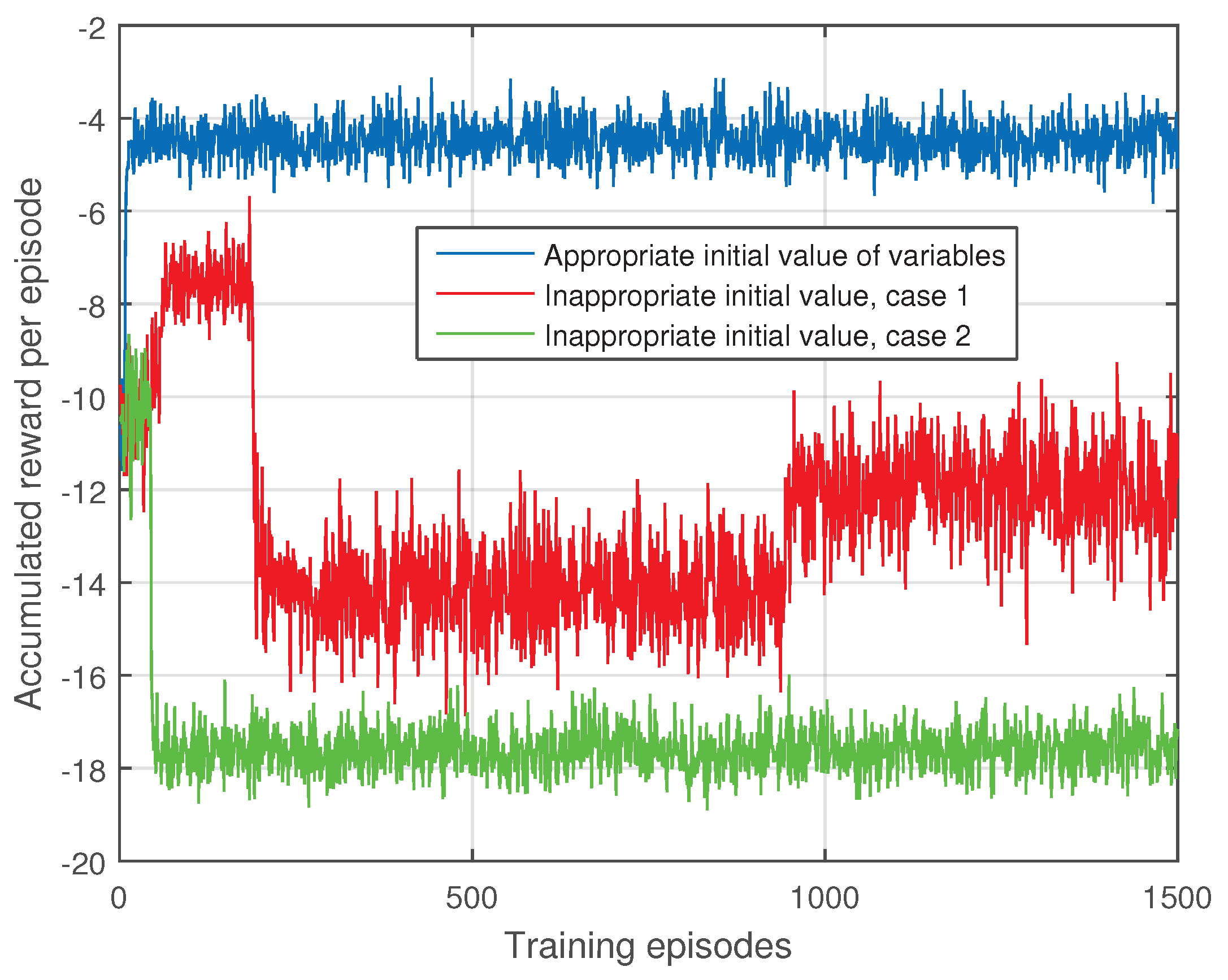
Figure 2 shows the impacts of the initial values of $\mathit{\theta }$ and $\mathbf{w}$ on the accumulated reward. The iterative algorithms are susceptible to the initial value of variables. In our paper, the initial value of $\mathit{\theta }$ and $\mathbf{w}$ are randomly given, which is a common way in DRL algorithms. It can be seen from Figure 2 that different initial values of $\mathit{\theta }$ and $\mathbf{w}$ have deep influences on the convergence performance of the our DRL based algorithm. In order to guarantee the performance of the algorithm, we must run the algorithm multiple times and select the one has best performance as the final output.

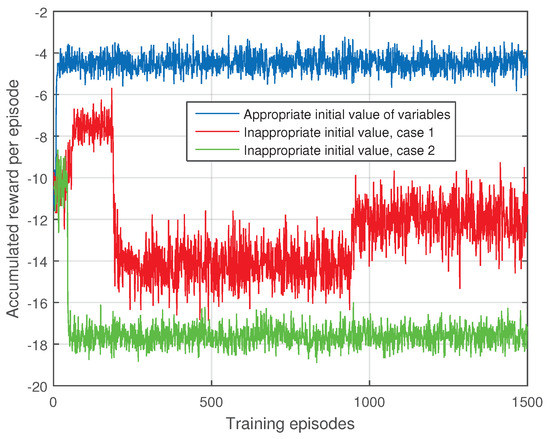
Figure 2. The impacts of the initial value of $\mathit{\theta }$ and $\mathbf{w}$ on the accumulated reward.

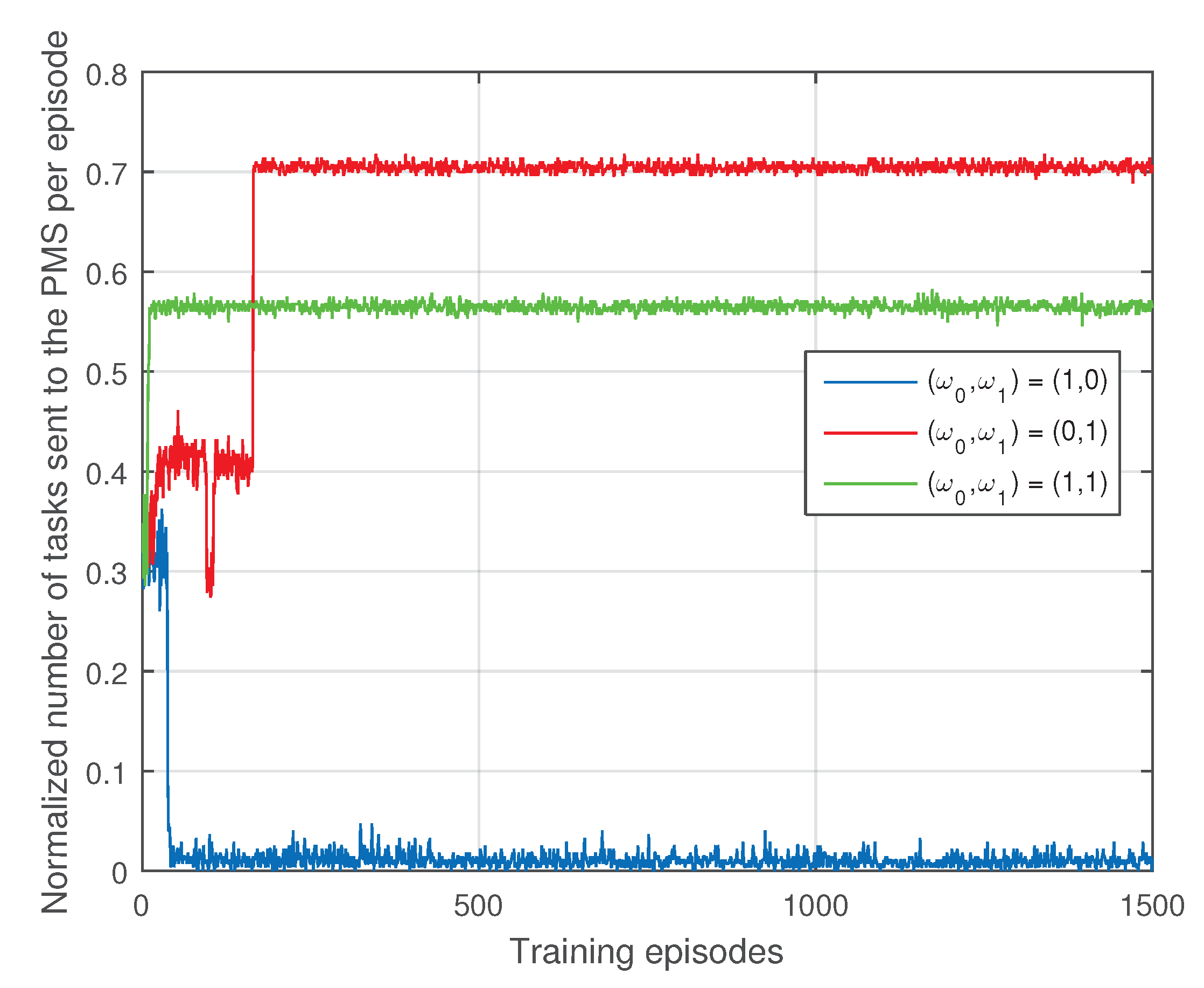
Figure 3 shows the impact of the weights on the normalized number of tasks sent to the PMS per episode. It can be seen from Figure 3 that the case $\left({\omega }_0,{\omega }_1\right)=\left(1,0\right)$ has the smallest number of tasks sent to the PMS. This is because the VSO only concerns the computing pressure of the PMS when $\left({\omega }_0,{\omega }_1\right)=\left(1,0\right)$. When $\left({\omega }_0,{\omega }_1\right)=\left(0,1\right)$, the VSO mainly tries to find a policy to minimize the number of dropped tasks, namely, to make the problem ${\mathrm{P}}_{3,km}$ solvable. As the PMS has strongest computing power, the VSO will allocate many tasks to the PMS, which can be proofed by Figure 3. Finally, when $\left({\omega }_0,{\omega }_1\right)=\left(1,1\right)$, the VSO must make a trade-off between the computing pressure on the PMS and the task dropping cost. Hence, when $\left({\omega }_0,{\omega }_1\right)=\left(1,1\right)$, the number of tasks sent to the PMS per episode is higher than the case $\left({\omega }_0,{\omega }_1\right)=\left(1,0\right)$ but smaller than the case $\left({\omega }_0,{\omega }_1\right)=\left(0,1\right)$.

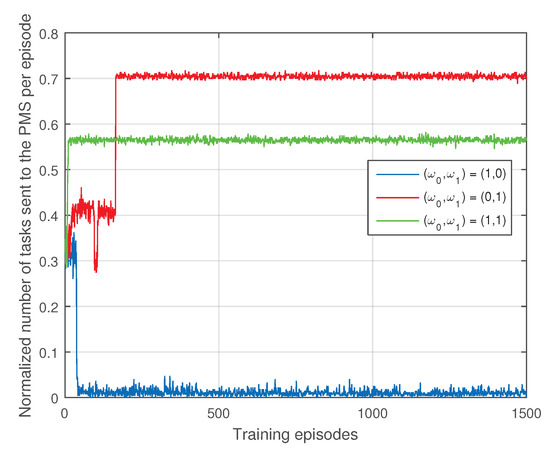
Figure 3. The impact of the weights on the normalized number of tasks sent to the PMS per episode.

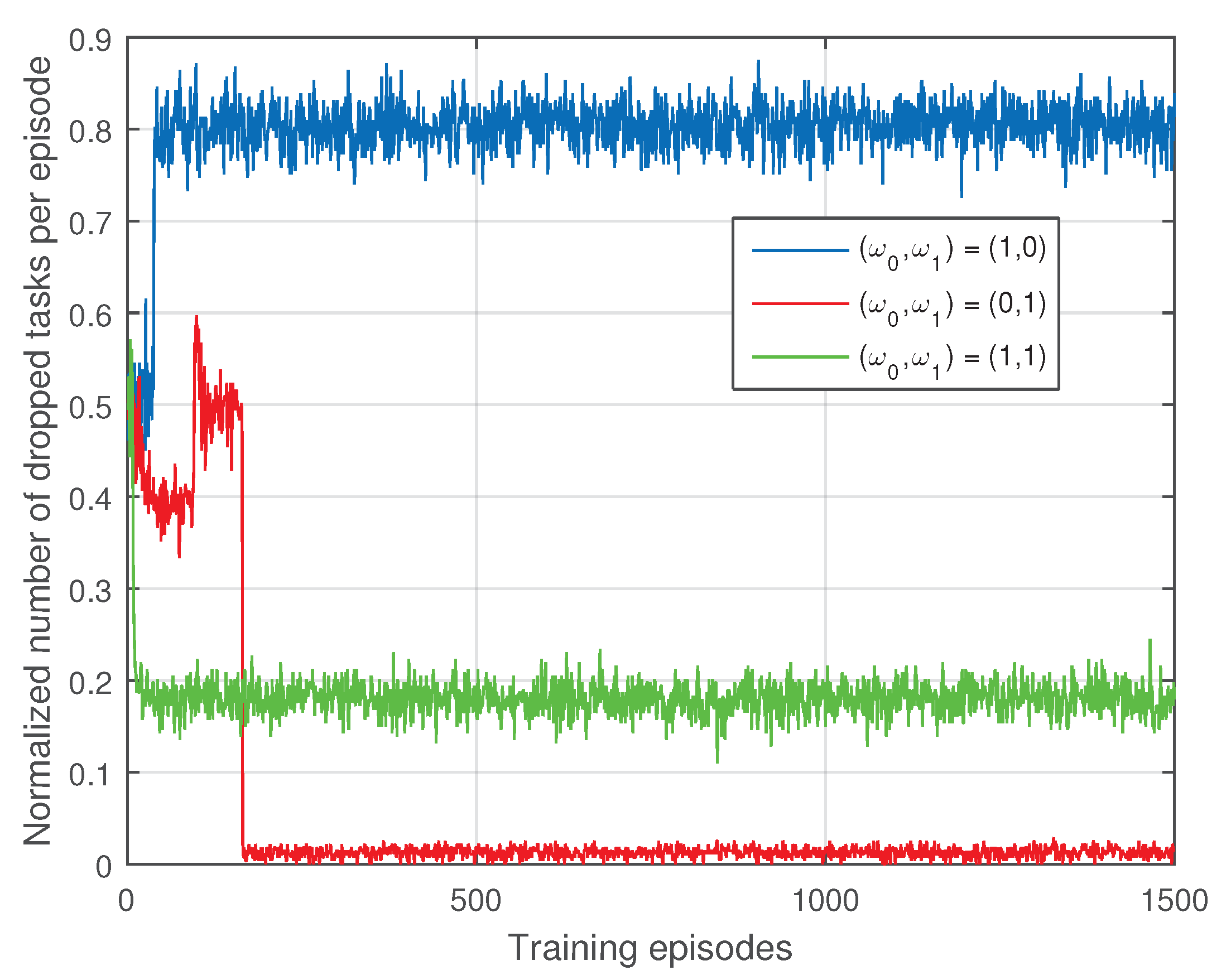
Figure 4 shows the impact of the weights on the normalized number of dropped tasks per episode. When $\left({\omega }_0,{\omega }_1\right)=\left(1,0\right)$, most of the tasks are allocated to the SMSs to reduce the computing pressure of the PMS. Since the computing power of the SMSs are weak, many tasks may be dropped. The case $\left({\omega }_0,{\omega }_1\right)=\left(0,1\right)$ has the smallest normalized number of dropped tasks per episode, which is explained in Figure 3. Similar to that in Figure 3, the case $\left({\omega }_0,{\omega }_1\right)=\left(1,1\right)$ has middle number of dropped tasks per episode.

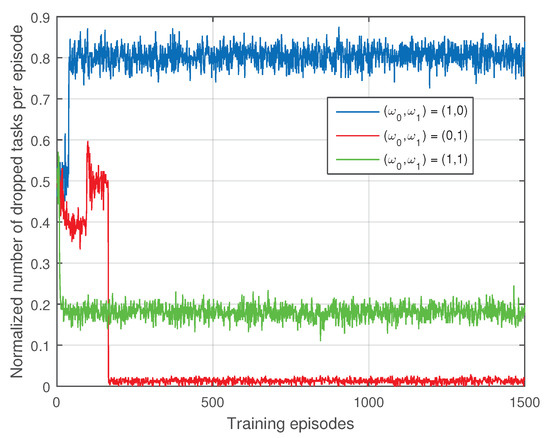
Figure 4. The impact of the weights on the normalized number of dropped tasks per episode.

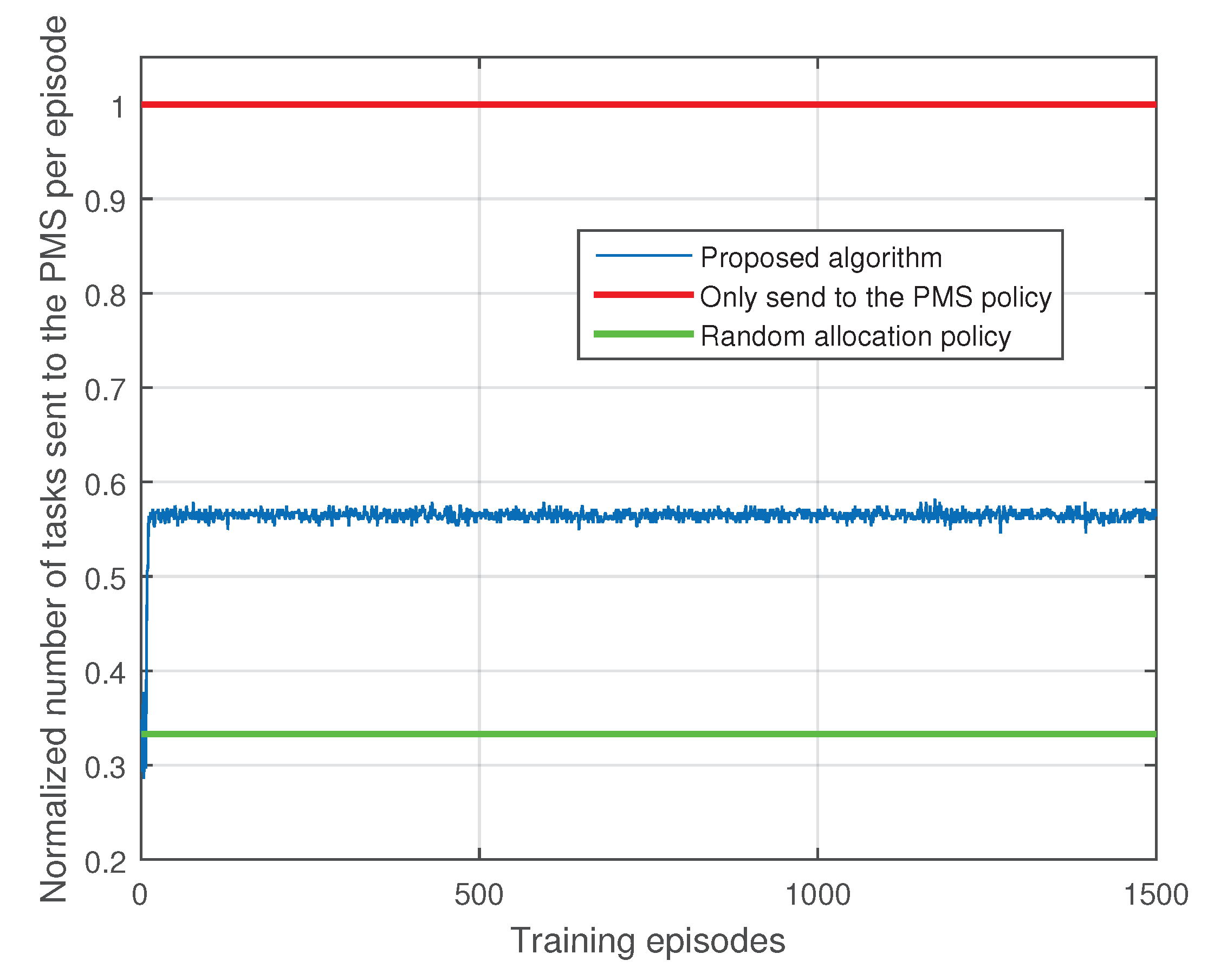
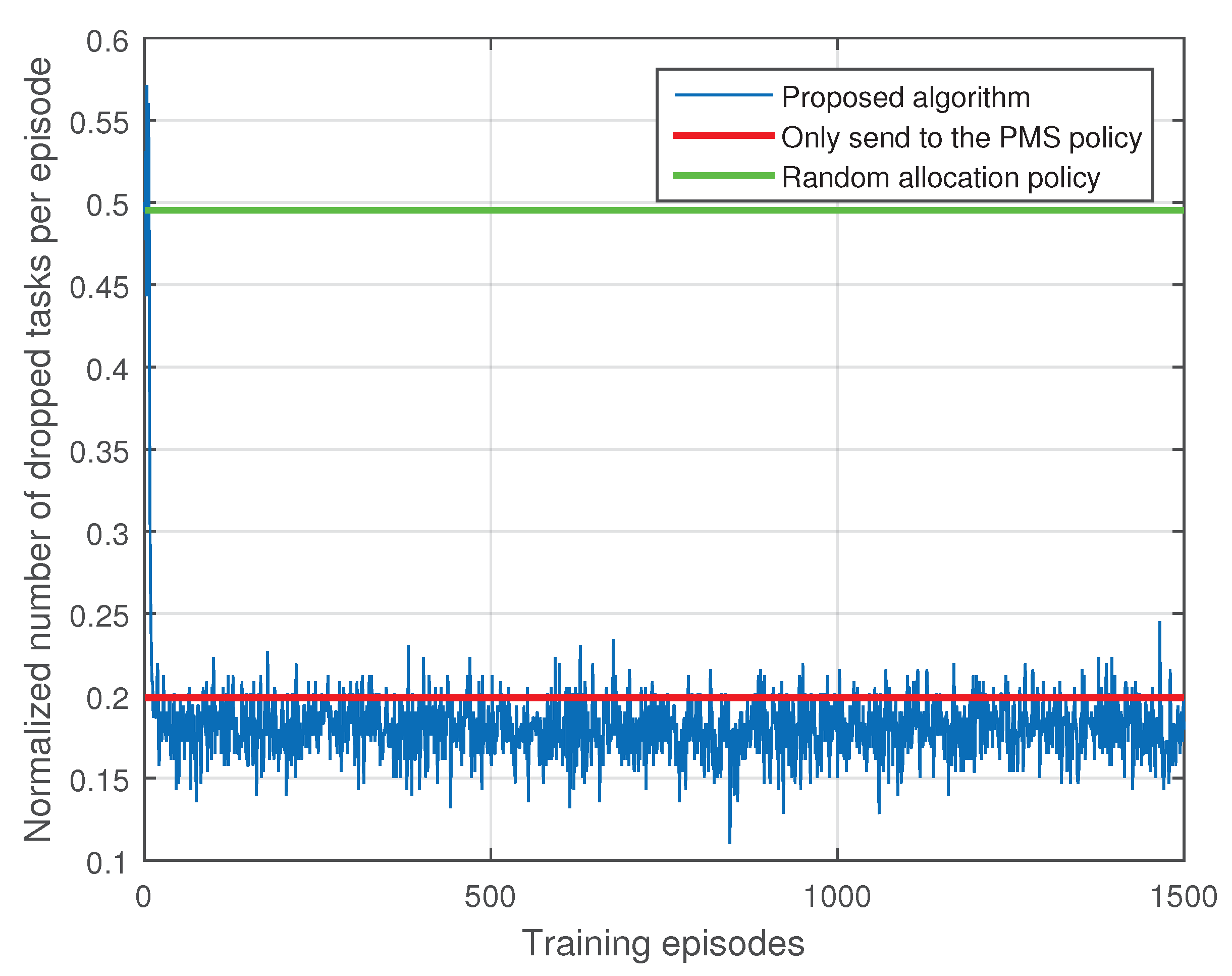
Figure 5 and Figure 6 show performance comparisons between our proposed algorithm ($\left({\omega }_0,{\omega }_1\right)=\left(1,1\right)$) and two benchmark polices: only send to the PMS policy and random allocation policy. Only send to the PMS policy allocate all the IoT devices’ tasks to the PMS, which is a policy adopted in typical single MEC server deployment scenario. Random allocation policy allocates each IoT device’s task randomly to the $M+1$ MEC servers. The two benchmark policies are both short-term optimization policies, we plot the mean value of the normalized number of tasks sent to the PMS and dropped tasks per episode in Figure 5 and Figure 6. As shown in Figure 5 and Figure 6, our proposed algorithm achieve superior performances on computing pressure of the PMS and tasks dropped cost than the only send to the PMS policy. In order to obtain a lower task dropped cost, our algorithm has larger computing pressure on the PMS than the random allocation policy. However, we have significant performance gain in term of task dropped cost compared with the random allocation policy. Hence, our proposed algorithm is more practical than the random allocation policy.

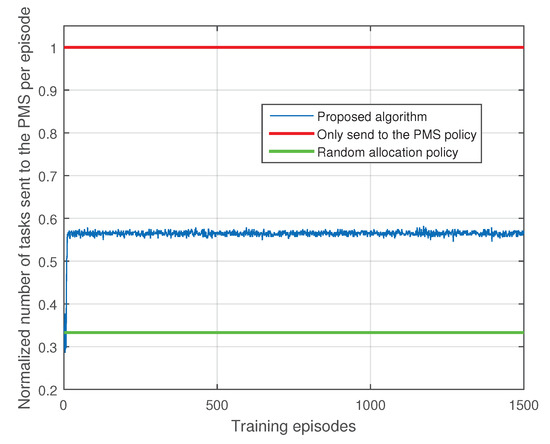
Figure 5. Comparison with benchmark polices in terms of normalized number of tasks sent to the PMS per episode.

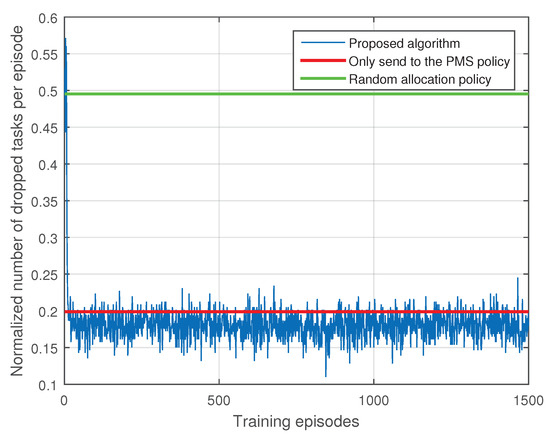
Figure 6. Comparison with benchmark polices in terms of normalized number of dropped tasks per episode.

6. Conclusions

We studied the problem of making trade-off among the computing pressure on the PMS, the sum of energy consumption of the IoT devices and all the MEC servers, and the task dropping cost. The formulated MINLP problem was solved by a proposed DRL-based optimization algorithm. The simulation results demonstrated the validity of the proposed algorithm.