Design of Compact Complex Impedance Transformer with Frequency and Terminal Impedance Tunability
Abstract
:1. Introduction
2. Design Methodology
3. Design Procedures
- ◆
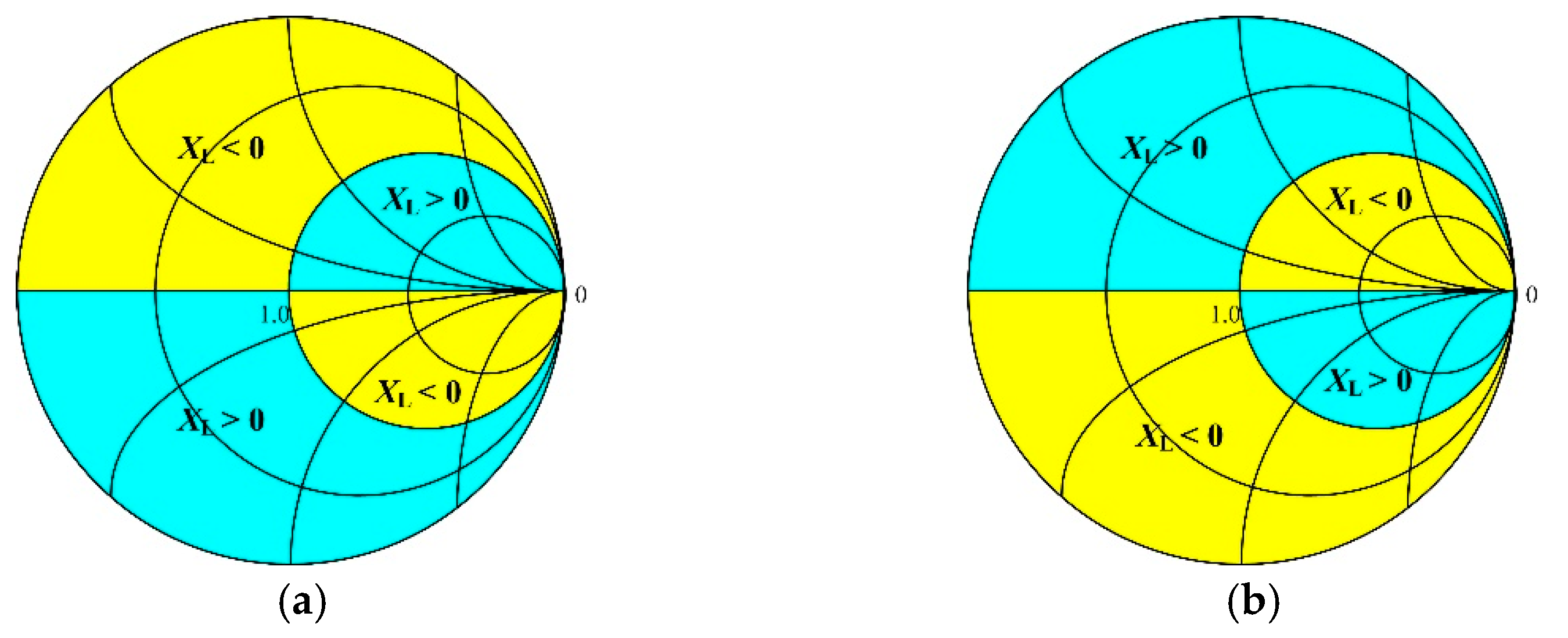
- The initial impedance RL is larger than Zg:
- (1)
- When the real part of the transformed complex impedance is greater than Zg, the imaginary part has the same sign as XL.
- (2)
- When the real part of the transformed complex impedance is smaller than Zg, the imaginary part has the opposite sign to XL.
- ◆
- The initial impedance RL is smaller than Zg:
- (1)
- When the real part of the transformed complex impedance is smaller than Zg, the imaginary part has the same sign as XL.
- (2)
- When the real part of the transformed complex impedance is larger than Zg, the imaginary part has the opposite sign to XL.
4. Implementation and Measurements
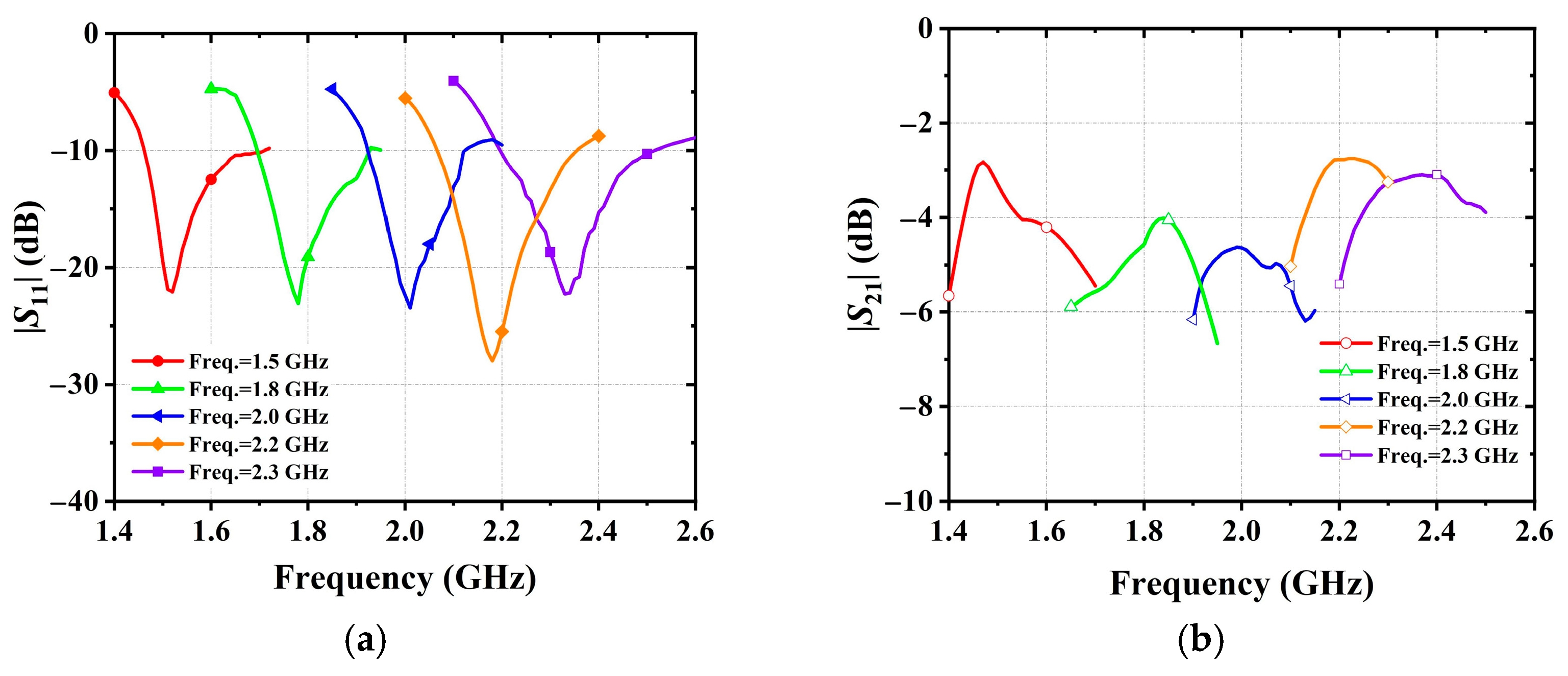
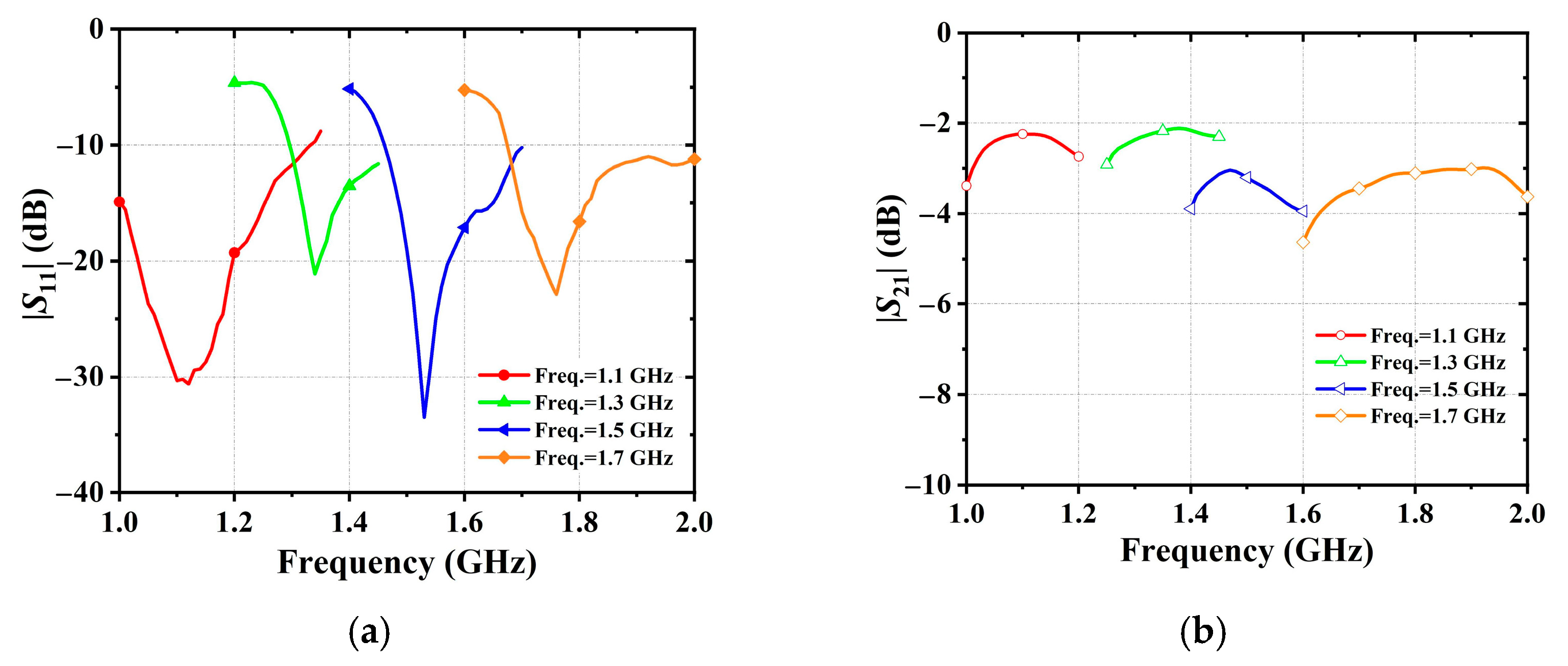
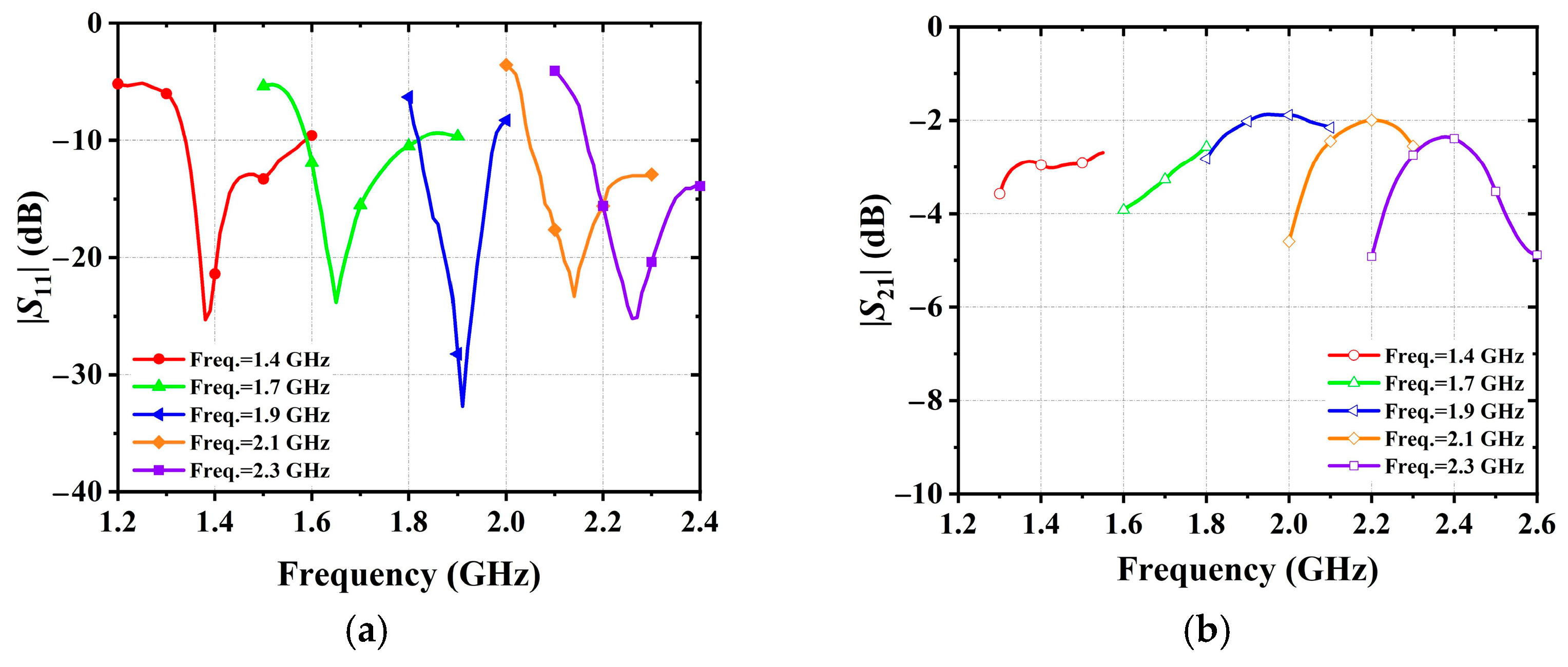
4.1. Frequency Tunable
4.2. Terminal Impedance Tunable
4.3. Both Frequency and Terminal Impedance Tunable
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
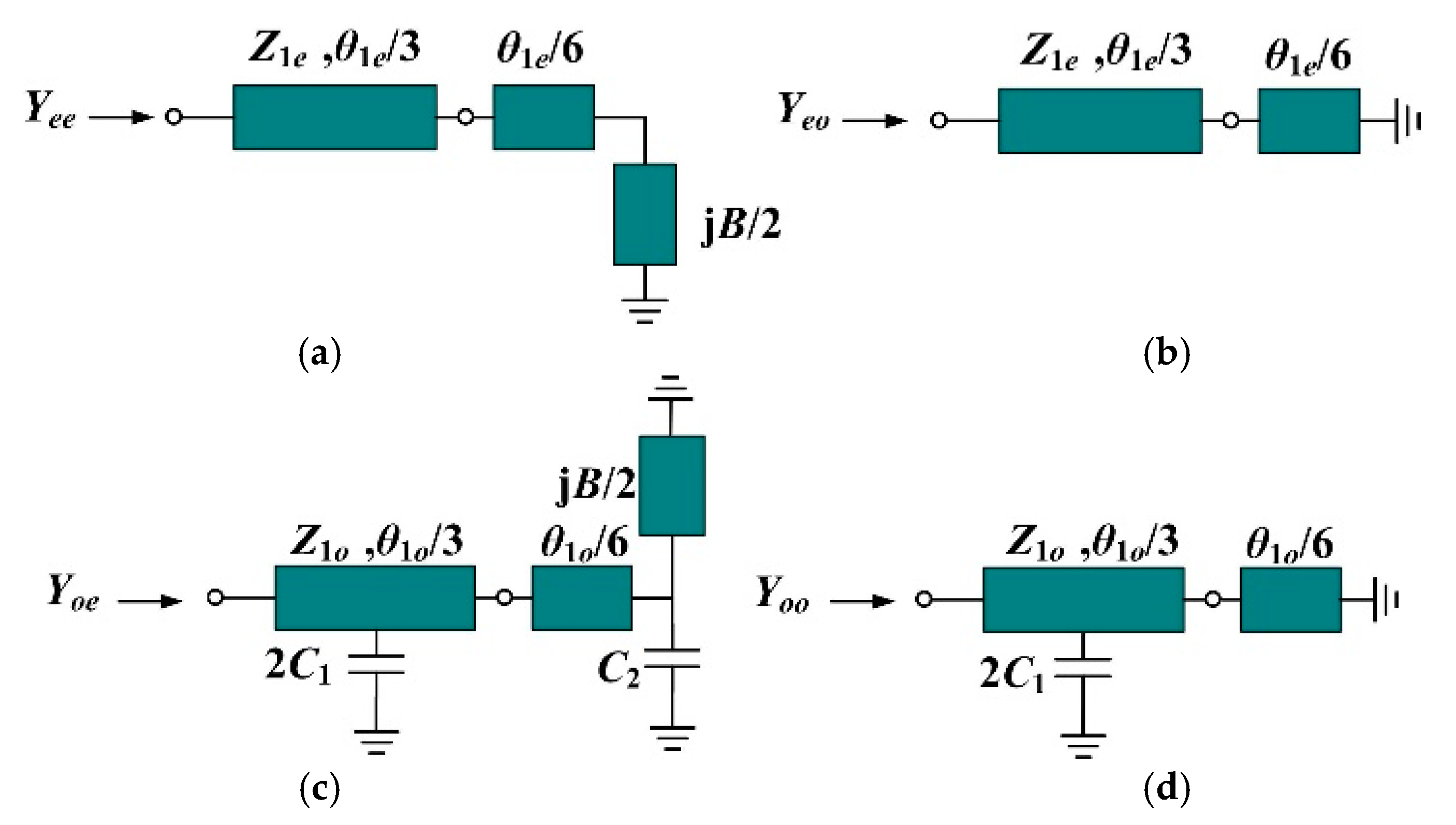
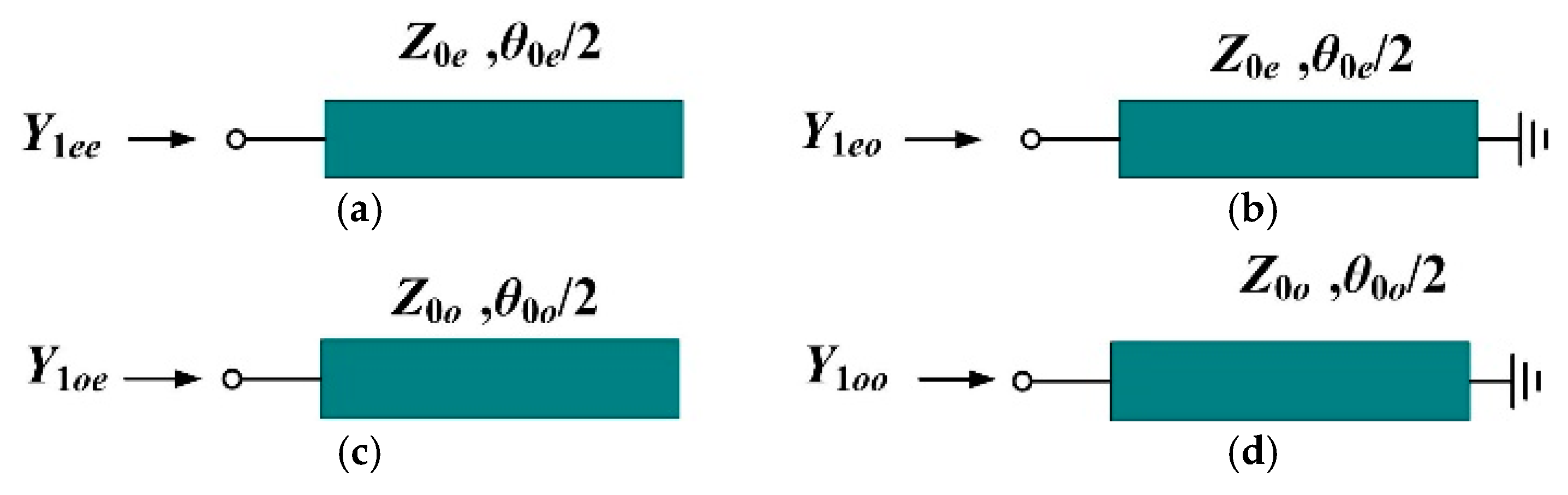
References
- Tsao, Y.-F.; Würfl, J.; Hsu, H.-T. Bandwidth Improvement of MMIC Single-Pole-Double-Throw Passive HEMT Switches with Radial Stubs in Impedance-Transformation Networks. Electronics 2020, 9, 270. [Google Scholar] [CrossRef] [Green Version]
- Kim, H.-W.; Ahn, M.; Lee, O.; Kim, H.; Kim, H.; Lee, C.-H. Analysis and Design of a Fully-Integrated High-Power Differential CMOS T/R Switch and Power Amplifier Using Multi-Section Impedance Transformation Technique. Electronics 2021, 10, 1028. [Google Scholar] [CrossRef]
- Ali, E.M.; Alibakhshikenari, M.; Virdee, B.S.; Soruri, M.; Limiti, E. Efficient Wireless Power Transfer via Magnetic Resonance Coupling Using Automated Impedance Matching Circuit. Electronics 2021, 10, 2779. [Google Scholar] [CrossRef]
- Lu, Z.; Zhao, Y.; Liu, D. Adaptive Impedance Matching Scheme for Magnetic MIMO Wireless Power Transfer System. Electronics 2021, 10, 2788. [Google Scholar] [CrossRef]
- Ahn, H.-R.; Tentzeris, M.M. Complex impedance transformers based on allowed and forbidden regions. IEEE Access 2019, 7, 39288–39298. [Google Scholar] [CrossRef]
- Manoochehri, O.; Asoodeh, A.; Forooraghi, K. Π-model dual-band impedance transformer for unequal complex impedance loads. IEEE Microw. Compon. Lett. 2015, 25, 238–240. [Google Scholar] [CrossRef]
- Chuang, M.; Wu, M. General dual-band impedance transformer with a selectable transmission zero. IEEE Trans. Compon. Packag. Manufact. Technol. 2016, 6, 1113–1119. [Google Scholar] [CrossRef]
- Xie, T.; Wang, X.; Ma, Z.; Chen, C.-P.; Lu, G. A novel analysis approach for dual-frequency parallel transmission-line transformer with complex terminal loads. IEEE Access 2020, 8, 57472–57482. [Google Scholar] [CrossRef]
- Chen, M.-G.; Hou, T.-B.; Tang, C.-W. Design of planar complex impedance transformers with the modified coupled line. IEEE Trans. Compon. Packag. Manufact. Technol. 2012, 2, 1704–1710. [Google Scholar] [CrossRef]
- Fang, S.; Jia, X.; Liu, H.; Wang, Z. Design of compact coupled-line complex impedance transformers with the series susceptance component. IEEE Trans. Circuits Syst. II Express Br. 2020, 67, 2482–2486. [Google Scholar] [CrossRef]
- Lu, P.; Yang, X.S.; Li, J.L.; Wang, B.Z. Polarization reconfigurable broadband rectenna with tunable matching network for microwave power transmission. IEEE Trans. Antennas Propag. 2016, 64, 1136–1141. [Google Scholar] [CrossRef]
- Fu, J.-S.; Mortazawi, A. Improving power amplifier efficiency and linearity using a dynamically controlled tunable matching network. IEEE Trans. Microw. Theory Techn. 2008, 56, 3239–3244. [Google Scholar]
- Neo, W.C.E.; Lin, Y.; Liu, X.-D.; De Vreede, L.C.N.; Larson, L.E.; Spirito, M.; Pelk, M.J.; Buisman, K.; Akhnoukh, A.; De Graauw, A.; et al. Adaptive multi-band multi-mode power amplifier using integrated varactor-based tunable matching networks. IEEE J. Solid State Circuits 2006, 41, 2166–2176. [Google Scholar] [CrossRef]
- Ko, C.-H.; Rebeiz, G.M. A 1.4–2.3 GHz tunable diplexer based on reconfigurable matching networks. IEEE Trans. Microw. Theory Techn. 2015, 63, 1595–1602. [Google Scholar] [CrossRef]
- Vaha-Heikkila, T.; Lahdes, M.; Kantanen, M.; Tuovinen, J. On-wafer noise-parameter measurements at W-band. IEEE Trans. Microw. Theory Techn. 2003, 51, 1621–1628. [Google Scholar] [CrossRef]
- McIntosh, C.E.; Pollard, R.D.; Miles, R.E. Novel MMIC source-impedance tuners for on-wafer microwave noise-parameter measurements. IEEE Trans. Microw. Theory Techn. 1999, 47, 125–131. [Google Scholar] [CrossRef]
- MI-Nozahi, E.; Sanchez-Sinencio, E.; Entesari, K. A CMOS low noise amplifier with reconfigurable input matching network. IEEE Trans. Microw. Theory Techn. 2009, 57, 1054–1062. [Google Scholar] [CrossRef]
- Zhang, H.; Gao, H.; Li, G.-P. Broad-band power amplifier with a novel tunable output matching network. IEEE Trans. Microw. Theory Tech. 2005, 53, 3606–3614. [Google Scholar] [CrossRef]
- Lee, C.I.; Lin, W.C. A novel p-i-n inductor for tunable wideband matching network application. IEEE Trans. Electron Devices 2013, 60, 2611–2618. [Google Scholar] [CrossRef]
- Sanchez-Perez, C.; de Mingo, J.; Carro, P.L.; García-Dúcar, P. Design and applications of a 300–800 MHz tunable matching network. IEEE J. Emerg. Sel. Top. Circuits Syst. 2013, 3, 531–540. [Google Scholar] [CrossRef]
- Fouladi, S.; Domingue, F.; Zahirovica, N.; Mansour, R.R. Distributed MEMS tunable impedance-matching network based on suspended slow-wave structure fabricated in a standard CMOS technology. IEEE Trans. Microw. Theory Tech. 2010, 58, 1056–1064. [Google Scholar] [CrossRef]
- Hoarau, C.; Corrao, N.; Arnould, J.-D.; Ferrari, P.; Xavier, P. Complete Design and Measurement Methodology for a Tunable RF Impedance-Matching Network. IEEE Trans. Microw. Theory Tech. 2008, 56, 2620–2627. [Google Scholar] [CrossRef]
- Brito, K.; de Lima, R.N. Tunable impedance matching network. In Proceedings of the 2007 SBMO/IEEE MTT-S International Microwave and Optoelectronics Conference, Salvador, Brazil, 29 October–1 November 2007; pp. 117–121. [Google Scholar]
- Tombak, A. A Ferroelectric-Capacitor-Based Tunable Matching Network for Quad-Band Cellular Power Amplifiers. IEEE Trans. Microw. Theory Tech. 2007, 55, 370–375. [Google Scholar] [CrossRef]
- Arabi, E.; Morris, K.A.; Beach, M.A. Analytical Formulas for the Coverage of Tunable Matching Networks for Reconfigurable Applications. IEEE Trans. Microw. Theory Tech. 2017, 65, 3211–3220. [Google Scholar] [CrossRef] [Green Version]
- Shen, Q.; Barker, N.S. Distributed MEMS tunable matching network using minimal-contact RF-MEMS varactors. IEEE Trans. Microw. Theory Tech. 2006, 54, 2646–2658. [Google Scholar] [CrossRef]
- Jeong, H.T.; Kim, J.E.; Chang, I.S.; Kim, C.D. Tunable impedance transformer using a transmission line with variable characteristic impedance. IEEE Trans. Microw. Theory Tech. 2005, 53, 2587–2593. [Google Scholar] [CrossRef]
- Suvarna, A.R.; Bhagavatula, V.; Rudell, J.C. Transformer-Based Tunable Matching Network Design Techniques in 40-nm CMOS. IEEE Trans. Circuits Syst. II Express Br. 2016, 63, 658–662. [Google Scholar] [CrossRef]
- Jensen, T.; Zhurbenko, V.; Krozer, V.; Meincke, P. Coupled transmission lines as impedance transformer. IEEE Trans. Microw. Theory Tech. 2007, 55, 2957–2965. [Google Scholar] [CrossRef] [Green Version]



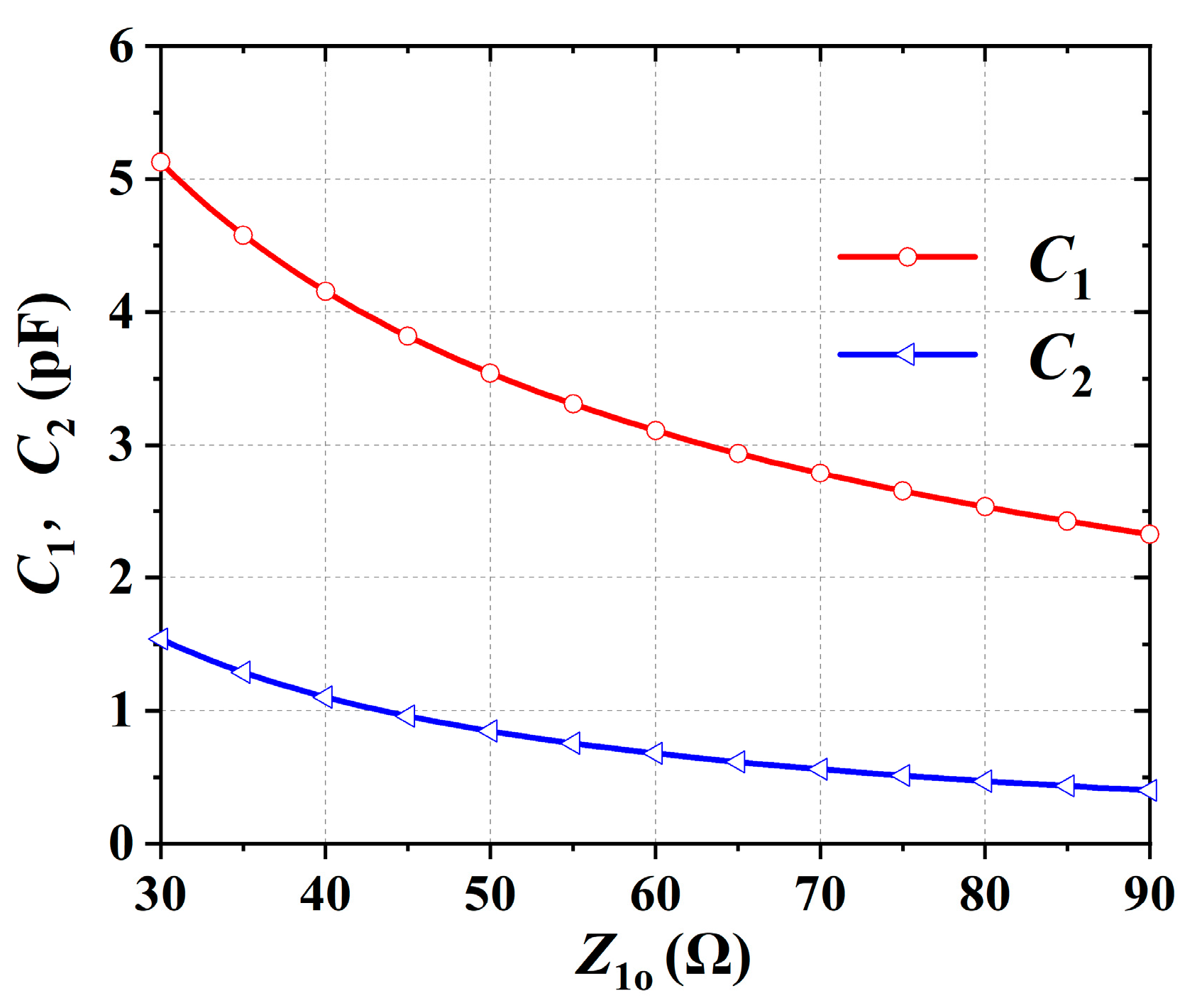
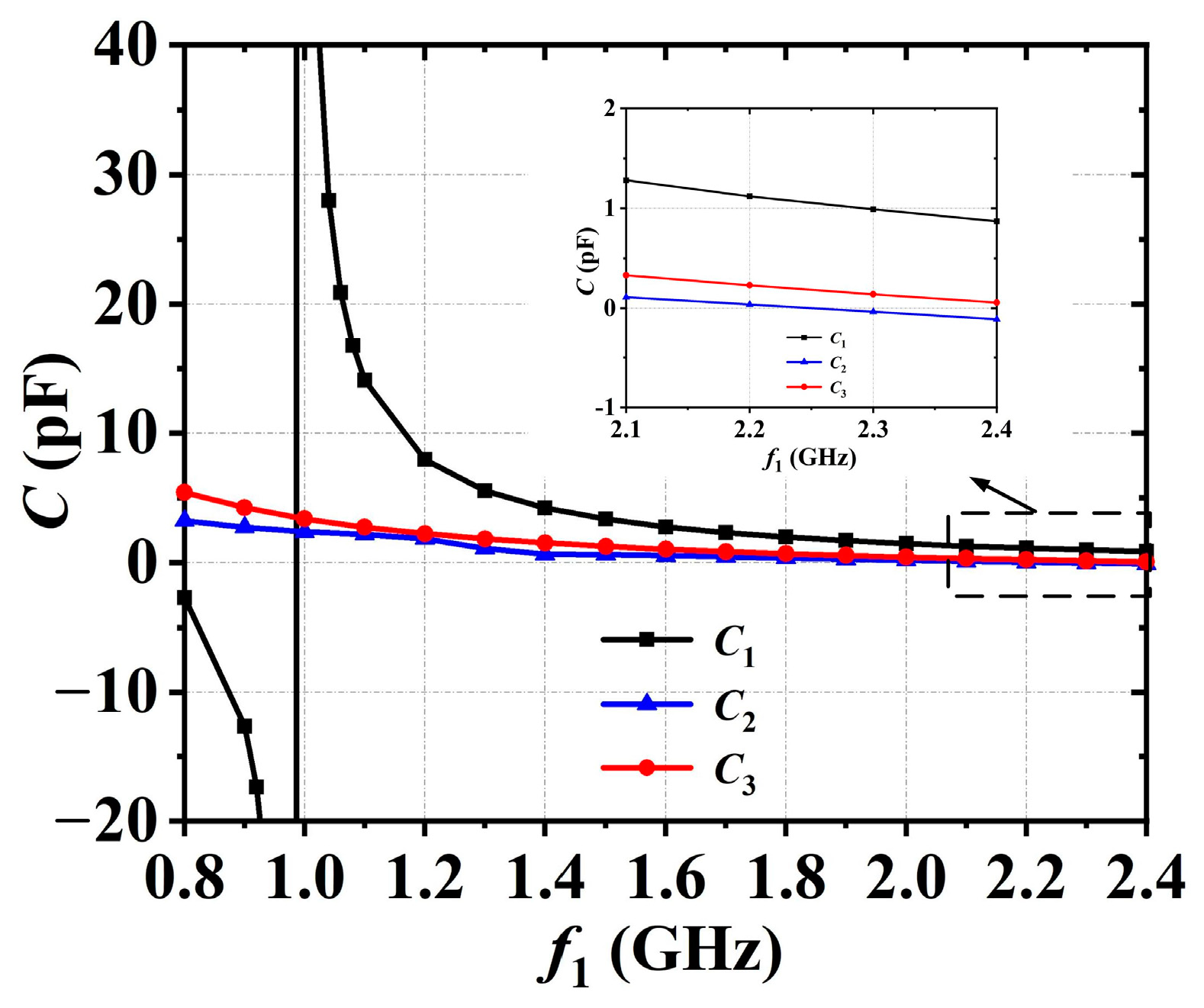
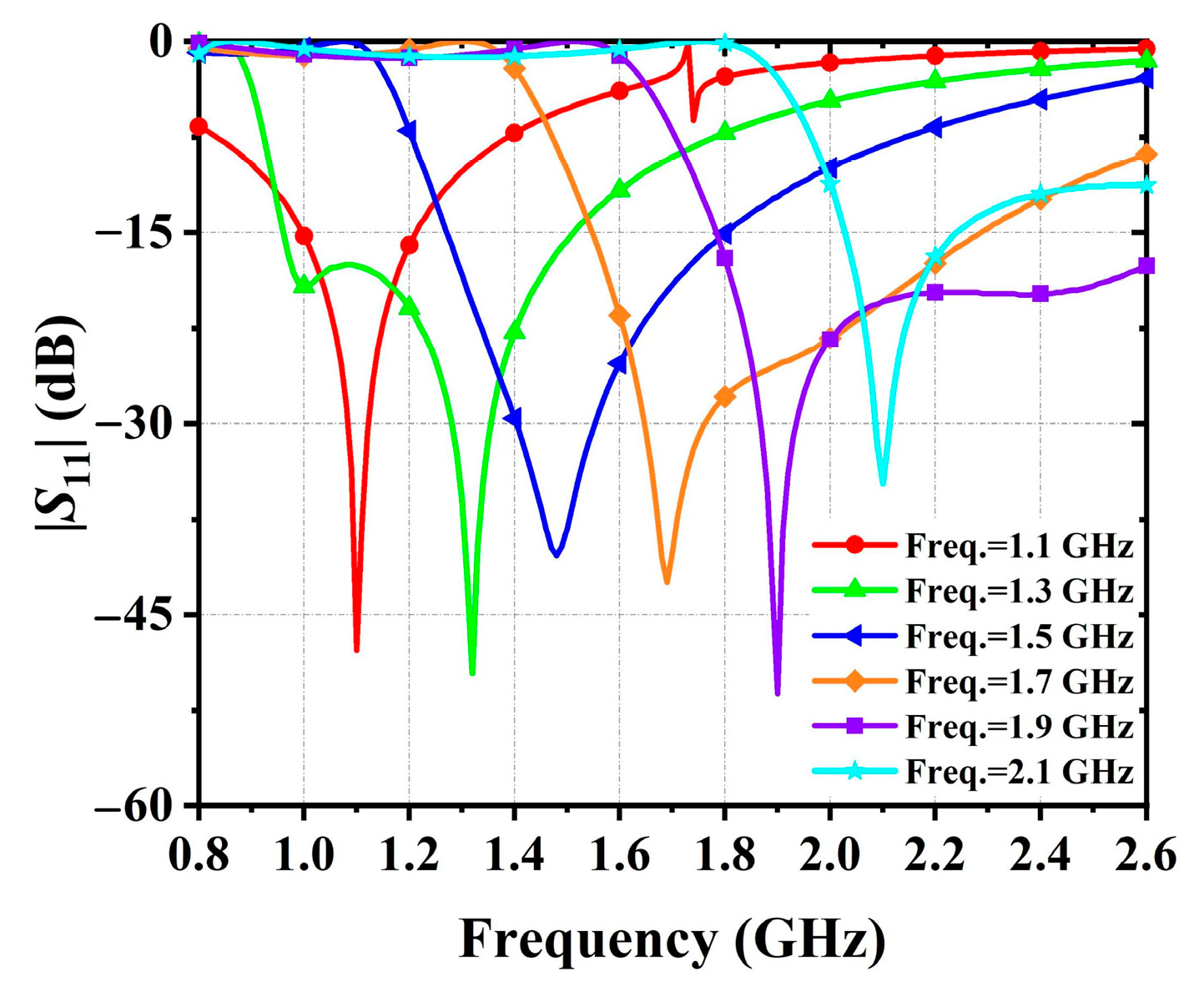
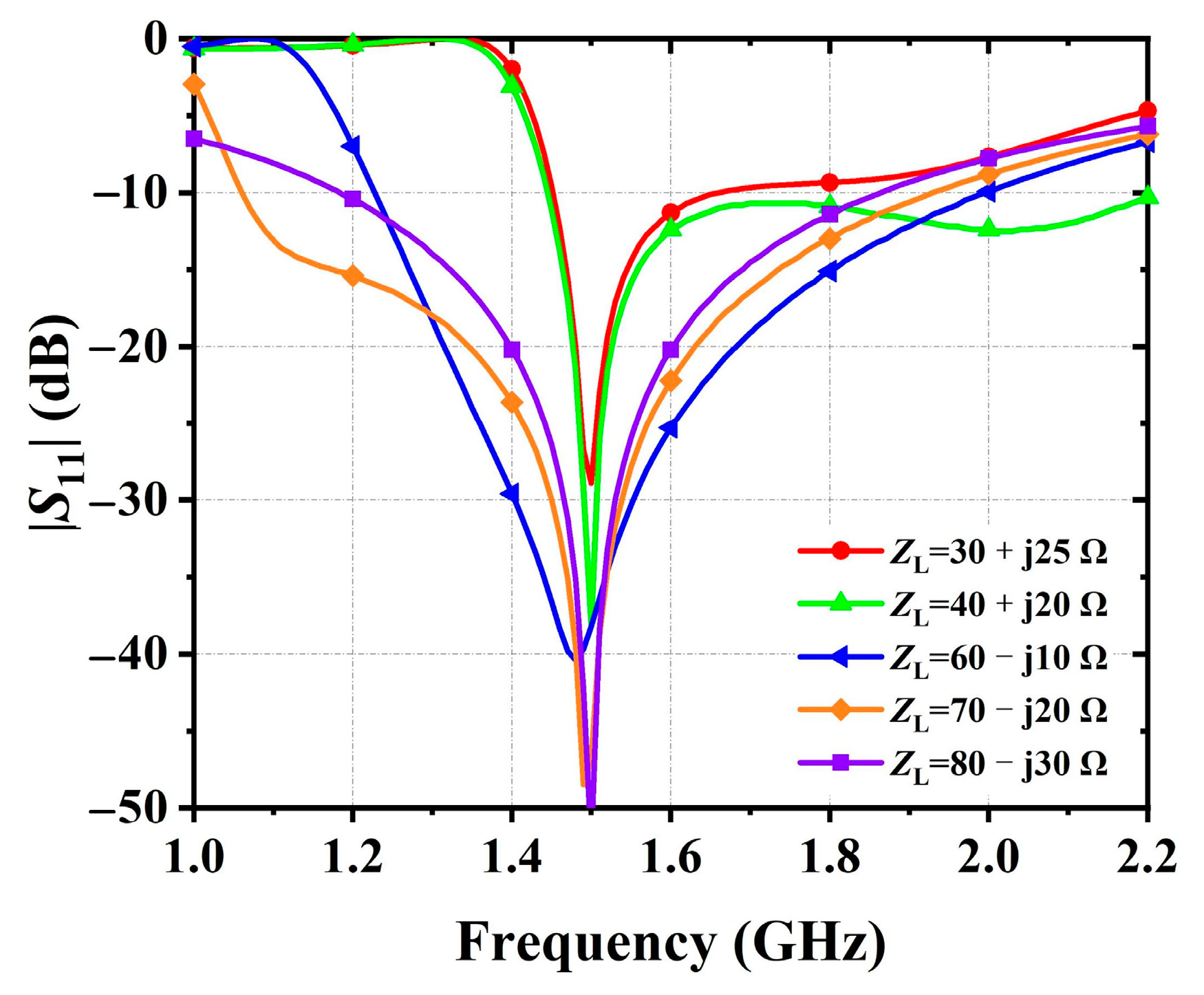

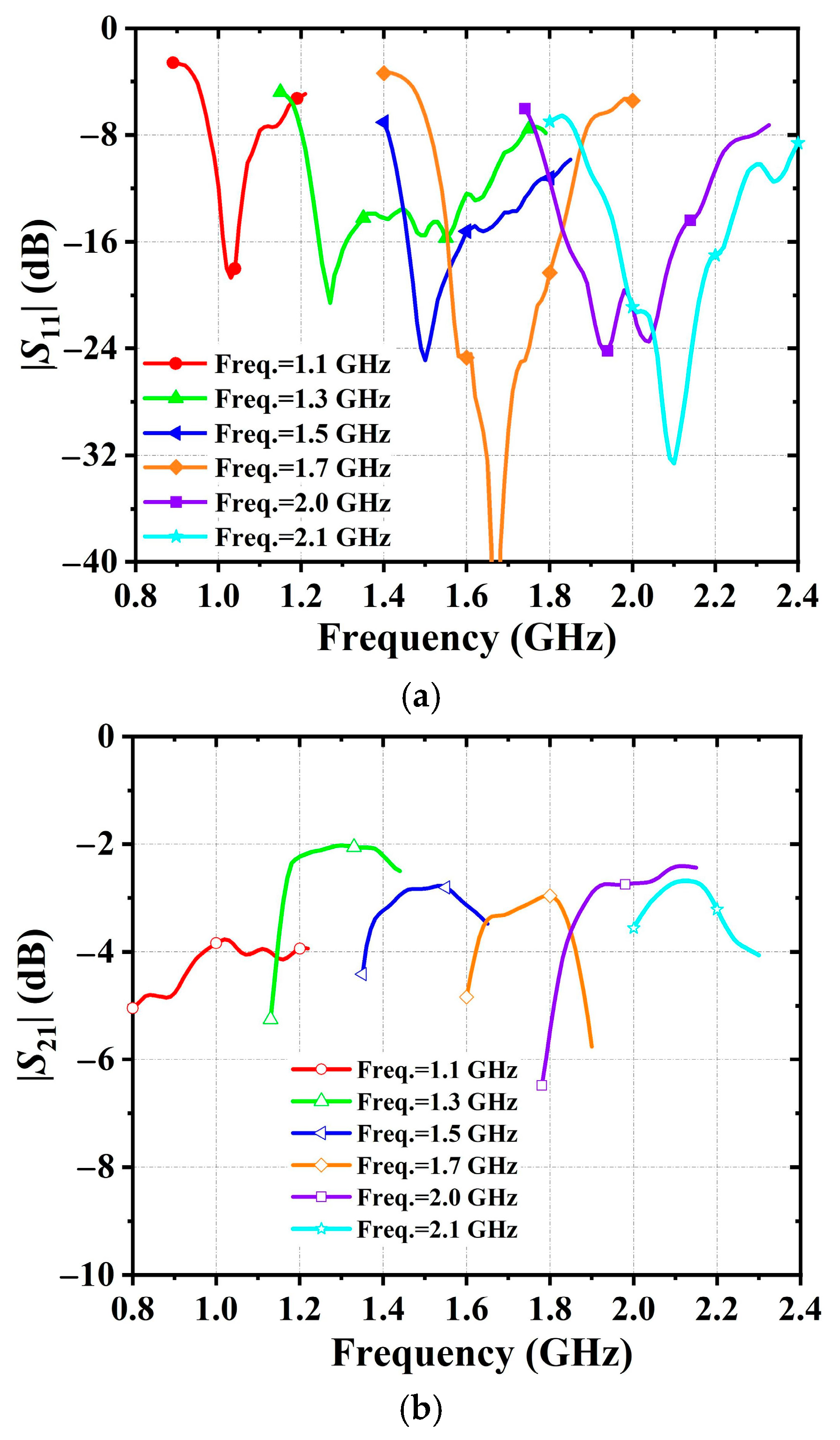


| f1 (GHz) | C1 (pF) | C2 (pF) | B (mS) | C3 (pF) |
|---|---|---|---|---|
| 1.1 | 13.8 | 2.2 | 1.3 | 2.7 |
| 1.3 | 5.5 | 0.2 | 0.1 | 1.8 |
| 1.5 | 3.4 | 0.7 | −1.1 | 1.3 |
| 1.7 | 2.3 | 0.5 | −2.3 | 0.9 |
| 1.9 | 1.7 | 0.3 | −3.6 | 0.6 |
| 2.1 | 1.2 | 0.2 | −4.9 | 0.3 |
| Zg (Ω) | 50 | Z1o (Ω) | 80 |
| ZL (Ω) | 60–j10 | θ1 (°) | 60 |
| f0 (GHz) | 1.5 | L1 (nH) | 8.2 |
| Z0e (Ω) | 138.3 | f1 (GHz) | 1.1–2.1 |
| Z0o (Ω) | 9.9 | C1 (pF) | 1.2–13.8 |
| θ0 (°) | 56 | C2 (pF) | 0.2–2.2 |
| Z1e (Ω) | 127.4 | C3 (pF) | 0.3–2.7 |
| ZL (Ω) | C1 (pF) | C2 (pF) | C3 (pF) |
|---|---|---|---|
| 80 − j30 | 7.88 | 0.99 | 1.22 |
| 70 − j20 | 4.41 | 1.01 | 1.24 |
| 60 − j10 | 3.40 | 0.70 | 1.30 |
| 40 + j20 | 2.33 | 0.80 | 0.99 |
| 30 + j25 | 2.32 | 0.82 | 1.23 |
| Freq. (GHz) | Biasing Conditions |
|---|---|
| 1.1 | V1 = 1.3 V, V2 = 2.7 V, V3 = 1.1 V |
| 1.3 | V1 = 2.7 V, V2 = 4.1 V, V3 = 2.2 V |
| 1.5 | V1 = 4.4 V, V2 = 5.0 V, V3 = 3.7 V |
| 1.7 | V1 = 7.1 V, V2 = 7.3 V, V3 = 6.4 V |
| 2.0 | V1 = 9.4 V, V2 = 8.6 V, V3 = 8.5 V |
| 2.1 | V1 = 12.9 V, V2 = 10.2 V, V3 = 12.6 V |
| ZL (Ω) | Biasing Conditions |
|---|---|
| 35 + j25 | V1 = 5.5 V, V2 = 4.7 V, V3 = 1.8 V |
| 40 + j20 | V1 = 5.2 V, V2 = 6.4 V, V3 = 1.8 V |
| 60 − j10 | V1 = 4.4 V, V2 = 5.0 V, V3 = 3.7 V |
| 75 − j15 | V1 = 5.4 V, V2 = 5.8 V, V3 = 4.4 V |
| ZL (Ω) | Freq. (GHz) | Biasing Conditions (V) |
|---|---|---|
| 35 + j25 | 1.5 | V1 = 5.5, V2 = 4.7, V3 = 1.8 |
| 1.8 | V1 = 7.1, V2 = 5.8, V3 = 3.1 | |
| 2.0 | V1 = 8.7, V2 = 7.2, V3 = 4.4 | |
| 2.2 | V1 = 10.6, V2 = 8.5, V3 = 5.8 | |
| 2.3 | V1 = 13.2, V2 = 10.0, V3 = 7.6 | |
| 40 + j20 | 1.3 | V1 = 3.9, V2 = 4.6, V3 = 0.9 |
| 1.5 | V1 = 5.2, V2 = 6.4, V3 = 1.8 | |
| 1.8 | V1 = 6.7, V2 = 7.1, V3 = 3.1 | |
| 2.1 | V1 = 8.2, V2 = 8.7, V3 = 4.4 | |
| 2.2 | V1 = 9.6, V2 = 12.4, V3 = 6.1 | |
| 75 − j15 | 1.1 | V1 = 1.7, V2 = 3.4, V3 = 1.5 |
| 1.3 | V1 = 3.5, V2 = 4.4, V3 = 2.7 | |
| 1.5 | V1 = 5.4, V2 = 5.8, V3 = 4.4 | |
| 1.7 | V1 = 6.8, V2 = 7.2, V3 = 5.9 | |
| 80 − j30 | 1.4 | V1 = 4.7, V2 = 6.4, V3 = 4.9 |
| 1.7 | V1 = 6.2, V2 = 8.0, V3 = 6.9 | |
| 1.9 | V1 = 8.4, V2 = 9.9, V3 = 10.7 | |
| 2.1 | V1 = 10.6, V2 = 12.2, V3 = 13.8 | |
| 2.3 | V1 = 11.9, V2 = 13.6, V3 = 16.0 |
| Ref. | Technology | Tuning | Insertion Loss | |
|---|---|---|---|---|
| Frequency | Impedance | |||
| [17] | Tunable inductor | Δf/f0 = 23.3% (Continuous) | NO | -- |
| [18] | Pin diodes | 0.9 GHz, 2.0 GHz | NO | -- |
| [19] | Pin inductor at RF breakdown | Δf/f0 = 44.4% (Continuous) | YES (Discrete) | 2–3.5 dB |
| [20] | Pin diodes | NO | YES (Discrete) | -- |
| [21] | Switched MEMS capacitors | NO | YES (Discrete) | 0.4–7.55 dB |
| [22] | Varactor | Δf/f0 = 50% (Continuous) | YES (Continuous) | 2.5–3.5 dB |
| [23] | MEMS-based switches | NO | YES (Discrete) | 0.7–2.1 dB |
| [24] | Ferroelectric capacitors | NO | YES (Continuous) | 1.4–2.5 dB |
| [25] | Varactor | NO | YES (Continuous) | -- |
| [26] | RF-MEMS varactors | NO | YES (Continuous) | 2.5–5 dB |
| [27] | Pin diodes | NO | YES (Discrete) | About 0.2 dB |
| [28] | NMOS switches | NO | YES (Discrete) | 1.8–4 dB |
| This work | Varactor | Δf/f0 = 62.5% (Continuous) | YES (Continuous) | 2–4.5 dB |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, H.; Guo, Y.; Wang, X.; Fang, S.; Wang, Z. Design of Compact Complex Impedance Transformer with Frequency and Terminal Impedance Tunability. Electronics 2022, 11, 983. https://doi.org/10.3390/electronics11070983
Liu H, Guo Y, Wang X, Fang S, Wang Z. Design of Compact Complex Impedance Transformer with Frequency and Terminal Impedance Tunability. Electronics. 2022; 11(7):983. https://doi.org/10.3390/electronics11070983
Chicago/Turabian StyleLiu, Hongmei, Yongquan Guo, Xinshuo Wang, Shaojun Fang, and Zhongbao Wang. 2022. "Design of Compact Complex Impedance Transformer with Frequency and Terminal Impedance Tunability" Electronics 11, no. 7: 983. https://doi.org/10.3390/electronics11070983
APA StyleLiu, H., Guo, Y., Wang, X., Fang, S., & Wang, Z. (2022). Design of Compact Complex Impedance Transformer with Frequency and Terminal Impedance Tunability. Electronics, 11(7), 983. https://doi.org/10.3390/electronics11070983







