Throughput Multiplexing Efficiency for High-Order Handset MIMO Antennas

Abstract

In multipath environments, multiple-input multiple-output (MIMO) terminals typically suffer from non-zero correlations due to limited handset space and power imbalances due to different antenna efficiencies or partial hand blockage. These antenna–channel impairments can lead to significant throughput performance degradation of MIMO terminals. The multiplexing efficiency was proposed to quantitatively assess this performance degradation. Previous work only derived the analytical expression of the throughput-based multiplexing efficiency of two-port MIMO antennas for user equipment (UE). However, the fifth-generation (5G) UE dictates four or more antennas. In this paper, we extend the multiplexing efficiency metric to high-order MIMO UEs. Both correlation-based channel models and geometry-based stochastic channel models were used for validation. Besides dipole antennas, two representative terminal antennas were also employed for simulation verifications in this work.

1. Introduction

With the development of multiple-input multiple-output (MIMO) technology in recent years, performance characterization of MIMO antenna has been widely concerned by academia and industry [1,2,3,4,5,6,7,8]. In reality, MIMO terminals have limited space, limited incident wave angle spread [9], and different antenna efficiencies among different antenna elements, resulting in non-zero correlations and power imbalances between the MIMO antenna. Additionally, the existence of non-zero correlation and power imbalance can cause severe performance degradation in the MIMO system.

Traditionally, the performance of a MIMO antenna has been characterized by the measured channel capacity, to name a few [4]. The performance of a MIMO antenna was also characterized by the measured throughput [5]. However, channel capacity and throughput are system-level metrics and cannot directly reflect the impact of different MIMO antenna–channel impairments on the system performance [10]. Antenna engineers need a more intuitive power-related metric to evaluate the designed MIMO antenna. For instance, at a low signal-to-noise ratio (SNR) regime, diversity gain is usually used to characterize the diversity performance of the MIMO antenna. At a high SNR regime, spatial multiplexing is the core technology to improve spectrum efficiency. Therefore, spatial multiplexing (SM) efficiency was first proposed in [11] to characterize the spatial multiplexing effect of the MIMO antenna. The SM efficiency in [11] was defined as the SNR degradation due to non-zero correlations and power imbalance of the MIMO antenna at a given channel capacity level. However, the channel capacity is just an information-theoretic value (denoting the maximum data transmission rate of the channel), which can seldom be achieved in practice. As a result, a throughput-based SM efficiency that is more consistent with the measurement results was proposed in [12,13], where it was shown that the capacity-based SM efficiency would underestimate the performance degradation caused by imperfect MIMO antennas.

The new contributions of this work are summarized as follows:

(1)

Previous works [12,13] only considered the (throughput) SM efficiency in the case of two-port MIMO antennas, which limits the usability of the SM efficiency in high-order MIMO antennas. With the development of the fifth-generation (5G) technology, the user equipment (UE) is typically equipped with four or more antennas. In this paper, we extended the SM efficiency to characterize the performance of high-order MIMO UEs;

(2)

Conflicting with the previous finding that the correlation and power imbalance effects are separable for two-port antennas, it was shown that the two effects become inter-related in a high-order MIMO system, which motivates the derivation of closed-form expressions of SM efficiencies in high-order MIMO systems;

(3)

In order to verify the derived SM efficiency, we use both the correlation-based channel model and the more realistic geometry-based stochastic channel model. In the former case, the simulated and theoretical SM efficiencies show perfect agreement. In the latter case, some deviations are observed for the correlation effect on the SM efficiency, and explanations are given. In addition, unlike the previous works [12,13] (where only over-simplified antennas were used), two typical terminal antennas are employed (in addition to dipole antennas) for simulation verifications in this work.

2. Methods

By considering a flat fading channel, the MIMO system can be modeled as $\mathit{y}=\mathit{H}\mathit{x}+\mathit{n}$, where $\mathit{H}$ is the $N_R\times N_T$ channel matrix, $\mathit{x}$ is the transmitted signal vector, $\mathit{y}$ is the received signal vector, and $\mathit{n}$ is the noise vector with independent and identically distributed (i.i.d.) Gaussian variables. For better illustration, only the effect of transmit antennas was studied (assuming ideal receive antennas). As is shown later, the effect of receive antennas on the MIMO throughput is similar. The MIMO channel can be expressed as [14]

$$\mathit{H}={\mathit{H}}_{\mathit{w}}{\mathit{R}}^{1/2}$$

(1)

where ${\mathit{H}}_{\mathit{w}}$ denotes the Rayleigh fading MIMO channel with i.i.d. complex Gaussian variables, $\mathit{R}$ denotes the correlation matrix describing the effects of imperfect antennas on the channel. ${\mathit{R}}^{1/2}$ represents the Hermitian square root of the correlation matrix $\mathit{R}$, which is defined as [11]

$$\mathit{R}={\mathit{e}}^{1/2}\mathit{\Phi }{\mathit{e}}^{1/2}$$

(2)

where $\mathit{\Phi }$ is a matrix consisting of the correlation coefficients, and $\mathit{e}$ denotes a diagonal matrix composed of the mean effective gains (MEGs) [15] of all the transmit antennas. The MEG depends not only on the antenna itself but also on the propagation environment. It reduces to half of the efficiency in an isotropic scattering environment [13]. Since most antenna engineers are not familiar with the MEG, we will use the efficiency in the following expressions, bearing in mind that one can simply replace the efficiency with the MEG in a general multipath environment. Note that in simulations, the power imbalances are calculated as the ratios between different receiving branches, and thus the efficiency/MEG notation does not affect the simulation results. Moreover, note that the correlations in (1) include the mutual coupling effect already [10,11,12,13].

By assuming a zero-forcing (ZF) detector in an open-loop MIMO system, the signal-to-noise ratio (SNR) of the ith data stream can be derived as [14]

$${\gamma }_i=\frac{{\overline{\gamma }}_0}{{[{({\mathit{H}}^{\mathit{H}}\mathit{H})}^{-1}]}_{i,i}}$$

(3)

where ${\overline{\gamma }}_0=E[{|x_i|}^2]/E[{|n_i|}^2]$ with $x_i$ and $n_i$ denoting the ith elements of $\mathit{x}$ and $\mathit{n}$, respectively, and ${[\mathit{X}]}_{i,i}$ denotes the ith diagonal element of the matrix $\mathit{X}$.

Following the same derivation as [12], for a given average SNR ${\overline{\gamma }}_i$ and threshold ${\gamma }_{th}$, the cumulative distribution function (CDF) of ${\gamma }_i$ can be obtained as

$$F\left({\gamma }_{th};{\overline{\gamma }}_i\right)={\rm Y}\left(N_R-N_T+1,\frac{{\gamma }_{th}}{{\overline{\gamma }}_i}\right)/\Gamma \left(N_R-N_T+1\right)$$

(4)

where ${\rm Y}$ is the lower incomplete gamma function, ${\overline{\gamma }}_i={\mu }_i{\overline{\gamma }}_0$, ${\mu }_i=1/{[{\mathit{R}}^{-1}]}_{i,i}$, and $\Gamma$ denotes the Gamma function.

The throughput model was derived in [16]. For a MIMO system, the throughput $T_{put}$ represents the total throughput of all the streams and can be modeled as

$$T_{put}\left(\overline{\gamma }\right)=\frac{T_{put,max}}{N_T}\cdot {\displaystyle \sum }_{i=1}^{N_T}\left(1-F\left({\gamma }_{th};{\overline{\gamma }}_i\right)\right)$$

(5)

where $T_{put,max}$ is the maximum throughput (achieved at a high SNR regime) and $\overline{\gamma }=N_T{\overline{\gamma }}_0$. For simplicity, the relative throughput is adopted in this work, which is defined as $T_{put}/T_{put,max}$.

For a fixed modulation and coding scheme, the SM efficiency can be expressed as [12]

$$e_{mux}=\frac{\overline{\gamma }\left(T_{ref}=x\right)}{\overline{\gamma }\left(T=x\right)}$$

(6)

where $x$ is the relative throughput level, $T_{ref}$ and T denote the relative throughput in an ideal fading channel (with no power imbalance or correlation) and an actual multipath channel (with antenna impairments), respectively, and $\overline{\gamma }\left(T=x\right)$ represents the required SNR value when the relative throughput $T=x$. In this work, 95% was adopted. Note that the SM efficiency is insensitive to the level, and a different level results in an almost identical result.

In order to show the effects of antenna–channel impairments on throughput explicitly, a two-port antenna in $N_R\times 2$ and $N_R\times N_T$ MIMO systems were considered, and we assumed that both cases have $N_R$ ideal receive antennas and focus on the transmit MIMO antenna. The derived results are also applicable to receiving MIMO antenna evaluation with $N_T$ ideal transmit antennas.

2.1. N_R × 2 MIMO System

In this case, ${\mu }_i=e_i(1-{|\rho |}^2)$. At high SNR, the CDF of ${\gamma }_i$ (4) boils down to

$$F({\gamma }_{th};{\overline{\gamma }}_0{e}_i(1-{|\rho |}^2))\approx \frac{{[{\gamma }_{th}/({\overline{\gamma }}_0{e}_i(1-{|\rho |}^2))]}^{N_R-1}}{(N_R-1)!}$$

(7)

where $\rho$ and $e_i \left(i =1, 2\right)$ denote the transmit correlation coefficient and antenna efficiencies (or MEGs), respectively, and $!$ is the factorial operator. By combining (5)–(7), the SM efficiency can be obtained as

$$e_{mux}=2^{\frac{1}{N_R-1}}\cdot {\left(\frac{1}{e_1^{N_R-1}}+\frac{1}{e_2^{N_R-1}}\right)}^{-\left(\frac{1}{N_R-1}\right)}\cdot \left(1-{\left|\rho \right|}^2\right)$$

(8)

For a $2\times 2$ MIMO system, (8) reduces to [12]

$$e_{mux}=2\cdot {\left(\frac{1}{e_1}+\frac{1}{e_2}\right)}^{-1}\cdot \left(1-{\left|\rho \right|}^2\right)$$

(9)

It can be seen that in the case of a $2\times 2$ MIMO system, the impact of power imbalance and correlation on throughput is separable.

2.2. N_R × N_T MIMO System

In this work, we are mainly interested in extending the SM efficiency to high-order MIMO cases, where the UE is equipped with four or more antennas. The corresponding CDF of ${\gamma }_i$ (at high SNR) comes

$$F\left({\gamma }_{th};{\overline{\gamma }}_0{\mu }_i\right)\approx \frac{{\left[{\gamma }_{th}/\left({\overline{\gamma }}_0{\mu }_i\right)\right]}^{N_R-N_T+1}}{\left(N_R-N_T+1\right)!}$$

(10)

By substituting (10) into (5), then the required SNRs to reach the relative throughput level $x$ in the ideal fading channel and the actual multipath channel can be obtained respectively as

$$\overline{\gamma }\left(T_{ref}=x\right)={\gamma }_{th}{N}_T{}^{\frac{1}{N_R-N_T+1}}{\left(\frac{1}{N_T\left(1-x\right)\left(N_R-N_T+1\right)!}\right)}^{\frac{1}{N_R-N_T+1}}$$

(11)

$$\begin{gathered} \overline{\gamma }\left(T=x\right)={\gamma }_{th}{\left(\frac{1}{{\mu }_1^{N_R-N_T+1}}+\frac{1}{{\mu }_2^{N_R-N_T+1}}+\cdots +\frac{1}{{\mu }_{N_T}^{N_R-N_T+1}}\right)}^{\frac{1}{N_R-N_T+1}} \\ {\left(\frac{1}{N_T\left(1-x\right)\left(N_R-N_T+1\right)!}\right)}^{\frac{1}{N_R-N_T+1}}. \end{gathered}$$

(12)

Then, the SM efficiency of the high-order MIMO system can be obtained as

$$e_{mux}=N_T{}^{\frac{1}{N_R-N_T+1}}{\left(\frac{1}{{\mu }_1^{N_R-N_T+1}}+\frac{1}{{\mu }_2^{N_R-N_T+1}}+\cdots +\frac{1}{{\mu }_{N_T}^{N_R-N_T+1}}\right)}^{-\left(\frac{1}{N_R-N_T+1}\right)}$$

(13)

the current 5G UEs are generally equipped with four antennas. For the most commonly used $4\times 4$ MIMO system, (13) reduces to

$$e_{mux}=4{\left(\frac{1}{{\mu }_1}+\frac{1}{{\mu }_2}+\frac{1}{{\mu }_3}+\frac{1}{{\mu }_4}\right)}^{-1}$$

(14)

Unlike previous work, where the 2-port MIMO antennas have only one correlation coefficient, the 4-port MIMO antennas have six non-redundant correlation coefficients. They are all characterized in the correlation matrix $\mathit{R}$:

$$\mathit{R}=\left[\begin{array}{cc}\begin{array}{cc}{e}_1& r_{12}\sqrt{e_1{e}_2}\\ r_{12}^{\ast }\sqrt{e_1{e}_2}& e_2\end{array}& \begin{array}{cc}{r}_{13}\sqrt{e_1{e}_3}& r_{14}\sqrt{e_1{e}_4}\\ r_{23}\sqrt{e_2{e}_3}& r_{24}\sqrt{e_2{e}_4}\end{array}\\ \begin{array}{cc}{r}_{13}^{\ast }\sqrt{e_1{e}_3}& r_{23}^{\ast }\sqrt{e_2{e}_3}\\ r_{14}^{\ast }\sqrt{e_1{e}_4}& r_{24}^{\ast }\sqrt{e_2{e}_4}\end{array}& \begin{array}{cc}{e}_3& r_{34}\sqrt{e_3{e}_4}\\ r_{34}^{\ast }\sqrt{e_3{e}_4}& e_4\end{array}\end{array}\right]$$

(15)

where $r_{\mathrm{mn}}$ represents the correlation coefficient between antenna elements $\mathrm{m}$ and $\mathrm{n}$. Thus, the 4-port MIMO antennas’ SM efficiency is more complicated than in the previous case. Nevertheless, according to the positions of the four antenna elements in the handset, two cases can be assumed to simplify the analyses.

The first case assumes that only element 1 is related to element 2, and element 3 is related to element 4, ignoring the correlations between other elements. (This case is referred to as case A in the sequel. It is a reasonable assumption for self-decoupled antenna pair [17], where two elements in a pair are closely arranged while different antenna pairs can be sufficiently separated. A corresponding handset example is given in Section 3.2.2) The value of $\mu$ can be expressed as

$$\begin{array}{cc}{\mu }_1=e_1\left(1-{\left|r_{12}\right|}^2\right)& {\mu }_1=e_2\left(1-{\left|r_{12}\right|}^2\right)\\ {\mu }_3=e_3\left(1-{\left|r_{34}\right|}^2\right)& {\mu }_4=e_4\left(1-{\left|r_{34}\right|}^2\right)\end{array}$$

(16)

The second case assumes that the correlation only exists between adjacent antenna elements. (This case is referred to as case B in the sequel, and a corresponding handset example is given in Section 3.2.2) The value of $\mu$ can be expressed as

$$\begin{array}{cc}{\mu }_1=e_1\left[1-\frac{{\left|r_{12}\right|}^2-{\left|r_{12}\right|}^2{\left|r_{34}\right|}^2}{1-{\left|r_{23}\right|}^2-{\left|r_{34}\right|}^2}\right]& {\mu }_2=e_2\left[1-{\left|r_{12}\right|}^2-\frac{{\left|r_{23}\right|}^2}{1-{\left|r_{34}\right|}^2}\right]\\ {\mu }_3=e_3\left[1-{\left|r_{34}\right|}^2-\frac{{\left|r_{23}\right|}^2}{1-{\left|r_{12}\right|}^2}\right]& {\mu }_4=e_4\left[1-\frac{{\left|r_{34}\right|}^2-{\left|r_{12}\right|}^2{\left|r_{34}\right|}^2}{1-{\left|r_{12}\right|}^2-{\left|r_{23}\right|}^2}\right]\end{array}$$

(17)

The two cases cover most of the four-port handset antennas. Unlike the previous conclusion for two-port antennas, it can be seen that in the case of $4\times 4$ (high-order) MIMO system, the impact of power imbalance and correlation on throughput is no longer independent.

Furthermore, although the previous derivations are based on transmitting antennas, the results can also be used to characterize receiving antennas [12].

3. Simulations and Results

In this section, we studied the performance degradation caused by joint antenna channel impairments at the receiver. Two channel models were used for simulations. The first one was the correlation-based Kronecker channel model [14] (where the corresponding correlations and power imbalances can be easily specified by (1) and (2)). The second one is the QuaDRiGa channel model [18], which is a geometry-based stochastic channel model (GSCM). (The GSCM was successfully used for MIMO antenna evaluations in realistic multipath scenarios.) The QuaDRiGa channel model was calibrated using measurements from different propagation scenarios. Therefore, the QuaDRiGa channel model was more realistic than the Kronecker channel model. In the following, we show the simulation results using these two channel models separately.

3.1. Simulations with Kronecker Channel Model

In order to characterize the receiver alone, it was assumed that the antennas at the transmitter are uncorrelated. In the simulations, we first generated 10,000 snapshots of the i.i.d. Gaussian matrix $H_w$. Furthermore, correlation and power imbalance could be easily introduced into the MIMO channel via (1) and (2). Based on the channel snapshots, 10,000 instantaneous SNRs were calculated using the ZF algorithm (3). The corresponding empirical CDF was obtained based on these 10,000 SNR samples, and then (5) could be used to calculate the relative throughput.

In order to demonstrate that the derived SM efficiency of a high-order MIMO system can quantitatively describe the degradation of throughput performance, we performed multiple simulations for different correlations and power imbalances, respectively. In this work, the power imbalance was introduced by reducing the efficiency of one of the antennas. Note that in the simulations, the power imbalance has values in the range [0, 10] (unit: dB), with the interval in 1 dB. The range of correlation is [0, 0.9], with an interval of 0.1. 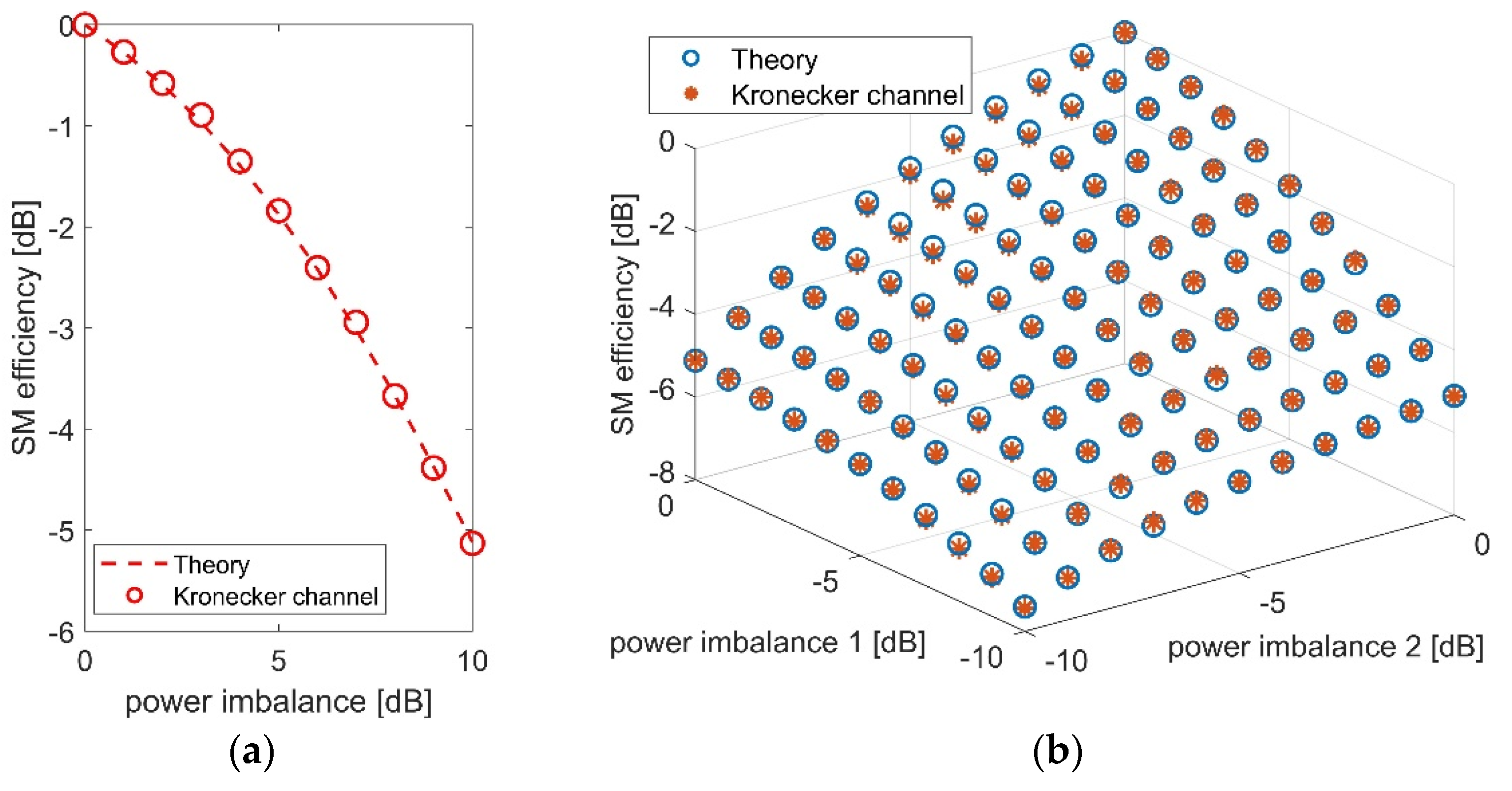Figure 1 shows the SM efficiency of the MIMO antenna in a 4 × 4 MIMO system with power imbalances. (Different power imbalances between all the four branches are inconvenient to exhibit in a graph and thus are omitted here. The corresponding difference is numerically shown in

Table 1. RMSEs (dB) between simulated and theoretical SM efficiencies under different conditions.

Case	Power Imbalances Introduced by Reducing the Efficiency/Efficiencies of			Correlation
	One Element	Two Elements	Three Elements	Case A	Case B
A	0.0359	0.0792	0.0797	0.0221	-
B				-	0.0714

instead.) The results show that the theoretically derived SM efficiency of a high-order MIMO system is in good agreement with simulations. In addition, it can be seen in Figure 1a that the SM efficiency is about −5.1 dB (greater than −7.2 dB in [12]) at a 10-dB power imbalance. This is because the power imbalance in Figure 1a is introduced by reducing the efficiency of one element while the other elements are unchanged, which has a less adverse effect on the throughput performance of a 4-port MIMO antenna than a 2-port MIMO antenna. Figure 2 shows the relationship between correlation and the SM efficiency of case A. It can be seen that the empirical SM efficiency obtained from the simulation agrees perfectly with the theoretical one.

In order to show the agreement between the simulated and the theoretical SM efficiencies in different conditions quantitively, we used the root mean square error (RMSE) to represent the difference between simulation and theory. As shown in Table 1, the RMSEs between the simulated and theoretical SM efficiencies for case A and case B remain at a very low level (less than 0.1) under all conditions.

3.2. Simulations with QuaDRiGa Channel Model

In order to obtain more specific antenna examples, we used the QuaDRiGa channel model for simulations. The QuaDRiGa channel model can support more realistic channel simulations by importing the actual antenna patterns and simulating the channel impulse responses (CIR). However, it is important to note that we cannot directly specify correlations and power imbalances in the QuaDRiGa channel model. Instead, we needed to change the spacing and angle between the antennas to control the power imbalances and correlations indirectly. In the following, we presented the simulation results using the dipole antennas and the actual terminal antennas at the UE, respectively.

3.2.1. Simulations with Dipoles

The simulation parameters are listed in

Table 2. List of simulation parameters.

Scenario	Cluster	Inter-Antenna Spacing of BS	UE Distribution Radius	Drops
Indoor	16	5 wavelengths	15~25 m	10,000
UMa	25		50~1000 m

. We chose the indoor non-line-of-sight (NLOS) and the urban-macrocell (UMa) NLOS scenarios in the QuaDRiGa channel model for simulations at 5 GHz. In order to make the correlation and power imbalance controllable, we assumed that both the base station (BS) and the UE are linear arrays of four half-wave dipoles. Since we mainly studied the handset antennas, it was assumed that the BS is located in the center of the environment, and the BS dipoles are vertically polarized with an inter-antenna spacing of five wavelengths (ensuring negligible correlations at the BS side). For the indoor scenario, the UE was randomly distributed around the BS with a distance range of 15 to 25 m from the BS (i.e., a typical radius setting for the indoor hotspot scenario [19]). For the UMa scenario, the UE has a distance range of 50 to 1000 m from the BS. By changing the settings (angle and spacing) of the UE dipoles, we could obtain different power imbalances and correlations. Ten thousand drops were generated for every setting of the UE dipoles.

In order to study the power imbalance effect alone, the UE dipoles were assumed to be vertically polarized with an inter-antenna spacing of four wavelengths (ensuring negligible correlations). By gradually rotating one (or two) antennas from vertical to horizontal polarization, we created different power imbalances thanks to the cross-polarization ratio of the propagation channel. In order to study the correlation effect without power imbalance, the UE dipoles were fixed to be vertically polarized. By gradually reducing the antenna spacing from 4 wavelengths to 0.1 wavelengths, different correlations could be realized.

Figure 3 and Figure 4 show the SM efficiencies of the MIMO antennas with different power imbalances and correlations, respectively. For the power imbalance effect, we can see that the theoretically derived SM efficiency can be a good predictor of the simulated SM efficiency using the QuaDRiGa channel model. (Since the results of UMa are similar to those of the indoor case, only the results in the indoor scenario are shown here.) However, for the correlation effect, there is a noticeable deviation between the simulation results and the theoretical ones in the indoor scenario (as shown in Figure 4a). The discrepancy is mainly attributed to the fact that the MIMO channel simulated using the QuaDRiGa channel model does not satisfy joint Gaussianity or multivariate normality (MVN) [20], whereas the theoretical SM efficiency is derived based on the assumptions that the MIMO channel H is jointly Gaussian so that H^HH follows the Wishart distribution [21]. Therefore, due to the non-MVN of the simulated MIMO channel, there will be modeling errors.

In order to explain this further, we examined the simulated SM efficiency of the correlation effect in the UMa scenario (as shown in Figure 4b). It can be seen that the simulation results were greatly improved and are in good agreement with the theoretical ones. This is because there are only 16 clusters in the indoor scenario, while the UMa scenario has 24 clusters. More clusters mean richer multipath, which results in better Gaussianity of the simulated MIMO channel. Therefore, the modeling errors in the UMa scenario would be reduced. Furthermore, such results further illustrate that the proposed SM efficiency is more applicable for the environment of Gaussian channels.

Moreover, we used RMSE as the quantitative metric to represent the difference between the simulated and the theoretical SM efficiencies in different scenarios, as shown in

Table 3. RMSEs (dB) between simulated and theoretical SM efficiencies with the QuaDRiGa channel model.

Power Imbalances Introduced by Rotating (Indoor)		Correlation
One Element	Two Elements	Indoor	UMa
0.09	0.18	2.92	0.87

. For the power imbalance effect, the RMSEs between the simulated and theoretical SM efficiencies remained at a very low level. For the correlation effect, the RMSE was as high as 2.92 for the indoor scenario, while the error of the UMa scenario (with better Gaussianity) was greatly improved (dropped to 0.87).

3.2.2. Simulations with Representative Terminal Antennas

In order to have specific antenna examples, we used two types of representative terminal antennas [17,22] as MS for channel simulations. Figure 5 shows the perspective views of the two terminal MIMO antenna models, respectively. To simplify, we refer to Figure 5a as handset 1 and Figure 5b as handset 2. More detailed antenna parameters can be found in [17,22]. In the following, we considered both four-port and eight-port MIMO antennas for channel simulations (where the four-port case only contains four antennas on one side of the handsets). For the four-port MIMO antenna, we can see that handset 1 is similar to case A as we mentioned before (i.e., only element 1 is related to element 2, and element 3 is related to element 4. For example, the simulation results in the indoor scenario show that $r_{12}$ and $r_{34}$ are about 0.37, and the other correlations are lower than 0.1), and handset 2 is similar to case B (i.e., the correlation only exists between adjacent antenna elements. For example, the simulation results in the indoor scenario show that the correlations between elements are all below 0.1). In addition, the simulation frequencies of handsets 1 and 2 were set to 3.66 GHz and 3.5 GHz, respectively. The other scenario parameters are the same as in Table 3.

The results are shown in

Table 4. SM efficiencies (dB) of two types of terminal MIMO antennas.

MIMO Order	Scenario	Handset 1 (Theory/Simulation)	Handset 2 (Theory/Simulation)
4 × 4	Indoor	−1.24/−3.73 (dB)	−0.20/−2.21 (dB)
	UMa	−0.44/−0.99 (dB)	−0.29/−0.46 (dB)
8 × 8	Indoor	−1.26/−3.82 (dB)	−0.42/−3.75 (dB)
	UMa	−0.52/−1.50 (dB)	−0.53/−0.90 (dB)

. We can see that in the indoor scenario, the simulated SM efficiency differs from the theoretical one by 2~3 dB due to the presence of modeling errors, as explained before. However, for the UMa channel environment with better Gaussianity, the error between the simulated results and the theoretical one can be controlled within 1 dB.

4. Conclusions

In this work, we extended the SM efficiency metric for evaluating the throughput performance of high-order handset MIMO antennas. It was found that the effects of power imbalances and correlations on throughput are no longer separable in a high-order MIMO system. In addition, both the correlation-based and geometry-based stochastic channel models were employed to verify the derived SM efficiency. In the case of the Kronecker channel model, the simulated SM efficiency is in perfect agreement with the theoretical SM efficiency. In the case of the QuaDRiGa channel model, mild deviations of the correlation effect on the SM efficiency were observed. This is because the SM efficiency model is derived under the assumption of the MVN channel, while the simulated MIMO channel is not jointly Gaussian, which is the main contribution to the modeling error. Therefore, the SM efficiency model derived in this paper is more inclined to be used for evaluating Gaussian-like channel scenarios (i.e., rich multipath environments), which may be strenuous for non-Gaussian channels (i.e., sparse multipath environments). Nevertheless, the agreements are still reasonable, and the theoretical SM efficiency predicts the same trend as the simulated one. More importantly, the derived SM efficiency offers insight into the antenna impairments in high-order MIMO systems.