An Efficient Random Access Reception Algorithm for ToA Estimation in NB-IoT
Abstract
:1. Introduction
2. System Model
2.1. Basics in Random Access of the NB-IoT
2.2. Random Access Procedure
3. Proposed Method for ToA Estimation
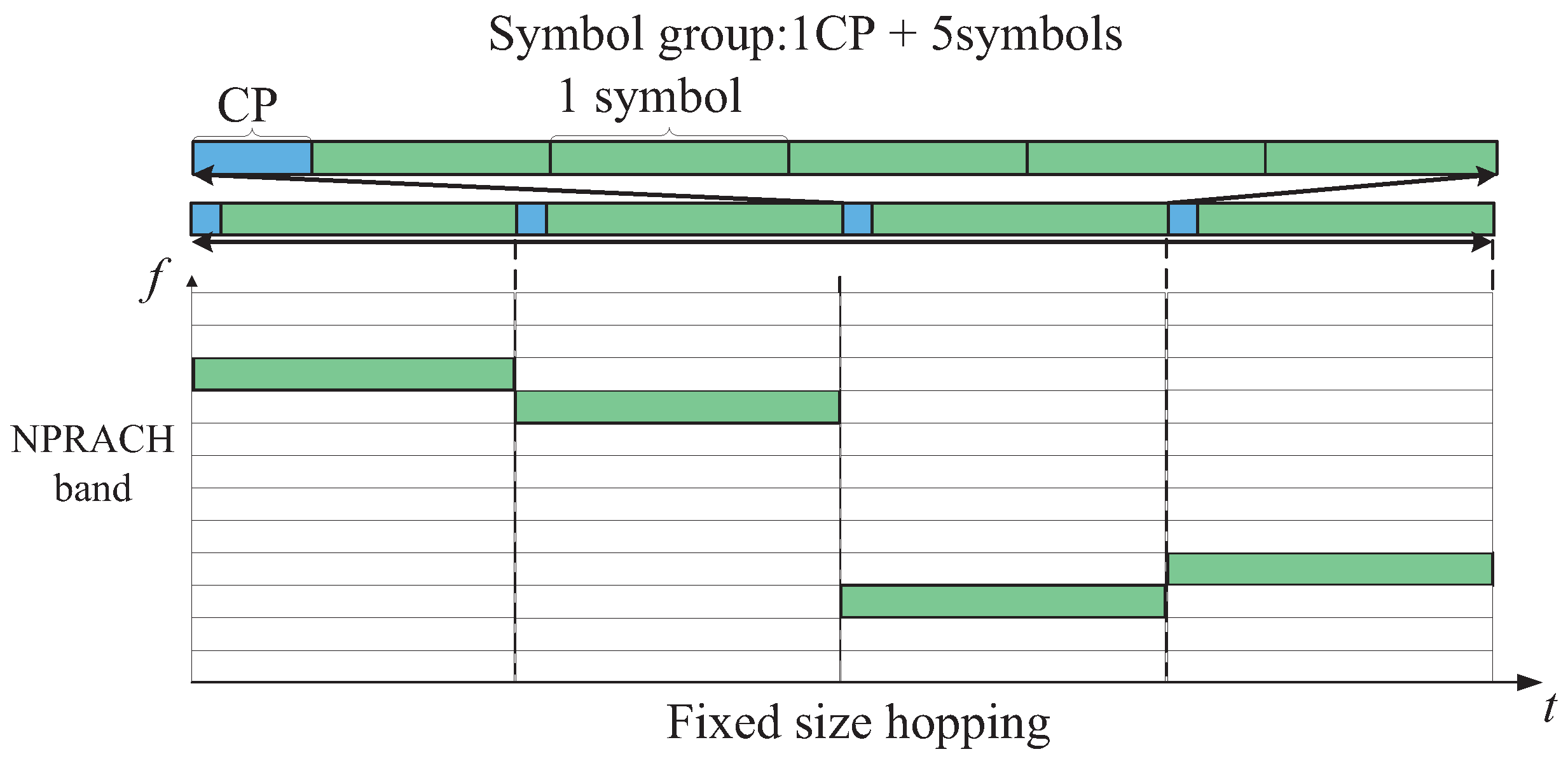
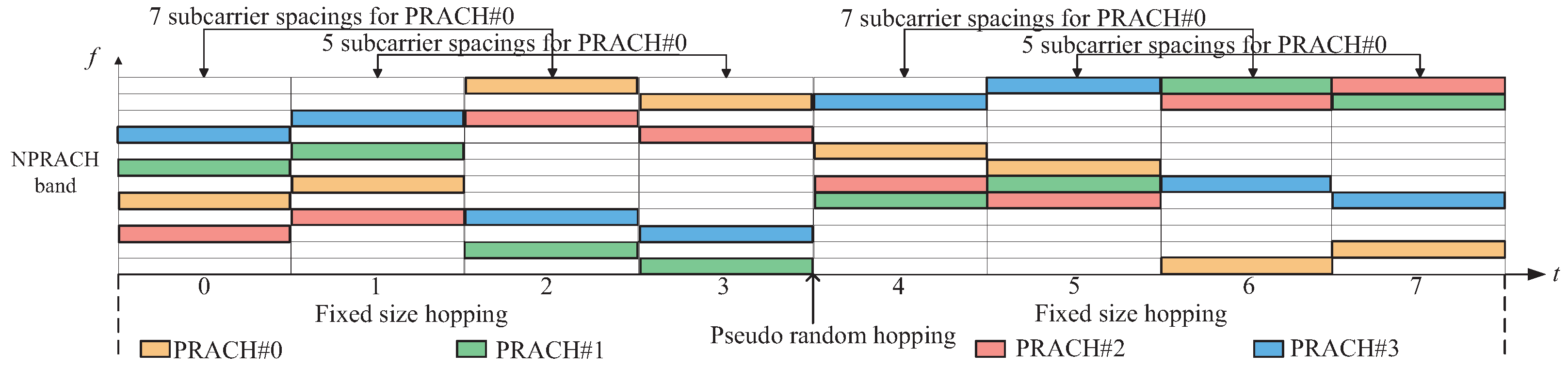
3.1. Effect of the Hopping Distance on ToA Estimation
3.2. Proposed Reception Algorithm
3.3. Complexity Analysis
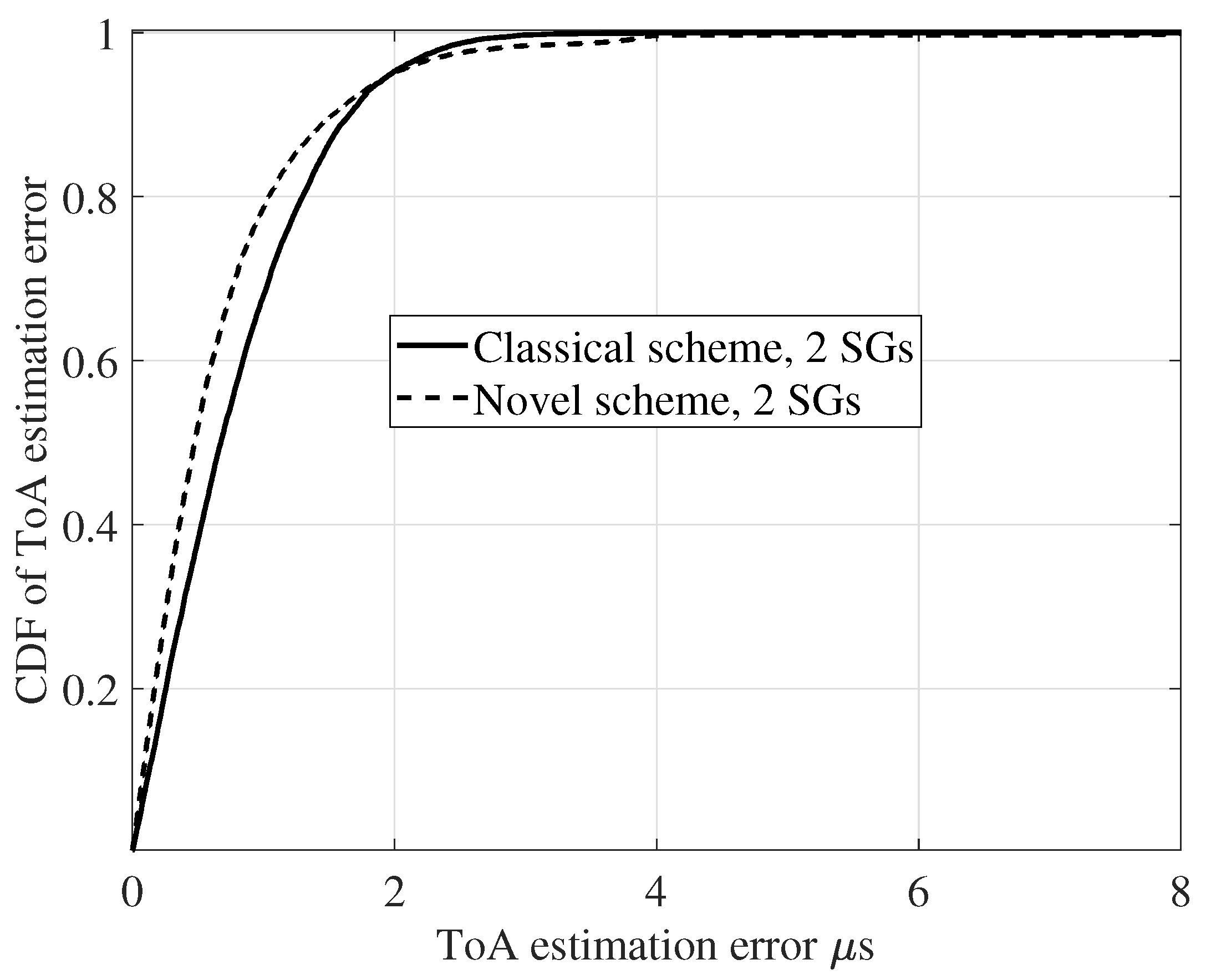
4. Simulation Results
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Kong, D.; Xu, Y.; Song, G.; Li, J.; Jiang, T. A CP reduction scheme based on symbol repetition for Narrow-Band IoT systems. IEEE Internet Things J. 2021, 8, 12880–12891. [Google Scholar] [CrossRef]
- Kanj, M.; Savaux, V.; Le Guen, M. A tutorial on NB-IoT physical layer design. IEEE Commun. Surv. Tutor. 2020, 22, 2408–2446. [Google Scholar] [CrossRef]
- Jeon, W.S.; Seo, S.B.; Jeong, D.G. Effective frequency hopping pattern for ToA estimation in NB-IoT random access. IEEE Trans. Veh. Technol. 2018, 67, 10150–10154. [Google Scholar] [CrossRef]
- Yu, T.; Zhuang, C.; Zhang, Z.; Zhou, W. Joint DOA and TOA Estimation for Multipath OFDM Signals Based on Gram Matrix. In Proceedings of the 2021 7th International Conference on Computer and Communications (ICCC), Chengdu, China, 10–13 December 2021; pp. 479–484. [Google Scholar]
- Li, Y.; Long, Q.; Wang, C.; Zhou, Z.; Jin, T.; Oh, D. Adaptive Subspace Classification Technique Using Fuzzy Support Vector Machine for Supspace-based TOA Estimation in a Multipath Channel. In Proceedings of the 2022 IEEE 5th International Conference on Electronic Information and Communication Technology (ICEICT), Hefei, China, 21–23 August 2022; pp. 543–547. [Google Scholar]
- Shimoshige, K.; Tategami, K.; Fujimoto, M. Acceleration of DOA-TOA Simultaneous Estimation by Matrix Based Compressed Sensing with Zero Bin Removal. In Proceedings of the 2020 International Symposium on Antennas and Propagation (ISAP), Osaka, Japan, 25–28 January 2021; pp. 605–606. [Google Scholar]
- Li, H.; Fan, Y. Fast Joint TOA and AOA Estimation for Multipath Signals Based on Improved Propagator Method. In Proceedings of the 2022 IEEE 5th Advanced Information Management, Communicates, Electronic and Automation Control Conference (IMCEC), Chongqing, China, 16–18 December 2022; Volume 5, pp. 934–940. [Google Scholar]
- Nouali, I.Y.; Slimane, Z.; Abdelmalek, A. Change Point Detection-Based TOA Estimation in UWB Indoor Ranging Systems. In Proceedings of the 2022 45th International Conference on Telecommunications and Signal Processing (TSP), Prague, Czech Republic, 13–15 July 2022; pp. 329–332. [Google Scholar]
- Wu, M.; Hao, C. Super-Resolution TOA and AOA Estimation for OFDM Radar Systems Based on Compressed Sensing. IEEE Trans. Aerosp. Electron. Syst. 2022, 58, 5730–5740. [Google Scholar] [CrossRef]
- Pan, M.; Liu, P.; Liu, S.; Qi, W.; Huang, Y.; You, X.; Jia, X.; Li, X. Efficient Joint DOA and TOA Estimation for Indoor Positioning With 5G Picocell Base Stations. IEEE Trans. Instrum. Meas. 2022, 71, 8005219. [Google Scholar] [CrossRef]
- Bang, J.H.; Park, D.H.; Kim, H.N. Improved TOA and Pulse Width Estimation for Wideband Signal in Electronic Warfare Systems. In Proceedings of the 2022 19th European Radar Conference (EuRAD), Milan, Italy, 28–30 September 2022; pp. 73–76. [Google Scholar]
- Pan, M.; Liu, P.; Li, X.; Liu, S.; Qi, W.; Huang, Y. A Low-Complexity Joint AOA and TOA Estimation Method for Positioning with 5G Signals. In Proceedings of the 2021 CIE International Conference on Radar (Radar), Haikou, China, 15–19 December 2021; pp. 2912–2916. [Google Scholar]
- Gong, Z.; Wu, L.; Zhang, Z.; Dang, J.; Zhu, B.; Jiang, H.; Li, G.Y. Joint TOA and DOA Estimation with CFO Compensation Using Large-Scale Array. IEEE Trans. Signal Process. 2021, 69, 4204–4218. [Google Scholar] [CrossRef]
- Pan, M.; Liu, P.; Jia, X.; Liu, S.; Qi, W.; Huang, Y. A Joint DOA and TOA Estimation Scheme for 5G Signals Under Array Modeling Errors. In Proceedings of the 2021 CIE International Conference on Radar (Radar), Haikou, China, 15–19 December 2021; pp. 1822–1826. [Google Scholar]
- Zhu, J.; Kouda, E.; Hou, P.; Nagayama, K.; Hou, Y.; Denno, S. Indoor Simultaneous TOA Estimation of Multiple Users Using Leaky Coaxial Cable. In Proceedings of the 2022 IEEE 4th Global Conference on Life Sciences and Technologies (LifeTech), Osaka, Japan, 7–9 March 2022; pp. 297–298. [Google Scholar]
- Ramirez-Arroyo, A.; Alex-Amor, A.; Padilla, P.; Valenzuela-Valdes, J.F. Joint Direction-of-Arrival and Time-of-Arrival Estimation with Ultra-wideband Elliptical Arrays. IEEE Trans. Wirel. Commun. 2023. [Google Scholar] [CrossRef]
- Wei, Q.; Chen, X.; Jiang, C.; Huang, Z. Time-of-Arrival Estimation for Integrated Satellite Navigation and Communication Signals. IEEE Trans. Wirel. Commun. 2023. [Google Scholar] [CrossRef]
- Liu, Z.; Chen, L.; Zhou, X.; Jiao, Z.; Guo, G.; Chen, R. Machine Learning for Time-of-Arrival Estimation With 5G Signals in Indoor Positioning. IEEE Internet Things J. 2023, 10, 9782–9795. [Google Scholar] [CrossRef]
- Chougrani, H.; Kisseleff, S.; Chatzinotas, S. Efficient preamble detection and Time-of-Arrival estimation for single-tone frequency hopping random access in NB-IoT. IEEE Internet Things J. 2021, 8, 7437–7449. [Google Scholar] [CrossRef]
- Lin, X.; Adhikary, A.; Wang, Y.P.E. Random access preamble design and detection for 3GPP Narrowband IoT systems. IEEE Wirel. Commun. Lett. 2016, 5, 640–643. [Google Scholar] [CrossRef] [Green Version]
- Chakrapani, A. NB-IoT uplink receiver design and performance study. IEEE Internet Things J. 2020, 7, 2469–2482. [Google Scholar] [CrossRef] [Green Version]
- 3GPP TS 36.211. Physical Channels and Modulation; Release 13 V13.7.1; ETSI: Sophia Antipolis, France, 2017.
- Dian, F.J.; Vahidnia, R. NB-IoT preamble signal: A survey. In Proceedings of the 2021 IEEE 7th World Forum on Internet of Things (WF-IoT), New Orleans, LA, USA, 14 June–31 July 2021; pp. 107–112. [Google Scholar]
- R1-160025. NB-PRACH design. In Proceedings of the 3GPP TSG RAN WG1 NB-IoT Ad-Hoc Meeting, Sophia Antipolis, France, 22–24 March 2016.
- 3GPP TS 36.104. Base Station (BS) Radio Transmission and Reception; Release 14 V14.5.0; ETSI: Sophia Antipolis, France, 2017.

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, S.; Xiang, T.; Huang, D.; Han, L.; Wu, Q.; Kong, D. An Efficient Random Access Reception Algorithm for ToA Estimation in NB-IoT. Electronics 2023, 12, 2636. https://doi.org/10.3390/electronics12122636
Li S, Xiang T, Huang D, Han L, Wu Q, Kong D. An Efficient Random Access Reception Algorithm for ToA Estimation in NB-IoT. Electronics. 2023; 12(12):2636. https://doi.org/10.3390/electronics12122636
Chicago/Turabian StyleLi, Shengyong, Tian Xiang, Ding Huang, Ling Han, Qi Wu, and Dejin Kong. 2023. "An Efficient Random Access Reception Algorithm for ToA Estimation in NB-IoT" Electronics 12, no. 12: 2636. https://doi.org/10.3390/electronics12122636





