Abstract
Aiming at the problem of low throughput and energy efficiency caused by the mutual restriction of energy efficiency and spectral efficiency in massive MIMO systems and the fact that resource allocation does not consider the factors of user service QoS and the upper and lower speed limits, a resource joint optimization method based on user service QoS guarantee is proposed. The method first performs user scheduling according to service delay and channel state under the condition of equal power distribution and calculates the current system capacity, and then combines transmit antenna power and service QoS constraints to redistribute power, and corrects the system capacity, establishing the objective function for the joint optimization of the spectral efficiency and energy efficiency. An algorithm combining deep learning and Q learning is used to solve the problem, and finally, the purpose of joint optimization is achieved. The simulation shows that the joint optimization method proposed in this paper can control the timeout of user data packets more finely and, at the same time, obtain greater energy efficiency and throughput.
1. Introduction
Multiple-Input and Multiple-Output (MIMO) technology has gradually matured after years of development and has become one of the key technologies used in intelligent communication [1], and this technology enables communication systems to obtain higher transmission rates, system capacity, and spectral efficiency [2]. In the field of wireless communication, because different types of services have different requirements for QoS (quality of service, QoS) latency and rate, and when considering resource allocation, it is necessary to take user service as the premise. Due to the limited spectrum resources and the demand for high-rate capacity, spectrum efficiency as a traditional performance index has long been widely studied [3]. At the same time, with the need for the future development of green communication, the spectrum efficiency of the system is no longer blindly pursued; therefore, the optimization index of energy efficiency has emerged, and the improved energy efficiency means that the energy consumption of the system can be reduced [4]. In the real environment, the RF link corresponding to each antenna in the MIMO system has a certain power consumption, and in the traditional MIMO system, due to the small number of antennas, the power consumption generated by this part of the RF link can usually be ignored. However, massive MIMO systems are equipped with a large number of antennas, resulting in circuit power consumption that cannot be ignored anymore [5]. With an increasing number of antennas, the spectral efficiency of the system will continue to increase, while the energy efficiency will increase to a certain extent and then begin to decline, and the two restrict each other, presenting a contradictory relationship [6], and it is difficult to achieve relative optimization at the same time. Therefore, for massive MIMO systems, the joint optimization of spectral efficiency and energy efficiency is still worth exploring.
Many scholars, both domestically and internationally, have conducted research on this topic. The research in [7] proposes a power allocation method based on the maximum and minimum fairness criteria under massive MIMO systems, which maximizes the worst signal-to-noise ratio of all users and ensures the average performance for the users but does not consider the type of service and does not meet the QoS requirements of the users. The research conducted in [8] studies the power allocation problem of massive MIMO systems and proposes a power allocation method using the asymptotic concave formation of the system sum rate, and the sum rate of the system increases with the increased number of antennas but ignores the index of spectral efficiency. The research in [9] proposes a beam allocation and power optimization scheme, which is solved by expressing the problem of beam allocation and power optimization as a multivariate mixed integer nonlinear programming problem. This scheme has certain research value but does not consider the user’s QoS index. The research carried out in [10] considers the QoS delay requirements of user services and the fairness of occupying wireless channels, and a power allocation strategy based on user expectations and pre-allocation is proposed to improve user satisfaction and fairness between users but the influence of channel status information is not considered. The research in [11] uses power allocation to obtain optimal energy efficiency, but the default number of users meets the antenna restriction conditions, which is not in line with the access situation of users in practical applications. The research in [12] obtains optimal energy efficiency through power allocation but does not add the limitation of the transmission power of the base station antenna, which will cause the power allocation to lose practical significance. The research in [13] proposes a joint optimization design method for antenna selection and power distribution in massive MIMO systems. The research in [14] optimizes energy efficiency under the constraints of spectral efficiency. The research in [15] proposes an optimization algorithm for the energy efficiency of a massive MIMO system based on the particle swarm optimization algorithm, which takes the transmit power and the number of antennas in the system as the decision variables in the optimization, and uses the improved particle swarm optimization algorithm to solve it, which has certain advantages, but does not consider the factors of the number of users and user service. The research in [16] takes the transmit power and the number of transmitting antennas as the decision variables to obtain the joint optimization problem of spectral efficiency and energy efficiency and then maps it to the NSGA-II algorithm for solving but does not consider the user-side situation, and there are few comparative experiments. With the continuous development of deep learning, neural networks have been applied to resource allocation, electromagnetism, and antenna fields. As described in document [17], neural networks have been used in the field of communication resource allocation. Using a well-trained network to solve the resource allocation problem has very close performance and low computational complexity compared with traditional mathematics algorithms. The research in [18] points out that neural networks in deep learning have made a breakthrough in terms of the antenna used for environmental sensing. The research in [19] utilized deep neural networks for resource allocation among multiple users in MIMO systems. Firstly, the objective function is optimized based on the multi-objective sine c–sine algorithm. Secondly, the demand level of each user is identified, and a deep neural network algorithm is used to solve the problem, which to some extent, improves the system performance. However, the default number of users is less than the antenna limit, and there is no user scheduling, which is not in line with the actual situation.
According to the above analysis, there is little literature that has studied the joint optimization problem of energy efficiency and spectral efficiency based on the user service QoS guarantee. Therefore, the research in this paper is carried out in two steps, firstly, user scheduling is carried out under the condition of ensuring the QoS delay requirements of users, and the system capacity is maximized on the basis of equal power distribution. Then, the power of the scheduled users is re-distributed, the system energy efficiency is optimized on the basis of the refined QoS rate requirements, and the system capacity after adjusting the power is not lower than the system capacity in the first step of scheduling so as to establish a joint optimization problem, and finally, the Deep Q-Leaning Network (DQN) algorithm is to solve the problem.
The main contributions of this article are as follows: Before resource allocation, users are scheduled based on their business latency and channel state information to improve the satisfaction of different users. Based on the refinement of the QoS rate requirements, optimize system energy efficiency and ensure that the system capacity after power adjustment is not lower than the system capacity during the first step of scheduling in order to establish a joint optimization problem. Utilize the DQN algorithm to solve problems and improve system performance.
2. Problem Modeling
Firstly, a multi-user massive MIMO system model is established, and the block diagonalization precoding method is used under this system model equivalent to the multi-user system as a single-user system in order to eliminate the interference of other users [20]. Then, based on the average power allocation, user scheduling is carried out based on service QoS delay requirements and channel status, and the system capacity is calculated. Then, under the requirements of ensuring the upper and lower limits of transmitter power and QoS rate, the selected users are reallocated to optimize the system’s energy efficiency, the system capacity in the scheduling stage is corrected, and the objective function of the spectrum efficiency and energy efficiency joint optimization is established to achieve a compromise between the two.
2.1. System Model
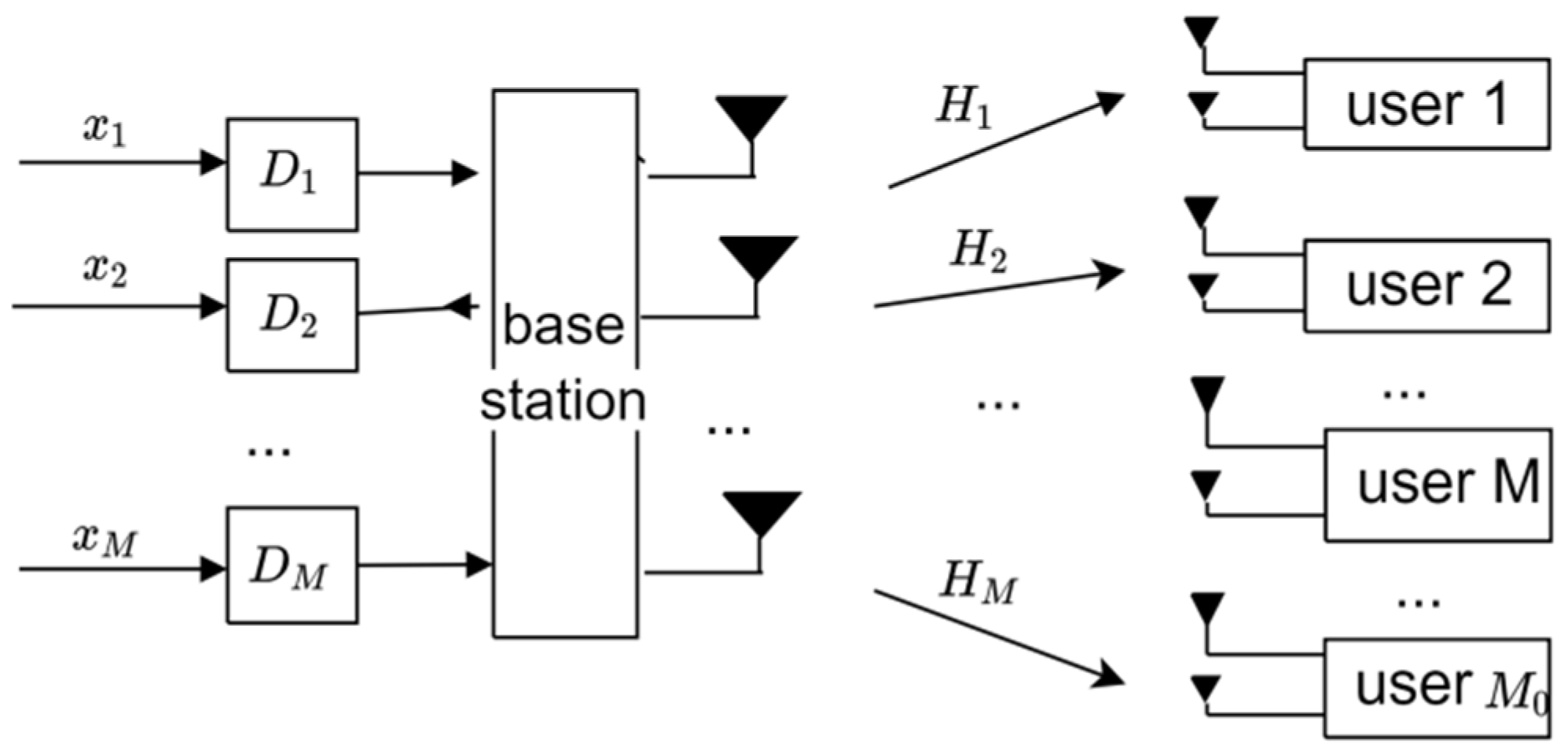
This paper takes the downlink of a multi-user massive MIMO system as the background, assuming that the base station has transmitting antennas and users, and if the number of receiving antennas for the mth user is , the base station can support M users to communicate at the same time in each scheduling time slot. The system model is shown in Figure 1.
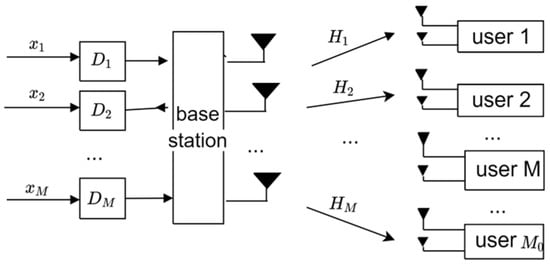
Figure 1.
Downlink channel model of multi-user MIMO system.
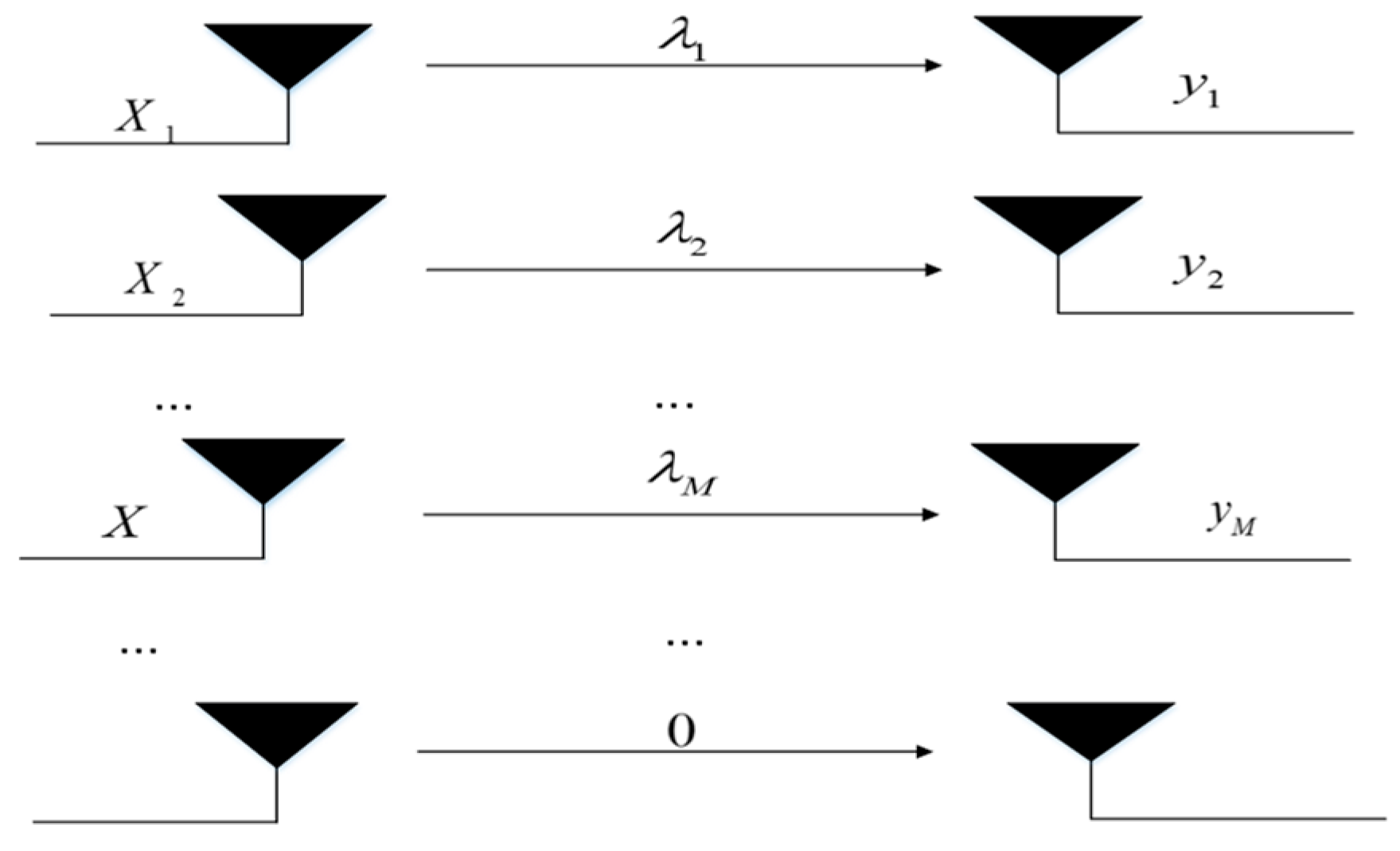
In a massive MIMO system, in order to improve the spectral efficiency of the system, all users are allowed to reuse the same time–frequency resources. In this way, each user will receive signals from other users in addition to receiving the signals they need, resulting in inter-user interference. Therefore, in the transmitter end of the downlink system, it is generally necessary to use precoding technology to preprocess the transmitted signal in order to increase the signal-to-noise ratio, thereby accelerating the data transmission rate and improving the performance of the entire system. In this paper, block diagonalization precoding is used to decompose the downstream channel matrix of a multi-user MIMO system into a block diagonalized form, which is equivalent to multiple single-user MIMO systems that do not interfere with each other, eliminating interference from other users. The equivalent channel model is shown in Figure 2.
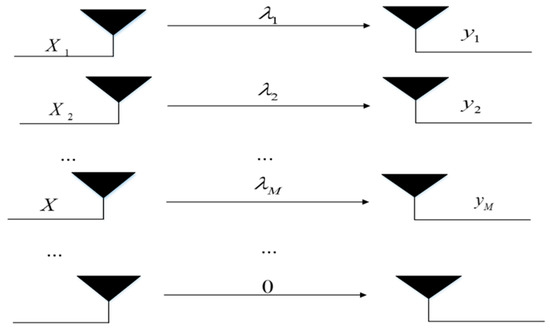
Figure 2.
Equivalent channel model.
Assuming that the channel state information of the base station transmitter is known, represents the transmit signal vector of the mth user, and represents the received signal vector of the mth user, and then there are:
where represents the signal required by the mth user, represents interference from other users, and represents additive white Gaussian noise in the mth user channel. represents the complex Gaussian random channel matrix for the mth bit, and represents the precoded matrix for the mth use. Block diagonalization is applied to find the pre-coded matrix, , so that the interference from other users is zero, and for the mth user, the matrix consisting of the channel matrix of the other users is as follows:
where is the -dimensional full-rank matrix. Decomposing by singular value yields the following:
where is the unitary matrix of order , is a diagonal matrix composed of non-zero singular values of , is the conjugate transpose matrix of , consisting of and , is composed of right singular vectors corresponding to non-zero singular values of , and is composed of right singular vectors corresponding to zero singular values.
According to the unitary matrix property: ; therefore, Equation (3) can be written as follows:
Multiplying the left and right of formula (6) together gives:
According to (7), for the mth user, can eliminate the interference of other users, and in order to solve the equation system, needs to be satisfied, which is the use of the block diagonalization method to remove multi-user interference on the user scheduling scheme constraints; that is, the maximum number of simultaneous communication users M limit.
Further, let and perform singular value decomposition to obtain:
where is an -dimensional matrix, is a -dimensional unitary matrix, is a -dimensional matrix, is a diagonal matrix composed of non-zero singular values, and is composed of right singular vectors corresponding to non-zero singular values of .
Take the block diagonalized precoded matrix of and substitute into Equation (1) to obtain the following:
where is the equivalent channel matrix. Substituting Equation (8) into (9) yields:
Multiply on both sides to obtain:
where and are the diagonal matrices in which the diagonal elements are not zero and the other elements are all zero. Let the diagonal element of be and let to have .
Block diagonalized precoding equates multi-user channels to multiple independent single-user channels, which in turn can be equivalent to multiple parallel channels. At this point, the data rate of the mth user after bandwidth normalization can be expressed as follows:
where represents the signal power of the mth user on the kth parallel channel, the diagonal element of represents the channel fading coefficient, and represents the power of additive white Gaussian noise.
2.2. User Scheduling
In practical applications, due to the burstiness of users, the number of users accessing the system will be greater than the limit of the number of antennas at the base station end; therefore, user scheduling is required first in resource allocation, and M users are selected in each scheduling time slot to maximize system throughput while ensuring user service QoS requirements.
This article discusses four types of user services: conversational class, streaming class, interaction class, and background class. The conversational class focuses on real-time requirements, and the most critical QoS indicator is latency, which is very severe and will cause the session to fail to proceed normally; therefore, latency is listed as an important indicator affecting the conversational class. The streaming class does not require interactions between two users, and data are only transmitted in one direction; therefore, the service has certain real-time requirements but is not as strict as the conversational class. Compared with the previous two, the delay requirements of the interactive class are not high. The background class basically has no hard requirements in terms of delay. Therefore, this article takes latency as the indicator of the QoS requirements in the user scheduling stage and specifies that the delay requirement is the maximum time that data are waiting in the queue. Table 1 shows the rate and delay requirements of the four services.

Table 1.
Business Description.
Among them, the conversation class pays the most attention to real-time experiences, and the most critical QoS indicator is delay, which will cause the session to not continue normally when the delay is very serious. In the streaming class, data are transmitted in one direction, which has certain real-time requirements, but it is not as strict as that of the conversational class. Compared with the previous two, the delay requirements of the interactive class are not so strict. The background class only cares about whether the data are transmitted correctly and almost do not require delay. In summary, this chapter takes delay as the QoS metric in the user scheduling stage and specifies that the delay requirement is the maximum time that data wait in the queue.
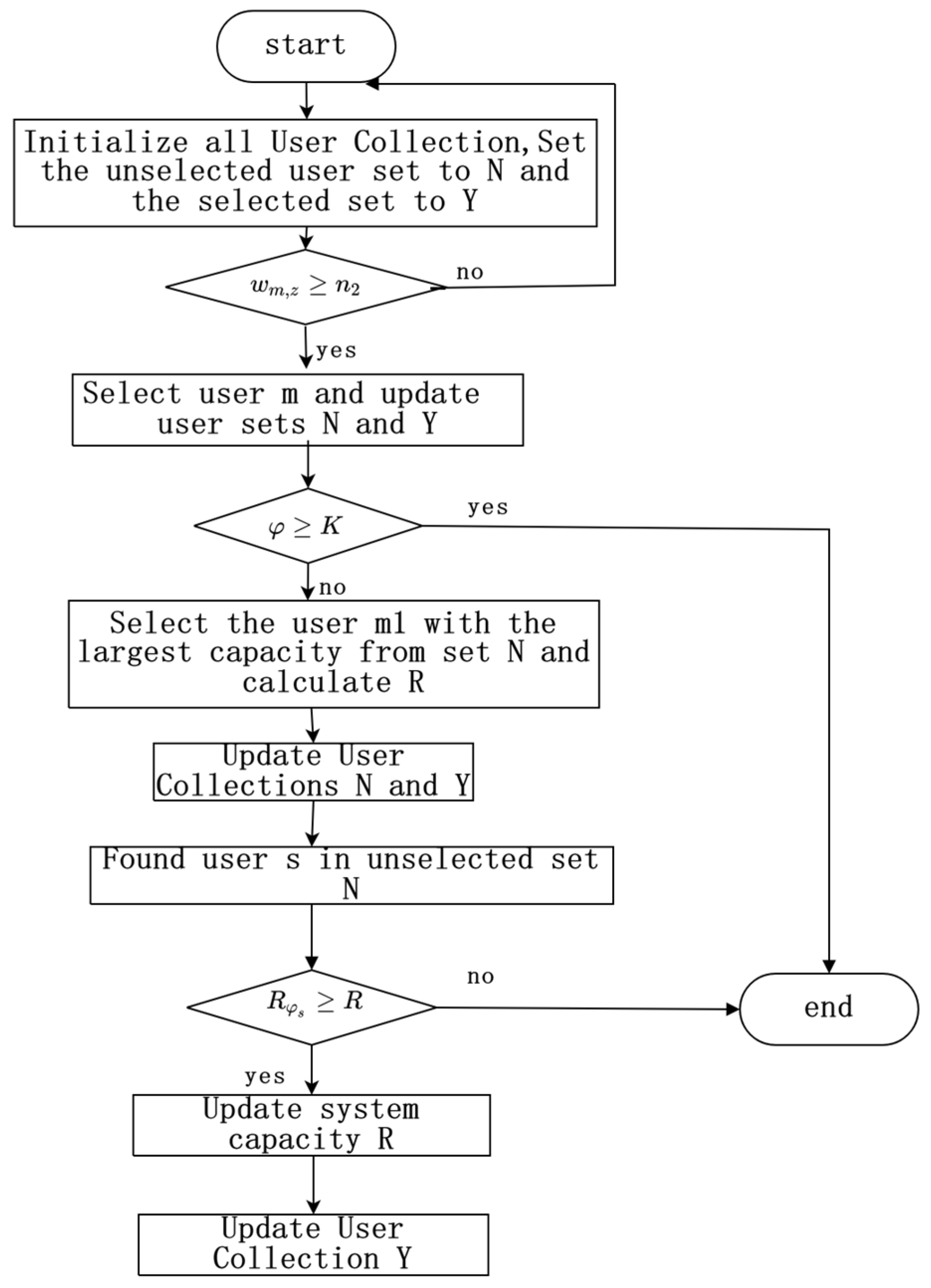
The number of antennas used in real life is not enough for users to use according to the above business characteristics, which for delay requirements, often need user scheduling in order to be achieved, assuming that users only use one service in a certain time slot, in the user scheduling stage, consider the user’s service delay and channel status, set the number of user waiting time slots to , the maximum number of waiting time slots to , set a scheduling cycle to t, and the delay requirement is expressed by the maximum number of waiting cycles: . When scheduling, first dispatch the user services that is about to reach or exceed , and if all the users who meet the conditions have been accessed but there are still antennas left, the channel state information of the user is considered. The user scheduling process is shown in Figure 3:
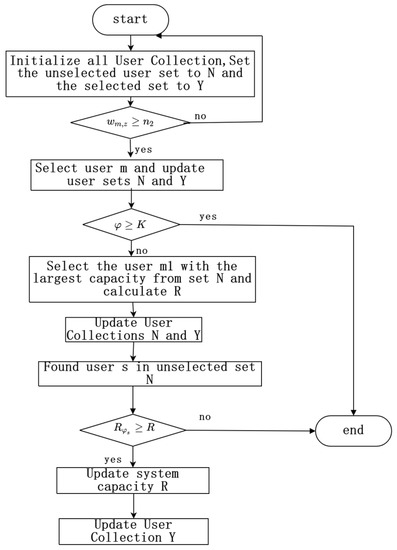
Figure 3.
User scheduling flow chart.
As can be seen from the above flowchart, the specific execution method of user scheduling is:
- Step 1: Initialize all user collections, set the unchecked collection to and the selected collection to .
- Step 2: Determine the number of waiting time slots for each service , and if , select User M. Update the user collection, selected, unchecked.
- Step 3: If the number of selected users exceeds the antenna limit, it ends. Otherwise, select User that satisfies . At this point , update the user collection , .
- Step 4: Iterate through the remaining user collection N. For each user s in N, define and calculate the capacity of set : . In set N, if a user satisfies , let at this time. Otherwise, end the algorithm and then update and update user collection , .
- Step 5: Repeat step 4 to finally update the user collection.
2.3. Joint Optimization Function Establishment
After user scheduling, it can ensure the delay requirements of the user’s business. However, this stage is performed under the circumstances of average power distribution. Therefore, it is necessary to redistribute power and optimize the system capacity obtained during the scheduling phase. To ensure the normal progress of the business, the lowest limit of is set to set the rate. Similarly, in order to avoid waste of resources, try not to exceed the user m rate upper limit of . Therefore, the rate of user m is limited as follows:
The total rate of all selected users is:
The optimization objective of this article is not only to maximize the throughput of the scheduled user set but also to consider energy efficiency as an important indicator in this article. Assuming that is the upper limit of the transmitting power of the i-root antenna, the power limit of the launch antenna is as follows:
In summary, the total launch power of the base station can be expressed as follows:
among them, is the efficiency of the base station power amplifier. is the power consumption of the circuit component, which is a fixed value, defining the energy efficiency as follows:
Therefore, the optimization proposed in this article is as follows:
It can be observed that if is maximized, the greater the power consumption, the worse the energy efficiency . The two restrict each other and are difficult to optimize at the same time. The total capacity after power redistribution should be greater than the total capacity at average allocation in order to be meaningful. Therefore, this article uses the main objective method to transform the problem, with as the main optimization objective and as the constraint, thus transforming the problem into:
3. Solving the Combination Optimization Problem Based on DQN Algorithm
The joint optimization problem proposed above is the problem of NP-difficulty non-convex optimization. It is more complicated to use traditional methods when solving this problem. Therefore, for this decision-making problem, this article uses the DQN model in deep Q learning to solve this problem. Among them, the neural network of the Q value function is selected from the deep neural network of the full connection. In the above resource allocation, define each user as an intelligent agent. At the moment of , the user observes the current status of the environment , then use the strategy to adopt action from the allowable set of action set and obtain a reward , and then obtain the status and reward in the next moment.
Status collection: set as the maximum waiting cycle of the user, and record the status corresponding to the -transmission time of the learning process as follows:
Action collection: Define actions as selecting users and allocating power and record the action corresponding to the t-th transmission time interval of the learning process as . Among them, is a dual variable, and its value is determined by using :
To reduce the set of actions, simplify the actions as follows:
Instantaneous reward is defined as energy efficiency, and the instantaneous reward for executing action in state is recorded as follows:
Cumulative reward: the cumulative reward for executing action in state is defined as the state action value function and expressed as incremental updates:
among them, represents the current value function of action executed in state at time , and represents the maximum value function corresponding to various actions taken by time in state . represents the learning rate, usually taken as a very small value. represents the discount factor related to the future.
The objective value function of executing action in state is denoted as the sum of the maximum Q value of the reward and the discount in the next state:
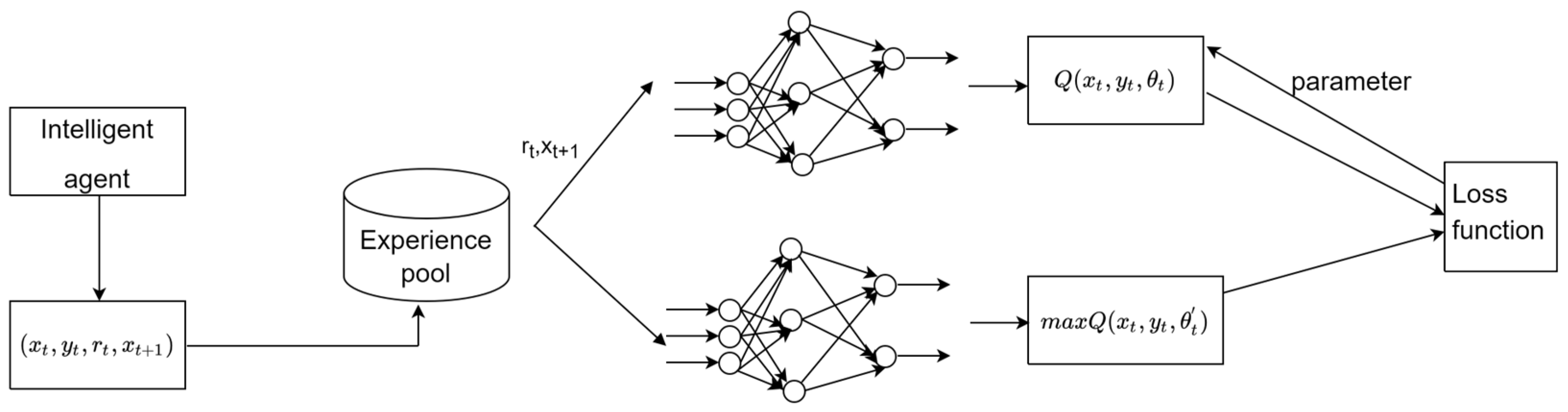
The DQN model adopts a dual network structure, which records the current Q value and the target Q value separately. The purpose of training the neural network is to reduce the difference between the current Q value and the target Q value by minimizing the loss function. The loss function is defined as follows:
The solution model based on DQN is as Figure 4, after each action selection, the intelligent agent will store the state, action, rewards obtained, and the state of the next time in the experience pool. When the experience pool is full, the network starts to update. The reward and the next moment’s state are used to calculate the Q value, and the target Q value is calculated from the Q value, and then the loss function value is calculated until convergence.
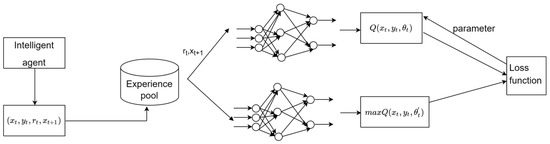
Figure 4.
DQN algorithm diagram.
It can be seen from the above that the pseudocode for solving the above optimization problem with DQN is as follows (Algorithm 1):
| Algorithm 1: DQN |
| Initialize experience playback pool and capacity ; Initialize parameter of the current Q-value network ; Initialize parameter of target Q-value network , i.e., ; for episode = 1, M do Randomly select initial state ; for t = 1, T do if random < do Select actions based on the strategy and randomly select action with probability ; else Select action end if Execute action , observe reward and the next state ; Store memory, store in experience playback pool ; Batch extract sample data from to train the current Q-value network; Using the function, the parameter is updated through the gradient back propagation of the neural network; Copy and update the target Q-value network parameter every T round of cycling; end for end for |
4. Experimental Simulation and Analysis
4.1. Feature Extraction and Analysis
The network parameters and deep learning algorithm parameter values for this experiment are shown in Table 2 and Table 3. The neural network used for training is a fully connected neural network containing two hidden layers, and the activation function used by each neuron is a modified linear unit (ReLU).

Table 2.
Wireless network parameter values.

Table 3.
Parameter values of DQN algorithm.
4.2. Analysis of Simulation Results
To avoid repeated experiments, this chapter only discusses two types of business: conversation and background. The comparative experiment selects the following three algorithms: algorithm a, which is based on the user’s channel state; greedy algorithms are used to schedule and select users, aiming to maximize system capacity, and then, energy efficiency is optimized based on this scheduling. This method does not consider the QoS latency requirements of users. The default number of antennas used in reference [11] is required to meet the number of user accesses, and there is no user scheduling. If the number of connected users exceeds the set number of antennas, random scheduling may be carried out, and some users may not be able to access the services, which does not meet the user’s QoS requirements. The comparison algorithm, b, limits the QoS rate of users based on the above. The comparison algorithm, c, is the algorithm taken from the research [16], which jointly optimizes spectral efficiency and energy efficiency and then maps it to the NSGA-II algorithm to provide the solution without taking into account the QoS of the user service.
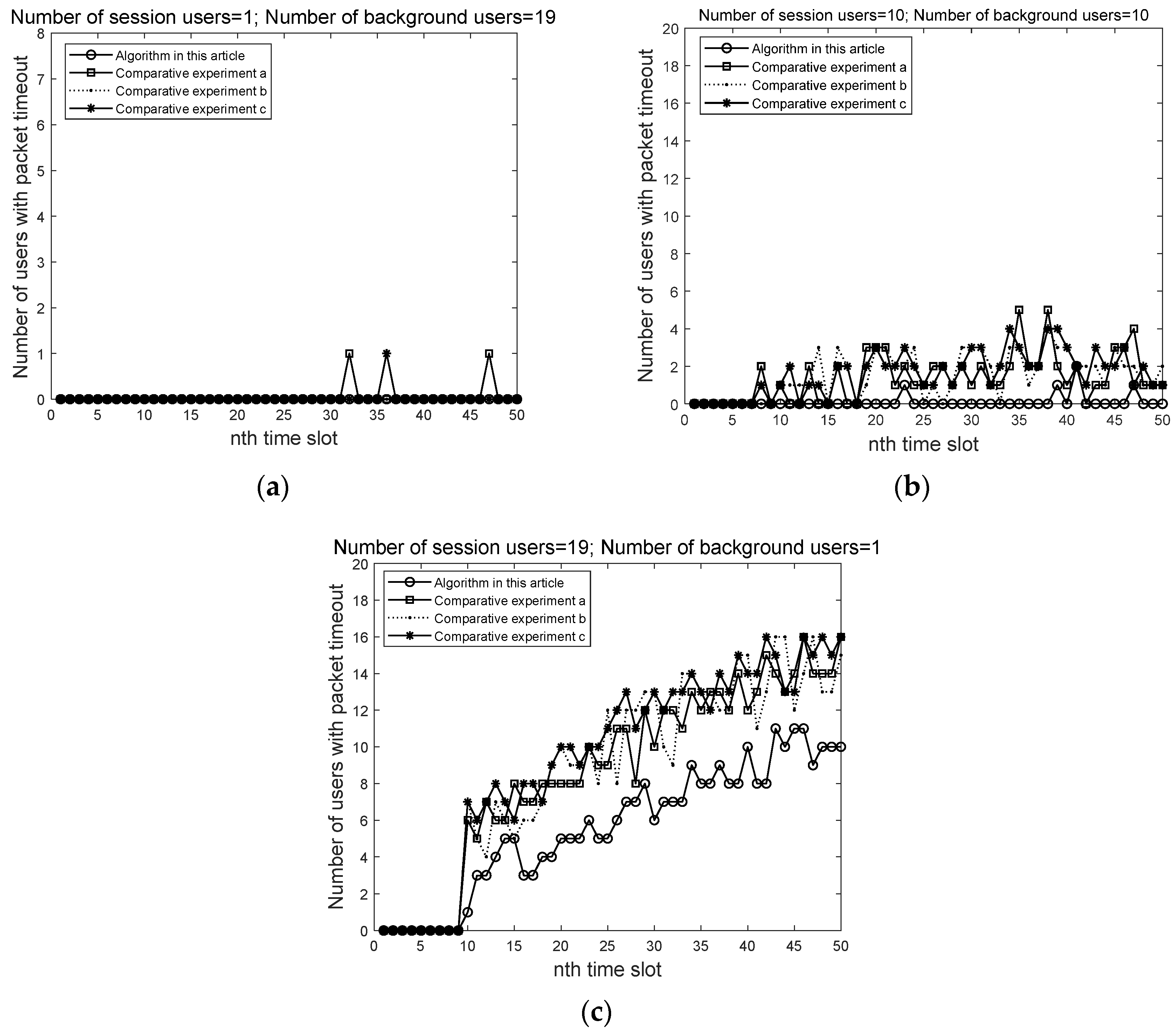
Assuming that for each scheduling slot, the number of waiting slots for a user’s data packet increases by 1, reflecting user satisfaction as the number of users who have timed out the data packet, the fewer timeout users, the higher user satisfaction. Assuming there are a total of 20 users who use session-based and background-based services extremely and evenly, the user satisfaction of the algorithm under different situations is shown in Figure 5:
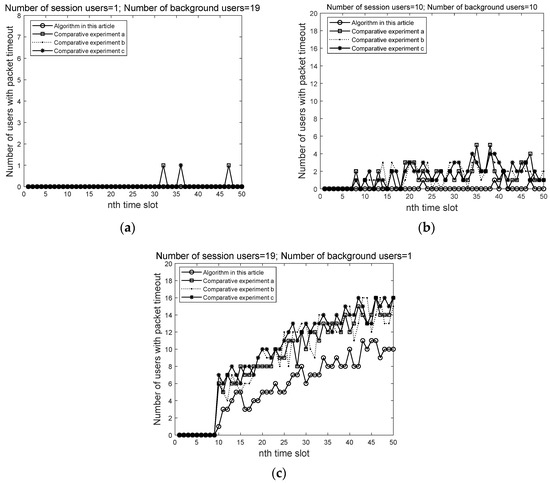
Figure 5.
Comparison of data packet timeouts of different algorithms. (a) Packet timeout when the number of session users is 1 and background users are 19; (b) Packet timeout when the number of session users is 10 and background users are 10; (c) Packet timeout when the number of session users is 19 and the background user is 1.
From Figure 5a, it can be seen that when the number of users using background services is 19 and the number of session users is 1, the user data packets in all of the algorithms almost do not time out because background services do not require latency; therefore, whether the algorithm considers the delay requirements during user scheduling has little impact on the results. From Figure 5b, it can be seen that when the number of session-type users and background-type users is half, whether the algorithm considers delay requirements has a significant impact on the results because session-type services have strict requirements in terms of delay. The algorithm proposed in this article minimizes the number of timeout packets, ensuring the user’s business latency requirements. Algorithms a, b, and c did not consider the business latency requirements during the user scheduling process, resulting in a significant increase in the number of timeout packets, which cannot be met by users using session-based services. As shown in Figure 5c, when the number of session-based business users is 19 and the number of background-based business users is 1, the number of timeout users in all algorithms will increase. However, compared to the other three algorithms, the scheduling scheme proposed in this paper still has fewer timeout users starting around the 10th time slot. In summary, the user scheduling scheme proposed in this paper can alleviate the situation of packet timeout and improve user satisfaction.
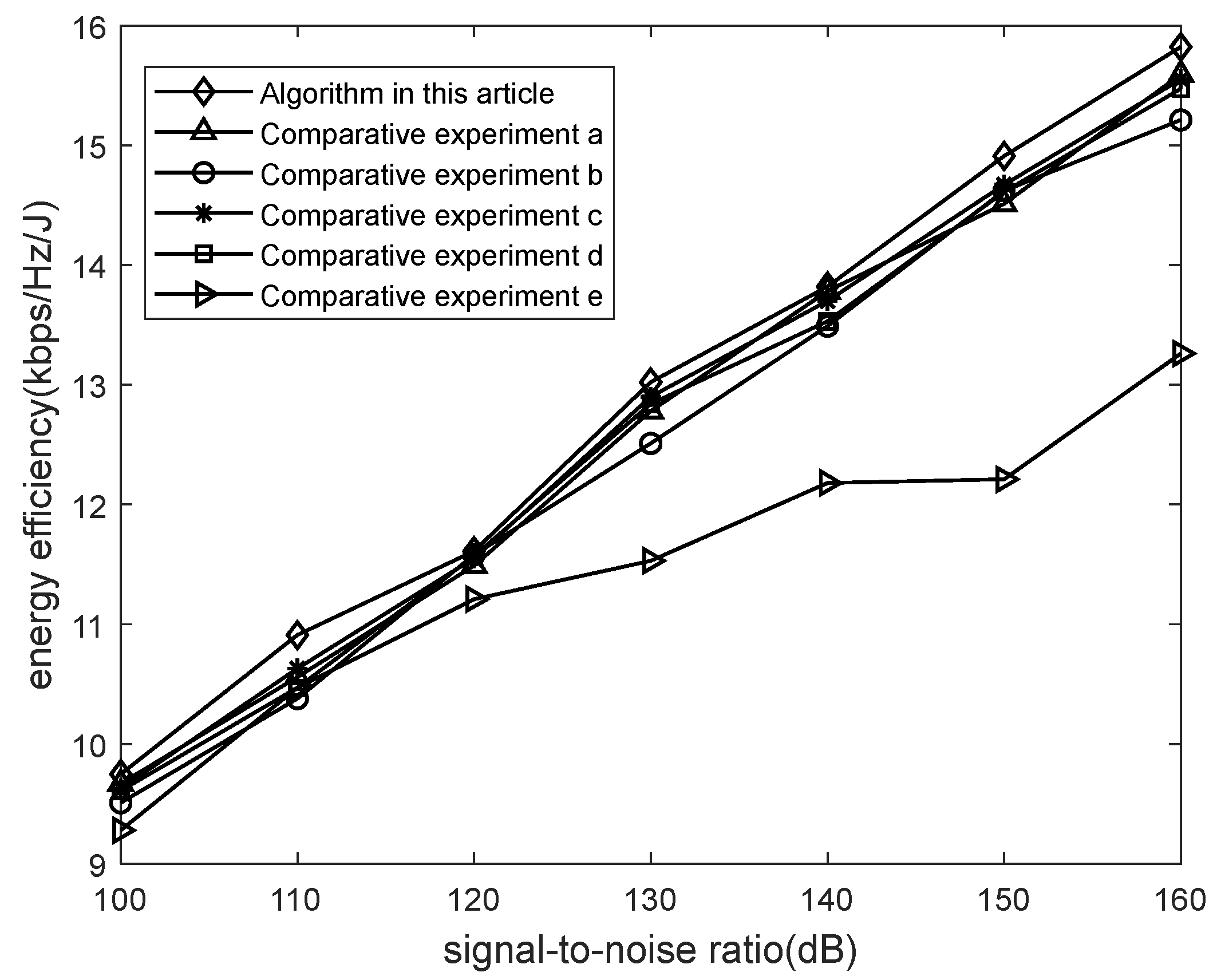
In order to demonstrate the advantages of the proposed method in the joint optimization of energy efficiency and system capacity, two algorithms were added for comparison on the basis of comparative experiments a, b, and c. Comparative algorithm d was an algorithm used in reference [11], which optimized energy efficiency but did not consider the user’s business delay requirements and the upper and lower limit requirements in terms of rate. The comparison algorithm e only considers the throughput indicator under the same scheduling scheme without considering the energy efficiency indicator in green communication.
Let the signal-to-noise ratio be calculated as follows: . In the experiment, the signal-to-noise ratio is changed by changing the value of . In order to verify that the method proposed in this article can achieve high energy efficiency, the efficiency of different algorithms under different signal-to-noise ratios is compared, as shown in Figure 6.
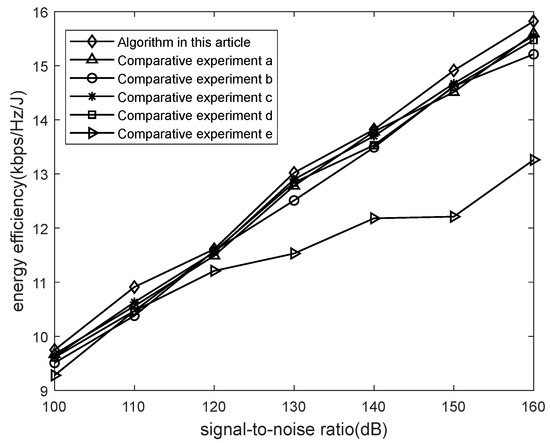
Figure 6.
Comparison of energy efficiency under different signal-to-noise ratios.
From Figure 6, it can be seen that as the signal-to-noise ratio (SNR) continues to increase, the energy efficiency of all algorithms increases accordingly. It should be noted that the energy efficiency of algorithm e starts to slowly increase after increasing to a certain extent. This is because the algorithm aims to improve system throughput, resulting in higher energy consumption and having advantages in optimizing throughput alone. From the graph, it can also be observed that the algorithm proposed in this article and the comparison algorithms a, b, c, and d have a similar growth rate as the signal-to-noise ratio increases. This is because these algorithms are all optimized based on energy efficiency. However, compared to this, the method proposed in this article still has a slight advantage, indicating that the algorithm proposed in this article can improve throughput while not affecting energy efficiency.
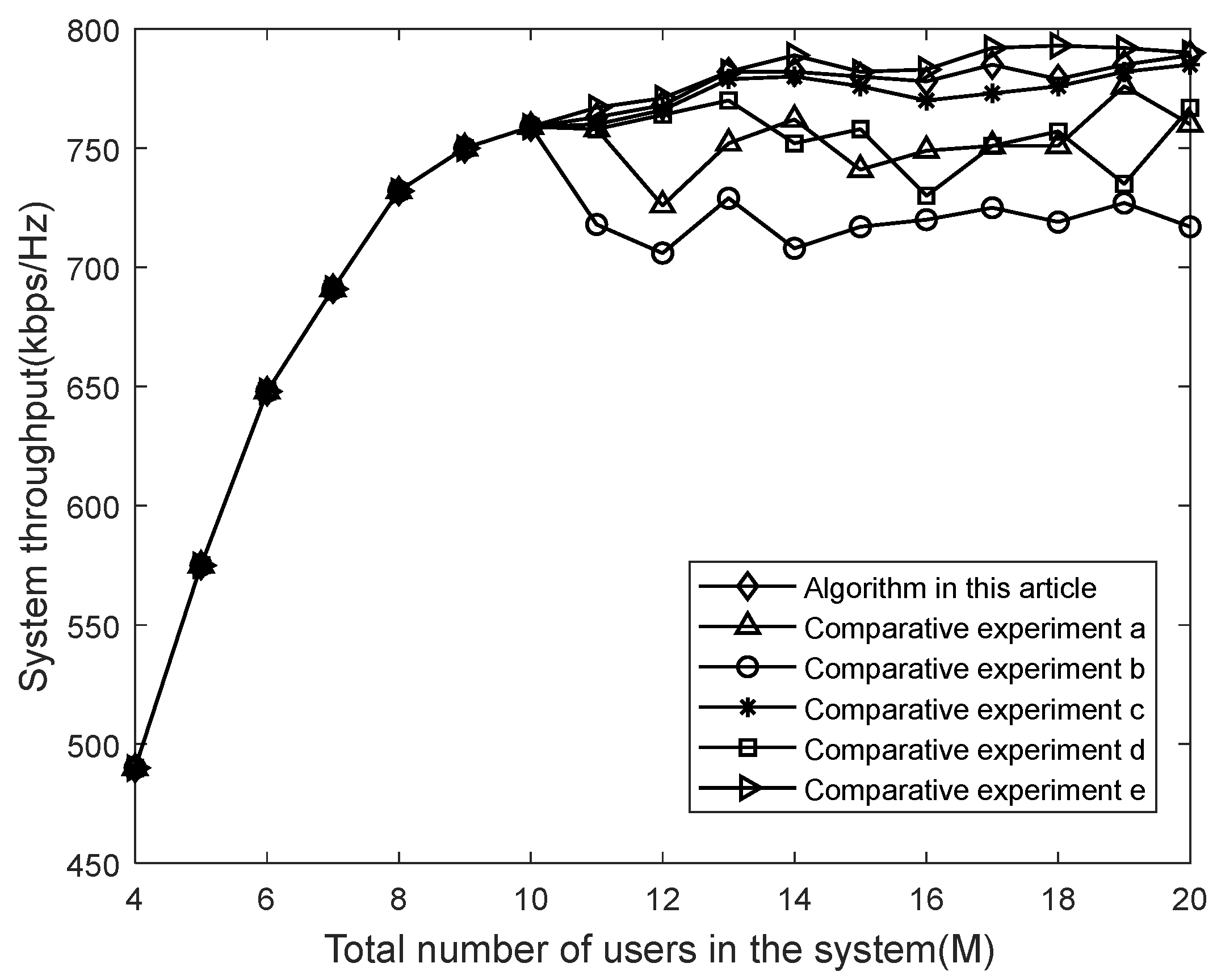
In order to further verify the advantages of the algorithm proposed in this article in terms of system capacity compared to other algorithms mentioned above, different algorithms were compared as the number of users in the system continued to increase, as shown in Figure 7.
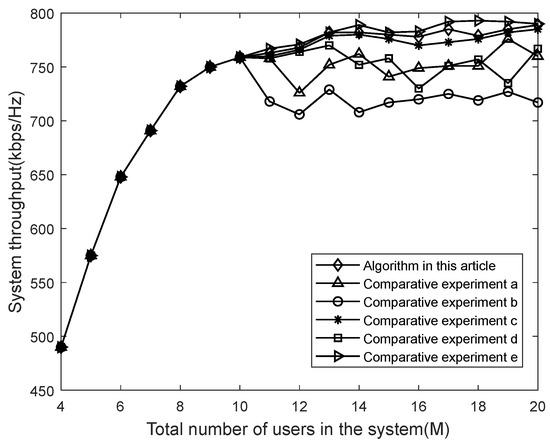
Figure 7.
Comparison of system throughput obtained by different algorithms.
From Figure 7, it can be observed that when the number of users is small, the throughput obtained by all of the comparison algorithms increases rapidly without any difference as the total number of users increases. When the total number of users exceeds the maximum number of users served simultaneously set by the system, the throughput obtained by all of the algorithms will no longer continue to increase. As the total number of users continues to increase, the system throughput begins to fluctuate. Note that the fluctuation range of algorithm e is small and that the system throughput is maximum because this algorithm only aims to improve system throughput. Compared to the other algorithms, achieving higher throughput is reasonable, but it ignores the indicator of energy efficiency. Among the remaining four algorithms, the system throughput fluctuation range of the proposed algorithm and algorithm c is relatively small and relatively high. In summary, Figure 6 and Figure 7, combined from the perspectives of energy efficiency and throughput, demonstrate that the algorithm proposed in this paper can effectively balance these two objectives, achieving a relatively optimal combination of the two. Although algorithm c can also effectively improve energy efficiency and throughput, it can be seen from Figure 5 that the packet timeout situation of this algorithm is severe and user satisfaction is low. Therefore, overall, the algorithm proposed in this paper has good performance.
5. Conclusions
Aiming at the problem of low throughput and energy efficiency in large-scale MIMO systems due to the mutual constraints between energy efficiency and spectral efficiency and the lack of consideration of user service QoS and the rate of the upper and lower limits in resource allocation, a method based on the combined optimization of spectrum and energy resources under QoS guarantees is proposed. This method is divided into two steps. First, greedy algorithms are used to schedule users based on their latency requirements. Then, a joint optimization problem model is established by setting upper and lower rate requirements for the selected users. Finally, the DQN method is used to solve the problem. The simulation results show that the algorithm proposed in this article can ensure user QoS requirements and improve user satisfaction while also improving throughput and energy efficiency to a certain extent.
This article focuses on the downlink of multi-user massive MIMO systems. The next step is to focus on the multi-objective optimization problem of the uplink of massive MIMO systems. In the future, more resource allocation issues will be considered, including power, bandwidth, antenna number, etc. This joint resource allocation problem is very useful for future communication users.
Author Contributions
Conceptualization, Q.L. and R.L.; methodology, Q.L.; software, R.L.; validation, R.L. and M.L.; formal analysis, R.L.; investigation, R.L. and M.L.; resources, Q.L.; data curation, R.L.; writing, original draft preparation, R.L.; writing, review and editing, Q.L., R.L. and M.L.; visualization, R.L.; supervision, M.L.; project administration, M.L.; funding acquisition, Q.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China, grant number 61931004, and the APC was funded by Dalian University.
Data Availability Statement
The processed data required to reproduce these findings cannot be shared as the data also form part of an ongoing study.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Ke, W. The Development Trend and Key Technologies of 5G Mobile Communication. Comput. Telecommun. 2017, 1, 46–47. [Google Scholar]
- Ni, Y.; Liang, J.; Shi, X. Research on key technology in 5G mobile communication network. In Proceedings of the 2019 International Conference on Intelligent Transportation, Big Data & Smart City (ICITBS), Changsha, China, 12–13 January 2019. [Google Scholar]
- Larsson, E.G.; Edfors, O.; Tufvesson, F.; Marzetta, T.L. Massive MIMO for next generation wireless systems. IEEE Commun. Mag. 2014, 52, 186–195. [Google Scholar] [CrossRef]
- Chen, Y.; Zhang, S.; Xu, S.; Li, G.Y. Fundamental trade-offs on green wireless networks. IEEE Commun. Mag. 2012, 49, 30–37. [Google Scholar] [CrossRef]
- Chen, Q.; Su, S.; Lei, G. Channel estimation based on compressive sensing for multi-user massive MIMO systems. J. Phys. Conf. Ser. 2021, 1865, 042057. [Google Scholar] [CrossRef]
- Sboui, L.; Rezki, Z.; Sultan, A.; Alouini, M.S. A new relation between energy efficiency and spectral efficiency in wireless communications systems. IEEE Wirel. Commun. 2019, 26, 168–174. [Google Scholar] [CrossRef]
- Chaves, R.S.; Cetin, E.; Lima, M.V.; Martins, W.A. On the convergence of max-min fairness power allocation in massive MIMO systems. IEEE Commun. Lett. 2020, 24, 2873–2877. [Google Scholar] [CrossRef]
- Hu, A.; Pan, P. Concavity approximation based power allocation in millimeter-wave MIMO systems. IEEE Access 2017, 5, 25731–25740. [Google Scholar] [CrossRef]
- Maimaiti, S.; Chuai, G.; Gao, W.; Zhang, J. Beam Allocation and Power Optimization for Energy-Efficiency in Multiuser mmWave Massive MIMO System. Sensors 2021, 21, 2550. [Google Scholar] [CrossRef]
- Liu, X.; Li, C.; Xie, J. Research on Optimization Algorithm of Power Allocation for High-Speed Railway Mobile Communications. In Proceedings of the 2021 IEEE 4th International Conference on Electronics and Communication Engineering (ICECE), Xi’an, China, 17–19 December 2021. [Google Scholar]
- Xiao, X.; Tao, X.; Lu, J. QoS-guaranteed energy-efficient power allocation in downlink multi-user MIMO-OFDM systems. In Proceedings of the 2014 IEEE International Conference on Communications (ICC), Sydney, Australia, 10–14 June 2014. [Google Scholar]
- Valls, V.; Leith, D.J. Proportional fair MU-MIMO in 802.11 WLANs. IEEE Wirel. Commun. Lett. 2014, 3, 221–224. [Google Scholar] [CrossRef]
- Joung, J.; Chia, Y.K.; Sun, S. Energy-efficient, large-scale distributed-antenna system (L-DAS) for multiple users. IEEE J. Sel. Top. Signal Process. 2014, 8, 954–965. [Google Scholar] [CrossRef]
- Huq, K.M.S.; Mumtaz, S.; Rodriguez, J.; Aguiar, R.L. Energy efficiency optimization in MU-MIMO system with spectral efficiency constraint. In Proceedings of the 2014 IEEE Symposium on Computers and Communications (ISCC), Funchal, Portugal, 23–26 June 2014. [Google Scholar]
- Zhang, J.; Deng, H.; Li, Y.; Zhu, Z.; Liu, G.; Liu, H. Energy Efficiency Optimization of Massive MIMO System with Uplink Multi-Cell Based on Imperfect CSI with Power Control. Symmetry 2022, 14, 780. [Google Scholar] [CrossRef]
- Zhang, Q.; Sun, X.; Chen, D. Application of NSGA-II Algorithm to Energy and Spectral Efficiency Trade-off in Massive MIMO Systems with Antenna Selection. In Signal and Information Processing, Networking and Computers: Proceedings of the 3rd International Conference on Signal and Information Processing, Networking and Computers (ICSINC) 3; Springer: Singapore, 2018. [Google Scholar]
- Chen, L.; Sun, F.; Li, K.; Chen, R.; Yang, Y.; Wang, J. Deep reinforcement learning for resource allocation in massive MIMO. In Proceedings of the 2021 29th European Signal Processing Conference (EUSIPCO), Dublin, Ireland, 23–27 August 2021. [Google Scholar]
- Lalbakhsh, A.; Simorangkir, R.B.; Bayat-Makou, N.; Kishk, A.A.; Esselle, K.P. Advancements and artificial intelligence approaches in antennas for environmental sensing. In Artificial Intelligence and Data Science in Environmental Sensing; Academic Press: Cambridge, MA, USA, 2022; pp. 19–38. [Google Scholar]
- Purushothaman, K.E.; Nagarajan, V. Evolutionary multi-objective optimization algorithm for resource allocation using deep neural network in 5G multi-user massive MIMO. Int. J. Electron. 2021, 108, 1214–1233. [Google Scholar] [CrossRef]
- Zhang, X.; Zhao, F. Hybrid Precoding Algorithm for Millimeter-Wave Massive MIMO Systems with Subconnection Structures. Wirel. Commun. Mob. Comput. 2021, 2021, 5532939. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).