Trajectory Tracking Control of Unmanned Surface Vehicles Based on a Fixed-Time Disturbance Observer
Abstract
:1. Introduction
2. Preliminaries and Mathematical Model
2.1. Preliminaries
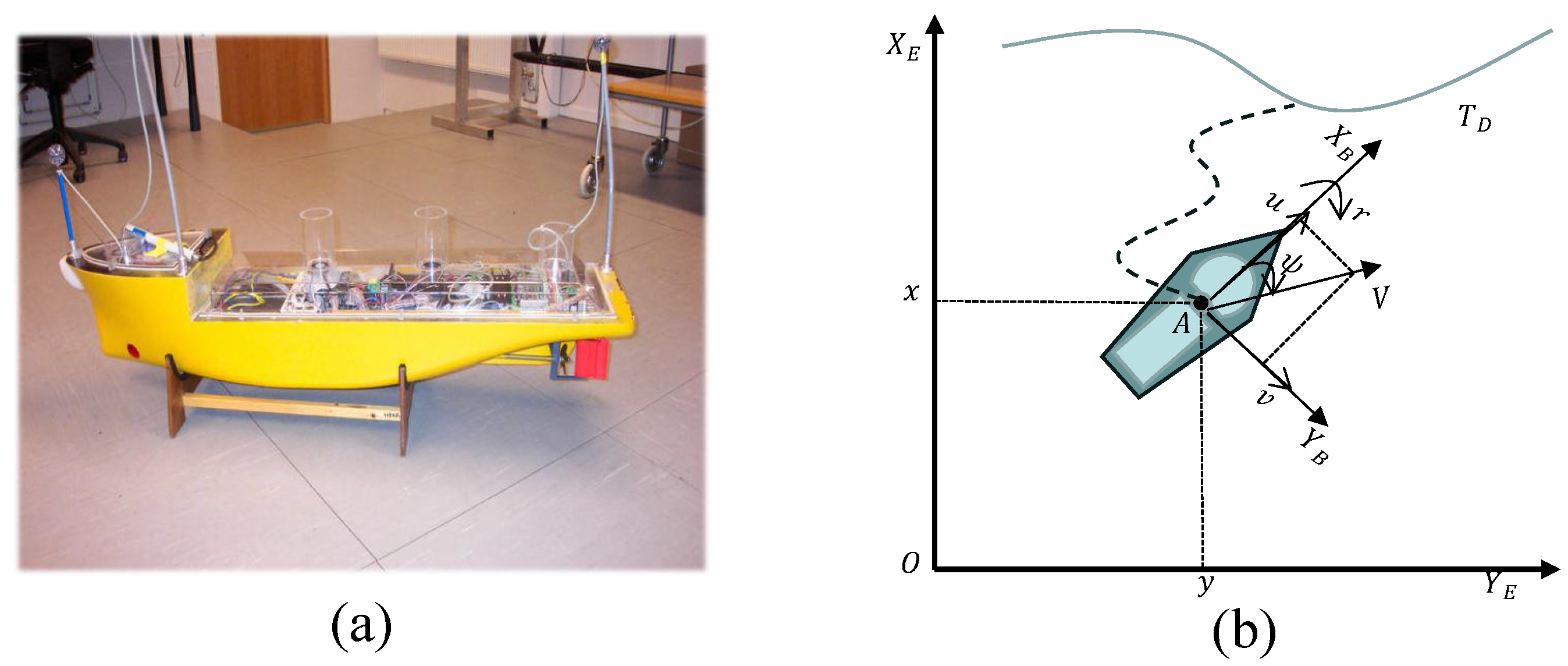
2.2. Mathematical Model
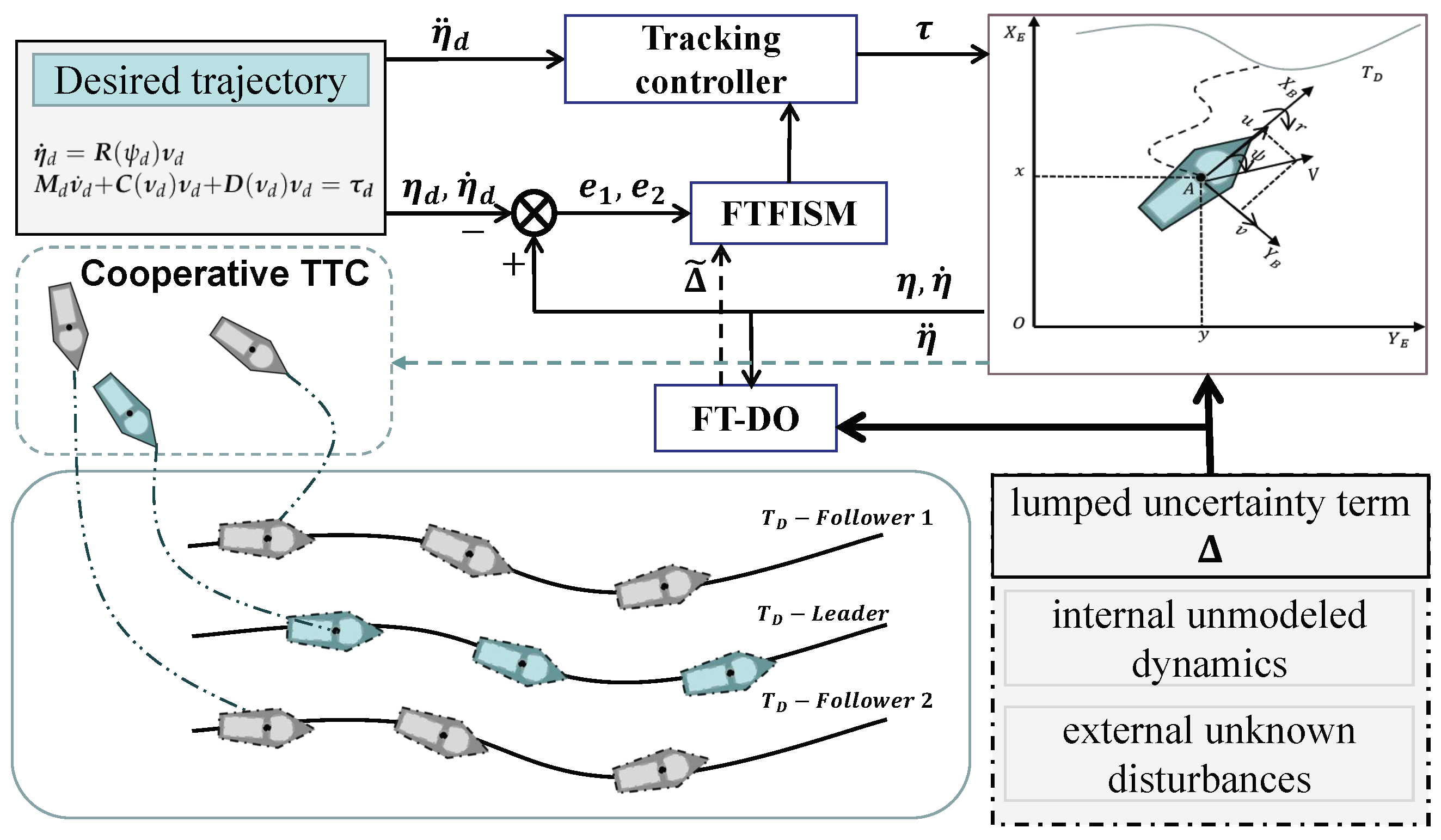
3. Disturbance Identification and Trajectory Tracking Controller Design
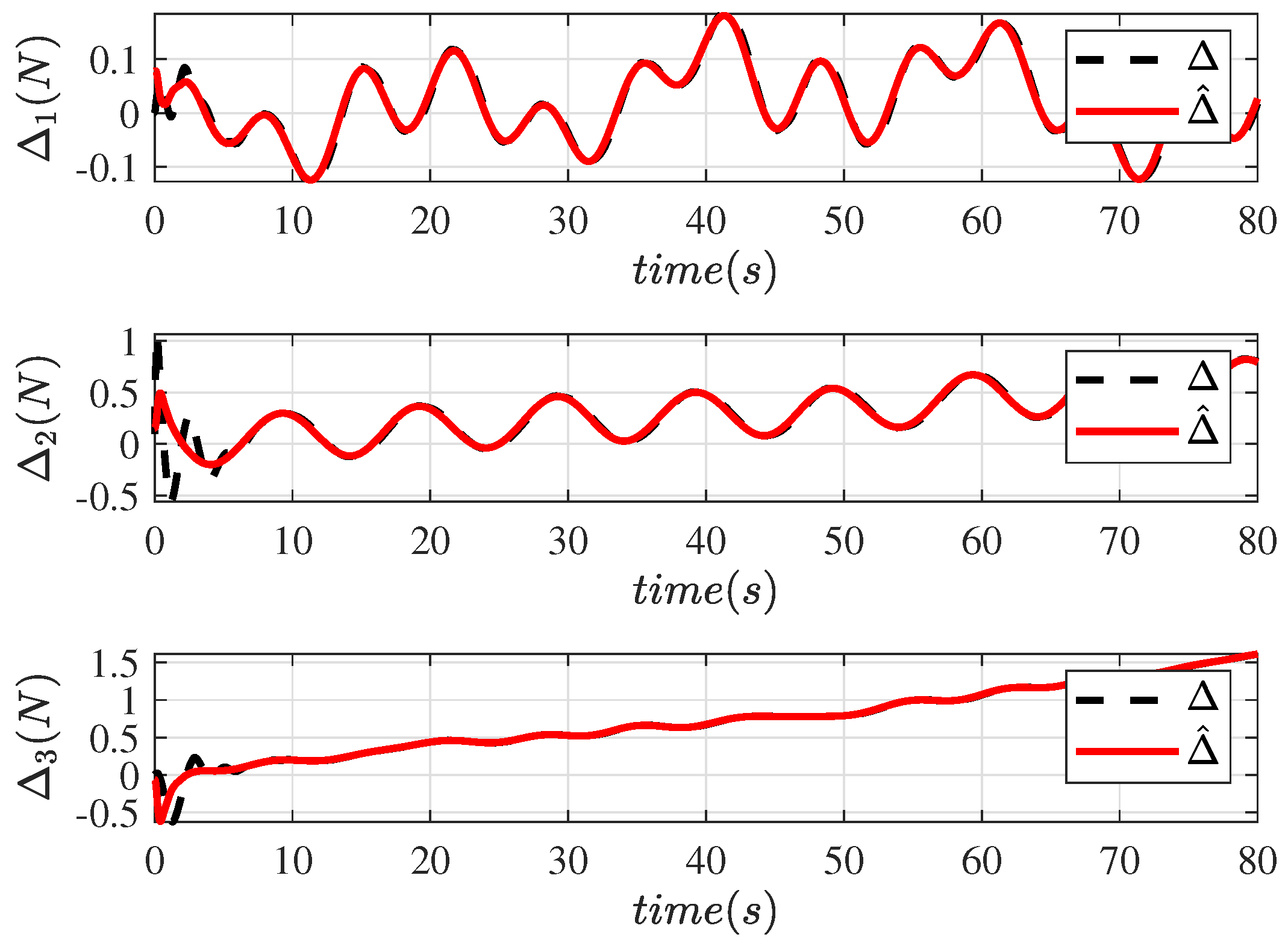
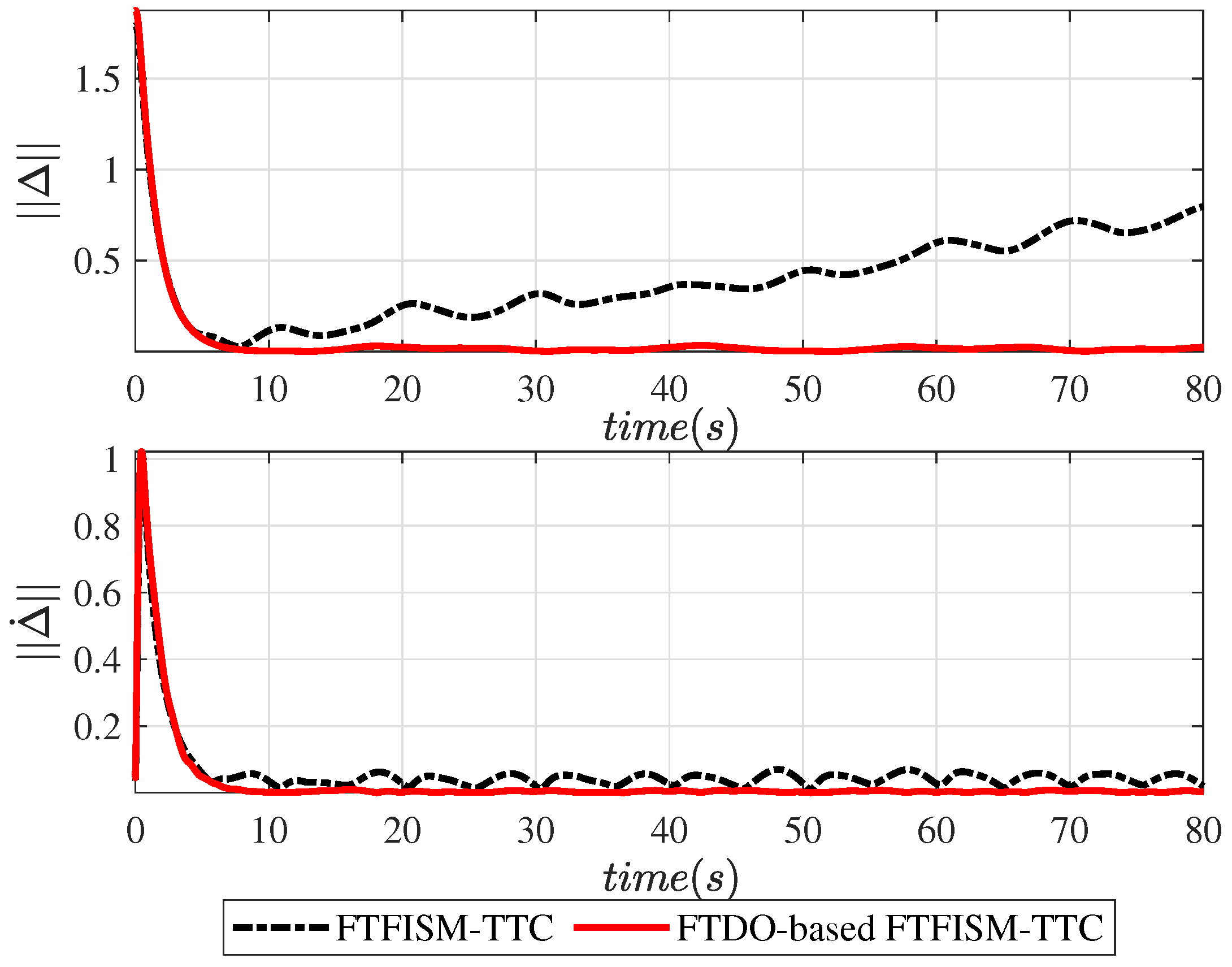
3.1. Design and Analysis of the Stability of the FT-DO
3.2. Design and Analysis of the Stability of the FTFISM-TTC
3.3. Design of the Cooperative Trajectory Tracking Controller
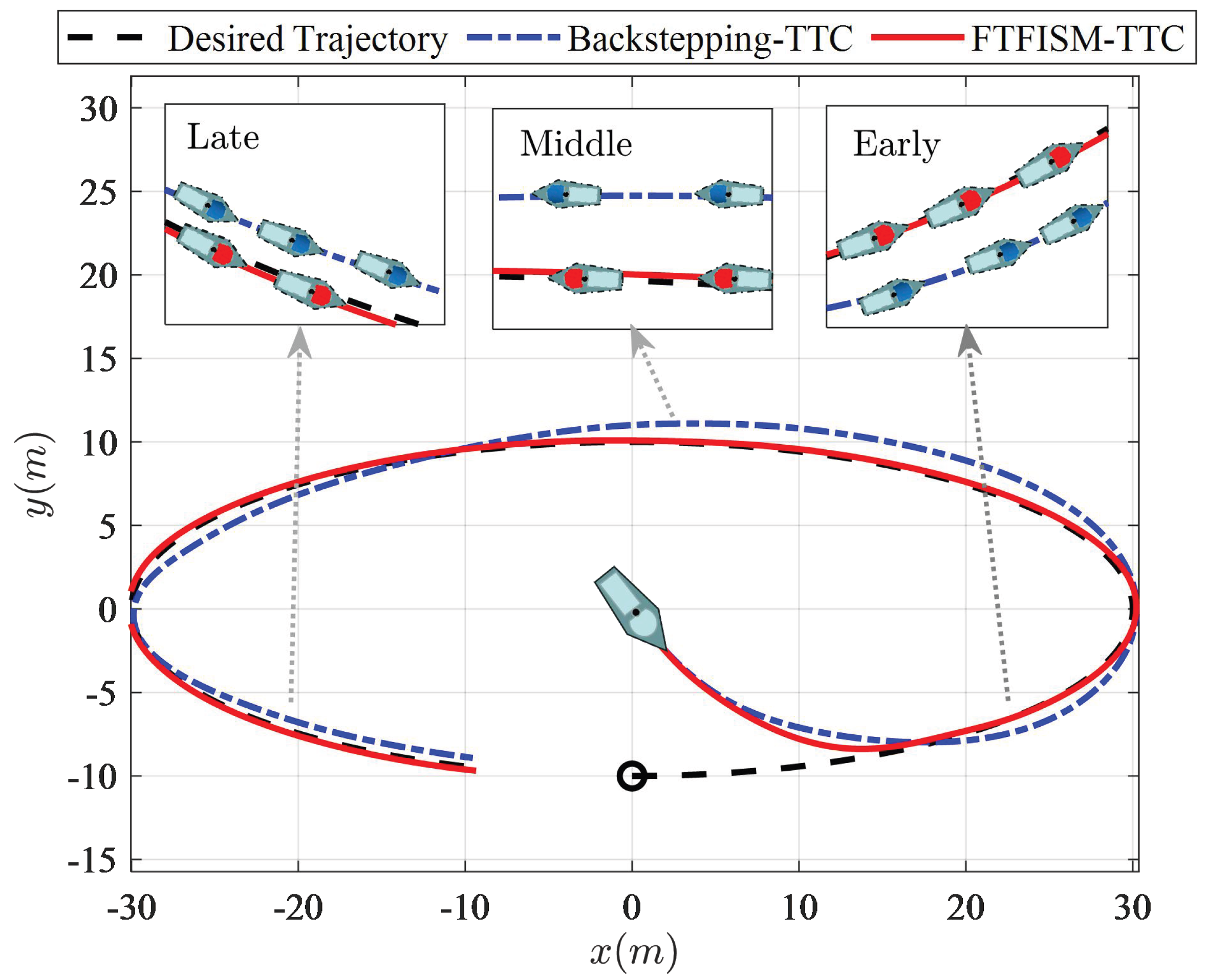
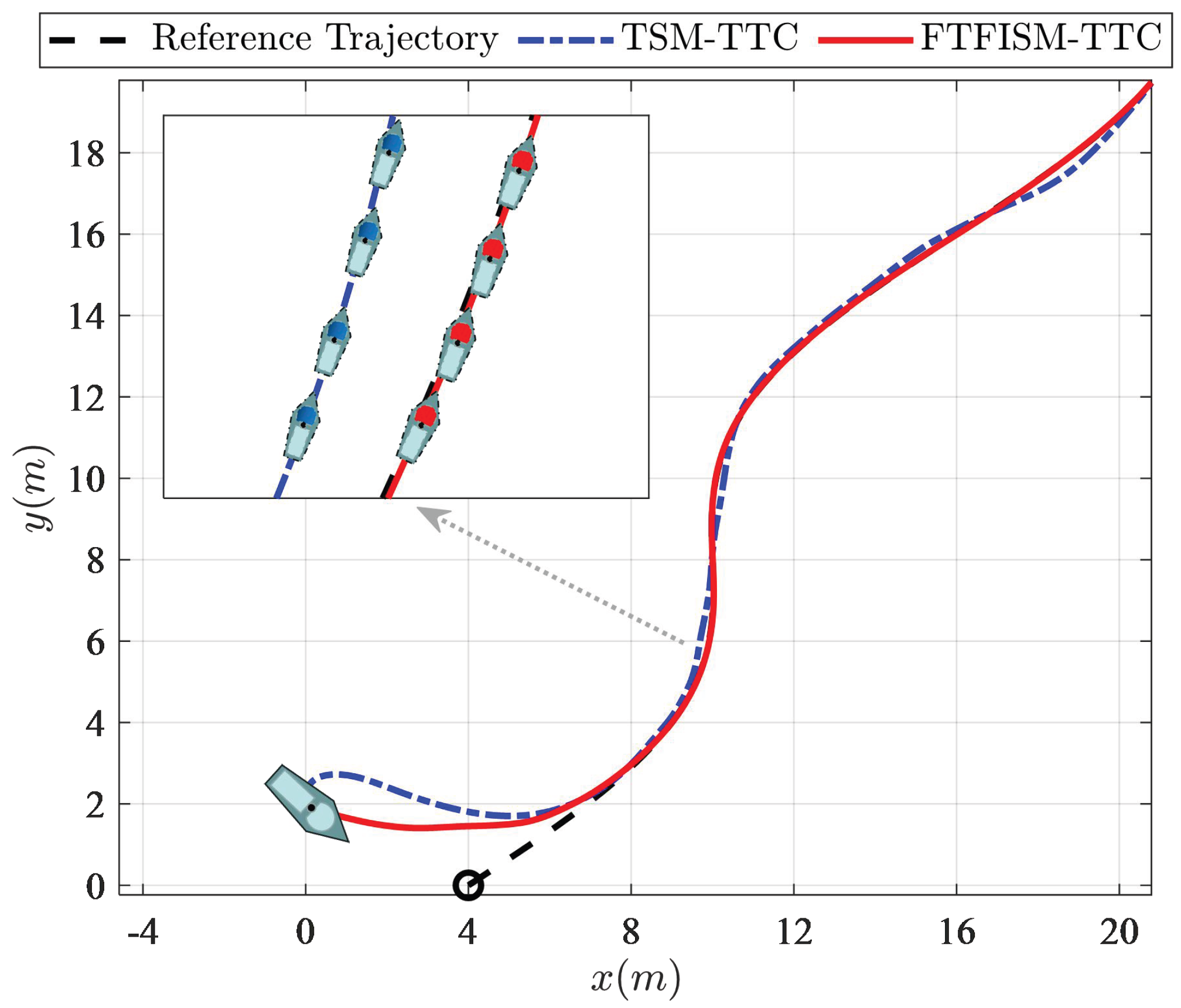
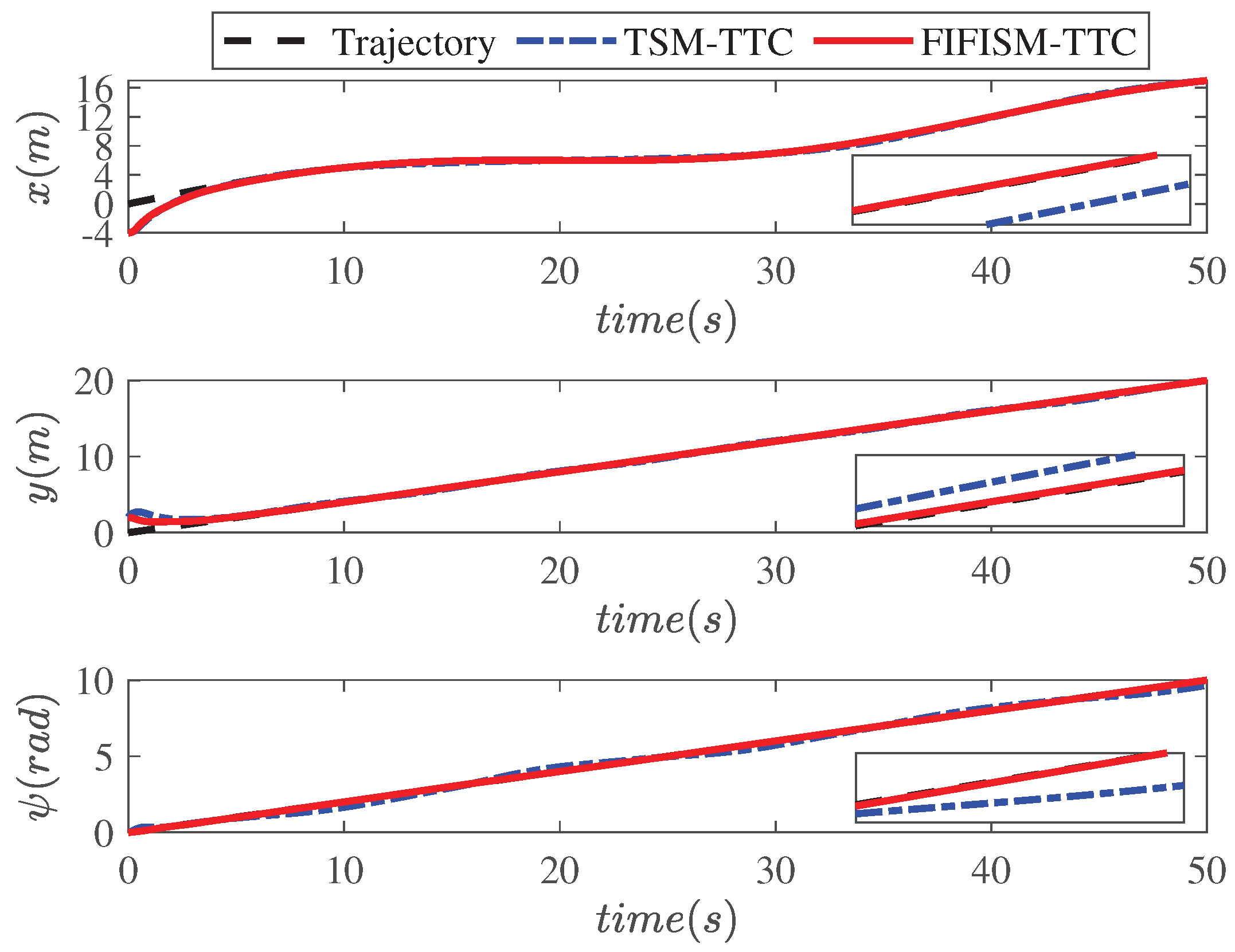
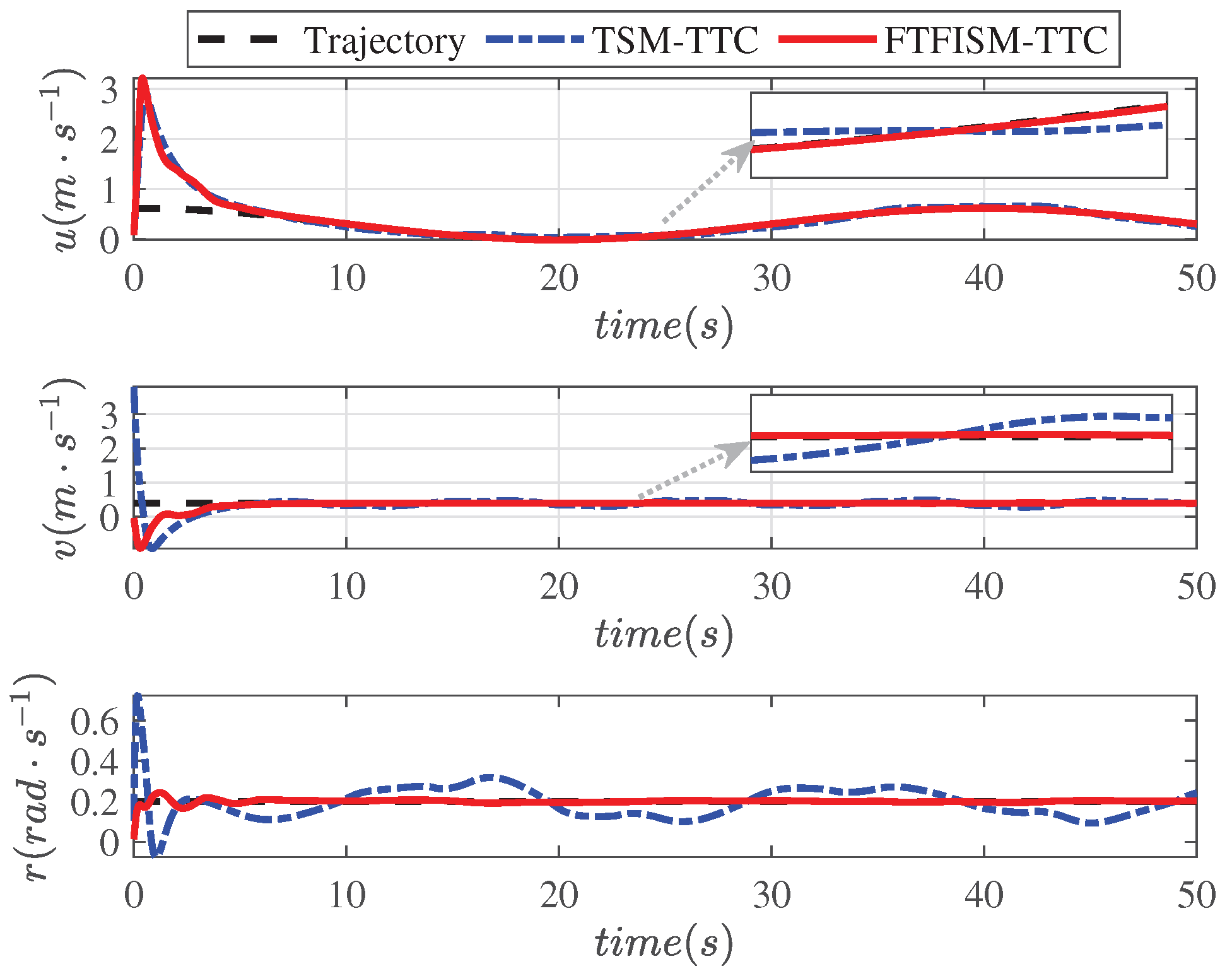
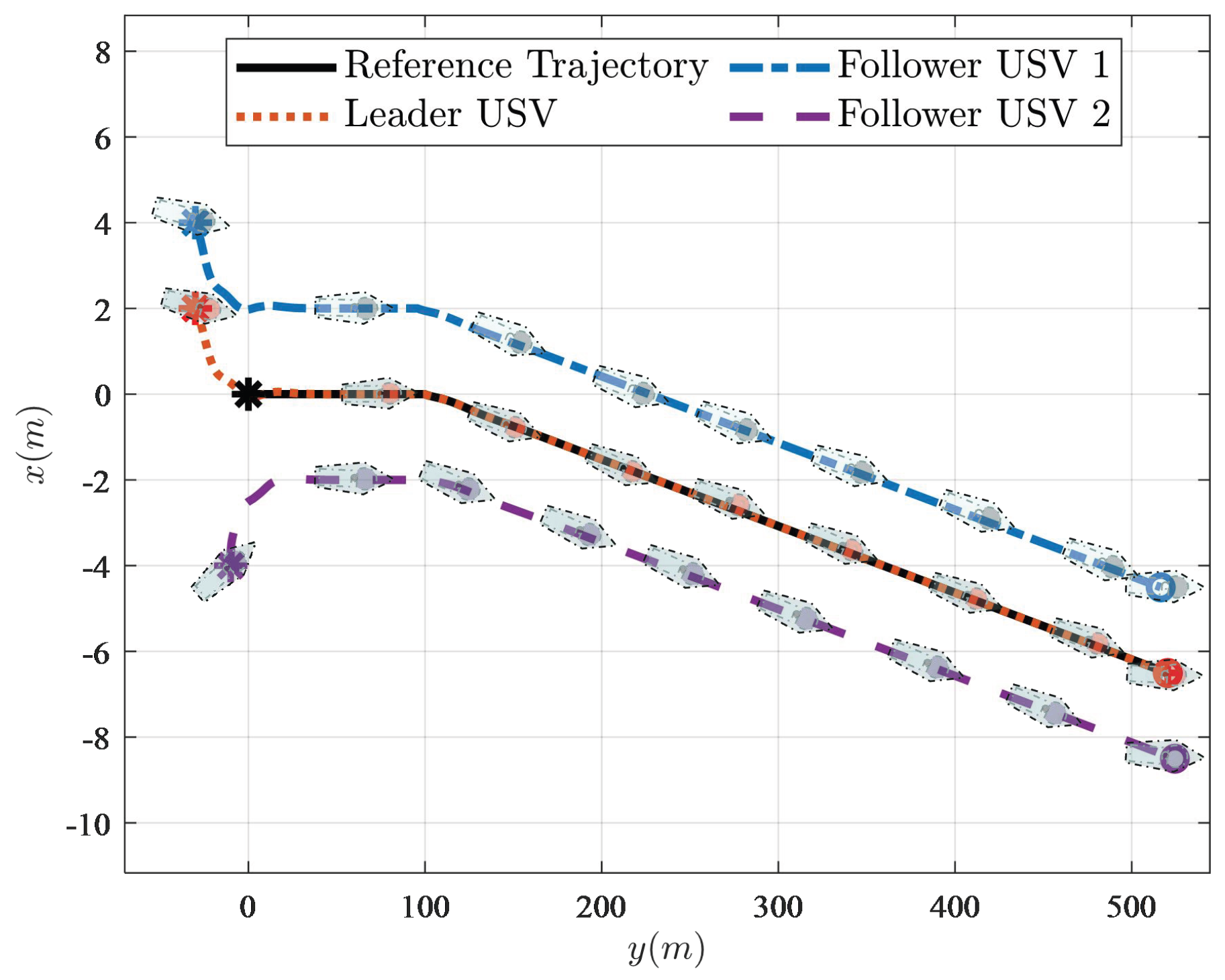
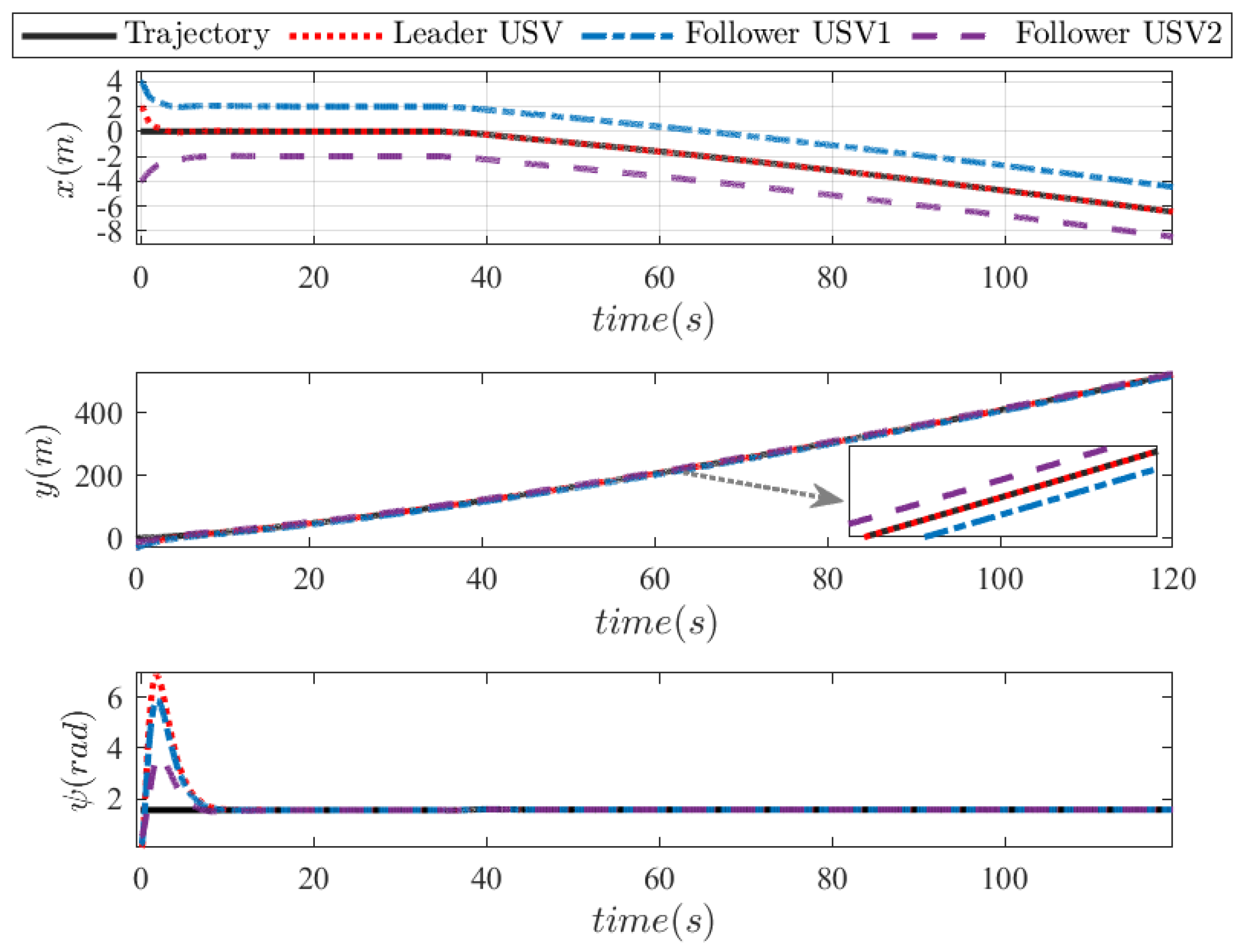
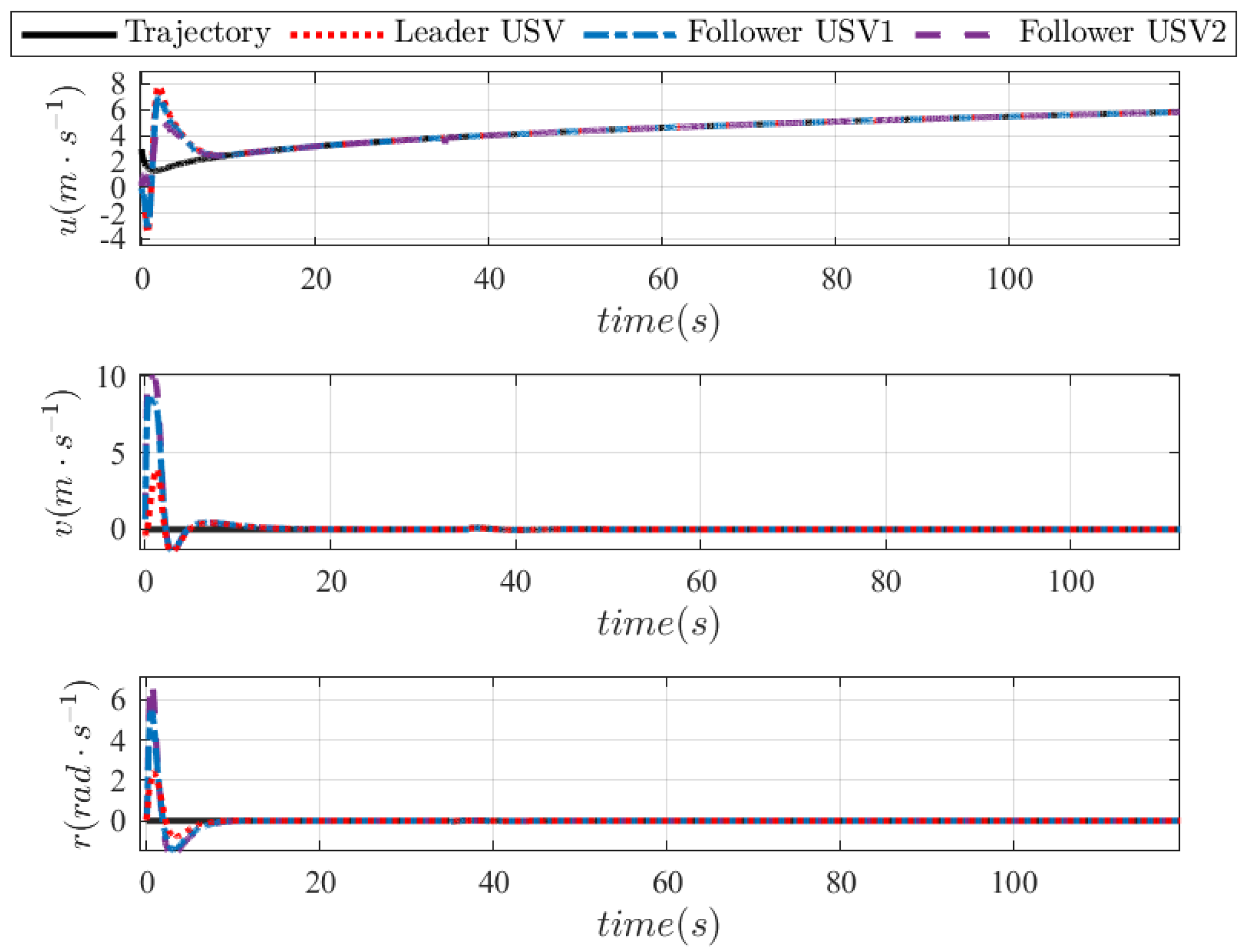
4. Simulations and Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Peng, Y.; Li, Y. Autonomous Trajectory Tracking Integrated Control of Unmanned Surface Vessel. J. Mar. Sci. Eng. 2023, 11, 568. [Google Scholar] [CrossRef]
- Lee, J.-H.; Jeong, S.-K.; Ji, D.-H.; Park, H.-Y.; Kim, D.-Y.; Choo, K.-B.; Jung, D.-W.; Kim, M.-J.; Oh, M.-H.; Choi, H.-S. Unmanned Surface Vehicle Using a Leader–Follower Swarm Control Algorithm. Appl. Sci. 2023, 13, 3120. [Google Scholar] [CrossRef]
- Xu, H.; Zhang, X.K. Tracking Control of Ship at Sea based on MPC with Virtual Ship Bunch under Frenet Frame. Ocean Eng. 2022, 247, 110737. [Google Scholar]
- Yang, T.T.; Zhang, P.F.; Chen, H.Y. Distributed Prescribed-Time Leader–Follower Formation Control of Surface Vehicles with Unknowns and Input Saturation. Ocean Eng. 2023, 134, 16–27. [Google Scholar] [CrossRef]
- Song, H.; Hu, S.; Jiang, W.; Guo, Q.; Zhu, M. Artificial Potential Field-Based Multi-UAV Formation Control and Target Tracking. Int. J. Aerosp. Eng. 2022, 2022, 4253558. [Google Scholar] [CrossRef]
- Wen, J.B.; Yang, J.C.; Li, Y.; He, J.Y.; Li, Z.J.; Song, H.B. Behavior-Based Formation Control Digital Twin for Multi-AUG in Edge Computing. IEEE Trans. Netw. Sci. Eng. 2022, 1–11. [Google Scholar] [CrossRef]
- Zhen, Q.Z.; Wan, L.; Li, Y.L.; Jiang, D.P. Formation Control of A Multi-AUVs System based on Virtual Structure and Artificial Potential Field on SE(3). Ocean Eng. 2022, 253, 111148. [Google Scholar] [CrossRef]
- Pang, W.; Zhu, D.Q.; Liu, C.X.; Wang, L.L. The Multi-AUV Time-Varying Formation Reconfiguration Control based on Rigid-Graph Theory and Affine Transformation. Ocean Eng. 2023, 270, 113521. [Google Scholar] [CrossRef]
- Wang, D.; Kong, M.; Zhang, G.; Liang, X. Adaptive Second-Order Fast Terminal Sliding-Mode Formation Control for Unmanned Surface Vehicles. J. Mar. Sci. Eng. 2022, 10, 1782. [Google Scholar] [CrossRef]
- Liu, Z.; Cai, W.; Zhang, M.; Lv, S. Improved Integral Sliding Mode Control-Based Attitude Control Design and Experiment for High Maneuverable AUV. J. Mar. Sci. Eng. 2022, 10, 795. [Google Scholar] [CrossRef]
- Nguyen, N.P.; Park, D.; Ngoc, D.N.; Xuan-Mung, N.; Huynh, T.T.; Nguyen, T.N.; Hong, S.K. Quadrotor Formation Control via Terminal Sliding Mode Approach: Theory and Experiment Results. Drones 2022, 6, 172. [Google Scholar] [CrossRef]
- Souissi, S.; Boukattaya, M. Time-Varying Nonsingular Terminal Sliding Mode control of Autonomous Surface Vehicle with predefined convergence time. Ocean Eng. 2022, 263, 112264. [Google Scholar] [CrossRef]
- Oliveira, T.R.; Melo, T.G.; Hsu, L.; Cunha, J.P.V.S. Monitoring Functions Applied to Adaptive Sliding Mode Control for Disturbance Rejection. IFAC Papers-OnLine 2017, 50, 2684–2689. [Google Scholar] [CrossRef]
- Hsu, L.; Oliveira, T.R.; Cunha, J.P.V.; Yan, L. Adaptive Unit Vector Control of Multivariable Systems Using Monitoring Functions. Int. J. Robust Nonlinear Control 2019, 29, 583–600. [Google Scholar] [CrossRef]
- Wang, N.; Deng, Z.C. Finite-time Fault Estimator based Fault-Tolerance Control for A Surface Vehicle with Input Saturations. IEEE Trans. Ind. Inform. 2020, 16, 1172–1181. [Google Scholar] [CrossRef]
- Wang, N.; Karimi, H.R. Successive Waypoints Tracking of An Underactuated Surface Vehicle. IEEE Trans. Ind. Inform. 2020, 16, 898–908. [Google Scholar] [CrossRef]
- Wang, N.; Su, S.F. Finite-time Unknown Observer-based Interactive Trajectory Tracking Control of Asymmetric Underactuated Surface Vehicles. IEEE Trans. Control Syst. Technol. 2021, 29, 794–803. [Google Scholar] [CrossRef]
- Chen, D.; Zhang, J.; Li, Z. A Novel Fixed-Time Trajectory Tracking Strategy of Unmanned Surface Vessel Based on the Fractional Sliding Mode Control Method. Electronics 2022, 11, 726. [Google Scholar] [CrossRef]
- Vo, A.T.; Truong, T.N.; Kang, H.J. A Novel Fixed-Time Control Algorithm for Trajectory Tracking Control of Uncertain Magnetic Levitation Systems. IEEE Access 2021, 9, 47698–47712. [Google Scholar] [CrossRef]
- Polyakov, A. Nonlinear Feedback Design for Fixed-Time Stabilization of Linear Control Systems. IEEE Trans. Automat. Control 2012, 57, 2106–2110. [Google Scholar] [CrossRef] [Green Version]
- Liu, W.; Ye, H.; Yang, X. Super-Twisting Sliding Mode Control for the Trajectory Tracking of Underactuated USVs with Disturbances. J. Mar. Sci. Eng. 2023, 11, 636. [Google Scholar] [CrossRef]
- Gu, N.; Peng, Z.H.; Wang, D.; Liu, L.; Jiang, Y. Nonlinear Observer Design for A Robotic Unmanned Surface Vehicle with Experiment Results. Appl. Ocean. Res. 2020, 95, 102028. [Google Scholar] [CrossRef]
- Wang, N.; Zhu, Z.; Qin, H.; Deng, Z.; Sun, Y. Finite-Time Extended State Observer-based Exact Tracking Control of An Unmanned Surface Vehicle. Int. J. Robust Nonlinear Control 2021, 31, 1704–1719. [Google Scholar] [CrossRef]
- Wang, N.; Ki Ahn, C. Hyperbolic-Tangent LOS Guidance-Based Finite-Time Path Following of Underactuated Marine Vehicles. IEEE Trans. Ind. Electron. 2020, 67, 8566–8575. [Google Scholar] [CrossRef]
- Lu, L.; Dan, W.; Peng, Z.H. Eso-based Line-of-Sight Guidance Law for Path Following of Underactuated Marine Surface Vehicles with Exact Sideslip Compensation. IEEE J. Ocean. Eng. 2017, 42, 477–487. [Google Scholar] [CrossRef]
- Pinto, H.L.C.P.; Oliveira, T.R.; Hsu, L. Fault Reconstruction for Delay Systems via Least Squares and Time-Shifted Sliding Mode Observers. Asian J. Control 2019, 21, 52–69. [Google Scholar] [CrossRef]
- Pinto, H.L.C.P.; Oliveira, T.R.; Hsu, L. Sliding Mode Observer for Fault Reconstruction of Time-Delay and Sampled-Output Systems-A Time Shift Approach. Automatica 2019, 106, 390–400. [Google Scholar] [CrossRef]
- Wang, N.; He, L. Leader-Follower Formation Control of Surface Vehicles: A Fixed-Time Control Approach. ISA. Trans. 2022, 124, 356–364. [Google Scholar] [CrossRef]
- Bhat, S.P.; Bernstein, D.S. Continuous Finite-Time Stabilization of The Translational and Rotational Double Integrators. IEEE Trans. Automat. Control 1998, 43, 678–682. [Google Scholar] [CrossRef] [Green Version]
- Zuo, Z. Nonsingular Fixed-Time Consensus Tracking for Second-Order Multi-Agent Networks. Automatica 2015, 54, 305–309. [Google Scholar] [CrossRef]
- Zuo, Z.; Tian, B.; Defoort, M. Fixed-Time Consensus Tracking for Multiagent Systems with High-Order Integrator Dynamics. IEEE Trans. Autom. Control 2017, 63, 563–570. [Google Scholar] [CrossRef] [Green Version]
- Fiori, S. Model Formulation Over Lie Groups and Numerical Methods to Simulate the Motion of Gyrostats and Quadrotors. Mathematics 2019, 7, 935. [Google Scholar] [CrossRef] [Green Version]
- Tarsi, A.; Fiori, S. Lie-Group Modeling and Numerical Simulation of a Helicopter. Mathematics 2021, 9, 2682. [Google Scholar] [CrossRef]
- Skjetne, R.; Smogeli, Ø.; Fossen, T.I. Modeling, Identification, and Adaptive Maneuvering of Cybership II: A Complete Design with Experiments. IFAC Proc. 2004, 37, 203–208. [Google Scholar] [CrossRef]




| Parameter | Formula | Parameter | Formula |
|---|---|---|---|
| Parameters | Values | Parameters | Values | Parameters | Values |
|---|---|---|---|---|---|
| 1 | 0.15 | 0.15 | |||
| 0.15 | 0.85 | 1.15 | |||
| 1 | 4 | 4 | |||
| 0.3 | 1.3 | 0.1 | |||
| 0.7 | 0.5 | 5, 7 |
| Parameters | Values | Parameters | Values | Parameters | Values |
|---|---|---|---|---|---|
| m | 23.8000 | −0.8612 | −2.0 | ||
| 1.7600 | −36.2823 | −10.0 | |||
| 0.460 | 0.1079 | 0.0 | |||
| −0.7225 | 0.1052 | 0.0 | |||
| −1.3274 | 5.0437 | −1.0 | |||
| −5.8664 |
| T | 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 |
|---|---|---|---|---|---|---|---|---|
| 0.1157 | 0.2548 | 0.3180 | 0.3547 | 0.4444 | 0.5966 | 0.7173 | 0.7962 | |
| 0.0360 | 0.0274 | 0.0194 | 0.0264 | 0.0279 | 0.0275 | 0.0195 | 0.0200 | |
| 0.0689 | 0.2221 | 0.0770 | 0.2174 | 0.0714 | 0.2192 | 0.0713 | 0.2370 | |
| 0.0392 | 0.0363 | 0.0400 | 0.0381 | 0.0372 | 0.0446 | 0.0392 | 0.0486 | |
| Parameters | Values | Parameters | Values |
|---|---|---|---|
| Figure 7 | Figure 7 | ||
| Figure 7 | Figure 7 | ||
| Figure 10 | Figure 10 | ||
| Figure 10 | Figure 10 |
| Parameters | Values | Parameters | Values |
|---|---|---|---|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, X.; Li, X.; Ma, D.; Kong, X. Trajectory Tracking Control of Unmanned Surface Vehicles Based on a Fixed-Time Disturbance Observer. Electronics 2023, 12, 2896. https://doi.org/10.3390/electronics12132896
Li X, Li X, Ma D, Kong X. Trajectory Tracking Control of Unmanned Surface Vehicles Based on a Fixed-Time Disturbance Observer. Electronics. 2023; 12(13):2896. https://doi.org/10.3390/electronics12132896
Chicago/Turabian StyleLi, Xiaosong, Xiaochen Li, Dianguang Ma, and Xianwei Kong. 2023. "Trajectory Tracking Control of Unmanned Surface Vehicles Based on a Fixed-Time Disturbance Observer" Electronics 12, no. 13: 2896. https://doi.org/10.3390/electronics12132896
APA StyleLi, X., Li, X., Ma, D., & Kong, X. (2023). Trajectory Tracking Control of Unmanned Surface Vehicles Based on a Fixed-Time Disturbance Observer. Electronics, 12(13), 2896. https://doi.org/10.3390/electronics12132896





