An In-Phase/Quadrature Index Modulation-Aided Spread Spectrum Communication System for Underwater Acoustic Communication †
Abstract
:1. Introduction
2. System Model
2.1. The Transmitter
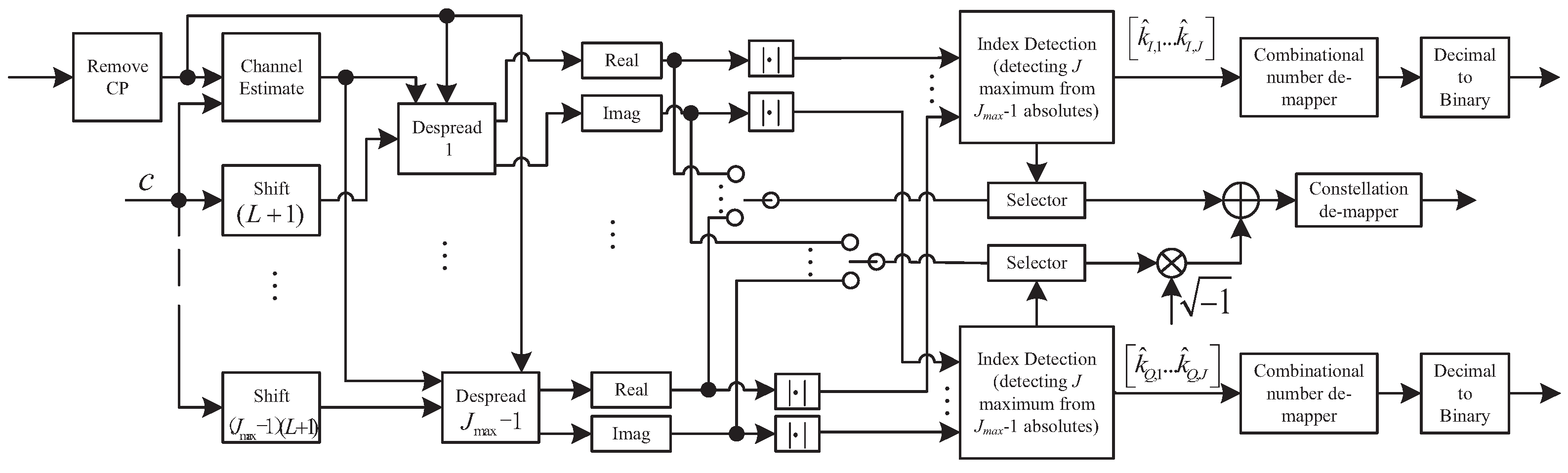
2.2. The Receiver
| Algorithm 1: To Estimate the Indexes , . |
| Input: J and |
| 1: for |
| 2: |
| 3: |
| 4: end for |
| 5: |
| 6: |
| Output: |
3. Performance Analysis
3.1. Bit Error Probability of MSSS-I/Q-IM
3.2. Erroneous Index Detection Probability
3.3. Demodulation Error Probability of Constellation Symbols
4. Numerical Results and Discussion
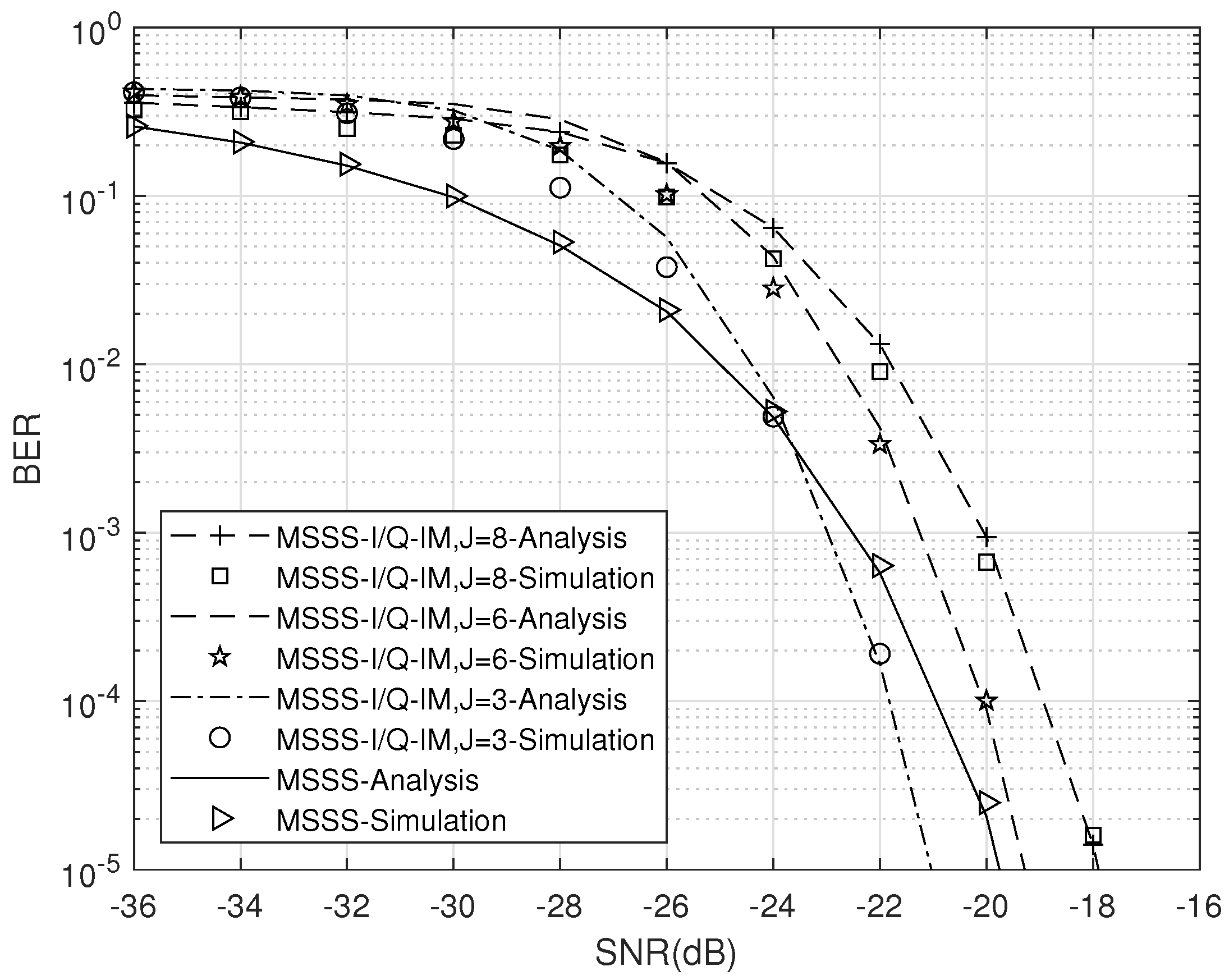
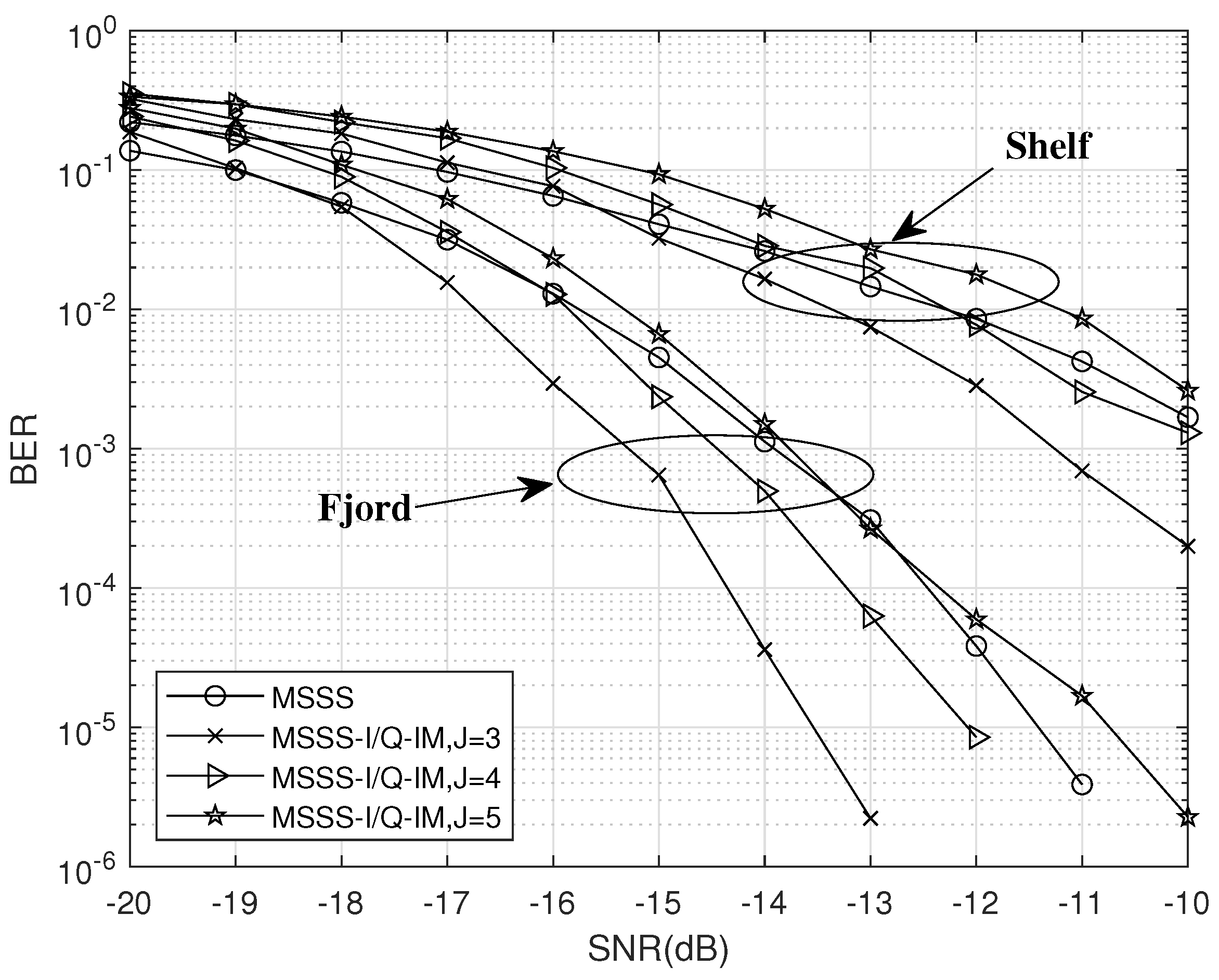
4.1. BER Performance over an AWGN Channel
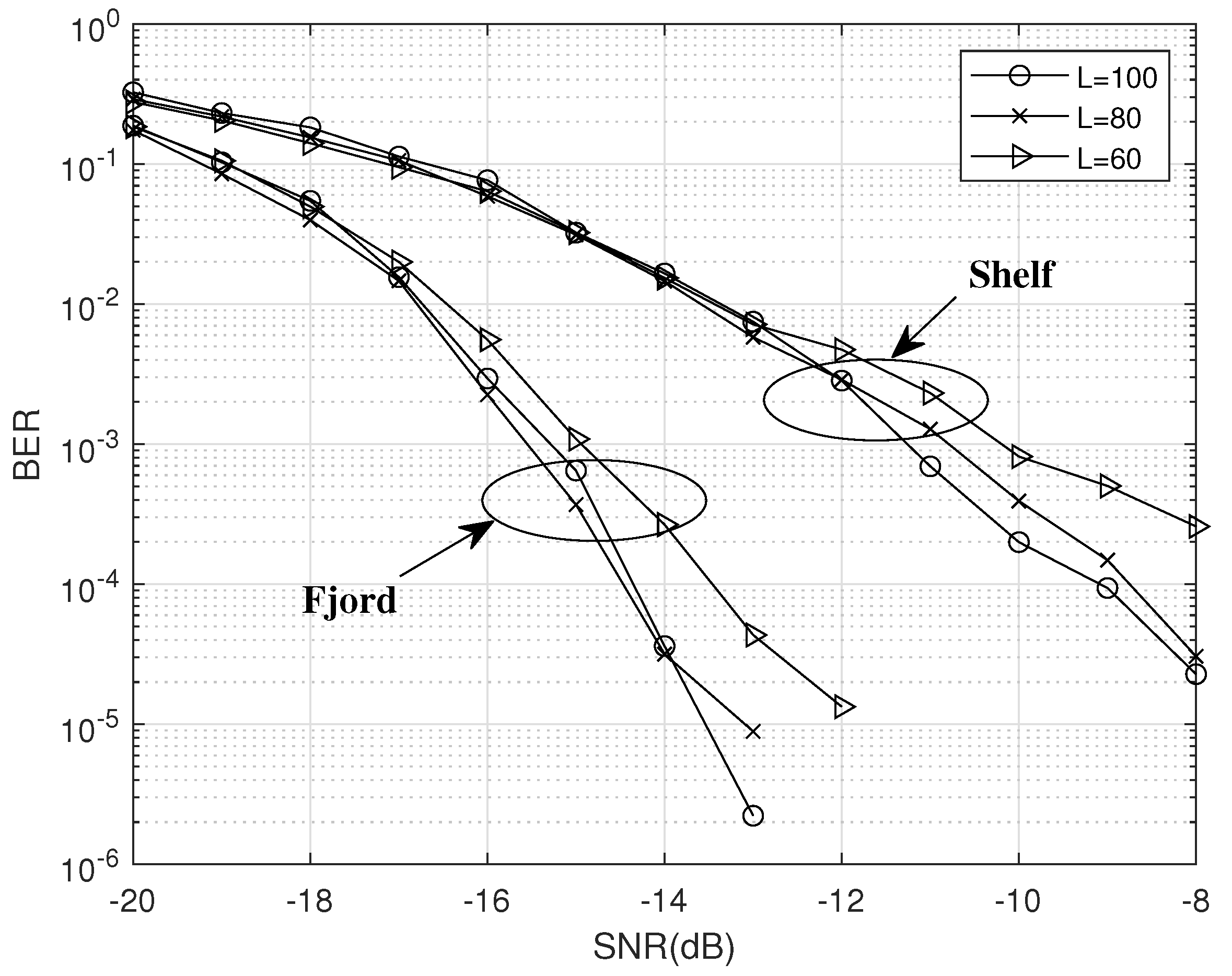
4.2. BER Performance over a UWA Channel
4.3. Water Pool Experiments
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Farr, N.; Bowen, A.; Ware, J.; Pontbriand, C.; Tivey, M. An integrated, underwater optical/acoustic communications system. In Proceedings of the OCEANS’10 IEEE SYDNEY, Sydney, NSW, Australia, 24–27 May 2010; pp. 1–6. [Google Scholar]
- Brekhovskikh, L.; Lysanov, Y.P. Fundamentals of Ocean Acoustics; Acoustical Society of America; Springer: Berlin/Heidelberg, Germany, 2004. [Google Scholar]
- Diamant, R.; Lampe, L. Low probability of detection for underwater acoustic communication: A review. IEEE Access. 2018, 6, 19099–19112. [Google Scholar] [CrossRef]
- Zhou, Y.; Tong, F. Channel estimation based equalizer for underwater acoustic multiple-inputmultiple-output communication. IEEE Access. 2019, 7, 79005–79016. [Google Scholar] [CrossRef]
- Dillard, G.M.; Reuter, M.; Zeidler, J.; Zeidler, B. Cyclic code shift keying: A low probability of intercept communication technique. IEEE Trans. Aerosp. Electron. Syst. 2003, 39, 786–798. [Google Scholar] [CrossRef] [Green Version]
- He, C.B.; Huang, J.G.; Han, J.; Zhang, Q.F. Cyclic shift keying spread spectrum underwater acoustic communication. Acta Phys. Sinica. 2009, 58, 8379–8385. [Google Scholar]
- He, C.; Zhang, Q.; Huang, J. Passive time reversal communication with cyclic shift keying over underwater acoustic channels. Appl. Acoust. 2015, 96, 132–138. [Google Scholar] [CrossRef]
- Yang, Y.U.; Feng, Z.H.O.U.; Gang, Q.I.A.O.; Donghu, N.I.E. Orthogonal M-ary code shift keying spread spectrum underwater acoustic communication. Chin. J. Acoust. 2014, 33, 279. [Google Scholar]
- Zhou, F.; Liu, B.; Nie, D.; Yang, G.; Zhang, W.; Ma, D. M-ary cyclic shift keying spread spectrum underwater acoustic communications based on virtual time-reversal mirror. Sensors 2019, 19, 3577. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lu, Q.; Hu, X.; Wang, D.; Zhou, S. Parallel combinatory multicarrier modulation in underwater acoustic communications. IET Commun. 2017, 11, 1331–1337. [Google Scholar] [CrossRef]
- Qu, F.; Qin, X.; Yang, L.; Yang, T.C. Spread-spectrum method using multiple sequences for underwater acoustic communications. IEEE J. Ocean. Eng. 2017, 43, 1215–1226. [Google Scholar] [CrossRef]
- Ishikawa, N.; Sugiura, S.; Hanzo, L. 50 years of permutation, spatial and index modulation: From classic rf to visible light communications and data storage. IEEE Commun. Surv. Tutor. 2018, 20, 1905–1938. [Google Scholar] [CrossRef] [Green Version]
- Sugiura, S.; Ishihara, T.; Nakao, M. State-of-the-art design of index modulation in the space, time, and frequency domains: Benefits and fundamental limitations. IEEE Access 2017, 5, 21774–21790. [Google Scholar] [CrossRef]
- Kaddoum, G.; Nijsure, Y.; Tran, H. Generalized code index modulation technique for high-data-rate communication systems. IEEE Trans. Veh. Technol. 2015, 65, 7000–7009. [Google Scholar] [CrossRef] [Green Version]
- Wen, M.; Cheng, X.; Yang, L.; Li, Y.; Cheng, X.; Ji, F. Index modulated OFDM for underwater acoustic communications. IEEE Commun. Mag. 2015, 54, 132–137. [Google Scholar] [CrossRef]
- Qasem, Z.A.H.; Wang, J.; Leftah, H.A.; Sun, H.; Hong, S.; Qi, J.; Esmaiel, H. Real signal DHT-OFDM with index modulation for underwater acoustic communication. IEEE J. Ocean. Eng. 2023, 48, 246–259. [Google Scholar] [CrossRef]
- Quan, L.; Xu, W.; Wang, D.; Wang, L. A multiple sequences spread-spectrum system with in-phase/quadrature index modulation for underwater acoustic communications. In Proceedings of the 15th International Symposium on Medical Information and Communication Technology (ISMICT), Xiamen, China, 14–16 April 2021; pp. 29–34. [Google Scholar]
- van Walree, P.A.; Socheleau, F.X.; Otnes, R.; Jenserud, T. The watermark benchmark for underwater acoustic modulation schemes. IEEE J. Ocean. Eng. 2017, 42, 1007–1018. [Google Scholar] [CrossRef] [Green Version]
- Başar, E.; Aygölü, Ü.; Panayırcı, E.; Poor, H.V. Orthogonal frequency division multiplexing with index modulation. IEEE Trans. Signal Process. 2013, 61, 5536–5549. [Google Scholar] [CrossRef]
- Cai, X.; Xu, W.; Wang, L.; Kolumbán, G. Multicarrier m-ary orthogonal chaotic vector shift keying with index modulation for high data rate transmission. IEEE Trans. Commun. 2019, 68, 974–986. [Google Scholar] [CrossRef]




| MSSS | MSSS-I/Q-IM | ||
|---|---|---|---|
| 18 | |||
| 22 | 24 | 18 | |
| MSSS | MSSS-I/Q-IM | |
|---|---|---|
| 228.77 bit/s | 228.77 bit/s | |
| 254.19 bit/s | ||
| 279.61 bit/s | ||
| Parameters | Value |
|---|---|
| Distance | 10 m |
| Sample Rate | 100 kHz |
| Carrier Frequency | 25 kHz |
| Synchronization Signal | LFM Signal |
| Bandwidth | 6 kHz |
| Attenuation Factor | Estimated SNR | MSSS | MSSS-I/Q-IM | ||
|---|---|---|---|---|---|
| J = 3 | J = 2 | J = 1 | |||
| 10 | −10.62 | 0 | 0 | 0 | 0 |
| 20 | −11.61 | 0 | 0 | 0 | 0 |
| 50 | −14.83 | 0.0650 | 0.1610 | 0.0772 | 0.0027 |
| 100 | −20.55 | 0.2592 | 0.3560 | 0.3166 | 0.1347 |
| Attenuation Factor | Estimated SNR | L = 200 | L = 150 | L = 100 |
|---|---|---|---|---|
| 20 | −8.67 | 0 | 0.0712 | 0.0101 |
| 25 | −9.36 | 0 | 0.1566 | 0.0652 |
| 100/3 | −11.24 | 0 | 0.1610 | 0.0572 |
| 50 | −12.75 | 0.0121 | 0.2083 | 0.1092 |
| Attenuation Factor | Estimated SNR | M = 1023 | M = 1023 |
|---|---|---|---|
| 50 | −6.01 | 0.0103 | 0.1340 |
| 100 | −9.97 | 0.3405 | 0.4787 |
| 125 | −12.37 | 0.3454 | 0.4183 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wei, Y.; Quan, L.; Xu, W.; Wang, D.; Wang, L. An In-Phase/Quadrature Index Modulation-Aided Spread Spectrum Communication System for Underwater Acoustic Communication. Electronics 2023, 12, 2919. https://doi.org/10.3390/electronics12132919
Wei Y, Quan L, Xu W, Wang D, Wang L. An In-Phase/Quadrature Index Modulation-Aided Spread Spectrum Communication System for Underwater Acoustic Communication. Electronics. 2023; 12(13):2919. https://doi.org/10.3390/electronics12132919
Chicago/Turabian StyleWei, Yunlong, Lingmiao Quan, Weikai Xu, Deqing Wang, and Lin Wang. 2023. "An In-Phase/Quadrature Index Modulation-Aided Spread Spectrum Communication System for Underwater Acoustic Communication" Electronics 12, no. 13: 2919. https://doi.org/10.3390/electronics12132919
APA StyleWei, Y., Quan, L., Xu, W., Wang, D., & Wang, L. (2023). An In-Phase/Quadrature Index Modulation-Aided Spread Spectrum Communication System for Underwater Acoustic Communication. Electronics, 12(13), 2919. https://doi.org/10.3390/electronics12132919







