A Federated Learning Method Based on Blockchain and Cluster Training
Abstract
:1. Introduction
- In terms of algorithms, this paper improves upon the federated learning algorithm based on odd–even round cluster training by incorporating blockchain instead of a central server. This enhancement provides higher levels of data privacy, security, and traceability while reducing the risk of a single point of failure;
- In terms of data compression, the model parameters obtained from local training on the client side are subjected to sparse quantization operations and integrated into the Quantization and Value–Coordinate Separated Storage (QVCSS) format proposed in this paper before being transmitted, thereby reducing the communication cost;
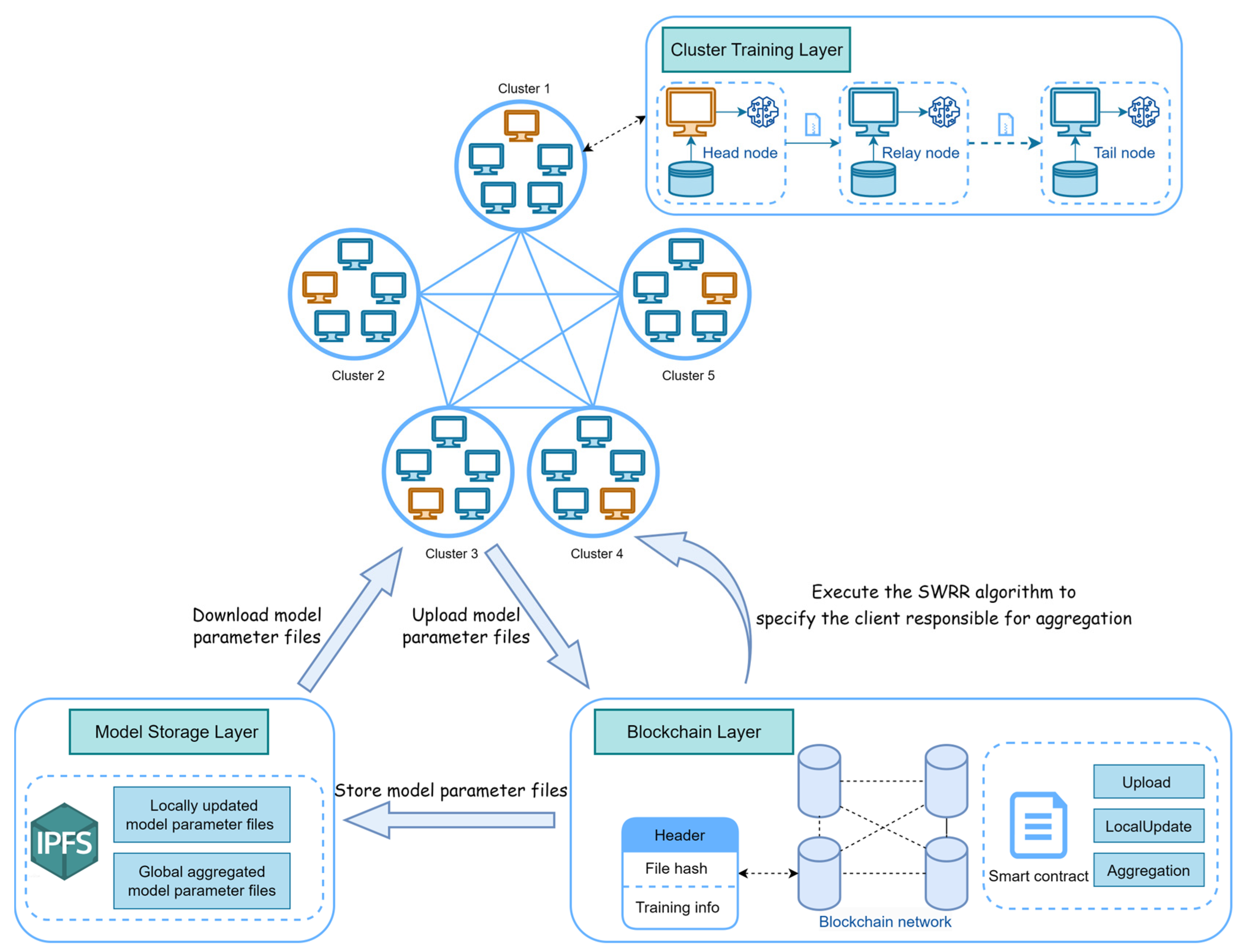
- In terms of architecture, a decentralized federated learning architecture based on blockchain and IPFS is proposed. First, instead of relying on a central server, a smart contract is designed to implement the Smooth Weighted Round-Robin (SWRR) algorithm to select the client responsible for global gradient aggregation in each round, which effectively avoids the single-point failure of the central server in traditional federated learning. Second, a consortium chain is adopted, which is more suitable for scenarios such as federated learning that require efficient processing of large amounts of data, as the consortium chain can improve performance by limiting the number of participants and using more efficient consensus algorithms. In addition, the use of IPFS optimizes the high overhead problem of storing model parameter files in the consortium chain.
2. Related Work
3. Design of BCFL Method
3.1. System Architecture
3.2. Federated Learning Algorithm Based on Odd–Even Round Cluster Training
| Algorithm 1: FedOEC |
 |
3.3. Model Parameter Compression
3.3.1. Top-K Operation
3.3.2. Storage Format Based on Quantization and Value–Coordinate Separation
3.4. Model Parameter Storage
4. Smart Contract Design
4.1. Upload() Function
- (1)
- Read model parameters: the function is executed after local updating or global model parameter aggregation and retrieves the model parameters from the local client;
- (2)
- Perform sparse and quantization processing: Judge whether to perform sparse or quantization operations, and if necessary, execute the function to integrate the model parameters in QVCSS format. In particular, the deflate compression algorithm is used to compress the array in QVCSS format, which further reduces the storage space and transmission cost of the model parameters;
- (3)
- Store the model parameters: Store the processed model parameters in IPFS and then generate the hash value corresponding to the model parameter file. The hash value and the related training information are packaged and stored in a block of the consortium chain so that other participants can access them.
4.2. LocalUpdate() Function
- (1)
- Download the model file: First, determine whether the client node is the head node in the cluster; if so, then download the global model file of the previous round from IPFS according to the hash value. Otherwise, download the model file of the predecessor node in the current round;
- (2)
- Verify the file hash: Determine the hash value of the downloaded model file and compare the calculated value with the provided value. If they match, then the file is complete and correct;
- (3)
- Load model parameters: load the model parameters from the model file and apply them to local training.
4.3. Aggregation() Function
4.3.1. FL Aggregation Node Selection Method Based on SWRR Algorithm
4.3.2. Design of Function
- (1)
- Read the current round: first, read the information of each cluster in the current round;
- (2)
- Execute the SWRR algorithm: use the information of the current round as the input of the SWRR algorithm and calculate the weight array corresponding to the nodes responsible for aggregation.
- (3)
- Specify the client responsible for aggregation: according to the result of the SWRR algorithm, specify the aggregation node for the current round;
- (4)
- Download and verify the model file from IPFS: the aggregation node downloads the model parameter files that were uploaded by the tail nodes of other clusters in the current round from IPFS and performs a hash verification;
- (5)
- Load model parameters: the aggregation node loads the model parameters from the model files;
- (6)
- Aggregate the model parameters: the aggregation node carries out weighted averaging of the model parameters of all clusters to obtain the global model parameter.
5. Experimental Implementation and Evaluation
5.1. Experimental Environment
5.2. Experimental Dataset
- (1)
- MNIST dataset
- (2)
- CIFAR-10 dataset
5.3. Experimental Metrics
5.4. Experimental Setting and Implementation
5.5. Security Evaluation
- (1)
- Integrity protection
- (2)
- Consensus mechanism protection
- (3)
- Decentralized storage
5.6. Experimental Results
- (1)
- Accuracy and communication cost analysis
- Experiment results of MNIST dataset
- 2.
- Experiment results of CIFAR-10 dataset
- 3.
- Experiment results analysis
- (2)
- Time consumption analysis
6. Conclusions and Future Work
- Optimization of client clustering partitioning strategies: In the algorithm proposed in this paper, client cluster partitioning is based on a simple random grouping strategy. Future research can explore more optimal client cluster partitioning strategies by considering specific application requirements and data distributions. This can further enhance the speed and accuracy of model convergence;
- Strengthening of security mechanisms: While the BCFL architecture proposed in this paper exhibits a high level of trustworthiness and robustness, it still has certain potential security risks and vulnerabilities. The utilization of blockchain technology in federated learning may face issues related to the abuse of decentralized authority. Additionally, consensus mechanisms in blockchain technology can be susceptible to attacks, such as the 51% attack, and smart contracts may contain security vulnerabilities that could be exploited by malicious actors [25]. Future research should focus on implementing effective oversight and governance mechanisms, continually improving and updating consensus mechanisms, and conducting security audits and vulnerability fixes for smart contract development—all of which are aimed at strengthening the system’s security mechanisms;
- Adaptation to heterogeneous devices and resource constraints: In practical application scenarios, clients participating in federated learning training may possess varying computational capabilities and resource constraints, such as IoT devices and edge computing systems. Future research can focus on several aspects to enhance the adaptability and practicality of federated learning algorithms. These aspects include reducing communication costs arising from limited device bandwidth, optimizing resource allocation, and enhancing the ability to combat malicious participants [26];
- Cross-domain applications of FL: This paper primarily focuses on the fundamental issues and methods of federated learning without delving into specific application domains. FL technology holds extensive potential applications in fields such as healthcare, finance, and transportation, among others. In the future, it will be possible to design cross-domain FL methods and application frameworks tailored to the characteristics and requirements of various domains.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- The Mobile Economy 2023. Available online: https://data.gsmaintelligence.com/research/research/research-2023/the-mobile-economy-2023 (accessed on 10 May 2023).
- Complete Guide to GDPR Compliance. Available online: https://gdpr.eu/ (accessed on 12 May 2023).
- Yin, X.; Zhu, Y.; Hu, J. A comprehensive survey of privacy-preserving federated learning: A taxonomy, review, and future directions. ACM Comput. Surv. (CSUR) 2021, 54, 1–36. [Google Scholar] [CrossRef]
- Kouhizadeh, M.; Sarkis, J. Blockchain practices, potentials, and perspectives in greening supply chains. Sustainability 2018, 10, 3652. [Google Scholar] [CrossRef]
- McMahan, B.; Moore, E.; Ramage, D.; Hampson, S.; Arcas, B.A. Communication-efficient learning of deep networks from decentralized data. In Artificial Intelligence and Statistics; PMLR: New York, NY, USA, 2017; pp. 1273–1282. [Google Scholar]
- Konecny, J.; McMahan, H.B.; Felix, X.Y.; Richtárik, P.; Suresh, A.T.; Bacon, D. Federated learning: Strategies for improving communication efficiency. arXiv 2016, arXiv:1610.05492. [Google Scholar]
- Briggs, C.; Fan, Z.; Andras, P. Federated learning with hierarchical clustering of local updates to improve training on non-IID data. In Proceedings of the 2020 International Joint Conference on Neural Networks (IJCNN), Glasgow, UK, 19–24 July 2020; pp. 1–9. [Google Scholar]
- Aji, A.F.; Heafield, K. Sparse communication for distributed gradient descent. arXiv 2017, arXiv:1704.05021. [Google Scholar]
- Jhunjhunwala, D.; Gadhikar, A.; Joshi, G.; Eldar, Y.C. Adaptive quantization of model updates for communication-efficient federated learning. In Proceedings of the ICASSP 2021—2021 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Toronto, ON, Canada, 6–11 June 2021; pp. 3110–3114. [Google Scholar]
- Li, C.; Li, G.; Varshney, P.K. Communication-efficient federated learning based on compressed sensing. IEEE Internet Things J. 2021, 8, 15531–15541. [Google Scholar] [CrossRef]
- Sattler, F.; Wiedemann, S.; Müller, K.R.; Samek, W. Robust and communication-efficient federated learning from non-iid data. IEEE Trans. Neural Netw. Learn. Syst. 2019, 31, 3400–3413. [Google Scholar] [CrossRef]
- Haddadpour, F.; Kamani, M.M.; Mokhtari, A.; Mahdavi, M. Federated learning with compression: Unified analysis and sharp guarantees. PMLR 2021, 130, 2350–2358. [Google Scholar]
- Seol, M.; Kim, T. Performance Enhancement in Federated Learning by Reducing Class Imbalance of Non-IID Data. Sensors 2023, 23, 1152. [Google Scholar] [CrossRef] [PubMed]
- Zhao, L.; Huang, J. A distribution information sharing federated learning approach for medical image data. Complex Intell. Syst. 2023, 1–12. [Google Scholar] [CrossRef] [PubMed]
- Chen, F.; Wan, H.; Cai, H.; Cheng, G. Machine learning in/for blockchain: Future and challenges. Can. J. Stat. 2021, 49, 1364–1382. [Google Scholar] [CrossRef]
- Tsai, C.W.; Chen, Y.P.; Tang, T.C.; Luo, Y.C. An efficient parallel machine learning-based blockchain framework. Ict Express 2021, 7, 300–307. [Google Scholar] [CrossRef]
- Lo, S.K.; Liu, Y.; Lu, Q.; Wang, C.; Xu, X.; Paik, H.Y.; Zhu, L. Toward trustworthy ai: Blockchain-based architecture design for accountability and fairness of federated learning systems. IEEE Internet Things J. 2022, 10, 3276–3284. [Google Scholar] [CrossRef]
- Jiang, T.; Shen, G.; Guo, C.; Cui, Y.; Xie, B. BFLS: Blockchain and Federated Learning for sharing threat detection models as Cyber Threat Intelligence. Comput. Netw. 2023, 224, 109604. [Google Scholar] [CrossRef]
- Zhang, W.; Wang, Z.; Li, X. Blockchain-based decentralized federated transfer learning methodology for collaborative machinery fault diagnosis. Reliab. Eng. Syst. Saf. 2023, 229, 108885. [Google Scholar] [CrossRef]
- Zhang, Y.; Wu, Y.; Li, T.; Zhou, H.; Chen, Y. Vertical Federated Learning Based on Consortium Blockchain for Data Sharing in Mobile Edge Computing. CMES-Comput. Model. Eng. Sci. 2023, 137, 345–361. [Google Scholar] [CrossRef]
- Fu, X.; Peng, R.; Yuan, W.; Ding, T.; Zhang, Z.; Yu, P.; Kadoch, M. Federated learning-based resource management with blockchain trust assurance in smart IoT. Electronics 2023, 12, 1034. [Google Scholar] [CrossRef]
- Li, Y.; Liu, Z.; Huang, Y.; Xu, P. FedOES: An Efficient Federated Learning Approach. In Proceedings of the 2023 3rd International Conference on Neural Networks, Information and Communication Engineering (NNICE), Guangzhou, China, 24–26 February 2023; pp. 135–139. [Google Scholar]
- Davis, T.A.; Hu, Y. The University of Florida sparse matrix collection. ACM Trans. Math. Softw. 2011, 38, 1–25. [Google Scholar] [CrossRef]
- Zheng, Z.; Xie, S.; Dai, H.; Chen, X.; Wang, H. An overview of blockchain technology: Architecture, consensus, and future trends. In Proceedings of the 2017 IEEE International Congress on Big Data (BigData Congress), Honolulu, HI, USA, 25–30 June 2017; pp. 557–564. [Google Scholar]
- Li, X.; Jiang, P.; Chen, T.; Luo, X.; Wen, Q. A survey on the security of blockchain systems. Future Gener. Comput. Syst. 2020, 107, 841–853. [Google Scholar] [CrossRef]
- Lim, W.Y.B.; Luong, N.C.; Hoang, D.T.; Jiao, Y.; Liang, Y.C.; Yang, Q.; Niyato, D.; Miao, C. Federated learning in mobile edge networks: A comprehensive survey. IEEE Commun. Surv. Tutor. 2020, 22, 2031–2063. [Google Scholar] [CrossRef]














| Selected Aggregation Node | |||
|---|---|---|---|
| 1 | [1, 1, 3, 2, 1] | [1, 1, −5, 2, 1] | |
| 2 | [2, 2, −2, 4, 2] | [2, 2, −2, −4, 2] | |
| 3 | [3, 3, 1, −2, 3] | [−5, 3, 1, −2, 3] | |
| 4 | [−4, 4, 4, 0, 4] | [−4, −4, 4, 0, 4] | |
| 5 | [−3, −3, 7, 2, 5] | [−3, −3, −1, 2, 5] | |
| 6 | [−2, −2, 2, 4, 6] | [−2, −2, 2, 4, −2] | |
| 7 | [−1, −1, 5, 6, −1] | [−1, −1, 5, −2, −1] | |
| 8 | [0, 0, 8, 0, 0] | [0, 0, 0, 0, 0] | |
| 9 | [1, 1, 3, 2, 1] | [1, 1, −5, 2, 1] |
| Pattern | Sparsity Used? | Quantization Used? |
|---|---|---|
| Pattern 1 (P1) | No | No |
| Pattern 2 (P2) | Yes | No |
| Pattern 3 (P3) | Yes | Yes |
| Round of Communication | Algorithm Type | Accuracy (IID) | Accuracy (Non-IID) | Communication Cost (Upload) | Communication Cost (Download) |
|---|---|---|---|---|---|
| 5th round | BCFL (p1) | 97.80% | 96.59% | 22.47 MB | 4.49 MB |
| BCFL (p2) | 97.07% | 95.52% | 16.26 MB | 3.25 MB | |
| BCFL (p3) | 97.30% | 93.89% | 10.76 MB | 2.15 MB | |
| FedAvg | 95.06% | 88.98% | 44.94 MB | 44.94 MB | |
| 20th round | BCFL (p1) | 98.81% | 98.20% | 89.87 MB | 17.97 MB |
| BCFL (p2) | 98.38% | 97.47% | 65.04 MB | 13.01 MB | |
| BCFL (p3) | 98.26% | 97.27% | 43.05 MB | 8.61 MB | |
| FedAvg | 96.63% | 95.73% | 179.74 MB | 179.74 MB | |
| 100th round | BCFL (p1) | 99.15% | 98.84% | 449.35 MB | 89.87 MB |
| BCFL (p2) | 98.85% | 98.53% | 325.21 MB | 65.04 MB | |
| BCFL (p3) | 98.81% | 98.51% | 215.23 MB | 43.05 MB | |
| FedAvg | 98.83% | 98.29% | 898.71 MB | 898.71 MB |
| Round of Communication | Algorithm Type | Accuracy (IID) | Accuracy (Non-IID) | Communication Cost (Upload) | Communication Cost (Download) |
|---|---|---|---|---|---|
| 5th round | BCFL(p1) | 73.06% | 58.77% | 1.18 GB | 0.24 GB |
| BCFL (p2) | 71.15% | 58.98% | 1.03 GB | 0.21 GB | |
| BCFL(p3) | 71.01% | 57.27% | 0.72 GB | 0.14 GB | |
| FedAvg | 63.21% | 55.51% | 2.36 GB | 2.36 GB | |
| 20th round | BCFL(p1) | 80.87% | 71.09% | 4.71 GB | 0.94 GB |
| BCFL(p2) | 78.78% | 71.05% | 4.12 GB | 0.82 GB | |
| BCFL(p3) | 78.28% | 71.50% | 2.87 GB | 0.57 GB | |
| FedAvg | 76.01% | 70.87% | 9.43 GB | 9.43 GB | |
| 100th round | BCFL(p1) | 81.98% | 78.41% | 23.57 GB | 4.71 GB |
| BCFL(p2) | 80.82% | 78.50% | 20.60 GB | 4.12 GB | |
| BCFL(p3) | 81.20% | 77.83% | 14.35 GB | 2.87 GB | |
| FedAvg | 81.44% | 77.88% | 47.14 GB | 47.14 GB |
| File Type | |||||
|---|---|---|---|---|---|
| MNIST (p1) | — | — | 0.718 s | — | 0.718 s |
| MNIST (p2) | — | 0.058 s | 0.526 s | 0.062 s | 0.646 s |
| MNIST (p3) | 0.00017 s | 0.061 s | 0.362 s | 0.064 s | 0.487 s |
| CIFAR-10 (p1) | — | — | 37.712 s | — | 37.712 s |
| CIFAR-10 (p2) | — | 3.397 s | 32.972 s | 3.427 s | 39.796 s |
| CIFAR-10 (p3) | 0.0048 s | 3.542 s | 22.978 s | 3.452 s | 29.972 s |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Y.; Yan, Y.; Liu, Z.; Yin, C.; Zhang, J.; Zhang, Z. A Federated Learning Method Based on Blockchain and Cluster Training. Electronics 2023, 12, 4014. https://doi.org/10.3390/electronics12194014
Li Y, Yan Y, Liu Z, Yin C, Zhang J, Zhang Z. A Federated Learning Method Based on Blockchain and Cluster Training. Electronics. 2023; 12(19):4014. https://doi.org/10.3390/electronics12194014
Chicago/Turabian StyleLi, Yue, Yiting Yan, Zengjin Liu, Chang Yin, Jiale Zhang, and Zhaohui Zhang. 2023. "A Federated Learning Method Based on Blockchain and Cluster Training" Electronics 12, no. 19: 4014. https://doi.org/10.3390/electronics12194014
APA StyleLi, Y., Yan, Y., Liu, Z., Yin, C., Zhang, J., & Zhang, Z. (2023). A Federated Learning Method Based on Blockchain and Cluster Training. Electronics, 12(19), 4014. https://doi.org/10.3390/electronics12194014






