Multi-Type Electric Vehicle Scheduling Optimization Considering Load Capacity, Battery-Allowed Mileage, and Recharging Duration
Abstract
:1. Introduction
1.1. Literature Review
1.2. Contributions
2. Problem Statement
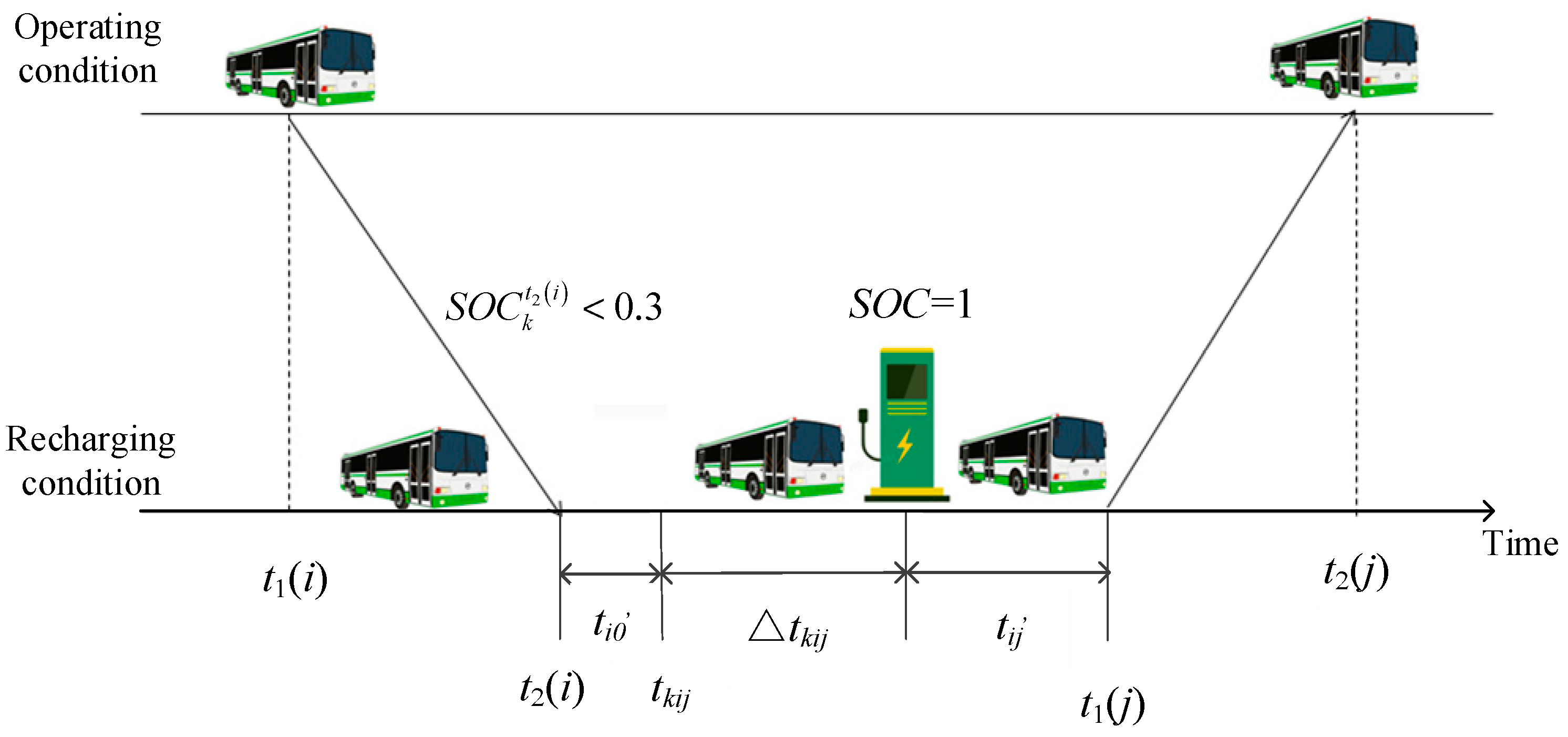
2.1. Vehicle Scheduling
- (1)
- Normal trip: A normal trip refers to a planned journey with scheduling departure/arrival times, which includes necessary information, i.e., the bus line number, the first and last station, the running time, and the vehicle number.
- (2)
- Idle trip: An idle trip refers to a trip undertaken by vehicles without carrying passengers. There are several reasons for conducting idle trips, such as the following: (i) when a bus completes a trip, and the last stop of the previous trip is different from the first stop of the next trip, an idle trip is necessary in order to maintain the schedule; (ii) in order to maintain a balanced distribution of buses among depots throughout the day, idle trips are used to allocate vehicles at the end of operations; (iii) to ensure the smooth operation of the bus network, buses that are temporarily idle at certain depots may need to be dispatched to depots with demand to participate in subsequent trips; and (iv) idle trips also facilitate vehicle inspection, maintenance, refueling, charging, and other necessary activities. Reasonable idle trip management can effectively improve the PT operational efficiency and reduce the required fleet size.
- (3)
- Trip chain: A trip chain represents the complete schedule of a vehicle for a day, encompassing both normal trips and idle trips. It records the entire process of a bus leaving the depot, completing all of the trips, and returning to the depot.
- (4)
- Depot: A depot is a designated facility used for parking and maintaining buses. Typically, depots are equipped with garages, maintenance rooms, gas stations, charging stations, and other necessary buildings and equipment.
2.2. Assumptions
- (1)
- The recharging infrastructures (rechargers) are located at the depot, and there is only one depot considered in the model. For a medium-sized PT company, a single depot is enough for storing the overall fleet sizes.
- (2)
- Recharging queuing is not considered in this study. It means the number of rechargers is sufficient for recharging.
- (3)
- The vehicles strictly adhere to the timetable, regardless of operational delays.
- (4)
- The electrovalence value is fixed, according to the local policy.
- (5)
- A discharge depth of 70–80% is beneficial for electric vehicle battery health. Thus, once the discharge depth exceeds 70%, the electric vehicles need to recharge.
2.3. Notations
3. Model Formulation
3.1. Objective Function
3.2. Constraints
4. Solution Algorithm
4.1. Preprocessing Procedure
4.2. Genetic Algorithm
- (1)
- Encoding
- Vehicle 1: Depot → Trip 1 → Trip 5 → Trip 7 → Depot
- Vehicle 2: Depot → Trip 4 → Trip 8 → Depot
- Vehicle 3: Depot → Trip 2 → Trip 3 → Depot
- Vehicle 4: Depot → Trip 6 → Depot
- Vehicle 5: No trip to operate
- (2)
- Initialization
- (3)
- Fitness function
- (4)
- Selection
- (5)
- Crossover
- (6)
- Mutation
- (7)
- Termination criterion
5. Case Study
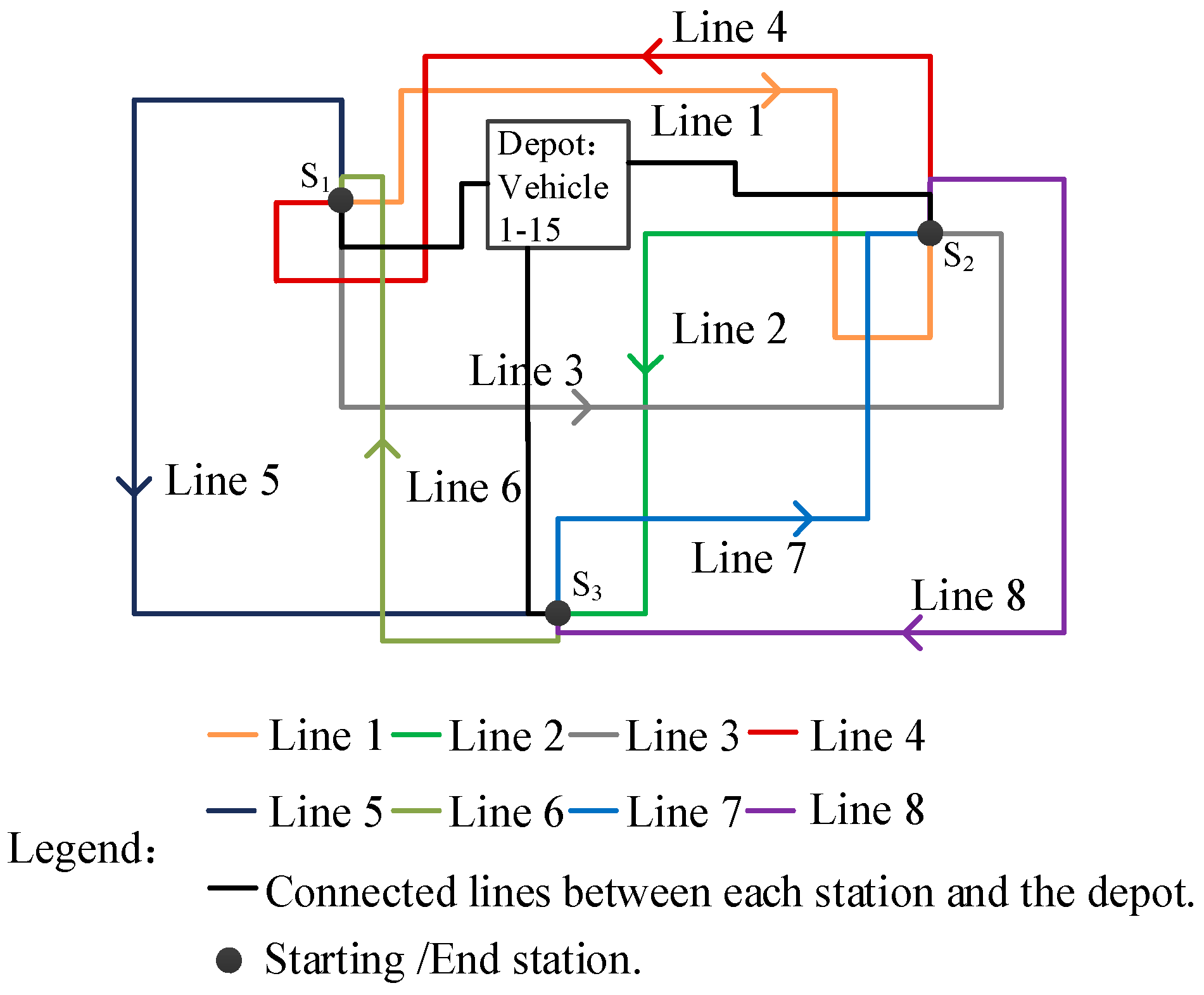
5.1. Data and Parameter Settings
5.2. Result Analysis
5.2.1. Scenario 1: One-Trip Frequency Scenario
- (1)
- Single-one-type vehicle scheduling
- (2)
- Two-type vehicle scheduling
- (3)
- Multi-type vehicle scheduling
5.2.2. Scenario 2: Two-Trip Frequency Scenario
- (1)
- Single-one-type vehicle scheduling scheme
- (2)
- Two-type vehicle scheduling
- (3)
- Multi-type vehicle scheduling
5.2.3. Scenario 3: Three-Trip Frequency Scenario
- (1)
- Single-one-type vehicle scheduling
- (2)
- Two-type vehicle scheduling
- (3)
- Multi-type vehicle scheduling
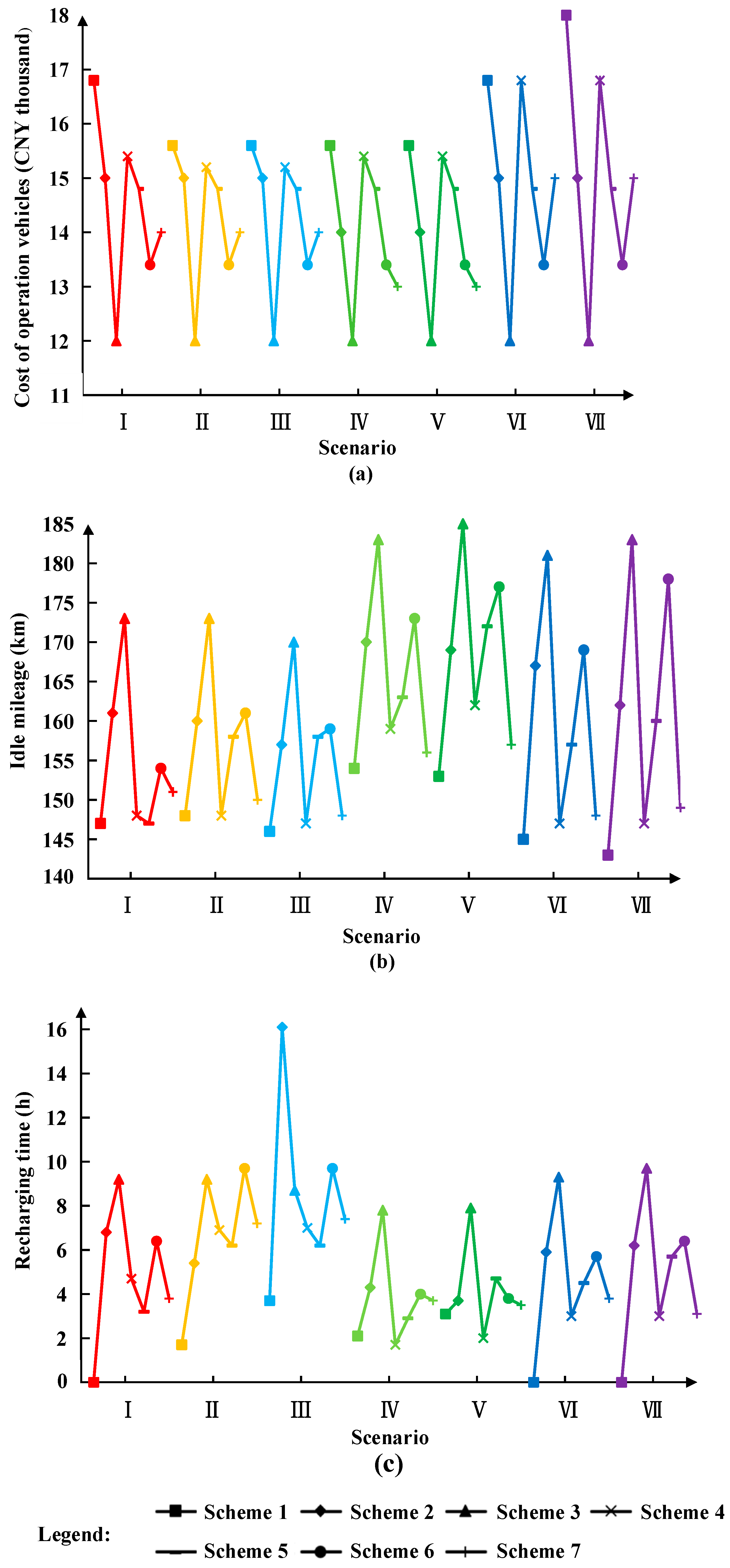
5.3. Sensitivity Analysis
- Scheme 1: single large-type vehicle;
- Scheme 2: single medium-type vehicle;
- Scheme 3: single small-type vehicle;
- Scheme 4: large- and medium-type vehicle;
- Scheme 5: large- and small-type vehicle,
- Scheme 6: medium- and small-type vehicle;
- Scheme 7: multi-type vehicle.
6. Conclusions
- Expanding the optimization problem to multiple depots and addressing the network-level synchronization of scheduling problems.
- Considering the influence of emergencies, traffic congestion, and other special conditions on vehicle scheduling. Techniques such as GIS technology can be employed to study dynamic traffic network planning for pure electric vehicles.
- Simultaneously considering various charger types to optimize the charging infrastructure and scheduling process.
- Exploring the collaborative optimization of vehicle scheduling with crew scheduling to enhance the overall operational efficiency and cost-effectiveness.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Gavish, B.; Shlifer, E. An approach for solving a class of transportation scheduling problems. Eur. J. Oper. Res. 1979, 3, 122–134. [Google Scholar] [CrossRef]
- Wang, Y.; Liao, Z.; Tang, T.; Ning, B. Train scheduling and circulation planning in urban rail transit lines. Control Eng. Pract. 2017, 61, 112–123. [Google Scholar] [CrossRef]
- Mancini, S.; Gansterer, M. Vehicle scheduling for rental-with-driver services. Transp. Res. Part E Logist. Transp. Rev. 2021, 156, 102530. [Google Scholar] [CrossRef]
- Olariu, F.E.; Frasinaru, C. Multiple-Depot Vehicle Scheduling Problem Heuristics. arXiv 2020, arXiv:2004.14951. [Google Scholar] [CrossRef]
- Wu, M.; Yu, C.; Ma, W.; An, K.; Zhong, Z. Joint optimization of timetabling, vehicle scheduling, and ride-matching in a flexible multi-type shuttle bus system. Transp. Res. Part C Emerg. Technol. 2022, 139, 103657. [Google Scholar] [CrossRef]
- Jin, L. Study on the Matching Relationship between Electric Bus Battery State and Operation. Master’s Thesis, Beijing Jiaotong University, Beijing, China, 2011. (In Chinese). [Google Scholar]
- Sebastiani, M.T.; Lüders, R.; Fonseca, K.V.O. Evaluating Electric Bus Operation for a Real-World BRT Public Transportation Using Simulation Optimization. IEEE Trans. Intell. Transp. Syst. 2016, 17, 2777–2786. [Google Scholar] [CrossRef]
- Wang, Y.; Huang, Y.; Xu, J.; Barclay, N. Optimal recharging scheduling for urban electric buses: A case study in Davis. Transp. Res. Part E Logist. Transp. Rev. 2017, 100, 115–132. [Google Scholar] [CrossRef]
- Rogge, M.; Van der Hurk, E.; Larsen, A.; Sawer, D.U. Electric bus fleet size and mix problem with optimization of recharging infrastructure. Appl. Energy 2018, 211, 282–295. [Google Scholar] [CrossRef]
- Tang, X.; Lin, X.; He, F. Robust scheduling strategies of electric buses under stochastic traffic conditions. Transp. Res. Part C Emerg. Technol. 2019, 105, 163–182. [Google Scholar] [CrossRef]
- He, Y.; Liu, Z.; Song, Z. Optimal recharging scheduling and management for a fast-recharging battery electric bus system. Transp. Res. Part E Logist. Transp. Rev. 2020, 142, 102056. [Google Scholar]
- Yao, E.; Liu, T.; Lu, T.; Yang, Y. Optimization of electric vehicle scheduling with multiple vehicle types in public transport. Sustain. Cities Soc. 2020, 52, 101862. [Google Scholar] [CrossRef]
- Wang, J.; Kang, L.; Liu, Y. Optimal scheduling for electric bus fleets based on dynamic programming approach by considering battery capacity fade. Renew. Sustain. Energy Rev. 2020, 130, 109978. [Google Scholar] [CrossRef]
- Wu, W.; Lin, Y.; Liu, R.; Jin, W. The multi-depot electric vehicle scheduling problem with power grid characteristics. Transp. Res. Part B Methodol. 2022, 155, 322–347. [Google Scholar] [CrossRef]
- Liu, T.; Ceder, A.A. Battery-electric transit vehicle scheduling with optimal number of stationary chargers. Transp. Res. Part C Emerg. Technol. 2020, 114, 118–139. [Google Scholar] [CrossRef]
- Uslu, T.; Kaya, O. Location and capacity decisions for electric bus recharging stations considering waiting times. Transp. Res. Part D Transp. Environ. 2021, 90, 102645. [Google Scholar] [CrossRef]
- He, J.; Yang, H.; Tang, T.Q.; Huang, H.J. An optimal recharging station location model with the consideration of electric vehicle’s driving range. Transp. Res. Part C Emerg. Technol. 2018, 86, 641–654. [Google Scholar] [CrossRef]
- Ma, T.Y.; Xie, S. Optimal fast recharging station locations for electric ridesharing with vehicle-recharging station assignment. Transp. Res. Part D Transp. Environ. 2021, 90, 102682. [Google Scholar] [CrossRef]
- Xue, H. Multi-Vehicle Pure Electric Bus Timetable and Vehicle Scheduling Integration and Optimization. Master’s Thesis, Dalian Maritime University, Dalian, China, 2022. (In Chinese). [Google Scholar]
- Katoch, S.; Chauhan, S.S.; Kumar, V. A review on genetic algorithm: Past, present, and future. Multimed. Tools Appl. 2020, 80, 8091–8126. [Google Scholar] [CrossRef] [PubMed]








| Publication | Charging Method | Multi Depot | Multi-Type: Heterogeneous/Optimized | Model Structure | Solution Method |
|---|---|---|---|---|---|
| Sebastiani et al., (2016) [7] | Recharging | No | No/No | Simulation | GA |
| Wang et al., (2017) [2] | Recharging (at intermediate stations) | No | No/No | MILP | CPLEX |
| Rogge et al., (2018) [9] | Recharging | No | Yes/Yes | MILP | GGA |
| Tang et al., (2019) [10] | Recharging | No | No/Yes | MILP | CPLEX |
| He et al., (2020) [11] | Recharging | Yes | No/No | MILP | CPLEX |
| Yao et al., (2020) [12] | Recharging | No | Yes/Yes | MILP | Heuristic |
| Wang et al., (2020) [13] | Battery swapping or recharging | No | No/No | MILP | DP |
| Liu et al., (2020) [15] | Recharging | No | No/Yes | DP/IP | Heuristic/AMF |
| Wu et al., (2022) [14] | Recharging | No | No/No | MILP | BP |
| This paper (2023) | Recharging | No | Yes/Yes | MINLP | GA |
| Notations | Definition |
|---|---|
| Total cost. | |
| The number of buses in a line, where m0 stands for the capacity of the depot. | |
| Index of vehicle, . | |
| The number of trips, determined by the timetable. | |
| Index of trip, . | |
| Cost per unit distance (unit: CNY, the abbreviation of China Yuan). | |
| Battery-allowed mileage of vehicle k (unit: km). | |
| Idle mileage between trip i and trip j (unit: km). | |
| Distance from depot to first station of trip i (unit: km). | |
| Distance returning to the depot after executing the trip j (unit: km). | |
| Idle time between trip i and depot (unit: min). | |
| Running distance of trip i (unit: km). | |
| Starting time of trip i. | |
| End time of trip i. | |
| Connection time between trip i and trip j (unit: min). | |
| Idle time between trip i and trip j (unit: min). | |
| Recharging time of vehicle k during idle time between trip i and trip j (unit: min). | |
| Starting time of recharging between trip i and trip j of vehicle k. | |
| Binary variable. If vehicle k is included in the scheduling, ; otherwise, . | |
| Total number of trips that vehicle k performs. | |
| Binary variable. If the vehicle k executes trip i and trip j orderly, ; otherwise, . | |
| Binary variable. If vehicle k executes trip i from the depot, ; otherwise, . | |
| Binary variable. If vehicle k returns to the depot after trip j, ; otherwise, . | |
| Remaining energy of vehicle k at time . | |
| The number of passengers who need to board during trip i. | |
| Maximum capacity of vehicle k. | |
| Q | Set of vehicles that are not assigned for service trips. |
| Y | Set of vehicles that execute service trips. |
| Trip Index | Start Time | End Time |
|---|---|---|
| 1 | 8:00 | 9:00 |
| 2 | 8:20 | 9:20 |
| 3 | 8:40 | 9:40 |
| 4 | 9:20 | 10:20 |
| 5 | 9:30 | 10:00 |
| 6 | 10:40 | 11:20 |
| 7 | 11:40 | 12:20 |
| 8 | 12:20 | 13:30 |
| Line | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 3 | 4 | 3 | 4 | 3 | 5 | 5 | 4 |
| 1 | 4 | 0 | 0 | 7 | 0 | 7 | 9 | 9 | 0 |
| 2 | 5 | 8 | 0 | 8 | 9 | 8 | 0 | 0 | 9 |
| 3 | 4 | 7 | 0 | 0 | 0 | 7 | 9 | 9 | 0 |
| 4 | 3 | 0 | 7 | 0 | 0 | 0 | 8 | 8 | 7 |
| 5 | 5 | 8 | 9 | 8 | 9 | 0 | 0 | 0 | 9 |
| 6 | 4 | 0 | 7 | 0 | 7 | 0 | 0 | 8 | 7 |
| 7 | 4 | 7 | 0 | 7 | 0 | 7 | 9 | 0 | 0 |
| 8 | 5 | 8 | 9 | 8 | 9 | 8 | 0 | 0 | 0 |
| Line | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 6 | 8 | 6 | 8 | 6 | 10 | 10 | 8 |
| 1 | 8 | 0 | 0 | 14 | 0 | 14 | 18 | 18 | 0 |
| 2 | 10 | 16 | 0 | 16 | 18 | 16 | 0 | 0 | 18 |
| 3 | 8 | 14 | 0 | 0 | 0 | 14 | 18 | 18 | 0 |
| 4 | 6 | 0 | 14 | 0 | 0 | 0 | 16 | 16 | 14 |
| 5 | 10 | 16 | 18 | 16 | 18 | 0 | 0 | 0 | 18 |
| 6 | 6 | 0 | 14 | 0 | 14 | 0 | 0 | 16 | 14 |
| 7 | 8 | 14 | 0 | 14 | 0 | 14 | 18 | 0 | 0 |
| 8 | 10 | 16 | 18 | 16 | 18 | 16 | 0 | 0 | 0 |
| Line | Mileage |
|---|---|
| 1 | 30 |
| 2 | 40 |
| 3 | 30 |
| 4 | 30 |
| 5 | 20 |
| 6 | 20 |
| 7 | 40 |
| 8 | 40 |
| Vehicle Type | Large-Type | Medium-Type | Small-Type |
|---|---|---|---|
| Energy consumption (kWh/km) | 1.2 | 1 | 0.8 |
| Battery capacity ((kWh) | 182 | 121 | 86 |
| Recharging duration (h) | 4.7 | 3.1 | 2.2 |
| Maximum battery-allowed mileage (km) | 106 | 85 | 75 |
| Weight of vehicle operation cost | 1.2 | 1 | 0.8 |
| Line | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|---|---|
| The number of passengers in 1st trip | 35 | 28 | 65 | 21 | 17 | 27 | 19 | 47 |
| Vehicle Index | Trips Performed by Vehicles (Idle Mileage) |
|---|---|
| The 1st Scheme | |
| 1 | 0 → 4th trip → 6th trip → 0 (16 km) |
| 2 | 0 → 1st trip → 5th trip → 0 (15 km) |
| 3 | 0 km |
| 4 | 0 → 2nd trip → 7th trip → 0 (8 km) |
| 5 | 0 → 3rd trip → 8th trip → 0 (8 km) |
| Scheme Index | No. Large-Type | No. Medium-Type | No. Small-Type | Idle Mileage(km) | Operation Cost Z1 | Idle MileageCost Z2 | Recharging Time Cost Z3 | Total Cost Z |
|---|---|---|---|---|---|---|---|---|
| 1st | 4 | 0 | 0 | 47 | 4.8 | 0.0047 | 0 | 4.8047 |
| Vehicle Index | Trips Performed by Vehicles (Idle Mileage) | |
|---|---|---|
| The 2nd Scheme | The 3rd Scheme | |
| 1 | 0 → 5th trip → 7th trip → 0 (7 km) | 0 → 3th trip → 8th trip → 0 (8 km) |
| 2 | 0 km | 0 → 1st trip → 5th trip → 6th trip → 0 (7 km) |
| 3 | 0 → 1st trip → 4th trip → 6th trip → 0 (15 km) | 0 → 1st trip → 0 (7 km) |
| 4 | 0 → 3rd trip → 8th trip → 0 (8 km) | 0 → 2nd trip → 4th trip → 0 (16 km) |
| 5 | 0 → 2nd trip → 0 (9 km) | 0 → 7th trip → 0 (9 km) |
| Scheme Index | No. Large-Type | No. Medium-Type | No. Small-Type | Idle Mileage(km) | Operation Cost Z1 | Idle MileageCost Z2 | Recharging Time Cost Z3 | Total Cost Z |
|---|---|---|---|---|---|---|---|---|
| 2nd | 2 | 2 | 0 | 39 | 4.4 | 0.0039 | 0 | 4.4039 |
| 3rd | 2 | 0 | 3 | 47 | 4.8 | 0.0047 | 0 | 4.8047 |
| Vehicle Index | Trips Performed by Vehicles (Idle Mileage) |
|---|---|
| The 4th Scheme | |
| 1 | 0 → 1st trip → 5th trip → 8th trip → 0 (24 km) |
| 2 | 0 → 2nd trip → 0 (9 km) |
| 3 | 0 → 4th trip → 6th trip → 0 (16 km) |
| 4 | 0 → 3rd trip → 7th trip → 0 (16 km) |
| 5 | 0 km |
| Scheme Index | No. Large-Type | No. Medium-Type | No. Small-Type | Idle Mileage(km) | Operation Cost Z1 | Idle MileageCost Z2 | Recharging Time Cost Z3 | Total Cost Z |
|---|---|---|---|---|---|---|---|---|
| 1st | 4 | 0 | 0 | 47 | 4.8 | 0.0047 | 0 | 4.8047 |
| 2nd | 2 | 2 | 0 | 39 | 4.4 | 0.0039 | 0 | 4.4039 |
| 3rd | 2 | 0 | 3 | 47 | 4.8 | 0.0047 | 0 | 4.8047 |
| 4th | 1 | 1 | 2 | 65 | 3.8 | 0.0065 | 0.101 | 3.8075 |
| Line | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|---|---|
| The number of passengers on 1st trip | 35 | 28 | 65 | 21 | 17 | 27 | 19 | 47 |
| The number of passengers on 2nd trip | 62 | 14 | 33 | 28 | 13 | 39 | 12 | 18 |
| Scheme Index | No. Large-Type | No. Medium-Type | No. Small-Type | Idle Mileage (km) | Operation Cost Z1 | Idle Mileage Cost Z2 | Recharging Time Cost Z3 | Total Cost Z |
|---|---|---|---|---|---|---|---|---|
| 1st | 8 | 0 | 0 | 88 | 9.6 | 0.0088 | 0.0015 | 9.6103 |
| 2nd | 0 | 8 | 0 | 96 | 8 | 0.0096 | 0.0015 | 8.0111 |
| 3rd | 0 | 0 | 10 | 85 | 8 | 0.0085 | 0.0015 | 8.0100 |
| 4th | 3 | 5 | 0 | 83 | 8.6 | 0.0083 | 0.0014 | 8.6097 |
| 5th | 4 | 0 | 4 | 97 | 8 | 0.0097 | 0.0014 | 8.0111 |
| 6th | 0 | 5 | 5 | 112 | 9 | 0.0112 | 0.0019 | 9.0131 |
| Scheme Index | No. Large-Type | No. Medium-Type | No. Small-Type | Idle Mileage (km) | Operation Cost Z1 | Idle Mileage Cost Z2 | Recharging Time Cost Z3 | Total Cost Z |
|---|---|---|---|---|---|---|---|---|
| 1st | 8 | 0 | 0 | 88 | 9.6 | 0.0088 | 0.0015 | 9.6103 |
| 2nd | 0 | 8 | 0 | 96 | 8 | 0.0096 | 0.0015 | 8.0111 |
| 3rd | 0 | 0 | 10 | 85 | 8 | 0.0085 | 0.0015 | 8.0100 |
| Line | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|---|---|
| The number of passengers on 1st trip | 35 | 28 | 65 | 21 | 17 | 27 | 19 | 47 |
| The number of passengers on 2nd trip | 62 | 14 | 33 | 28 | 13 | 39 | 12 | 18 |
| The number of passengers on 3rd trip | 16 | 21 | 32 | 18 | 20 | 18 | 26 | 29 |
| Scheme Index | No. Large-Type | No. Medium-Type | No. Small-Type | Idle Mileage (km) | Operation Cost Z1 | Idle Mileage Cost Z2 | Recharging Time Cost Z3 | Total Cost Z |
|---|---|---|---|---|---|---|---|---|
| 1st | 11 | 0 | 0 | 157 | 13.2 | 0.0157 | 0.0045 | 13.2202 |
| 2nd | 0 | 13 | 0 | 167 | 13 | 0.0167 | 0.0030 | 13.0244 |
| 3rd | 0 | 0 | 15 | 150 | 12 | 0.0150 | 0.0040 | 12.0154 |
| 4th | 5 | 7 | 0 | 151 | 13 | 0.0151 | 0.0036 | 13.0187 |
| 5th | 7 | 0 | 6 | 161 | 11.8 | 0.0161 | 0.0041 | 11.8219 |
| 6th | 0 | 6 | 8 | 156 | 13.6 | 0.0156 | 0.0062 | 13.6218 |
| 7th | 4 | 4 | 4 | 150 | 12 | 0.0150 | 0.0063 | 12.0213 |
| Scheme Index | No. Large-Type | No. Medium-Type | No. Small-Type | Idle Mileage (km) | Operation Cost Z1 | Idle Mileage Cost Z2 | Recharging Time Cost Z3 | Total Cost Z |
|---|---|---|---|---|---|---|---|---|
| 1st | 11 | 0 | 0 | 157 | 13.2 | 0.0157 | 0.0045 | 13.2202 |
| 2nd | 0 | 13 | 0 | 167 | 13 | 0.0167 | 0.0030 | 13.0244 |
| 3rd | 0 | 0 | 15 | 150 | 12 | 0.0150 | 0.0040 | 12.0154 |
| Scenario | Scheme | Cost of Operation Vehicles (CNY Thousand) | Idle Mileage (km) | Recharging Time (h) | Total Cost Z (CNY Thousand) | Total Cost Z Saving Percentage |
|---|---|---|---|---|---|---|
| I C1 = 1 C2 = 1 C3 = 1 | 1 | 16.8 | 147 | 0 | 163.8 | 15.65% |
| 2 | 15 | 161 | 6.8 | 182.8 | 5.87% | |
| 3 | 12 | 173 | 9.2 | 194.2 | - | |
| 4 | 15.4 | 148 | 4.7 | 168.1 | 13.44% | |
| 5 | 14.8 | 147 | 3.2 | 165 | 15.04% | |
| 6 | 13.4 | 154 | 6.4 | 173.8 | 10.51% | |
| 7 | 14 | 151 | 3.8 | 168.8 | 13.08% | |
| II C1 = 1 C2 = 1 C3 = 0.001 | 1 | 15.6 | 148 | 1.7 | 163.6017 | 11.57% |
| 2 | 15 | 160 | 5.4 | 175.0054 | 5.41% | |
| 3 | 12 | 173 | 9.2 | 185.0092 | - | |
| 4 | 15.2 | 148 | 6.9 | 163.2069 | 11.78% | |
| 5 | 14.8 | 158 | 6.2 | 172.8062 | 6.60% | |
| 6 | 13.4 | 161 | 9.7 | 174.4097 | 5.73% | |
| 7 | 14 | 150 | 7.2 | 164.0072 | 11.35% | |
| III C1 = 1 C2 = 1 C3 = 0.0001 | 1 | 15.6 | 146 | 3.7 | 161.60037 | 11.21% |
| 2 | 15.0 | 157 | 16.1 | 172.00061 | 5.49% | |
| 3 | 12.0 | 170 | 8.7 | 182.00087 | - | |
| 4 | 15.2 | 147 | 7.0 | 162.2007 | 10.88% | |
| 5 | 14.8 | 158 | 6.2 | 172.80062 | 5.06% | |
| 6 | 13.4 | 159 | 9.7 | 172.40097 | 5.27% | |
| 7 | 14.0 | 148 | 7.4 | 162.00074 | 10.99% | |
| IV C1 = 1 C2 = 0.001 C3 = 1 | 1 | 15.6 | 154 | 2.1 | 17.854 | 10.65% |
| 2 | 14.0 | 170 | 4.3 | 18.47 | 7.57% | |
| 3 | 12.0 | 183 | 7.8 | 19.983 | - | |
| 4 | 15.4 | 159 | 1.7 | 17.259 | 13.63% | |
| 5 | 14.8 | 163 | 2.9 | 17.863 | 10.61% | |
| 6 | 13.4 | 173 | 4.0 | 17.573 | 12.06% | |
| 7 | 13.0 | 156 | 3.7 | 16.856 | 15.65% | |
| V C1 = 1 C2 = 0.0001 C3 = 1 | 1 | 15.6 | 153 | 3.1 | 18.7153 | 6.04% |
| 2 | 14.0 | 169 | 3.7 | 17.7169 | 11.05% | |
| 3 | 12.0 | 185 | 7.9 | 19.9185 | - | |
| 4 | 15.4 | 162 | 2.0 | 17.4162 | 12.56% | |
| 5 | 14.8 | 172 | 4.7 | 19.5172 | 2.01% | |
| 6 | 13.4 | 177 | 3.8 | 17.2177 | 13.56% | |
| 7 | 13 | 157 | 3.5 | 16.5157 | 17.08% | |
| VI C1 = 0.001 C2 = 1 C3 = 1 | 1 | 16.8 | 145 | 0 | 145.0168 | 23.80% |
| 2 | 15.0 | 167 | 5.9 | 172.9150 | 9.14% | |
| 3 | 12.0 | 181 | 9.3 | 190.312 | - | |
| 4 | 16.8 | 147 | 3.0 | 150.0168 | 21.17% | |
| 5 | 14.8 | 157 | 4.5 | 161.5148 | 15.13% | |
| 6 | 13.4 | 169 | 5.7 | 174.7134 | 8.20% | |
| 7 | 15.0 | 148 | 3.8 | 151.815 | 20.23% | |
| VII C1 = 0.0001 C2 = 1 C3 = 1 | 1 | 18.0 | 143 | 0 | 143.0018 | 25.79% |
| 2 | 15.0 | 162 | 6.2 | 168.2015 | 12.71% | |
| 3 | 12.0 | 183 | 9.7 | 192.7012 | - | |
| 4 | 16.8 | 147 | 3.0 | 150.00168 | 22.16% | |
| 5 | 14.8 | 160 | 5.7 | 165.70148 | 14.01% | |
| 6 | 13.4 | 178 | 6.4 | 181.40134 | 5.86% | |
| 7 | 15.0 | 149 | 3.1 | 152.1015 | 21.07% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cao, Z.; Mao, Z.; Wang, Y.; Zhang, S. Multi-Type Electric Vehicle Scheduling Optimization Considering Load Capacity, Battery-Allowed Mileage, and Recharging Duration. Electronics 2023, 12, 4655. https://doi.org/10.3390/electronics12224655
Cao Z, Mao Z, Wang Y, Zhang S. Multi-Type Electric Vehicle Scheduling Optimization Considering Load Capacity, Battery-Allowed Mileage, and Recharging Duration. Electronics. 2023; 12(22):4655. https://doi.org/10.3390/electronics12224655
Chicago/Turabian StyleCao, Zhichao, Zhimin Mao, Yaoyao Wang, and Silin Zhang. 2023. "Multi-Type Electric Vehicle Scheduling Optimization Considering Load Capacity, Battery-Allowed Mileage, and Recharging Duration" Electronics 12, no. 22: 4655. https://doi.org/10.3390/electronics12224655
APA StyleCao, Z., Mao, Z., Wang, Y., & Zhang, S. (2023). Multi-Type Electric Vehicle Scheduling Optimization Considering Load Capacity, Battery-Allowed Mileage, and Recharging Duration. Electronics, 12(22), 4655. https://doi.org/10.3390/electronics12224655







