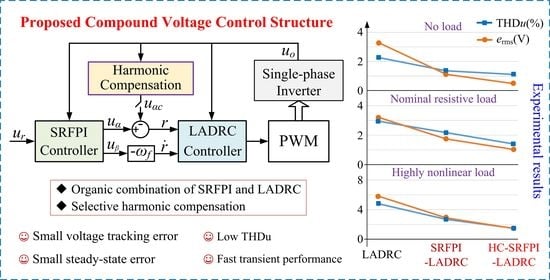
SRFPI-LADRC Based Control Strategy for Off-Grid Single-Phase Inverter: Design, Analysis, and Verification
Abstract
1. Introduction
- (1)
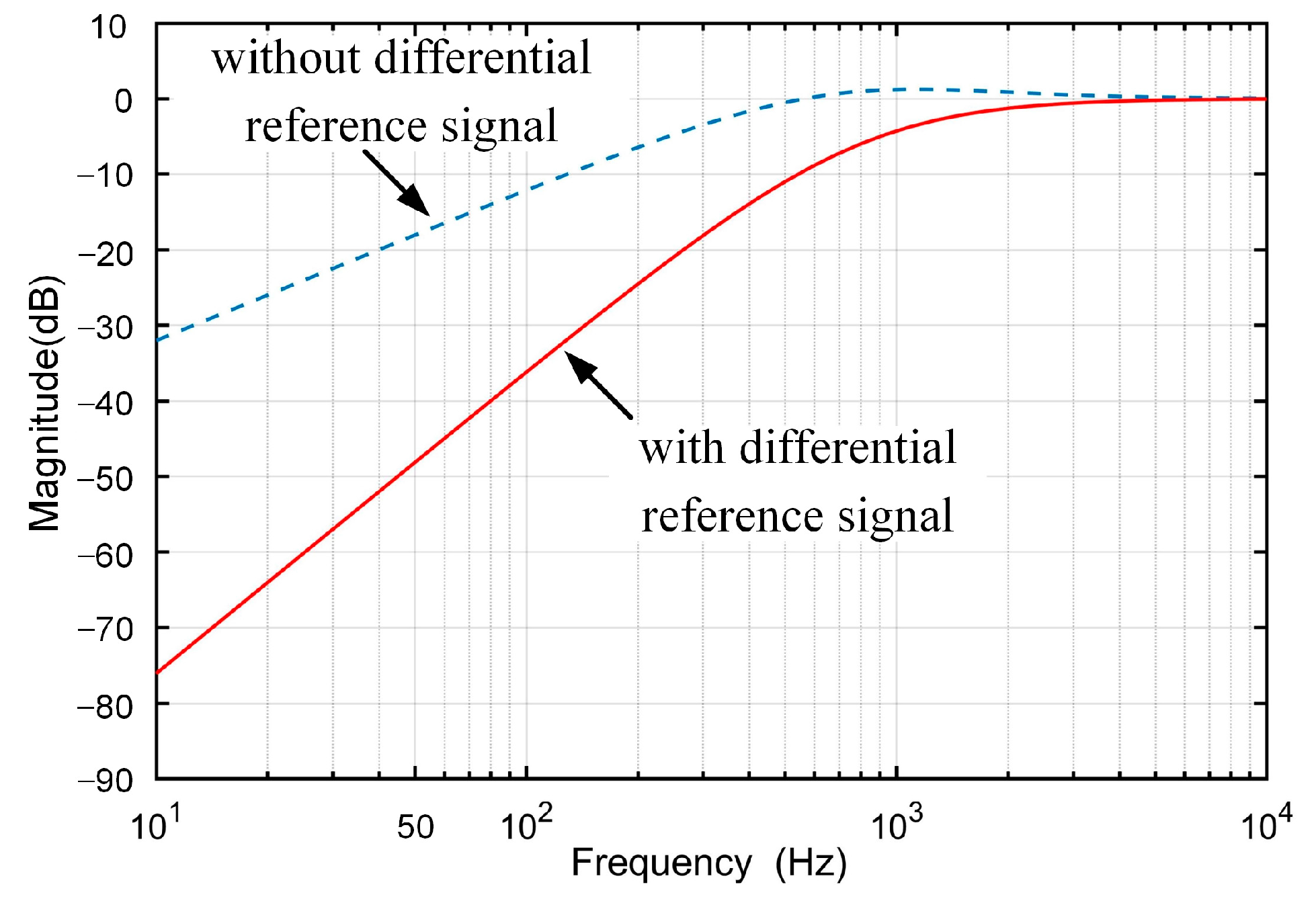
- The benefits of introducing a differential reference into LADRC is analyzed. Detailed theoretical analyses of the SRFPI-LADRC-based strategy, including system stability, robustness, performance of the voltage tracking error and disturbance rejection are presented, which indicate that the organic combination of SRFPI and LADRC fuses the merits of both without adding complexity to the parameters design.
- (2)
- The HC, consisting of paralleled multiple SRFPI controllers corresponding to harmonic frequencies, is built to remove the selective harmonic components. The HC also enhances the performance of the disturbance rejection.
- (3)
- Contrast experiments are conducted, and the findings verify that the proposed method significantly improves the system performance in terms of the tracking error and steady-error, dynamic response, and voltage THD (THDu).
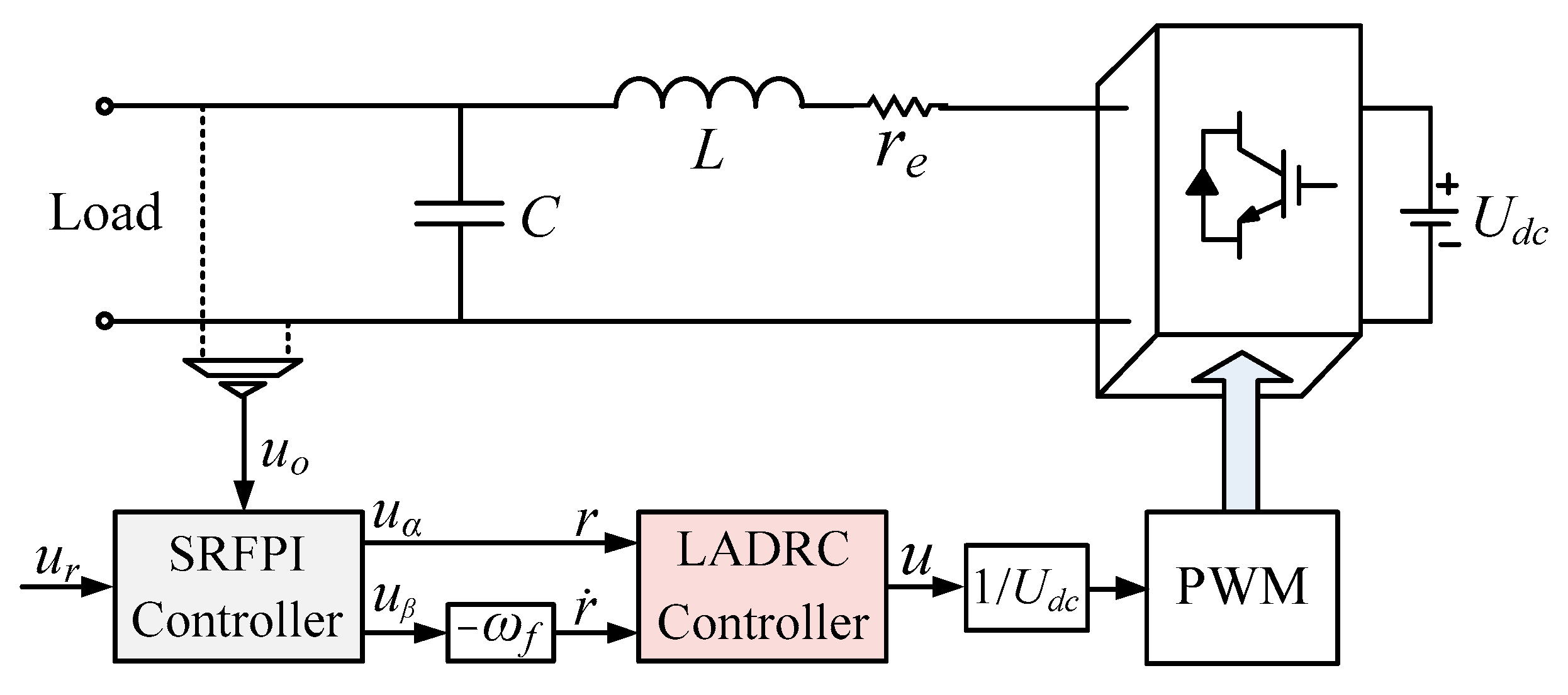
2. Design of LADRC for Single-Phase Inverter
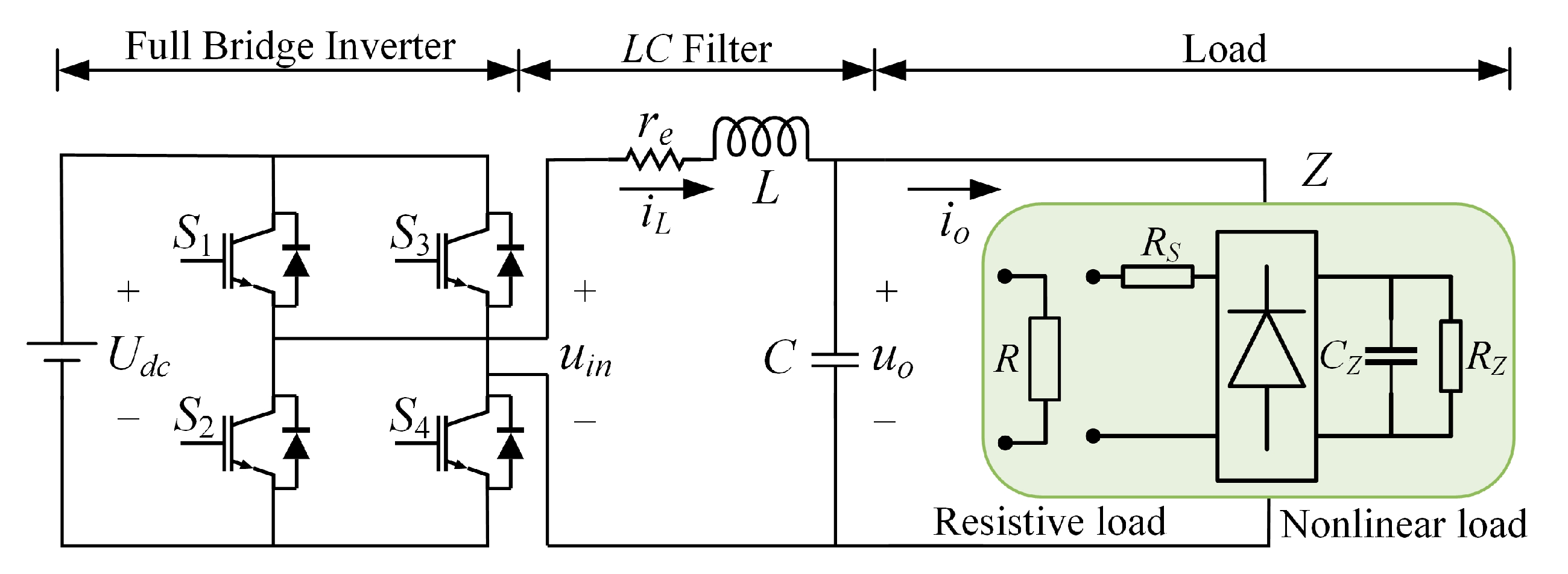
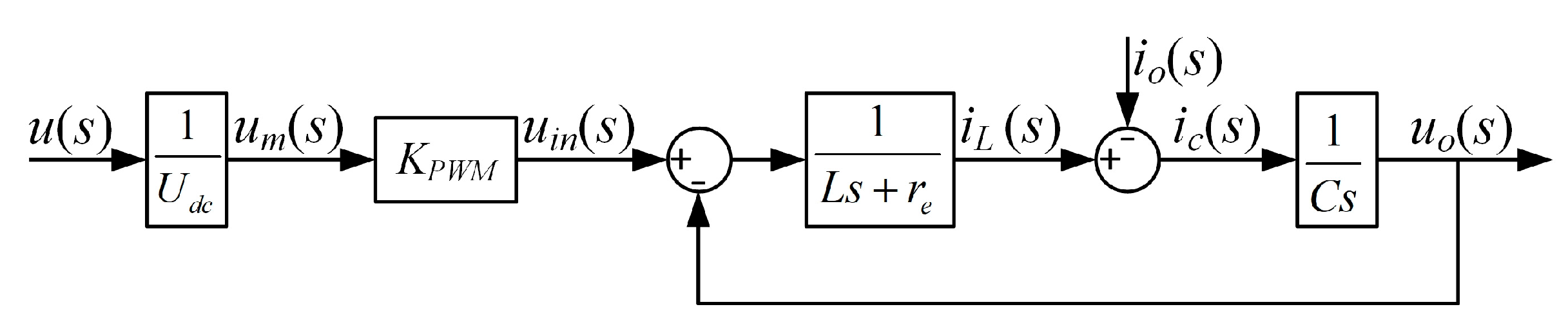
2.1. Modeling of Single-Phase Inverter
2.2. Design of LADRC
3. Design and Analysis of SRFPI-LADRC
3.1. Introduction of SRFPI
3.2. Modeling of SRFPI-LADRC Based Inverter
3.3. Stability Analysis and Parameters Design
3.4. Robustness Analysis
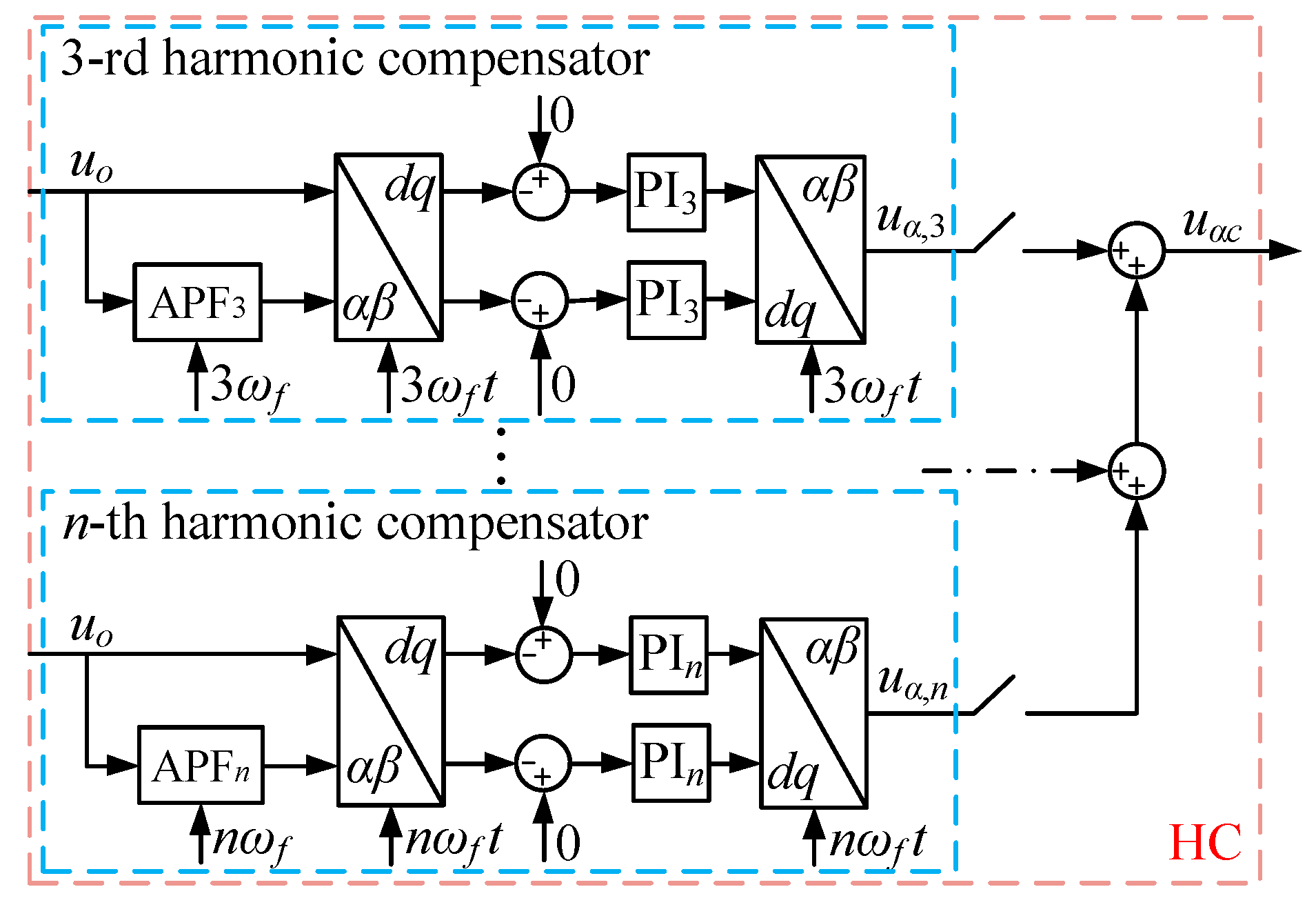
4. Design and Analysis of HC-SRFPI-LADRC
4.1. Harmonic Compensation
4.2. Disturbance Supperssion Analysis
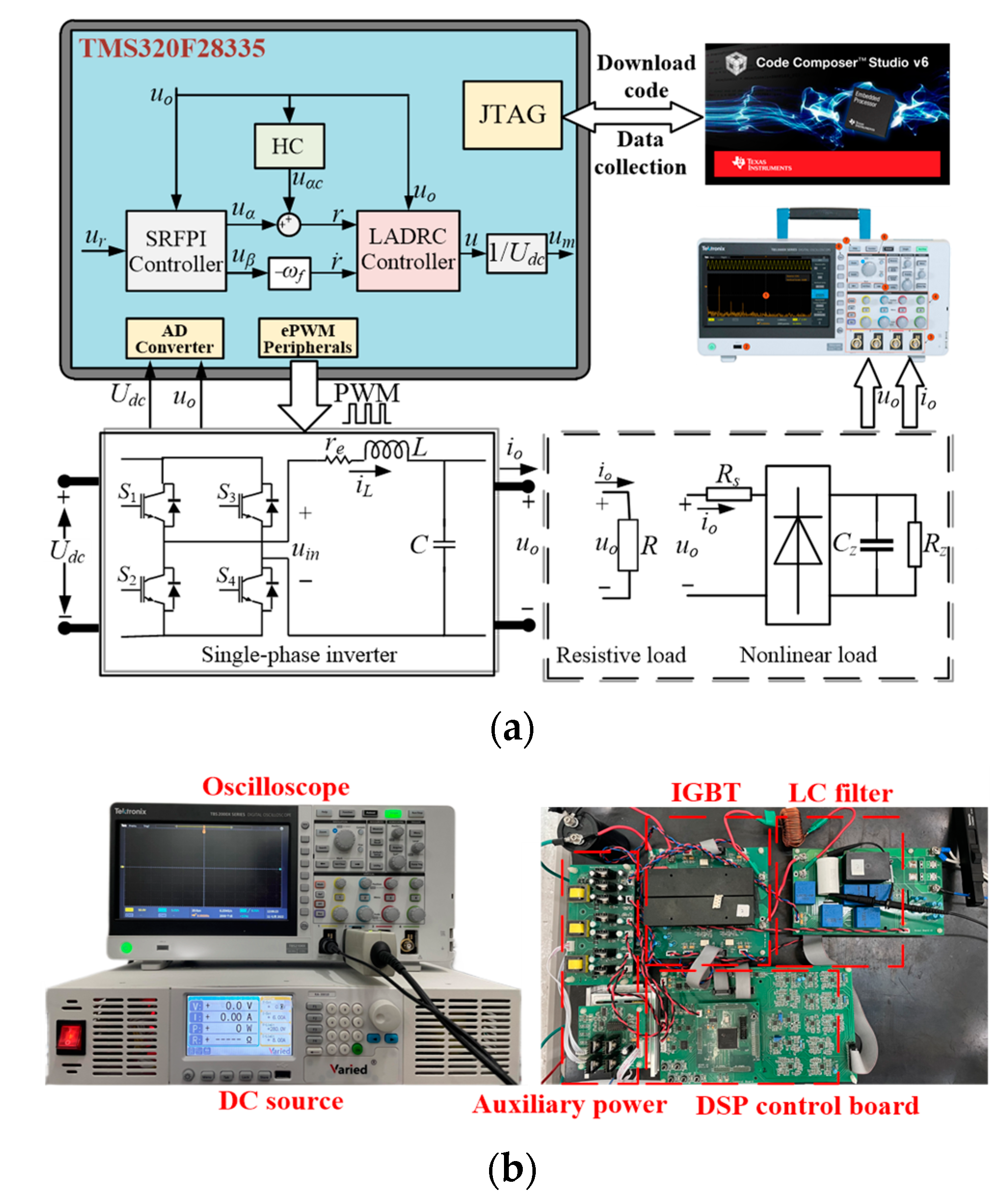
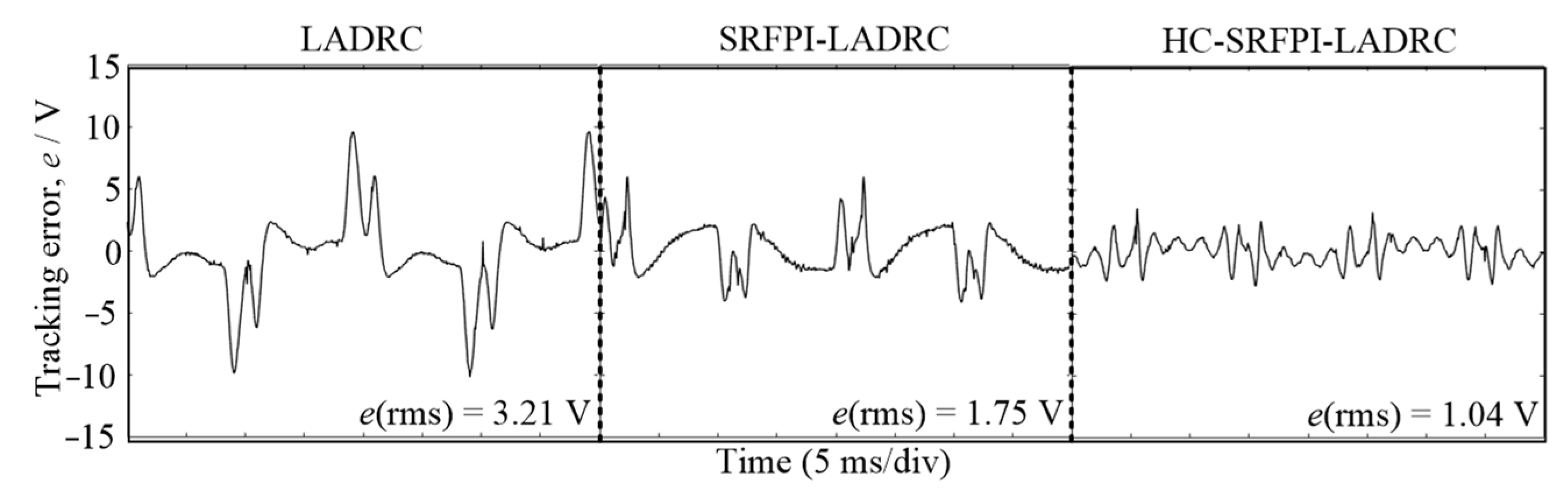
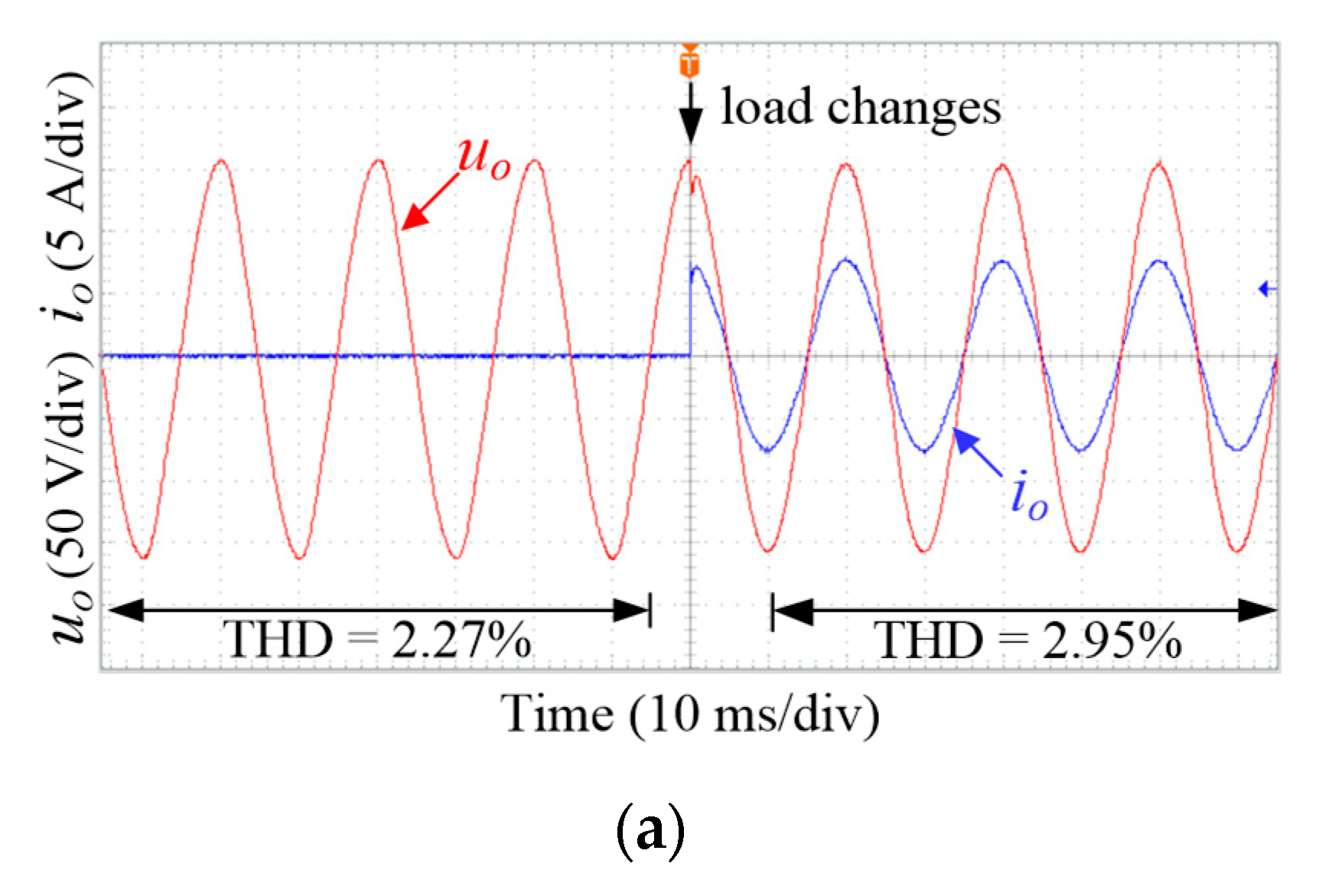
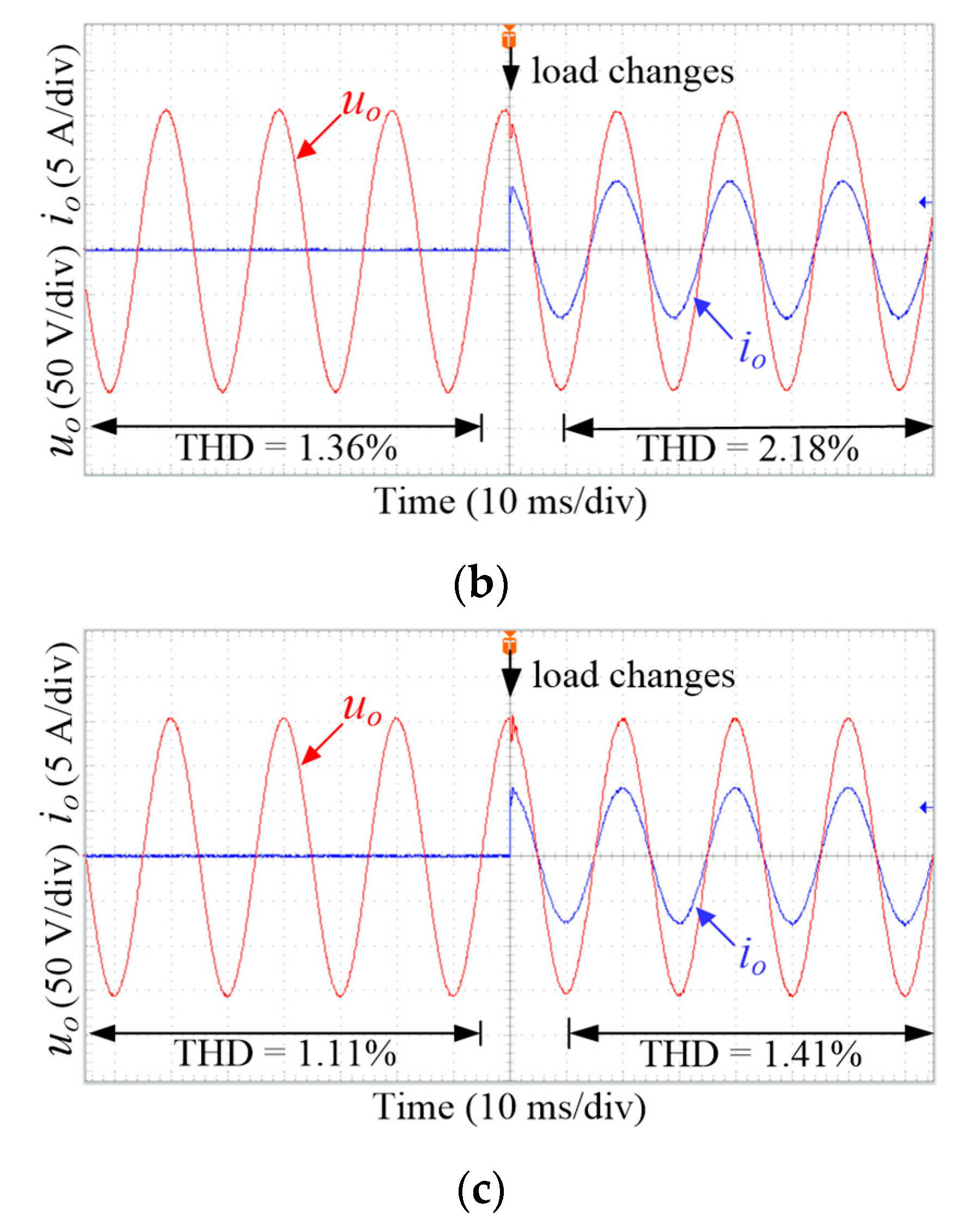
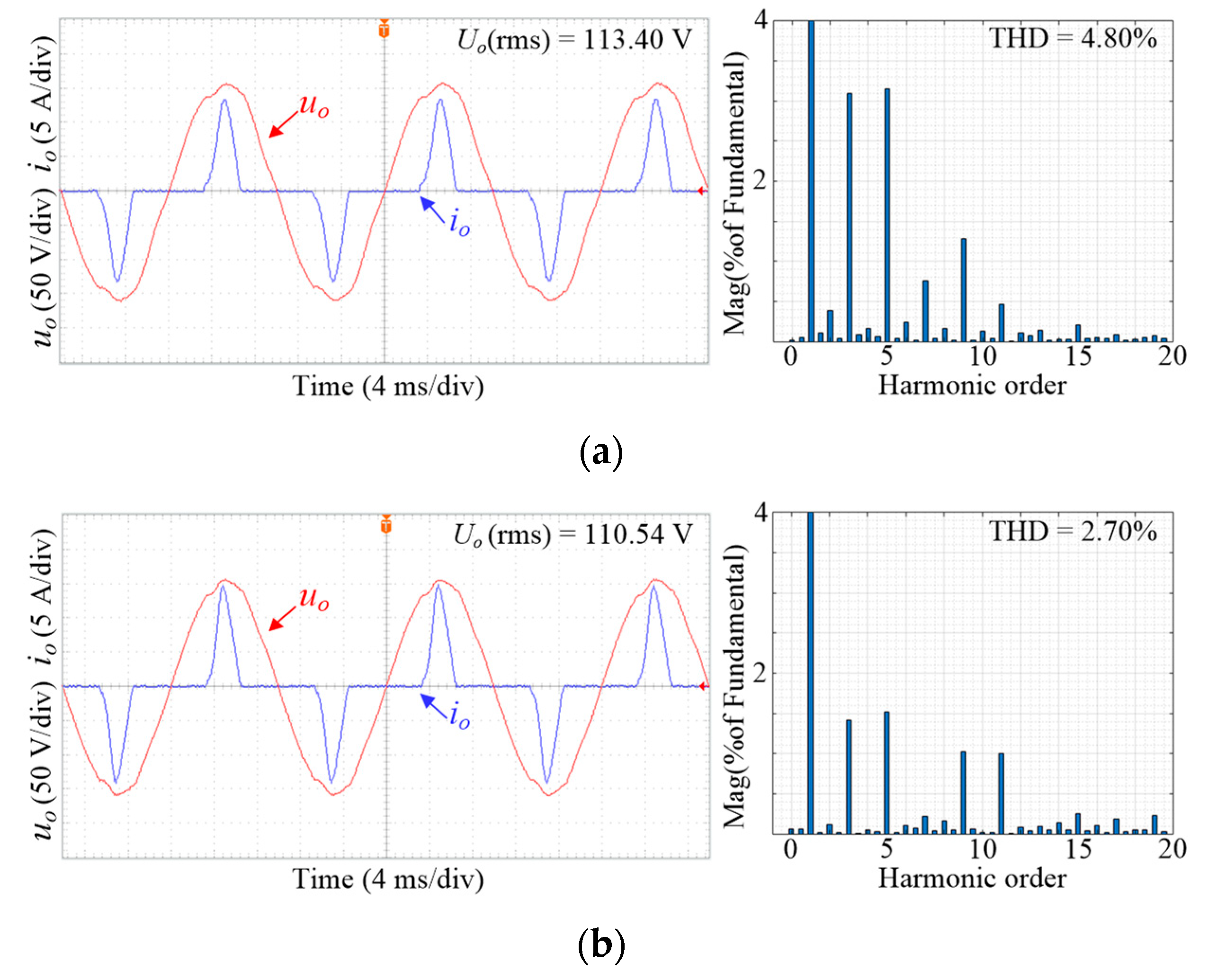
5. Experimental Results
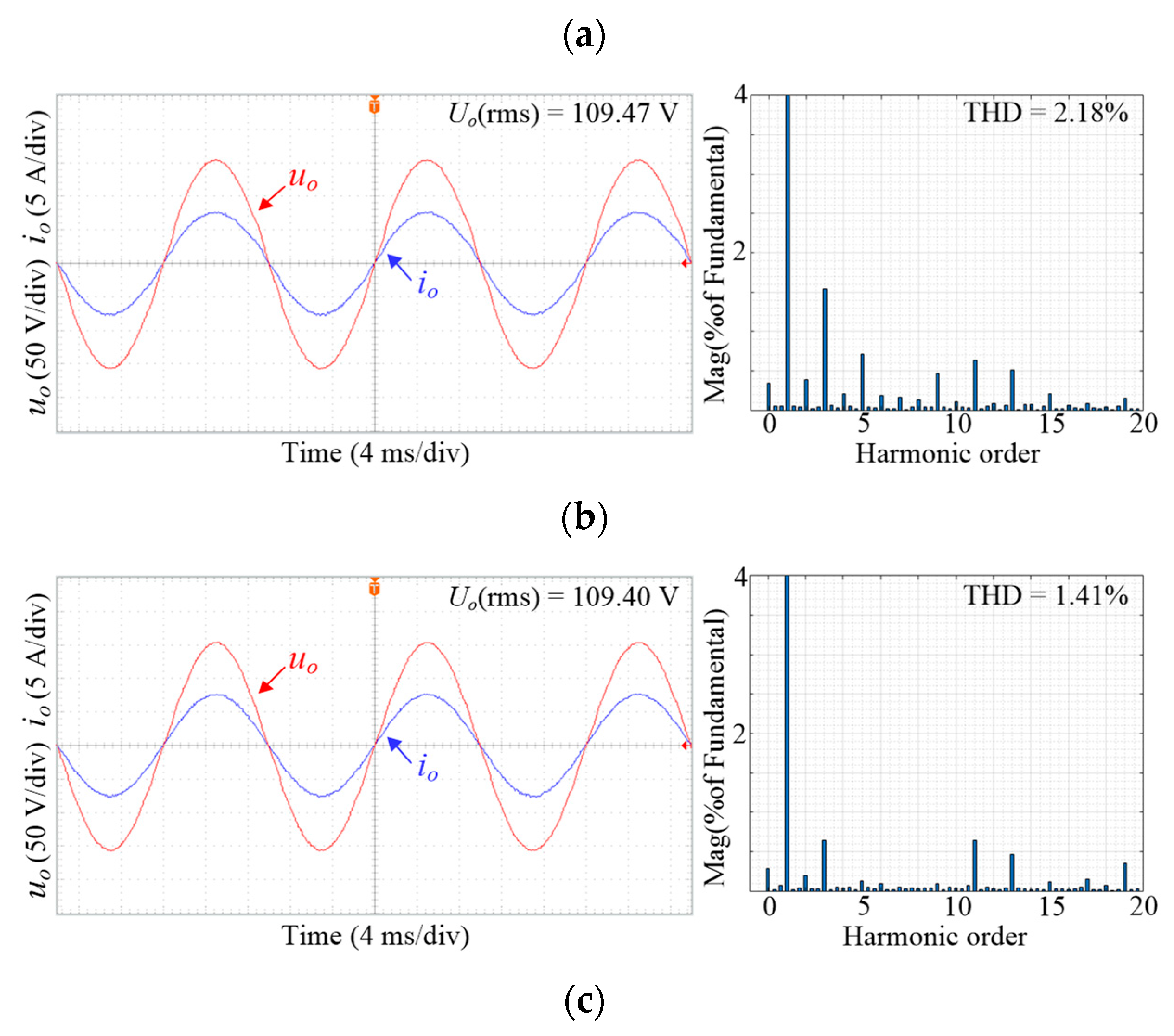
5.1. Contrast Experiments under Rated Resistive Load
5.2. Contrast Experiments under Step Load
5.3. Contrast Experiments under Nonlinear Load
5.4. Robustness Experiments under Nonlinear Load
5.5. Relevant Experimental Data Collection
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| Acronym | Definition |
| UPS | Uninterrupted power supply |
| PID | Proportional-integral-derivative |
| 2DOF | Two degrees of freedom |
| ADRC | Active disturbance rejection control |
| LADRC | Linear ADRC |
| ESO | Extended state observer |
| LESO | Linear ESO |
| SRF | Synchronous reference frame |
| SRFPI | SRF proportional-integral |
| OSG | Orthogonal-signal-generation |
| HC | Harmonic compensator |
| THD | Total harmonic distortion |
| THDu | Voltage THD |
| ESR | Equivalent series resistance |
| APF | All-pass filter |
References
- Li, J.; Sun, Y.; Li, X.; Xie, S.; Lin, J.; Su, M. Observer-Based Adaptive Control for Single-Phase UPS Inverter Under Nonlinear Load. IEEE Trans. Transp. Electrif. 2022, 8, 2785–2796. [Google Scholar] [CrossRef]
- He, J.; You, C.C.; Zhang, X.; Li, Z.; Liu, Z. An Adaptive Dual-Loop Lyapunov-Based Control Scheme for a Single-Phase UPS Inverter. IEEE Trans. Power Electron. 2020, 35, 8886–8891. [Google Scholar] [CrossRef]
- Han, Y.; Fang, X.; Yang, P.; Wang, C.; Xu, L.; Guerrero, J.M. Stability Analysis of Digital-Controlled Single-Phase Inverter with Synchronous Reference Frame Voltage Control. IEEE Trans. Power Electron. 2018, 33, 6333–6350. [Google Scholar] [CrossRef]
- Lorenzini, C.; Pereira, L.F.A.; Bazanella, A.S.; da Silva, G.R.G. Single-Phase Uninterruptible Power Supply Control: A Model-Free Proportional-Multiresonant Method. IEEE Trans. Ind. Electron. 2022, 69, 2967–2975. [Google Scholar] [CrossRef]
- Tian, H.; Chen, M.; Liang, G.; Xiao, X. Single-Phase Rectifier with Reduced Common-Mode Current, Auto-PFC, and Power Decoupling Ability. IEEE Trans. Power Electron. 2022, 37, 6873–6882. [Google Scholar] [CrossRef]
- Peng, Y.; Sun, W.; Deng, F. Internal Model Principle Method to Robust Output Voltage Tracking Control for Single-Phase UPS Inverters With Its SPWM Implementation. IEEE Trans. Energy Convers. 2021, 36, 841–852. [Google Scholar] [CrossRef]
- Chen, W.; Yang, J.; Guo, L.; Li, S. Disturbance-Observer-Based Control and Related Methods—An Overview. IEEE Trans. Ind. Electron. 2016, 63, 1083–1095. [Google Scholar] [CrossRef]
- Xue, W.; Madonski, R.; Lakomy, K.; Gao, Z.; Huang, Y. Add-on module of active disturbance rejection for set-point tracking of motion control systems. IEEE Trans. Ind. Appl. 2017, 53, 4028–4040. [Google Scholar] [CrossRef]
- Wu, Y.; Ye, Y. Internal Model-Based Disturbance Observer with Application to CVCF PWM Inverter. IEEE Trans. Ind. Electron. 2018, 65, 5743–5753. [Google Scholar] [CrossRef]
- Wu, Y.; Ye, Y.; Zhao, Q.; Cao, Y.; Xiong, Y. Discrete-Time Modified UDE-Based Current Control for LCL-Type Grid-Tied Inverters. IEEE Trans. Ind. Electron. 2020, 67, 2143–2154. [Google Scholar] [CrossRef]
- Zhou, R.; Tan, W. Analysis and Tuning of General Linear Active Disturbance Rejection Controllers. IEEE Trans. Ind. Electron. 2019, 66, 5497–5507. [Google Scholar] [CrossRef]
- Li, Y.; Qi, R.; Dai, M.; Zhang, X.; Zhao, Y. Linear Active Disturbance Rejection Control Strategy with Known Disturbance Compensation for Voltage-Controlled Inverter. Electronics 2021, 10, 1137. [Google Scholar] [CrossRef]
- Cao, Y.; Zhao, Q.; Ye, Y.; Xiong, Y. ADRC-Based Current Control for Grid-Tied Inverters: Design, Analysis, and Verification. IEEE Trans. Ind. Electron. 2020, 67, 8428–8437. [Google Scholar] [CrossRef]
- Han, J. From PID to Active Disturbance Rejection Control. IEEE Trans. Ind. Electron. 2009, 56, 900–906. [Google Scholar] [CrossRef]
- Gao, Z. Scaling and bandwidth-parameterization based controller tuning. In Proceedings of the 2003 American Control Conference, Denver, CO, USA, 4–6 June 2003; pp. 4989–4996. [Google Scholar]
- Godbole, A.A.; Kolhe, J.P.; Talole, S.E. Performance Analysis of Generalized Extended State Observer in Tackling Sinusoidal Disturbances. IEEE Trans. Control. Syst. Technol. 2013, 21, 2212–2223. [Google Scholar] [CrossRef]
- Yang, Y.; Zhou, K.; Cheng, M.; Zhang, B. Phase Compensation Multiresonant Control of CVCF PWM Converters. IEEE Trans. Power Electron. 2013, 28, 3923–3930. [Google Scholar] [CrossRef]
- Sayem, A.H.M.; Cao, Z.; Man, Z. Model Free ESO-Based Repetitive Control for Rejecting Periodic and Aperiodic Disturbances. IEEE Trans. Ind. Electron. 2017, 64, 3433–3441. [Google Scholar] [CrossRef]
- Dong, D.; Thacker, T.; Burgos, R.; Wang, F.; Boroyevich, D. On Zero Steady-State Error Voltage Control of Single-Phase PWM Inverters with Different Load Types. IEEE Trans. Power Electron. 2011, 26, 3285–3297. [Google Scholar] [CrossRef]
- Han, Y.; Lin, X.; Fang, X.; Xu, L.; Yang, P.; Hu, W.; Coelho, E.A.A.; Blaabjerg, F. Floquet-Theory-Based Small-Signal Stability Analysis of Single-Phase Asymmetric Multilevel Inverters with SRF Voltage Control. IEEE Trans. Power Electron. 2020, 35, 3221–3241. [Google Scholar] [CrossRef]
- Monfared, M.; Golestan, S.; Guerrero, J.M. Analysis, Design, and Experimental Verification of a Synchronous Reference Frame Voltage Control for Single-Phase Inverters. IEEE Trans. Ind. Electron. 2014, 61, 258–269. [Google Scholar] [CrossRef]
- Lin, L.; Li, H.; Zhu, K.; Shi, L.; Li, P. Analysis and Verification of Compound SRFPI-LADRC Strategy for an Off-Grid Single-Phase Inverter. Int. Trans. Electr. Energy Syst. 2022, 2022, 1–14. [Google Scholar] [CrossRef]
- Li, H.; Shi, L.; Lin, L. An Improved SRFPI-LADRC-based Voltage Control for Single-Phase Inverter. In Proceedings of the 3rd IEEE International Power Electronics and Application Conference and Exposition, Xiamen, China, 4–7 November 2022. [Google Scholar]
- Yoo, D.; Yau, S.S.-T.; Gao, Z. Optimal fast tracking observer bandwidth of the linear extended state observer. Int. J. Control. 2007, 80, 102–111. [Google Scholar] [CrossRef]
- Zmood, D.N.; Holmes, G. Stationary frame current regulation of PWM inverters with zero steady state error. IEEE Trans. Power Electron. 2003, 18, 814–822. [Google Scholar] [CrossRef]










| Comparative Item | Single/Dual-Loop PID Control | SRFPI Control | LADRC | SRFPI-LADRC |
|---|---|---|---|---|
| System robustness | Medium | Medium | Good | Good |
| Steady-state performance | Medium | Good | Medium | Good |
| Transient performance | Medium | Good | Good | Good |
| Virtual orthogonal signals | Not required | Required | Not required | Required |
| Hardware cost | Low | Low | Low | Medium |
| s5 | 1 | A2 | A4 |
| s4 | A1 | A3 | A5 |
| s3 | B1 | B2 | |
| s2 | C1 | C2 | |
| s1 | D1 | ||
| s0 | E1 |
| Parameter | Value | Parameter | Value |
|---|---|---|---|
| switching frequency, fs | 20 kHz | rated output voltage, Uo | 110 V |
| fundamental frequency, ωf | 100π rad/s | proportional factor of PI controller, kp | 1.2 |
| nominal filter inductance, L | 700 μH | integral factor of PI controller, ki | 100 |
| ESR of the inductance, re | 0.1 Ω | bandwidth of the controller, ωc | 5000 rad/s |
| nominal filter capacitance, C | 40 μF | bandwidth of the observer, ωo | 10,000 rad/s |
| dc-link voltage, Udc | 190 V | dead time, td | 1.3 μs |
| Control Method | Load Type | THDu | e (rms)/V | Uo (rms)/V |
|---|---|---|---|---|
| LADRC | No load | 2.27% | 3.29 | 111.65 |
| Nominal resistive load | 2.95% | 3.21 | 110.72 | |
| Highly nonlinear load | 4.80% | 5.82 | 113.40 | |
| SRFPI-LADRC (without differential reference [22]) | No load | 1.47% | 1.15 | 109.40 |
| Nominal resistive load | 2.26% | 1.82 | 109.37 | |
| Highly nonlinear load | 2.96% | 3.15 | 109.48 | |
| SRFPI-LADRC (with differential reference) | No load | 1.36% | 1.12 | 109.52 |
| Nominal resistive load | 2.18% | 1.75 | 109.47 | |
| Highly nonlinear load | 2.70% | 2.90 | 110.54 | |
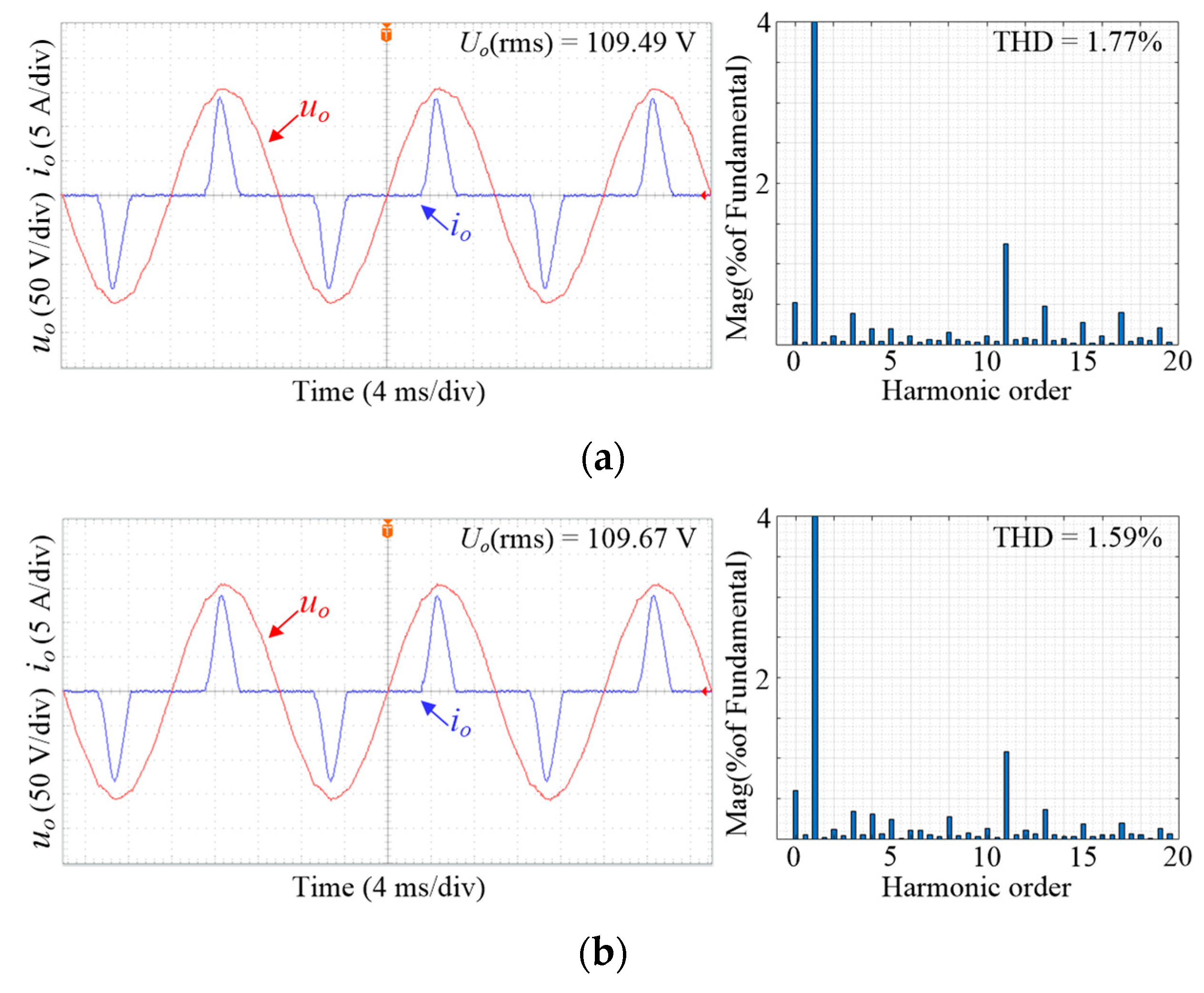
| HC-SRFPI-LADRC | No load | 1.11% | 0.48 | 109.46 |
| Nominal resistive load | 1.41% | 1.04 | 109.40 | |
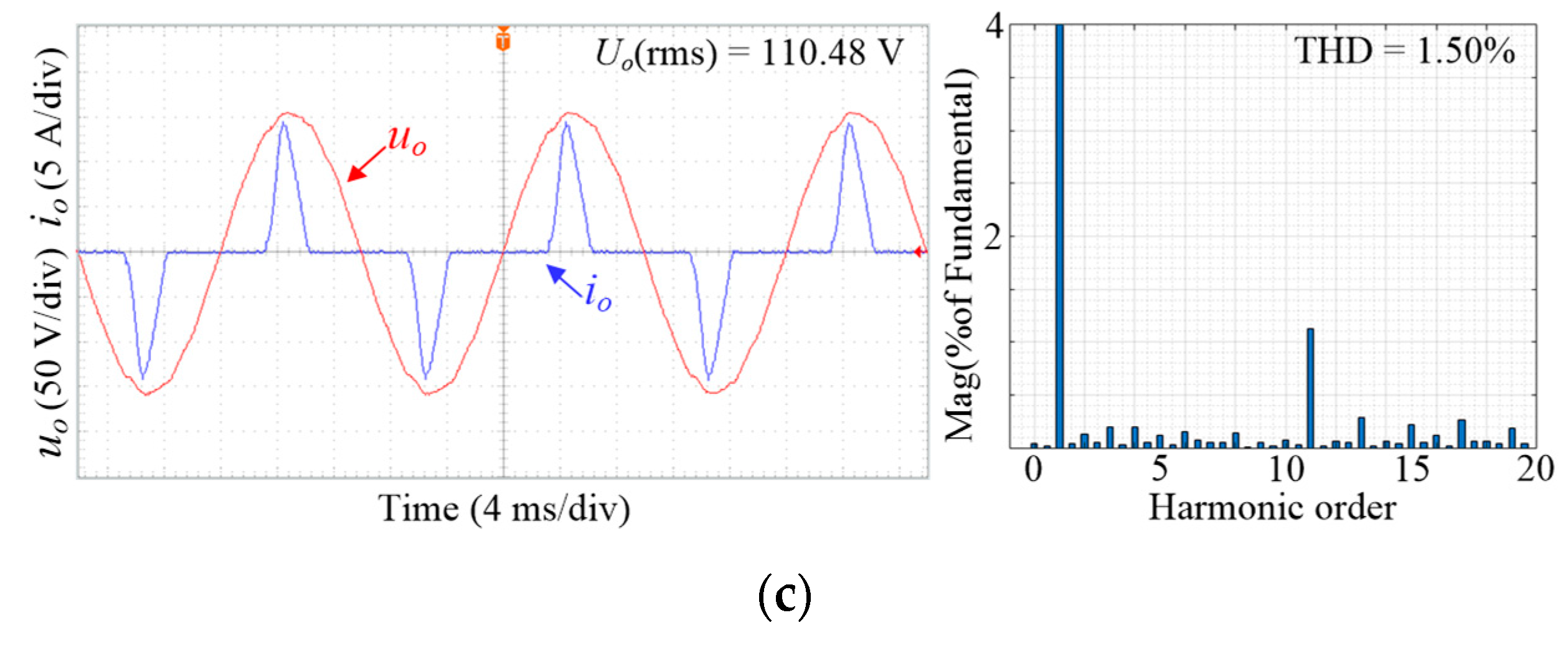
| Highly nonlinear load | 1.50% | 1.47 | 110.48 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lin, L.; Li, H.; Zhu, K.; Shi, L. SRFPI-LADRC Based Control Strategy for Off-Grid Single-Phase Inverter: Design, Analysis, and Verification. Electronics 2023, 12, 962. https://doi.org/10.3390/electronics12040962
Lin L, Li H, Zhu K, Shi L. SRFPI-LADRC Based Control Strategy for Off-Grid Single-Phase Inverter: Design, Analysis, and Verification. Electronics. 2023; 12(4):962. https://doi.org/10.3390/electronics12040962
Chicago/Turabian StyleLin, Liaoyuan, Haoda Li, Kai Zhu, and Lingling Shi. 2023. "SRFPI-LADRC Based Control Strategy for Off-Grid Single-Phase Inverter: Design, Analysis, and Verification" Electronics 12, no. 4: 962. https://doi.org/10.3390/electronics12040962
APA StyleLin, L., Li, H., Zhu, K., & Shi, L. (2023). SRFPI-LADRC Based Control Strategy for Off-Grid Single-Phase Inverter: Design, Analysis, and Verification. Electronics, 12(4), 962. https://doi.org/10.3390/electronics12040962