High Precision Sinusoidal Position Tracking of a Voice-Coil Linear Servomotor Using Resonant Control
Abstract
:1. Introduction
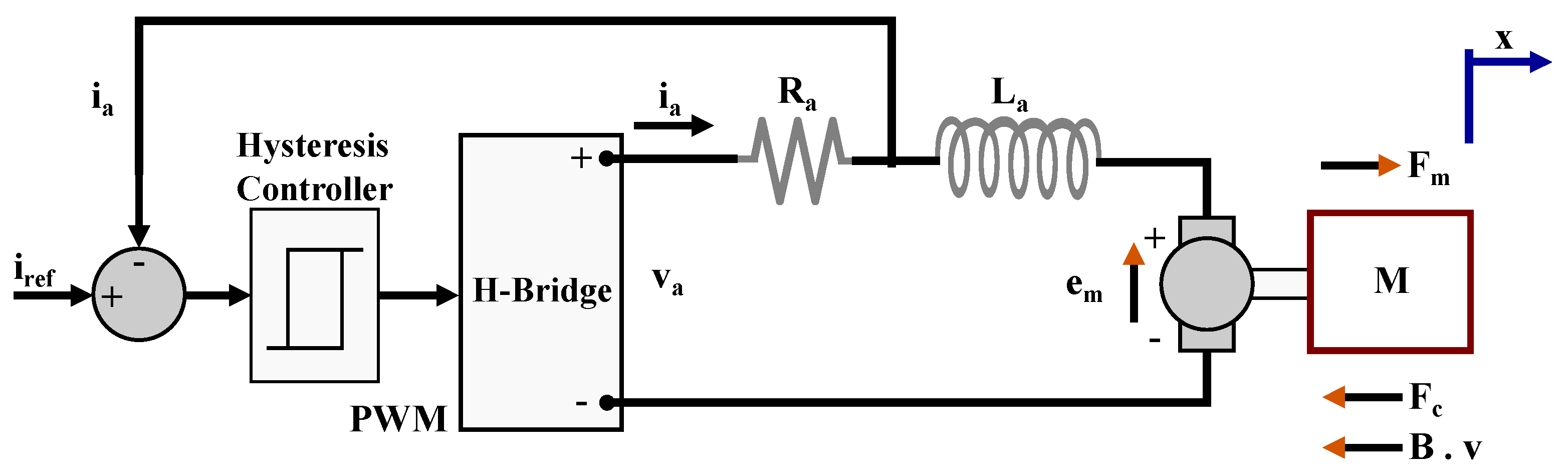
2. System Modeling
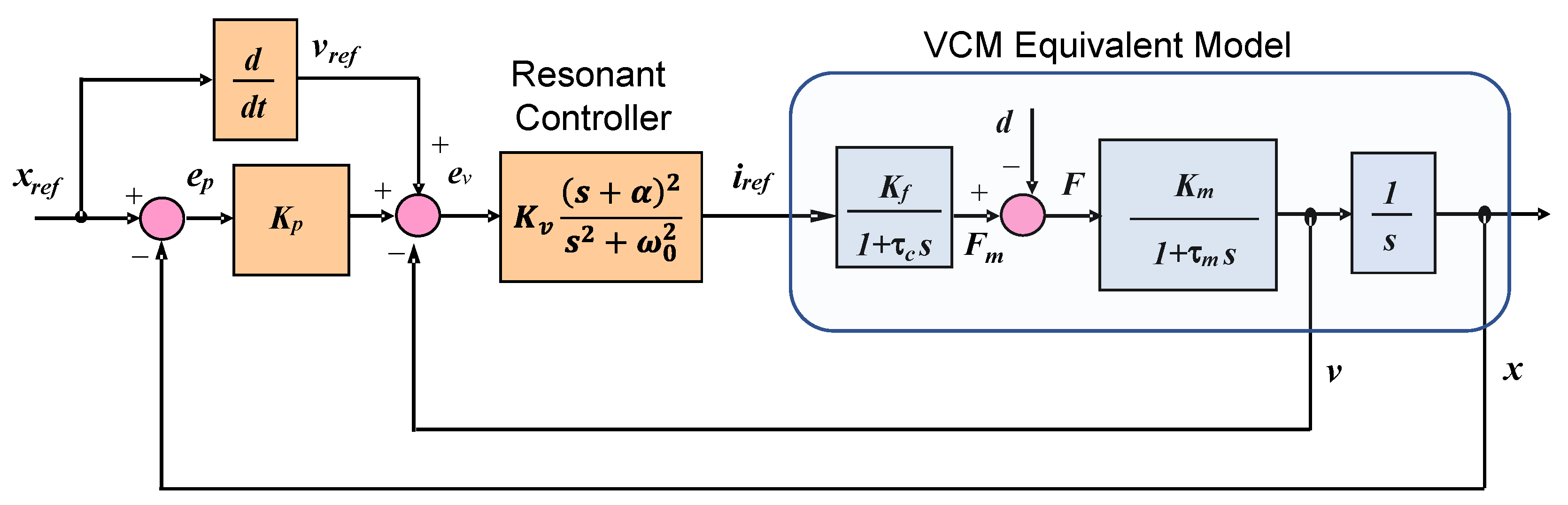
3. Controller Design
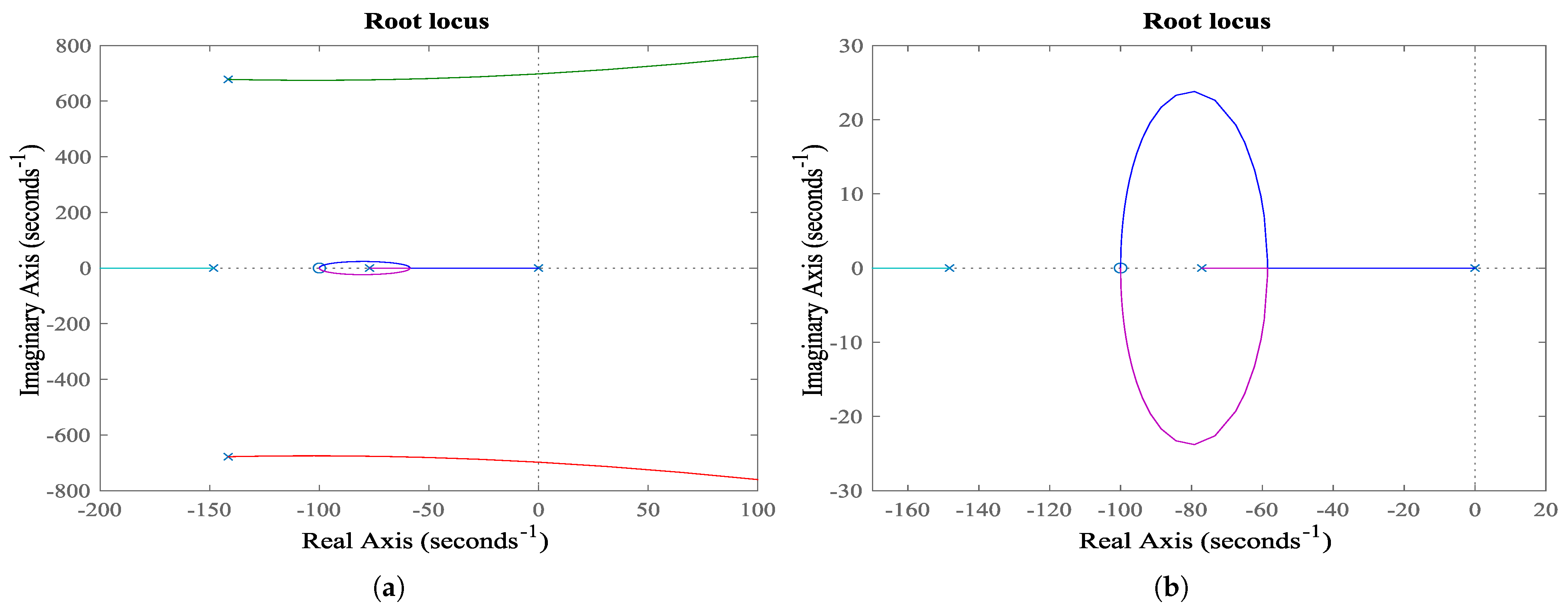
3.1. Velocity Controller Design
- •
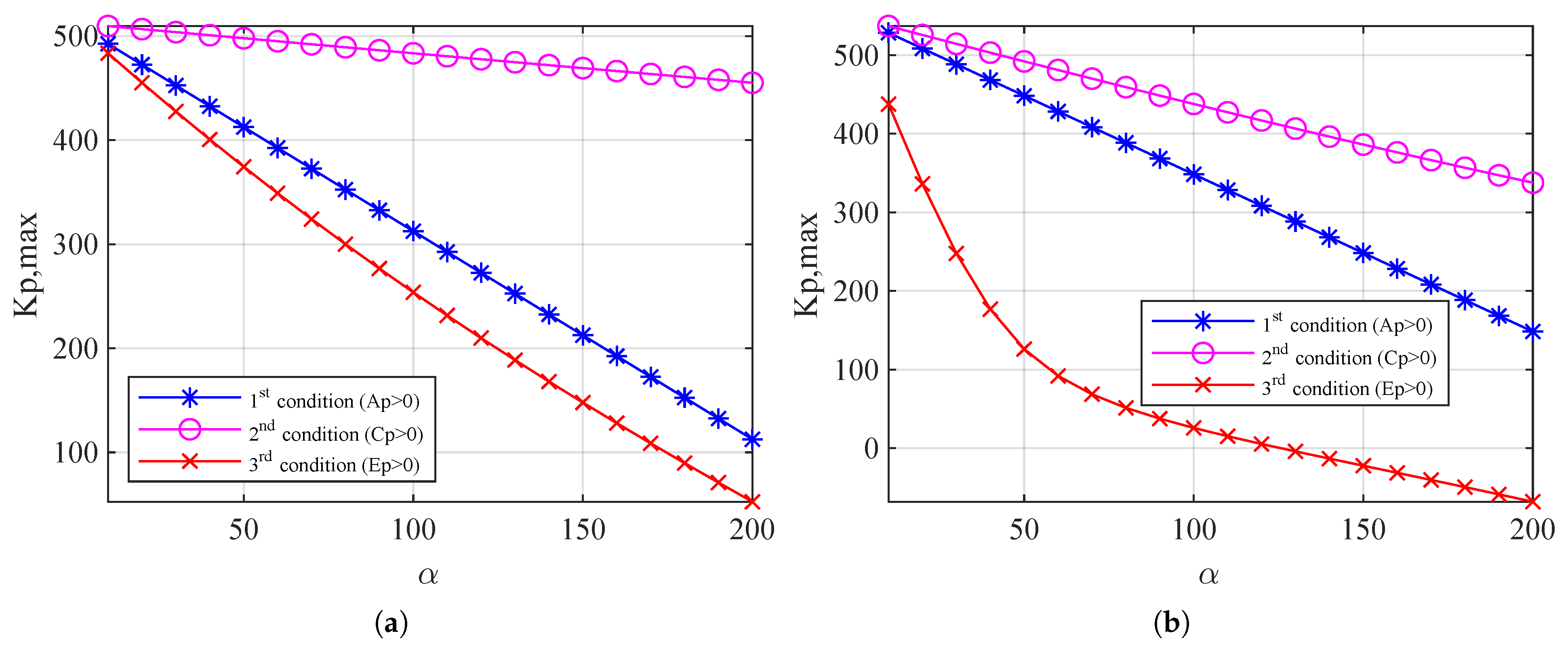
- The variable is selected to satisfy the condition given in (29).
- •
- The gain is selected to satisfy the condition given in (32).
- •
- The above two conditions can be achieved without the exact knowledge of the mechanical system parameters , , , and . Only approximate values of these parameters are needed to select the appropriate controller variables and assure system stability.
- •
- The current control loop time constant is usually very small compared to the mechanical time constant . Therefore, . This gives more flexibility in the selection on the variable .
3.2. Position Controller Design
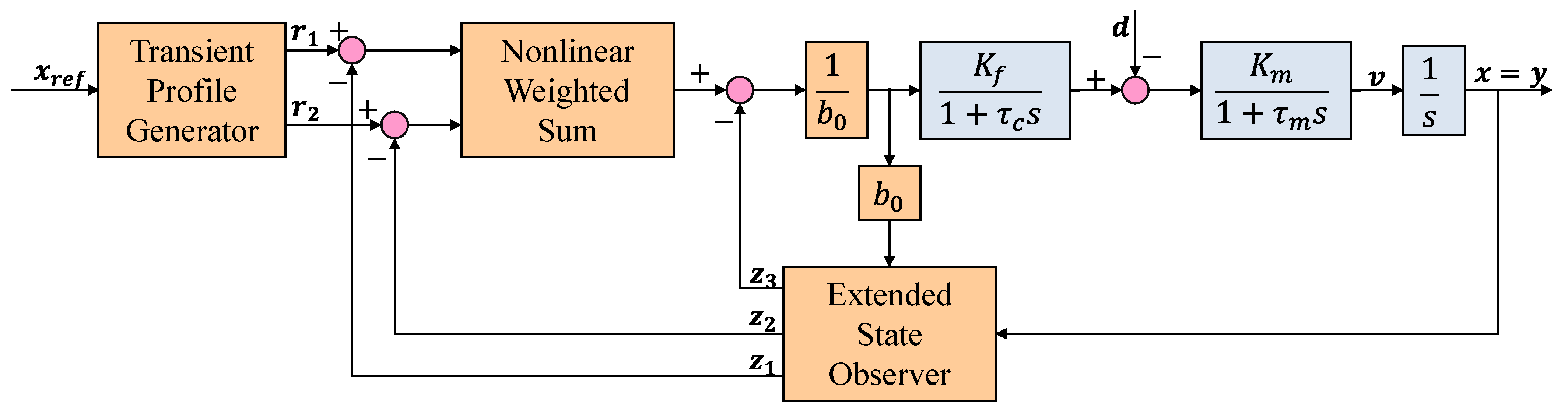
4. Active Disturbance Rejection Controller
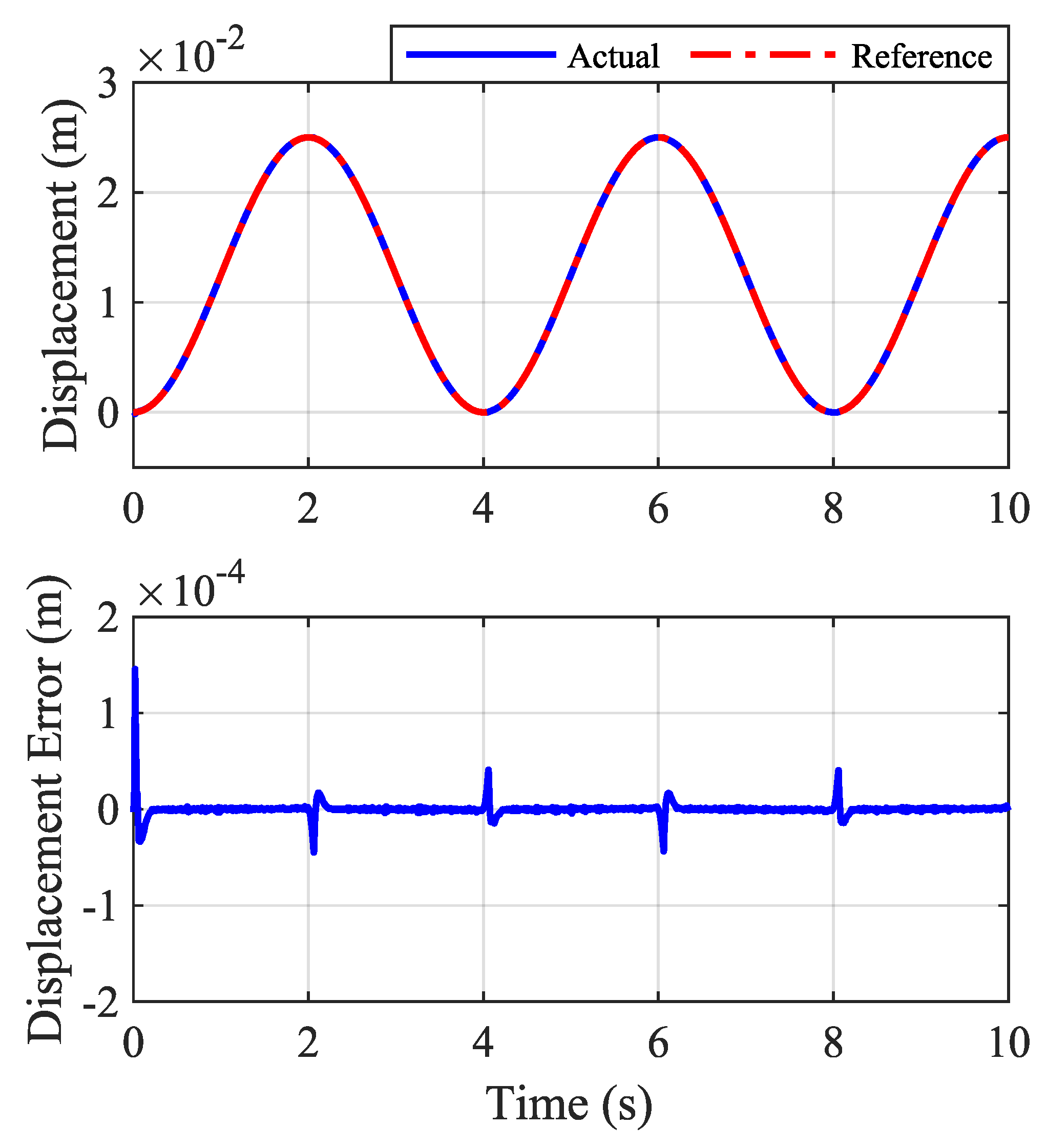
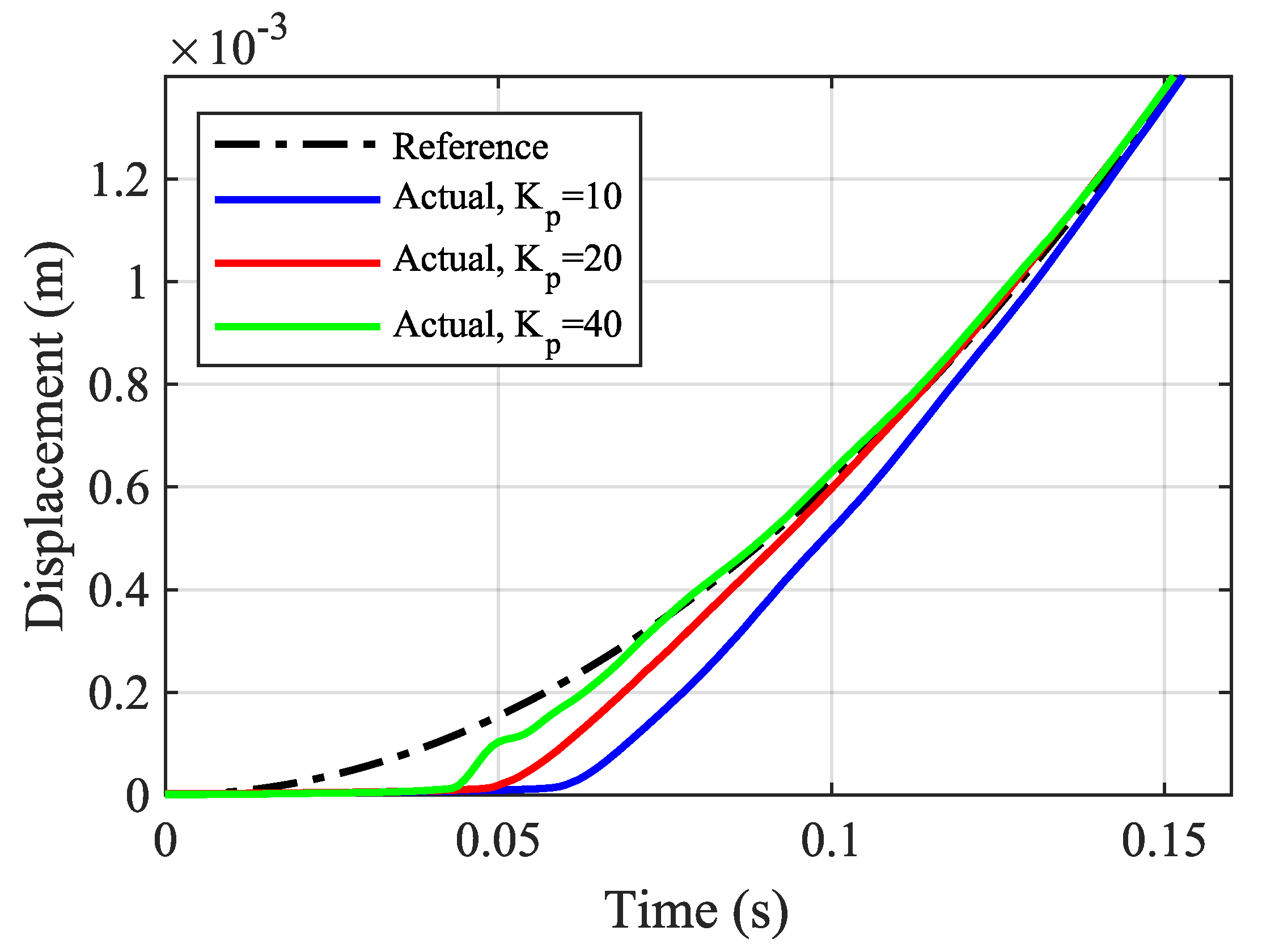
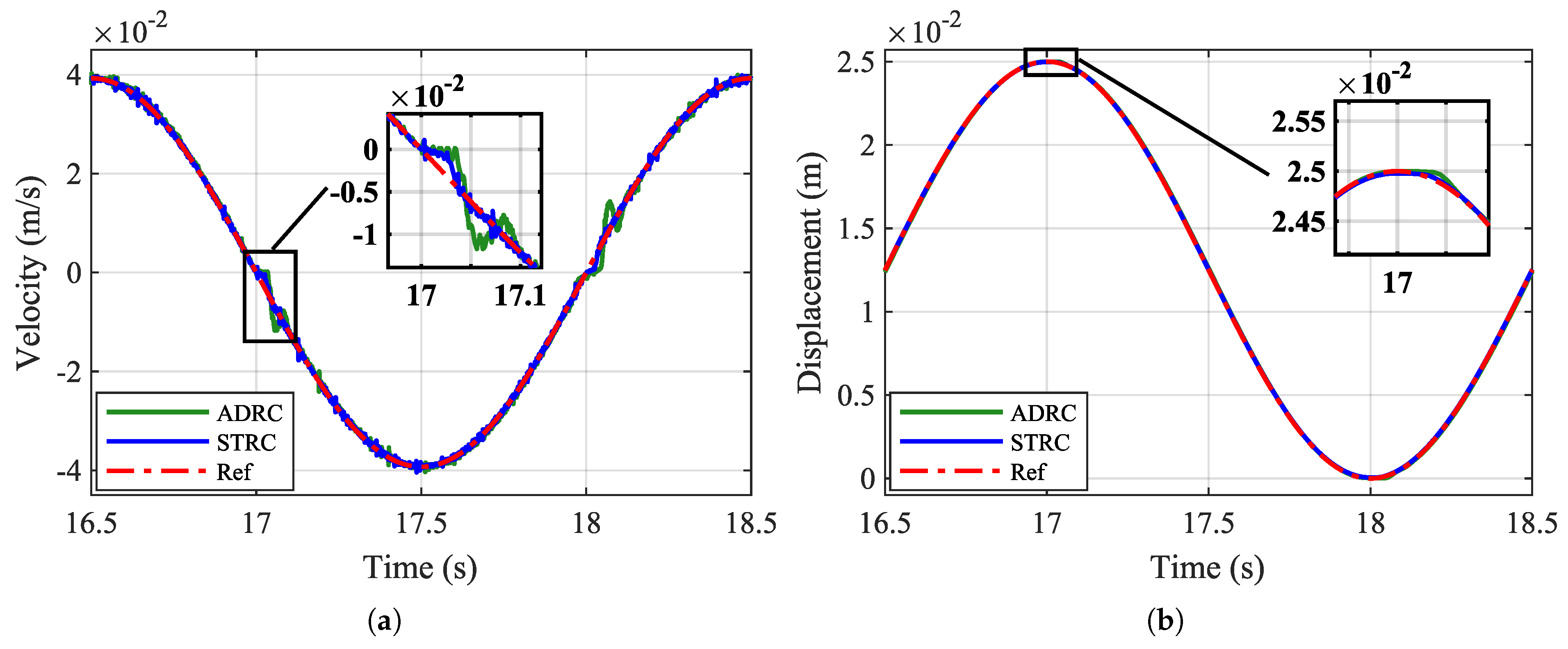
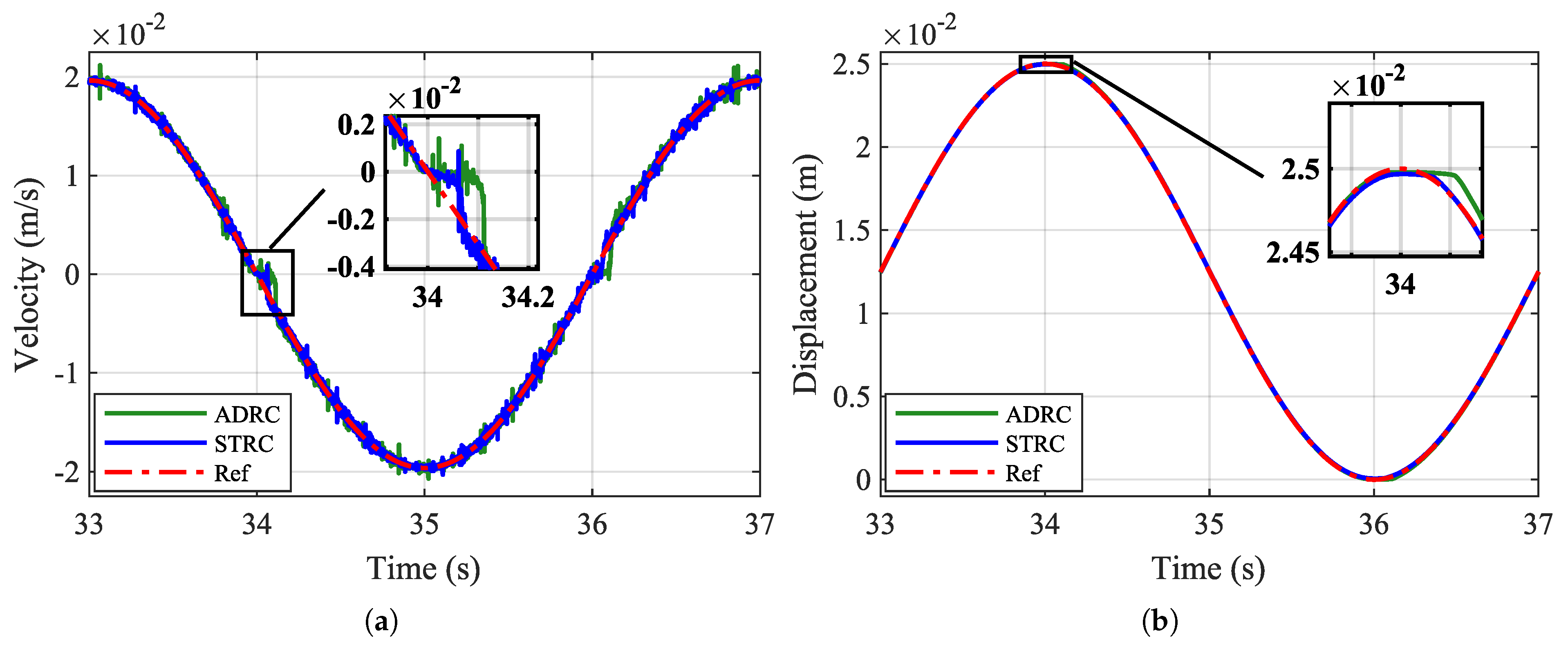
5. Results and Discussion
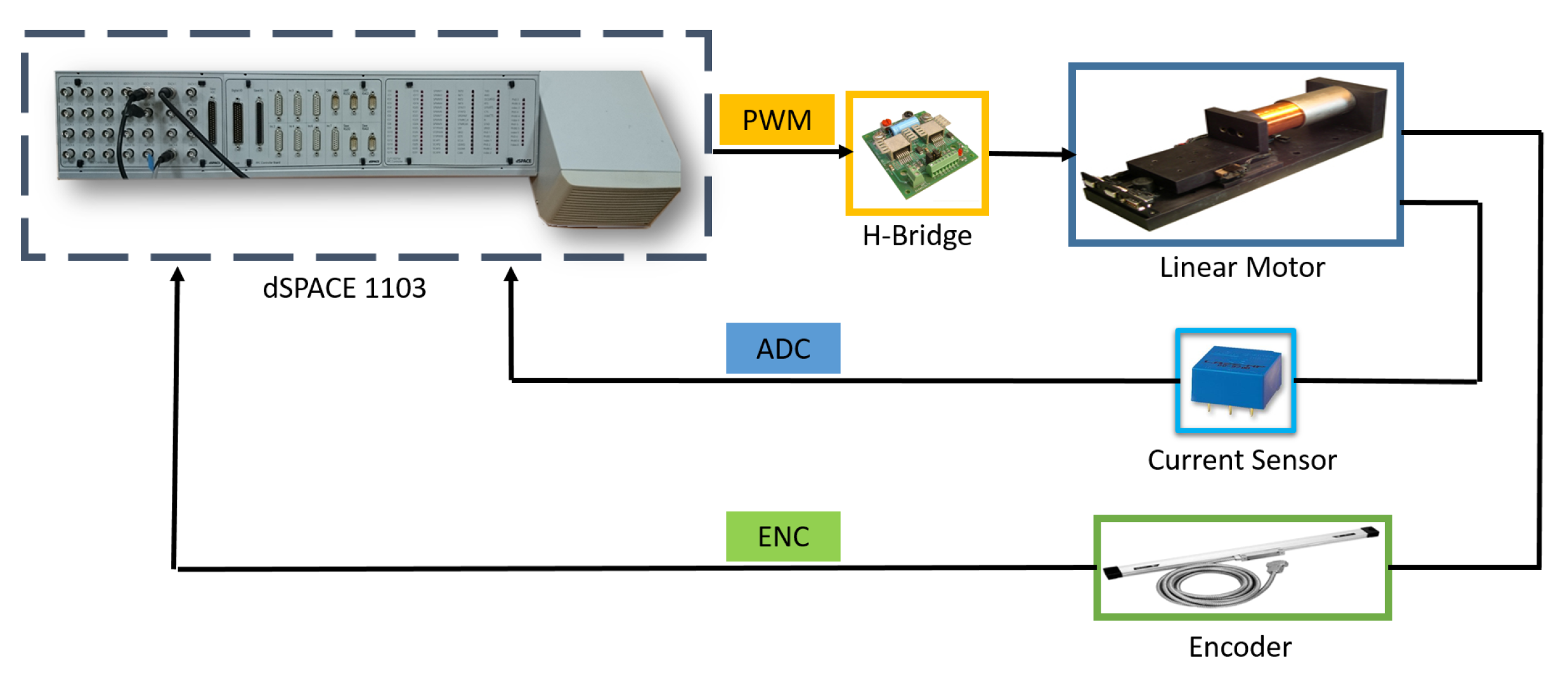
5.1. Experimental Setup
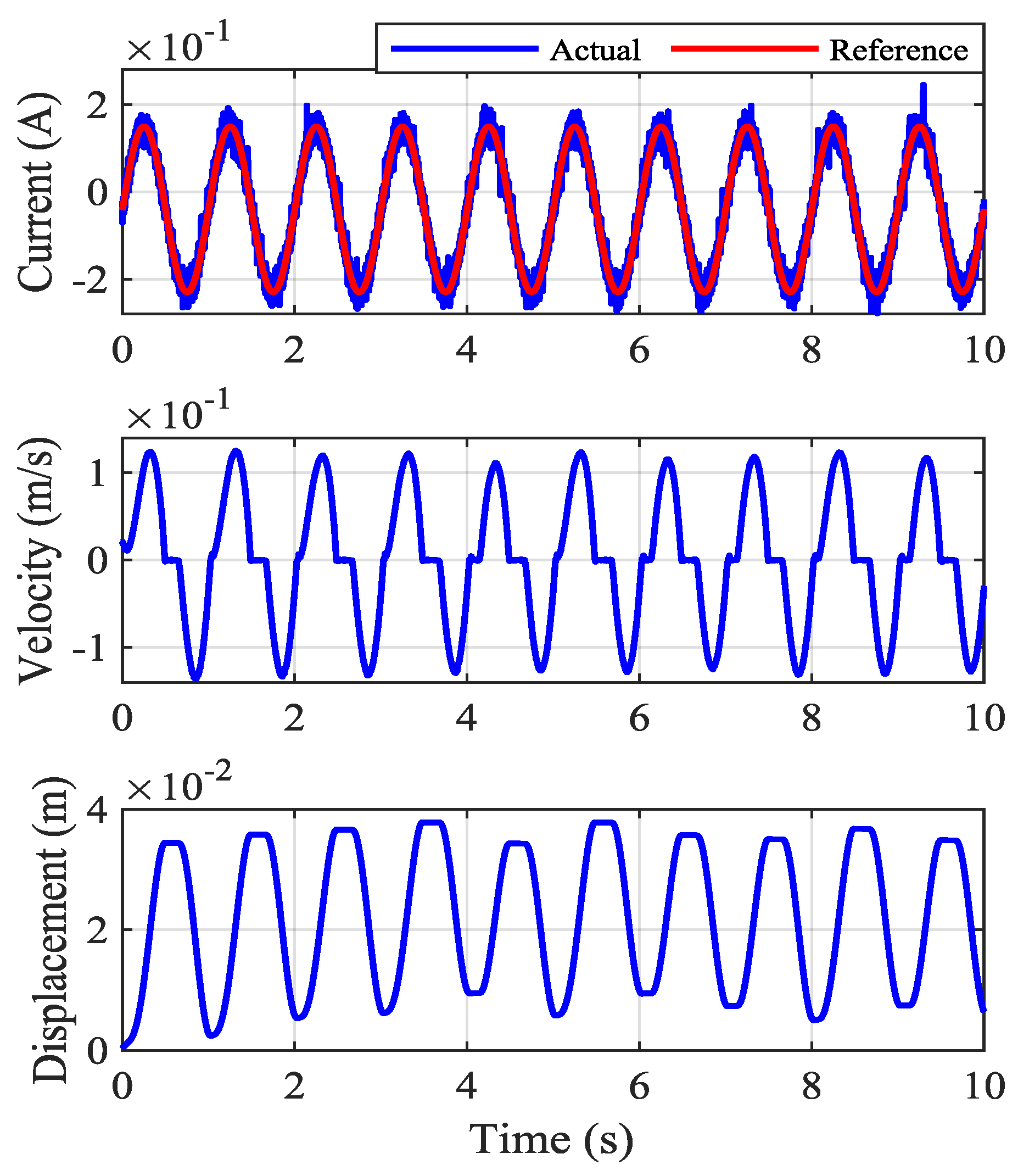
5.2. STRC Response at Different Frequencies
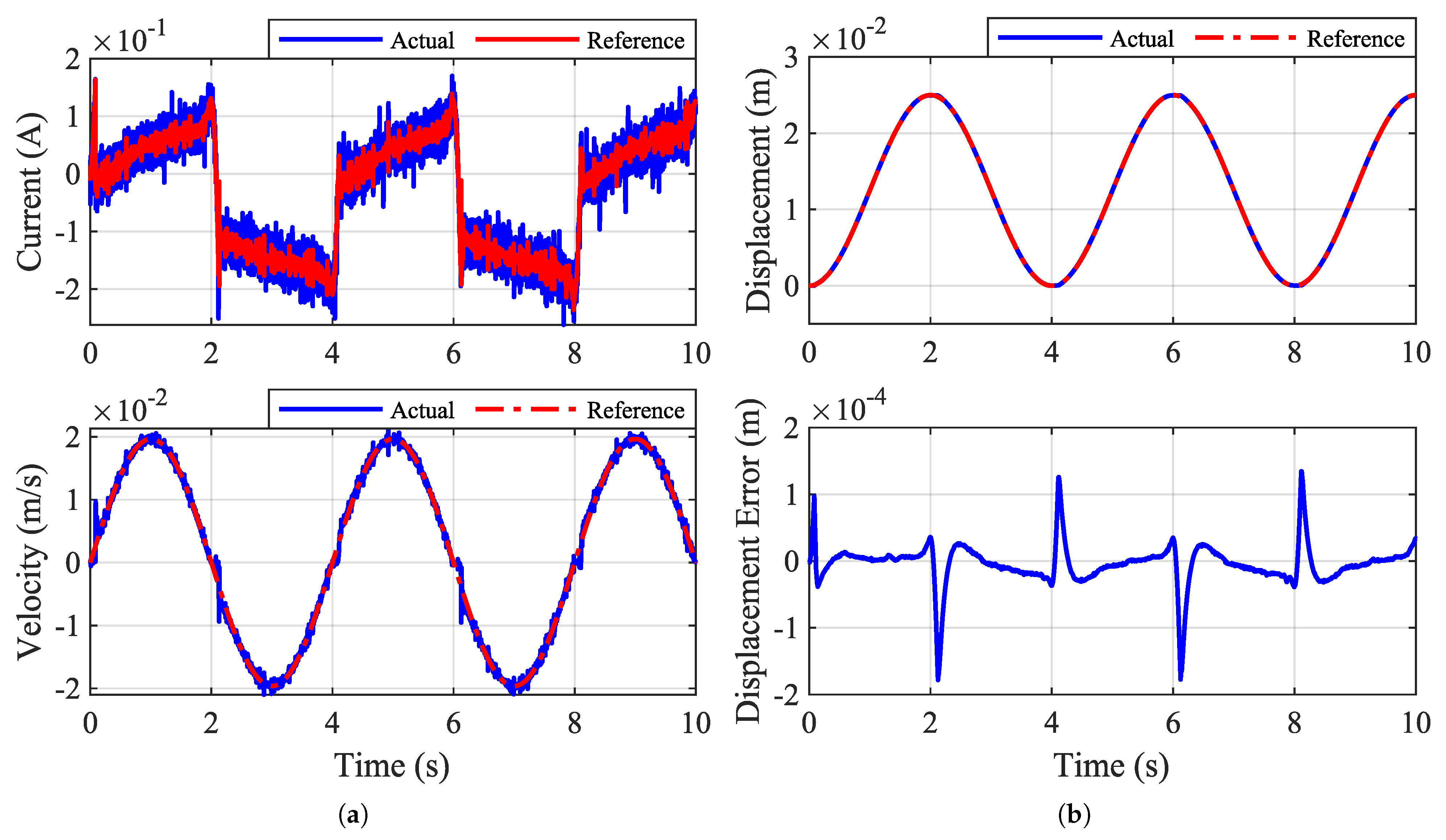
5.3. Comparative Analysis of STRC with ADRC
5.4. Response to System Parameters Variation
5.5. STRC Performance with Higher-Order Dynamics
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| STRC | Sinusoidal Tracking Resonant-based Controller |
| VCA | Voice-Coil Actuator |
| VCM | Voice-Coil Motor |
| PID | Proportional–Integral–Derivative |
| ADRC | Adaptive Disturbance Rejection Control |
| EMF | Back Electromotive Force |
| TPG | Tracking Profile Generator |
| NWS | Nonlinear Weighted Sum |
| ESO | Extended State Observer |
| RMSE | Root Mean Square Error |
| 2MM | Two Mass Model |
References
- Zheng, J.; Fu, M.; Lu, R.; Xie, S. Design, Identification, and Control of a Linear Dual-Stage Actuation Positioning System. J. Frankl. Inst. 2018, 355, 5018–5036. [Google Scholar] [CrossRef]
- Huang, D.; Venkataramanan, V.; Xu, J.X.; Huynh, T.C.T. Contact-Induced Vibration in Dual-Stage Hard Disk Drive Servo Systems and Its Compensator Design. IEEE Trans. Ind. Electron. 2014, 61, 4052–4060. [Google Scholar] [CrossRef]
- Landolsi, T.; Dhaouadi, R.; Aldabbas, O. Beam-Stabilized Optical Switch Using a Voice-Coil Motor Actuator. J. Frankl. Inst. 2011, 348, 1–11. [Google Scholar] [CrossRef]
- Smith, K.J.; Graham, D.J.; Neasham, J.A. Design and Optimization of a Voice Coil Motor with a Rotary Actuator for an Ultrasound Scanner. IEEE Trans. Ind. Electron. 2015, 62, 7073–7078. [Google Scholar] [CrossRef]
- Ryoo, J.R.; Jin, K.B.; Moon, J.H.; Chung, M.J. Track-Following Control Using a Disturbance Observer with Asymptotic Disturbance Rejection in High-Speed Optical Disk Drives. IEEE Trans. Consum. Electron. 2003, 49, 1178–1185. [Google Scholar] [CrossRef]
- Shinshi, T.; Shimizu, D.; Kodeki, K.; Fukushima, K. A Fast Steering Mirror Using a Compact Magnetic Suspension and Voice Coil Motors for Observation Satellites. Electronics 2020, 9, 1997. [Google Scholar] [CrossRef]
- Shen, C.; Chen, N.; Tan, R.; Fan, S.; Fan, D. Modeling and Stability Analysis of Coarse–Fine Composite Mechatronic System in UAV Multi-Gimbal Electro-Optical Pod. Electronics 2020, 9, 769. [Google Scholar] [CrossRef]
- Liu, C.S.; Wu, Y.C.; Lan, Y.J. Design of 4-DOF Voice Coil Motor with Function of Reducing Laser Geometrical Fluctuations. Actuators 2021, 10, 320. [Google Scholar] [CrossRef]
- Lin, Y.H.; Liu, C.S.; Yeh, C.N. Design and Simulation of Novel 3-DOF Spherical Voice Coil Motor. Actuators 2021, 10, 155. [Google Scholar] [CrossRef]
- Armstrong-Helouvry, B.; Dupont, P.; Canudasdewit, C. Survey of Models, Analysis Tools and Compensation Methods for the Control of Machines with Friction. Automatica 1994, 30, 1083–1138. [Google Scholar] [CrossRef]
- Tan, K.; Huang, S.; Lee, T. Robust Adaptive Numerical Compensation for Friction and Force Ripple in Permanent-Magnet Linear Motors. IEEE Trans. Magn. 2002, 38, 221–228. [Google Scholar] [CrossRef]
- Lin, C.J.; Yau, H.T.; Tian, Y.C. Identification and Compensation of Nonlinear Friction Characteristics and Precision Control for a Linear Motor Stage. IEEE/ASME Trans. Mechatron. 2013, 18, 1385–1396. [Google Scholar] [CrossRef]
- Verbert, K.A.J.; Tóth, R.; Babuška, R. Adaptive Friction Compensation: A Globally Stable Approach. IEEE/ASME Trans. Mechatron. 2016, 21, 351–363. [Google Scholar] [CrossRef] [Green Version]
- Nie, K.; Xue, W.; Zhang, C.; Mao, Y. Disturbance Observer-Based Repetitive Control with Application to Optoelectronic Precision Positioning System. J. Frankl. Inst. 2021, 358, 8443–8469. [Google Scholar] [CrossRef]
- Lan, Y.H.; He, J.L.; Li, P.; She, J.H. Optimal Preview Repetitive Control with Application to Permanent Magnet Synchronous Motor Drive System. J. Frankl. Inst. 2020, 357, 10194–10210. [Google Scholar] [CrossRef]
- Kerschen, G.; Worden, K.; Vakakis, A.F.; Golinval, J.C. Past, Present and Future of Nonlinear System Identification in Structural Dynamics. Mech. Syst. Signal Process. 2006, 20, 505–592. [Google Scholar] [CrossRef] [Green Version]
- Ljung, L. Identification of Nonlinear Systems; Other academic LiTH-ISY-R, 2784; Department of Electrical Engineering, Linköping University: Linköping, Sweden, 2007. [Google Scholar]
- Waleed, D.; Usman, H.M.; Dhaouadi, R. Dynamic Friction Characterization of a Linear Servo Motor Using an Optimal Sinusoidal Reference Tracking Controller. J. Robot. Mechatronics 2018, 30, 1014–1018. [Google Scholar] [CrossRef]
- Noorbakhsh, M.; Yazdizadeh, A. Adaptive Friction Compensation in a Two-Link Planar Robot Manipulator Using a New Lyapunov-Based Controller. In Proceedings of the IEEE ICCA 2010, Xiamen, China, 9–11 June 2010; pp. 2132–2137. [Google Scholar] [CrossRef]
- Ryu, J.H.; Song, J.; Kwon, D.S. A Nonlinear Friction Compensation Method Using Adaptive Control and its Practical Application to an In-Parallel Actuated 6-DOF Manipulator. Control. Eng. Pract. 2001, 9, 159–167. [Google Scholar] [CrossRef]
- Kim, W.; Shin, D.; Won, D.; Chung, C.C. Disturbance-Observer-Based Position Tracking Controller in the Presence of Biased Sinusoidal Disturbance for Electrohydraulic Actuators. IEEE Trans. Control. Syst. Technol. 2013, 21, 2290–2298. [Google Scholar] [CrossRef]
- Wang, Z.; Wang, H.; Li, Y.; Blaabjerg, F. A Single Position Loop Control Strategy for High-Speed Voice Coil Motor Based on Active Disturbance Rejection Control. In Proceedings of the 2017 IEEE 26th International Symposium on Industrial Electronics (ISIE), Edinburgh, UK, 19–21 June 2017; pp. 220–225. [Google Scholar] [CrossRef]
- Gao, Y. Active Disturbance-Rejection Control of Voice Coil Motor Based on RBF Neural Network. In Proceedings of the 2011 International Conference on Consumer Electronics, Communications and Networks (CECNet), Xianning, China, 16–18 April 2011; pp. 3895–3898. [Google Scholar] [CrossRef]
- Gao, Z. Scaling and Bandwidth-Parameterization Based Controller Tuning. In Proceedings of the 2003 American Control Conference, Denver, CO, USA, 4–6 June 2003; Volume 6, pp. 4989–4996. [Google Scholar] [CrossRef]
- Chen, Q.; Li, L.; Wang, M.; Pei, L. The Precise Modeling and Active Disturbance Rejection Control of Voice Coil Motor in High Precision Motion Control System. Appl. Math. Model. 2015, 39, 5936–5948. [Google Scholar] [CrossRef]
- Chatterjee, A.; Mohanty, K.B. Current Control Strategies for Single Phase Grid Integrated Inverters for Photovoltaic Applications- A Review. Renew. Sustain. Energy Rev. 2018, 92, 554–569. [Google Scholar] [CrossRef]
- Ming, L.; Xin, Z.; Kong, X.; Yin, C.; Loh, P.C. Power Factor Correction and Harmonic Elimination for LCL-Filtered Three-Level Photovoltaic Inverter with Inverter-Side Current Control. In Proceedings of the IECON 2019—45th Annual Conference of the IEEE Industrial Electronics Society, Lisbon, Portugal, 14–17 October 2019; Volume 1, pp. 3405–3410. [Google Scholar] [CrossRef]
- Santiprapan, P.; Areerak, K.; Areerak, K. The Implementation of Active Power Filter using Proportional plus Resonant Controller. Eng. J. 2017, 21, 69–80. [Google Scholar] [CrossRef]
- Xu, Q.; Jia, M. Model Reference Adaptive Control with Perturbation Estimation for a Micropositioning System. IEEE Trans. Control. Syst. Technol. 2014, 22, 352–359. [Google Scholar] [CrossRef]
- Esbrook, A.; Guibord, M.; Tan, X.; Khalil, H.K. Control of Systems with Hysteresis via Servocompensation and its Application to Nanopositioning. In Proceedings of the 2010 American Control Conference, Baltimore, MD, USA, 30 June–2 July 2010; pp. 6531–6536. [Google Scholar] [CrossRef]
- Yepes, A.G.; Freijedo, F.D.; Doval-Gandoy, J.; Lopez, O.; Malvar, J.; Fernandez-Comesaña, P. Effects of Discretization Methods on the Performance of Resonant Controllers. IEEE Trans. Power Electron. 2010, 25, 1692–1712. [Google Scholar] [CrossRef]
- Nian, H.; Wu, C.; Cheng, P. Direct Resonant Control Strategy for Torque Ripple Mitigation of DFIG Connected to DC Link through Diode Rectifier on Stator. IEEE Trans. Power Electron. 2017, 32, 6936–6945. [Google Scholar] [CrossRef]
- Wang, X.; Sun, D.; Zhu, Z.Q. Resonant Based Backstepping Direct Power Control Strategy for DFIG Under Both Balanced and Unbalanced Grid Conditions. In Proceedings of the IEEE Energy Conversion Congress and Exposition (ECCE), Milwaukee, WI, USA, 18–22 September 2016; pp. 1–8. [Google Scholar] [CrossRef]
- Touati, Z.; Pereira, M.; Araújo, R.E.; Khedher, A. Comparative Study of Discrete PI and PR Controller Implemented in SRG for Wind Energy Application: Theory and Experimentation. Electronics 2022, 11, 1285. [Google Scholar] [CrossRef]
- Cordero, R.; Estrabis, T.; Brito, M.A.; Gentil, G. Development of a Resonant Generalized Predictive Controller for Sinusoidal Reference Tracking. IEEE Trans. Circuits Syst. II Express Briefs 2022, 69, 1218–1222. [Google Scholar] [CrossRef]
- Zhou, Z.; Xia, C.; Yan, Y.; Wang, Z.; Shi, T. Disturbances Attenuation of Permanent Magnet Synchronous Motor Drives Using Cascaded Predictive-Integral-Resonant Controllers. IEEE Trans. Power Electron. 2018, 33, 1514–1527. [Google Scholar] [CrossRef]
- Turner, M.C.; Sofrony, J.; Prempain, E. Anti-windup for model-reference adaptive control schemes with rate-limits. Syst. Control. Lett. 2020, 137, 104630. [Google Scholar] [CrossRef]
- Hosseinzadeh, M.; Yazdanpanah, M.J. Performance enhanced model reference adaptive control through switching non-quadratic Lyapunov functions. Syst. Control. Lett. 2015, 76, 47–55. [Google Scholar] [CrossRef]
- Kahani, R.; Jamil, M.; Iqbal, M.T. Direct Model Reference Adaptive Control of a Boost Converter for Voltage Regulation in Microgrids. Energies 2022, 15, 5080. [Google Scholar] [CrossRef]
- Takrouri, M.; Dhaouadi, R. ADALINE-based friction identification of a linear voice coil DC motor. In Proceedings of the 2016 American Control Conference (ACC), Boston, MA, USA, 6–8 July 2016; pp. 3062–3068. [Google Scholar] [CrossRef]
- Dorf, R.C.; Bishop, R.H. Modern Control Systems, 13th ed.; Pearson: Hoboken, NJ, USA, 2017. [Google Scholar]
- Al Kalbani, F.K.; Zhang, J. Inferential Active Disturbance Rejection Control of a Heat Integrated Distillation Column. In Proceedings of the 2016 14th International Conference on Control, Automation, Robotics and Vision (ICARCV), Phuket, Thailand, 13–15 November 2016; pp. 1–6. [Google Scholar] [CrossRef]
- Han, J. From PID to Active Disturbance Rejection Control. IEEE Trans. Ind. Electron. 2009, 56, 900–906. [Google Scholar] [CrossRef]
- Gao, Z. From Linear to Nonlinear Control Means: A Practical Progression. ISA Trans. 2002, 41, 177–189. [Google Scholar] [CrossRef] [PubMed]
- Moticont. Linear Voice Coil Motors. 2023. Available online: http://moticont.com/voice-coil-motor.htm (accessed on 3 January 2023).





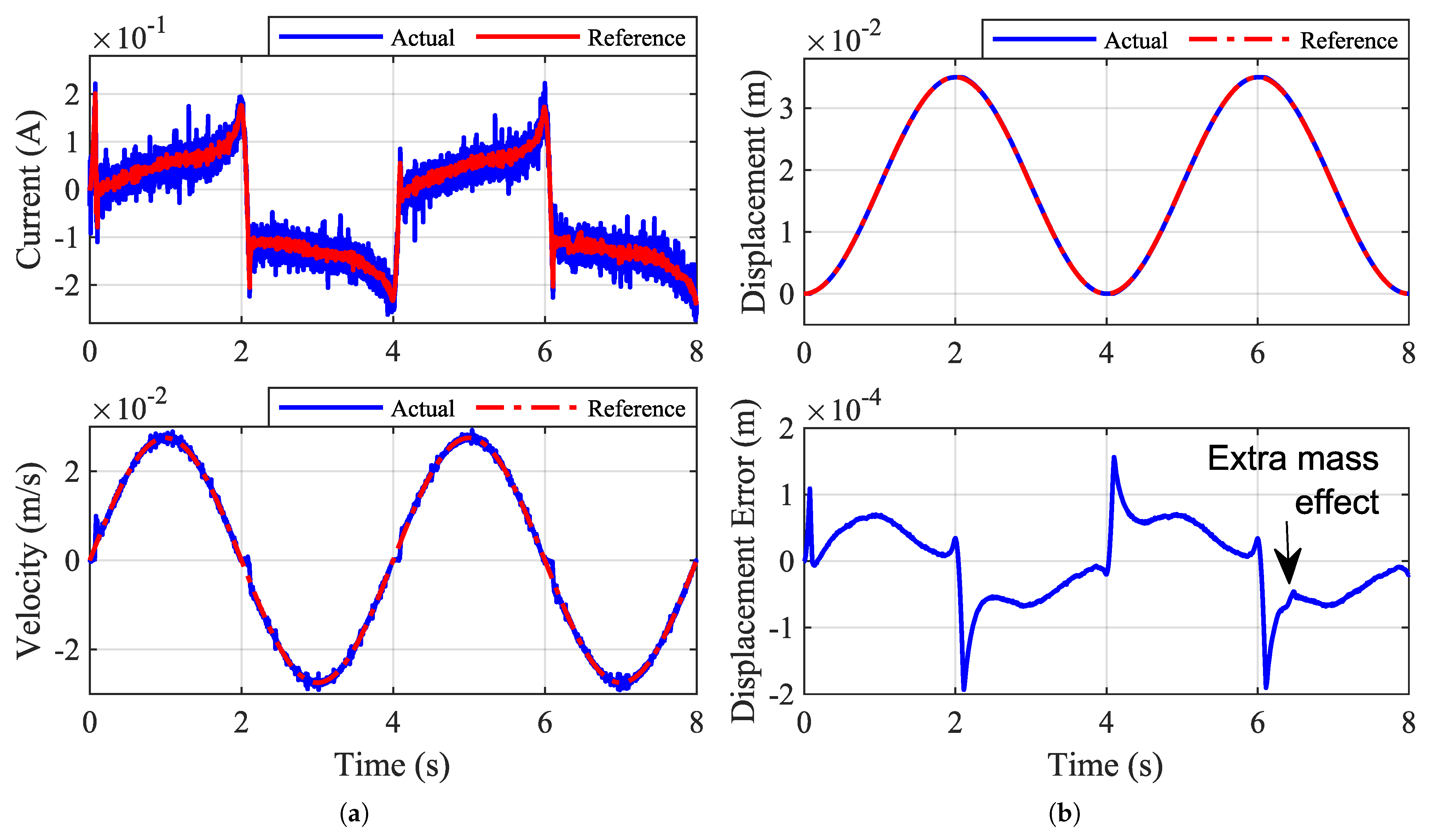
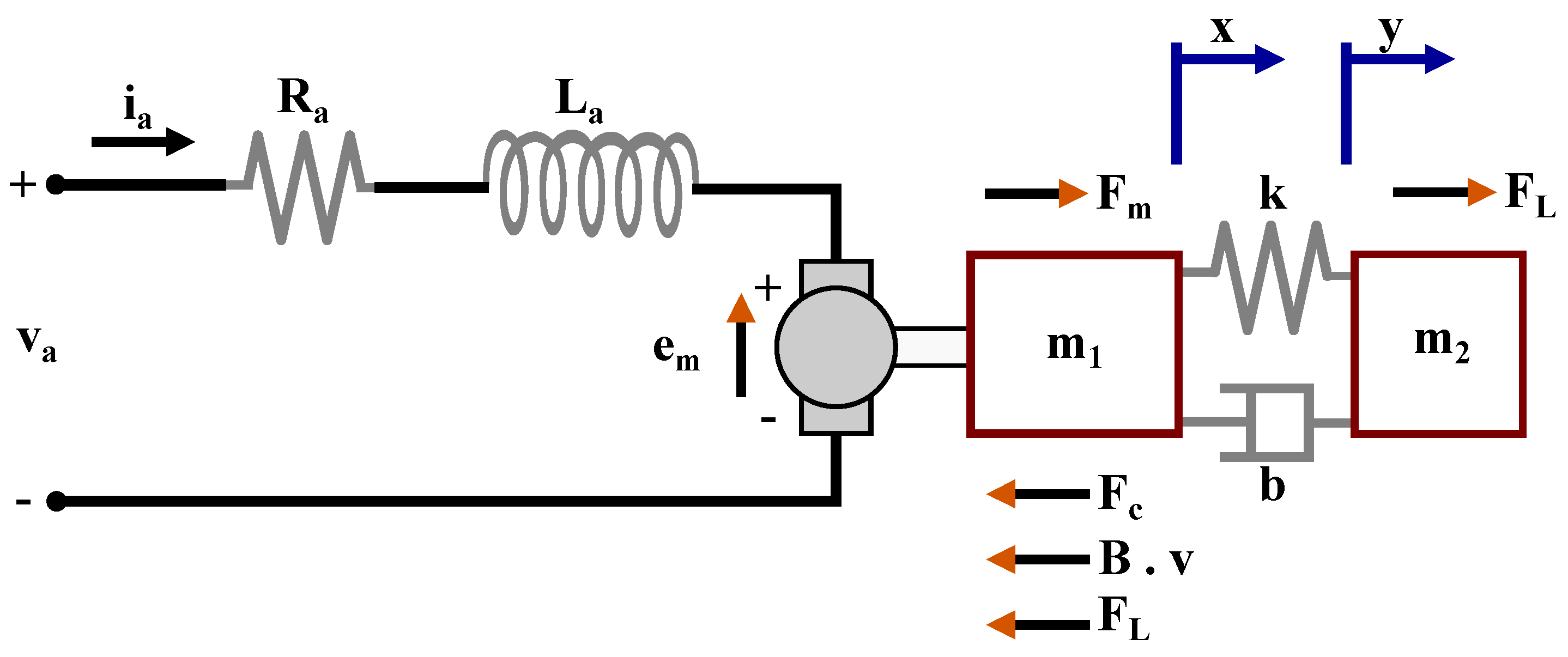


| 0 | |||
| 0 | |||
| 0 |
| 0 | |||
| 0 | |||
| 0 |
| Parameter | Value |
|---|---|
| M (Kg) | 0.9232 |
| B (N.s/m) | 7.9124 |
| (N) | 0.5035 |
| (N/A) | 10.1 |
| (m/N.s) | 0.1264 |
| (s) | 0.1167 |
| (s) | 0.002 |
| Frequency | RMSE Position | RMSE Velocity | ||
|---|---|---|---|---|
| STRC | ADRC | STRC | ADRC | |
| 1.00 Hz | ||||
| 0.50 Hz | ||||
| 0.25 Hz | ||||
| Frequency | RMSE Position | RMSE Velocity | ||
|---|---|---|---|---|
| STRC | STRC-2MM | STRC | STRC-2MM | |
| 0.25 Hz | ||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dhaouadi, R.; Takrouri, M.; Hafez, I. High Precision Sinusoidal Position Tracking of a Voice-Coil Linear Servomotor Using Resonant Control. Electronics 2023, 12, 977. https://doi.org/10.3390/electronics12040977
Dhaouadi R, Takrouri M, Hafez I. High Precision Sinusoidal Position Tracking of a Voice-Coil Linear Servomotor Using Resonant Control. Electronics. 2023; 12(4):977. https://doi.org/10.3390/electronics12040977
Chicago/Turabian StyleDhaouadi, Rached, Mohannad Takrouri, and Ishaq Hafez. 2023. "High Precision Sinusoidal Position Tracking of a Voice-Coil Linear Servomotor Using Resonant Control" Electronics 12, no. 4: 977. https://doi.org/10.3390/electronics12040977
APA StyleDhaouadi, R., Takrouri, M., & Hafez, I. (2023). High Precision Sinusoidal Position Tracking of a Voice-Coil Linear Servomotor Using Resonant Control. Electronics, 12(4), 977. https://doi.org/10.3390/electronics12040977










