Sensorless Field Oriented Control of Synchronous Machines for Low and High Speeds with Space Vector Modulation-Based Direct Flux Control Measurement Sequence
Abstract
:1. Introduction
2. SVM-Based DFC Measurement Sequence
2.1. Voltage Equation at the Machine’s Star Point
2.2. Standard Voltage Vectors and Voltage between the Star Points
2.3. Space Vector Modulation with DFC Measurement Sequence
3. Sensorless Speed Closed Loop Control with Field Oriented Control and SVM-Based DFC Measurement Sequence
3.1. Rotor Position Estimation Using DFC
3.2. DFC-Based Rotor Speed Estimation
3.3. Sensorless Speed Closed Loop Control with Field Oriented Control Structure
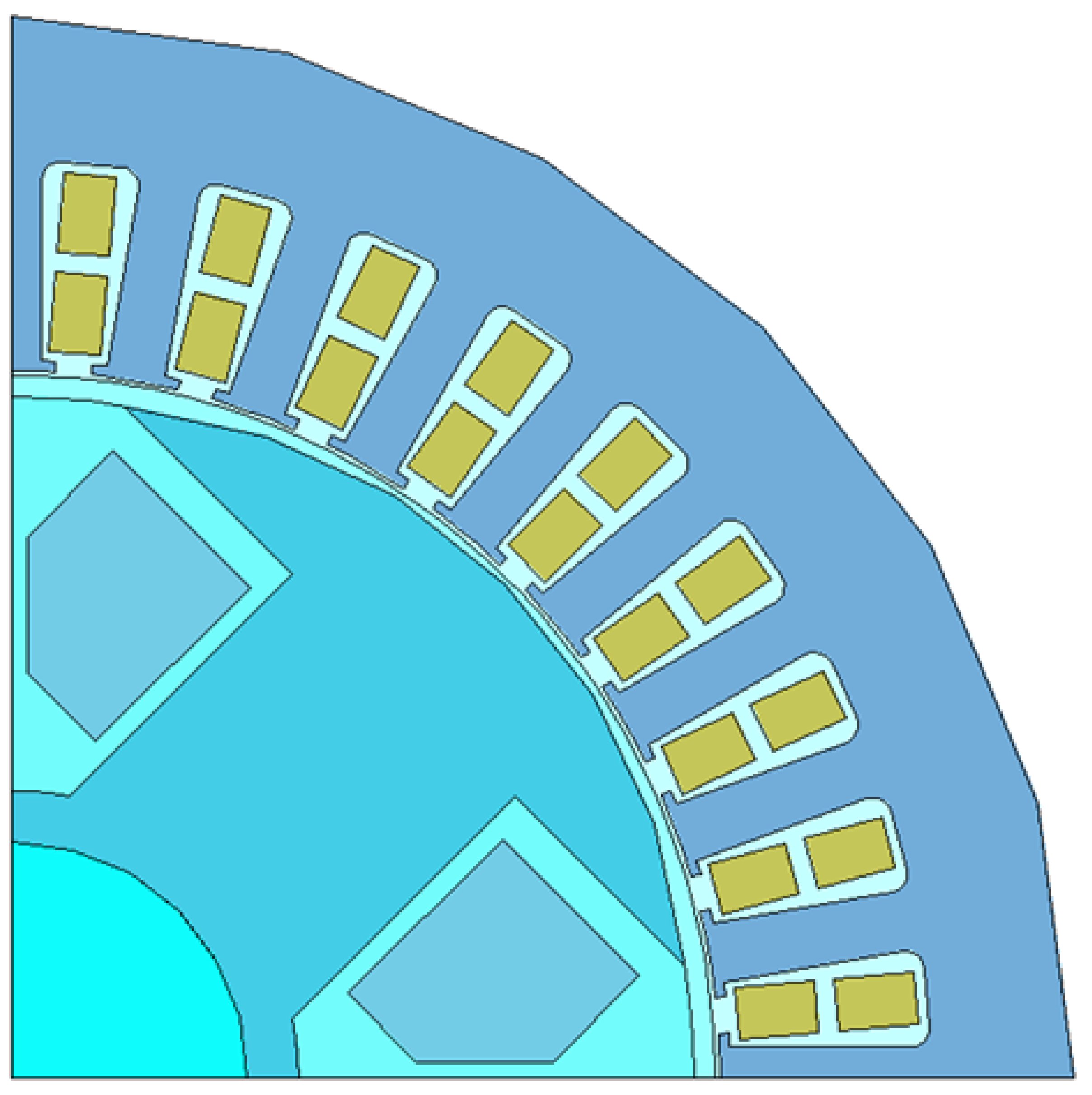
4. Finite Element Model of the Synchronous Machine
4.1. WRSESM Model Reduction
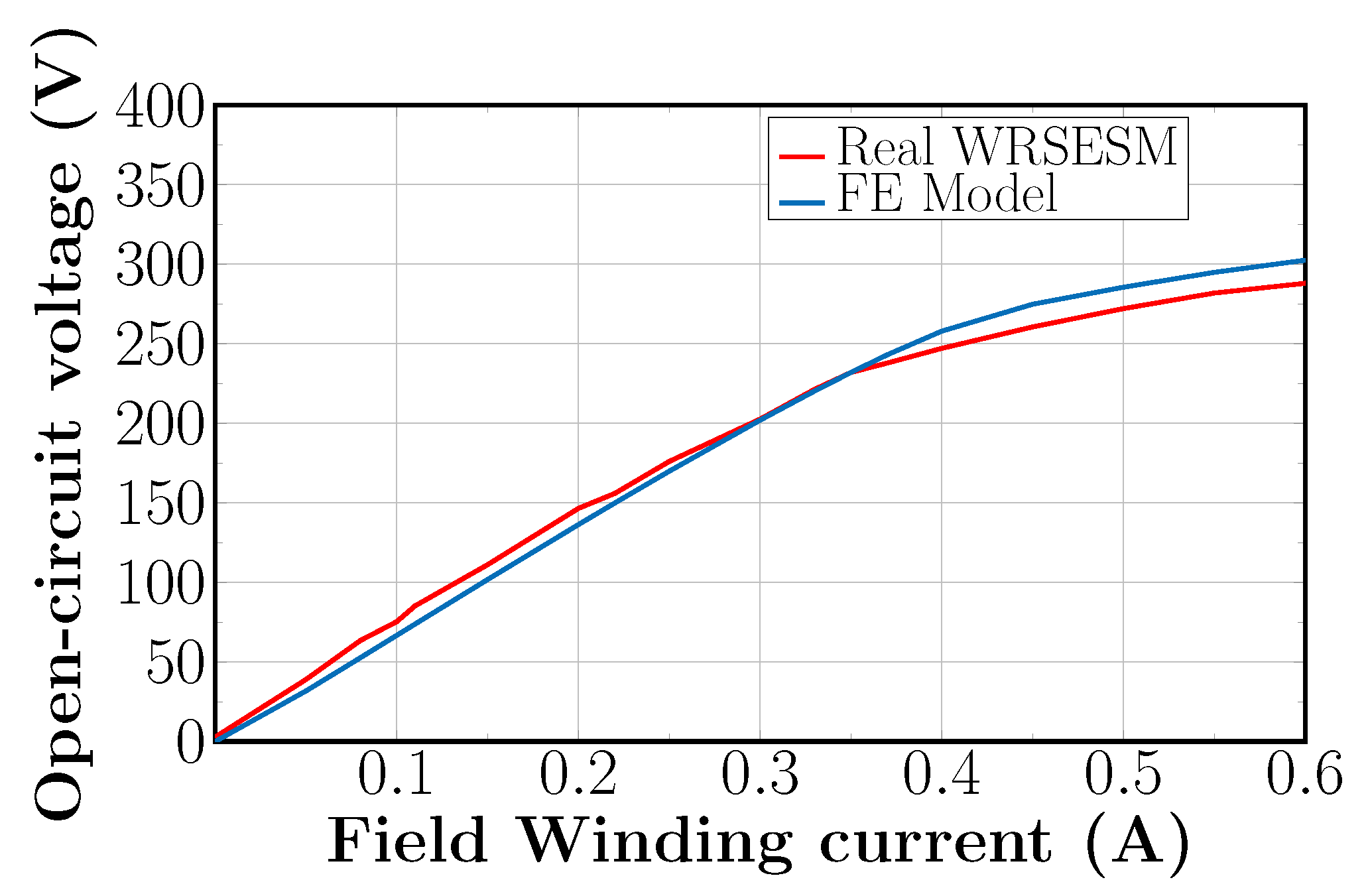
4.2. Model Validation
5. Simulation Validation
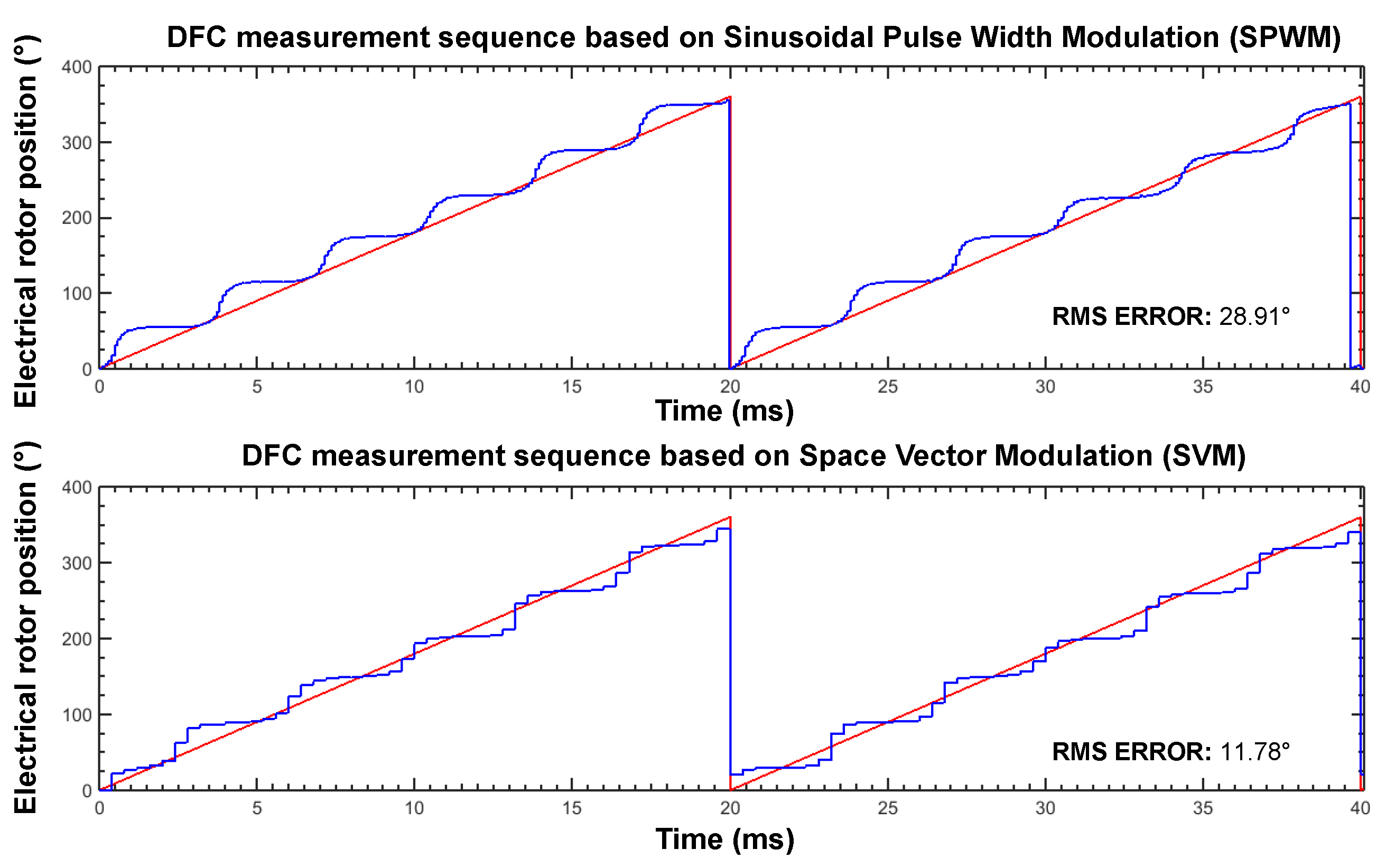
5.1. Comparison: SVM-Based DFC and SPWM-Based DFC
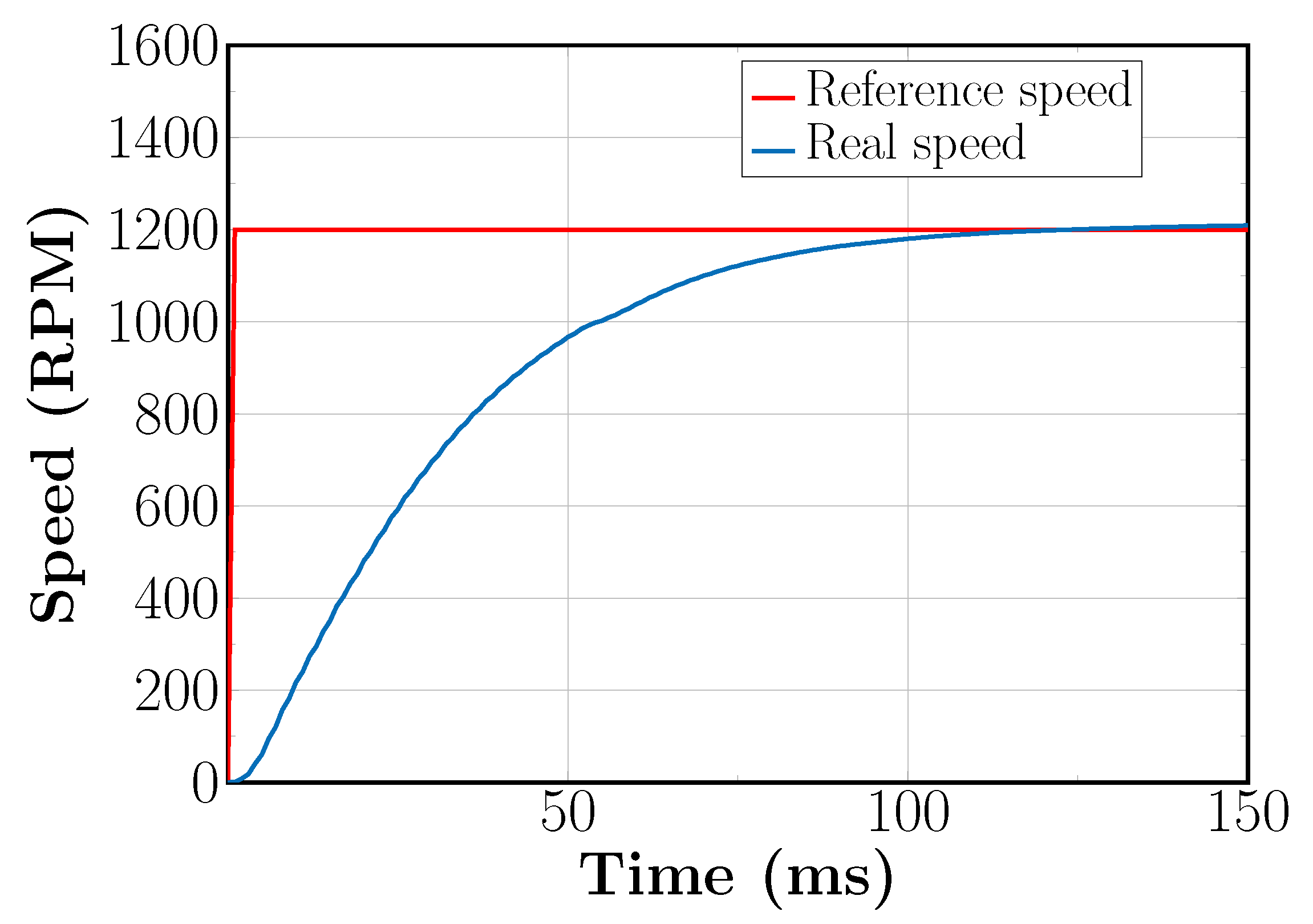
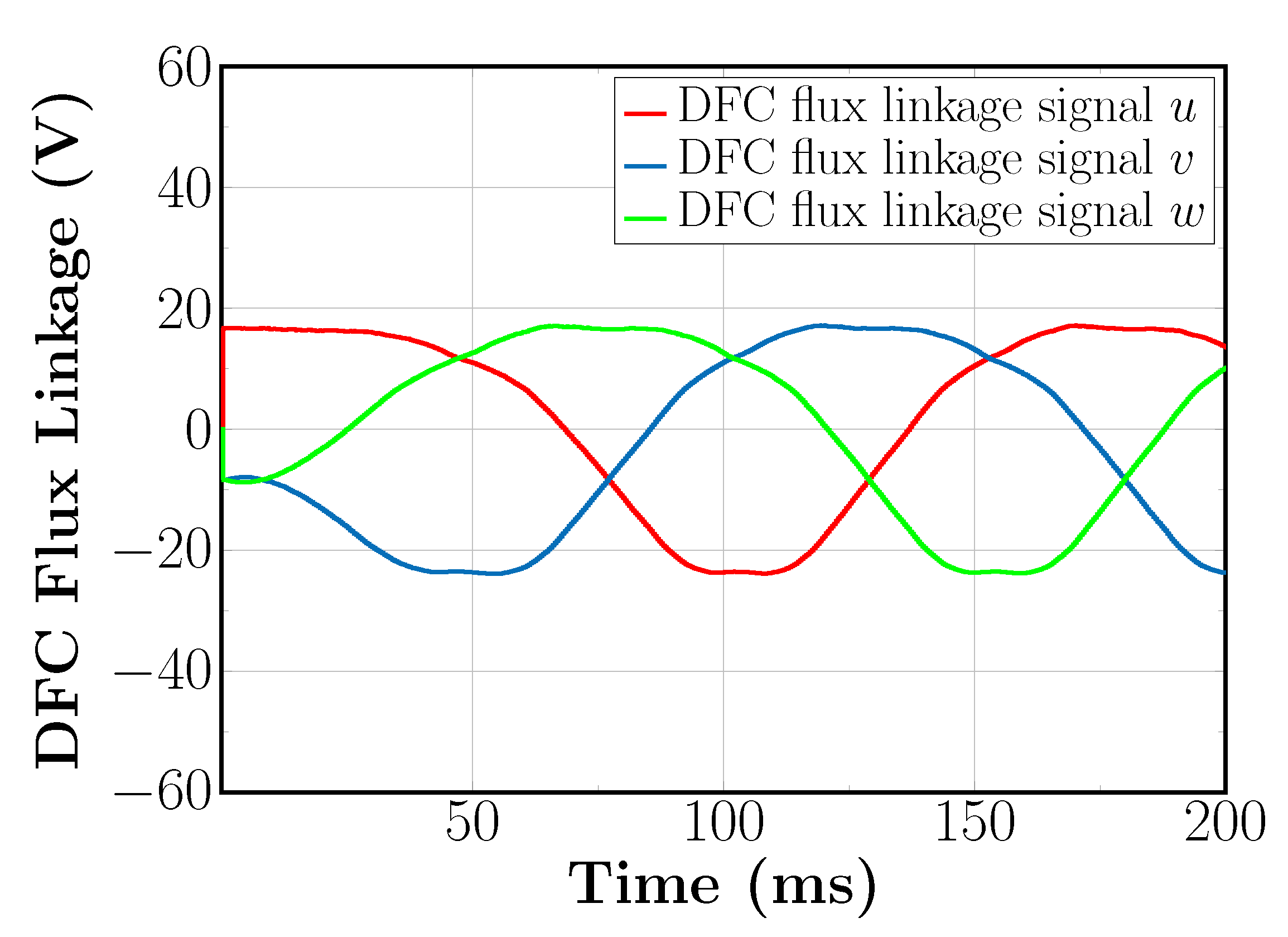
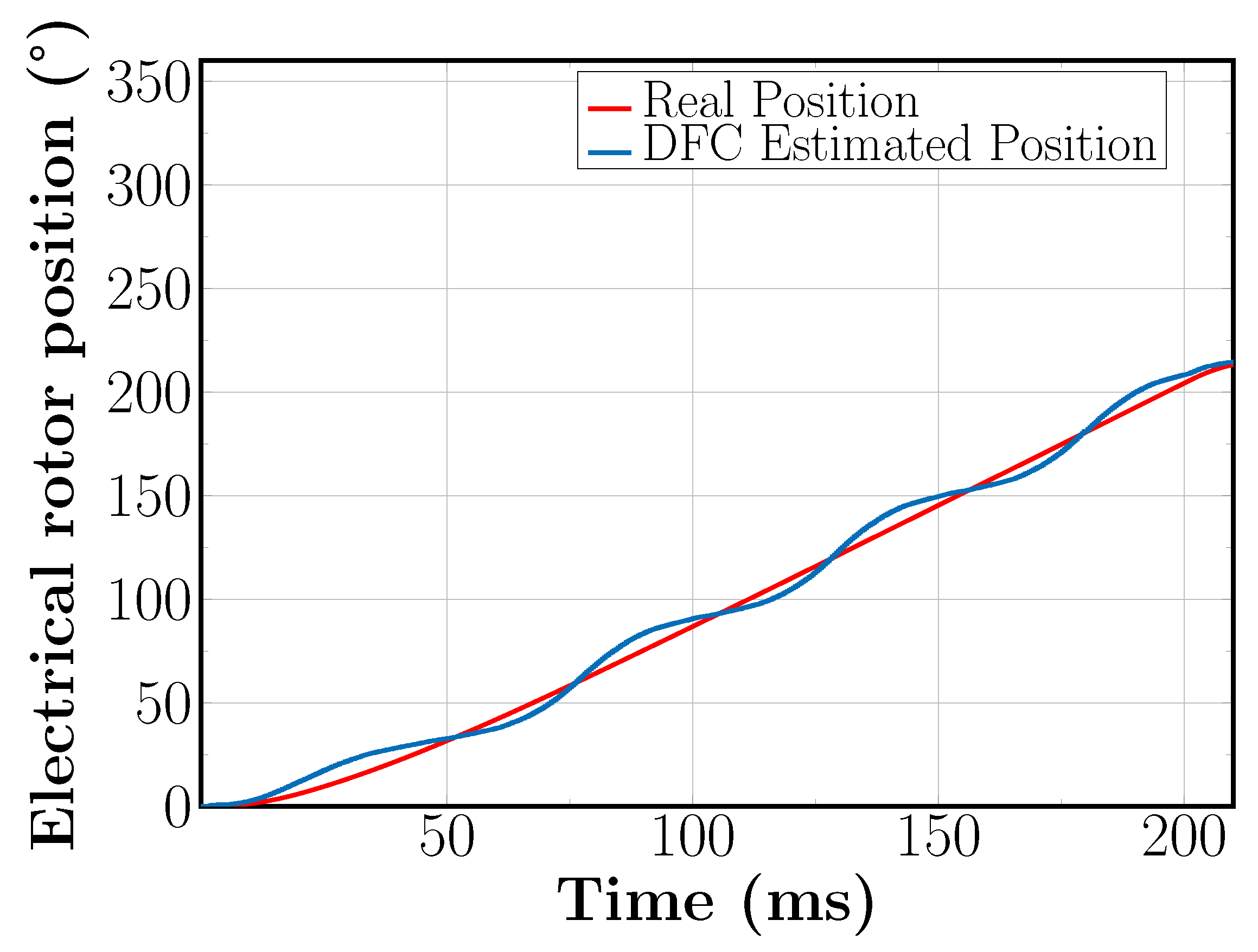
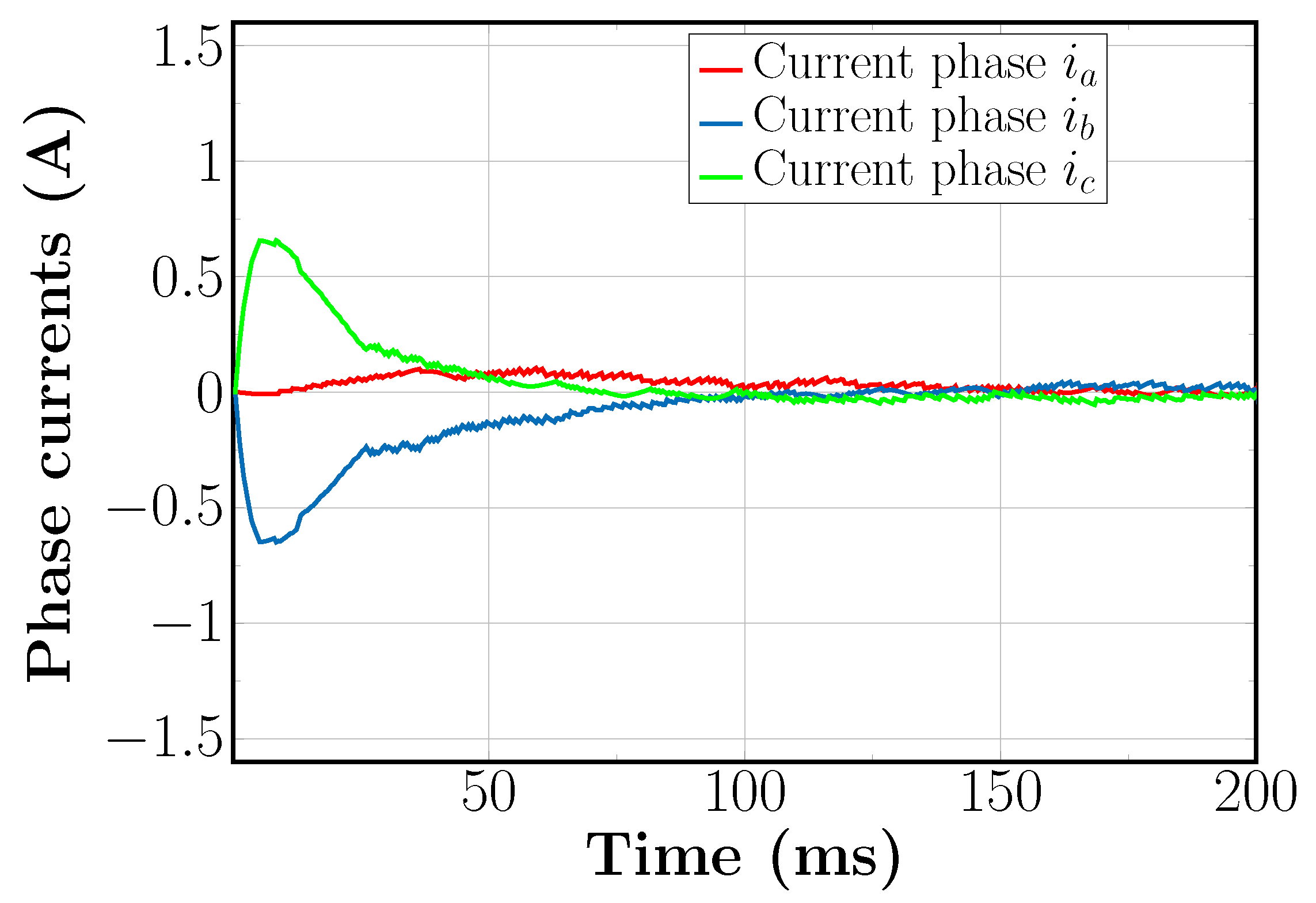
5.2. Sensorless Field Oriented Control with SVM-Based DFC for High Speed Reference
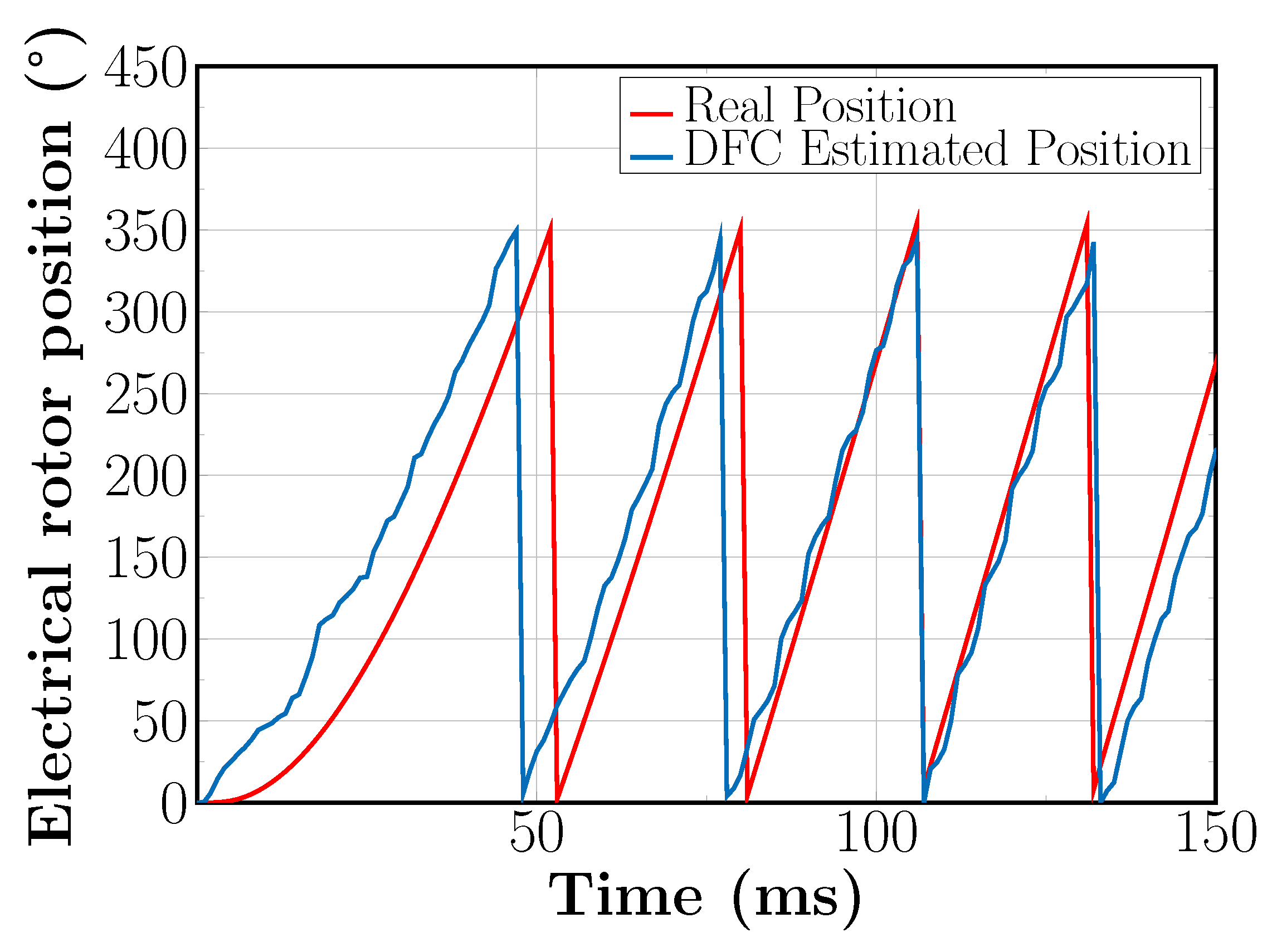
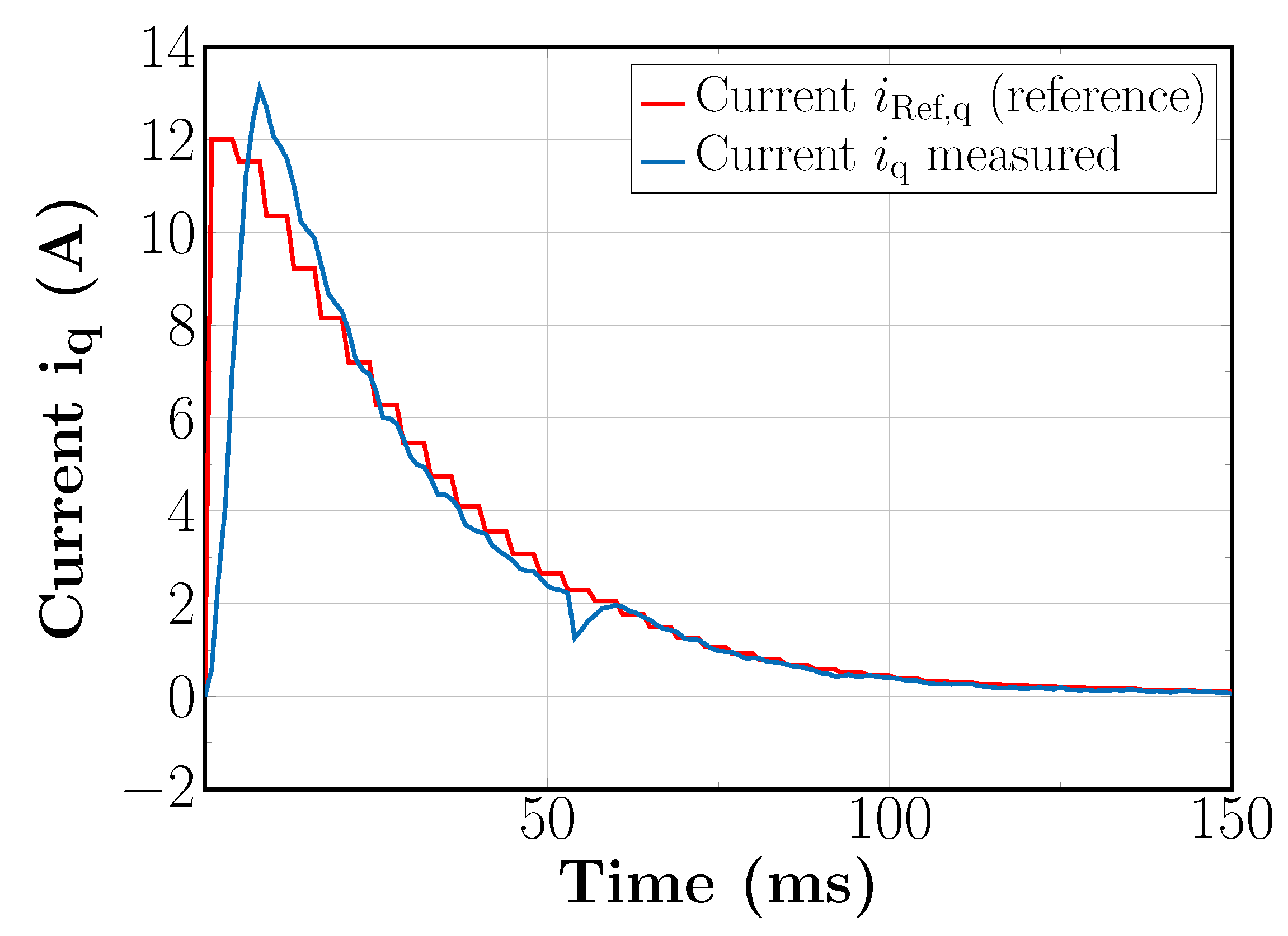
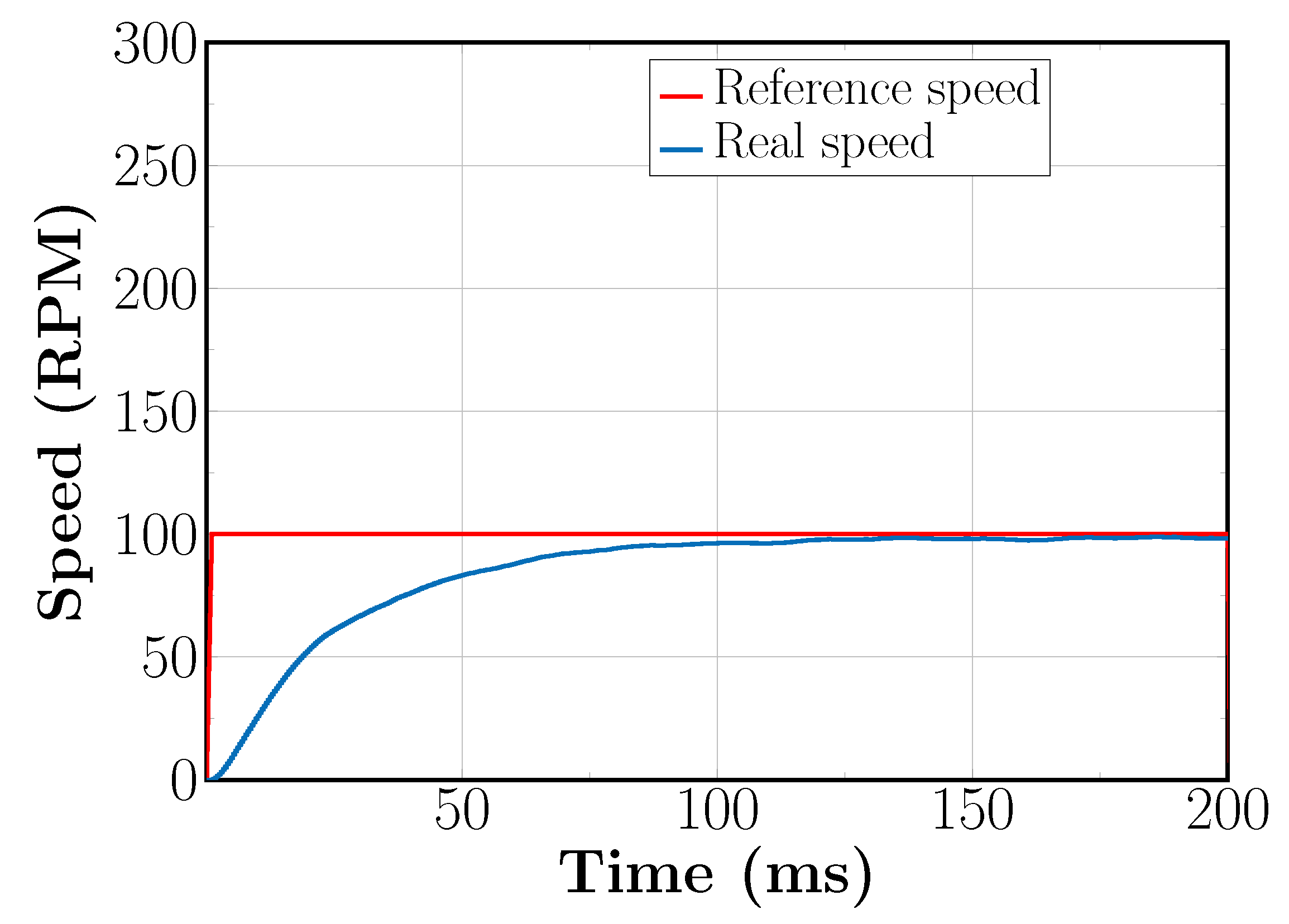
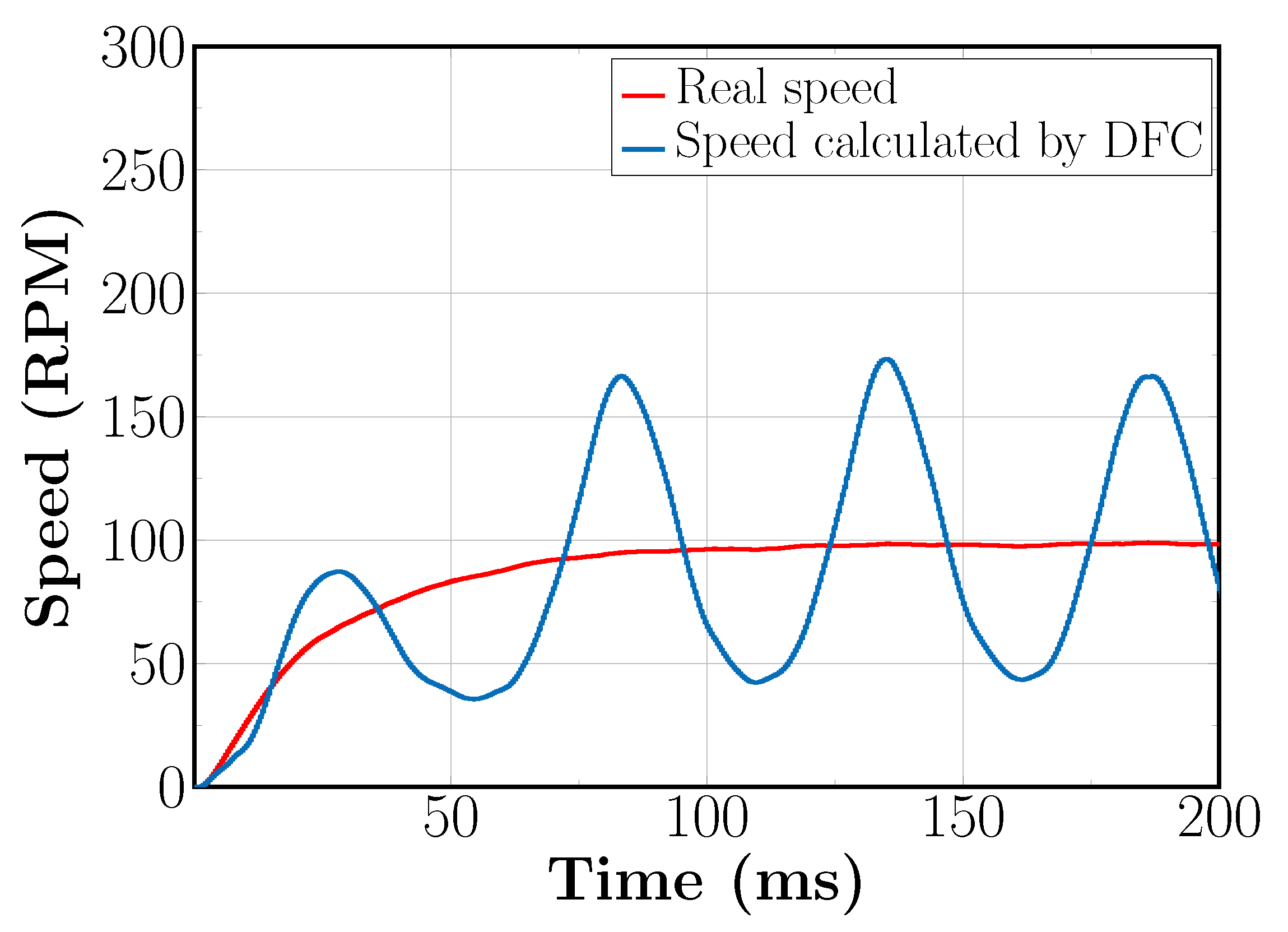
5.3. Sensorless Field Oriented Control with SVM-Based DFC for Low Speed Reference
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| DFC | Direct Flux Control |
| SVM | Space Vector Modulation |
| SM | Synchronous Machines |
| PMSM | Permanent Magnet Synchronous Machines |
| PWM | Pulse Width Modulation |
| SPWM | Sinusoidal Pulse Width Modulation |
| EMI | Electromagnetic Interference |
| FEM | Finite Element Model |
| FE | Finite Element |
Appendix A. Machine’s Star Voltage Equation
Appendix B. Finite Element Model (FEM) Synchronous Machine Data
References
- Liu, Y.; Laghrouche, S.; Depernet, D.; Djerdir, A.; Cirrincione, M. Disturbance-Observer-Based Complementary Sliding-Mode Speed Control for PMSM Drives: A Super-Twisting Sliding-Mode Observer-Based Approach. IEEE J. Emerg. Sel. Top. Power Electron. 2021, 9, 5416–5428. [Google Scholar] [CrossRef]
- Wang, G.; Zhang, G.; Xu, D. Position Sensorless Control Techniques for Permanent Magnet Synchronous Machine Drives; Springer: Singapore, 2020; pp. 2–10. [Google Scholar]
- Tapani, J.; Hrabovcova, V.; Pyrhonen, J. Design of Rotating Electrical Machines; John Wiley & Sons: Hoboken, NJ, USA, 2013. [Google Scholar]
- Li, C.; Elbuluk, M. A sliding mode observer for sensorless control of permanent magnet synchronous motors. In Proceedings of the Conference Record of the 2001 IEEE Industry Applications Conference—36th IAS Annual Meeting (Cat. No. 01CH37248), Chicago, IL, USA, 30 September–4 October 2001; Volume 2, pp. 1273–1278. [Google Scholar]
- Weidauer, J.; Messer, R. Electrical Drives: Principles, Planning, Applications, Solutions; John Wiley & Sons: Hoboken, NJ, USA, 2014; pp. 152–153. [Google Scholar]
- Sandre-Hernandez, O.; Morales-Caporal, R.; Rangel-Magdaleno, J.; Peregrina-Barreto, H.; Hernandez-Perez, J.N. Parameter identification of PMSMs using experimental measurements and a PSO algorithm. IEEE Trans. Instrum. Meas. 2015, 64, 2146–2154. [Google Scholar] [CrossRef]
- Lara, J.; Xu, J.; Chandra, A. Effects of rotor position error in the performance of field-oriented-controlled PMSM drives for electric vehicle traction applications. IEEE Trans. Ind. Electron. 2016, 63, 4738–4751. [Google Scholar] [CrossRef]
- Podder, A.; Pandit, D. Study of Sensorless Field-Oriented Control of SPMSM Using Rotor Flux Observer & Disturbance Observer Based Discrete Sliding Mode Observer. In Proceedings of the 2021 IEEE 22nd Workshop on Control and Modelling of Power Electronics (COMPEL), Cartagena, Colombia, 2–5 November 2021; pp. 1–8. [Google Scholar]
- DPulle, W.; Darnell, P.; Veltman, A. Applied Control of Electrical Drives; Springer: Berlin/Heidelberg, Germany, 2015; pp. 18–31. [Google Scholar]
- Jung, S.; Nam, K. PMSM Control Based on Edge-Field Hall Sensor Signals Through ANF-PLL Processing. IEEE Trans. Ind. Electron. 2011, 58, 5121–5129. [Google Scholar] [CrossRef]
- Sul, S.-K. Control of Electric Machine Drive System; IEEE Press: Piscataway, NJ, USA, 2011. [Google Scholar]
- Sul, S.-K. Motor Drive and Sensorless Control; 3rd Asian PhD School on Advanced Power Electronics: Chengdu, China, 2021. [Google Scholar]
- Wolf, C.M.; Lorenz, R.D. Using the Motor Drive as a Sensor to Extract Spatially Dependent Information for Motion Control Applications. IEEE Trans. Ind. Appl. 2011, 47, 1344–1351. [Google Scholar] [CrossRef]
- Qu, L.; Qiao, W.; Qu, L. An Enhanced Linear Active Disturbance Rejection Rotor Position Sensorless Control for Permanent Magnet Synchronous Motors. IEEE Trans. Power Electron. 2020, 35, 6175–6184. [Google Scholar] [CrossRef]
- Rashed, M.; MacConnell, P.F.A.; Stronach, A.F.; Acarnley, P. Sensorless Indirect-Rotor-Field-Orientation Speed Control of a Permanent-Magnet Synchronous Motor With Stator-Resistance Estimation. IEEE Trans. Ind. Electron. 2007, 54, 1664–1675. [Google Scholar] [CrossRef]
- Chi, S.; Zhang, Z.; Xu, L. Sliding-Mode Sensorless Control of Direct-Drive PM Synchronous Motors for Washing Machine Applications. IEEE Trans. Ind. Appl. 2009, 45, 582–590. [Google Scholar] [CrossRef]
- Ye, S.; Yao, X. An Enhanced SMO-Based Permanent-Magnet Synchronous Machine Sensorless Drive Scheme With Current Measurement Error Compensation. IEEE J. Emerg. Sel. Top. Power Electron. 2021, 9, 4407–4419. [Google Scholar] [CrossRef]
- Raca, D.; Garcia, P.; Reigosa, D.D.; Briz, F.; Lorenz, R.D. Carrier signal selection for sensorless control of PM synchronous machines at zero and very low speeds. Proc. IEEE Ind. Appl. 2009, 46, 167–178. [Google Scholar] [CrossRef]
- Liu, J.M.; Zhu, Z.Q. Sensorless control strategy by square-waveform high-frequency pulsating signal injection into stationary reference frame. IEEE J. Emerg. Sel. Topics Power Electron. 2014, 2, 171–180. [Google Scholar] [CrossRef]
- Xu, P.L.; Zhu, Z.Q. Novel square-wave signal injection method using zero-sequence voltage for sensorless control of PMSM drives. IEEE Trans. Ind. Electron. 2016, 63, 7444–7454. [Google Scholar] [CrossRef]
- Schrödl, M.; Lambeck, M. Statistic properties of the INFORM-method in highly dynamics sensorless PM motor control applications down to standstill. Eur. Power Electron. Drives 2003, 13, 22–29. [Google Scholar] [CrossRef]
- Zentai, A.; Daboczi, T. Improving INFORM calculation method on permanent magnet synchronous machines. In Proceedings of the 2007 IEEE Instrumentation & Measurement Technology Conference (IMTC 2007), Warsaw, Poland, 1–3 May 2007; pp. 1–6. [Google Scholar]
- Thiemann, P.; Mantala, C.; Mueller, T.; Strothmann, R.; Zhou, E. Direct Flux Control (DFC): A New Sensorless Control Method for PMSM. In Proceedings of the 2011 46th International Universities’ Power Engineering Conference (UPEC), Soest, Germany, 5–8 September 2011; pp. 1–6. [Google Scholar]
- Müller, T.; See, C.; Ghani, A.; Bati, A.; Thiemann, P. Direct flux control–sensorless control method of PMSM for all speeds–basics and constraints. Electron. Lett. 2017, 53, 1110–1111. [Google Scholar] [CrossRef] [Green Version]
- Grasso, E.; Palmieri, M.; Mandriota, R.; Cupertino, F.; Nienhaus, M.; Kleen, S. Analysis and Application of the Direct Flux Control Sensorless Technique to Low-Power PMSMs. Energies 2020, 13, 1453. [Google Scholar] [CrossRef] [Green Version]
- Robeischl, E.; Schroedl, M. Optimized INFORM measurement sequence for sensorless PM synchronous motor drives with respect to minimum current distortion. IEEE Trans. Ind. Appl. 2004, 40, 591–598. [Google Scholar] [CrossRef]
- Strothmann, R. Device for Obtaining Information about the Rotor Position of Electric Machines. DE Patent WO 2007/073854, 5 July 2007. [Google Scholar]
- Thiemann, P.; Mantala, C.; Mueller, T.; Strothmann, R.; Zhou, E. Sensorless control for buried magnet PMSM based on direct flux control and fuzzy logic. In Proceedings of the 8th IEEE Symposium on Diagnostics for Electrical Machines, Power Electronics & Drives, Bologna, Italy, 5–8 September 2011; pp. 405–412. [Google Scholar]
- Müller, T.; See, C.; Ghani, A.; Thiemann, P. Simulation of PMSM in maxwell 3D/simplorer to optimize direct flux control. In Proceedings of the 2017 IEEE 26th International Symposium on Industrial Electronics (ISIE), Edinburgh, UK, 19–21 June 2017; pp. 368–373. [Google Scholar]
- Mantala, C. Sensorless Control of Brushless Permanent Magnet Motors. Ph.D. Thesis, University of Bolton, Bolton, UK, 2013. [Google Scholar]
- Thiemann, P.; Mantala, C.; Hördler, J.; Groppe, D.; Trautmann, A.; Strothmann, R.; Zhou, E. PMSM sensorless rotor position detection for all speeds by Direct Flux Control. In Proceedings of the 2011 IEEE International Symposium on Industrial Electronics, Gdansk, Poland, 27–30 June 2011; pp. 673–678. [Google Scholar]
- Thiemann, P.; Mantala, C.; Mueller, T.; Strothmann, R.; Zhou, E. PMSM sensorless control with Direct Flux Control for all speeds. In Proceedings of the 3rd IEEE International Symposium on Sensorless Control for Electrical Drives (SLED 2012), Catania, Italy, 21–22 September 2012; pp. 1–6. [Google Scholar]
- Iturra, R.G.; Thiemann, P. Sensorless Rotor Position detection of Synchronous Machine using Direct Flux Control—Comparative evaluation of rotor position estimation methods. In Proceedings of the 2021 XVIII International Scientific Technical Conference Alternating Current Electric Drives (ACED), Ekaterinburg, Russia, 24–27 May 2021; pp. 1–6. [Google Scholar]
- Merl, D.; Grasso, E.; Schwartz, R.; Nienhaus, M. A Direct Flux Observer Based on a Fast Resettable Integrator Circuitry for Sensorless Control of PMSMs. In Proceedings of the 16th International Conference on New Actuators (ACTUATOR 2018), Bremen, Germany, 25–27 June 2018; pp. 1–4. [Google Scholar]
- Grasso, E.; Mandriota, R.; König, N.; Nienhaus, M. Analysis and Exploitation of the Star-Point Voltage of Synchronous Machines for Sensorless Operation. Energies 2019, 12, 4729. [Google Scholar] [CrossRef] [Green Version]
- Schuhmacher, K.; Grasso, E.; Nienhaus, M. Improved rotor position determination for a sensorless star-connected PMSM drive using Direct Flux Control. J. Eng. 2019, 17, 3749–3753. [Google Scholar] [CrossRef]
- Iturra, R.G.; Thiemann, P. Sensorless Field Oriented Control of PMSM using Direct Flux Control with improved measurement sequence. In Proceedings of the 2021 XVIII International Scientific Technical Conference Alternating Current Electric Drives (ACED), Ekaterinburg, Russia, 24–27 May 2021; pp. 1–6. [Google Scholar]
- Holmes, D.; Lipo, T.A. Pulse Width Modulation for Power Converters: Principles and Practice; John Wiley & Sons: Hoboken, NJ, USA, 2003; Volume 18. [Google Scholar]
- Teaching Old Motors New Tricks. Available online: https://e2e.ti.com/blogs_/b/industrial_strength/posts/teaching-old-motors-new-tricks (accessed on 6 April 2016).
- Umans, S.; Fitzgerald, E.; Kingsley, C. Electric Machinery; McGraw-Hill Higher Education: New York, NY, USA, 2013. [Google Scholar]
- Mohan, N.; Undeland, T.M.; Williams, P. Power Electronics: Converters, Applications, and Design; John Wiley & Sons: Hoboken, NJ, USA, 2003. [Google Scholar]
- Quang, N.; Nguyen, P.; Dittrich, J. Vector Control of Three-Phase AC Machines; Springer: Berlin/Heidelberg, Germany, 2008; Volume 2. [Google Scholar]
- van der Broeck, C.; Petit, M.; De Doncker, R. Tutorial: Physics-based Modelling and Control of PWM Converters. In Proceedings of the 2020 IEEE Energy Conversion Congress and Exposition (ECCE), Detroit, MI, USA, 11–15 October 2020. [Google Scholar]
- Ansoft Corporation. User Guide—Maxwell 2D v15.0: Electronic Design and Automation Software; Ansoft: Pittsburgh, PA, USA, 2016; pp. 6–9. [Google Scholar]

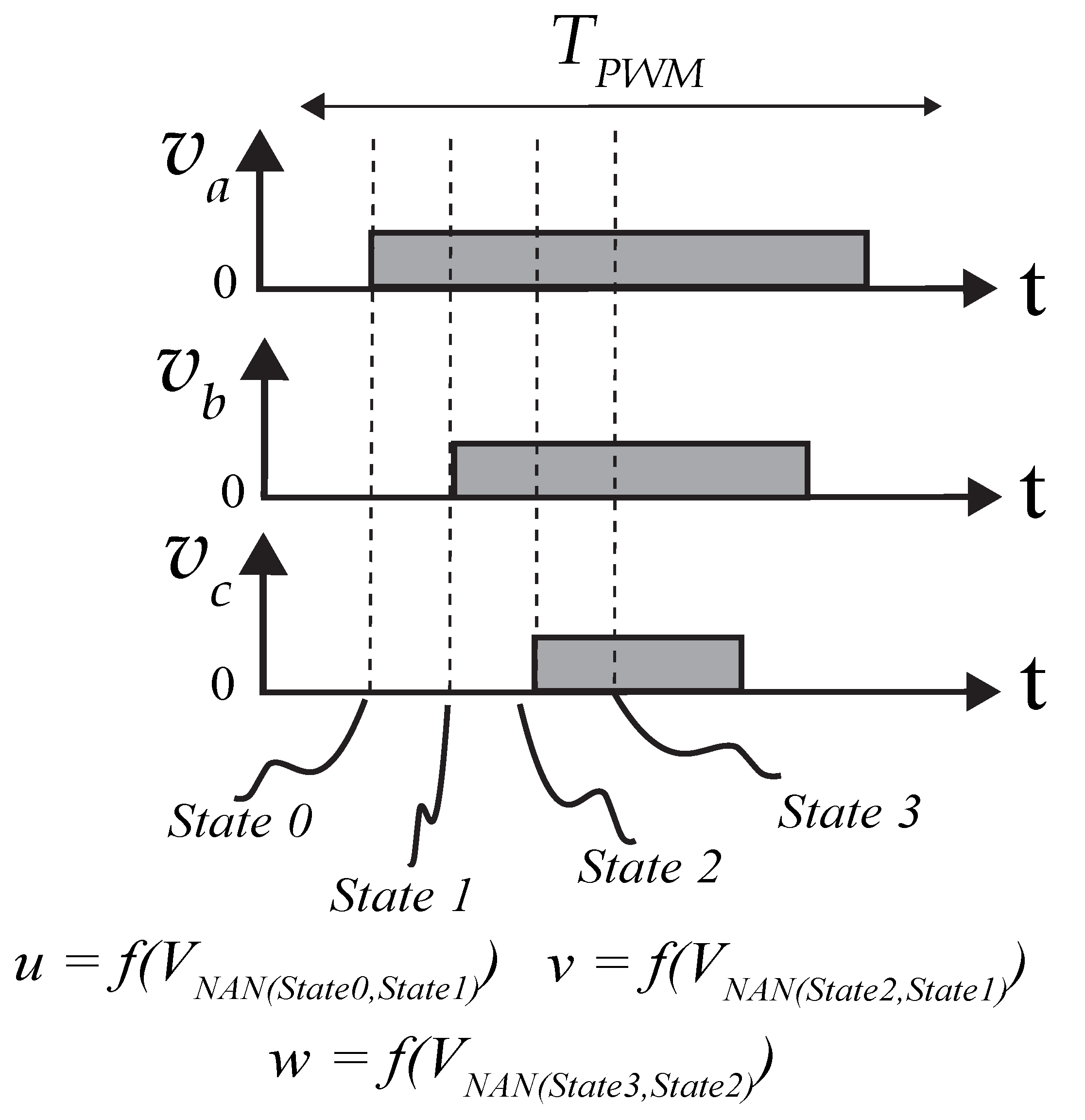

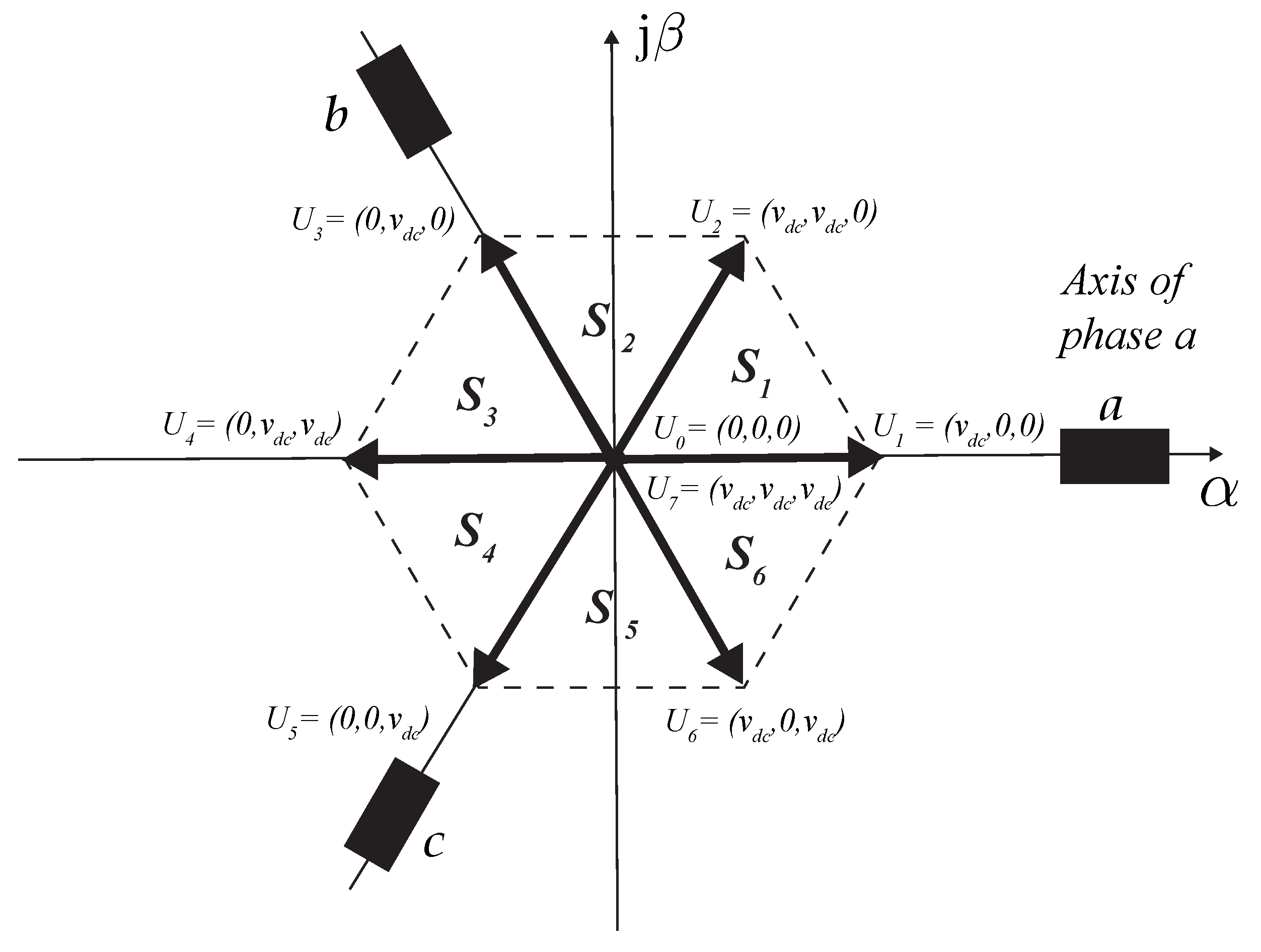
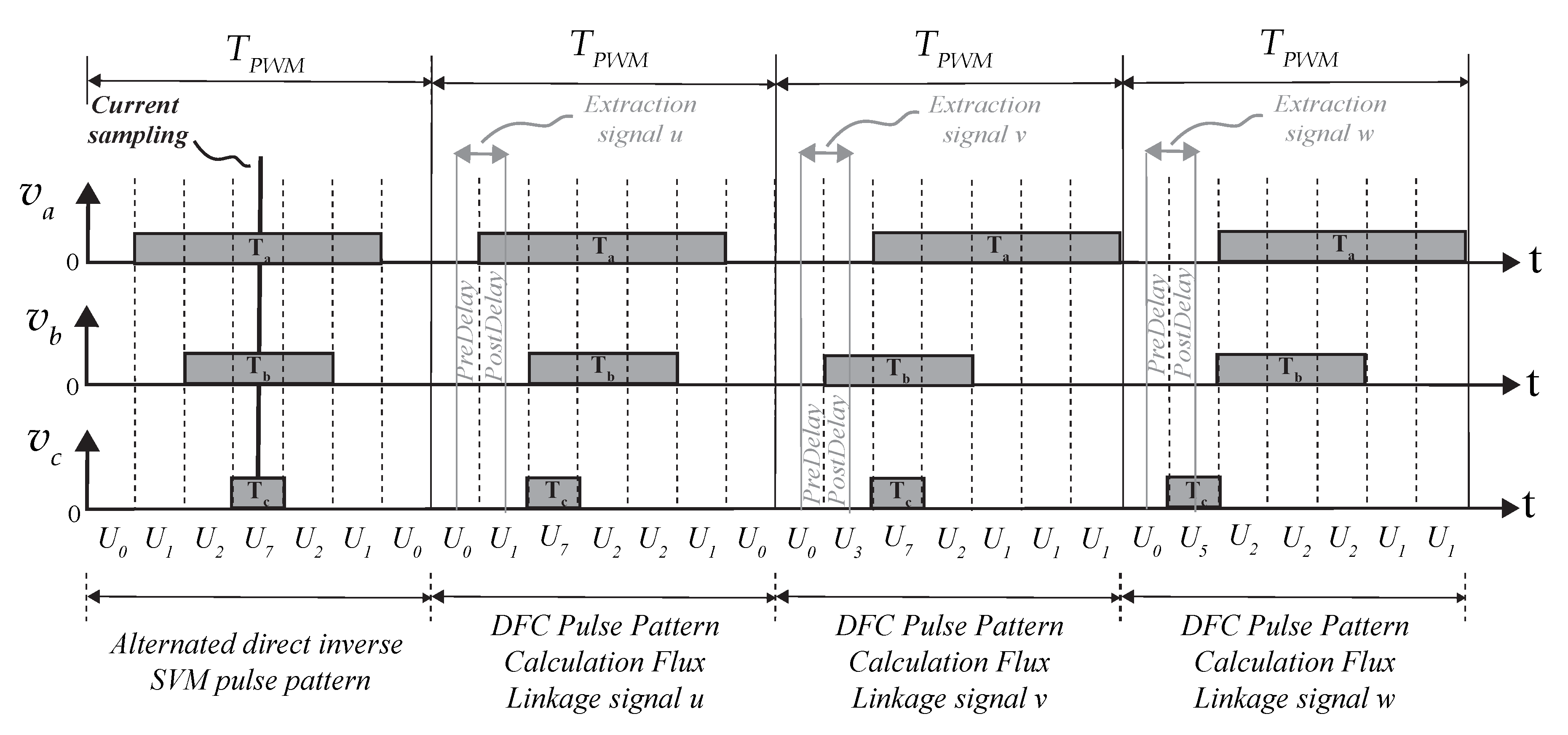
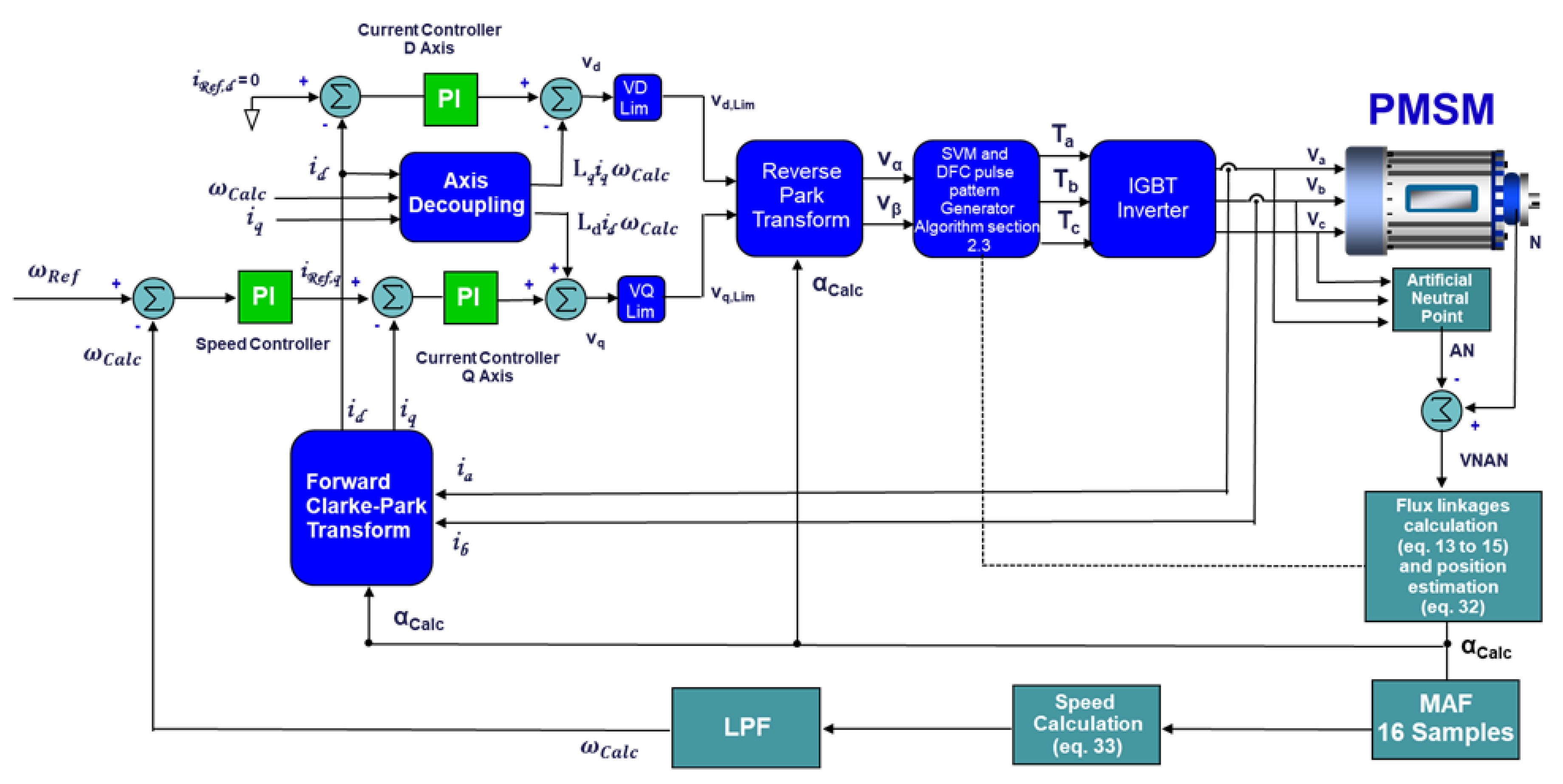











| Standard | Voltage |
|---|---|
| Vector | |
| . | |
| . | |
| . | |
| . | |
| . | |
| . | |
| and | . |
| Parameter | Value | Unit | Description |
|---|---|---|---|
| Type | W3375-4A | Three-phase SM | |
| with salient pole rotor | |||
| (4 poles) | |||
| 50 | Hz | Electrical frequency | |
| 1500 | rpm | Mechanical speed | |
| 0.8–1–0.8 | rpm | Power factor | |
| S | 1 | kVA | Rated apparent power |
| P | 0.8 | kW | Real power at = 0.8 |
| 400 | V | Nominal phase voltage | |
| 1.52 | A | Nominal phase current | |
| at leading = 0.8 | |||
| 220 | V | Nominal field winding voltage | |
| 0.6 | A | Nominal field winding current |
| Parameter | Value | Description |
|---|---|---|
| Inverter parameters | ||
| 565 V | DC-Link voltage | |
| 10 kHz | Inverter switching frequency | |
| 100 s | PWM Switching period | |
| DFC parameters | ||
| 2 s | DFC Pre-delay time | |
| 2 s | DFC Post-delay time | |
| Mechanical parameters | ||
| J | 0.07 kg · m2 | Total moment of inertia |
| WRSESM Electrical Parameters | ||
| 0.3957 H | d-Axis Inductance | |
| 0.1511 H | q-Axis Inductance | |
| 14.62 Ohms | Stator’s winding resistor | |
| 2.9 H | WRSESM Rotor self-inductance | |
| 0.4 A | Rotor self-inductance | |
| 1.16 Vs | Rotor flux linkage | |
| Current controller d-Axis | ||
| 98.93 V/A | Proportional gain | |
| 3655 (Vs)/(A) | Integral gain | |
| 250 Hz | Closed loop bandwidth | |
| Current controller q-Axis | ||
| 72.38 V/A | Proportional gain | |
| 7000 (Vs)/(A) | Integral gain | |
| 500 Hz | Closed loop bandwidth | |
| Speed controller | ||
| LPF | 50 Hz | Low Pass Filter (LPF) cut-off frequency |
| 0.5 A/(rad/s) | Proportional gain | |
| 0.0050 A/rad | Integral gain | |
| 5 Hz | Closed loop bandwidth | |
| Solver | ||
| 1 s | Simulation Time-step | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Iturra, R.G.; Thiemann, P. Sensorless Field Oriented Control of Synchronous Machines for Low and High Speeds with Space Vector Modulation-Based Direct Flux Control Measurement Sequence. Electronics 2023, 12, 1382. https://doi.org/10.3390/electronics12061382
Iturra RG, Thiemann P. Sensorless Field Oriented Control of Synchronous Machines for Low and High Speeds with Space Vector Modulation-Based Direct Flux Control Measurement Sequence. Electronics. 2023; 12(6):1382. https://doi.org/10.3390/electronics12061382
Chicago/Turabian StyleIturra, Rodrigo Guzman, and Peter Thiemann. 2023. "Sensorless Field Oriented Control of Synchronous Machines for Low and High Speeds with Space Vector Modulation-Based Direct Flux Control Measurement Sequence" Electronics 12, no. 6: 1382. https://doi.org/10.3390/electronics12061382





