1. Introduction
Radio communication is widely used in various fields as an important part of information technology. Initially, in radio communication, the signal is modulated by a transmitter into a constant-frequency radio frequency (RF) signal, which is then sent to a receiver. However, constant-frequency RF signals are very susceptible to interference from the complex surrounding electromagnetic environment and to eavesdropping by third parties [
1,
2]. In this case, frequency-hopping signals have gradually replaced constant-frequency RF signals due to their strong anti-interference capability and good confidentiality and are widely used for military communications and remote control [
3,
4,
5,
6,
7]. Since the introduction of FH technology in the military, research on jamming, counter jamming, counter sabotage and sabotage for FH technology has never stopped [
8]. The emergence of frequency-hopping signals with frequency-switching time is a good proof of this. In order to intercept and jam the frequency-hopping signals of non-cooperative targets, precise knowledge of the parameters of their transmitted FH signals is required [
9]. Therefore, parameter estimation of frequency-hopping (FH) signals is an important task for information interception and autonomous electronic countermeasures [
10,
11]. The battlefield environment is rapidly changing, and the fast estimation of FH signals in the case of unknown frequency, an unknown number of signals or signals with frequency-switching time is of great importance. The parameter estimation of FH signals includes hopping time, hopping speed and frequency [
12]. Researchers have conducted numerous studies on the estimation methods of FH signal parameters.
Time–frequency analysis algorithms, such as short-time Fourier transform (STFT) [
13,
14,
15] and the Wigner–Ville distribution (WVD) [
8,
16], are classical algorithms for estimating parameters of FH signals. Although the STFT algorithm is less computationally intensive, it cannot meet the high accuracy requirements of both the frequency and time domains at the same time [
17,
18]. When used to estimate the parameters of a multiple FH signal, the WVD algorithm is disrupted by cross terms [
19,
20]. In Ref. [
21], an algorithm for parameter estimation of FH signals based on adaptive smoothing of the Wigner–Ville distribution and instantaneous frequency (SWWVD-IF) was proposed. Although this algorithm can overcome the interference problem of cross terms, it has a high computational complexity. In Ref. [
22], a parameter estimation algorithm for multiple frequency-hopping signals based on short-time Fourier transform and smoothed pseudo Wigner–Ville distribution (STFT&SPWVD) was proposed. The STFT&SPWVD algorithm combines the advantages of STFT, which avoids cross-term interference, and SPWVD, which provides higher resolution in the frequency–time domain. However, the computational complexity of this algorithm is slightly higher than that of the SPWVD algorithm. With the development of frequency-hopping technology, the frequency-hopping signal hops over a larger frequency band. The time–frequency analysis algorithm based on Nyquist’s sampling theorem must obtain the entire signal at a high sampling rate [
23]. This poses a serious challenge for signal reception equipment.
Provided that the original signal is sparse or can be sparsely represented, compressive sensing theory allows the signal to be acquired at a frequency lower than the sub-Nyquist sampling frequency [
24,
25]. This has led to the increasing application of compressive sensing theory to FH signal processing. Popular algorithms based on this theory include sparse linear regression (SLR) algorithms [
26,
27,
28] and sparse Bayesian learning (SBL) algorithms [
20,
29,
30]. These algorithms are very computationally intensive. In Ref. [
31], a new algorithm combining orthogonal matching pursuit (OMP) and sparse linear regression named OSLR was introduced to reduce the computational effort of the algorithm. The OSLR algorithm has a lower time complexity than the SLR algorithm. However, it requires the number of signals of multiple FH signals as a priori information to achieve correct frequency estimation [
32], and when the signals have frequency-switching time, the number of signals changes during the frequency-switching time, so it cannot estimate the parameters of the signals with frequency-switching time. In [
32], a new parameter estimation algorithm (CSOMP-ASW) was introduced that combines compressed spectrum sensing, OMP, a frequency clustering algorithm and an adaptive sliding window algorithm. The CSOMP-ASW algorithm uses the compressed spectrum sensing algorithm to evaluate the sparsity of the signal, then uses the OMP algorithm and the clustering algorithm to estimate the frequency of the signal so that it is not fast enough to estimate the frequency.
In Ref. [
33], a frequency-hopping synchronization algorithm based on maximum likelihood (ML) theory was proposed. This algorithm is computationally intensive and is only applicable to parameter estimation of a single FH signal without frequency-switching time. To reduce the computational complexity required to estimate parameters of multiple frequency-hopping signals under conditions in which the number of signals is known, in our previous work, we proposed a frequency-hopping signal parameter estimation algorithm called OML [
34]. This algorithm estimates the frequency using the OMP algorithm and the hopping time using an algorithm traversing all time points based on the maximum likelihood theory, which partially improves the speed of hopping signal parameter estimation.
In summary, all the above research methods have different degrees of improvement in reducing the computational complexity and increasing the accuracy of parameter estimation, but there are still some shortcomings. In order to mitigate the limitations of the above methods and realize the fast estimation of frequency and hopping time of multiple FH signals under conditions in which the frequency is unknown, the number of signals is unknown or the signals have frequency-switching time, a new frequency-hopping algorithm (CSML) is proposed in this paper. First, based on the sparsity of multiple FH signals in the frequency domain, a combination of compressed spectrum sensing and kurtosis thresholding is used to estimate the frequencies. The ML-based hopping-time fast estimation algorithm is then used to estimate the hopping time. The main contributions of this paper are as follows:
An enhanced two-hop model (ETHM) is developed to characterize multiple FH signals; then, a likelihood function is derived from the model for the estimation of the parameters of the multiple FH signals. Based on this likelihood function, a hopping-time fast estimation algorithm is proposed that reduces the time required for estimation of the hopping time of multiple FH signals.
The algorithm based on compressed spectrum sensing has low accuracy in performing frequency estimation. The reasons for this phenomenon are explored, and a zero-setting method and averaging methods are proposed to improve the effectiveness of this algorithm. Satisfactory performance is still obtained for the estimation of multiple FH signal frequencies without the involvement of other algorithms such as OMP. Fast estimation of the frequency of multiple FH signals without a priori information is achieved.
The remainder of this paper is organized as follows. In
Section 2, an enhanced two-hop model is introduced.
Section 3 provides details of the proposed CSML algorithm.
Section 4 presents the simulations and results of the CSML algorithm. Finally, in
Section 5, we present our conclusions.
Notation:
—The transposition of ;
—The conjugate transposition of ;
—The inverse of ;
—The -dimensional zero vector;
—The -dimensional unit vector;
—Euclidean norm of ;
—The inner product of ;
—The estimated value of .
2. The Enhanced Two-Hop Model
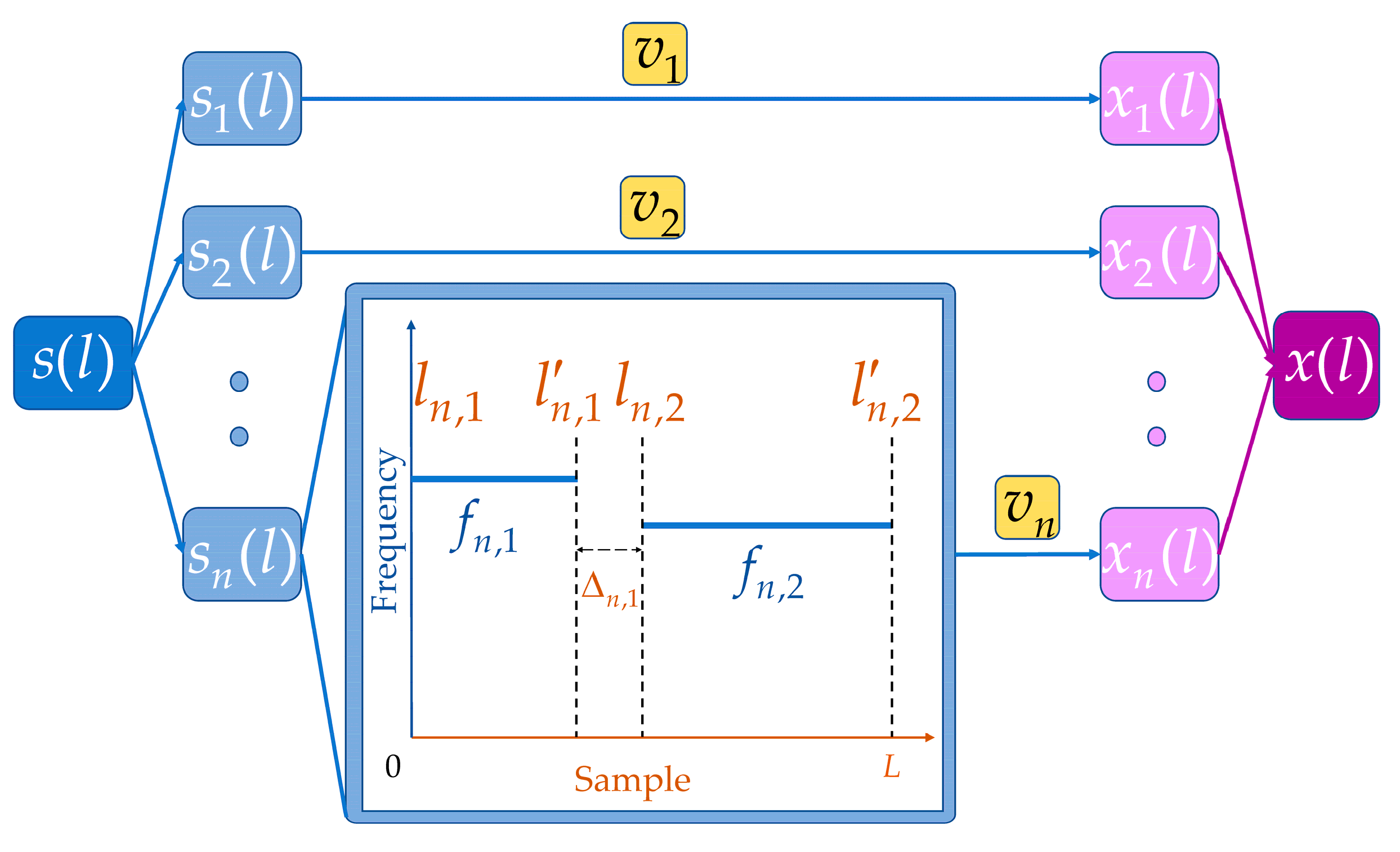
In order to realize the parameter estimation of multiple FH signals with frequency-switching time, a multiple FH signal model is developed in this paper. To distinguish it from the two-hop model proposed in [
33], it is named the enhanced two-hop model (ETHM). A schematic diagram of the ETHM is shown in
Figure 1. In
Figure 1,
is the total number of samples, and the rest of the notations are annotated under (1). The ETHM is composed of two FH signal models and two received signal models.
The
nth FH signal can be denoted as:
where
is the number of hops,
is the frequency of the
hop,
is the starting time of the
hop,
is the frequency-switching time between the
hop and the
hop,
is the stopping time of the
hop (denoted as
) and
is the sampling frequency.
The received signal corresponding to the
FH signal can be expressed as:
where
is the amplitude corresponding to the
hop of the
FH signal, and
is the additive Gaussian white noise.
The multiple FH signals (
), which are a mixture of
FH signals, can be indicated as:
The received signal corresponding to
can be represented as:
This paper only considers the case in which the spectrum of each hopping signal does not overlap.
3. CSML Algorithm
3.1. Likelihood Function
Under the condition in which the frequencies are known, the computational complexity of the ML-based algorithm is reduced by not traversing all frequencies and time points simultaneously. Furthermore, since the shape of the curve of the likelihood function is fixed, the correct hopping time can be obtained without traversing all time points. Therefore, the ML-based algorithm has the potential to estimate the hopping time quickly under the condition in which the frequency is known. The frequencies of multiple FH signals can also be provided by specialized frequency estimation algorithms (the frequency estimation algorithm used in this paper is based on the compressed spectrum sensing and kurtosis thresholding algorithm proposed in
Section 3.2).
According to Equations (1) and (2), the received signal corresponding to the
FH signal can be re-expressed as:
where:
According to Equations (5) and (6),
can be divided into two parts as follows:
where:
According to Equations (7) and (8), the following likelihood function can be derived:
Thus, the parameters
and
can be obtained by minimizing (10) and (11).
After derivation, the parameters
and
can be obtained by maximizing (A8), as shown in (12). The derivation procedure is shown in
Appendix A.
3.2. The Hopping-Time Fast Estimation Algorithm
As illustrated in (12), when estimating the hopping time of multiple FH signals, all the time points are traversed. This makes the CPU time consumed in the process of estimating the hopping time too long. To solve this problem, a fast estimation algorithm for hopping time is proposed in this subsection.
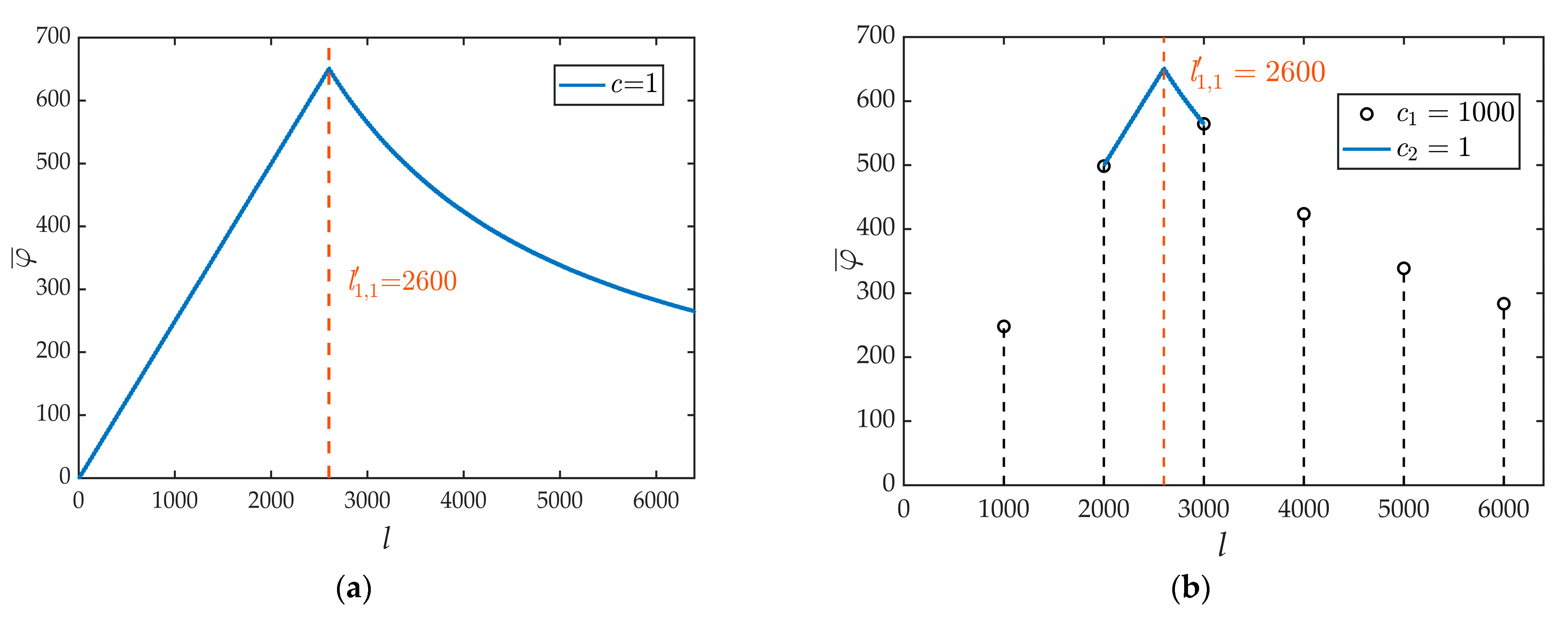
Assume that there is an FH signal with a length of 6400 (
) and a hopping time of 2600 (
). The variation of
with
for this FH signal is shown in
Figure 2a. The maximum
occurs when
is equal to
. When
is less than
, the
increases monotonically. When
is greater than
,
decreases monotonically. Due to the good monotonicity of
before and after the hopping time
, it is possible to select
uniformly at intervals of
in
; then, the
corresponding to
is calculated. This narrows the existence of
to
points.
Figure 2b shows the variation of
with
when
and
. The
of these six sampling points is calculated (marked by black circles in
Figure 2b,
), and the two largest
values correspond to
and
, respectively. This shows that the hopping time
is in the range of
. The hopping time
can be obtained by traversing
in the range of
(marked by the blue line in
Figure 2b,
). With this algorithm, only 1005 calculations of
are required to obtain an estimate of the hopping time
, which is only one-sixth of the previous workload. The optimal value of parameter
will be discussed in
Section 4.
The specific steps of the hopping-time fast estimation algorithm are described below:
Step 1: Select sampling points at intervals of and calculate using (A8);
Step 2: Compare the calculated in step 1, and select the sampling points with the two largest values;
Step 3: Calculate the of the sampling points between the two points selected in step 2.
Step 4: Compare the calculated in step 3, and select the sampling point with the largest value as the hopping time.
3.3. The Frequency Estimation Algorithm
As in [
32], the sparsity of the FH signal in the frequency domain is used to obtain the FH signal spectrum in the compressed domain. The relationship between the compressed sampled signal (
) and the received signal (
) can be expressed as:
where
is the compressed sampled signal of the received signal (
),
is the Gaussian random matrix,
is the Fourier orthogonal matrix,
is the compressed sensing matrix, and
is the factor matrix of the received signal (
) corresponding to
. The compression ratio is
, and
is equal to
. The
column of
can be expressed by the following equation:
Its corresponding frequency can be expressed as:
According to (13), the inner product of
and
can be expressed in the form of (16).
is the magnitude of the projection of the received signal (
) on the Fourier orthogonal matrix; therefore, the spectrum of
can be obtained.
Figure 3a illustrates the spectrum of the received signal at a signal-to-noise ratio (SNR) of 30 dB;
Figure 3b shows the spectrum of the noise signal.
where
.
As shown in
Figure 3a, the frequencies corresponding to the three peaks are 12 MHz, 18 MHz and 54 MHz, which are the frequencies of the multiple FH signals and can be obtained by comparing the magnitude of
in the spectrum. Due to the presence of noise, the spectrum contains a large number of non-zero values. It is risky to discriminate whether the frequency is the frequency of multiple FH signals by setting a threshold on the value of
.
The kurtosis value (
), defined by (17) [
35], is sensitive to the presence of peaks in the data; the spectrum in
Figure 3a contains three peaks, and the kurtosis value (
) of this spectrum is equal to 19.7, while the spectrum in
Figure 3b does not contain peaks, and the kurtosis value (
) of this spectrum is 1.6.
where
.
Taking
Figure 3 as an example, the frequency corresponding to the largest
value is taken as the frequency of the multiple FH signals and recorded, and the largest
value is set to zero (zero-setting method) or to the average of
on both sides of it (averaging method). After three operations, the spectrum of the received signal changes from that shown in
Figure 3a to that shown in
Figure 3b, and the kurtosis value (
)changes from 19.1 to 1.6. Therefore, a suitable kurtosis value can be selected as the stopping condition of the frequency estimation algorithm, known as the kurtosis threshold (
).
During the operation, it was found that the
(marked by the yellow triangle in
Figure 4a,b) on both sides of the maximum
was also large, as shown in
Figure 4a,b. This is the reason for the low accuracy of the frequency estimation algorithm based on compressed spectrum sensing. Therefore, the
on both sides of the maximum
should be processed using the zero-setting method or the averaging method.
Assuming that the
at 12 MHz is
(the 601st value in the vector
), the zero-setting method can be expressed as
, where
is the neighborhood radius.
Figure 5a shows the partial enlargement of the spectrogram at 12 MHz after using the zero-setting method when the neighborhood radius (
) is equal to 6. The averaging method can be expressed as
.
Figure 5b illustrates the partial enlargement of the spectrogram at 12 MHz after using the averaging method when the neighborhood radius (
) is equal to 6. The optimal values of the kurtosis threshold (
) and the neighborhood radius (
) will be further investigated in
Section 4.
3.4. Steps of the CSML Algorithm
Estimating the frequency and hopping time of multiple FH signals is the main task of the CSML algorithm proposed in this paper. The CSML algorithm estimates the frequency first, then the hopping time. A flow chart of the CSML algorithm is shown in
Figure 6.
The specific steps are described as follows:
Step 1: Split the received signal (
) into segments of size
, where
is the total number of signal segments:
Step 2: Obtain the compressed spectrum of the each segment using Equations (13), (15) and (16);
Step 3: Record the frequency corresponding to the maximum . Set the maximum to zero using the zero-setting method or the averaging method. Repeat this step until the kurtosis value () of this compressed spectrum is smaller than the kurtosis threshold ;
Step 4: Repeat step 3 for the compressed spectrum of the remaining signal segments until the frequencies of all signal segments are obtained. Compare the frequencies between adjacent segments to find the frequency of the multiple FH signals and the segment in which the frequency hopping occurred;
Step 5: Estimate the hopping time using the hopping-time fast estimation algorithm. Repeat this step until all hopping times are obtained.
The purposes of splitting the received signal are as follows:
Avoid processing large amounts of data at the same time and reduce the requirement for hardware devices;
By comparing the frequencies of each segment, the segments in which the frequency hopping occurs, as well as FH frequencies, are identified, in addition to preparing for the estimation of hopping time.
It is worth noting that it is not the entire received signal that is fed into the hopping-time fast estimation algorithm but the selected signal segments where frequency hopping occurs after frequency estimation. The length of these segments is . Therefore, the computational complexity of the fast estimation algorithm of the frequency-hopping signal parameters does not increase with the length of the received signal. To avoid errors, the size of the segments () should be smaller than the minimum FH signal duration.
3.5. Complexity Analysis
Continuing with the relevant symbols from the previous section, the number of FH signals is , the sampling length of the signal is , the received signal is divided into segments of length , is the total number of signal segments; the length of the compressed sampled signal is and the compression ratio of compressed sampling is . A slight difference is that is the total number of signal segments in which frequency hopping occurs.
The computational complexity of the compressed spectrum sensing part can be expressed as:
The computational complexity of the kurtosis value calculation once is
can be expressed as:
The computational complexity of the hopping-time fast estimation algorithm can be expressed as:
The computational complexity of the CSML algorithm proposed in this paper is:
The computational complexity of the ASW algorithm for one iteration can be expressed as [
32]:
The computational complexity of the ASW algorithm in the process of estimating the hopping time is as follows:
The computational complexity of the CSOMP-ASW algorithm [
32] is:
Usually, is much smaller than . Therefore, the computational complexity of the CSML algorithm proposed in this paper is smaller than that of CSOMP-ASW.
4. Simulations and Results
In this section, 100 Monte Carlo tests are performed on the proposed CSML algorithm to investigate the optimal values of the parameters
,
and
. Our simulations were performed on a desktop computer with an Intel(R) Core(TM) i5-9400F CPU @2.90 GHz processor. The operating system was Microsoft Windows 10, with 16 GB of RAM. The comparison with the four algorithms mentioned in
Section 1 is also performed. The sampling length
of the signal used in the simulations is 51200, and the sampling frequency (
) of the signal is 128 MHz.
The parameters of the multiple FH signals without frequency-switching time are shown in
Table 1, and a schematic diagram of the multiple FH signals is shown in
Figure 7. The multiple FH signals are used for the simulation tests in
Section 4.1,
Section 4.2,
Section 4.3 and
Section 4.4. FH signal No. 1 (
) starts at 12 MHz, and the frequency becomes 24 MHz when
; the starting frequency of FH signal No. 2 (
) is 54 MHz, and the frequency changes to 60 MHz when
; signal No. 3 (
) is a fixed-frequency signal with a frequency of 18 MHz.
Other necessary parameters are shown in
Table 2. The number of FH signals (
) is two; the sampling length of the signal (
) is 51,200; the sampling frequency (
) is 128 MHz; the received signal is divided into segments of length
, and the compression ratio of compressed sampling (
) is 8.
The SNR is given by:
where
is the multiple FH signals, and
is the variance of Gaussian white noise.
The common performance indicators of FH signal parameter estimation algorithms include mean square error (MSE), CPU time, accuracy, etc. In this paper, the frequency estimation accuracy and CPU time are used to evaluate the frequency estimation performance of the proposed algorithm; the mean square error (MSE) of the hopping time and CPU time are used to evaluate the hopping-time estimation performance of the proposed algorithm.
The frequency estimation accuracy is defined as:
where
is the total number of trials, and
is the number of frequencies that were correctly estimated in the
trial.
The mean square error (MSE) of the hopping-time estimation is defined as:
where
and
are the estimated values of
and
in the
trial, respectively.
4.1. The Effect of Parameters and on Frequency Estimation
The parameter
was set to 5, and the value of parameter
was selected within the range of
with an interval of 0.1. A total of 100 Monte Carlo tests were conducted under different SNR conditions. The results of the simulations are shown in
Figure 8.
Figure 8 illustrates that when
is less than 1.9, the frequency estimation accuracy is proportional to
. When
is between 1.9 and 2.1 and the SNR is greater than 0 dB, the frequency estimation accuracy can reach 100%; when
is greater than 2.1 and the SNR is 0 dB, the frequency estimation accuracy starts to decrease. The results show that either
being set either too high or too low reduced the frequency estimation accuracy. Therefore, the kurtosis threshold (
) was set to 2.0.
The parameter
was set to 2.0, and the SNR was set to 0 dB. The parameter
was selected sequentially in the range of
at intervals of 1. The
was processed by the zero-setting method and the averaging method, and 100 Monte Carlo tests were conducted. The results are shown in
Figure 9.
In
Figure 9, the frequency estimation accuracy with
is close to 0, which is consistent with the phenomenon mentioned in
Section 3.3. When
, the frequency estimation accuracy is 100% for both the averaging method and the zero-setting method. Therefore, in the subsequent simulations, the parameter
was set to 3, and the zero-setting method was chosen to process
.
4.2. The Effect of Parameter on Hopping-Time Estimation
The parameters of the multiple FH signals are the same as in
Section 4.1. The SNR is set to 30 dB, and the parameter
is selected at intervals in the range of
. A total of 100 Monte Carlo tests are conducted. The results are shown in
Figure 10.
In
Figure 10, the results for
correspond to the performance when the hopping-time fast estimation algorithm is not used, with an MSE equal to
and a CPU time equal to 0.475 s. When
is greater than 400, the MSE and CPU time of the hopping-time fast estimation algorithm increase with
, and the performance of the fast estimation algorithm gradually degrades. When
is too large, too few sampling points are selected in step 1 of the hopping-time fast estimation algorithm, the hopping time is not between the two sampling points selected in step 2 and the wrong hopping time is obtained. This is the main reason for the increase in MSE when
is too large. When
increases, the computation of step 3 in the hopping-time fast estimation algorithm increases, which leads to an increase in CPU time. When the parameter
is less than 400, the MSE is less than
, which is the same performance as when the hopping-time fast estimation algorithm is not used. As shown in
Figure 10b, the use of the hopping-time fast estimation algorithm leads to a significant decrease in the CPU time consumed during the hopping-time estimation, and the CPU time is the shortest at 0.293 s when parameter
equals 160. Therefore, in the subsequent simulations, parameter
is set to 160.
The sampling frequency selected in this paper is 128 MHz, and the signal fragment length is 3200, which is small enough for most signals to not miss the hopping time. The parameter obtained at this segment length has a wide applicability.
4.3. Frequency Estimation
A total of 100 Monte Carlo tests were conducted separately under different SNR conditions to compare the ability of the CSML algorithm with that of four other algorithms to estimate frequencies. The results are shown in
Figure 11 and
Figure 12. The minimum SNR for each algorithm to achieve 100% frequency estimation accuracy and the average CPU time consumed by each algorithm are shown in
Table 3.
In
Figure 11, the horizontal axis is the SNR, and the estimation of multiple FH signal parameters is severely affected by noise at 0 dB. The SWWVD-IF algorithm is unable to estimate the frequency of multiple FH signals at an SNR of 0 dB, and the frequency estimation accuracy of this algorithm is only 34% with an SNR of 10 dB. The frequency estimation accuracy of the CSOMP-ASW algorithm is 4% at an SNR of 0 dB, and the frequency estimation accuracy of this algorithm reaches 85% at an SNR of 10 dB. The STFT&SPWVD algorithm has a frequency estimation accuracy of 27% at an SNR of 0 dB and 91% at an SNR of 10 dB. The OSLR algorithm performs best, but it requires a priori information about the signal. The frequency estimation accuracy of the CSML algorithm proposed in this paper is 100% at an SNR of 0 dB. The CSML algorithm outperforms the CSOMP-ASW, SWWVD-IF and STFT&SPWVD algorithms under low-SNR conditions.
As shown in
Figure 12, the CPU time consumed by the five algorithms in estimating the frequency varies less with the SNR. As shown in
Table 3, the average CPU times of the OSLR, CSOMP-ASW, SWWVD-IF and STFT&SPWVD algorithms are 0.7277 s, 0.6796 s, 5.176 s and 5.5869 s, respectively. The average CPU time of the CSML algorithm is 0.2984 s. The CSML algorithm consumes the shortest CPU time, which is less than one-half that of the OSLR and CSOMP-ASW algorithms. Therefore, the CSML algorithm proposed in this paper can perform fast and accurate estimation of the frequencies of multiple FH signals without a priori information.
4.4. Hopping-Time Estimation
A total of 100 Monte Carlo tests were conducted separately under different SNR conditions to compare the ability of the CSML algorithm with that of four other algorithms to estimate the hopping time. The results are shown in
Figure 13 and
Figure 14.
Figure 13 and
Table 4 show the MSEs of the hopping-time estimation of the five algorithms at different SNRs. As the SNR increases, the MSEs of the hopping time estimated by the five algorithms decreases, finally converging to different values. When the SNR is greater than 10 dB, the MSEs of the CSOMP-ASW and STFT&SPWVD algorithms are basically unchanged at about
and
, respectively. When the SNR is greater than 15 dB, the MSE of the OSLR algorithm is less than
, and that of the CSML algorithm is less than
. When the SNR is greater than 20 dB, the MSE of the SWWVD-IF algorithm is less than
. Under the same SNR condition, the MSE of the CSML algorithm is smaller than that of the other four algorithms.
Figure 14 and
Table 5 reflect the CPU time consumed by the five algorithms. The estimation of hopping time by all five algorithms is based on the estimation of frequency. Therefore, the CPU time in this section includes the CPU time consumed during frequency estimation. The CPU time consumed by the OSLR algorithm fluctuates widely, with a minimum of 106.1 s and a maximum of 122.4 s. The CPU time consumed by the remaining four algorithms fluctuates very little. The average CPU times of the OSLR, CSOMP-ASW, SWWVD-IF and STFT&SPWVD algorithms are 116.87 s, 0.7646 s, 9.5659 s and 7.1659 s, respectively. The average CPU time of the CSML algorithm is 0.3088 s. Compared with the other four algorithms, the CSML algorithm can estimate the hopping time of multiple FH signals faster and more accurately.
4.5. Parameter Estimation Performance of the CSML Algorithm for Multiple FH Signals with Frequency-Switching Time
The parameters of the multiple FH signals used for the simulations in this section are shown in
Table 6, and a schematic diagram of this signal is shown in
Figure 15. The starting frequency of FH signal No. 1 (
) is 12 MHz; it enters the frequency-switching time at
, with a frequency-switching time of 1004, and the frequency becomes 24 MHz at
. The starting frequency of FH signal No. 2 (
) is 54 MHz; it enters the frequency-switching time at
, with a frequency-switching time of 4000, and the frequency changes to 60 MHz at
. The third signal is a fixed-frequency signal with a frequency of 18 MHz. Other necessary parameters are shown in
Table 2.
The OSLR, SWWVD-IF and STFT&SPWVD algorithms cannot estimate the parameters of the FH signals with frequency-switching time. In this section, only the CSML algorithm and the CSOMP-ASW algorithm are simulated. The results were shown in
Figure 16 and
Figure 17.
Figure 16a shows the correct rates of the CSML algorithm and the CSOMP-ASW algorithm for frequency estimation of multiple FH signals with frequency-switching time. When the SNR is greater than 0 dB, the frequency estimation accuracy of the CSML algorithm is 100%; when the SNR is greater than 10 dB, the frequency estimation accuracy of the CSOMP-ASW algorithm is greater than 98%; when the SNR is greater than 20 dB, the frequency estimation accuracy of the CSOMP-ASW algorithm is equal to 100%. As shown in
Figure 16b, the average CPU time consumed by the CSOMP-ASW algorithm is 0.7159 s, while that of the CSML algorithm is 0.2956 s.
Figure 17a shows the MSE of the estimated hopping time for the CSML algorithm and the CSOMP-ASW algorithm when estimating hopping time for multiple FH signals with frequency-switching time. When the SNR is greater than 5 dB, the MSE of the CSML algorithm is less than
, and the MSE of the CSOMP-ASW algorithm is less than
. As shown in
Figure 17b, the average CPU time consumed by the CSOMP-ASW algorithm is 0.768 s, while that of the CSML algorithm is 0.3032 s. Therefore, the CSML algorithm can perform fast and accurate estimation of the parameters of multiple FH signals with frequency-switching time.