A Three-Step Tapered Bit Period SAR ADC Using Area-Efficient Clock Generation
Abstract
:1. Introduction
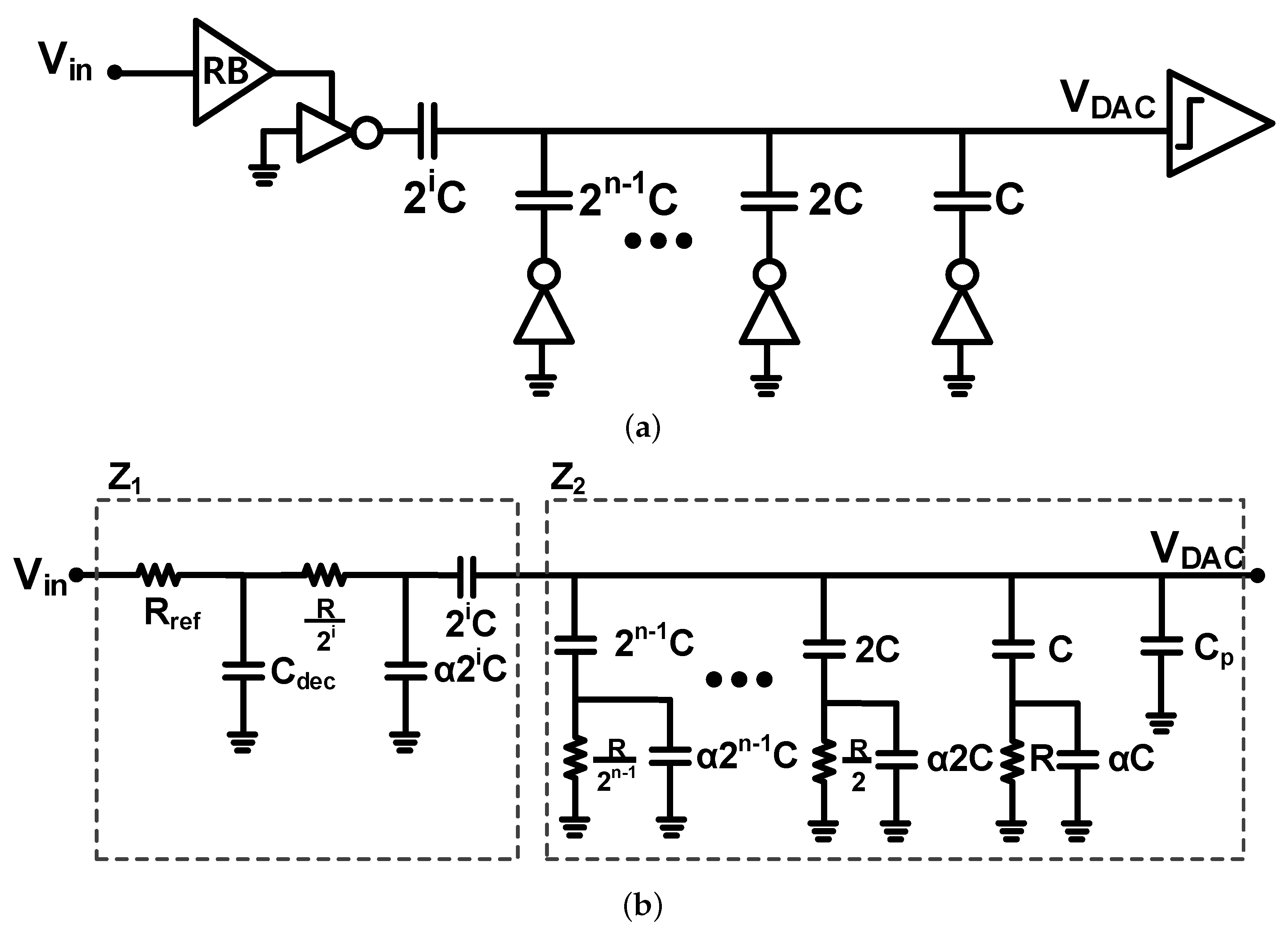
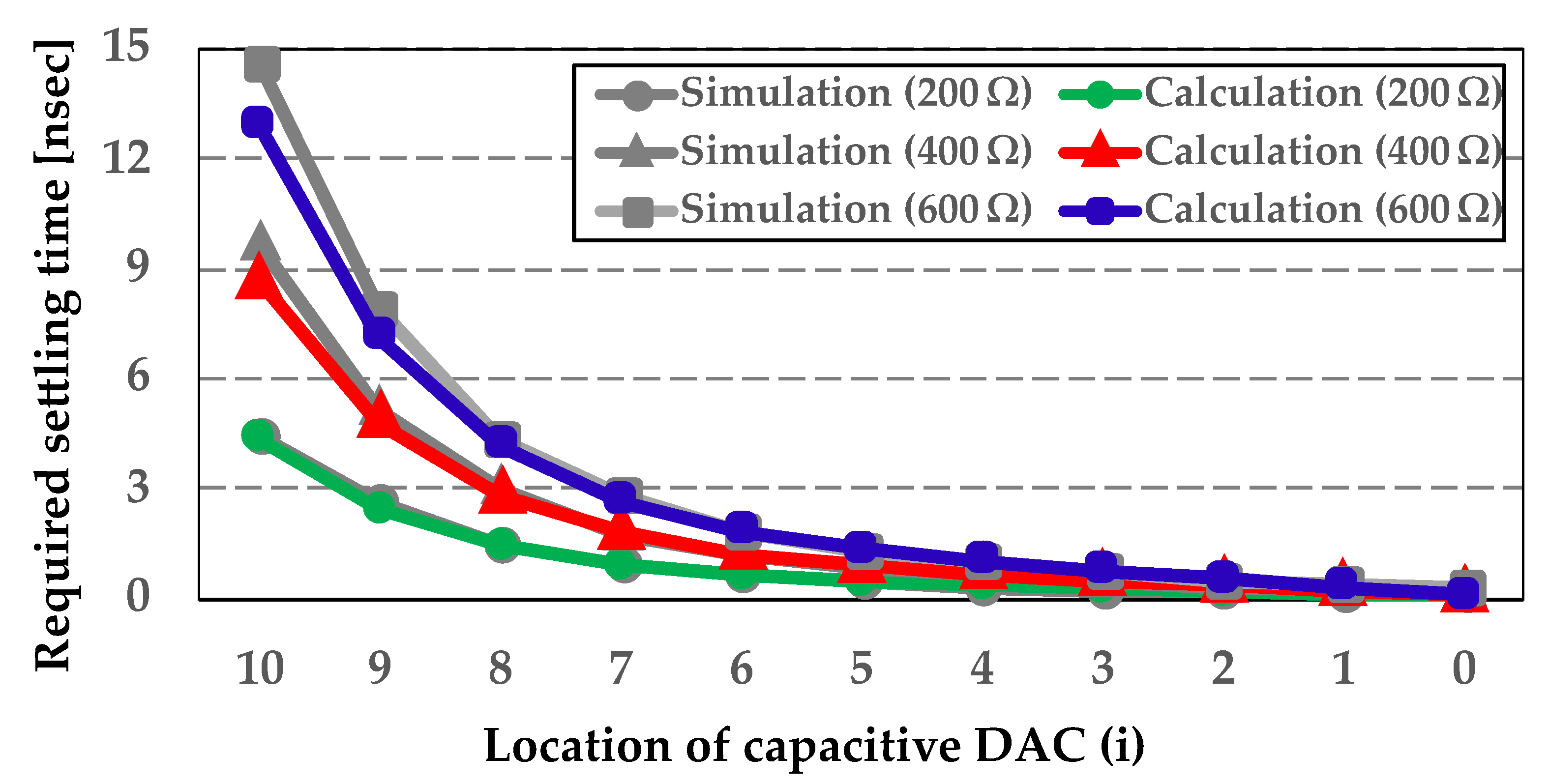
2. Analysis of Capacitive DAC Settling
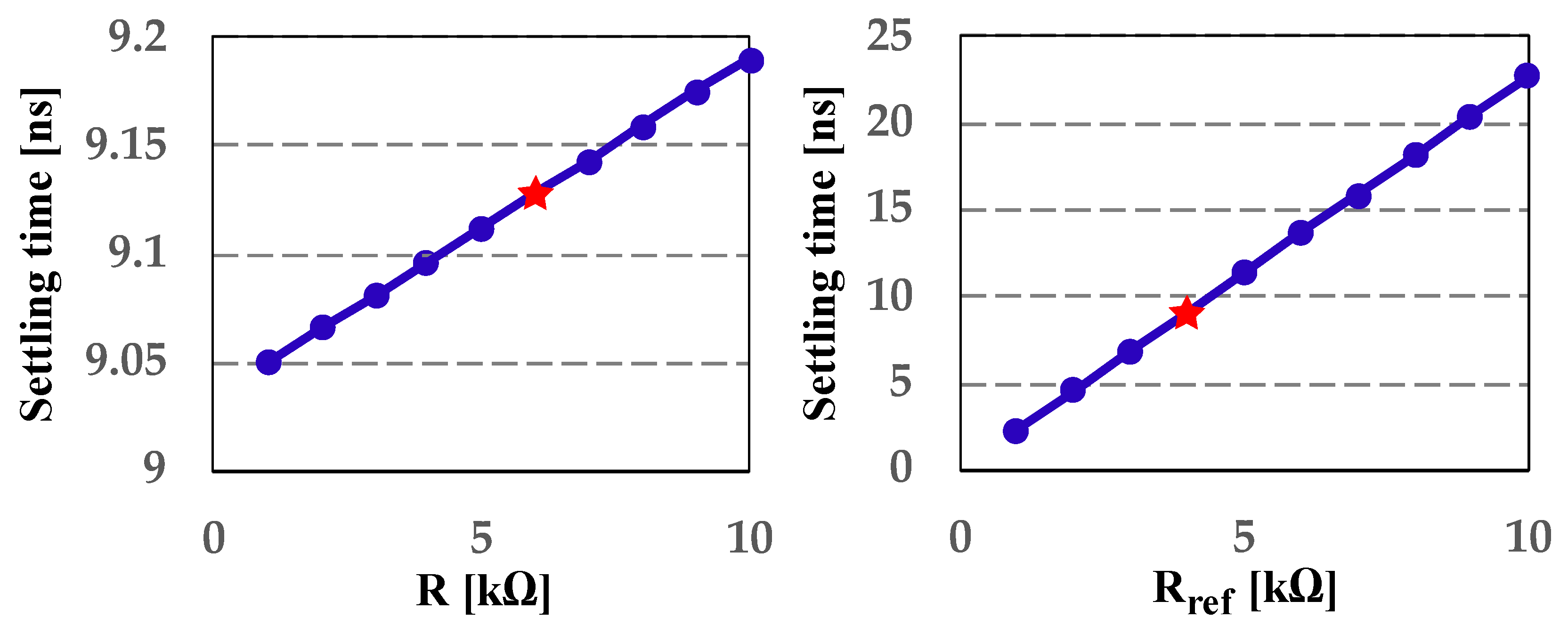
2.1. Equation of Required CDAC Settling Time with Reference Buffer
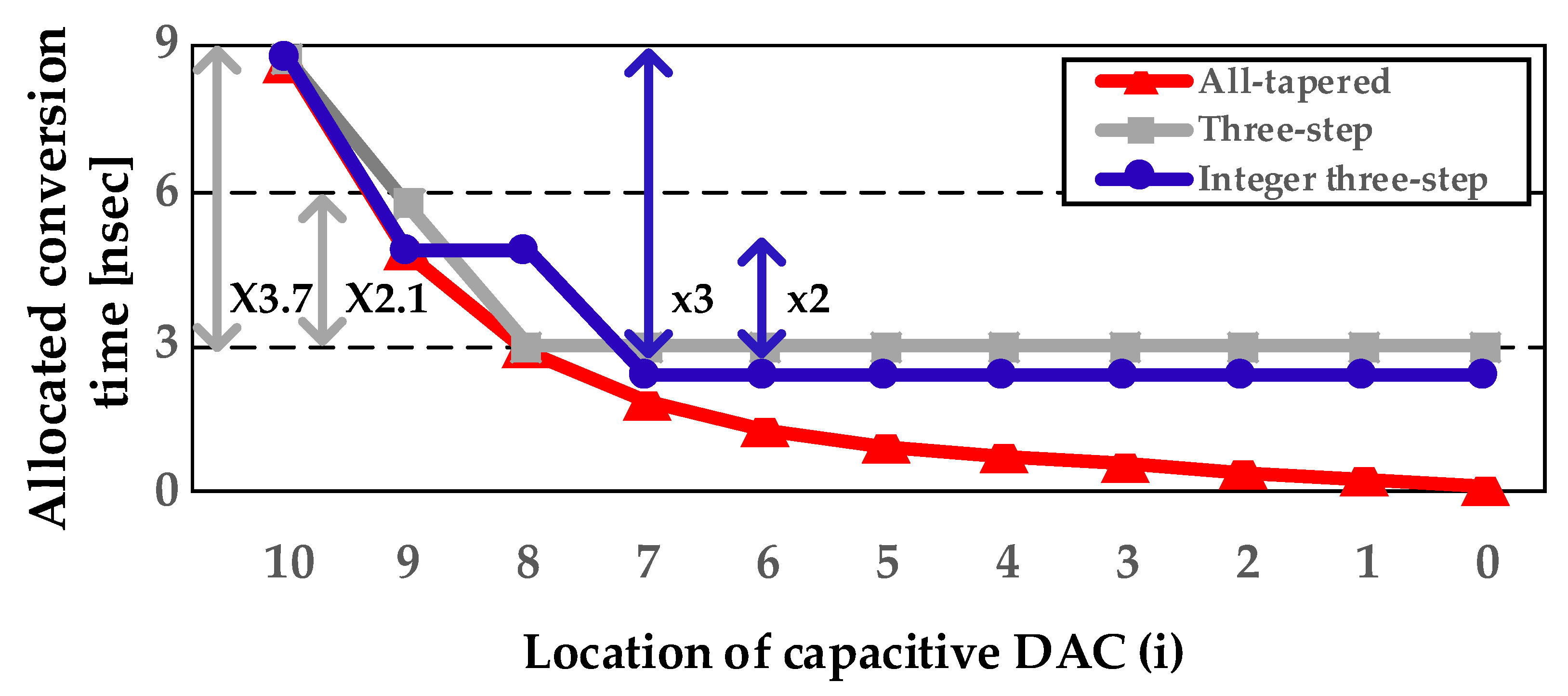
2.2. Analysis of Conversion Time According to Various Techniques
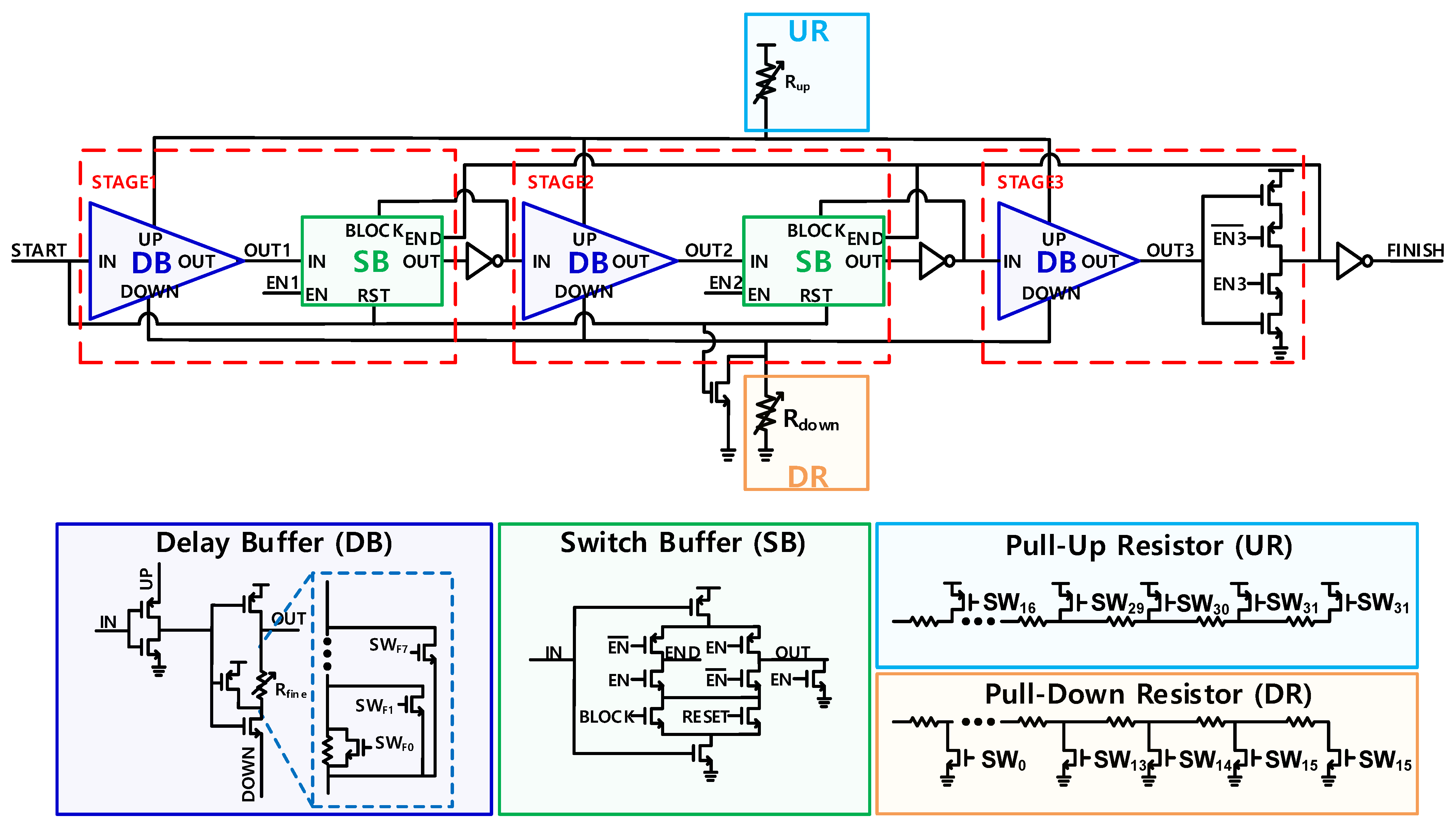
3. Proposed Three-Step Tapered Bit Period Clock Generator Circuit Implementation
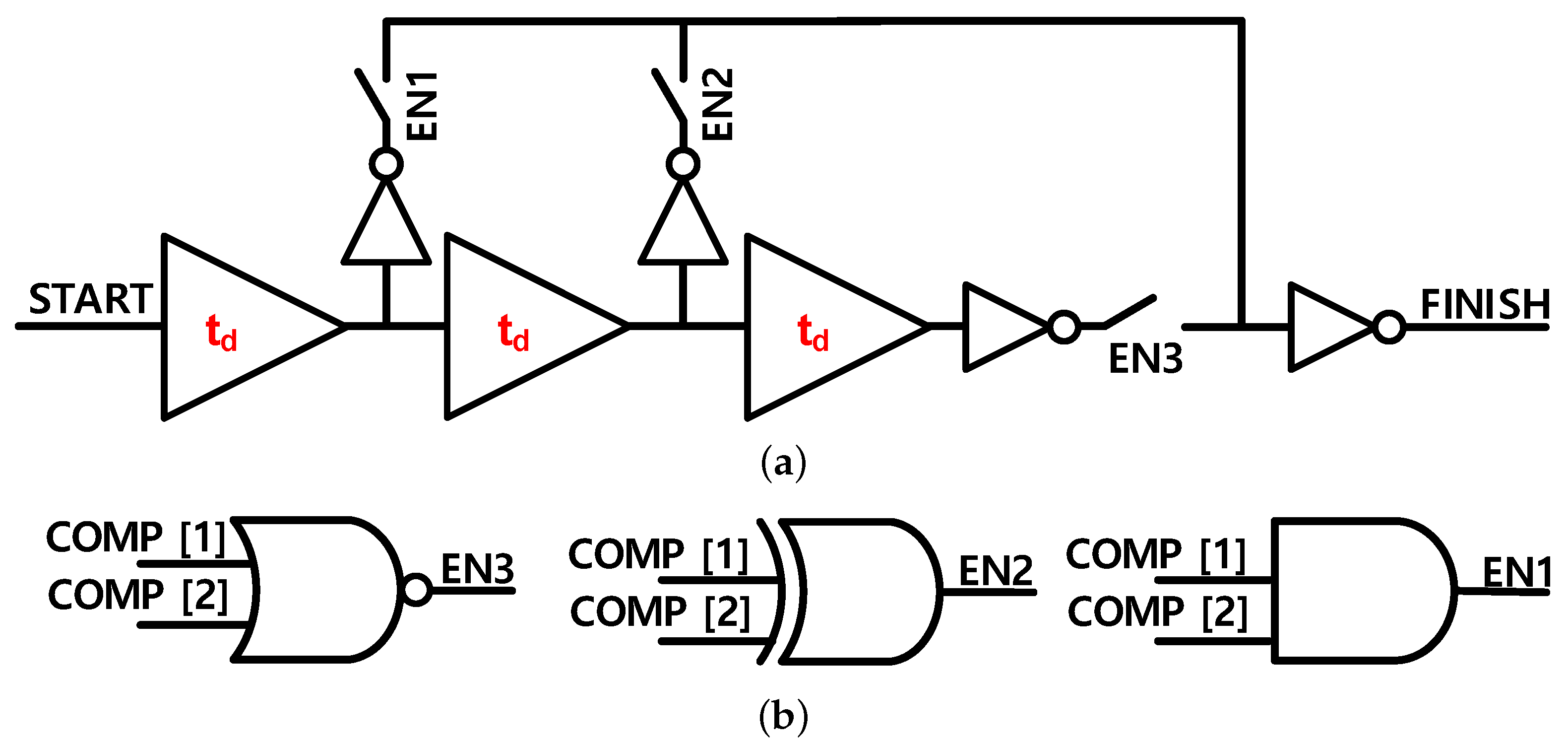
3.1. Asynchronous SAR Logic
3.2. Implementation of Delay Cell and Control Generator
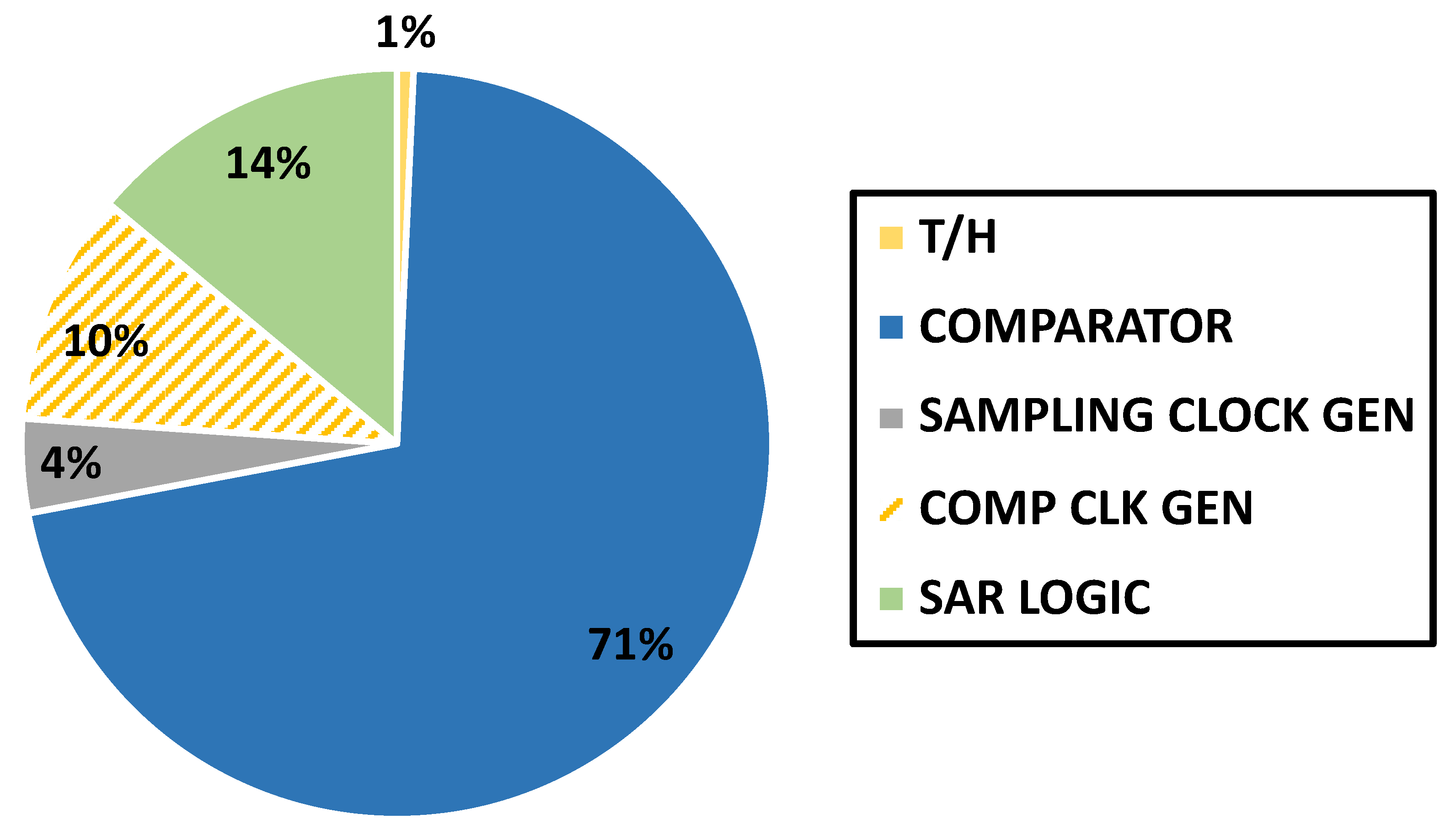
4. Post-Simulation Result
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Pietri, S.; Olmos, A.; Berens, M.; Boas, A.V.; Goes, M. A fully integrated touch screen controller based on 12b 825kS/s SAR ADC. In Proceedings of the Argentine School of Micro-Nanoelectronics, Technology and Applications, Bariloche, Argentina, 1–2 October 2009; pp. 66–70. [Google Scholar]
- Fan, H.; Heidari, H.; Maloberti, F.; Li, D.; Hu, D.; Cen, Y. High resolution and linearity enhanced SAR ADC for wearable sensing systems. In Proceedings of the IEEE International Symposium on Circuits and Systems (ISCAS), Baltimore, MD, USA, 28–31 May 2017; pp. 1–4. [Google Scholar]
- Liew, W.S.; Yao, L.; Lian, Y. A moving binary search SAR-ADC for low power biomedical data acquisition system. In Proceedings of the IEEE Asia Pacific Conference on Circuits and Systems (APCCAS), Macao, China, 30 November–3 December 2008; pp. 646–649. [Google Scholar]
- Pang, W.Y.; Wang, C.S.; Chang, Y.K.; Chou, N.K.; Wang, C.K. A 10-bit 500-KS/s low power SAR ADC with splitting comparator for bio-medical applications. In Proceedings of the IEEE Asian Solid-State Circuits Conference (A-SSCC), Taipei, Taiwan, 16–18 November 2009; pp. 149–152. [Google Scholar]
- Chang, Y.K.; Wang, C.S.; Wang, C.K. A 8-bit 500-KS/s low power SAR ADC for bio-medical applications. In Proceedings of the IEEE Asian Solid-State Circuits Conference (A-SSCC), Jeju, Republic of Korea, 12–14 November 2007; pp. 228–231. [Google Scholar]
- Chen, S.-L.; Villaverde, J.F.; Lee, H.-Y.; Chung, D.W.-Y.; Lin, T.-L.; Tseng, C.-H.; Lo, K.-A. A Power-Efficient Mixed-Signal Smart ADC Design With Adaptive Resolution and Variable Sampling Rate for Low-Power Applications. IEEE Sens. J. 2017, 17, 3461–3469. [Google Scholar] [CrossRef]
- Akbari, M.; Hashemipour, O.; Nazari, M.; Moradi, F.A. charge sharing–based switching scheme for SAR ADCs. Int. J. Circuit Theory Appl. 2019, 47, 1188–1198. [Google Scholar] [CrossRef]
- Yousefi, T.; Dabbaghian, A.; Yavari, M. An energy-efficient DAC switching method for SAR ADCs. IEEE Trans. Circuits Syst. II Express Briefs 2017, 65, 41–45. [Google Scholar] [CrossRef]
- Unno, Y.; Matsuura, T.; Kishida, R.; Hyogo, A. Examination of Incremental ADC with SAR ADC to Reduce Conversion Time with High Accuracy. In Proceedings of the International Symposium on Intelligent Signal Processing and Communication Systems (ISPACS), Taipei, Taiwan, 3–6 December 2019; pp. 1–2. [Google Scholar]
- Chen, S.-W.M.; Brodersen, R.W. A 6-bit 600-MS/s 5.3-mW Asynchronous ADC in 0.13-μm CMOS. IEEE J. Solid-State Circuits 2006, 41, 2669–2680. [Google Scholar] [CrossRef]
- Hu, Y.S.; Shih, C.H.; Tai, H.Y.; Chen, H.W.; Chen, H.S. A 0.6 V 6.4 fJ/conversion-step 10-bit 150MS/s subranging SAR ADC in 40nm CMOS. In Proceedings of the IEEE Asian Solid-State Circuits Conference (A-SSCC), Kaohsiung, Taiwan, 10–12 November 2014; pp. 81–84. [Google Scholar]
- Zhu, Y.; Chan, C.H.; Chio, U.F.; Sin, S.W.; Seng-Pan, U.; Martins, R.P.; Maloberti, F. A 10-bit 100-MS/s reference-free SAR ADC in 90 nm CMOS. IEEE J. Solid-State Circuits 2010, 17, 1111–1121. [Google Scholar] [CrossRef]
- Sekimoto, R.; Shikata, A.; Kuroda, T.; Ishikuro, H. A 40nm 50S/s–8MS/s ultra low voltage SAR ADC with timing optimized asynchronous clock generator. In Proceedings of the ESSCIRC (ESSCIRC), Helsinki, Finland, 12–16 September 2011; pp. 471–474. [Google Scholar]
- Huang, G.Y.; Chang, S.J.; Lin, Y.Z.; Liu, C.C.; Huang, C.P. A 10b 200MS/s 0.82 mW SAR ADC in 40nm CMOS. In Proceedings of the IEEE Asian Solid-State Circuits Conference (A-SSCC), Singapore, 11–13 November 2013; pp. 289–292. [Google Scholar]
- Wan, S.H.; Kuo, C.H.; Chang, S.J.; Huang, G.Y.; Huang, C.P.; Ren, G.J.; Ho, C.H. A 10-bit 50-MS/s SAR ADC with techniques for relaxing the requirement on driving capability of reference voltage buffers. In Proceedings of the IEEE Asian Solid-State Circuits Conference (A-SSCC), Singapore, 11–13 November 2013; pp. 293–296. [Google Scholar]
- Ju, H.; Lee, M. A 13-bit 3-MS/s asynchronous SAR ADC with a passive resistor based loop delay circuit. Electronics 2019, 8, 262. [Google Scholar] [CrossRef]
- Gu, W.; Zhou, H.; Lin, T.; Wang, Z.; Ye, F.; Ren, J. Power efficient SAR ADC with optimized settling technique. In Proceedings of the IEEE 56th International Midwest Symposium on Circuits and Systems (MWSCAS), Columbus, OH, USA, 4–7 August 2013; pp. 1156–1159. [Google Scholar]
- Janke, D.; Monk, A.; Swindlehurst, E.; Layton, K.; Chiang, S.H.W. A 9-Bit 10-MHz 28-μ W SAR ADC Using Tapered Bit Periods and a Partially Interdigitated DAC. IEEE Trans. Circuits Syst. II Express Briefs 2018, 66, 187–191. [Google Scholar] [CrossRef]
- Li, C.; Chan, C.H.; Zhu, Y.; Martins, R.P. Analysis of reference error in high-speed SAR ADCs with capacitive DAC. IEEE Trans. Circuits Syst. I Regular Pap. 2018, 66, 82–93. [Google Scholar] [CrossRef]
- Liu, C.C.; Chang, S.J.; Huang, G.Y.; Lin, Y.Z. A 10-bit 50-MS/s SAR ADC with a monotonic capacitor switching procedure. IEEE J. Solid-State Circuits 2010, 45, 731–740. [Google Scholar] [CrossRef]
- Shehzad, K.; Verma, D.; Khan, D.; Ain, Q.U.; Basim, M.; Kim, S.J.; Lee, K.Y. Design of a low power 10-b 8-MS/s asynchronous SAR ADC with on-chip reference voltage generator. Electronics 2020, 9, 872. [Google Scholar] [CrossRef]
- Park, J.; Hwang, Y.H.; Oh, J.; Song, Y.; Park, J.E.; Jeong, D.K. A mutual capacitance touch readout IC with 64% reduced-power adiabatic driving over heavily coupled touch screen. IEEE J. Solid-State Circuits 2019, 54, 1694–1704. [Google Scholar] [CrossRef]
- An, J.S.; Ra, J.H.; Kang, E.; Pertijs, M.A.; Han, S.H. A capacitive touch chipset with 33.9 dB charge-overflow reduction using amplitude-modulated multi-frequency excitation and wireless power and data transfer to an active stylus. In Proceedings of the IEEE International Solid-State Circuits Conference(ISSCC), San Francisco, CA, USA, 16–20 February 2020; pp. 430–432. [Google Scholar]
- Liu, C.C.; Kuo, C.H.; Lin, Y.Z. A 10 bit 320 MS/s low-cost SAR ADC for IEEE 802.11 ac applications in 20 nm CMOS. IEEE J. Solid-State Circuits 2017, 50, 2645–2654. [Google Scholar] [CrossRef]




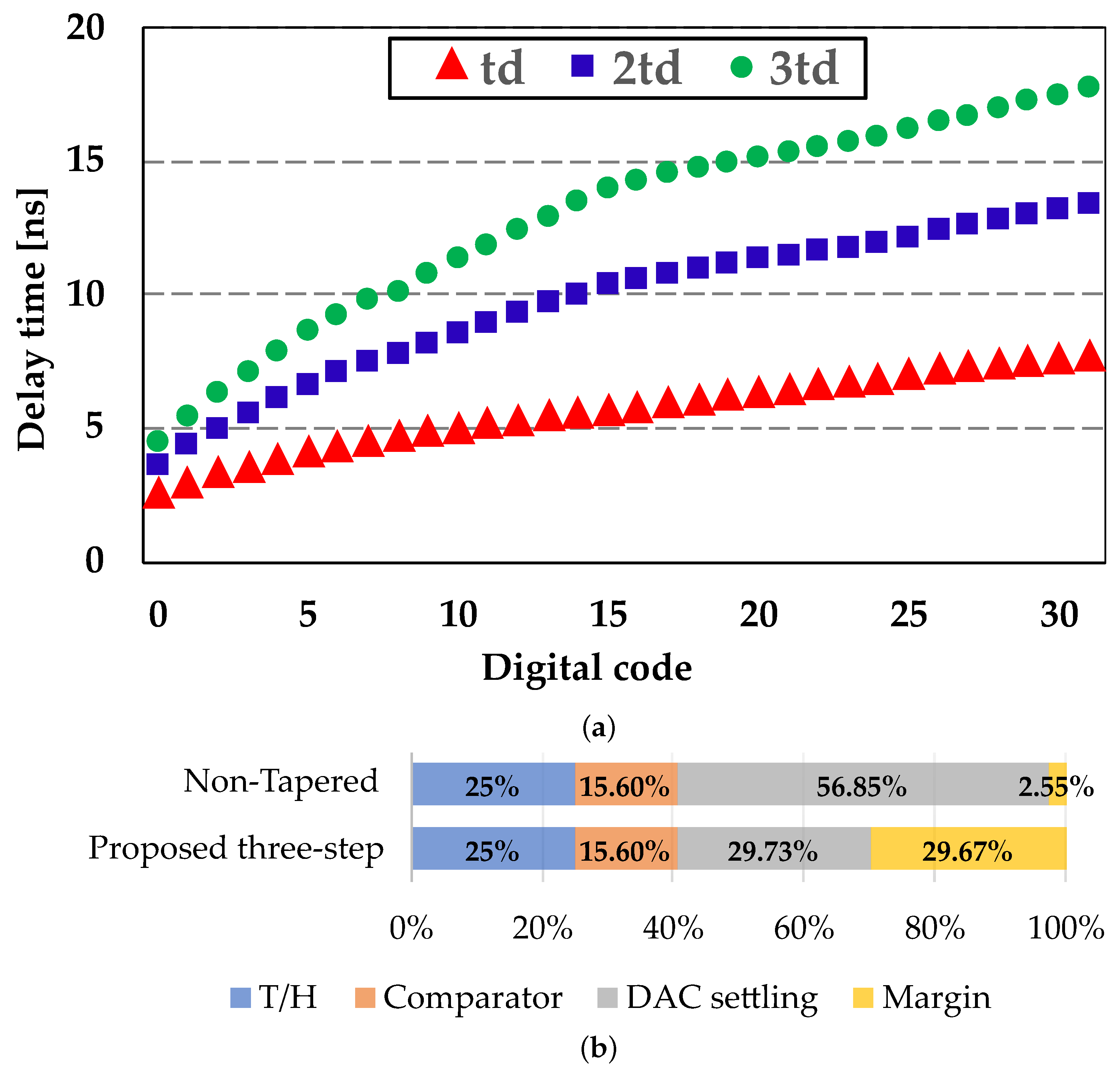
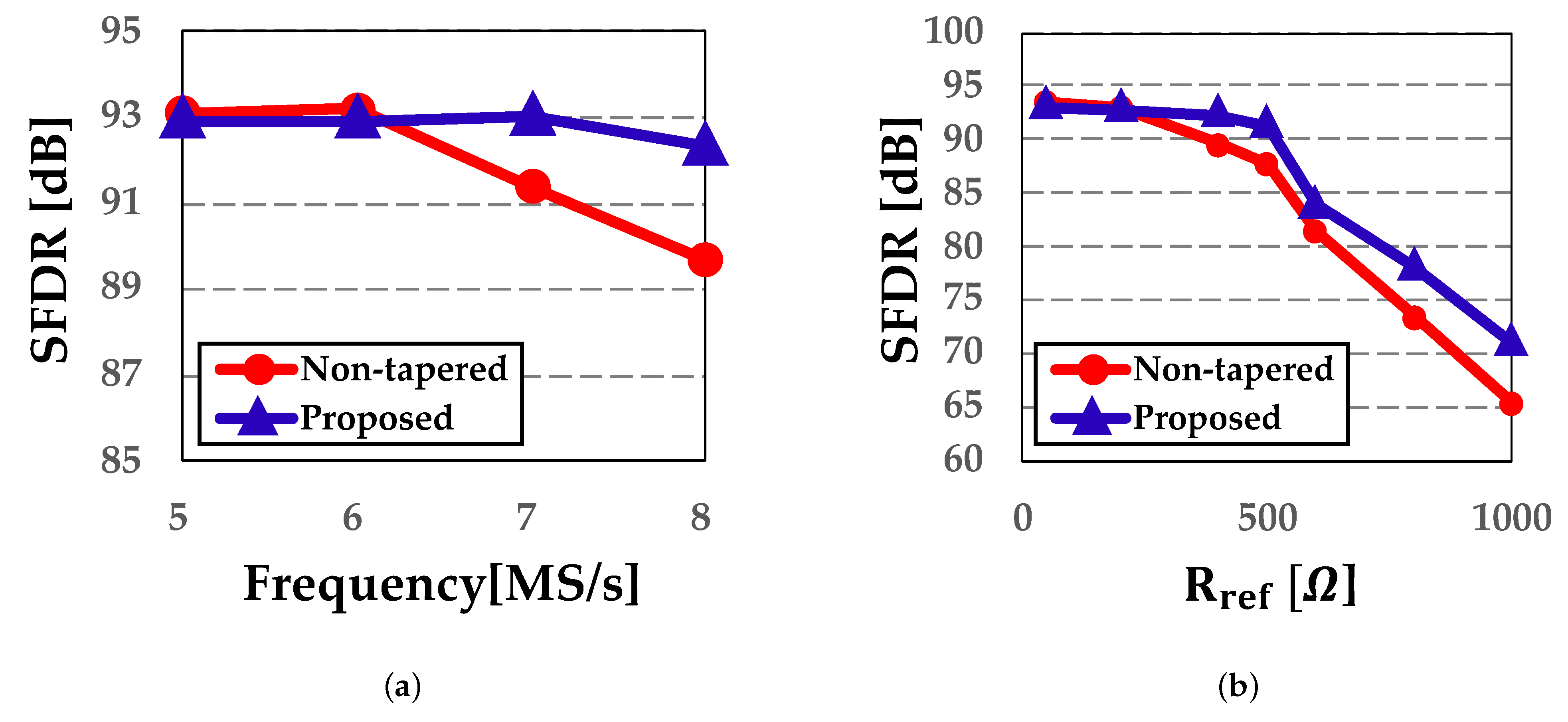

| Rref | 200 Ω | 300 Ω | 400 Ω | 500 Ω | 600 Ω | Average | |
|---|---|---|---|---|---|---|---|
| Technique | |||||||
| Non-tapered (one-step) | 47.87 ns (100%) | 71.32 ns (100%) | 94.76 ns (100%) | 118.21 ns (100%) | 141.66 ns (100%) | 94.76 ns (100%) | |
| All-tapered | 11.23 ns (23.45%) | 16.58 ns (23.25%) | 21.98 ns (23.19%) | 27.36 ns (23.15%) | 38.16 ns (23.11%) | 21.98 ns (23.23%) | |
| Limited all-tapered | 27.49 ns (57.42%) | 30.8 ns (43.19%) | 34.61 ns (36.53%) | 38.61 ns (32.66%) | 47.89 ns (30.32%) | 35.88 ns (40.02%) | |
| Two-step | 29.38 ns (61.36%) | 33.81 ns (47.41%) | 43.79 ns (46.21%) | 50.8 ns (42.98%) | 69.91 ns (42.69%) | 43.65 ns (48.13%) | |
| Three-step | 27.66 ns (57.78%) | 31.00 ns (43.47%) | 36.75 ns (38.78%) | 41.12 ns (34.78%) | 56.15 ns (34.8%) | 37.17 ns (41.92%) | |
| Four-step | 47.87 ns (100%) | 71.32 ns (100%) | 36.07 ns (38.06%) | 42.28 ns (35.76%) | 55.92 ns (34.79%) | 50.69 ns (61.72%) | |
| Integer three-step | 32.2 ns (67.26%) | 32.2 ns (45.15%) | 40.6 ns (42.84%) | 50.4 ns (42.64%) | 60.2 ns (42.5%) | 43.12 ns (48.08%) | |
| Proposed | Non-Tapered | [13] * | [16] * | [17] | [18] * | |
|---|---|---|---|---|---|---|
| Technology | 55 nm | 55 nm | 40 nm | 40 nm | 65 nm | 180 nm |
| Supply (V) | 1 | 1 | 0.7 ** | 1.1 | 1.2 | 1 |
| Frequency (MHz) | 8 | 8 | 2 | 3 | 50 | 10 |
| Resolution (bit) | 12 | 12 | 9 | 13 | 12 | 9 |
| Number of delay code | 256 | 256 | 32 | 256 | 1 | 1 |
| Number of step | 3 | 1 | 8 | 1 | 2 | 8 |
| Time reduction (%) | 47.7 | 0 | Not-mention | 0 | 25 | 32.6 |
| Delay cell structure | Poly-resistor | Poly-resistor | Inverter chain, Capacitor | Poly-resistor | Inverter chain | Current starved |
| () | 400 | 400 | Neglected | Neglected | Neglected | Neglected |
| SFDR (dB) | 89.8 | 86.2 | - | 68 | 82.1 | 71.6 |
| SNDR (dB) | 71.2 | 69.9 | 51.61 | 59.4 | 70.6 | 55.5 |
| Power (W) | 128.91 | - | 5.5 | 67 | 1663 | - |
| Area (mm) | 0.093 | - | 0.192 | 0.054 | - | 0.074 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kang, H.; Lee, S.; Lee, M. A Three-Step Tapered Bit Period SAR ADC Using Area-Efficient Clock Generation. Electronics 2023, 12, 1863. https://doi.org/10.3390/electronics12081863
Kang H, Lee S, Lee M. A Three-Step Tapered Bit Period SAR ADC Using Area-Efficient Clock Generation. Electronics. 2023; 12(8):1863. https://doi.org/10.3390/electronics12081863
Chicago/Turabian StyleKang, Hyein, Sewon Lee, and Minjae Lee. 2023. "A Three-Step Tapered Bit Period SAR ADC Using Area-Efficient Clock Generation" Electronics 12, no. 8: 1863. https://doi.org/10.3390/electronics12081863
APA StyleKang, H., Lee, S., & Lee, M. (2023). A Three-Step Tapered Bit Period SAR ADC Using Area-Efficient Clock Generation. Electronics, 12(8), 1863. https://doi.org/10.3390/electronics12081863







