A Sliding Mode Controller with Signal Transmission Delay Compensation for the Parallel DC/DC Converter’s Network Control System
Abstract
:1. Introduction
- Considering a parallel buck converter’s NCS with a random time delay, a master-slave current-sharing controller is designed based on the LSMC in the continuous domain. Then the zero-order holder (ZOH) is used to realize the discretization of the designed system, and the stability conditions of the discrete system are further determined through the Lyapunov equation;
- Based on the length characteristics of different transmission delays, the effects of uncertainty and randomness on performing parallel buck converter’s NCS with system disturbance are analyzed, which lays a foundation for the design of delay compensation strategy;
- In order to solve the problem of the influence of random delay on the system stability, the LSM controller is improved based on the multi-step prediction method, and the system parameter conditions are provided based on analyzing the stability of the designed control system;
- Designed simulations and experiments prove the effectiveness of the proposed method.
2. Design of SMC for the Parallel DC/DC Converter
2.1. Modeling of the Parallel Buck Converter System
2.2. Design of the SM Controller
2.3. Discretization and Stability Analysis of the System
3. Analysis of the Influence of Signal Transmission Delay on the System
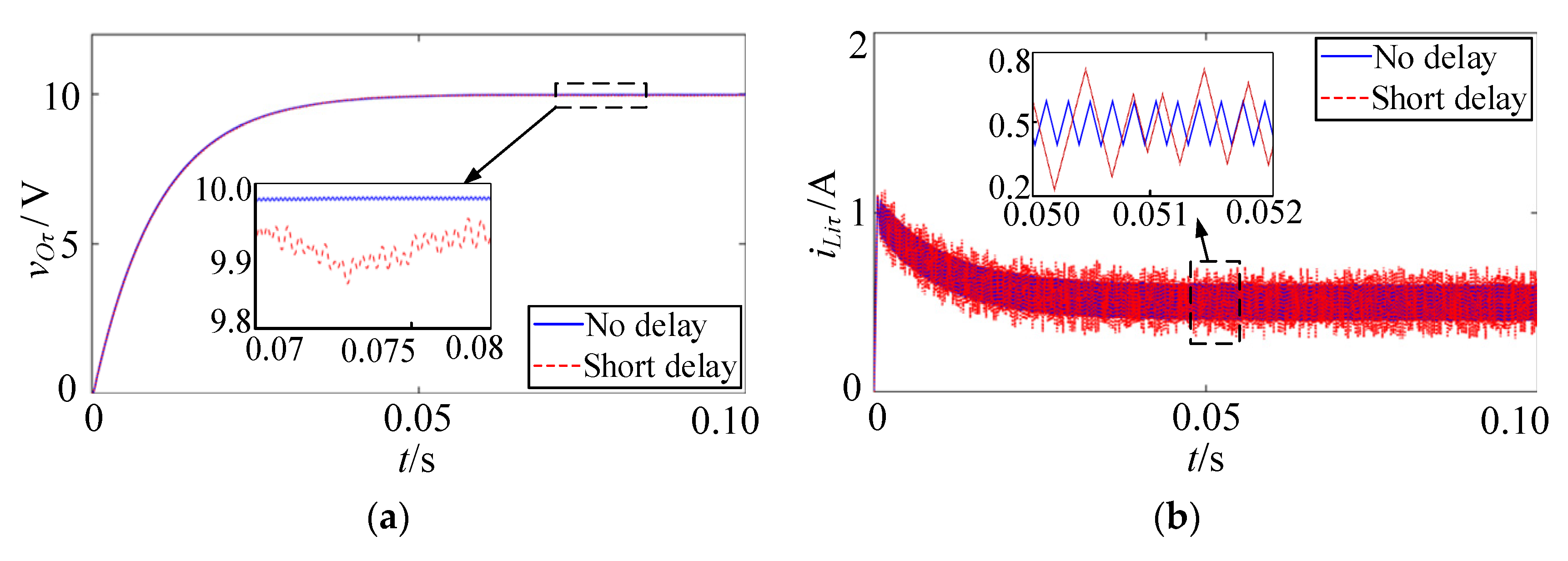
3.1. Analysis of the Influence of the Short Delay on the NCS
3.2. Analysis of the Influence of Long Delay on the NCS
4. Transmission Delay Compensation Strategy Based on Multi-Step Prediction Method
4.1. Design of the Sliding Mode Controller Based on Multi-Step Prediction Method
4.2. System Stability Analysis
- (1)
- When , from (36) we can get:
- (2)
- When , from (36) we can also get:
5. Simulation and Experimental Verification
5.1. Simulation Analysis and Verification
5.2. Experimental Verification
5.2.1. Verification of the Effect of Different Delays on NCS’s Output Performance
5.2.2. Verification of Compensation Strategy for NCS Transmitted Delay Signal Based on Multi-Step Prediction Method
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Peng, D.; Huang, M.; Li, J.; Sun, J.; Zha, X.; Wang, C. Large-signal stability criterion for parallel-connected DC–DC converters with current source equivalence. IEEE Trans. Circuits Syst. II Express Briefs 2019, 66, 2037–2041. [Google Scholar] [CrossRef]
- Li, H.; Ren, F.; Liu, C.; Guo, Z.; Lü, J.; Zhang, B.; Zheng, T.Q. An extended stability analysis method for paralleled dc-dc converters system with considering the periodic disturbance based on floquet theory. IEEE Access 2020, 8, 9023–9036. [Google Scholar] [CrossRef]
- Shi, J.; Zhou, L.; Li, J.; He, X. Common-duty-ratio control of input-parallel output-parallel (IPOP) connected DC–DC converter modules with automatic sharing of currents. IEEE Trans. Power Electron. 2012, 27, 3277–3291. [Google Scholar] [CrossRef]
- Panov, Y.; Jovanovic, M.M. Loop gain measurement of paralleled DC–DC converters with average-current-sharing control. IEEE Trans. Power Electron. 2008, 23, 2942–2948. [Google Scholar] [CrossRef]
- Xu, G.; Sha, D.; Liao, X. Decentralized inverse-droop control for input-series–output-parallel DC–DC converters. IEEE Trans. Power Electron. 2015, 30, 4621–4625. [Google Scholar] [CrossRef]
- Wang, R.; Liu, G.-P.; Wang, J.; Rees, D.; Zhao, Y.B. Guaranteed cost control for networked control systems based on an improved predictive control method. IEEE Trans. Control Syst. Technol. 2010, 18, 1226–1232. [Google Scholar] [CrossRef]
- Klügel, M.; Mamduhi, M.; Ayan, O.; Vilgelm, M.; Johansson, K.H.; Hirche, S.; Kellerer, W. Joint cross-layer optimization in real-time networked control systems. IEEE Trans. Control Netw. Syst. 2020, 7, 1903–1915. [Google Scholar] [CrossRef]
- Zhao, Y.-B.; Liu, G.-P.; Rees, D. Design of a packet-based control framework for networked control systems. IEEE Trans. Control Syst. Technol. 2009, 17, 859–865. [Google Scholar] [CrossRef]
- Wu, C.; Liu, J.; Jing, X.; Li, H.; Wu, L. Adaptive fuzzy control for nonlinear networked control systems. IEEE Trans. Syst. Man Cybern. Syst. 2017, 47, 2420–2430. [Google Scholar] [CrossRef]
- Xu, H.; Jagannathan, S. Neural network-based finite horizon stochastic optimal control design for nonlinear networked control systems. IEEE Trans. Neural Netw. Learn. Syst. 2015, 26, 472–485. [Google Scholar] [CrossRef]
- Shi, Y.; Yu, B. Output feedback stabilization of networked control systems with random delays modeled by markov chains. IEEE Trans. Autom. Control 2009, 54, 1668–1674. [Google Scholar]
- Qiu, J.; Gao, H.; Ding, S.X. Recent advances on fuzzy-model-based nonlinear networked control systems: A survey. IEEE Trans. Ind. Electron. 2016, 63, 1207–1217. [Google Scholar] [CrossRef]
- Tavassoli, B. Stability of nonlinear networked control systems over multiple communication links with asynchronous sampling. IEEE Trans. Autom. Control 2014, 59, 511–515. [Google Scholar] [CrossRef]
- Savkin, A.V.; Cheng, T.M. Detectability and output feedback stabilizability of nonlinear networked control systems. IEEE Trans. Autom. Control 2007, 52, 730–735. [Google Scholar] [CrossRef]
- Liu, K.-Z.; Wang, R.; Liu, G.-P. Tradeoffs between transmission intervals and delays for decentralized networked control systems based on a gain assignment approach. IEEE Trans. Circuits Syst. II Express Briefs 2016, 63, 498–502. [Google Scholar] [CrossRef]
- Maity, D.; Mamduhi, M.H.; Hirche, S.; Johansson, K.H. Optimal lqg control of networked systems under traffic-correlated delay and dropout. IEEE Control Syst. Lett. 2022, 6, 1280–1285. [Google Scholar] [CrossRef]
- Tang, B.; Wang, J.; Zhang, Y. A delay-distribution approach to stabilization of networked control systems. IEEE Trans. Control Netw. Syst. 2015, 2, 382–392. [Google Scholar] [CrossRef]
- Tan, C.; Zhang, H. Necessary and sufficient stabilizing conditions for networked control systems with simultaneous transmission delay and packet dropout. IEEE Trans. Autom. Control 2017, 62, 4011–4016. [Google Scholar] [CrossRef]
- Shangguan, X.-C.; Zhang, C.-K.; He, Y.; Jin, L.; Jiang, L.; Spencer, J.W.; Wu, M. Robust load frequency control for power system considering transmission delay and sampling period. IEEE Trans. Ind. Inform. 2021, 17, 5292–5303. [Google Scholar] [CrossRef]
- Pang, H.-p.; Liu, C.-j.; Liu, A.-z. Sliding Mode Control for Time-DELAY systems with Its Application to Networked Control Systems. In Proceedings of the Sixth International Conference on Intelligent Systems Design and Applications, Jian, China, 16–18 October 2006; pp. 192–197. [Google Scholar]
- Yan, S.; Shen, M.Q.; Nguang, S.K.; Zhang, G.M. Event-triggered H∞ control of networked control systems with distributed transmission delay. IEEE Trans. Autom. Control 2020, 65, 4295–4301. [Google Scholar] [CrossRef]
- Kim, D.S.; Choi, D.H.; Mohapatra, P. Real-time scheduling method for networked discrete control systems. Control Eng. Pract. 2009, 17, 564–570. [Google Scholar] [CrossRef]
- Heemels, W.P.M.H.; Teel, A.R.; van de Wouw, N.; Nesic, D. Networked control systems with communication constraints: Tradeoffs between transmission intervals, delays and performance. IEEE Trans. Autom. Control 2010, 55, 1781–1796. [Google Scholar] [CrossRef]
- Padhy, B.P.; Srivastava, S.C.; Verma, N.K. A Wide-Area Damping Controller Considering Network Input and Output Delays and Packet Drop. IEEE Trans. Power Syst. 2017, 32, 166–176. [Google Scholar] [CrossRef]
- Liu, G.P.; Chai, S.C.; Mu, J.X.; Rees, D. Networked Predictive Control of Systems with Random Delay in Signal Transmission Channels. Int. J. Syst. Sci. 2008, 39, 1055–1064. [Google Scholar] [CrossRef]
- Huangfu, Y.; Ma, R.; Zhao, B.; Liang, Z.; Ma, Y.; Wang, A.; Zhao, D.; Li, H.; Ma, R. A novel robust smooth control of input parallel output series quasi-z-source DC–DC converter for fuel cell electrical vehicle applications. IEEE Trans. Ind. Appl. 2021, 57, 4207–4221. [Google Scholar] [CrossRef]
- Mosayebi, M.; Gheisarnejad, M.; Khooban, M.H. An intelligent sliding mode control for stabilization of parallel converters feeding cpls in DC-microgrid. IET Power Electron. 2022, 15, 1596–1606. [Google Scholar] [CrossRef]
- Lee, S.; Jeung, Y.-C.; Lee, D.-C. Voltage balancing control of ipos modular dual active bridge DC/DC converters based on hierarchical sliding mode control. IEEE Access 2019, 7, 9989–9997. [Google Scholar] [CrossRef]
- Wei, Z.; Zhang, W.; Wang, Y. Sliding mode control for parallel DC–DC converter network systems with uniform quantization and discretization effects. IEEE Access 2023, 11, 99918–99934. [Google Scholar] [CrossRef]
- Lopez, M.; Vicuna, L.G.; Castilla, M.; Gaya, P.; Lopez, O. Current distribution control design for paralleled DC/DC converters using sliding-mode control. IEEE Trans. Ind. Electron. 2004, 51, 419–428. [Google Scholar] [CrossRef]
- Taheri, B.; Sedaghat, M.; Bagherpour, M.A.; Farhadi, P. A New Controller for DC-DC Converters Based on Sliding Mode Control Techniques. J. Control. Autom. Electr. Syst. 2019, 30, 63–74. [Google Scholar] [CrossRef]
- Alsmadi, Y.; Utkin, V.; Haj-ahmed, M.; Xu, L. Sliding mode control of power converters: DC/DC converters. Int. J. Control 2018, 91, 2472–2493. [Google Scholar] [CrossRef]
- Zhao, Y.; Qiao, W.; Ha, D. A sliding-mode duty-ratio controller for DC/DC buck converters with constant power loads. IEEE Trans. Ind. Appl. 2014, 50, 1448–1458. [Google Scholar] [CrossRef]









| Parameter | Value |
|---|---|
| Load resistance R | 10 Ω |
| Filter inductance Li | 1 mH |
| Filter capacitance Ci | 1000 μF |
| Reference voltage Vref | 10 V |
| Input DC voltage E | 20 V |
| Delay Type | τ (ms) | ΔvOτ (V) | ΔiLiτ (A) | System Current Mode |
|---|---|---|---|---|
| no delay | - | 0.07 | 0.21 | CCM |
| short delay | 0.05 | 0.09 | 0.38 | CCM |
| 0.10 | 0.12 | 0.57 | CCM | |
| long delay | 0.20 | 0.22 | 1.02 | CCM |
| 0.40 | 0.31 | 1.29 | DCM | |
| 0.60 | 0.35 | 1.61 | DCM |
| τ (ms) | Compensated State | ΔvOτ (V) | ΔvOτ_max (V) | ΔiLiτ (A) | ΔiLiτ_max (A) | System Current Mode |
|---|---|---|---|---|---|---|
| 0.2 | No | 0.22 | 0.78 | 1.02 | 0.44 | CCM |
| Yes | 0.02 | 0.01 | 0.81 | 0.37 | CCM | |
| 0.4 | No | 0.31 | 2.96 | 1.29 | 1.01 | DCM |
| Yes | 0.08 | 1.58 | 1.03 | 0.45 | CCM | |
| 0.6 | No | 0.35 | 2.41 | 1.61 | 1.39 | DCM |
| Yes | 0.11 | 1.42 | 1.38 | 0.67 | CCM |
| τ (ms) | Rise Time (ms) | Mean Steady-State Error (V) | Maximum Amplitude Error (V) |
|---|---|---|---|
| 0 | 103 | 0.22 | 0.37 |
| 0–0.1 | 122 | 0.40 | 0.50 |
| 0–0.2 | 138 | 0.74 | 1.01 |
| 0–0.4 | 148 | 0.89 | 1.41 |
| 0–0.6 | 173 | 0.91 | 1.61 |
| τ (ms) | Compensated State | Rise Time (ms) | Mean Steady-State Error (V) | Maximum Amplitude Error (V) |
|---|---|---|---|---|
| 0–0.4 | No | 148 | 0.89 | 0.99 |
| Yes | 64 | 0.48 | 0.78 | |
| 0–0.6 | No | 173 | 0.91 | 1.39 |
| Yes | 67 | 0.57 | 0.62 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yu, J.; Zhang, W.; Xiong, W.; Wang, Y. A Sliding Mode Controller with Signal Transmission Delay Compensation for the Parallel DC/DC Converter’s Network Control System. Electronics 2024, 13, 121. https://doi.org/10.3390/electronics13010121
Yu J, Zhang W, Xiong W, Wang Y. A Sliding Mode Controller with Signal Transmission Delay Compensation for the Parallel DC/DC Converter’s Network Control System. Electronics. 2024; 13(1):121. https://doi.org/10.3390/electronics13010121
Chicago/Turabian StyleYu, Juan, Weiqi Zhang, Wenwen Xiong, and Yanmin Wang. 2024. "A Sliding Mode Controller with Signal Transmission Delay Compensation for the Parallel DC/DC Converter’s Network Control System" Electronics 13, no. 1: 121. https://doi.org/10.3390/electronics13010121
APA StyleYu, J., Zhang, W., Xiong, W., & Wang, Y. (2024). A Sliding Mode Controller with Signal Transmission Delay Compensation for the Parallel DC/DC Converter’s Network Control System. Electronics, 13(1), 121. https://doi.org/10.3390/electronics13010121









