Diagnostics on Power Electronics Converters by Means of Autoregressive Modelling
Abstract
1. Introduction
- estimate an AR model of the measured signal (vibration, current, etc.);
- extract suitable features from the estimated model (prediction error variance, model coefficients, spectral density, etc.) that allow healthy conditions to be discriminated from faulty ones.
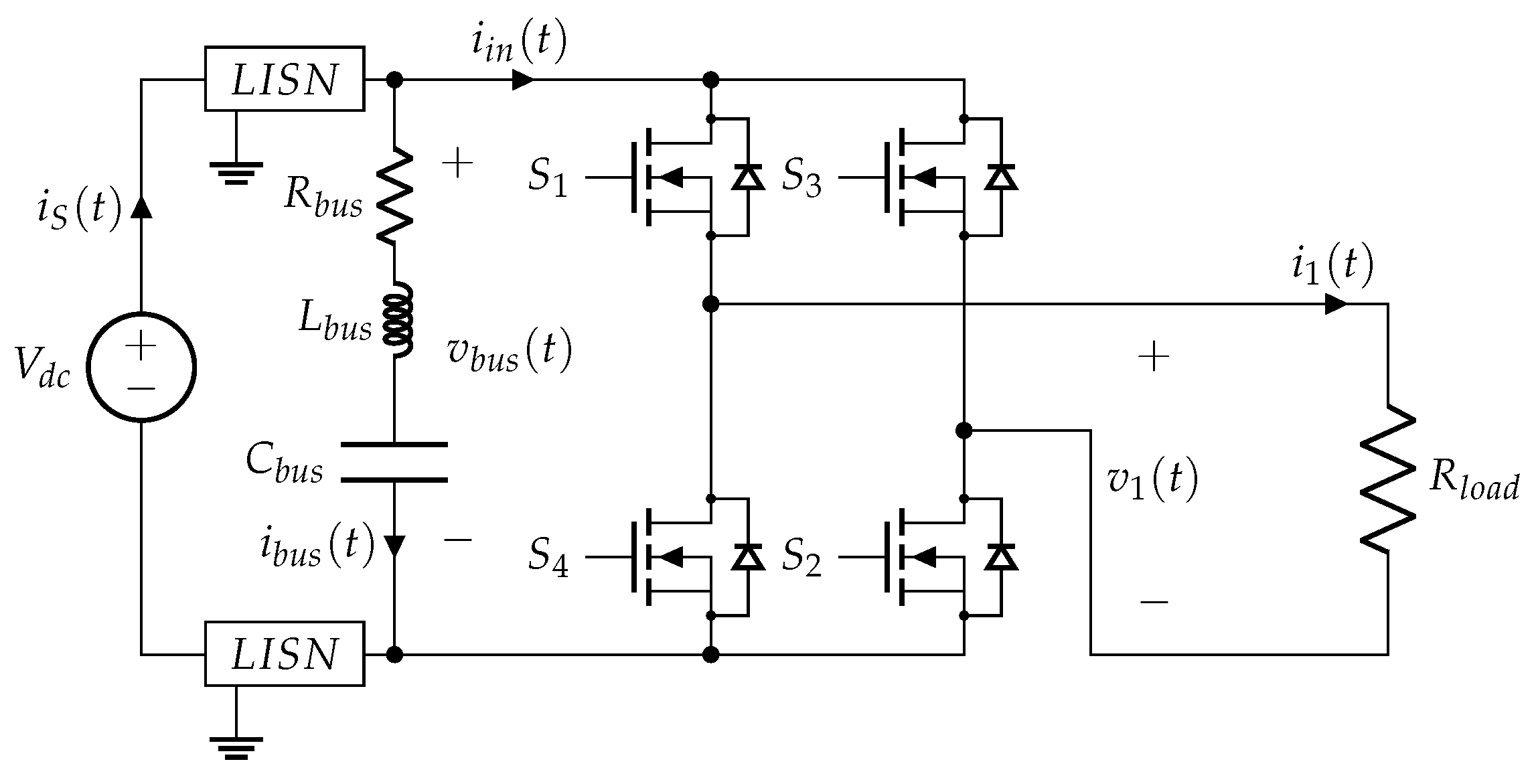
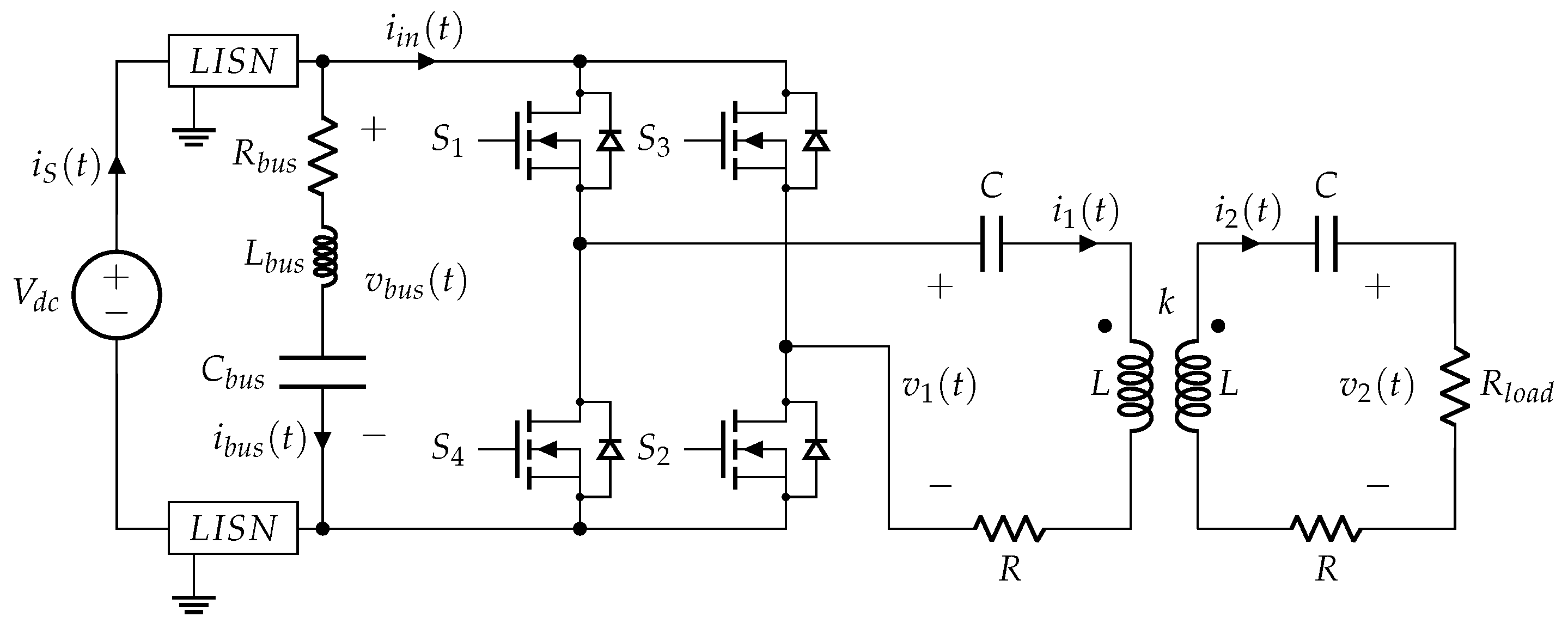
2. System Characteristics
3. Fault Diagnosis via Autoregressive Modelling
3.1. Autoregressive Modelling
3.2. Fault Diagnosis Procedure
4. Results
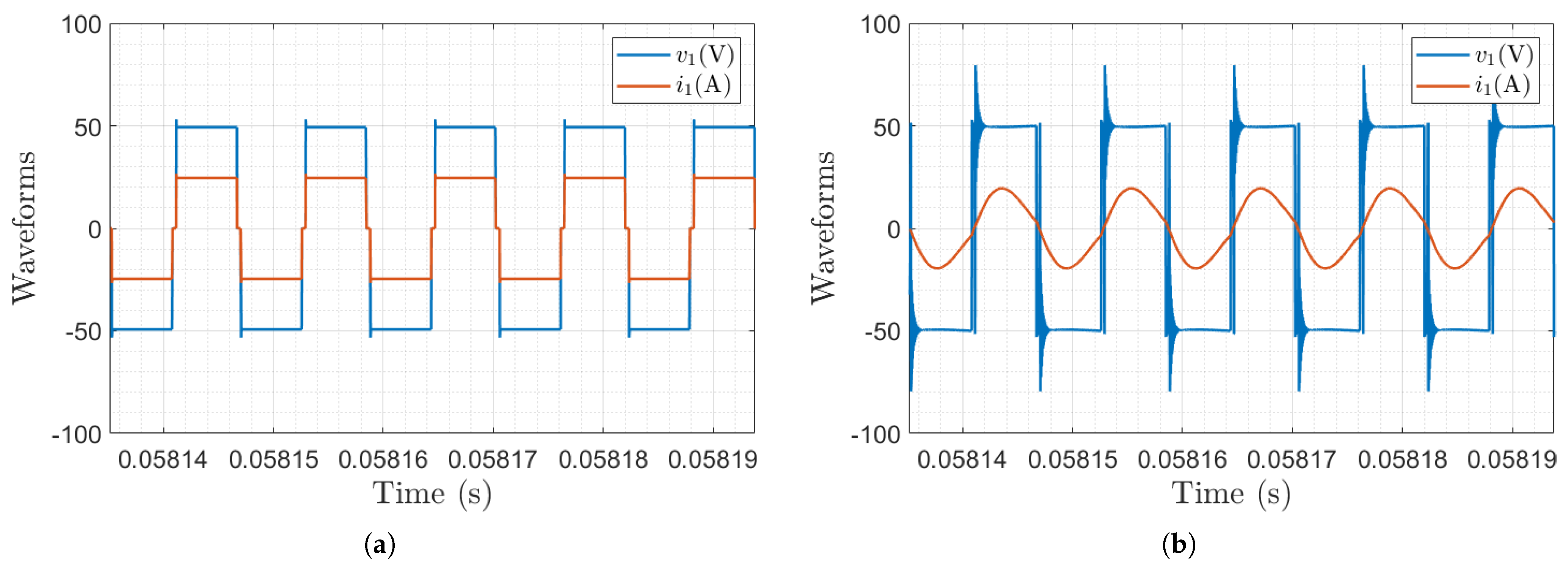
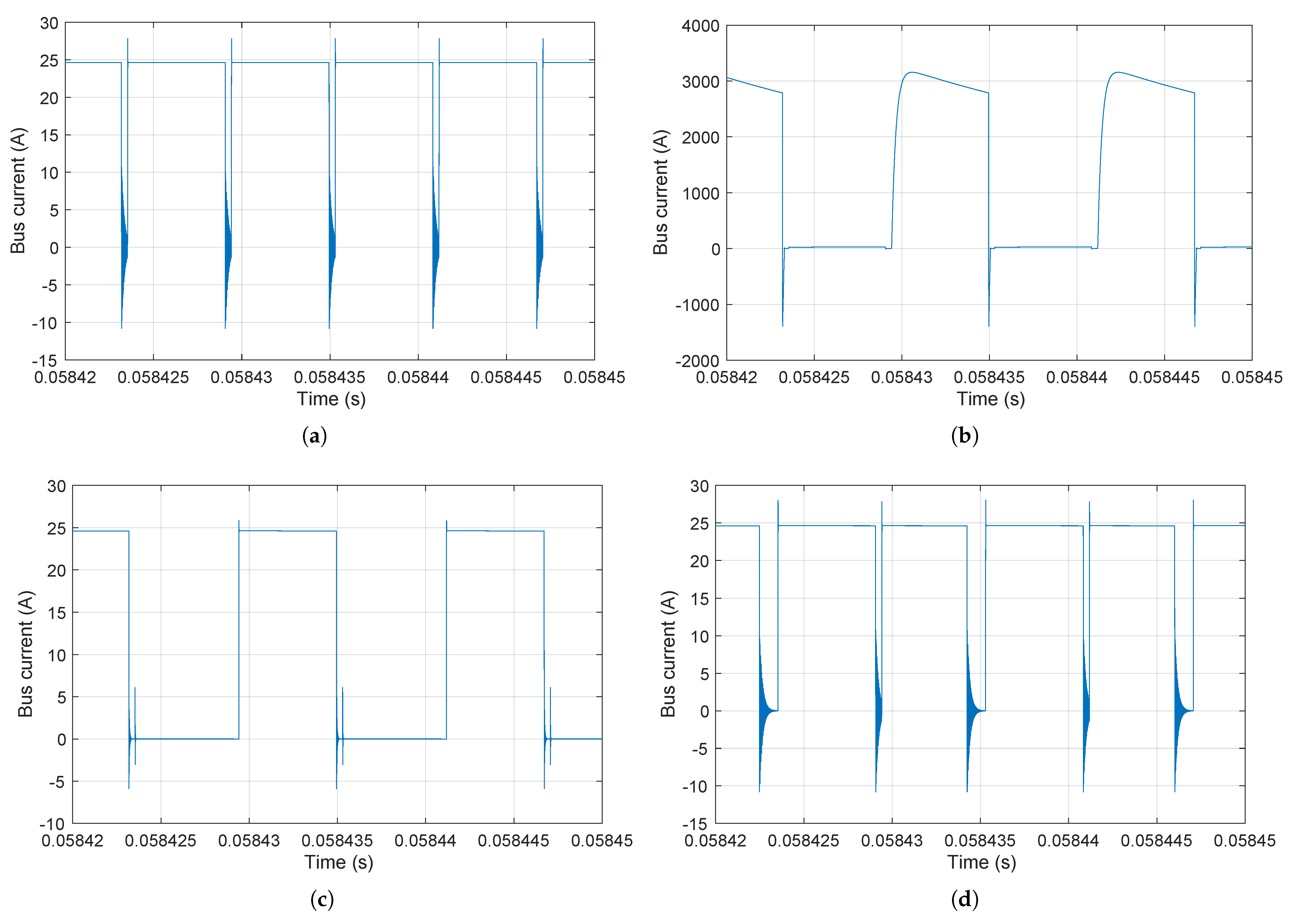
4.1. Non-Ideal Behavior and Fault Scenarios
4.1.1. Asymmetric Dead Time
4.1.2. Switch Fault
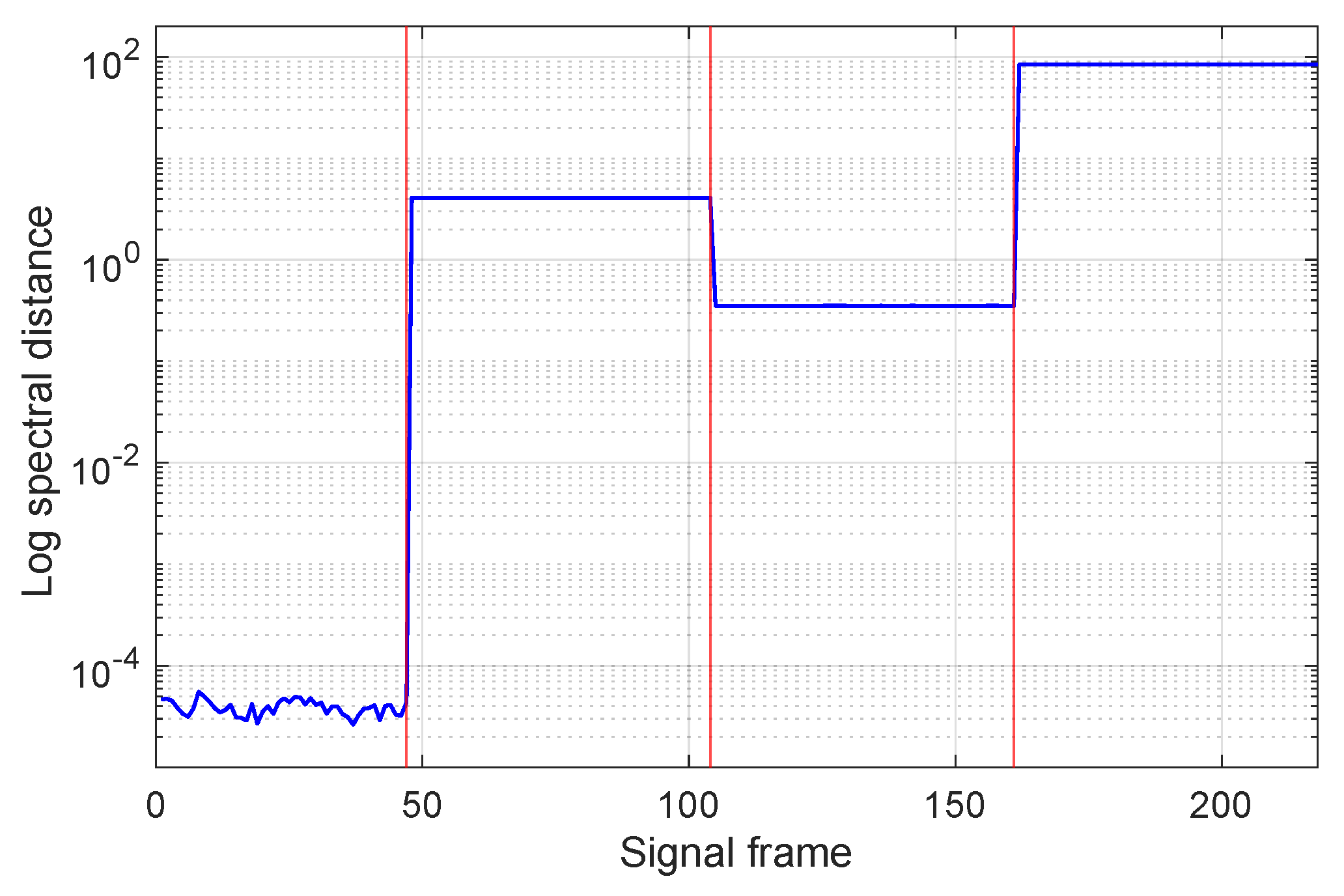
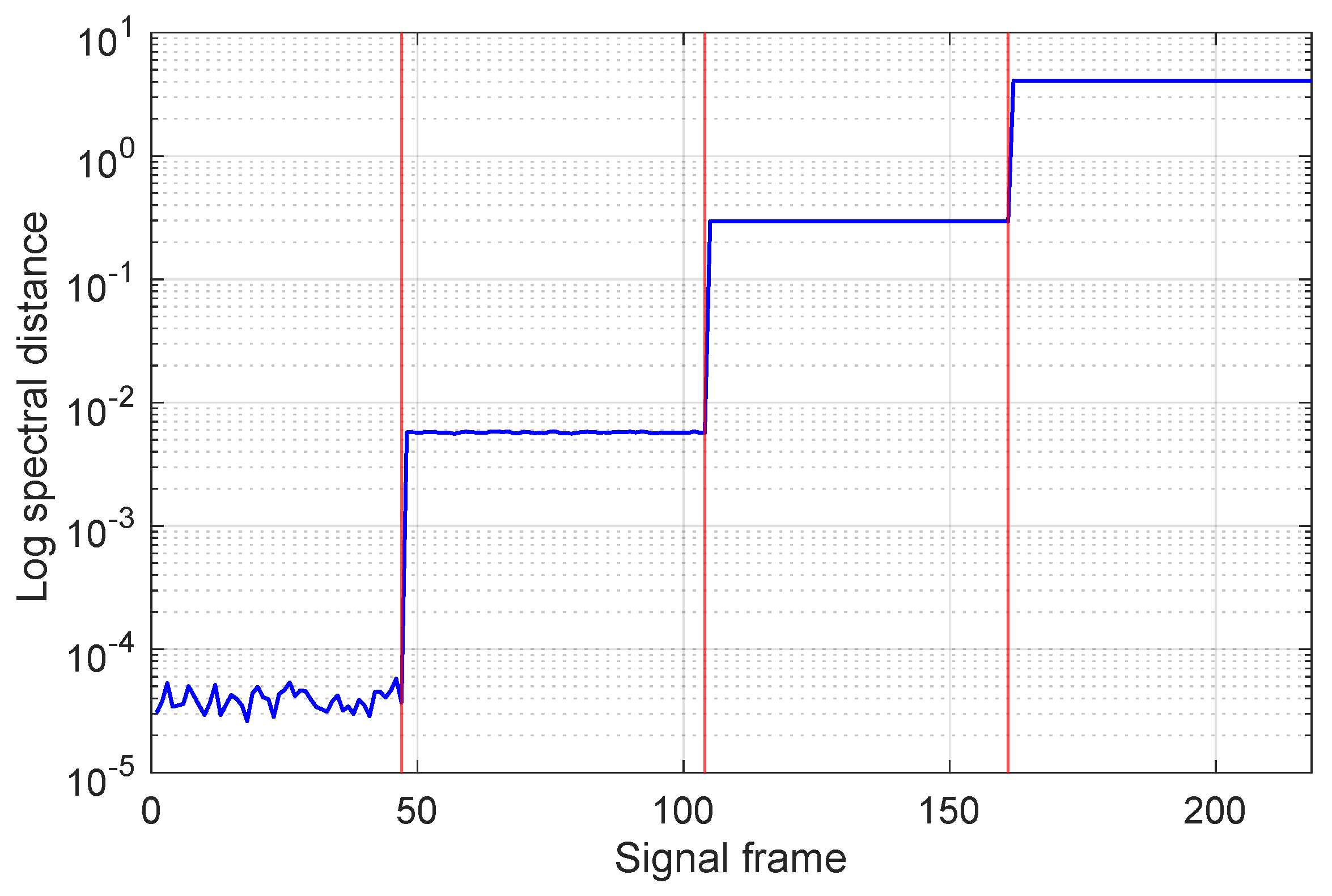
4.2. AR-Based FD: H-Bridge Inverter with Resistive Load
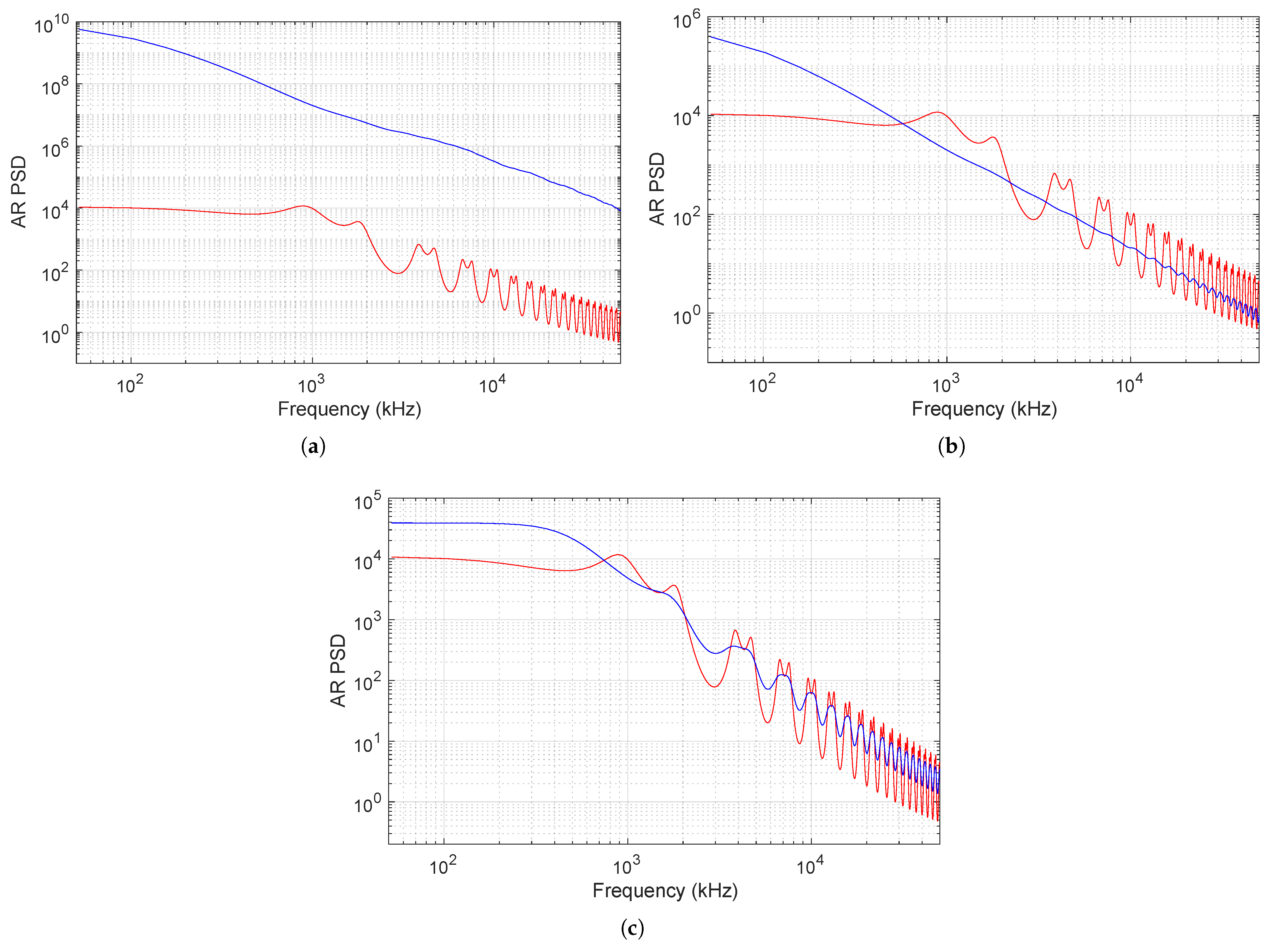
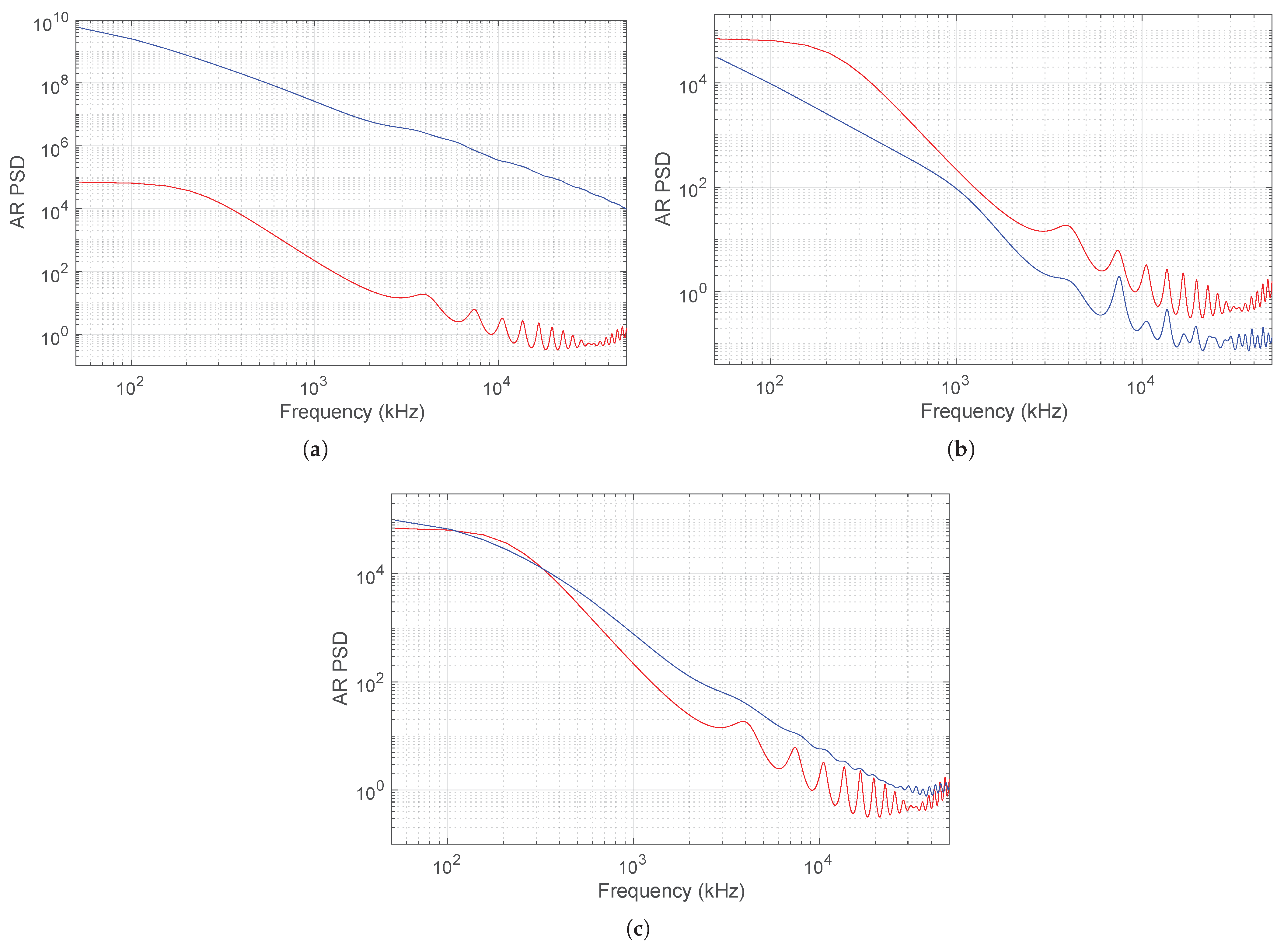
- First, a reference AR model is estimated by using a portion of the healthy signal and the corresponding PSD is computed from (11).
- Then, the remaining part of the healthy data and the faulty data are segmented into overlapping frames of length samples. For each sequence, an AR model of order is estimated and the associated PSD is computed.
- Finally, each current PSD is compared with the reference one through the health indicator (12).
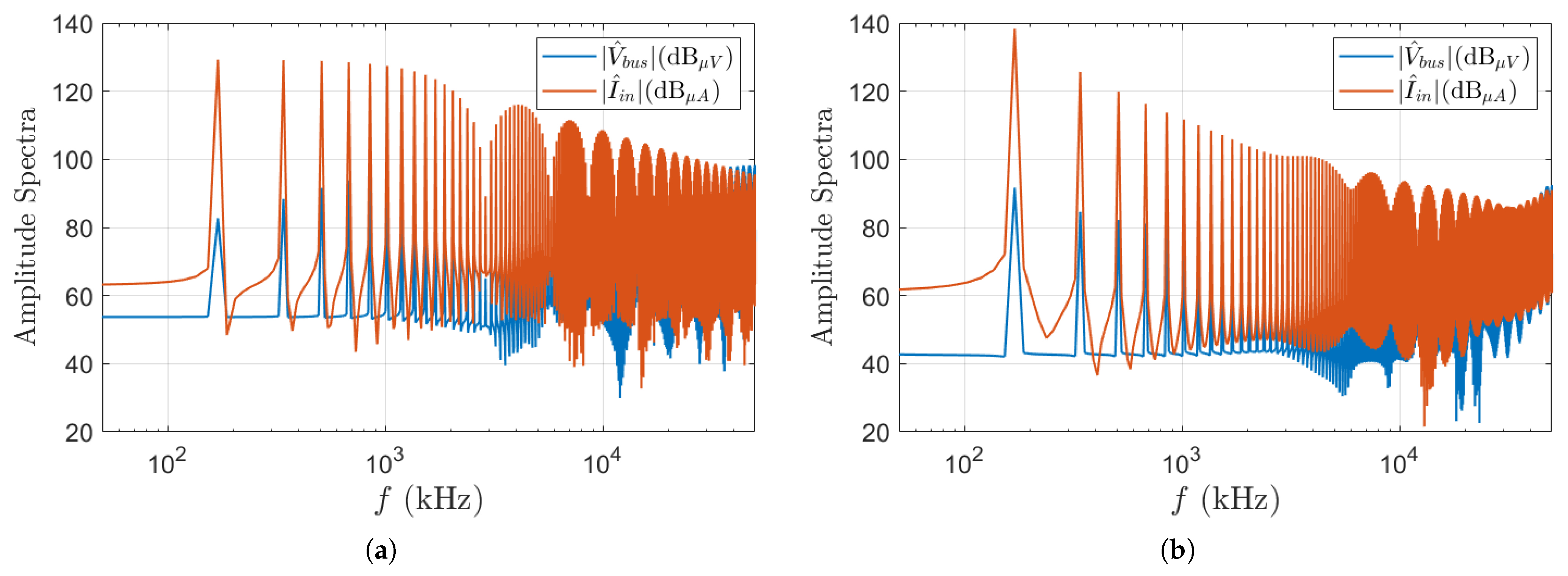
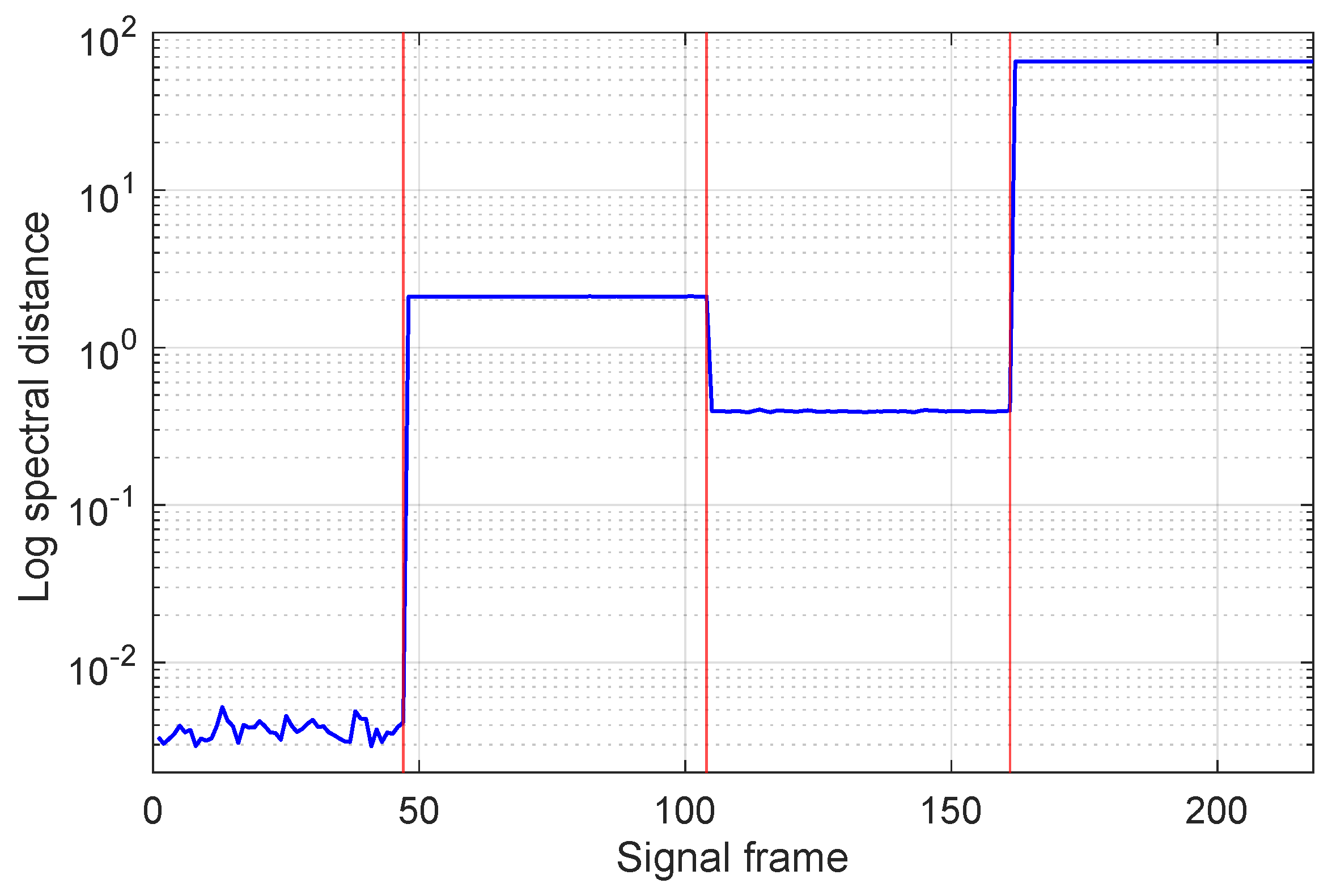
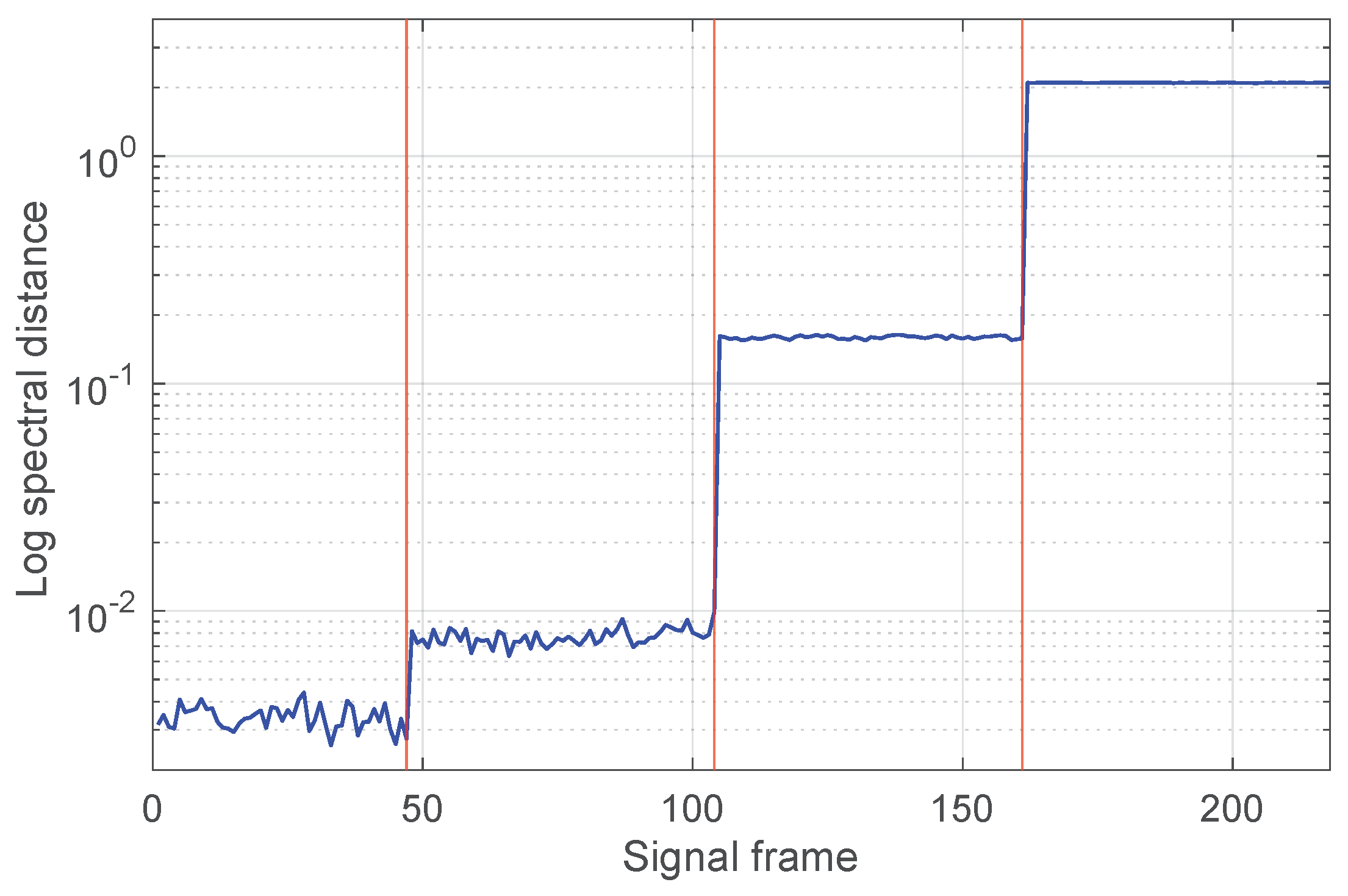
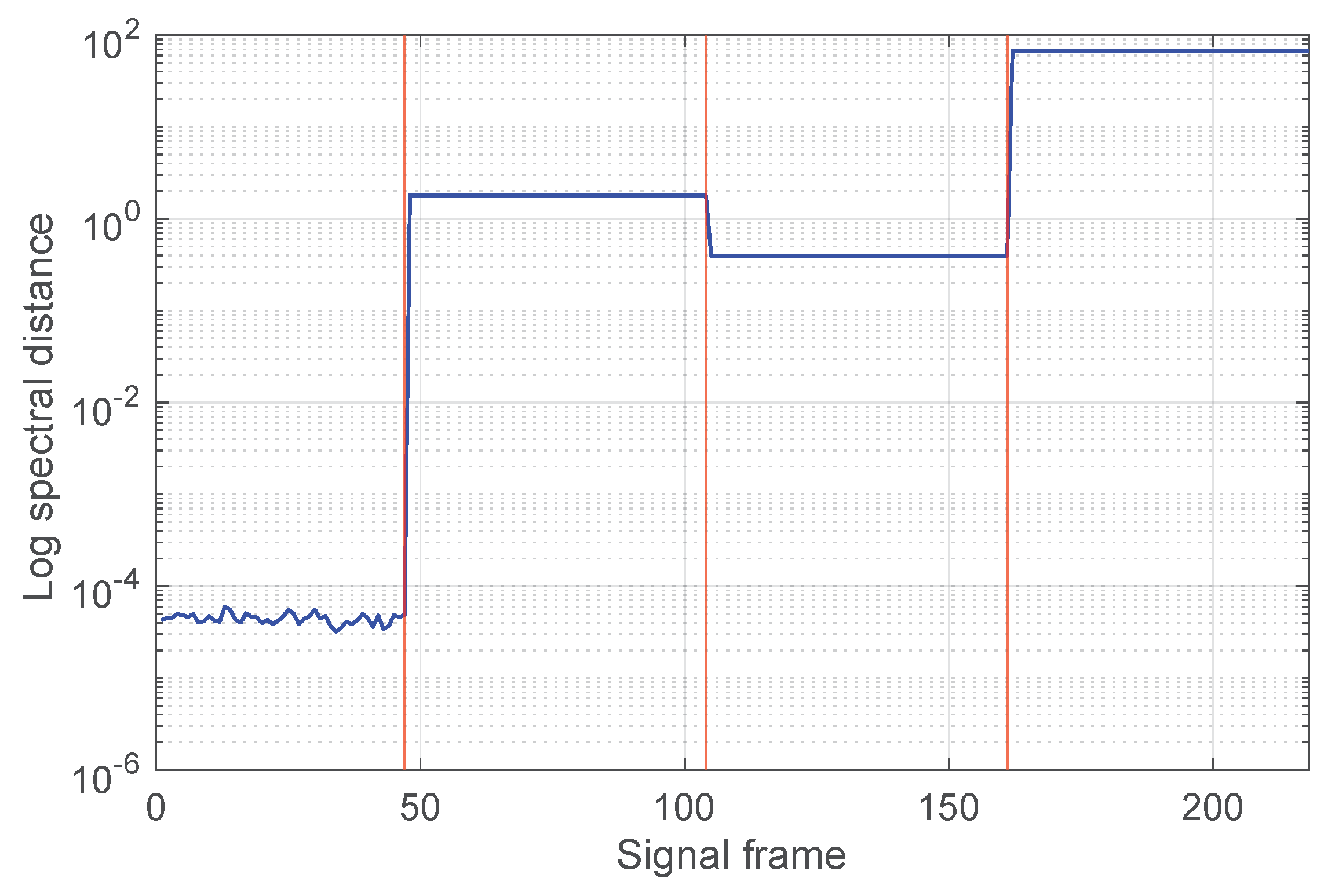
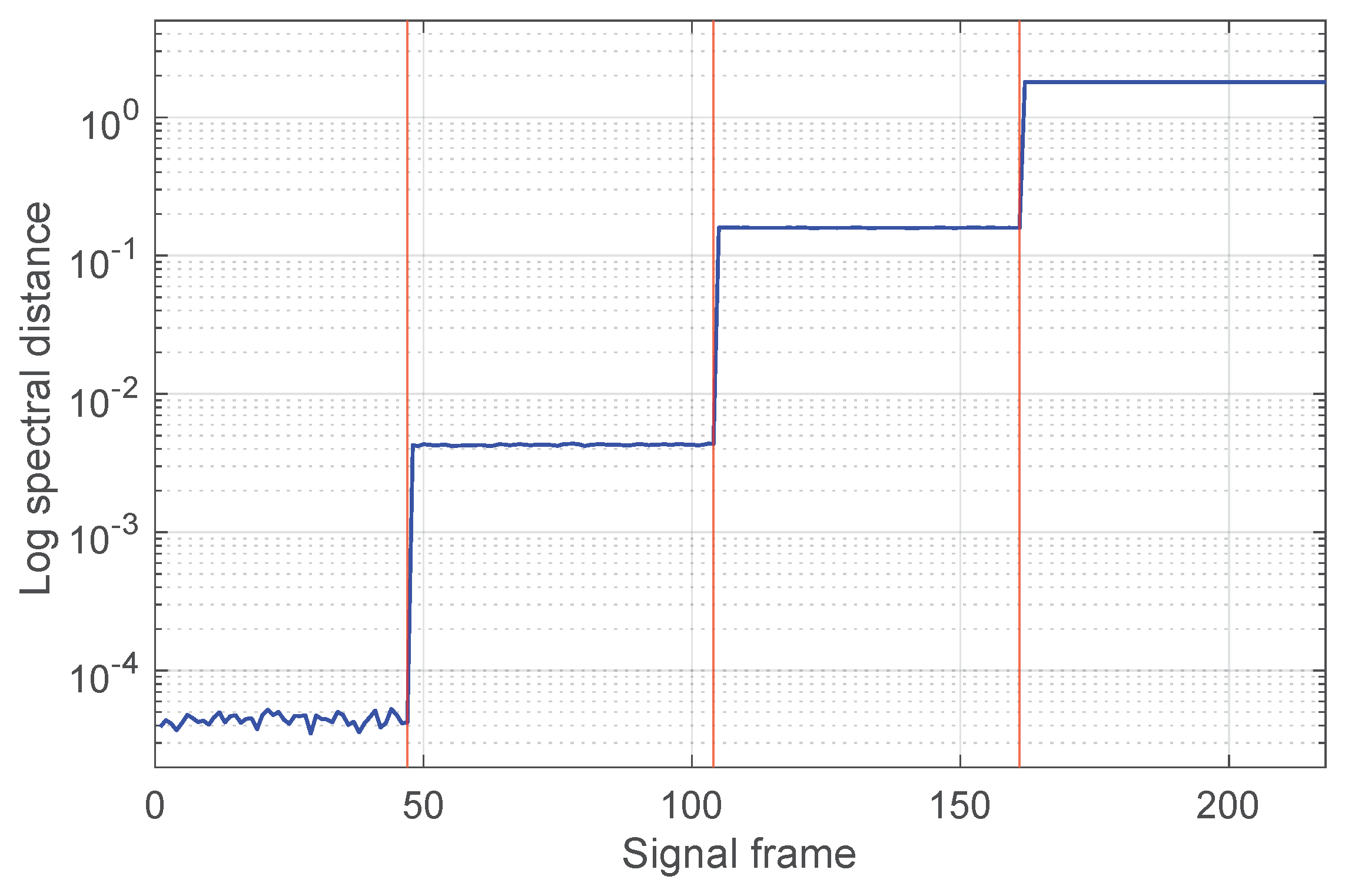
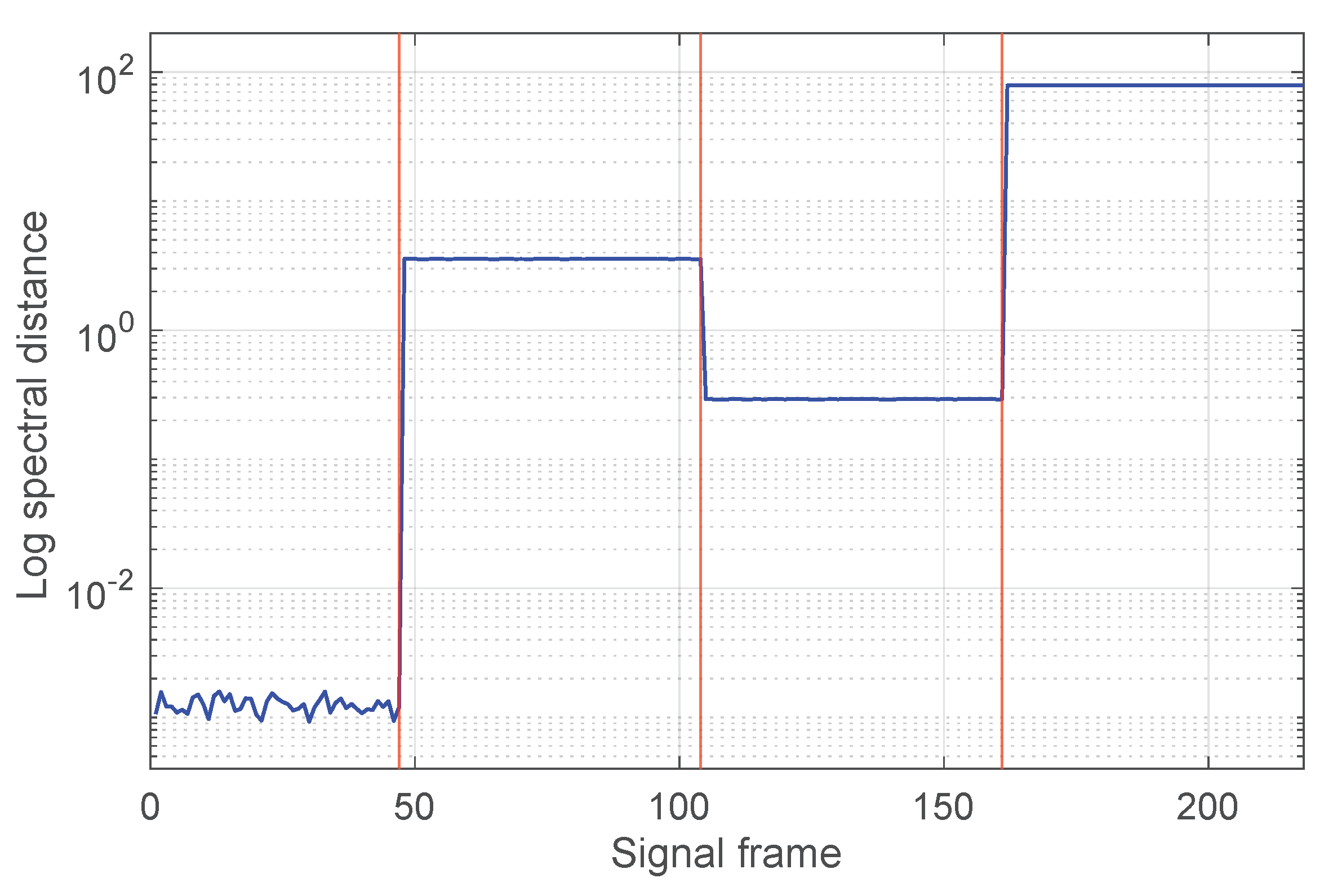
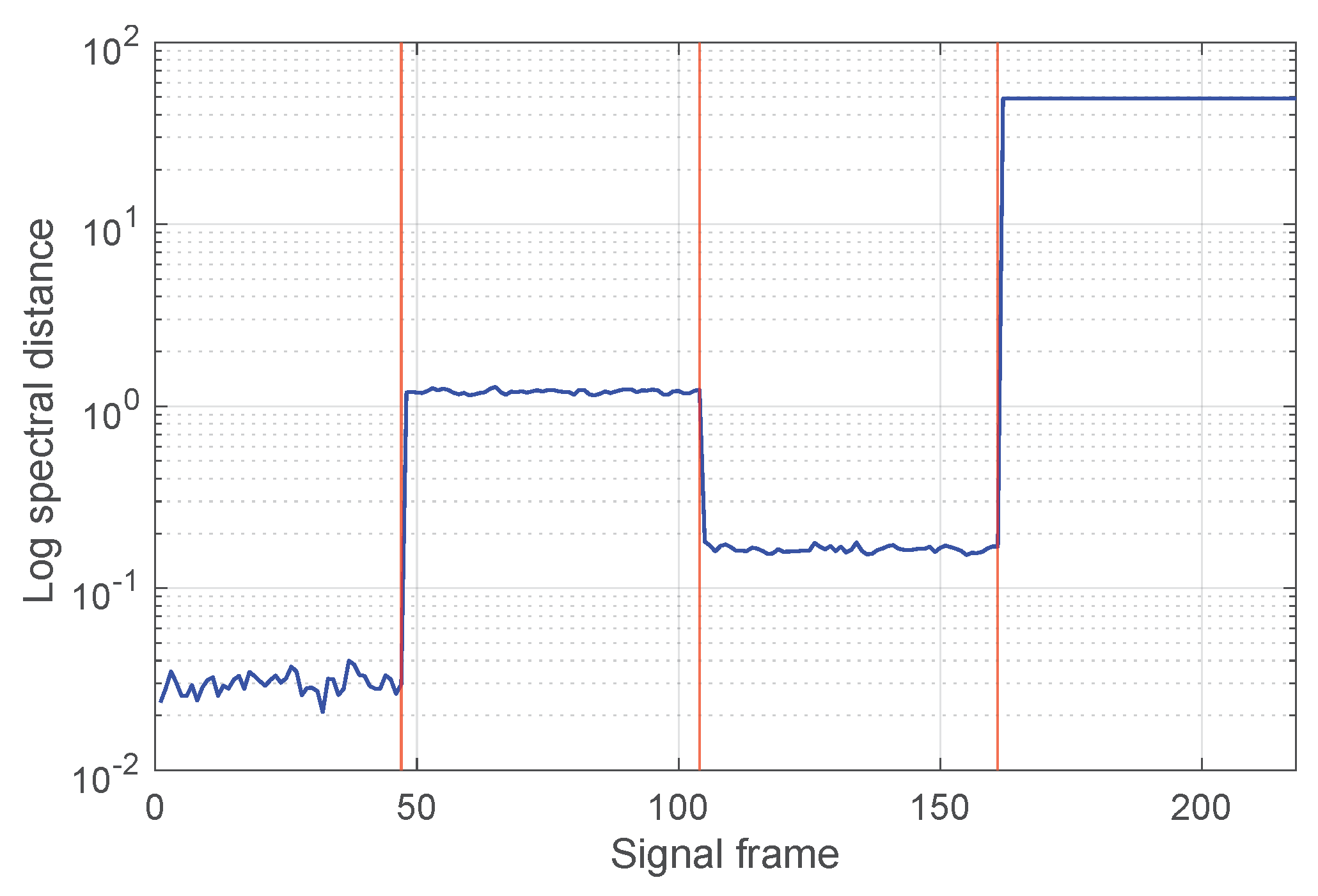
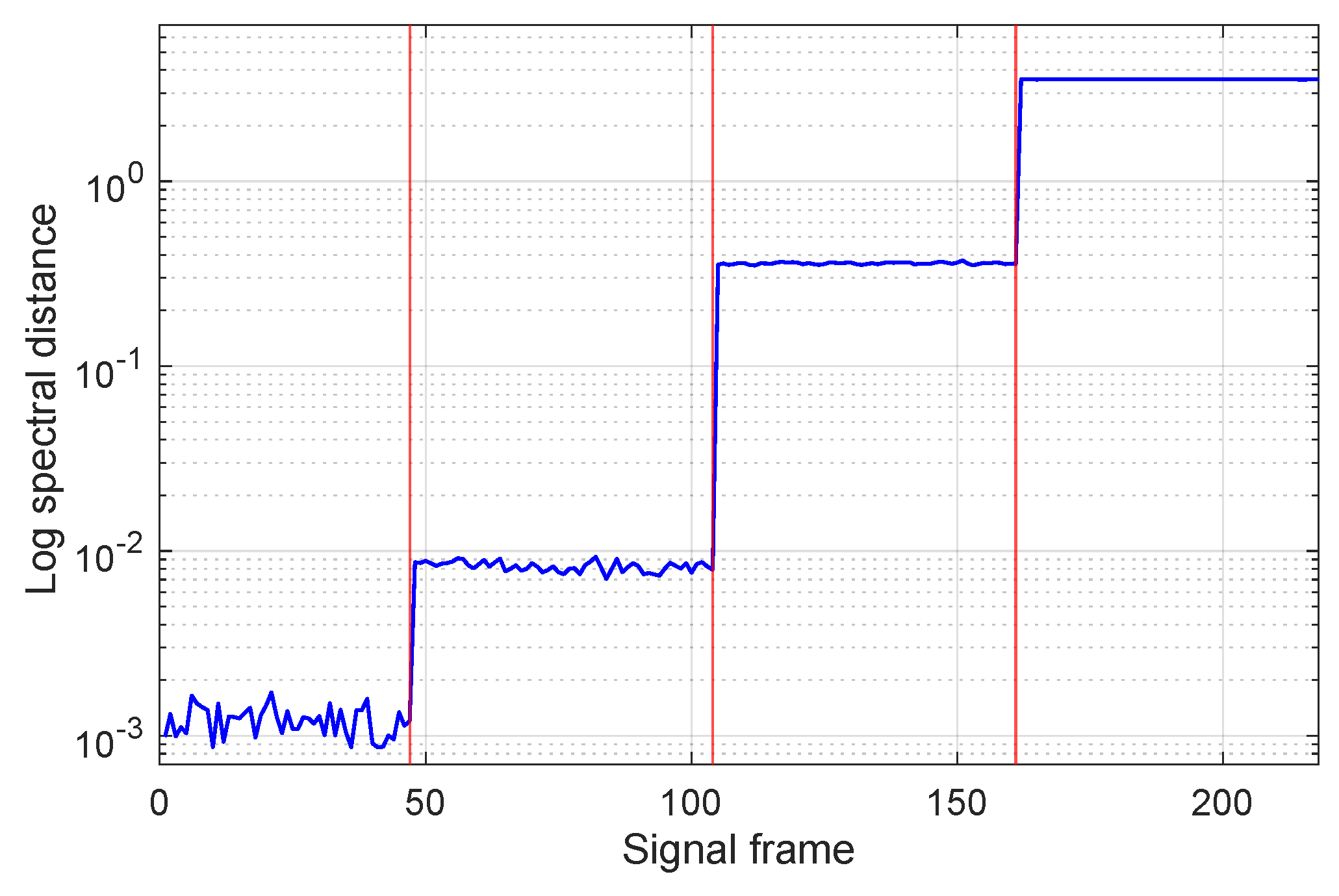
- The values corresponding to the four situations are different and, within each interval, the value of the indicator exhibits very small variations; this is consistent with the fact that the processed signal is due to the same fault type.
- Furthermore, the value of the spectral distance in the healthy case also remains almost constant and lower than in the other cases (by at least an order of magnitude), making the detection clear.
4.3. AR-Based FD: H-Bridge Inverter Supplying a WPT System
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Kumar, D.; Zare, F.; Ghosh, A. DC Microgrid Technology: System Architectures, AC Grid Interfaces, Grounding Schemes, Power Quality, Communication Networks, Applications, and Standardizations Aspects. IEEE Access 2017, 5, 12230–12256. [Google Scholar] [CrossRef]
- Bleilevens, R.; Priebe, J.; Wehbring, N.; Moser, A. Reliability Analysis of DC Distribution Grids. In Proceedings of the 2019 54th International Universities Power Engineering Conference (UPEC), Bucharest, Romania, 3–6 September 2019. [Google Scholar] [CrossRef]
- Zheng, K.; Yao, X.; Wang, W. Reliability Evaluation of Smart DC Microgrid. In Communications in Computer and Information Science; Springer International Publishing: Cham, Switzerland, 2022; pp. 595–605. [Google Scholar] [CrossRef]
- Weiss, R.; Ott, L.; Boeke, U. Energy efficient low-voltage DC-grids for commercial buildings. In Proceedings of the 2015 IEEE First International Conference on DC Microgrids (ICDCM), Atlanta, GA, USA, 7–10 June 2015. [Google Scholar] [CrossRef]
- Weckmann, S.; Sauer, A. DC Micro Grid for Energy Efficient and Flexible Production. Procedia Manuf. 2019, 39, 655–664. [Google Scholar] [CrossRef]
- Wang, H.; Pei, X.; Wu, Y.; Xiang, Y.; Kang, Y. Switch Fault Diagnosis Method for Series-Parallel Forward DC-DC Converter System. IEEE Trans. Ind. Electron. 2019, 66, 4684–4695. [Google Scholar] [CrossRef]
- Chen, F.; Zhong, Q.; Zhang, H.; Zhu, M.; Müller, S.; Meyer, J.; Huang, W. Survey of harmonic and supraharmonic emission of fast charging stations for electric vehicles in China and Germany. In Proceedings of the 26th International Conference and Exhibition on Electricity Distribution (CIRED), Online Conference, Nanjing, China, 24–27 August 2022; Institution of Engineering and Technology: Stevenage, UK, 2021. [Google Scholar] [CrossRef]
- Mariscotti, A. Harmonic and Supraharmonic Emissions of Plug-In Electric Vehicle Chargers. Smart Cities 2022, 5, 496–521. [Google Scholar] [CrossRef]
- Elsayed, A.T.; Mohamed, A.A.; Mohammed, O.A. DC microgrids and distribution systems: An overview. Electr. Power Syst. Res. 2015, 119, 407–417. [Google Scholar] [CrossRef]
- Hu, K.W.; Liaw, C.M. Incorporated operation control of DC microgrid and electric vehicle. IEEE Trans. Ind. Electron. 2016, 63, 202–215. [Google Scholar] [CrossRef]
- Baros, D.; Voglitsis, D.; Papanikolaou, N.P.; Kyritsis, A.; Rigogiannis, N. Wireless Power Transfer for Distributed Energy Sources Exploitation in DC Microgrids. IEEE Trans. Sustain. Energy 2019, 10, 2039–2049. [Google Scholar] [CrossRef]
- Simonazzi, M.; Sandrolini, L.; Mariscotti, A. Receiver–Coil Location Detection in a Dynamic Wireless Power Transfer System for Electric Vehicle Charging. Sensors 2022, 22, 2317. [Google Scholar] [CrossRef]
- Aviña-Corral, V.; Rangel-Magdaleno, J.d.J.; Barron-Zambrano, J.H.; Rosales-Nuñez, S. Review of fault detection techniques in power converters: Fault analysis and diagnostic methodologies. Measurement 2024, 234, 114864. [Google Scholar] [CrossRef]
- Collin, A.J.; Femine, A.D.; Landi, C.; Langella, R.; Luiso, M.; Testa, A. The Role of Supply Conditions on the Measurement of High-Frequency Emissions. IEEE Trans. Instrum. Meas. 2020, 69, 6667–6676. [Google Scholar] [CrossRef]
- Mariscotti, A.; Sandrolini, L.; Pasini, G. Variability Caused by Setup and Operating Conditions for Conducted EMI of Switched Mode Power Supplies Over the 2–1000 kHz Interval. IEEE Trans. Instrum. Meas. 2022, 71, 1501009. [Google Scholar] [CrossRef]
- Iqbal, M.N.; Kutt, L.; Asad, B.; Shabbir, N. Impact of Cable Impedance on the Harmonic Emission of LED Lamps. In Proceedings of the 2020 21st International Scientific Conference on Electric Power Engineering (EPE), Prague, Czech Republic, 19–21 October 2020. [Google Scholar] [CrossRef]
- Bollen, M.; Ronnberg, S.; Hooshyar, H. Spread of high frequency current emission. In Proceedings of the 22nd International Conference and Exhibition on Electricity Distribution (CIRED 2013), Stockholm, Sweden, 10–13 June 2013; Institution of Engineering and Technology: Stevenage, UK, 2013. [Google Scholar] [CrossRef]
- Suzuki, M.; Ogawa, K.; Shijo, T.; Kanekivo, Y.; Inoue, K.; Ogura, K.; Obayashi, S.; Ishida, M. Conducted Emission in an 85 kHz, 50 kW WPT System with Opposite-Phase Transfer and Spread Spectrum. In Proceedings of the 2019 IEEE PELS Workshop on Emerging Technologies: Wireless Power Transfer (WoW), London, UK, 18–21 June 2019; pp. 1–4. [Google Scholar] [CrossRef]
- Stepins, D.; Zakis, J.; Audze, J.; Husev, O.; Pakhaliuk, B.; Shevchenko, V. Reduction of Conducted Emissions Generated by WPT Systems with Multilevel Inverters using Spread Spectrum Approach. In Proceedings of the IECON 2020 the 46th Annual Conference of the IEEE Industrial Electronics Society, Singapore, 18–21 October 2020; pp. 3924–3929. [Google Scholar] [CrossRef]
- Simonazzi, M.; Campanini, A.; Sandrolini, L.; Rossi, C. Design Procedure Based on Maximum Efficiency for Wireless Power Transfer Battery Chargers with Lightweight Vehicle Assembly. Energies 2021, 15, 70. [Google Scholar] [CrossRef]
- Simonazzi, M.; Sandrolini, L.; Campanini, A. Input Current of H-bridge Inverters with Asymmetric Switch Parameters for Wireless Power Transfer Applications. In Proceedings of the 2023 IEEE 17th International Conference on Compatibility, Power Electronics and Power Engineering (CPE-POWERENG), Tallinn, Estonia, 14–16 June 2023; pp. 1–5. [Google Scholar] [CrossRef]
- Han, R.; Wang, R.; Zeng, G. Fault Diagnosis Method of Power Electronic Converter Based on Broad Learning. Complexity 2020, 2020, 7463291. [Google Scholar] [CrossRef]
- Januszewski, S.; Kociszewska-Szczerbik, M.; Swiaiek, H.; Swiatek, G. Semiconductor Device Failures in Power Converter Service Conditions. EPE J. 1998, 7, 12–17. [Google Scholar] [CrossRef]
- Valentine, N.; Das, D.; Sood, B.; Pecht, M. Failure Analyses of Modern Power Semiconductor Switching Devices. IMAPSource Proc. 2015, 2015, 690–695. [Google Scholar] [CrossRef]
- Hanif, A.; Yu, Y.; DeVoto, D.; Khan, F. A Comprehensive Review Toward the State-of-the-Art in Failure and Lifetime Predictions of Power Electronic Devices. IEEE Trans. Power Electron. 2019, 34, 4729–4746. [Google Scholar] [CrossRef]
- Fuchs, F. Some diagnosis methods for voltage source inverters in variable speed drives with induction machines—A survey. In Proceedings of the IECON’03. 29th Annual Conference of the IEEE Industrial Electronics Society (IEEE Cat. No.03CH37468), Roanoke, VA, USA, 2–6 November 2003; Volume 2, pp. 1378–1385. [Google Scholar] [CrossRef]
- Dhumale, R.; Lokhande, S. Neural Network Fault Diagnosis of Voltage Source Inverter under variable load conditions at different frequencies. Measurement 2016, 91, 565–575. [Google Scholar] [CrossRef]
- Zhao, H.; Cheng, L. Open-Switch Fault-Diagnostic Method for Back-to-Back Converters of a Doubly Fed Wind Power Generation System. IEEE Trans. Power Electron. 2018, 33, 3452–3461. [Google Scholar] [CrossRef]
- Mullali Kunnontakath Puthiyapurayil, M.R.; Nadir Nasirudeen, M.; Saywan, Y.A.; Ahmad, M.W.; Malik, H. A Review of Open-Circuit Switch Fault Diagnostic Methods for Neutral Point Clamped Inverter. Electronics 2022, 11, 3169. [Google Scholar] [CrossRef]
- Lee, J.; Choi, H.G.; Lee, K. Advanced Fault Diagnosis in Power Electronics: Switch Open Faults in DC-Link Shunt Sensor-Less Drives. J. Electr. Eng. Technol. 2024. [Google Scholar] [CrossRef]
- Isermann, R. Model-based fault-detection and diagnosis – status and applications. Annu. Rev. Control. 2005, 29, 71–85. [Google Scholar] [CrossRef]
- Hwang, I.; Kim, S.; Kim, Y.; Seah, C.E. A Survey of Fault Detection, Isolation, and Reconfiguration Methods. IEEE Trans. Control. Syst. Technol. 2010, 18, 636–653. [Google Scholar] [CrossRef]
- Alavi, M.; Luo, M.; Wang, D.; Zhang, D. Fault diagnosis for power electronic inverters: A model-based approach. In Proceedings of the 8th IEEE Symposium on Diagnostics for Electrical Machines, Power Electronics & Drives, Bologna, Italy, 5–8 September 2011; pp. 221–228. [Google Scholar] [CrossRef]
- Kou, L.; Liu, C.; Cai, G.W.; Zhang, Z. Fault Diagnosis for Power Electronics Converters based on Deep Feedforward Network and Wavelet Compression. Electr. Power Syst. Research 2020, 185, 106370. [Google Scholar] [CrossRef]
- Box, G.E.; Jenkins, G.M.; Reinsel, G.C.; Ljung, G.M. Time Series Analysis: Forecasting and Control; John Wiley & Sons: Hoboken, NJ, USA, 2015. [Google Scholar]
- Kay, S.M. Modern Spectral Estimation; Prentice Hall: Upper Saddle River, NJ, USA, 1988. [Google Scholar]
- Stoica, P.; Moses, R.L. Spectral Analysis of Signals; Pearson Prentice Hall Upper: Saddle River, NJ, USA, 2005. [Google Scholar]
- Baillie, D.; Mathew, J. A comparison of autoregressive modeling techniques for fault diagnosis of rolling element bearings. Mech. Syst. Signal Process. 1996, 10, 1–17. [Google Scholar] [CrossRef]
- Wang, W.; Wong, A.K. Autoregressive model-based gear fault diagnosis. J. Vib. Acoust. 2002, 124, 172–179. [Google Scholar] [CrossRef]
- Stack, J.; Habetler, T.; Harley, R. Bearing fault detection via autoregressive stator current modeling. IEEE Trans. Ind. Appl. 2004, 40, 740–747. [Google Scholar] [CrossRef]
- Isermann, R. Fault-Diagnosis Systems: An Introduction from Fault Detection to Fault Tolerance; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Junsheng, C.; Dejie, Y.; Yu, Y. A fault diagnosis approach for roller bearings based on EMD method and AR model. Mech. Syst. Signal Process. 2006, 20, 350–362. [Google Scholar] [CrossRef]
- Barbieri, M.; Diversi, R.; Tilli, A. Condition monitoring of ball bearings using estimated AR models as logistic regression features. In Proceedings of the 2019 18th European Control Conference (ECC), Naples, Italy, 25–28 June 2019; pp. 3904–3909. [Google Scholar] [CrossRef]
- Diversi, R.; Speciale, N.; Barbieri, M. Combining wavelets and AR identification for condition monitoring of electric-cam mechanisms using PLCopen readings of motor torque. Int. J. Progn. Health Manag. 2024, 15, 1–16. [Google Scholar] [CrossRef]
- Barbieri, M.; Bosso, A.; Conficoni, C.; Diversi, R.; Sartini, M.; Tilli, A. An Onboard Model-of-signals Approach for Condition Monitoring in Automatic Machines. In Enterprise Interoperability; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2018; Chapter 32; pp. 263–269. [Google Scholar] [CrossRef]
- Barbieri, M.; Nguyen, K.T.; Diversi, R.; Medjaher, K.; Tilli, A. RUL prediction for automatic machines: A mixed edge-cloud solution based on model-of-signals and particle filtering techniques. J. Intell. Manuf. 2021, 32, 1421–1440. [Google Scholar] [CrossRef]
- Lee, J.; Wu, F.; Zhao, W.; Ghaffari, M.; Liao, L.; Siegel, D. Prognostics and health management design for rotary machinery systems—Reviews, methodology and applications. Mech. Syst. Signal Process. 2014, 42, 314–334. [Google Scholar] [CrossRef]
- Atamuradov, V.; Medjaher, K.; Dersin, P.; Lamoureux, B.; Zerhouni, N. Prognostics and health management for maintenance practitioners - Review, implementation and tools evaluation. Int. J. Progn. Health Manag. 2017, 8, 1–31. [Google Scholar] [CrossRef]
- Soualhi, A.; Lamraoui, M.; Elyousfi, B.; Razik, H. PHM SURVEY: Implementation of Prognostic Methods for Monitoring Industrial Systems. Energies 2022, 15, 6909. [Google Scholar] [CrossRef]
- Ott, H.W. Electromagnetic Compatibility Engineering; John Wiley & Sons: Hoboken, NJ, USA, 2011. [Google Scholar]
- Mariscotti, A. Analysis of the DC-link current spectrum in voltage source inverters. IEEE Trans. Circuits Syst. Fundam. Theory Appl. 2002, 49, 484–491. [Google Scholar] [CrossRef]
- Cox, S.M. Voltage and current spectra for a single-phase voltage source inverter. IMA J. Appl. Math. 2009, 74, 782–805. [Google Scholar] [CrossRef]
- Pei, X.; Zhou, W.; Kang, Y. Analysis and Calculation of DC-Link Current and Voltage Ripples for Three-Phase Inverter with Unbalanced Load. IEEE Trans. Power Electron. 2015, 30, 5401–5412. [Google Scholar] [CrossRef]
- Abari, I.; Lahouar, A.; Hamouda, M.; Slama, J.B.H.; Al-Haddad, K. Fault Detection Methods for Three-Level NPC Inverter Based on DC-Bus Electromagnetic Signatures. IEEE Trans. Ind. Electron. 2018, 65, 5224–5236. [Google Scholar] [CrossRef]
- Linear Technology Corporation. LT Spice XVII (x64), Ver. 17.0.37.0. 2024. Available online: https://www.analog.com/en/resources/design-tools-and-calculators/ltspice-simulator.html (accessed on 24 July 2024).
- Basseville, M. Distance measures for signal processing and pattern recognition. Signal Process. 1989, 18, 349–369. [Google Scholar] [CrossRef]
- Mechefske, C.; Mathew, J. Fault detection and diagnosis in low speed rolling element bearings Part II: The use of nearest neighbour classification. Mech. Syst. Signal Process. 1992, 6, 309–316. [Google Scholar] [CrossRef]
- Dron, J.; Rasolofondraibe, L.; Bolaers, F.; Pavan, A. High-resolution methods in vibratory analysis: Application to ball bearing monitoring and production machine. Int. J. Solids Struct. 2001, 38, 4293–4313. [Google Scholar] [CrossRef]
- He, Q.; Du, D.; Wang, X. Autoregressive Model-Based Vibration Fault Diagnosis of Rolling Bearing. Noise Vib. Worldw. 2010, 41, 22–28. [Google Scholar] [CrossRef]
- Nikhar, N.K.; Patankar, S.S.; Kulkarni, J.V. Gear tooth fault detection by autoregressive modelling. In Proceedings of the 2013 Fourth International Conference on Computing, Communications and Networking Technologies (ICCCNT), Tiruchengode, India, 4–6 July 2013; pp. 1–6. [Google Scholar] [CrossRef]
- Quirk, M.; Liu, B. Improving resolution for autoregressive spectral estimation by decimation. IEEE Trans. Acoust. Speech Signal Process. 1983, 31, 630–637. [Google Scholar] [CrossRef]





| Quantity | Symbol | Value |
|---|---|---|
| Coil resistance | R | |
| Coil self-inductance | L | H |
| Coils mutual inductance | M | 5 H |
| Compensation capacitance | C | 280 nF |
| Resonance frequency | 85 kHz | |
| Load resistance | ||
| Source voltage | 50 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Diversi, R.; Sandrolini, L.; Simonazzi, M.; Speciale, N.; Mariscotti, A. Diagnostics on Power Electronics Converters by Means of Autoregressive Modelling. Electronics 2024, 13, 3083. https://doi.org/10.3390/electronics13153083
Diversi R, Sandrolini L, Simonazzi M, Speciale N, Mariscotti A. Diagnostics on Power Electronics Converters by Means of Autoregressive Modelling. Electronics. 2024; 13(15):3083. https://doi.org/10.3390/electronics13153083
Chicago/Turabian StyleDiversi, Roberto, Leonardo Sandrolini, Mattia Simonazzi, Nicolò Speciale, and Andrea Mariscotti. 2024. "Diagnostics on Power Electronics Converters by Means of Autoregressive Modelling" Electronics 13, no. 15: 3083. https://doi.org/10.3390/electronics13153083
APA StyleDiversi, R., Sandrolini, L., Simonazzi, M., Speciale, N., & Mariscotti, A. (2024). Diagnostics on Power Electronics Converters by Means of Autoregressive Modelling. Electronics, 13(15), 3083. https://doi.org/10.3390/electronics13153083









