Practical Verification of Diagnostic Capabilities of Methods for the Recreation of Voltage Fluctuations

Abstract

Voltage fluctuations are one of the most common problems in low-voltage networks. Very often, these disturbances cause damage to or the incorrect operation of electrical devices. Unfortunately, at present, the monitoring of these disturbances relies on short-term and long-term flicker indicators, which only assess the severity of one of the effects of voltage fluctuations. Another measure of voltage fluctuations that has greater diagnostic potential is voltage fluctuation indices, i.e., the amplitude and rate of voltage fluctuations. One advantage of these indices that has been highlighted in recent years is their potential ability to recreate voltage fluctuations using these indices. This article presents research results that allow for the verification of the potential of voltage fluctuation indices as a method for recreating voltage fluctuations. For verification purposes, various cases of voltage variation recorded in a modern low-voltage network are used. The analysis of the possibility of recreating voltage fluctuations from voltage fluctuation indices presented in this article, in association with previously carried out numerical simulation studies and experimental laboratory studies, constitutes a complementary whole and indicates further directions in voltage fluctuation research in terms of the electromagnetic compatibility of low-frequency conducted disturbances.

1. Introduction

Voltage fluctuations [1] are one of the most common disturbances of power quality in modern low-voltage power networks [2]. Voltage fluctuations can occur alone or simultaneously with other power quality disturbances [3]. If these disturbances occur simultaneously with the “clipped cosine” voltage distortion, which is typical for low-voltage networks as a result of the impact of the input stages of switching power supplies, the effects of voltage fluctuations can be intensified [4,5]. Such situations can also occur in the case of renewable energy source systems operating in a modern low-voltage power grid. Inverters cooperating with renewable energy sources, in which high-frequency switching is implemented, can cause flicker as a result of interaction with voltage distortions [4]. Voltage fluctuations often result in the deterioration of the operation of electrical loads, shortening their operating time and, in the worst case, damaging them [6,7,8,9]. If these electrical loads are light sources, flicker [10] can occur as a result of voltage fluctuations. In the case of modern light sources, it is difficult to associate voltage fluctuations with flicker [11] (e.g., for LED lamps, because of the power supplies with stabilizers of different topologies, it is not possible to clearly associate voltage fluctuations with flicker [12,13,14]). However, it is worth noting that flicker can also occur for some LED lamps [15,16,17]. If the electrical loads are, for example, electrical machines, there may be torque ripple [18], thermal transients [19], vibrations [20], and other states that shorten the life of these machines [21,22,23]. In recent years, more and more research results have quantitatively and qualitatively demonstrated the effects of voltage fluctuations on operations involving specific electrical loads [24,25,26].

However, even though voltage fluctuations occur frequently and cause real negative effects on the operation of commonly used electrical loads, there is still no comprehensive measure that accurately determines the severity of voltage fluctuations. One of the most commonly used measures of voltage fluctuations is short-term $P_{st}$ [27] and long-term $P_{lt}$ [28] flicker indicators that are measured using the IEC flickermeter [29,30]. The widespread use of these measures is due to the current normative requirements [3,30,31]. However, these measures only assess one effect of voltage fluctuations in the form of flicker [10], and even in this respect, the measure is limited because it includes the association between voltage fluctuations and flicker for one type of light source, i.e., an incandescent light source. Another measure of voltage fluctuations is the $\Delta V_{10}$ indicator [32], which is used in Asian countries. It is worth noting that the diagnostic capabilities of this measure of voltage fluctuations are similar to those of short-term $P_{st}$ and long-term $P_{lt}$ flicker indicators. In analyzing various measures of voltage fluctuations presented in the scientific literature, it is evident that voltage fluctuation indices, i.e., the amplitude $\delta U$ and rate f_x−y of voltage fluctuations in specific periods of discrimination $T_w$ [33], have great potential. These indices enable, among others, the analysis of voltage variations in the power grid [34], the identification of sources of disturbances in the power grid [35], and the indication of their power supply point [36]. The greatest advantage of this measure of voltage fluctuations is that it stores information about specific variations in voltage [34], and the level of severity of voltage fluctuation is assessed only on the basis of the selected and applied curve for the characteristic ($\delta U$,f_x−y) [34]. Therefore, the recorded voltage fluctuation indices allow us to determine the severity of voltage fluctuations in association with the various consequences of this disturbance.

Taking into account the fact that voltage fluctuation indices contain information about the variation in the root mean square (rms) value over time, in recent years, various publications have presented proposals for the recreation of voltage fluctuations using these indices [37,38,39]. The recreation of voltage fluctuations allows for the conversion of voltage fluctuation indices into other measures of voltage fluctuations [40], a post-factum investigation of various electrical loads within states that actually occurred in the power grid, or the implementation of various complex algorithms based on voltage waveforms [41]. It is worth emphasizing that a post-factum investigation of various electrical devices is particularly important in assessments regarding electromagnetic compatibility in the field of conducted low-frequency disturbances. The accurate recreation of voltage fluctuations is not possible because coding information about voltage variation into voltage fluctuation indices is a lossy process. However, the more reliable the recreation of voltage fluctuation is, the more effective the practical use of information about the recreated voltage fluctuations would be [42]. Currently, in the literature, the assessment of the effectiveness of recreating voltage fluctuations is carried out by flicker comparison, i.e., in the process of recreating voltage fluctuations, the aim is to obtain a signal that recreates the same effect as the original signal occurring in the real network. This is a result of the fact that $P_{st}$/$P_{lt}$ indicators are now broadly used to assess the severity of voltage fluctuations (there is no other widely accepted alternative comparative measure). Nevertheless, it is worth noting that the methods currently proposed in the literature for the recreation of voltage fluctuations from voltage fluctuation indices are validated on the basis of the following elements:

• Numerical simulation studies using signal models of voltage fluctuations [38,39];
• Experimental laboratory tests using signal models of voltage fluctuations [38,42];
• Experimental laboratory tests using a model of a real power grid, in which there were only single sources of voltage fluctuations in a specific power supply circuit [43].

Taking into account the limited scope of this research, which only concerns methods that recreate voltage fluctuations from voltage fluctuation indices, this article presents the results of research on the possibility of recreating voltage fluctuations from voltage fluctuation indices within various states recorded on the real power grid. Therefore, the presented research results in this article in connection with the previously presented results of numerical simulation studies [38] and experimental laboratory studies [43], constitute a complementary whole that allows for a reliable assessment of the possibility of recreating voltage fluctuations using voltage fluctuation indices. It is worth noting that this article is an extension of a former conference paper [43].

The structure of the article is as follows: Section 2 presents a description of the way in which voltage fluctuation indices are determined within the current measurement infrastructure. Section 3 presents selected methods for recreating voltage fluctuations from voltage fluctuation indices, the diagnostic capabilities of which are evaluated for the purposes of this article. Section 4 describes the data used to verify the ability to recreate voltage fluctuations from voltage fluctuation indices. Section 5 presents the research results and their discussion. Section 6 presents the most important final conclusions and further directions for development. A diagram presenting the conceptual organization of the article is shown in Figure 1.

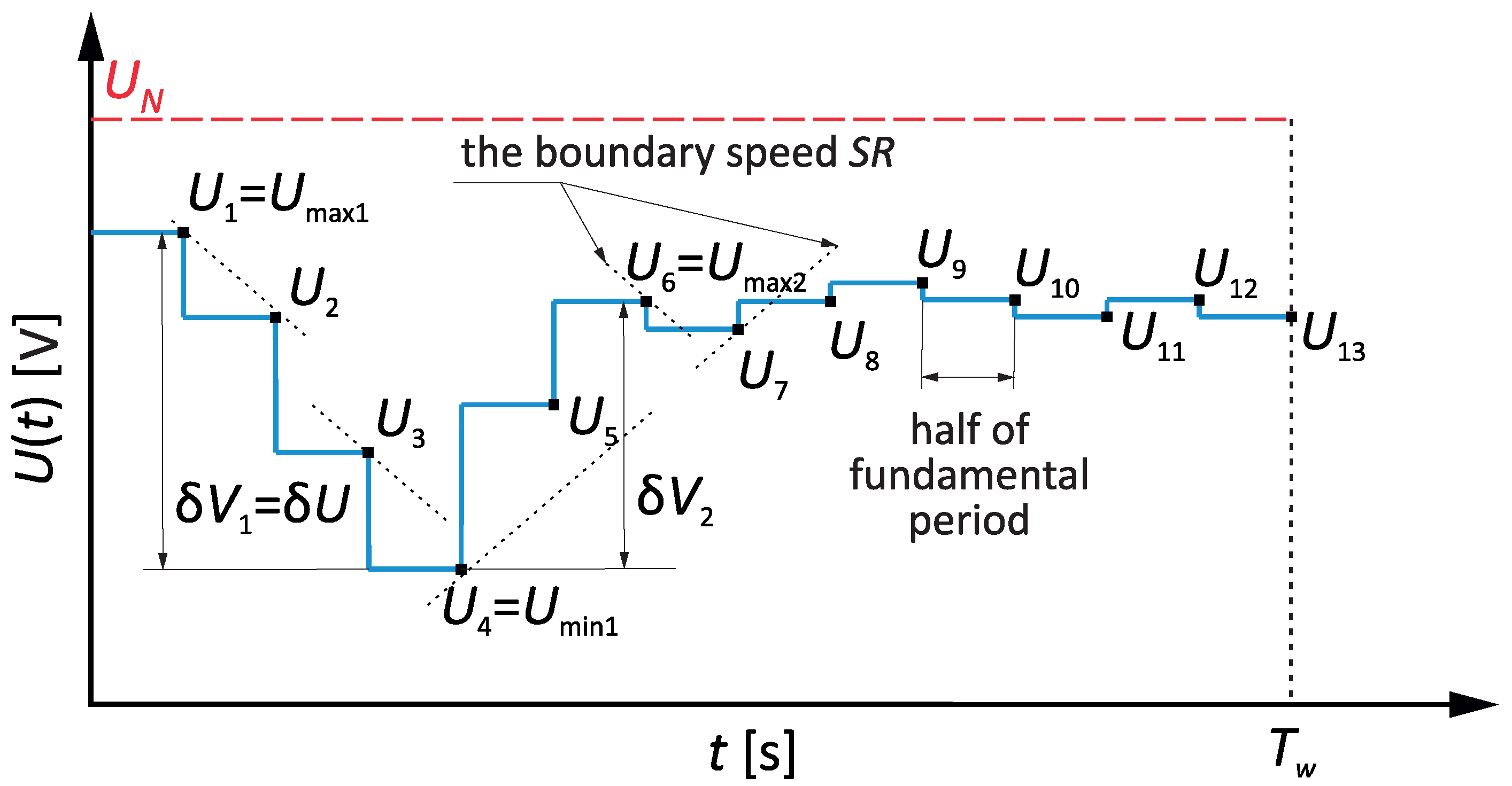
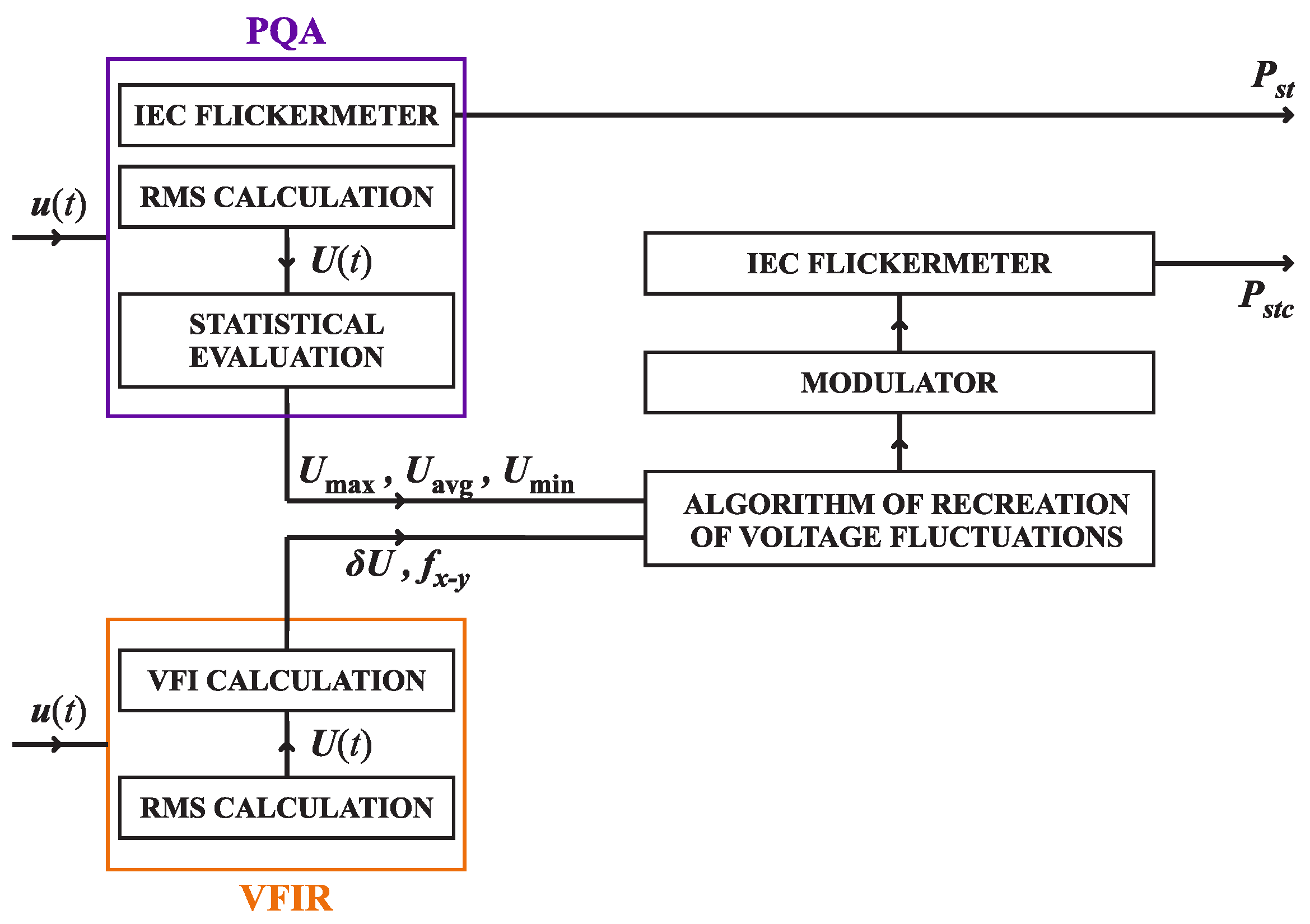
2. Brief Description of Voltage Fluctuation Indices

Voltage fluctuation indices are a measure that describes voltage fluctuations in terms of the amplitude $\delta U$ and the rate f_x−y of these voltage fluctuations [33,34]. Voltage fluctuation indices are determined on the basis of changes in the rms values of voltage $U\left(t\right)$ determined for the fundamental period of voltage T every half of this fundamental period T [33,34]. Much better diagnostic properties have analogous voltage fluctuation indices based on the voltage envelope $u_{\mathrm{env}}\left(t\right)$: $\delta U_e$ and $f_{e_{x-y}}$, determined on the basis of changes in the estimated voltage envelope $u_{\mathrm{env}}\left(t\right)$ by a demodulator with the estimation of the signal carrier [42]. However, the determination of voltage fluctuation indices from the estimated voltage envelope $u_{\mathrm{env}}\left(t\right)$, which is carried out with a demodulator with signal carrier estimation [42], requires significant changes in the signal chains of the measuring and recording devices used in practice. Therefore, for the purposes of this article, a conventional method is used to determine voltage fluctuation indices. The conventional approach allows for the direct possibility of the offline application of complex algorithms [41] to the recreated voltage fluctuations without modifying the currently used measuring and recording devices [33]. Moreover, the use of a conventional approach allows for a post-factum examination of states occurring in the power grid without the need to use long-term oscilloscope recordings, which results in significant memory consumption. Voltage fluctuation indices $\delta U$ and f_x−y directly describe changes in voltage classified as voltage fluctuations. Voltage fluctuation indices do not have a clear analytical definition, and their measurement is accomplished via an appropriate procedure. Similarly, the short-term flicker indicator $P_{st}$ does not have a clear analytical definition and is determined by an appropriate procedure specified in the appropriate standard [30]. The measurement of voltage fluctuation indices can be divided into two stages:

• The detection of the amplitudes $\delta V$ of subsequent changes in the rms values of voltage $U\left(t\right)$ in a given discrimination period $T_w$;
• The statistical assessment of the amplitudes $\delta V$ of subsequent changes recorded during the period of discrimination $T_w$, allowing for the determination of the final form of voltage fluctuation indices: the amplitude $\delta U$ and the rate f_x−y of voltage fluctuations.

The detection of the amplitudes $\delta V$ of subsequent changes in the rms values of the voltage $U\left(t\right)$ requires a preliminary determination of the speed $SR$ of changes in the rms values of the voltage $U\left(t\right)$. The change in the rms value of the voltage $U\left(t\right)$ is classified as amplitude $\delta V$ only when its speed SR exceeds the limit value, which is generally assumed in measuring and recording instruments to be equal to 1%$U_N/s$, where $U_N$ is the nominal rms value of voltage in the power network [33]. Based on the set of $\delta V$ values of subsequent changes in the rms values voltage $U\left(t\right)$, statistical analyses are performed, in which the number of occurrences of individual amplitudes $\delta V$ is determined in subsets related to the maximum $\delta V$ value in a given period $T_w$, which is taken as $\delta U$. For the purposes of this article, the following $\delta U$ sub-ranges are adopted: [1.0;0.9], (0.9;0.8], (0.8;0.7], (0.7;0.6], (0.6;0.5], (0.5;0.4], (0.4;0.0). For simplicity, they are written as $f_{1.0-0.9}$, $f_{0.9-0.8}$, $f_{0.8-0.7}$, $f_{0.7-0.6}$, $f_{0.6-0.5}$, $f_{0.5-0.4}$, $f_{0.4-0.0}$. The use of such sub-ranges is typical for measuring and recording devices that enable the recording of voltage fluctuation indices [33]. The process of determining the amplitudes $\delta V$ of subsequent changes in the rms voltage values $U\left(t\right)$ is shown in Figure 2.

3. Description of Selected Methods for Recreating Voltage Fluctuations

Selected methods for recreating voltage fluctuations, marked as M1, M2, and M3 [38,43], are used for the purposes of this research. Input data for individual methods (for periods of discrimination $T_w$ equal to 1 min and 5 min) are as follows:

• The minimum rms value of voltage $U_{\min }$ in $T_w$;
• The maximum rms value of voltage $U_{\max }$ in $T_w$;
• The average rms value of voltage $U_{\mathrm{avg}}$ in $T_w$;
• The amplitude of voltage fluctuations $\delta U$;
• The rate f_x−y of voltage fluctuations for individual sub-ranges $\delta U$: $f_{1.0-0.9}$, $f_{0.9-0.8}$, $f_{0.8-0.7}$, $f_{0.7-0.6}$, $f_{0.6-0.5}$, $f_{0.5-0.4}$, $f_{0.4-0.0}$.

In the recreation process, for research purposes, it is assumed that the amplitudes $\delta V$ of particular changes in the rms values of the voltage $U\left(t\right)$ are equal to the following:

• $\delta U$ in the sub-range $f_{1.0-0.9}$;
• 0.85$\delta U$ in the sub-range $f_{0.9-0.8}$;
• 0.75$\delta U$ in the sub-range $f_{0.8-0.7}$;
• 0.65$\delta U$ in the sub-range $f_{0.7-0.6}$;
• 0.55$\delta U$ in the sub-range $f_{0.6-0.5}$;
• 0.45$\delta U$ in the sub-range $f_{0.5-0.4}$;
• 0.39$\delta U$/0.3$\delta U$/0.2$\delta U$/0.1$\delta U$/0.01$\delta U$ in the sub-range $f_{0.4-0.0}$ (the number of changes in the sub-range is divided into five equal sets, and the rest falls on the central value).

Each method recreates subsequent changes in the rms values of voltage $U\left(t\right)$ in such a way that they oscillate around the average rms value of voltage $U_{\mathrm{avg}}$ and so that subsequent changes do not leave the range from $U_{\min }$ to $U_{\max }$. Differences between the process of recreating voltage fluctuations via individual methods M1 to M3 can be presented in detail as follows [38,43]:

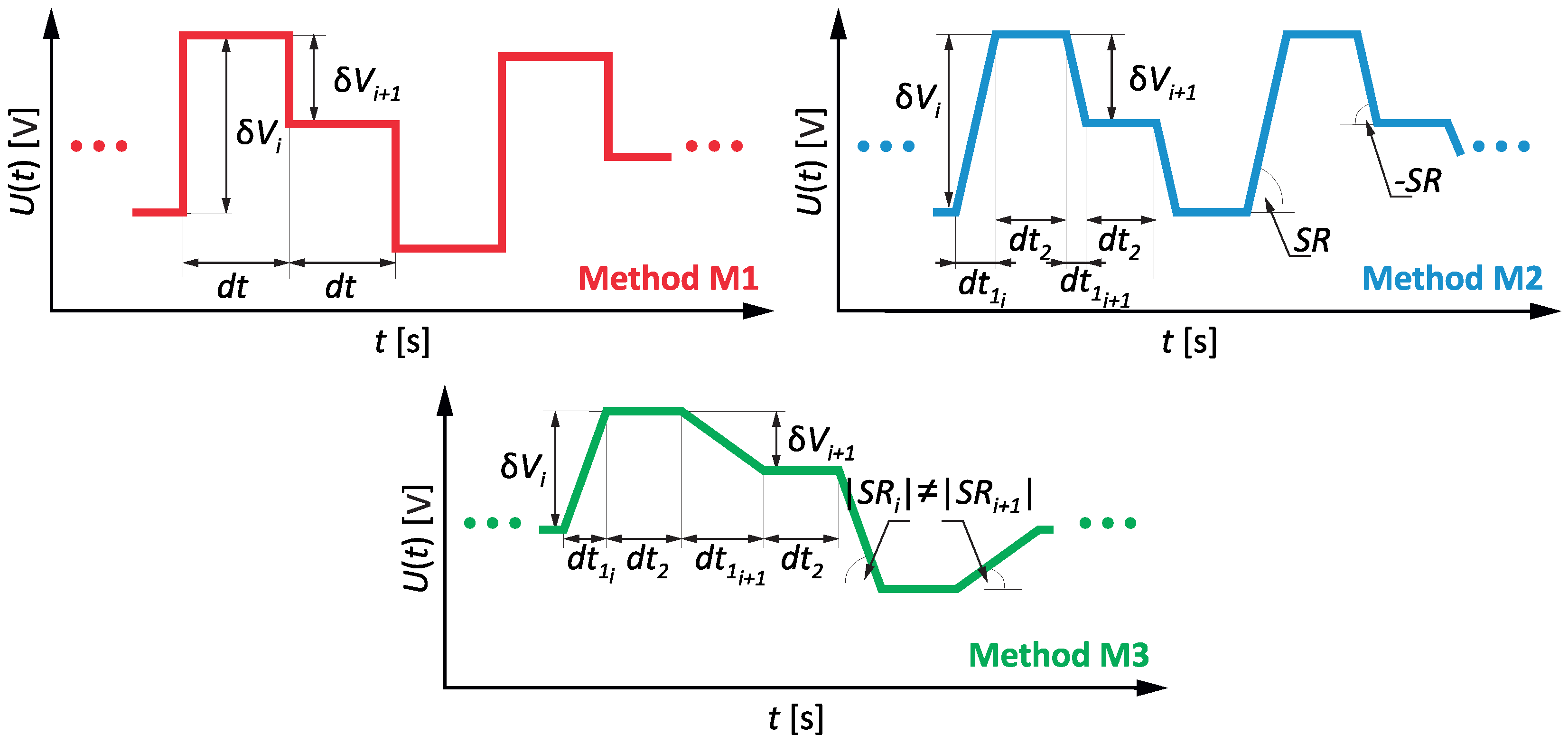
M1: 

This method recreates voltage fluctuations as step changes in the rms values of voltage $U\left(t\right)$, which correspond to the amplitude modulation with a square wave. The individual adopted amplitudes $\delta V$ of voltage changes are distributed evenly throughout the considered discrimination period $T_w$, and the order of their occurrence is random according to a uniform distribution. The subsequent assumed amplitudes $\delta V$ of voltage changes are distributed in such a way (by considering the sign of the voltage change) that they oscillate around the measured average rms value $U_{\mathrm{avg}}$ and that the recreated values within the range can be defined by the measured minimum $U_{\min }$ and maximum $U_{\max }$ rms values of voltage. An example fragment of the voltage fluctuations recreated using the M1 method is shown in Figure 3, where the time $dt$ is constant during the discrimination period $T_w$ and depends on the number of subsequent changes $\delta V$.

M2: 

This method recreates voltage fluctuations as trapezoidal changes in the rms values of the voltage $U\left(t\right)$, assuming a constant speed $SR$ of voltage fluctuations equal to $SR=300\%\delta U_N/s$. The individual adopted amplitudes $\delta V$ of voltage changes are evenly distributed throughout considered discrimination time $T_w$ considered, and the order of their occurrence is random according to a uniform distribution. The subsequently adopted amplitudes $\delta V$ of voltage changes in the rms values $U\left(t\right)$ are distributed in such a way (by considering the sign of the voltage change) that they oscillate around the measured average rms value $U_{\mathrm{avg}}$ and that the recreated values fall within the range defined by the measured minimum $U_{\min }$ and maximum $U_{\max }$ rms values of voltage. An example fragment of the voltage fluctuations recreated using the M2 method is shown in Figure 3, where the time $d{t}_2$ is constant during the discrimination period $T_w$ and depends on the number of subsequent changes $\delta V$, and the time $d{t}_1$ is variable and depends on the adopted constant value of the speed $SR$.

M3: 

This method recreates voltage fluctuations as trapezoidal changes in the rms values of voltage $U\left(t\right)$, assuming a variable speed $SR$ for recreation of voltage fluctuations. The individual speed $SR$ for the subsequent introduced amplitudes $\delta V$ of the voltage changes are randomized within a gamma distribution with a shape parameter of 1 and a scale parameter of 300. The individual adopted amplitudes $\delta V$ of voltage changes are evenly distributed throughout the considered discrimination time $T_w$, and the order of their occurrence is random, according to a uniform distribution. The subsequently assumed amplitudes $\delta V$ of voltage changes are distributed in such a way (by considering the sign of the change) that they oscillate around the measured average rms value $U_{\mathrm{avg}}$ and that the recreated values are within the range defined by the measured minimum $U_{\min }$ and maximum $U_{\max }$ rms values of voltage. An example fragment of the voltage fluctuations recreated using the M3 method is shown in Figure 3, where the time $d{t}_2$ is constant during the discrimination period $T_w$ and depends on the number of subsequent changes $\delta V$ and the time $d{t}_1$ is variable and depends on the random value of the speed $SR$.

Figure 3. Fragment of voltage fluctuations recreated by individual methods M1, M2, and M3.

Figure 3. Fragment of voltage fluctuations recreated by individual methods M1, M2, and M3.

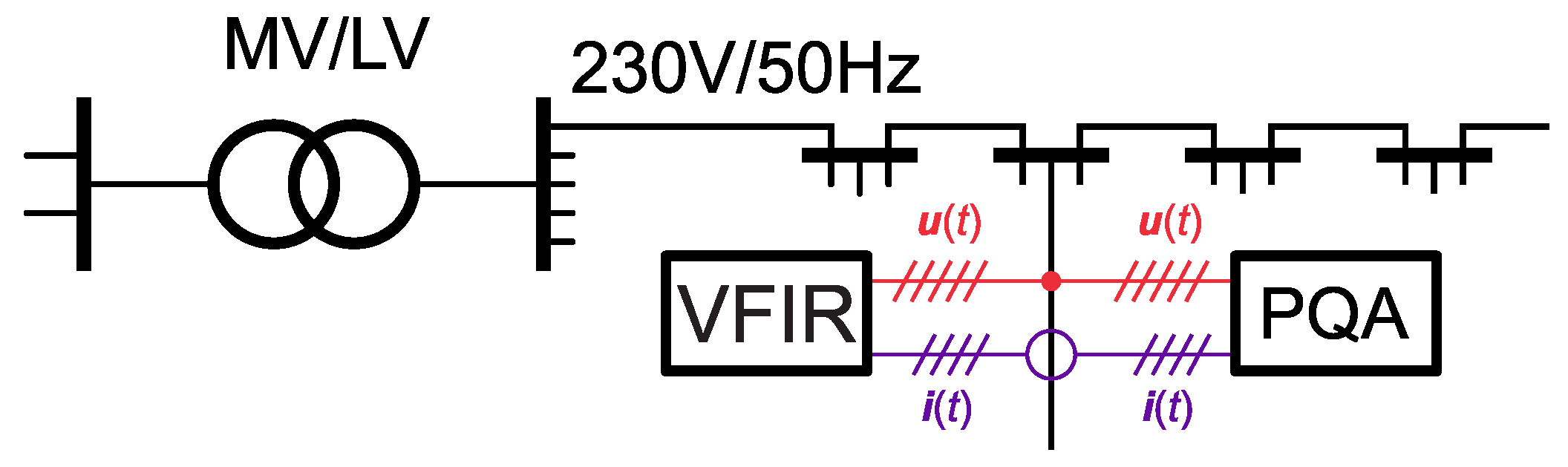
4. Description of Data Used for Verification

For verification purposes, 25 sets of measurement results were used, which were obtained via different power supply circuits of a three-phase low-voltage network. A simplified diagram of the measurement setup is shown in Figure 4.

A class A power quality analyzer (PQA) with a voltage fluctuation index recorder (VFIR) was used to record the selected parameters. The selected parameters, which are important for the verification of the selected algorithms that recreate voltage fluctuations, are as follows:

• The short-time $P_{st}$ and long-time $P_{lt}$ flicker indicator;
• The minimum rms value of voltage $U_{\min }$ in $T_w$;
• The maximum rms value of voltage $U_{\max }$ in $T_w$;
• The average rms value of voltage $U_{\mathrm{avg}}$ in $T_w$;
• The amplitude of voltage fluctuations $\delta U$;
• The rate f_x−y of voltage fluctuations for individual sub-ranges $\delta U$: $f_{1.0-0.9}$, $f_{0.9-0.8}$, $f_{0.8-0.7}$, $f_{0.7-0.6}$, $f_{0.6-0.5}$, $f_{0.5-0.4}$, and $f_{0.4-0.0}$.

Each set of measurement results includes periods during which voltage fluctuations of different degrees of severity occurred. Taking into account the fact that the measurements were taken on a real power grid, they include the resultant impacts from all loads operating during the recording. Therefore, it is not possible to indicate all sources of disturbance in detail. Depending on the power supply circuit within which the measurements were made, the dominant sources of disturbance could be pumps, welding machines, industrial machines (including systems equipped with soft starters), and resultant variable loads from production processes. Therefore, the obtained sets of measurement results contain registrations for states of voltage fluctuations caused by a wide range of electrical devices, which increases the reliability with which we can verify algorithms that recreate voltage fluctuations from the recorded data. The individual sets of measurement results are as follows:

• Case 1. Measurements taken over a period of 5 days, with the following settings:

  –

  The discrimination period $T_w$ of voltage fluctuation indices is 5 min;

  –

  $P_{st}$ values vary in the range from 0.29 to 2.14 (the average value of $P_{st}$ in this period is 1.19);

  –

  The maximum variability $\Delta U=U_{\max }-U_{\min }$ varies in the range from 0.40$\mathrm{V}$ to 41.27$\mathrm{V}$ (the average value of $\Delta U$ in this period is 6.98$\mathrm{V}$);

  –

  The amplitudes of voltage fluctuations $\delta U$ vary in the range from 0.00$\mathrm{V}$ to 27.68$\mathrm{V}$ (the average value of $\delta U$ in this period is 6.08$\mathrm{V}$);

  –

  The lowest rms value recorded in this period is 179.87$\mathrm{V}$;

  –

  The highest rms value recorded in this period is 242.76$\mathrm{V}$.

• Case 2. Measurements taken over a period of 7 days, with the following settings:

  –

  The discrimination period $T_w$ of voltage fluctuation indices is 5 min;

  –

  $P_{st}$ values vary in the range from 0.05 to 29.75 (the average value of $P_{st}$ in this period is 0.50);

  –

  The maximum variability $\Delta U=U_{\max }-U_{\min }$ varies in the range from 0.36$\mathrm{V}$ to 203.50$\mathrm{V}$ (the average value of $\Delta U$ in this period is 2.95$\mathrm{V}$);

  –

  The amplitudes of voltage fluctuations $\delta U$ vary in the range from 0.00$\mathrm{V}$ to 144.67$\mathrm{V}$ (the average value of $\delta U$ in this period is 2.39$\mathrm{V}$);

  –

  The lowest rms value recorded in this period is 48.29$\mathrm{V}$;

  –

  The highest rms value recorded in this period is 253.92$\mathrm{V}$.

• Case 3. Measurements taken over a period of 8 days, with the following settings:

  –

  The discrimination period $T_w$ of voltage fluctuation indices is 5 min;

  –

  $P_{st}$ values vary in the range from 0.05 to 2.16 (the average value of $P_{st}$ in this period is 0.45);

  –

  The maximum variability $\Delta U=U_{\max }-U_{\min }$ varies in the range from 0.57$\mathrm{V}$ to 29.31$\mathrm{V}$ (the average value of $\Delta U$ in this period is 4.26$\mathrm{V}$);

  –

  The amplitudes of voltage fluctuations $\delta U$ vary in the range from 0.00$\mathrm{V}$ to 28.43$\mathrm{V}$ (the average value of $\delta U$ in this period is 2.85$\mathrm{V}$);

  –

  The lowest rms value recorded in this period is 203.90$\mathrm{V}$;

  –

  The highest rms value recorded in this period is 236.43$\mathrm{V}$.

• Case 4. Measurements taken over a period of 6 days, with the following settings:

  –

  The discrimination period $T_w$ of voltage fluctuation indices is 5 min;

  –

  $P_{st}$ values vary in the range from 0.09 to 4.35 (the average value of $P_{st}$ in this period is 0.41);

  –

  The maximum variability $\Delta U=U_{\max }-U_{\min }$ varies in the range from 0.43$\mathrm{V}$ to 71.63$\mathrm{V}$ (the average value of $\Delta U$ in this period is 2.75$\mathrm{V}$);

  –

  The amplitudes of voltage fluctuations $\delta U$ vary in the range from 0.00$\mathrm{V}$ to 61.06$\mathrm{V}$ (the average value of $\delta U$ in this period is 1.88$\mathrm{V}$);

  –

  The lowest rms value recorded in this period is 159.91$\mathrm{V}$;

  –

  The highest rms value recorded in this period is 241.14$\mathrm{V}$.

• Case 5. Measurements taken over a period of 5 days, with the following settings:

  –

  The discrimination period $T_w$ of voltage fluctuation indices is 5 min;

  –

  $P_{st}$ values vary in the range from 0.09 to 1.71 (the average value of $P_{st}$ in this period is 0.42);

  –

  The maximum variability $\Delta U=U_{\max }-U_{\min }$ varies in the range from 0.45$\mathrm{V}$ to 26.35$\mathrm{V}$ (the average value of $\Delta U$ in this period is 2.78$\mathrm{V}$);

  –

  The amplitudes of voltage fluctuations $\delta U$ vary in the range from 0.00$\mathrm{V}$ to 20.16$\mathrm{V}$ (the average value of $\delta U$ in this period is 1.83$\mathrm{V}$);

  –

  The lowest rms value recorded in this period is 209.05$\mathrm{V}$;

  –

  The highest rms value recorded in this period is 239.74$\mathrm{V}$.

• Case 6. Measurements taken over a period of 6 days, with the following settings:

  –

  The discrimination period $T_w$ of voltage fluctuation indices is 5 min;

  –

  $P_{st}$ values vary in the range from 0.14 to 6.27 (the average value of $P_{st}$ in this period is 0.36);

  –

  The maximum variability $\Delta U=U_{\max }-U_{\min }$ varies in the range from 0.44$\mathrm{V}$ to 70.18$\mathrm{V}$ (the average value of $\Delta U$ in this period is 2.30$\mathrm{V}$);

  –

  The amplitudes of voltage fluctuations $\delta U$ vary in the range from 0.28$\mathrm{V}$ to 46.23$\mathrm{V}$ (the average value of $\delta U$ in this period is 1.82$\mathrm{V}$);

  –

  The lowest rms value recorded in this period is 161.73$\mathrm{V}$;

  –

  The highest rms value recorded in this period is 235.19$\mathrm{V}$.

• Case 7. Measurements taken over a period of 2 days, with the following settings:

  –

  The discrimination period $T_w$ of voltage fluctuation indices is 5 min;

  –

  $P_{st}$ values vary in the range from 0.06 to 7.28 (the average value of $P_{st}$ in this period is 0.35);

  –

  The maximum variability $\Delta U=U_{\max }-U_{\min }$ varies in the range from 0.37$\mathrm{V}$ to 120.41$\mathrm{V}$ (the average value of $\Delta U$ in this period is 2.20$\mathrm{V}$);

  –

  The amplitudes of voltage fluctuations $\delta U$ vary in the range from 0.00$\mathrm{V}$ to 108.05$\mathrm{V}$ (the average value of $\delta U$ in this period is 1.81$\mathrm{V}$);

  –

  The lowest rms value recorded in this period is 119.76$\mathrm{V}$;

  –

  The highest rms value recorded in this period is 242.39$\mathrm{V}$.

• Case 8. Measurements taken over a period of 2 days, with the following settings:

  –

  The discrimination period $T_w$ of voltage fluctuation indices is 5 min;

  –

  $P_{st}$ values vary in the range from 0.06 to 0.95 (the average value of $P_{st}$ in this period is 0.10);

  –

  The maximum variability $\Delta U=U_{\max }-U_{\min }$ varies in the range from 0.26$\mathrm{V}$ to 15.24$\mathrm{V}$ (the average value of $\Delta U$ in this period is 0.88$\mathrm{V}$);

  –

  The amplitudes of voltage fluctuations $\delta U$ vary in the range from 0.00$\mathrm{V}$ to 11.62$\mathrm{V}$ (the average value of $\delta U$ in this period is 0.26$\mathrm{V}$);

  –

  The lowest rms value recorded in this period is 221.94$\mathrm{V}$;

  –

  The highest rms value recorded in this period is 241.65$\mathrm{V}$.

• Case 9. Measurements taken over a period of 3 days, with the following settings:

  –

  The discrimination period $T_w$ of voltage fluctuation indices is 5 min;

  –

  $P_{st}$ values vary in the range from 0.06 to 1.40 (the average value of $P_{st}$ in this period is 0.12);

  –

  The maximum variability $\Delta U=U_{\max }-U_{\min }$ varies in the range from 0.29$\mathrm{V}$ to 16.34$\mathrm{V}$ (the average value of $\Delta U$ in this period is 0.93$\mathrm{V}$);

  –

  The amplitudes of voltage fluctuations $\delta U$ vary in the range from 0.00$\mathrm{V}$ to 13.49$\mathrm{V}$ (the average value of $\delta U$ in this period is 0.47$\mathrm{V}$);

  –

  The lowest rms value recorded in this period is 220.71$\mathrm{V}$;

  –

  The highest rms value recorded in this period is 242.02$\mathrm{V}$.

• Case 10. Measurements taken over a period of 4 days, with the following settings:

  –

  The discrimination period $T_w$ of voltage fluctuation indices is 5 min;

  –

  $P_{st}$ values vary in the range from 0.66 to 2.20 (the average value of $P_{st}$ in this period is 1.03);

  –

  The maximum variability $\Delta U=U_{\max }-U_{\min }$ varies in the range from 0.79$\mathrm{V}$ to 23.44$\mathrm{V}$ (the average value of $\Delta U$ in this period is 6.41$\mathrm{V}$);

  –

  The amplitudes of voltage fluctuations $\delta U$ vary in the range from 2.29$\mathrm{V}$ to 19.99$\mathrm{V}$ (the average value of $\delta U$ in this period is 5.08$\mathrm{V}$);

  –

  The lowest rms value recorded in this period is 191.51$\mathrm{V}$;

  –

  The highest rms value recorded in this period is 243.02$\mathrm{V}$.

• Case 11. Measurements taken over a period of 3 days, with the following settings:

  –

  The discrimination period $T_w$ of voltage fluctuation indices is 5 min;

  –

  $P_{st}$ values vary in the range from 0.05 to 1.71 (the average value of $P_{st}$ in this period is 0.10);

  –

  The maximum variability $\Delta U=U_{\max }-U_{\min }$ varies in the range from 0.50$\mathrm{V}$ to 87.41$\mathrm{V}$ (the average value of $\Delta U$ in this period is 1.45$\mathrm{V}$);

  –

  The amplitudes of voltage fluctuations $\delta U$ vary in the range from 0.00$\mathrm{V}$ to 68.54$\mathrm{V}$ (the average value of $\delta U$ in this period is 0.38$\mathrm{V}$);

  –

  The lowest rms value recorded in this period is 146.76$\mathrm{V}$;

  –

  The highest rms value recorded in this period is 236.03$\mathrm{V}$.

• Case 12. Measurements taken over a period of 3 days, with the following settings:

  –

  The discrimination period $T_w$ of voltage fluctuation indices is 5 min;

  –

  $P_{st}$ values vary in the range from 0.06 to 1.71 (the average value of $P_{st}$ in this period is 0.11);

  –

  The maximum variability $\Delta U=U_{\max }-U_{\min }$ varies in the range from 0.55$\mathrm{V}$ to 22.52$\mathrm{V}$ (the average value of $\Delta U$ in this period is 1.45$\mathrm{V}$);

  –

  The amplitudes of voltage fluctuations $\delta U$ vary in the range from 0.00$\mathrm{V}$ to 18.00$\mathrm{V}$ (the average value of $\delta U$ in this period is 0.37$\mathrm{V}$);

  –

  The lowest rms value recorded in this period is 209.99$\mathrm{V}$;

  –

  The highest rms value recorded in this period is 236.02$\mathrm{V}$.

• Case 13. Measurements taken over a period of 5 days, with the following settings:

  –

  The discrimination period $T_w$ of voltage fluctuation indices is 5 min;

  –

  $P_{st}$ values vary in the range from 0.14 to 4.86 (the average value of $P_{st}$ in this period is 0.73);

  –

  The maximum variability $\Delta U=U_{\max }-U_{\min }$ varies in the range from 0.45$\mathrm{V}$ to 60.73$\mathrm{V}$ (the average value of $\Delta U$ in this period is 4.14$\mathrm{V}$);

  –

  The amplitudes of voltage fluctuations $\delta U$ vary in the range from 0.28$\mathrm{V}$ to 37.16$\mathrm{V}$ (the average value of $\delta U$ in this period is 2.94$\mathrm{V}$);

  –

  The lowest rms value recorded in this period is 179.02$\mathrm{V}$;

  –

  The highest rms value recorded in this period is 289.16$\mathrm{V}$.

• Case 14. Measurements taken over a period of 5 days, with the following settings:

  –

  The discrimination period $T_w$ of voltage fluctuation indices is 5 min;

  –

  $P_{st}$ values vary in the range from 0.29 to 2.40 (the average value of $P_{st}$ in this period is 1.01);

  –

  The maximum variability $\Delta U=U_{\max }-U_{\min }$ varies in the range from 0.62$\mathrm{V}$ to 30.99$\mathrm{V}$ (the average value of $\Delta U$ in this period is 6.27$\mathrm{V}$);

  –

  The amplitudes of voltage fluctuations $\delta U$ vary in the range from 0.79$\mathrm{V}$ to 21.84$\mathrm{V}$ (the average value of $\delta U$ in this period is 5.21$\mathrm{V}$);

  –

  The lowest rms value recorded in this period is 183.45$\mathrm{V}$;

  –

  The highest rms value recorded in this period is 240.19$\mathrm{V}$.

• Case 15. Measurements taken over a period of 3 days, with the following settings:

  –

  The discrimination period $T_w$ of voltage fluctuation indices is 5 min;

  –

  $P_{st}$ values vary in the range from 0.13 to 1.63 (the average value of $P_{st}$ in this period is 0.38);

  –

  The maximum variability $\Delta U=U_{\max }-U_{\min }$ varies in the range from 0.54$\mathrm{V}$ to 21.37$\mathrm{V}$ (the average value of $\Delta U$ in this period is 2.84$\mathrm{V}$);

  –

  The amplitudes of voltage fluctuations $\delta U$ vary in the range from 0.20$\mathrm{V}$ to 16.23$\mathrm{V}$ (the average value of $\delta U$ in this period is 1.93$\mathrm{V}$);

  –

  The lowest rms value recorded in this period is 216.95$\mathrm{V}$;

  –

  The highest rms value recorded in this period is 247.66$\mathrm{V}$.

• Case 16. Measurements taken over a period of 3 days, with the following settings:

  –

  The discrimination period $T_w$ of voltage fluctuation indices is 5 min;

  –

  $P_{st}$ values vary in the range from 0.16 to 2.04 (the average value of $P_{st}$ in this period is 0.43);

  –

  The maximum variability $\Delta U=U_{\max }-U_{\min }$ varies in the range from 0.60$\mathrm{V}$ to 25.56$\mathrm{V}$ (the average value of $\Delta U$ in this period is 3.10$\mathrm{V}$);

  –

  The amplitudes of voltage fluctuations $\delta U$ vary in the range from 0.34$\mathrm{V}$ to 14.14$\mathrm{V}$ (the average value of $\delta U$ in this period is 2.13$\mathrm{V}$);

  –

  The lowest rms value recorded in this period is 215.07$\mathrm{V}$;

  –

  The highest rms value recorded in this period is 248.21$\mathrm{V}$.

• Case 17. Measurements taken over a period of 7 days, with the following settings:

  –

  The discrimination period $T_w$ of voltage fluctuation indices is 5 min;

  –

  $P_{st}$ values vary in the range from 0.05 to 4.27 (the average value of $P_{st}$ in this period is 0.26);

  –

  The maximum variability $\Delta U=U_{\max }-U_{\min }$ varies in the range from 0.31$\mathrm{V}$ to 63.88$\mathrm{V}$ (the average value of $\Delta U$ in this period is 1.52$\mathrm{V}$);

  –

  The amplitudes of voltage fluctuations $\delta U$ vary in the range from 0.00$\mathrm{V}$ to 59.43$\mathrm{V}$ (the average value of $\delta U$ in this period is 1.61$\mathrm{V}$);

  –

  The lowest rms value recorded in this period is 178.57$\mathrm{V}$;

  –

  The highest rms value recorded in this period is 244.86$\mathrm{V}$.

• Case 18. Measurements taken over a period of 5 days, with the following settings:

  –

  The discrimination period $T_w$ of voltage fluctuation indices is 5 min;

  –

  $P_{st}$ values vary in the range from 0.05 to 0.65 (the average value of $P_{st}$ in this period is 0.16);

  –

  The maximum variability $\Delta U=U_{\max }-U_{\min }$ varies in the range from 0.27$\mathrm{V}$ to 10.80$\mathrm{V}$ (the average value of $\Delta U$ in this period is 1.02$\mathrm{V}$);

  –

  The amplitudes of voltage fluctuations $\delta U$ vary in the range from 0.00$\mathrm{V}$ to 5.42$\mathrm{V}$ (the average value of $\delta U$ in this period is 0.57$\mathrm{V}$);

  –

  The lowest rms value recorded in this period is 226.93$\mathrm{V}$;

  –

  The highest rms value recorded in this period is 243.21$\mathrm{V}$.

• Case 19. Measurements taken over a period of 5 days, with the following settings:

  –

  The discrimination period $T_w$ of voltage fluctuation indices is 5 min;

  –

  $P_{st}$ values vary in the range from 0.13 to 3.92 (the average value of $P_{st}$ in this period is 1.19);

  –

  The maximum variability $\Delta U=U_{\max }-U_{\min }$ varies in the range from 0.38$\mathrm{V}$ to 27.46$\mathrm{V}$ (the average value of $\Delta U$ in this period is 5.64$\mathrm{V}$);

  –

  The amplitudes of voltage fluctuations $\delta U$ vary in the range from 0.00$\mathrm{V}$ to 19.46$\mathrm{V}$ (the average value of $\delta U$ in this period is 3.97$\mathrm{V}$);

  –

  The lowest rms value recorded in this period is 187.96$\mathrm{V}$;

  –

  The highest rms value recorded in this period is 243.68$\mathrm{V}$.

• Case 20. Measurements taken over a period of 7 days, with the following settings:

  –

  The discrimination period $T_w$ of voltage fluctuation indices is 1 min;

  –

  $P_{st}$ values vary in the range from 0.11 to 2.77 (the average value of $P_{st}$ in this period is 0.73);

  –

  The maximum variability $\Delta U=U_{\max }-U_{\min }$ varies in the range from 0.44$\mathrm{V}$ to 34.02$\mathrm{V}$ (the average value of $\Delta U$ in this period is 4.45$\mathrm{V}$);

  –

  The amplitudes of voltage fluctuations $\delta U$ vary in the range from 0.00$\mathrm{V}$ to 28.96$\mathrm{V}$ (the average value of $\delta U$ in this period is 1.85$\mathrm{V}$);

  –

  The lowest rms value recorded in this period is 210.98$\mathrm{V}$;

  –

  The highest rms value recorded in this period is 248.60$\mathrm{V}$.

• Case 21. Measurements taken over a period of 4 days, with the following settings:

  –

  The discrimination period $T_w$ of voltage fluctuation indices is 1 min;

  –

  $P_{st}$ values vary in the range from 0.05 to 29.57 (the average value of $P_{st}$ in this period is 1.38);

  –

  The maximum variability $\Delta U=U_{\max }-U_{\min }$ varies in the range from 0.04$\mathrm{V}$ to 247.45$\mathrm{V}$ (the average value of $\Delta U$ in this period is 5.97$\mathrm{V}$);

  –

  The amplitudes of voltage fluctuations $\delta U$ vary in the range from 0.00$\mathrm{V}$ to 110.27$\mathrm{V}$ (the average value of $\delta U$ in this period is 2.59$\mathrm{V}$);

  –

  The lowest rms value recorded in this period is 0.00$\mathrm{V}$;

  –

  The highest rms value recorded in this period is 253.99$\mathrm{V}$.

• Case 22. Measurements taken over a period of 4 days, with the following settings:

  –

  The discrimination period $T_w$ of voltage fluctuation indices is 1 min;

  –

  $P_{st}$ values vary in the range from 0.05 to 31.71 (the average value of $P_{st}$ in this period is 0.96);

  –

  The maximum variability $\Delta U=U_{\max }-U_{\min }$ varies in the range from 0.02$\mathrm{V}$ to 245.97$\mathrm{V}$ (the average value of $\Delta U$ in this period is 4.61$\mathrm{V}$);

  –

  The amplitudes of voltage fluctuations $\delta U$ vary in the range from 0.00$\mathrm{V}$ to 36.85$\mathrm{V}$ (the average value of $\delta U$ in this period is 1.71$\mathrm{V}$);

  –

  The lowest rms value recorded in this period is 0.00$\mathrm{V}$;

  –

  The highest rms value recorded in this period is 252.99$\mathrm{V}$.

• Case 23. Measurements taken over a period of 5 days, with the following settings:

  –

  The discrimination period $T_w$ of voltage fluctuation indices is 1 min;

  –

  $P_{st}$ values vary in the range from 0.08 to 1.90 (the average value of $P_{st}$ in this period is 0.36);

  –

  The maximum variability $\Delta U=U_{\max }-U_{\min }$ varies in the range from 0.44$\mathrm{V}$ to 17.28$\mathrm{V}$ (the average value of $\Delta U$ in this period is 2.14$\mathrm{V}$);

  –

  The amplitudes of voltage fluctuations $\delta U$ vary in the range from 0.00$\mathrm{V}$ to 10.18$\mathrm{V}$ (the average value of $\delta U$ in this period is 0.73$\mathrm{V}$);

  –

  The lowest rms value recorded in this period is 222.60$\mathrm{V}$;

  –

  The highest rms value recorded in this period is 249.42$\mathrm{V}$.

• Case 24. Measurements taken over a period of 5 days, with the following settings:

  –

  The discrimination period $T_w$ of voltage fluctuation indices is 1 min;

  –

  $P_{st}$ values vary in the range from 0.05 to 30.71 (the average value of $P_{st}$ in this period is 0.92);

  –

  The maximum variability $\Delta U=U_{\max }-U_{\min }$ varies in the range from 0.02$\mathrm{V}$ to 251.05$\mathrm{V}$ (the average value of $\Delta U$ in this period is 4.35$\mathrm{V}$);

  –

  The amplitudes of voltage fluctuations $\delta U$ vary in the range from 0.00$\mathrm{V}$ to 34.99$\mathrm{V}$ (the average value of $\delta U$ in this period is 1.55$\mathrm{V}$);

  –

  The lowest rms value recorded in this period is 0.00$\mathrm{V}$;

  –

  The highest rms value recorded in this period is 254.22$\mathrm{V}$.

• Case 25. Measurements taken over a period of 5 days, with the following settings:

  –

  The discrimination period $T_w$ of voltage fluctuation indices is 1 min;

  –

  $P_{st}$ values vary in the range from 0.05 to 31.22 (the average value of $P_{st}$ in this period is 1.27);

  –

  The maximum variability $\Delta U=U_{\max }-U_{\min }$ varies in the range from 0.03$\mathrm{V}$ to 254.08$\mathrm{V}$ (the average value of $\Delta U$ in this period is 5.76$\mathrm{V}$);

  –

  The amplitudes of voltage fluctuations $\delta U$ vary in the range from 0.00$\mathrm{V}$ to 53.23$\mathrm{V}$ (the average value of $\delta U$ in this period is 2.06$\mathrm{V}$);

  –

  The lowest rms value recorded in this period is 0.00$\mathrm{V}$;

  –

  The highest rms value recorded in this period is 259.35$\mathrm{V}$.

It is worth noting that the above cases also include states of momentary (short-term) voltage outages, as evidenced by the minimum rms values $U_{\min }$ close to 0$\mathrm{V}$. Amplitudes of voltage fluctuations $\delta U$ usually have maximum values $\delta U_{\max }$ that are smaller than the maximum variability $\Delta U=U_{\max }-U_{\min }$, which is a result of the fact that not every voltage change qualifies as a voltage fluctuation. Moreover, it is worth noting that even if significant amplitudes of voltage fluctuations $\delta U_{\max }$ occur, they are not very frequent, because the average values of the amplitudes of voltage fluctuations $\delta U_{\mathrm{avg}}$ are usually much smaller than the maximum values of these amplitudes $\delta U_{\max }$. It is also worth noting that the length of results recorded in individual cases is not related to the operation of algorithms. The monitoring time for individual cases is the effect of implementing activities for the electricity operator or the results of periodic consent in order to take measurements at a specific point of the power grid.

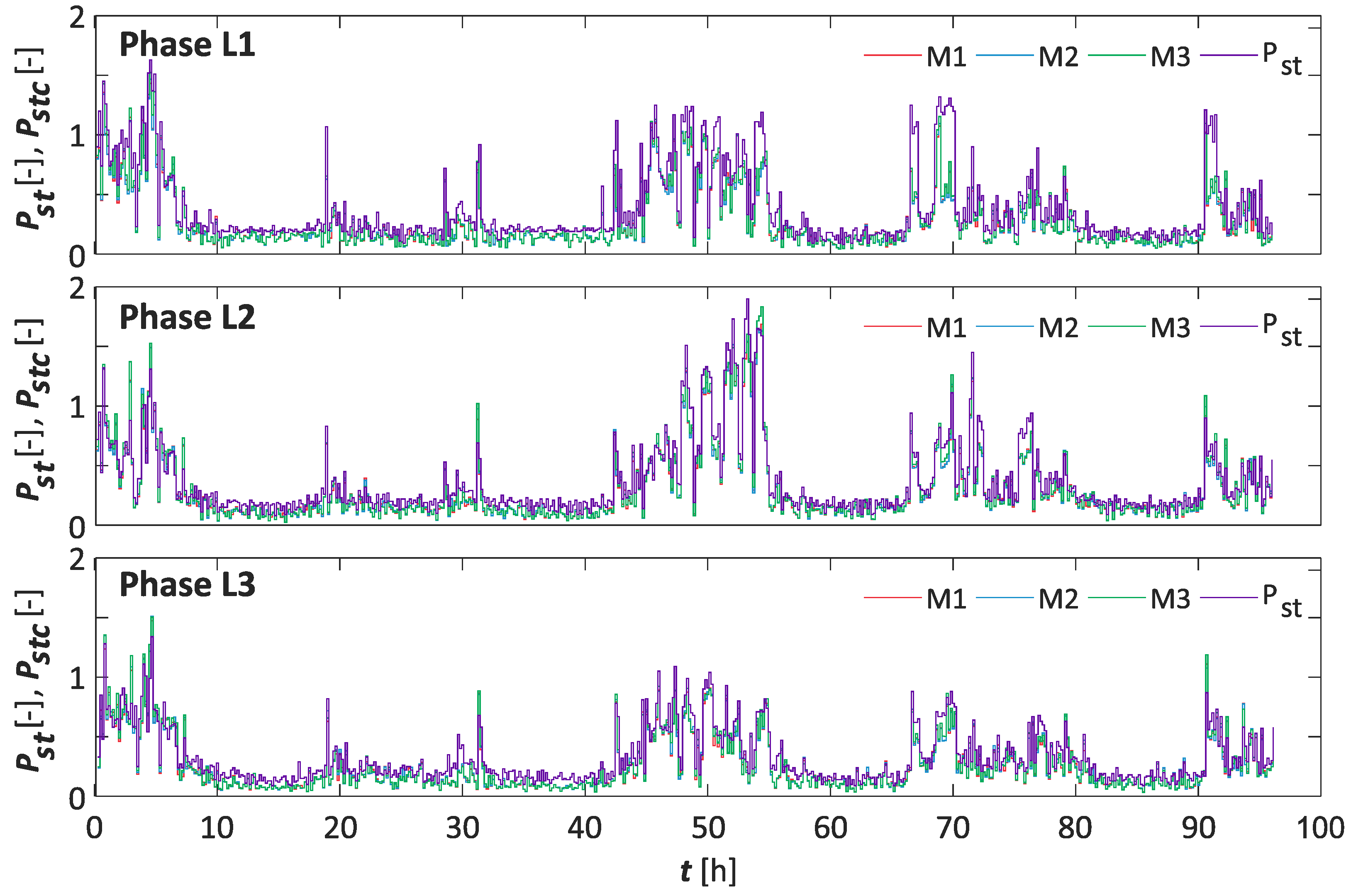
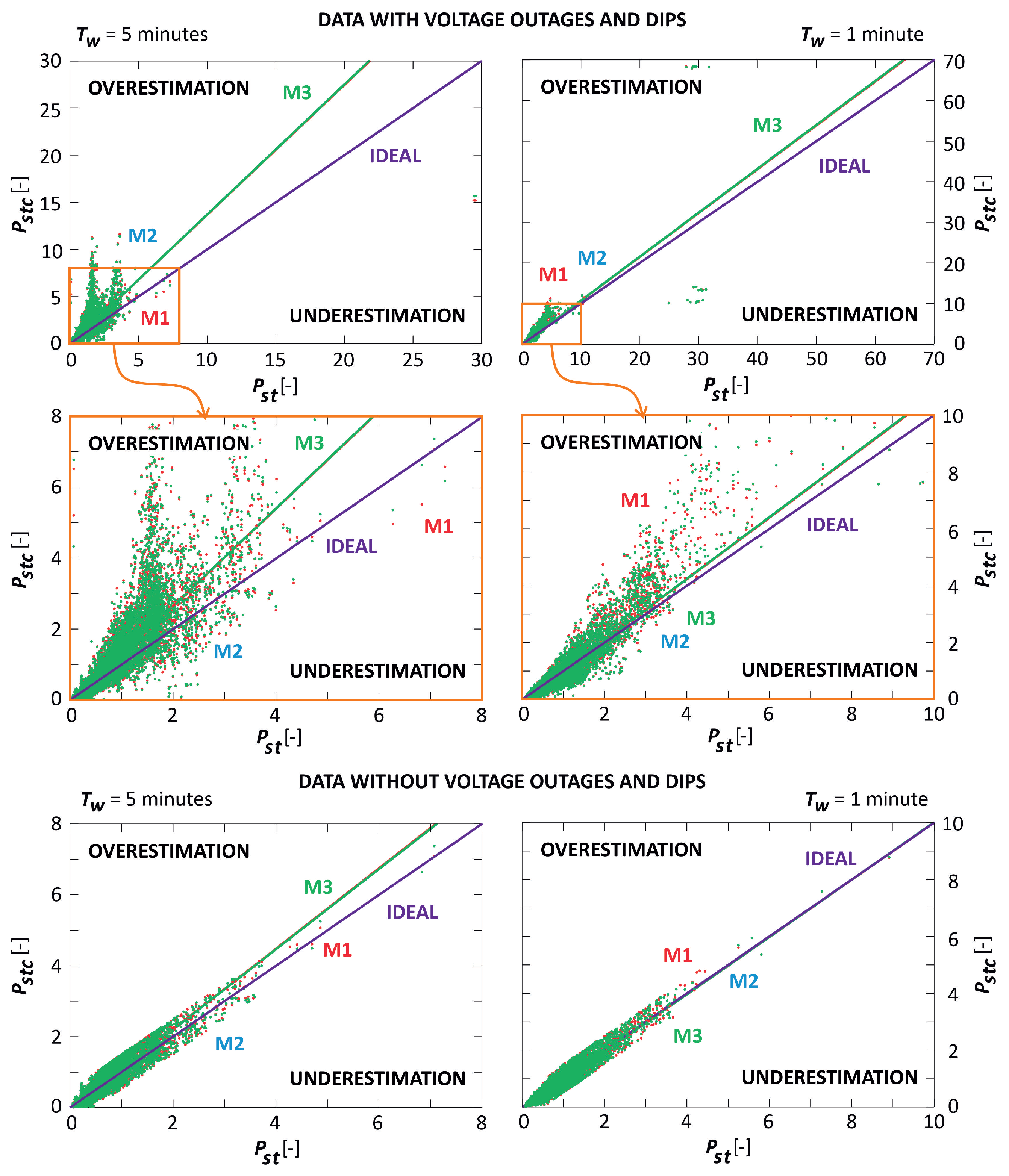
5. Research Results and Discussion

For the purpose of verifying the ability to recreate voltage fluctuations via individual methods M1 to M3, the measurement results described in Section 4 were used. Voltage fluctuations were recreated within individual discrimination periods $T_w$; and then, based on the individual $T_w$ segments connected in 10 min blocks, the value of the short-term flicker indicator $P_{stc}$ was determined in accordance with the diagram shown in Figure 5. In order to determine the $P_{stc}$ values, the recreated voltage fluctuations were used in a modulation process, where a nominal sinusoidal signal was assumed as the carrier signal, and then the signal thus modulated, which reflects the reconstructed instantaneous voltage signal in the power network, was input in the IEC flickermeter, which generated the $P_{stc}$ values as output.

The determined $P_{stc}$ values were compared with $P_{st}$ values measured on the real power grid. If the algorithm proved able to recreate voltage fluctuations that cause the same flicker effect as the signal occurring in the real network, then the $P_{st}$ and $P_{stc}$ values should be equal. Taking into account the fact that individual sets of measurement results contain multi-day registrations, which makes the comparative analysis of $P_{st}$ and $P_{stc}$ values at individual points difficult, two parameters were used for this analysis. The first parameter is the r-Pearson coefficient $r_{P_{st}}$ [44], which determines the linear correlation between individual $P_{st}$ and $P_{stc}$ values. The r-Pearson coefficient $r_{P_{st}}$ is determined with the following equation [44]:

$$r_{P_{st}}={\displaystyle \frac{{\sum }_{i=1}^N\left(P_{{st}_i}-\frac{1}{N}{\sum }_{j=1}^N{P}_{{st}_j}\right)\left(P_{{stc}_i}-\frac{1}{N}{\sum }_{j=1}^N{P}_{{stc}_j}\right)}{\sqrt{{\sum }_{i=1}^N{\left(P_{{st}_i}-\frac{1}{N}{\sum }_{j=1}^N{P}_{{st}_j}\right)}^2}\sqrt{{\sum }_{i=1}^N{\left(P_{{stc}_i}-\frac{1}{N}{\sum }_{j=1}^N{P}_{{stc}_j}\right)}^2}}},$$

(1)

where N is the number of 10 min segments that are analyzed. If individual algorithms proved able to recreate a signal that cause the same effect as the original signal, the r-Pearson coefficient $r_{P_{st}}$ should be equal to 1. The closer the value of this coefficient is to 0, the greater the dispersion is between the $P_{st}$ and $P_{stc}$ values, and the closer the value of $r_{P_{st}}$ is to 1, the better the nature of the recreated voltage fluctuations. It is worth noting, that $r_{P_{st}}$ determines the linear correlation between the $P_{st}$ and $P_{stc}$ values and therefore does not provide information about the convergence of absolute values. For this purpose, a second parameter was used, i.e., the slope coefficient $a_{P_{st}}$ of the characteristic $P_{stc}$ = f($P_{st}$), which is determined as follows:

$$a_{P_{st}}={\displaystyle \frac{{\sum }_{i=1}^N{P}_{{st}_i}{P}_{{stc}_i}-\frac{1}{N}{\sum }_{i=1}^N{P}_{{st}_i}{\sum }_{i=1}^N{P}_{{stc}_i}}{{\sum }_{i=1}^N{P_{{st}_i}}^2-\frac{1}{N}{\left({\sum }_{i=1}^N{P}_{{st}_i}\right)}^2}},$$

(2)

where N is the number of 10 min segments analyzed. If individual algorithms made it possible to recreate a signal causing the same effect as the original signal, the slope coefficient $a_{P_{st}}$ would be 1. The closer the slope coefficient $a_{P_{st}}$ is to 1, the better the absolute convergence of the individual values of $P_{stc}$ and $P_{st}$. If the slope coefficient $a_{P_{st}}$ produces a value greater than 1, overestimation is implied, i.e., the recreation of voltage fluctuations with more serve flicker than the original fluctuations. If the slope coefficient $a_{P_{st}}$ is less than 1, underestimation is implied, i.e., the recreation of voltage fluctuations with less serve flicker than the original fluctuations.

Figure 6 shows the determined coefficients $a_{P_{st}}$ and $r_{P_{st}}$ for all individual 10 min blocks for each set of measurement results separately. The determined coefficients are grouped separately for the discrimination window of 5 min and 1 min. Analyzing the research results presented in Figure 6, the convergence of the results between individual methods becomes evident (the results for individual methods M1–M3 overlap) both when the discrimination window is 5 min and 1 min. Therefore, contrary to the results presented in publications [38,43], there are no visible significant differences between individual methods in terms of recreating voltage fluctuations focused on obtaining the same flicker severity as the original. This conclusion is important from the point of view of the practical use of the methods, because the methods differ in computational complexity, as shown in [43]. Analyzing the obtained results, it can also be noted that, apart from case no. 11, the M1–M3 methods allow for maintaining the nature of the voltage fluctuations’ severity in the recreated voltage fluctuations (large value of the coefficient $r_{P_{st}}$). However, the values of the coefficient $a_{P_{st}}$ suggest that individual methods in most cases overestimate or underestimate the recreation of the original flicker severity (in some cases even twice). In order to determine the causes of such large errors during the recreation of voltage fluctuations by individual methods M1–M3, the time characteristics $P_{st}$ = $\mathrm{f}\left(t\right)$ and $P_{stc}$ = $\mathrm{f}\left(t\right)$ are analyzed. In the case of numerical data [38] or data from laboratory tests [43], such significant errors in the recreation of voltage fluctuations by individual methods do not occur.

Figure 7 shows the time characteristics $P_{st}$ = $\mathrm{f}\left(t\right)$ and $P_{stc}$ = $\mathrm{f}\left(t\right)$ for the case in which one of the best results is obtained (coefficients $r_{P_{st}}$ and $a_{P_{st}}$ close to 1), i.e., case no. 23. Analyzing the obtained research results, a slight asymmetry between the individual phases can be noticed. Again, as before, the convergence of results between the individual methods M1–M3 (the results for individual methods M1–M3 overlap), as well as the convergence of the results with the originally measured indicator $P_{st}$, is visible. All of the analyzed methods for this particular case showed good properties in terms of recreating voltage fluctuations. Therefore, the causes of the errors visible in Figure 6 can be found for the worst cases.

Figure 8 shows the time characteristics $P_{st}$ = $\mathrm{f}\left(t\right)$ and $P_{stc}$ = $\mathrm{f}\left(t\right)$ for the case in which one of the worst results is obtained (coefficients $r_{P_{st}}$ and $a_{P_{st}}$ significantly different from the value equal to 1), i.e., case no. 21. Analyzing this case, it can be noticed that, as before, there is a convergence of the results between individual methods M1–M3 (the results for the individual methods M1–M3 overlap). It can also be seen that the voltage fluctuations recreated by individual methods retain the nature of flicker severity changes as those originally occurring in the power grid. However, when the indicator $P_{st}$ reaches significant values for a short period of time ($P_{st}$ values greater than 5), there is a significant overestimation of the flicker intensity in the recreated voltage fluctuations (in other cases, it is an underestimation). Analyzing the changes in the minimum and maximum rms values of voltage separately, it can be seen that these moments correspond to short-term (momentary) voltage decays, outages, or dips. This observed fact allows for the conclusion that individual methods are generally highly effective in recreating voltage fluctuations when there are no additional anomalies in the form of sudden voltage outages or dips (voltage distortion or transient states such as overvoltages resulting from commutation are not a problem because individual datasets contain these disturbances, and no errors in the operation of individual methods have been noticed for these states). In order to verify this conclusion, fragments of the measurement results including voltage outages and dips were removed from individual sets of measurement results, and then the coefficients $a_{P_{st}}$ and $r_{P_{st}}$ were determined again. The results of these calculations are presented in Figure 9.

Analyzing the results presented in Figure 9, a significant improvement in the individual methods M1–M3 in terms of recreating voltage fluctuations can be observed. For each analyzed case, $a_{P_{st}}$ and $r_{P_{st}}$ values close to 1 are obtained. Moreover, slight differences in the performance of individual methods M1–M3 are highlighted. In general, the best results are obtained for the M3 method, with the highest computational complexity, as in the case of numerical data or data from laboratory tests. It is worth noting that there is also a significant impact of the discrimination window on the obtained research results. The best results are obtained for a shorter discrimination window $T_w$ of 1 min. In the research presented in [43], better results are also obtained for a shorter discrimination window $T_w$, but the difference is much smaller. For data from a real power grid, where there is a resultant impact from many sources of disturbance, the duration of the discrimination window $T_w$ is important. This state is associated with counting the amplitudes of voltage fluctuations $\delta V$ in the widest range (0.4;0.0)$\delta U$. This range usually contains the largest number of voltage fluctuation amplitudes $\delta V$, which is so important from the point of view of the operation of individual methods that at the stage of recreating voltage fluctuations, only a few arbitrary values of the voltage fluctuation amplitudes are assumed, while in reality, there can be voltage fluctuation amplitudes closer to one of the limit values of range (0.4;0.0)$\delta U$. In order to better highlight the influence of the duration of the discrimination window $T_w$ and momentary voltage outages and dips, a set of $P_{st}$ results and a set of $P_{stc}$ results were prepared, combining all analyzed cases into one, and the characteristics $P_{stc}$ = f($P_{st}$) were compared for states with and without voltage outages and dips, for discrimination windows $T_w$ of 5 min and 1 min. These results are presented in Figure 10.

Analyzing the results presented in Figure 10, it is possible to confirm the conclusions regarding the significant impact of discrimination window $T_w$ duration and voltage outages and dips on the aforementioned methods of recreating voltage fluctuations. If moments of voltage outages and dips are eliminated from the data and the discrimination window $T_w$ is 1 min, the linear regression curves for the methods M1–M3 coincide with the ideal curve with a slope coefficient of 1. In this case, there are also no noticeable differences between the operation of individual methods M1–M3; therefore, a method with low computational complexity, i.e., the M1 method, can also be effectively used. It is also worth noting that when a long discrimination window $T_w$ is involved, the removal of moments of voltage outages and dips improves the ability to more reliably recreate voltage fluctuations, but numerous overestimations or underestimations of the flicker severity still remain in the recreated voltage fluctuations.

6. Conclusions

This article presents a comprehensive verification of methods for recreating voltage fluctuations. For verification purposes, 25 sets of long-term measurement results taken from a real power grid were used. Individual sets of measurement results illustrate the impact of various sources of disturbance and take into account the simultaneous occurrence of many power quality disturbances. The presented research results complement and extend the preliminary research presented at a prior conference [43], which presents the results of verification of the operation of individual methods based on the data obtained in laboratory conditions using a model of a real power grid. The research results presented in this article in connection with the previously presented research results taking into account numerical data [38,39,40] and data from laboratory experimental tests [37,43] constitute a complementary whole in terms of assessing the possibility of recreating voltage fluctuations.

The research results presented in this article show that methods M1 to M3 are sensitive to the occurrence of voltage outages and dips. For the effective implementation of methods M1 to M3, it is necessary to remove voltage outages and dips. The presented research results also show the significant impact of the duration of the discrimination window $T_w$ on the utilization of methods M1 to M3. The shorter the discrimination window $T_w$ is, the more reliable the recreations of voltage fluctuations are within the said methods. Looking at the analyzed discrimination times $T_w$, when $T_w$ is 1 min, significant agreement was observed between the flicker severity of the real power grid’s state and the state recreated using voltage fluctuation indices. Moreover, it was found that there were no significant differences between the results for the individually analyzed methods M1 to M3; therefore, when utilizing data from a real power grid, the voltage fluctuation amplitudes $\delta V$ selected in the process of recreating voltage fluctuations are more important than the selected shape of the recreated voltage fluctuations. This conclusion indicates a potential avenue for further research, which should focus on long-term recordings of voltage fluctuation indices with a short discrimination time (1 min is sufficient from the diagnostic point of view) for various disturbances of power quality within the power grid and voltage fluctuations of various severity levels. Such recordings will allow for the determination of the appropriate probability density curve for a fairly wide range, within which the amplitudes of voltage fluctuations $\delta V$ with the smallest values may be determined. Such a density curve will allow for a more reliable recreation of voltage fluctuations for various states that are typical for modern power networks. The reliable recreation of voltage fluctuations may significantly support the assessment of electromagnetic compatibility in the field of low-frequency conducted disturbances (also in the case of other specific types of power networks, such as railway supply networks [45] or micro-grid networks [46,47]). It is also worth emphasizing that the proposed possibility of recreating voltage fluctuations could also become a tool for performing predictive maintenance in low-voltage networks (for the protection of consumers sensitive to such voltage fluctuations).