A Method for Power Flow Calculation in AC/DC Hybrid Distribution Networks Considering the Electric Energy Routers Based on an Alternating Iterative Approach
Abstract
1. Introduction
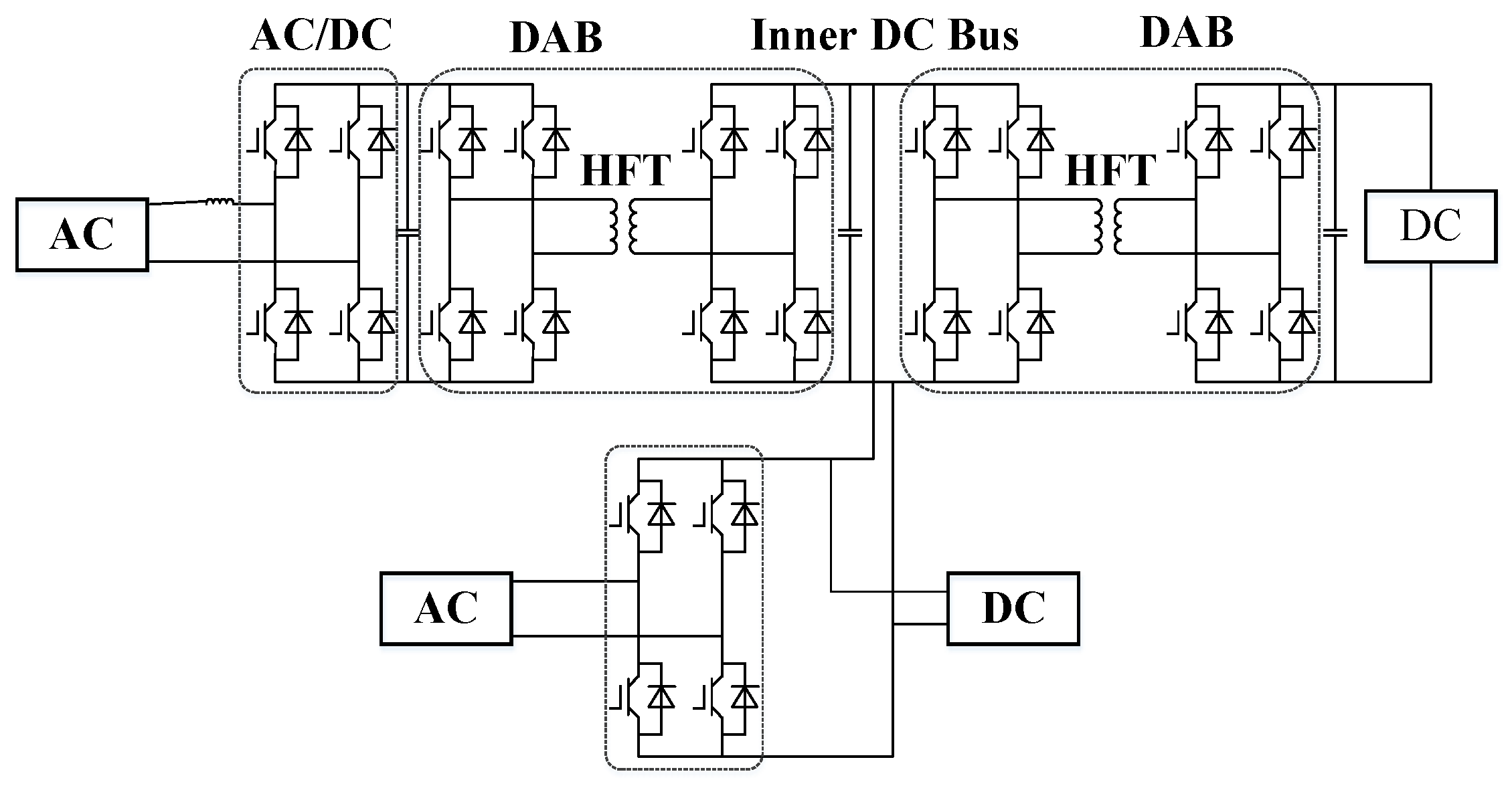
2. The Construction of a Multi-Port EER Model
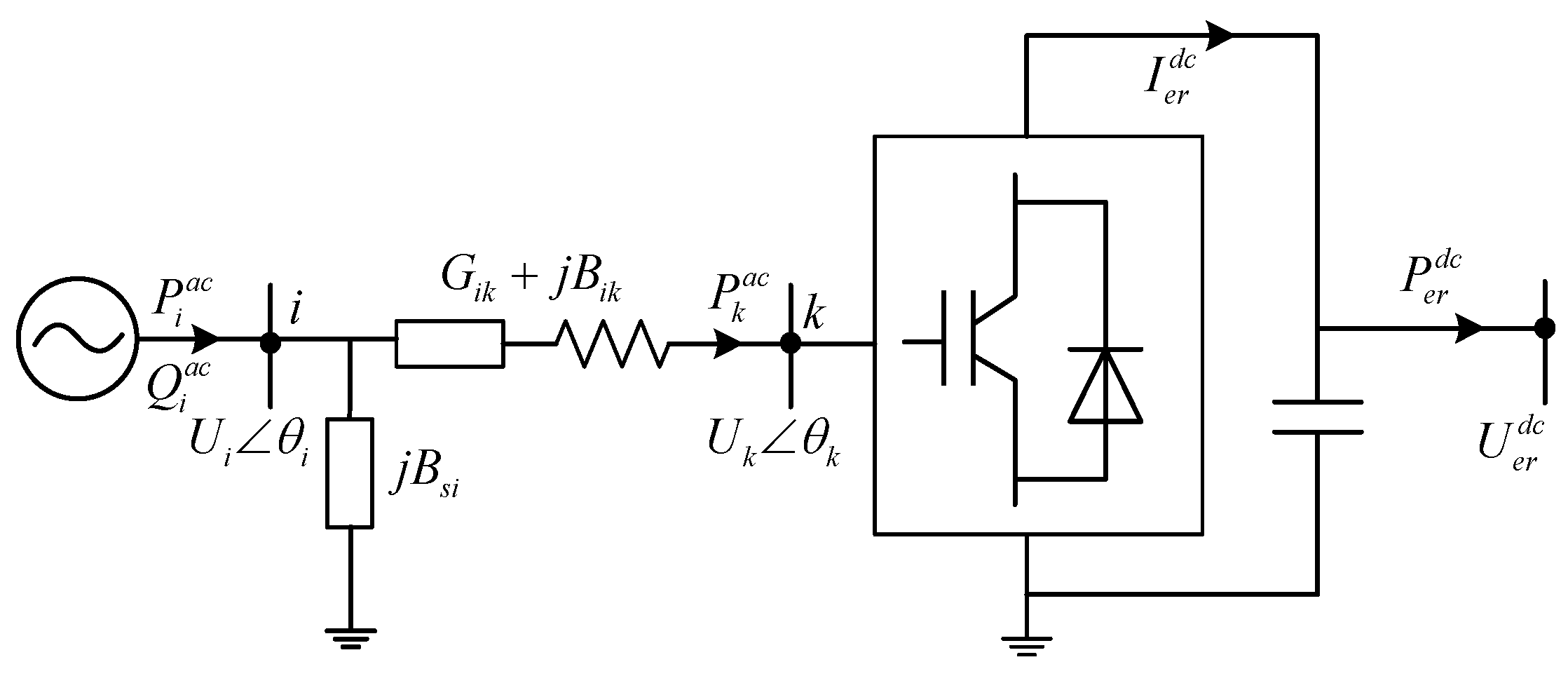
2.1. Steady-State Model of EER Port
2.2. The Construction of the Internal Power Model of the EER
2.3. Loss Situation and Control Methods of EER
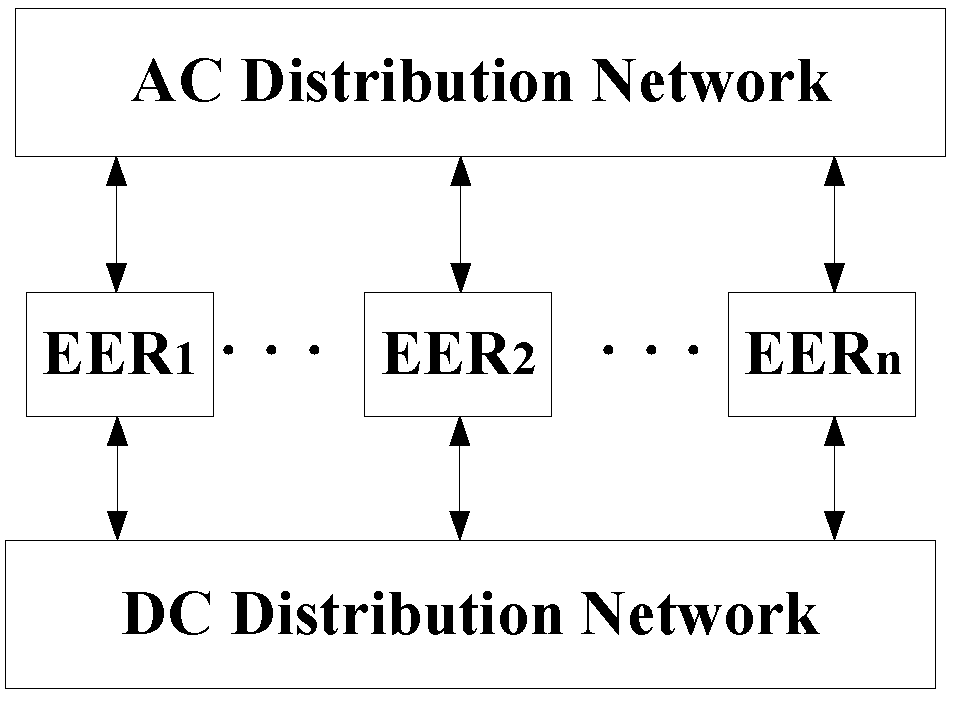
3. Hybrid Power Flow Calculation Model Construction
3.1. AC Distribution Network Power Flow Calculation
3.2. DC Distribution Network Power Flow Calculation
3.3. EER Power Flow Calculation
4. The Power Flow Calculation for AC/DC Hybrid Distribution Networks Considering EERs
5. Case Study Analysis
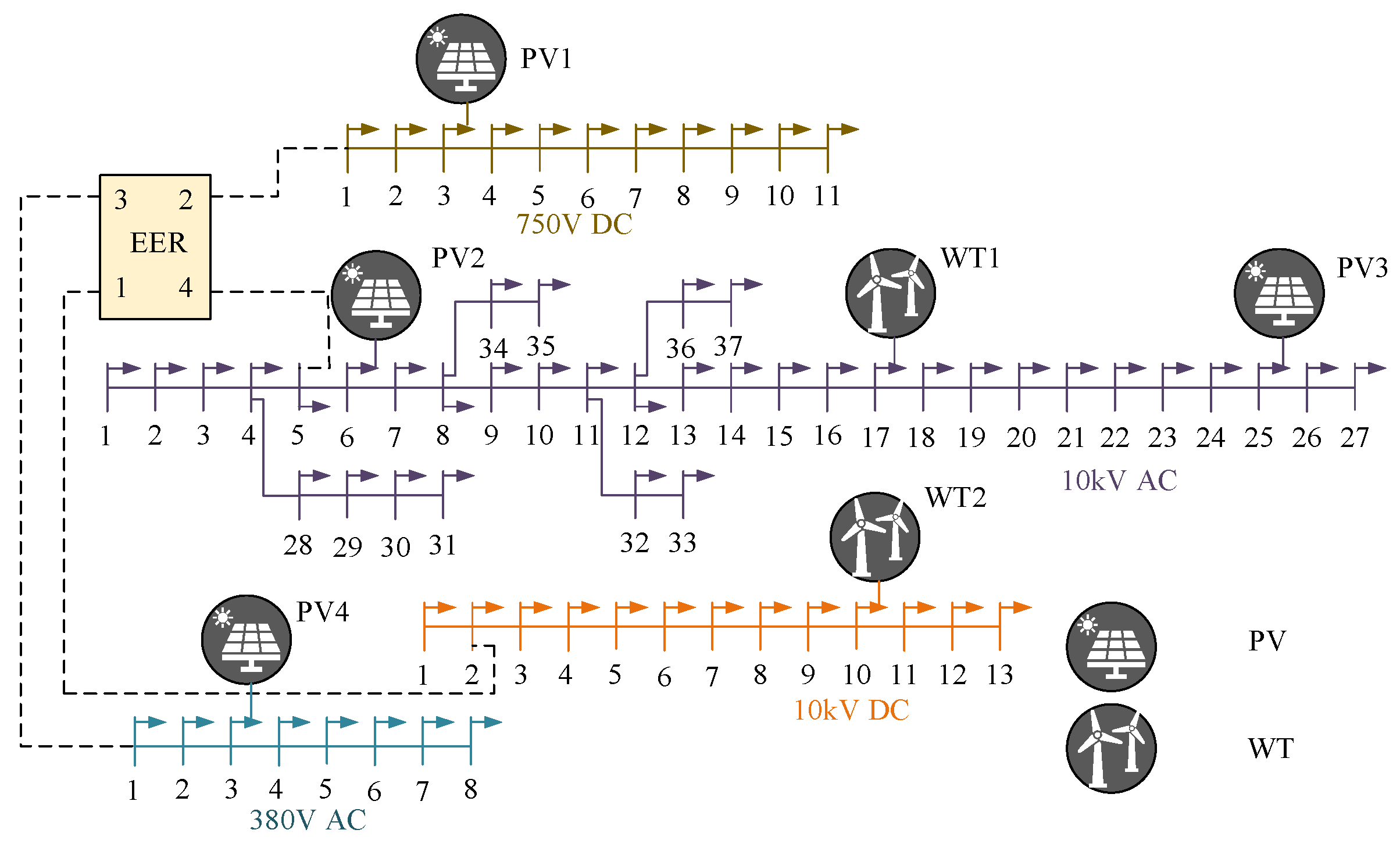
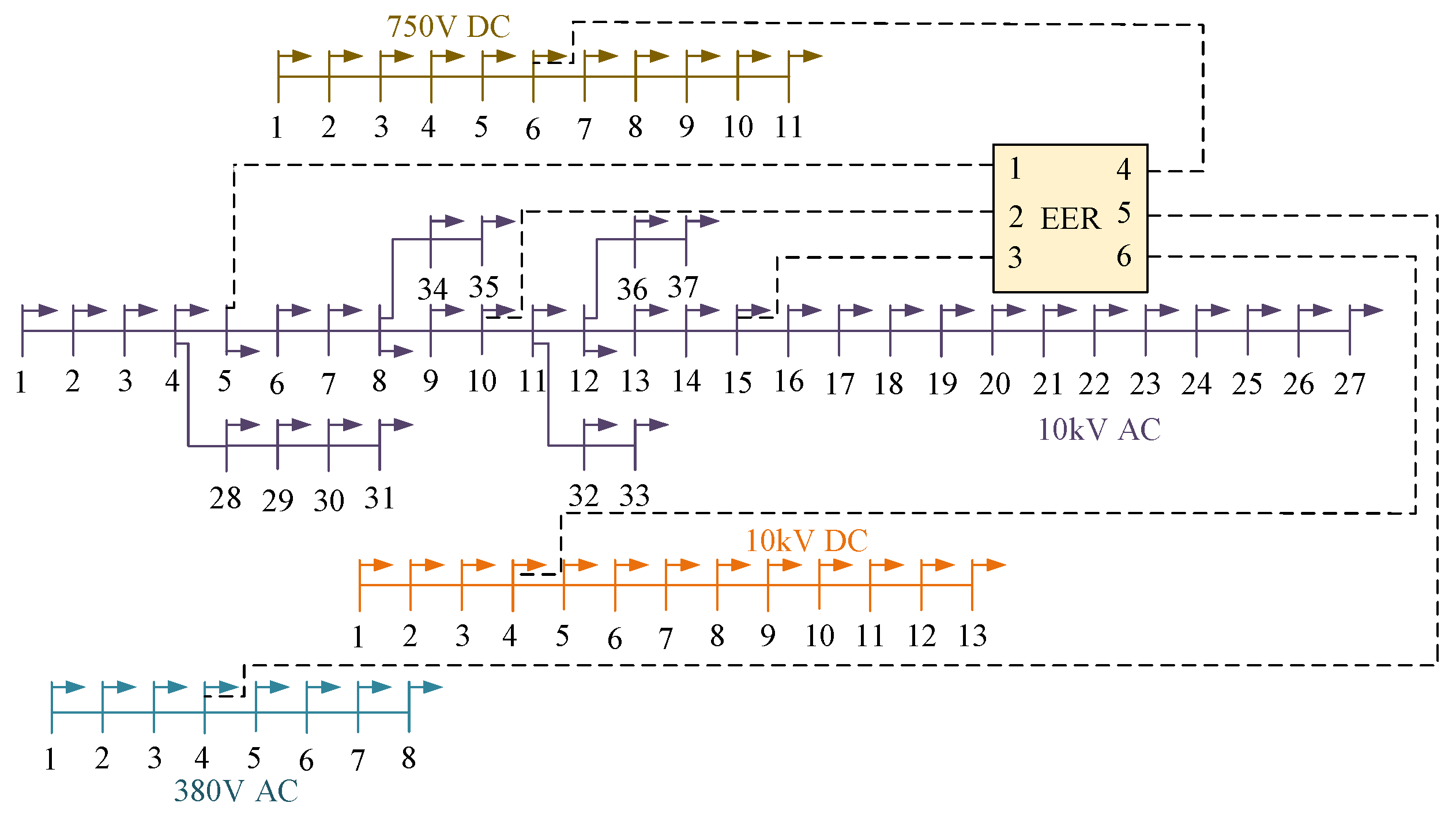
5.1. The Verification of Power Flow Calculation for Multi-Port EERs
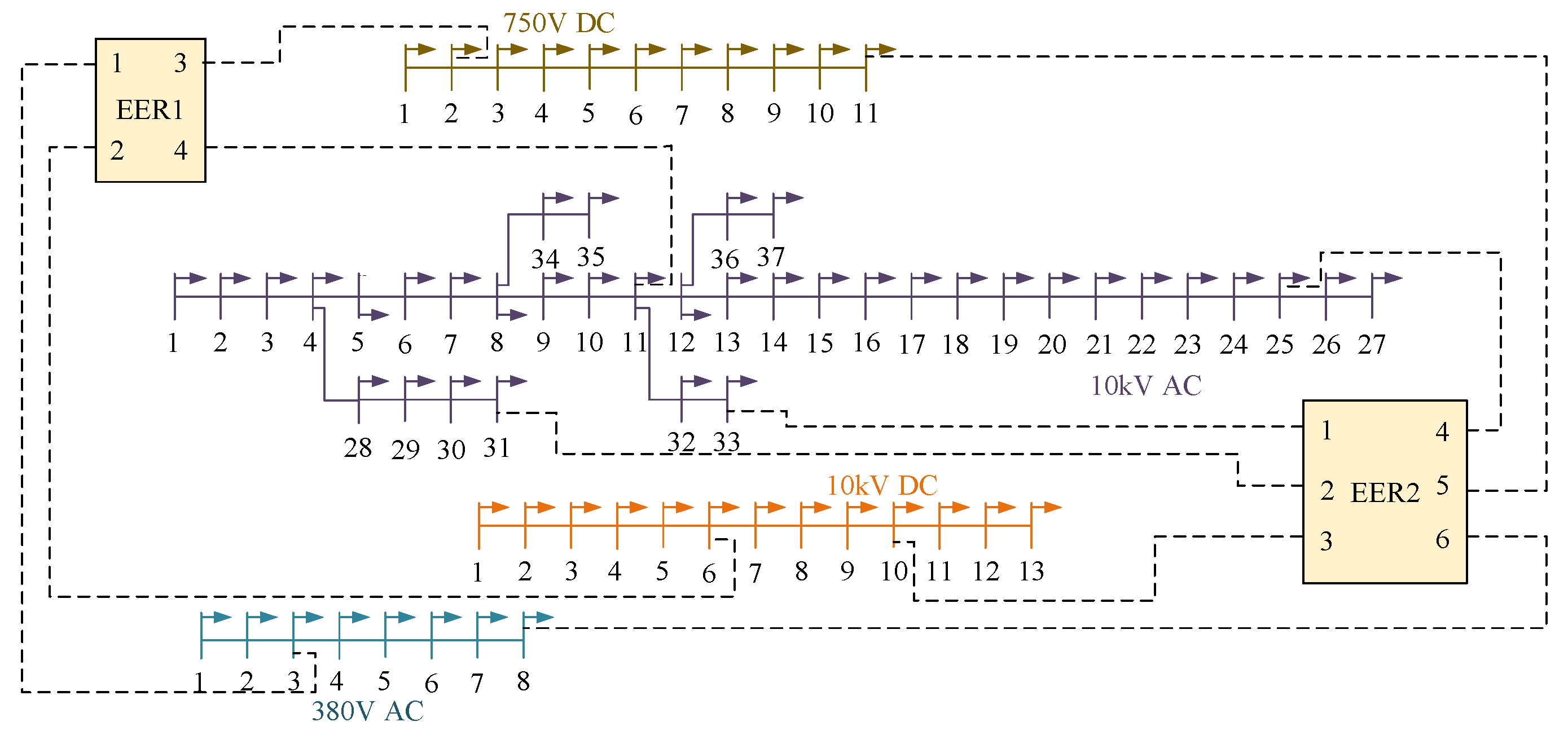
5.2. The Validation of Power Flow Calculation for Multi-Port and Multi-Quantity EERs
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- National Development and Reform Commission; National Energy Administration. Guidelines for high-quality development of distribution networks under new circumstances. Pop. Util. Electr. 2024, 39, 8–11. [Google Scholar]
- Wu, Y.; Liu, H.; Xiao, Z.; Chen, Z.; Liu, P.; Hou, H.; Tang, A.; Cui, R. Review of incremental distribution network planning considering the uncertainty of source- network-load. Power Syst. Prot. Control. 2021, 49, 177–187. [Google Scholar]
- Ye, J.; Li, B.; Zhang, Y.; Li, M.; Shi, B.; Wang, H. Energy Storage Requirements and Configuration Analysis Based on Typical Characteristics of Global Energy Internet. Power Gener. Technol. 2021, 42, 20–30. [Google Scholar] [CrossRef]
- Song, C.; Zhao, D.; Yin, J.; Zhang, Q. Coordinated Control Strategy of AGC and AVC Based on Multi-Agent System. In Proceedings of the 2018 2nd IEEE Conference on Energy Internet and Energy System Integration (EI2), Beijing, China, 20–22 October 2018; pp. 1–5. [Google Scholar]
- Asuhaimi, F.; Bu, S.; Nadas, J.; Imran, M. Delay-aware energy-efficient joint power control and mode selection in device-to-device communications for FREEDM systems in smart grids. IEEE Access 2019, 7, 87369–87381. [Google Scholar] [CrossRef]
- Xia, M.; Chen, M.; Chen, Q. Rule-based energy buffer strategy of energy router considering efficiency optimization. Int. J. Electr. Power Energy Syst. 2021, 125, 28–30. [Google Scholar] [CrossRef]
- Wang, J.; Wu, D.; Liu, C.; Sun, Y.; Chi, E. Application of multi-source micro-network based on energy router in oil field system. Electrotech. Appl. 2024, 43, 70–75. [Google Scholar]
- Ma, W.; Tai, Y.; Wang, Y.; Jiao, L.; Jin, Q.; Zhang, J. Mode switching coordination control strategy of an electrical energy router for new energy access. Power Syst. Prot. Control. 2023, 51, 52–61. [Google Scholar]
- Zhu, Y.; Wu, H.; Zhang, Z.; Zong, C.; Bi, K.; Xu, D. Power flow calculation of AC—DC hybrid distribution network with energy routers. Jiangsu Electr. Eng. 2024, 43, 136–145. [Google Scholar]
- Liang, D.; Zhou, J.; Lv, X.; Dong, Y. Research on the application of power router in interconnected micronetworks. Mech. Electr. Inf. 2024, 2, 9. [Google Scholar]
- Sheng, W.; Duan, Q.; Liang, Y.; Meng, X.; Shi, C. Research of Power Distribution and Application Grid Structure and Equipment for Future Energy Internet. Proc. CSEE 2015, 35, 3760–3769. [Google Scholar]
- Jingyuan, L.; Srikantha, P. Adaptive topology reconfiguration in smart distribution networks. IEEE Trans. Signal Inf. Process. Netw. 2021, 7, 716–729. [Google Scholar]
- Wang, C.; Sun, C.; Peng, K.; Li, Y.; Wu, Z. Study on AC-DC Hybrid Power Flow Algorithm for Microgrid. Proc. CSEE 2013, 33, 8–15. [Google Scholar]
- Ye, X.; Liu, K.; Meng, X. Power flow calculation for AC/DC hybrid distribution networks with distributed power sources. Distrib. Util. 2016, 33, 23–26. [Google Scholar]
- Lei, J.; An, T.; Du, Z.; Yuan, Z. A Unified AC/DC Power Flow Algorithm with DC Distribution. Proc. CSEE 2016, 36, 911–918. [Google Scholar]
- Lei, J.; An, T.; Du, Z.; Yuan, Z. A General Unified AC/DC Power Flow Algorithm with MTDC. IEEE Trans. Power Syst. 2016, 32, 2837–2846. [Google Scholar] [CrossRef]
- Sheng, W.; Li, P.; Duan, Q.; Li, Z.; Zhu, C. Research on Energy Management Strategy of Energy Hub with Energy Router Based on Lyapunov Optimization Method. Proc. CSEE 2019, 39, 6212–6225. [Google Scholar]
- Sheng, W.; Lan, Z.; Duan, Q.; Li, Y.; Ma, C.; Li, Z. Study on Self Energy Storage Based Energy Router. Power Syst. Technol. 2017, 41, 387–393. [Google Scholar]
- Xu, Y.; Zhang, J.; Wang, W.; Juneja, A.; Bhattacharya, S. Energy router: Architectures and functionalities toward energy internet. In Proceedings of the 2011 IEEE International Conference on Smart Grid Communications, Brussels, Belgium, 17–20 October 2011; IEEE: New York, NY, USA, 2011; pp. 31–36. [Google Scholar]
- Zheng, J.; Zhao, Z.; Shi, B.; Yu, Z.; Ju, J.; Fan, Z. A discrete state event driven simulation based losses analysis for multi-terminal megawatt power electronic transformer. CES Trans. Electr. Mach. Syst. 2020, 4, 275–284. [Google Scholar] [CrossRef]
- Zhang, Z.; Zheng, J.; Gui, Y.; Liu, Z.; Zhu, S. Multi-objective Optimal Operation of AC/DC Hybrid Microgrid Considering the Combination of Electric Energy Router Control Modes. In Proceedings of the 2021 IEEE Sustainable Power and Energy Conference (iSPEC), Nanjing, China, 23–25 December 2021; pp. 1430–1437. [Google Scholar]
- Peng, Q.; Qu, L.; Yuan, Z.; Wang, X.; Chen, Y.; Tian, B. Optimal Scheduling Strategy of AC/DC Hybrid Distribution Network Based on Power Electronic Transformer. Energies 2021, 14, 3219. [Google Scholar] [CrossRef]
- Rong, X.; Zhang, H.; Jia, C.; Zhao, J.; Ma, G.; He, Y. Power flow calculation of AC/DC hybrid distribution network considering energy router. In Proceedings of the Fifth International Conference on Energy Engineering and Environmental Protection, Xiamen, China, 17–19 November 2020; Volume 675, p. 012071. [Google Scholar]
- Luo, S.; Luan, L.; Cui, Y.; Xu, S.; Guo, Q.; Liu, T. Study on Optimal Operation of AC-DC Hybrid Distribution Network. J. Phys. Conf. Ser. 2021, 1952, 032025. [Google Scholar] [CrossRef]
- Bo, L.; Chen, Z.; Li, X.; Rodriguez, J.; Chong, K. Low voltage ride through enhancement of a permanent magnet synchronous generator based wind energy conversion system in an islanded microgrid: A dynamic matrix controlled virtual DC machine. Renew. Energy 2023, 228, 120680. [Google Scholar] [CrossRef]
- Wang, W.; Barnes, M. Power flow algorithms for multi-terminal VSC-HVDC with droop control. IEEE Trans. Power Syst. 2014, 29, 1721–1730. [Google Scholar] [CrossRef]
- Zhu, Y.; Wu, H.; Zhang, Z.; Zong, C.; Xu, D. Optimal power flow research of AC–DC hybrid grid with multiple energy routers. Electr. Power Syst. Res. 2024, 228, 110090. [Google Scholar] [CrossRef]
- Wang, J.; Ye, W.; Dong, Z.; Yu, J.; Peng, L.; Zheng, L. The Three-Level NPC Converter Based Energy Router and Its Application in Flexible Distribution Network Control. In Proceedings of the 2022 IEEE/IAS Industrial and Commercial Power System Asia (I&CPS Asia), Shanghai, China, 8–11 July 2022; pp. 978–983. [Google Scholar]
- Li, B.; Wang, W.; Liu, Y.; Li, B.; Wen, W. Research on power flow calculation method of true bipolar VSC-HVDC grids with different operation modes and control strategies. Int. J. Electr. Power Energy Syst. 2021, 126, 106558. [Google Scholar] [CrossRef]
- Chen, X.; Li, W.; Sun, L.; Xu, X. Power flow algorithm of DC distribution network with distributed energy access. In Proceedings of the 2018 International Conference on Power System Technology (POWERCON), Guangzhou, China, 6–9 November 2018; pp. 2414–2419. [Google Scholar]
- Ban, G.; Xu, Y.; Luo, Y.; Jian, L.; Ma, X.; Yuan, X. Flow Calculation of Flexible Interconnected Distribution Network with SOP. In Proceedings of the 2021 IEEE Sustainable Power and Energy Conference (iSPEC), Nanjing, China, 23–25 December 2021; pp. 1562–1569. [Google Scholar]
- Liu, Y.; Wang, Y.; Deng, H.; Tian, J.; Wang, F.; Zhuo, F. Research on Multi-Objective Optimization Scheme in Multi-Node Energy-Router-Based Network. In Proceedings of the 2023 IEEE 14th International Symposium on Power Electronics for Distributed Generation Systems (PEDG), Shanghai, China, 9–12 June 2023; pp. 613–619. [Google Scholar]
- Zhong, R.; Teng, Y.; Wang, X.; Zhu, Y.; Zhang, H. Probabilistic Optimal Power Flow Calculation of AC/DC Hybrid Distribution Network with Photovoltaic Power and Electric Vehicles. In Proceedings of the 2018 International Conference on Power System Technology (POWERCON), Guangzhou, China, 6–9 November 2018; pp. 20–27. [Google Scholar]
- Zhang, J.; Wang, B.; Ma, H.; He, Y.; Wang, Y.; Xue, Z. Reliability Evaluation of Cabled Active Distribution Network Considering Multiple Devices—A Generalized MILP Model. Processes 2023, 11, 3404. [Google Scholar] [CrossRef]
- Zhao, J.; Zhang, M.; Zhao, B.; Du, X.; Zhang, H.; Shang, L.; Wang, C. Integrated Reactive Power Optimisation for Power Grids Containing Large-Scale Wind Power Based on Improved HHO Algorithm. Sustainability 2022, 15, 12962. [Google Scholar] [CrossRef]
- Balasubramaniam, K.; Saraf, P.; Hadidi, R.; Makram, E.B. Energy management system for enhanced resiliency of microgrids during islanded operation. Electr. Power Syst. Res. 2016, 137, 133–141. [Google Scholar] [CrossRef]
- Ning, L.; Xie, C.; Bai, H.; Wu, D. The amelioration of control strategy of VSC-MTDC based on voltage droop control. In Proceedings of the 2017 2nd International Conference on Power and Renewable Energy (ICPRE), Chengdu, China, 20–23 September 2017; pp. 157–161. [Google Scholar]
- Alahmadi, A.; Chung, T.S. An Effective Selection of Memory Technologies for TCAM to Improve the Search Operations: Demonstration of Memory Efficiency in SDN Recovery. Electronics 2023, 13, 707. [Google Scholar] [CrossRef]
- Liu, Z.; Wang, J.; Guo, G.; Feng, K.; Zhan, X.; Peng, F.; Gong, D.; Tang, A.; Lulu, M.; Xiang, C. Research on the minimum network loss optimization control strategy of the active distribution network based on the distributed power flow controller. Front. Energy Res. 2024, 12, 1333171. [Google Scholar] [CrossRef]
- Zhu, L.; Rong, X.; Zhao, J.; Zhang, H.; Zhang, H.; Jia, C.; Ma, G. Topology optimization of AC/DC hybrid distribution network with energy router based on power flow calculation. Energy Rep. 2022, 8, 1622–1638. [Google Scholar] [CrossRef]
- Gilvanejad, M. A distributed energy resources control method to improve the loading profile of radial distribution feeders using solid-state transformer. Electr. Power Syst. Res. 2024, 228, 110110. [Google Scholar] [CrossRef]
- Shi, C.; Jin, G.; Yang, M.; Pan, D. Power flow calculation of chain-type AC-DC hybrid distribution network based on converter parameter identification. In Proceedings of the 2020 5th Asia Conference on Power and Electrical Engineering (ACPEE), Chengdu, China, 4–7 June 2020; pp. 1193–1196. [Google Scholar]
- Zhu, Z.; Liu, D.; Liao, Q.; Tang, F.; Zhang, J.; Jiang, H. Optimal Power Scheduling for a Medium Voltage AC/DC Hybrid Distribution Network. Sustainability 2018, 10, 318. [Google Scholar] [CrossRef]
- Wei, W.; Zhou, Y.; Zhu, J.; Hou, K.; Zhao, H.; Li, Z.; Xu, T. Reliability Assessment for AC/DC Hybrid Distribution Network with High Penetration of Renewable Energy. IEEE Access 2019, 7, 153141–153150. [Google Scholar] [CrossRef]
- Huang, L.; Zong, C.; Yang, X.; Chen, W.; Zhu, Y.; Bi, K. Power Flow Calculation of Distribution Network with Multiple Energy Routers. IEEE Access 2021, 9, 23489–23497. [Google Scholar] [CrossRef]
- Khanh, Q.B. A novel method for global voltage sag compensation in IEEE 69 bus distribution system by dynamic voltage restorers. Therm. Sci. Eng. Prog. 2019, 14, 1893–1911. [Google Scholar]
- Fan, Y.; Chi, Y.; Li, Y.; Wang, Z.; Liu, H.; Liu, W.; Li, X. Key technologies for medium and low voltage DC distribution system. Glob. Energy Interconnect. 2021, 4, 91–103. [Google Scholar] [CrossRef]
- Wang, J.; Yan, J.; Xu, Y.; Huang, K. Power flow calculation method for isolated microgrid considering the influence of harmonic power. J. Eng. 2017, 14, 2615–2621. [Google Scholar] [CrossRef]
- Shen, Y.; Zhu, F.; Zhang, C.; Cai, W.; Yuan, L.; Li, K.; Zhao, Z. Steady-state model of multi-port electric energy router and power flow analysis method of AC/DC hybrid system considering control strategies. J. Eng. 2019, 16, 2794–2799. [Google Scholar] [CrossRef]



| Port Type | Number of Ports | VSC Losses | DAB Losses |
|---|---|---|---|
| Medium-Voltage AC Port | M | √ | × |
| Low-Voltage AC Port | N | √ | √ |
| Medium-Voltage DC Port | K | × | × |
| Low-Voltage DC Port | T | × | √ |
| Port Type | Control Strategies |
|---|---|
| AC Port | PQ control (active power control uses fixed control; reactive power control uses fixed control) |
| PV control (active power control uses fixed control; reactive power control uses fixed control) | |
| DC Port | Fixed DC voltage control |
| Fixed DC active power control | |
| Droop control |
| Port Number | Connected Node | Control Method | |||||
|---|---|---|---|---|---|---|---|
| 1 | 10 kV AC Node 5 | PQ Control | 0.0276 | 0.0251 | 7.1617 | −30 | 0 |
| 2 | 10 kV AC Node 10 | PQ Control | 0.0276 | 0.0251 | 7.1617 | −2 | 19 |
| 3 | 10 kV AC Node 15 | PQ Control | 0.0276 | 0.0251 | 7.1617 | 0 | 0 |
| 4 | 750 V DC Node 6 | Constant P Control | 0.0578 | - | - | 8 | 0 |
| 5 | 380 V AC Node 4 | PQ Control | 0.0276 | 0.0251 | 7.1617 | 30 | 10 |
| 6 | 10 kV DC Node 4 | Constant P Control | 0.0355 | - | - | 122 | 0 |
| Port Number | ||||||
|---|---|---|---|---|---|---|
| 1 | −30 | 0 | 0.9997 | 1.0000 | 0.5572 | −46.7610 |
| 2 | −30 | 0 | 0.9889 | 1.0003 | 0.5631 | −46.7582 |
| 3 | 0 | 0 | 0.9786 | 1.0000 | 0 | 0 |
| 4 | 0 | 0 | 0.9999 | - | - | - |
| 5 | 10 | 0 | 0.9999 | 0.9995 | 0.8883 | 9.0150 |
| 6 | 50 | 0 | 0.9999 | - | - | - |
| EER Number | Port Number | Connected Node | Control Method | ||
|---|---|---|---|---|---|
| EER1 | 1 | 380 V AC Node 3 | PQ Control | 10 | 0 |
| 2 | 10 kV DC Node 6 | Constant P Control | 25 | 0 | |
| 3 | 750 V DC Node 2 | Constant P Control | 10 | 0 | |
| 4 | 10 kV AC Node 11 | PQ Control | −45 | 0 | |
| EER2 | 1 | 10 kV AC Node 33 | PQ Control | −40 | 0 |
| 2 | 10 kV AC Node 31 | PQ Control | −40 | 0 | |
| 3 | 10 kV DC Node 10 | Constant P Control | 35 | 0 | |
| 4 | 10 kV AC Node 25 | PQ Control | 35 | 0 | |
| 5 | 750 V DC Node 11 | Constant P Control | 0 | 0 | |
| 6 | 380 V AC Node 8 | PQ Control | 10 | 0 |
| EER Number | Port Number | ||||
|---|---|---|---|---|---|
| EER1 | 1 | 0.9999 | 1.0000 | 0.8879 | 9.0164 |
| 2 | 0.9999 | - | - | - | |
| 3 | 0.9999 | - | - | - | |
| 4 | 0.9882 | 1.0265 | 0.8237 | −47.0761 | |
| EER2 | 1 | 0.9882 | 1.000 | 0.7516 | −46.9965 |
| 2 | 0.9944 | 1.0003 | 0.7467 | −47.0031 | |
| 3 | 0.9999 | - | - | - | |
| 4 | 0.9748 | 0.9996 | 0.6669 | 132.8134 | |
| 5 | 0.9999 | - | - | - | |
| 6 | 0.9994 | 0.9997 | 0.8876 | 9.0267 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, J.; Dou, J.; Wu, Y.; Xia, H.; Duan, Q.; Dong, X.; Zhang, Y. A Method for Power Flow Calculation in AC/DC Hybrid Distribution Networks Considering the Electric Energy Routers Based on an Alternating Iterative Approach. Electronics 2024, 13, 3384. https://doi.org/10.3390/electronics13173384
Zhao J, Dou J, Wu Y, Xia H, Duan Q, Dong X, Zhang Y. A Method for Power Flow Calculation in AC/DC Hybrid Distribution Networks Considering the Electric Energy Routers Based on an Alternating Iterative Approach. Electronics. 2024; 13(17):3384. https://doi.org/10.3390/electronics13173384
Chicago/Turabian StyleZhao, Jie, Jinqiu Dou, Yunzhao Wu, Huaimin Xia, Qing Duan, Xuzhu Dong, and Yiyang Zhang. 2024. "A Method for Power Flow Calculation in AC/DC Hybrid Distribution Networks Considering the Electric Energy Routers Based on an Alternating Iterative Approach" Electronics 13, no. 17: 3384. https://doi.org/10.3390/electronics13173384
APA StyleZhao, J., Dou, J., Wu, Y., Xia, H., Duan, Q., Dong, X., & Zhang, Y. (2024). A Method for Power Flow Calculation in AC/DC Hybrid Distribution Networks Considering the Electric Energy Routers Based on an Alternating Iterative Approach. Electronics, 13(17), 3384. https://doi.org/10.3390/electronics13173384








