Design of Small-Size Lithium-Battery-Based Electromagnetic Induction Heating Control System
Abstract
:1. Introduction
2. Principles and Methods
2.1. Principle of Full-Bridge LC Series Resonant Electromagnetic Induction Heating
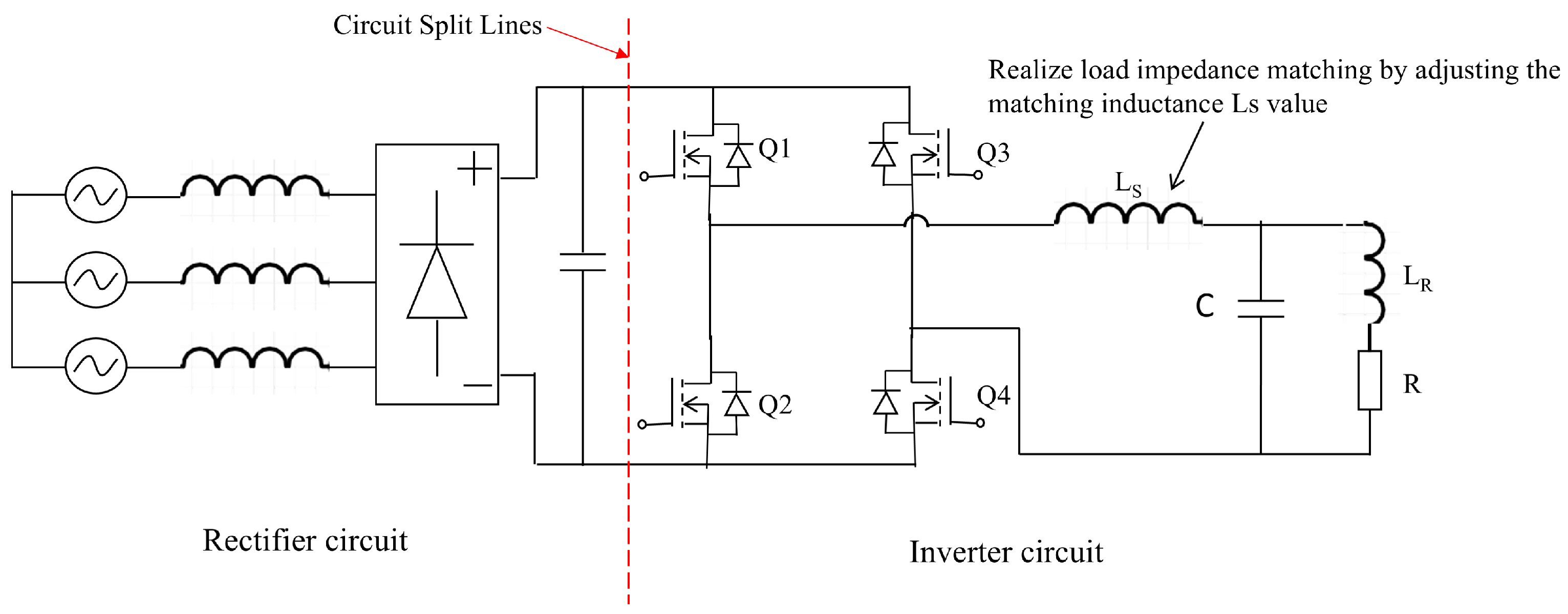
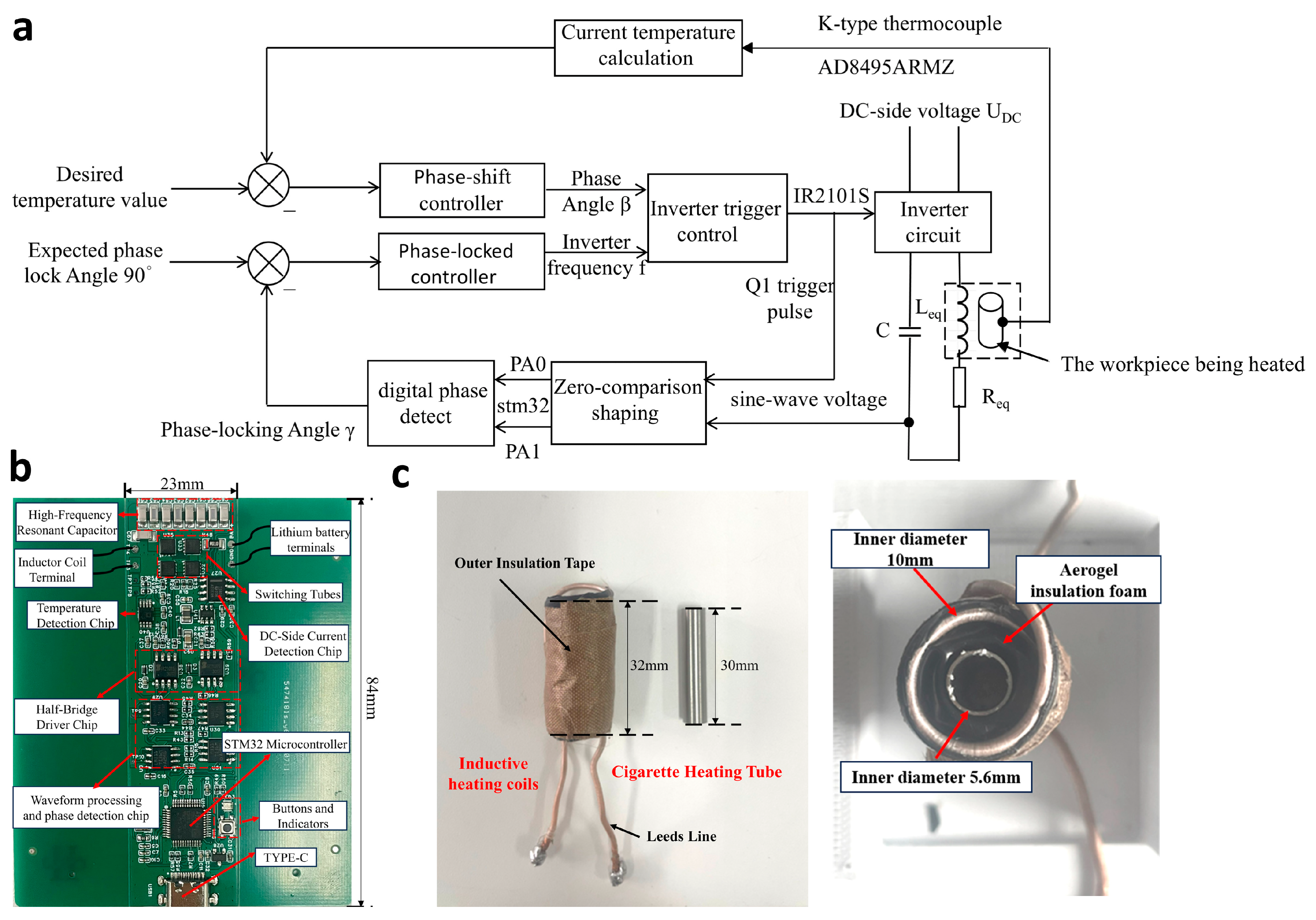
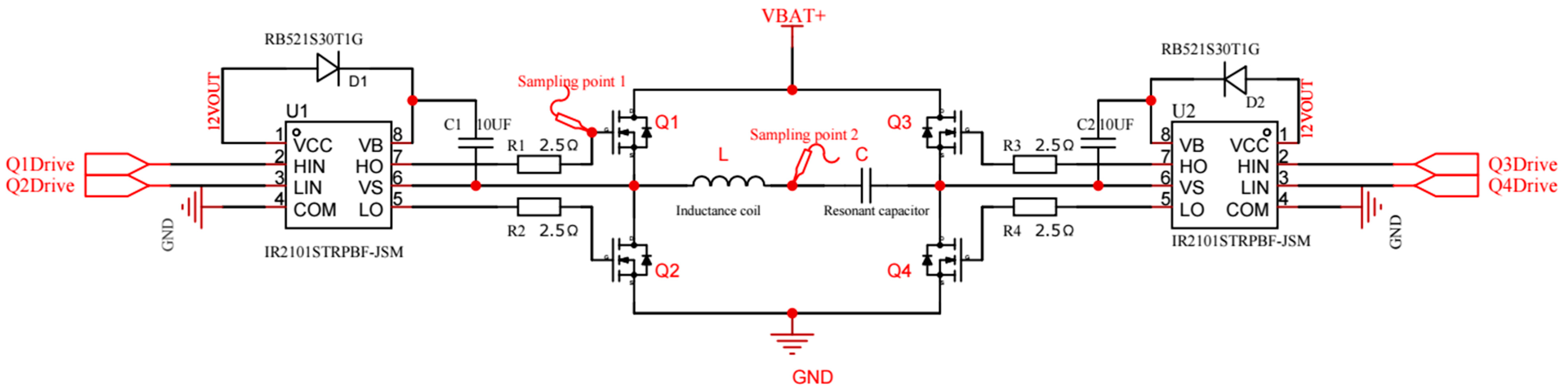
2.2. Low-Voltage-Powered Small-Size Electromagnetic Induction Heating Control System Structure and Circuit Principles
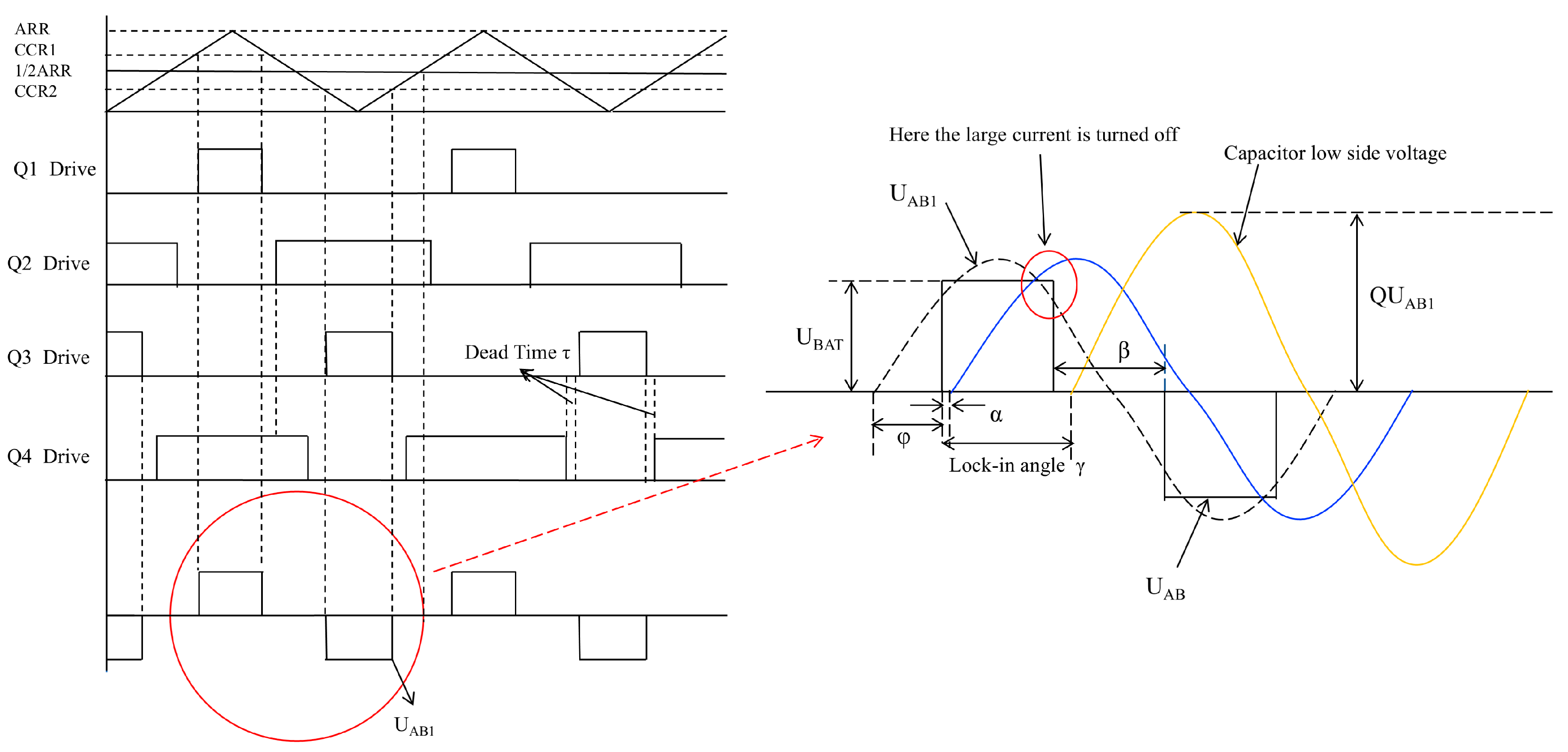
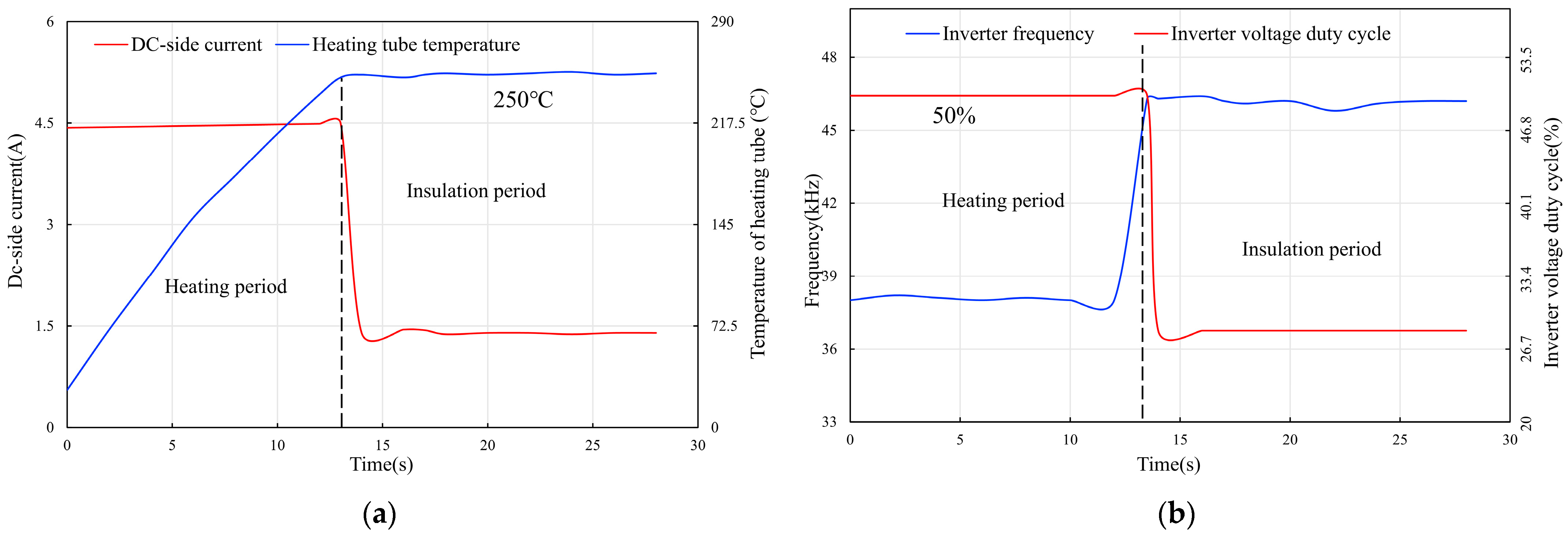
2.3. Electromagnetic Induction Heating Control System Work Process
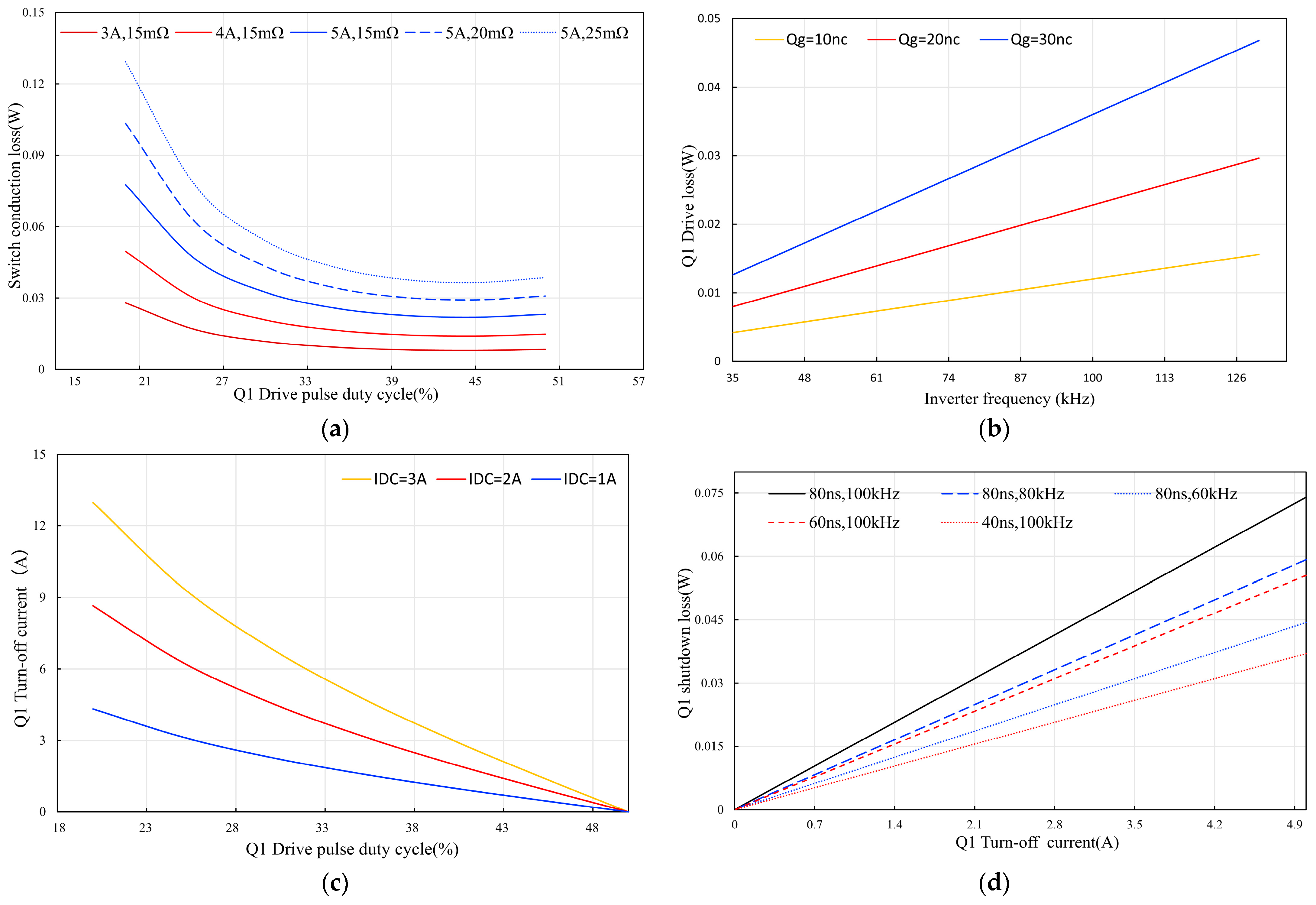
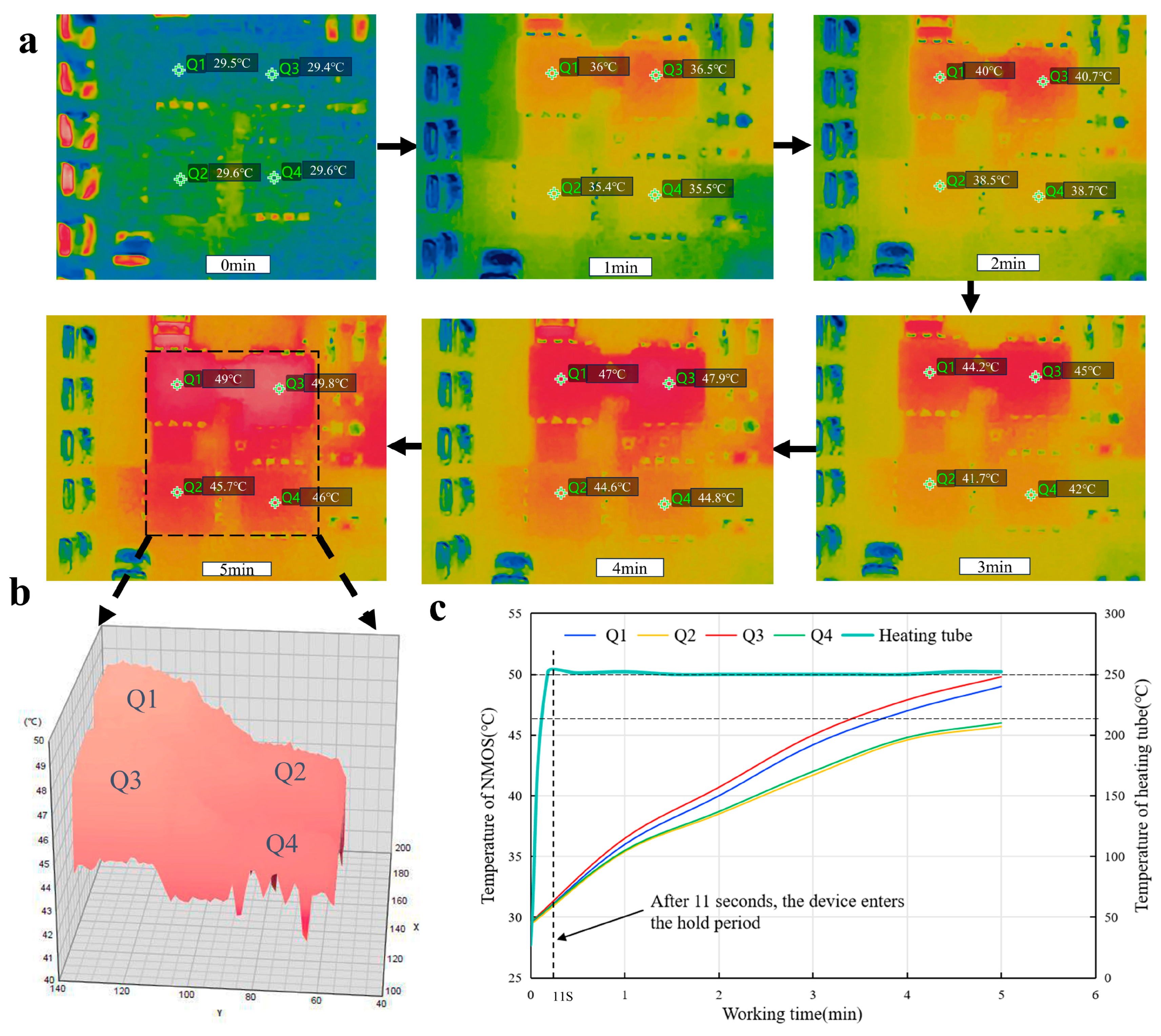
2.4. Impact Factor Analysis of NMOS Losses
2.5. Factors Affecting Resistance and Inductance of Coils
2.6. Experimental Setup
3. Results and Discussion
3.1. Effect of Resonant Capacitance Value on Heating Rate and NMOS Loss
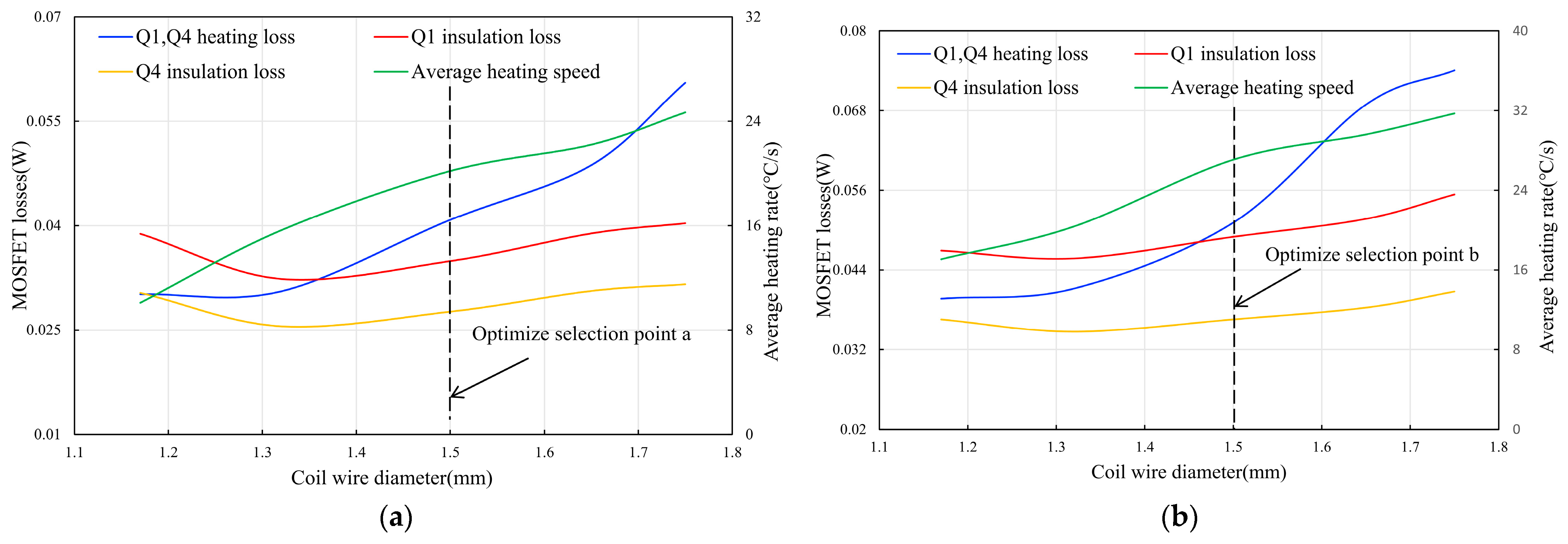
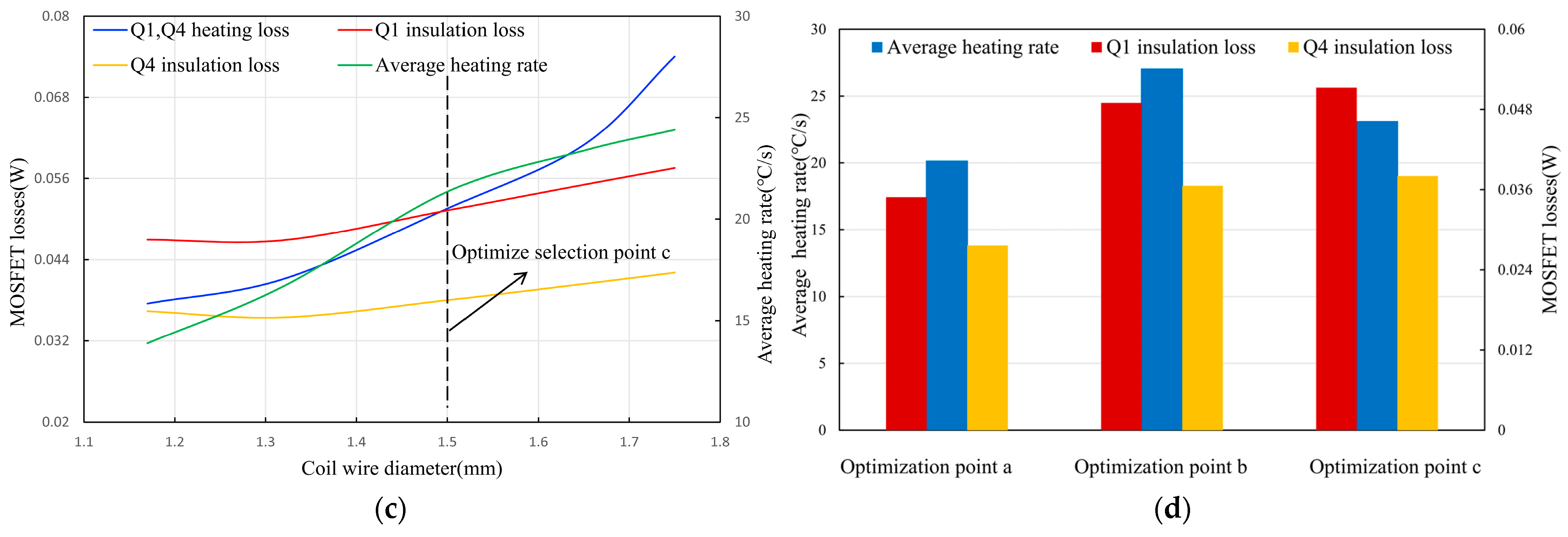
3.2. Effect of Induction Coil Wire Diameter on Heating Rate and NMOS Loss
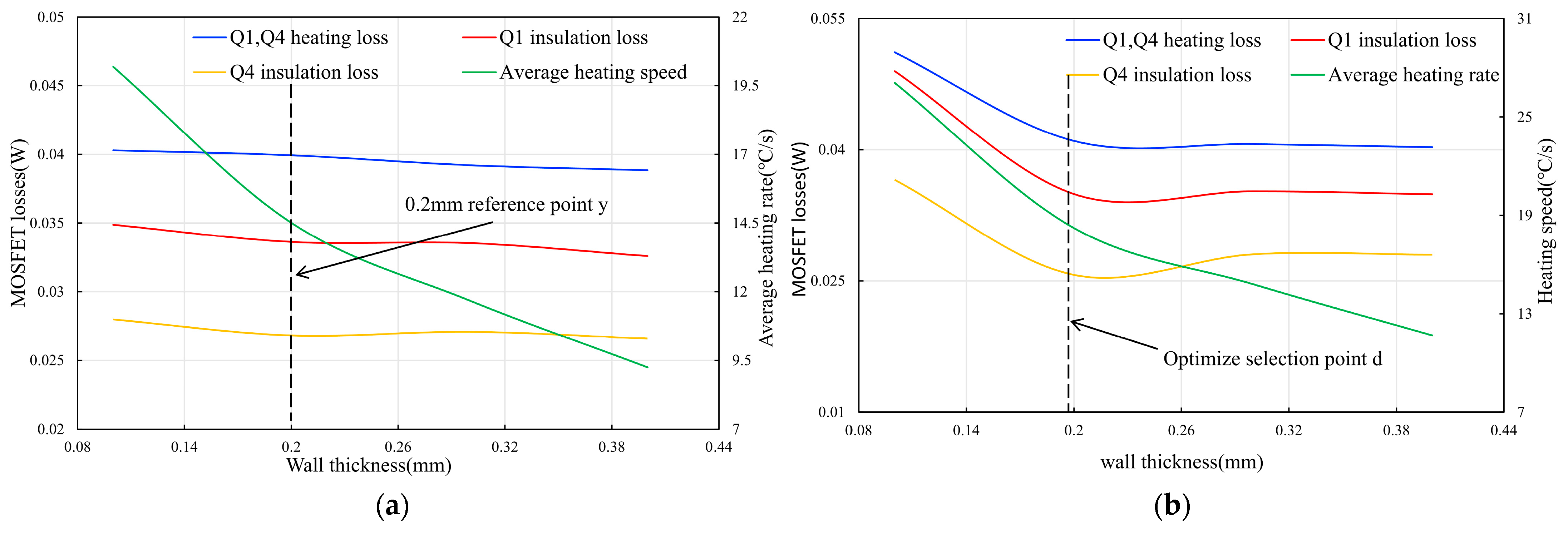
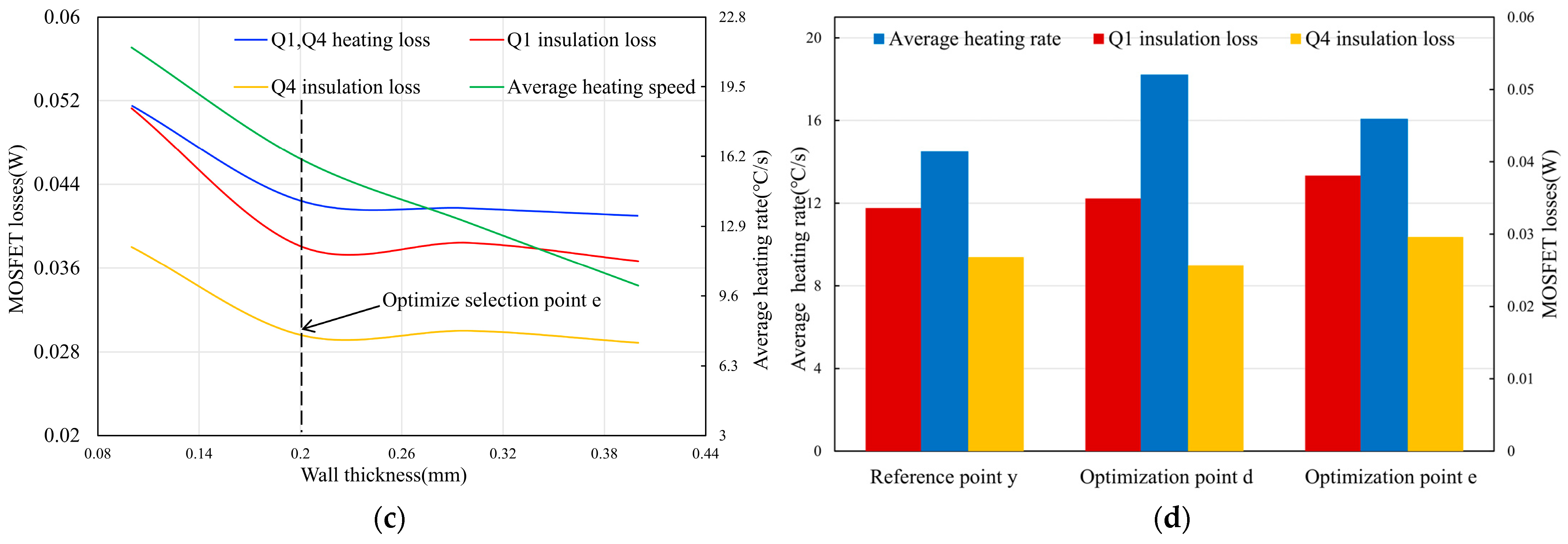
3.3. Effect of Heating Tube Wall Thickness on Heating Rate and NMOS Loss
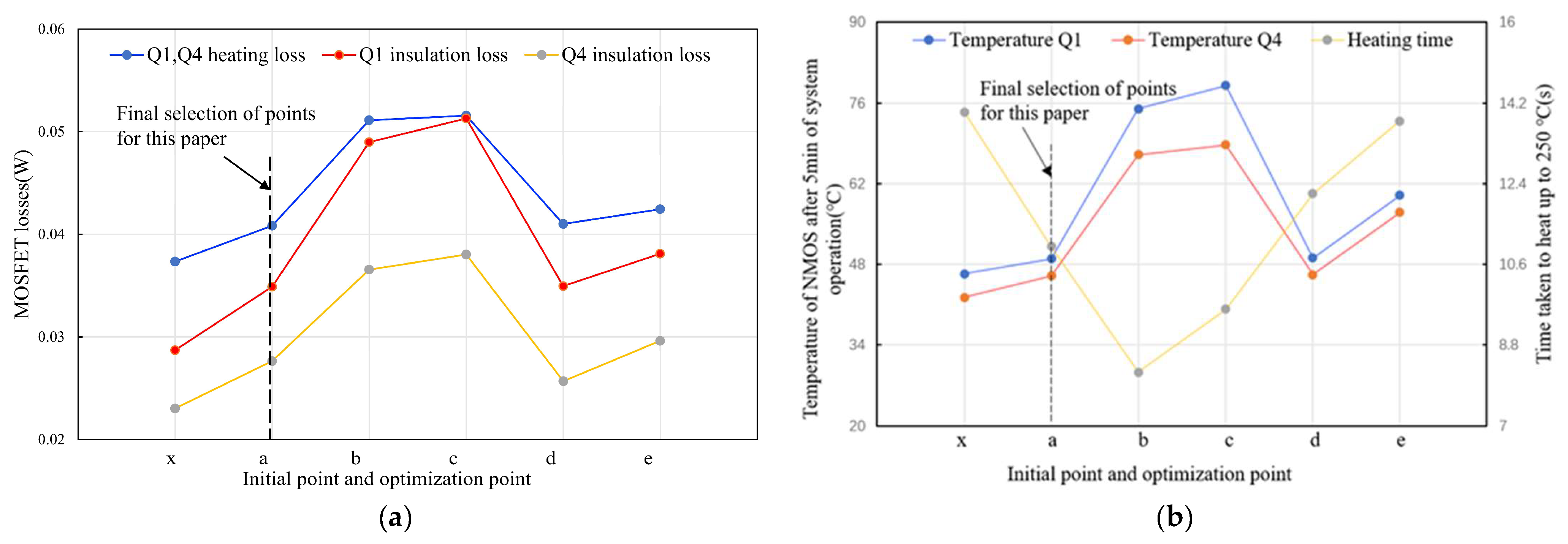
3.4. Comparison and Analysis of Initial Selection Point and Optimization Points
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Kukartsev, V.A.; Tynchenko, V.S.; Kukartsev, V.V. Steel smelting in induction crucible furnaces with industrial frequency. IOP Conf. Ser. Earth Environ. Sci. 2018, 194, 042024. [Google Scholar] [CrossRef]
- Phadungthin, R.; Haema, J. Full bridge resonant inverter for non-ferrous metal induction heating application. In Proceedings of the 2015 IEEE PES Asia-Pacific Power and Energy Engineering Conference (APPEEC), Brisbane, QLD, Australia, 15–18 November 2015; pp. 1–4. [Google Scholar]
- Phadungthin, R.; Haema, J. High frequency induction heating of full bridge resonant inverter application. In Proceedings of the 2016 International Symposium on Power Electronics, Electrical Drives, Automation and Motion (SPEEDAM), Capri, Italy, 22–24 June 2016; pp. 1383–1387. [Google Scholar]
- Smalcerz, A.; Wecki, B.; Blacha, L. Influence of the power of various types of induction furnaces on the shape of the metal bath surface. Adv. Sci. Technol. 2021, 15, 34–42. [Google Scholar] [CrossRef]
- El-Mashad, H.M.; Zhong, P. Application of induction heating in food processing and cooking. Food Eng. Rev. 2017, 9, 82–90. [Google Scholar] [CrossRef]
- Franco, C.; Acero, J.; Alonso, R.; Sagues, C. Inductive sensor for temperature measurement in induction heating applications. IEEE Sens. J. 2011, 12, 996–1003. [Google Scholar] [CrossRef]
- Meng, L.; Cheng, K.W.E.; Chan, K. Heating performance improvement and field study of the induction cooker. In Proceedings of the 2009 3rd International Conference on Power Electronics Systems and Applications (PESA), Hong Kong, China, 20–22 May 2009; pp. 1–5. [Google Scholar]
- Pijls, B.; Sanders, I.; Kuijper, E.; Nelissen, R. Segmental induction heating of orthopaedic metal implants. Bone Jt. Res. 2018, 7, 609–619. [Google Scholar] [CrossRef] [PubMed]
- Stauffer, P.R.; Cetas, T.C.; Jones, R.C. Magnetic induction heating of ferromagnetic implants for inducing localized hyperthermia in deep-seated tumors. IEEE Trans. Biomed. Eng. 1984, 31, 235–251. [Google Scholar] [CrossRef] [PubMed]
- Pijls, B.; Sanders, I.; Kuijper, E.; Nelissen, R. Non-contact electromagnetic induction heating for eradicating bacteria and yeasts on biomaterials and possible relevance to orthopaedic implant infections: In vitro findings. Bone Jt. Res. 2017, 6, 323–330. [Google Scholar] [CrossRef] [PubMed]
- Lucía, Ó.; Burdío, J.; Barragán, L.; Acero, J.; Millán, I. Series-resonant multiinverter for multiple induction heaters. IEEE Trans. Power Electron. 2010, 25, 2860–2868. [Google Scholar] [CrossRef]
- Park, H.P.; Jung, J.H. Load-adaptive modulation of a series-resonant inverter for all-metal induction heating applications. IEEE Trans. Ind. Electron. 2018, 65, 6983–6993. [Google Scholar] [CrossRef]
- Burdio, J.M.; Monterde, F.; Garcia, J.R.; Barragan, L.A.; Martinez, A. A two-output series-resonant inverter for induction-heating cooking appliances. IEEE Trans. Power Electron. 2005, 20, 815–822. [Google Scholar] [CrossRef]
- Bonert, R.; Lavers, J. Simple starting scheme for a parallel resonance inverter for induction heating. IEEE Trans. Power Electron. 1994, 9, 281–287. [Google Scholar] [CrossRef]
- Nam, I. Analysis and design method for parallel quasi resonant inverter in induction heating applications. In Proceedings of the 2018 IEEE Applied Power Electronics Conference and Exposition (APEC), San Antonio, TX, USA, 4–8 March 2018; pp. 1–5. [Google Scholar]
- Arslan, L.; Özbay, H. Modelling and simulation of D-class current-fed parallel resonant inverter for induction heating system. Aintelia Sci. Notes 2022, 1, 106–116. [Google Scholar]
- Kobos, W., Jr. Impedance matching of the inverter for induction heating. Relation 2018, 9, 1. [Google Scholar] [CrossRef]
- Esteve, V.; Jordán, J.; Dede, E.; Martinez, P.; Ferrara, K.; Bellido, J. Comparative analysis and improved design of LLC inverters for induction heating. IET Power Electron. 2023, 16, 1754–1764. [Google Scholar] [CrossRef]
- Esteve, V.; Jordán, J.; Dede, E.; Martinez, P.; Ferrara, K.; Bellido, J.L. Optimal LLC inverter design with SiC MOSFETs and phase shift control for induction heating applications. IEEE Trans. Ind. Electron. 2021, 69, 11100–11111. [Google Scholar] [CrossRef]
- Li, J.; Wang, L.; Sun, Q. Research on high-frequency induction heating load-matched based on LLC resonant circuit. In Proceedings of the 2014 International Power Electronics and Application Conference and Exposition, Shanghai, China, 5–9 November 2014; pp. 826–830. [Google Scholar]
- Kurre, M.; Banerjee, A. Zero voltage switching self-oscillating PWM inverter in induction heating applications. J. Eng. Res. 2022. [Google Scholar] [CrossRef]
- Yachiangkam, S.; Sangswang, A.; Naetiladdanon, S.; Koompai, C.; Koompai, C. Steady-state analysis of ZVS and NON-ZVS full-bridge inverters with asymmetrical control for induction heating applications. J. Power Electron. 2015, 15, 544–554. [Google Scholar] [CrossRef]
- Yongyuth, N.; Viriya, P.; Matsuse, K. Analysis of a full-bridge inverter for induction heating using asymmetrical phase-shift control under zvs and non-zvs operation. In Proceedings of the 2007 7th International Conference on Power Electronics and Drive Systems, Bangkok, Thailand, 27–30 November 2007; pp. 476–482. [Google Scholar]
- Kamli, M.; Yamamoto, S.; Abe, M. A 50–150 kHz half-bridge inverter for induction heating applications. IEEE Trans. Ind. Electron. 1996, 43, 163–172. [Google Scholar] [CrossRef]
- Lee, S.H.; Lim, S.; Song, S. Design of New Current Full-Bridge Resonant Inverter for Induction Heating System. J. Korean Inst. Illum. Electr. Install. Eng. 2012, 26, 59–69. [Google Scholar]
- Płatek, M.; Waradzyn, Z. Operation modes of full-bridge voltage-source series resonant inverter with PFM control for induction heating applications. Elektrotechnika Elektron. 2006, 25, 58–67. [Google Scholar]
- Lakkas, G. MOSFET power losses and how they affect power-supply efficiency. Analog. Appl. 2016, 10, 22–26. [Google Scholar]
- Kimball, J.W.; Chapman, P.L. Evaluating conduction loss of a parallel IGBT-MOSFET combination. In Proceedings of the Conference Record of the 2004 IEEE Industry Applications Conference, Seattle, WA, USA, 3–7 October 2004; pp. 22–26. [Google Scholar]
- Graovac, D.; Purschel, M.; Kiep, A. MOSFET power losses calculation using the data-sheet parameters. In Infineon Application Note; Infineon Technologies AG: Neubiberg, Germany, 2006; Volume 1. [Google Scholar]
- Esteve, V.; Jordan, J.; Sanchis, K.E.; Dede, E.J.; Maset, E.; Ejea, J.B.; Ejea, J. Enhanced pulse-density-modulated power control for high-frequency induction heating inverters. IEEE Trans. Ind. Electron. 2015, 62, 6905–6914. [Google Scholar] [CrossRef]
- Özbay, H. PDM-MPPT based solar powered induction heating system. Eng. Sci. Technol. 2020, 23, 1397–1414. [Google Scholar] [CrossRef]
- Yan, W.; Ji, Z.; Lu, X. Power control for induction heating by asymmetrical pulse density modulation. In Proceedings of the 2006 1ST IEEE Conference on Industrial Electronics and Applications, Singapore, 24–26 May 2006; pp. 1–5. [Google Scholar]
- Kumaraswamy, A.; Bhattacharya, A.; Sadhu, P. Dual output direct AC–AC series resonant converter for all metal induction heating system with a hybrid control technique. Electr. Eng. 2023, 105, 1363–1375. [Google Scholar] [CrossRef]
- Kwon, Y.S.; Lee, B.K.; Yoo, S.B. Half-Bridge Series Resonant Inverter for Induction Cooking Application with Load-Adaptive PFM Control Strategy. In ICPE (ISPE) Proceedings; Institute of Power Electronics: Seoul, Republic of Korea, 1998; Volume 10, pp. 1018–1023. [Google Scholar]
- Hu, J.; Bi, C.; Jia, K.; Xiang, Y. Power control of asymmetrical frequency modulation in a full-bridge series resonant inverter. IEEE Trans. Power Electron. 2015, 30, 7051–7059. [Google Scholar] [CrossRef]
- Zhou, M.; Li, Y.; Wang, J. Design of High Frequency Induction Heating Power Supply System. J. Harbin Univ. Sci. Technol. 2015, 20, 50. [Google Scholar]
- Jeong, W.; Heo, K.W.; Lee, J.S.; Jung, J.H. Phase-shifted third harmonic modulation technique for induction heating applications to improve soft switching capability. J. Power Electron. 2024, 24, 1014–1024. [Google Scholar] [CrossRef]
- Kifune, H.; Hatanaka, Y.; Nakaoka, M. Cost effective phase shifted pulse modulation soft switching high frequency inverter for induction heating applications. IEE Proc.-Electr. Power Appl. 2004, 151, 19–25. [Google Scholar] [CrossRef]





| Material | Density (g/cm3) | Relative Permeability | Thermal Conductivity (w/m·°C) | Specific Heat Capacity (J/kg·°C) |
|---|---|---|---|---|
| Pure iron | 7.86 | 4000 | 46.5 | 460 |
| 430 stainless steel | 7.75 | 500 | 23.9 | 460 |
| 1J50 soft magnetic alloy | 8.2 | 20,000 | 16.5 | 450 |
| Model | Qg (nc) | RDS(on) (mΩ) | QGD (nc) | QGS2 (nc) | toff (ns) |
|---|---|---|---|---|---|
| NCEP3065QU | About 30 | 1.9 | about 5 | about 3 | About 25 |
| Selection Point | Material | Coil Wire Diameter (mm) | Wall Thickness (mm) | Capacitance Value (uF) | Average Heating Power (W) | PWM Frequency for Heating and Holding Periods (kHz) | Equivalent Inductance (uH) | Coil DC Resistance (Ω) |
|---|---|---|---|---|---|---|---|---|
| x | Pure iron | 1.17 | 0.1 | 2.2 | about 17 | 38, 46 | 2.3 | 0.017 |
| a | Pure iron | 1.5 | 0.1 | 2.3 | about 17 | 43, 53.8 | 2.3 | 0.0085 |
| b | 1J50 alloy | 1.5 | 0.1 | 0.86 | about 17 | 73, 82.2 | 3.38 | 0.0085 |
| c | 430 steel | 1.5 | 0.1 | 0.96 | about 17 | 72, 84.5 | 2.61 | 0.0085 |
| d | 1J50 alloy | 1.5 | 0.2 | 1.95 | about 17 | 45, 53 | 3.2 | 0.0085 |
| e | 430 steel | 1.5 | 0.2 | 1.75 | about 17 | 49, 59 | 2.9 | 0.0085 |
| Optimal Point | Battery Output Current (A) | Heating Time (s) | Q1 Final Temperature (°C) | Q3 Final Temperature (°C) | Q2,Q4 Final Temperature (°C) | Coil Outer Temperature (°C) |
|---|---|---|---|---|---|---|
| a | 4.6A | 11 | 49 | 49.8 | About 46 | About 60 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liang, Y.; Song, S.; Xu, B.; Li, Z.; Li, X.; Mo, Z.; Li, J. Design of Small-Size Lithium-Battery-Based Electromagnetic Induction Heating Control System. Electronics 2024, 13, 3287. https://doi.org/10.3390/electronics13163287
Liang Y, Song S, Xu B, Li Z, Li X, Mo Z, Li J. Design of Small-Size Lithium-Battery-Based Electromagnetic Induction Heating Control System. Electronics. 2024; 13(16):3287. https://doi.org/10.3390/electronics13163287
Chicago/Turabian StyleLiang, Yuanjie, Shihao Song, Bocheng Xu, Zhuangzhuang Li, Xuelin Li, Zonglai Mo, and Jun Li. 2024. "Design of Small-Size Lithium-Battery-Based Electromagnetic Induction Heating Control System" Electronics 13, no. 16: 3287. https://doi.org/10.3390/electronics13163287
APA StyleLiang, Y., Song, S., Xu, B., Li, Z., Li, X., Mo, Z., & Li, J. (2024). Design of Small-Size Lithium-Battery-Based Electromagnetic Induction Heating Control System. Electronics, 13(16), 3287. https://doi.org/10.3390/electronics13163287






