Electromagnetic Fields Calculation and Optimization of Structural Parameters for Axial and Radial Helical Air-Core Inductors
Abstract
:1. Introduction
2. Finite Element Calculation of Electromagnetic Field for Air-Core Inductors
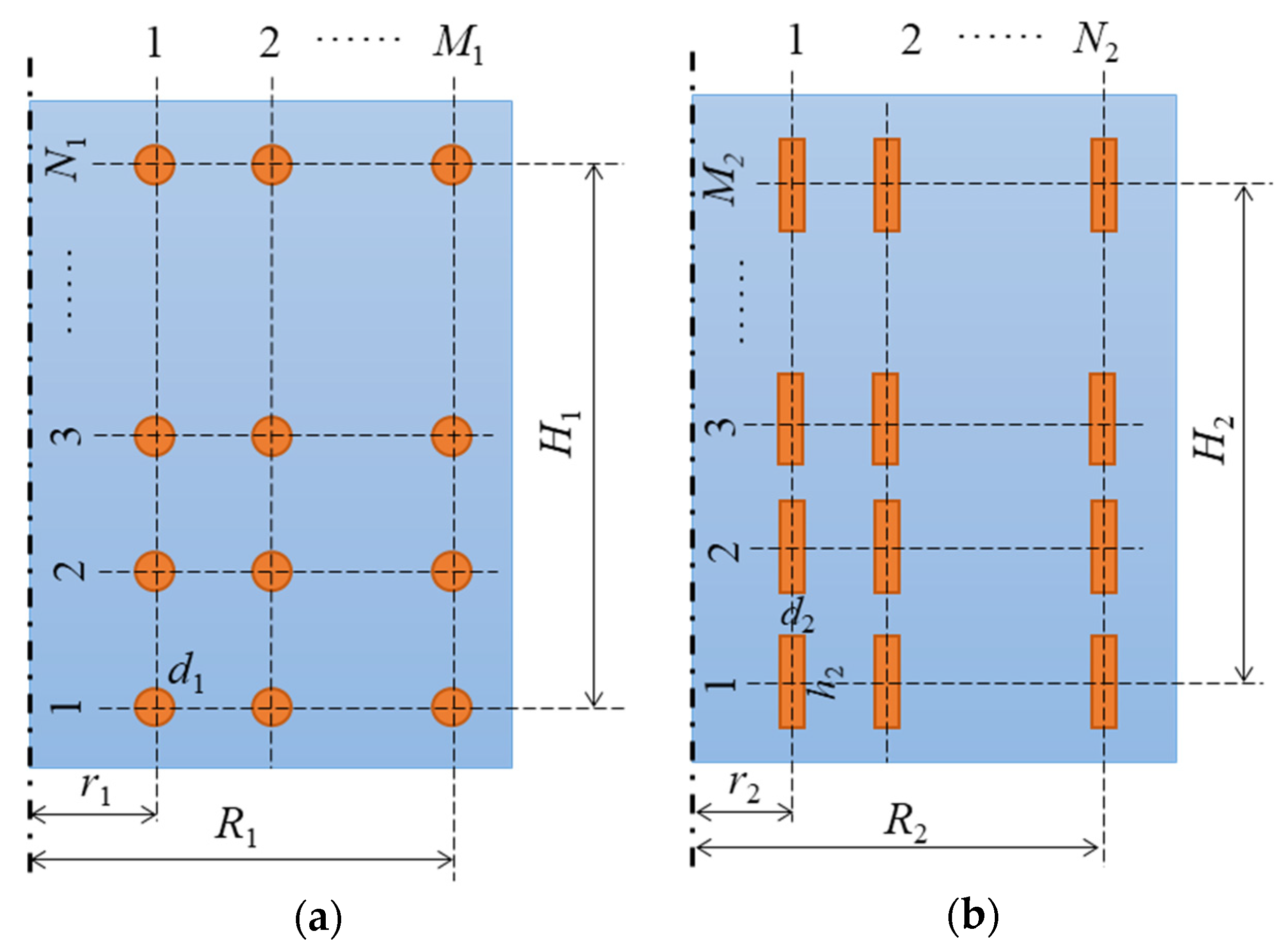
2.1. Two Types of Inductor Structures
2.2. Parameterized Finite Element Modeling
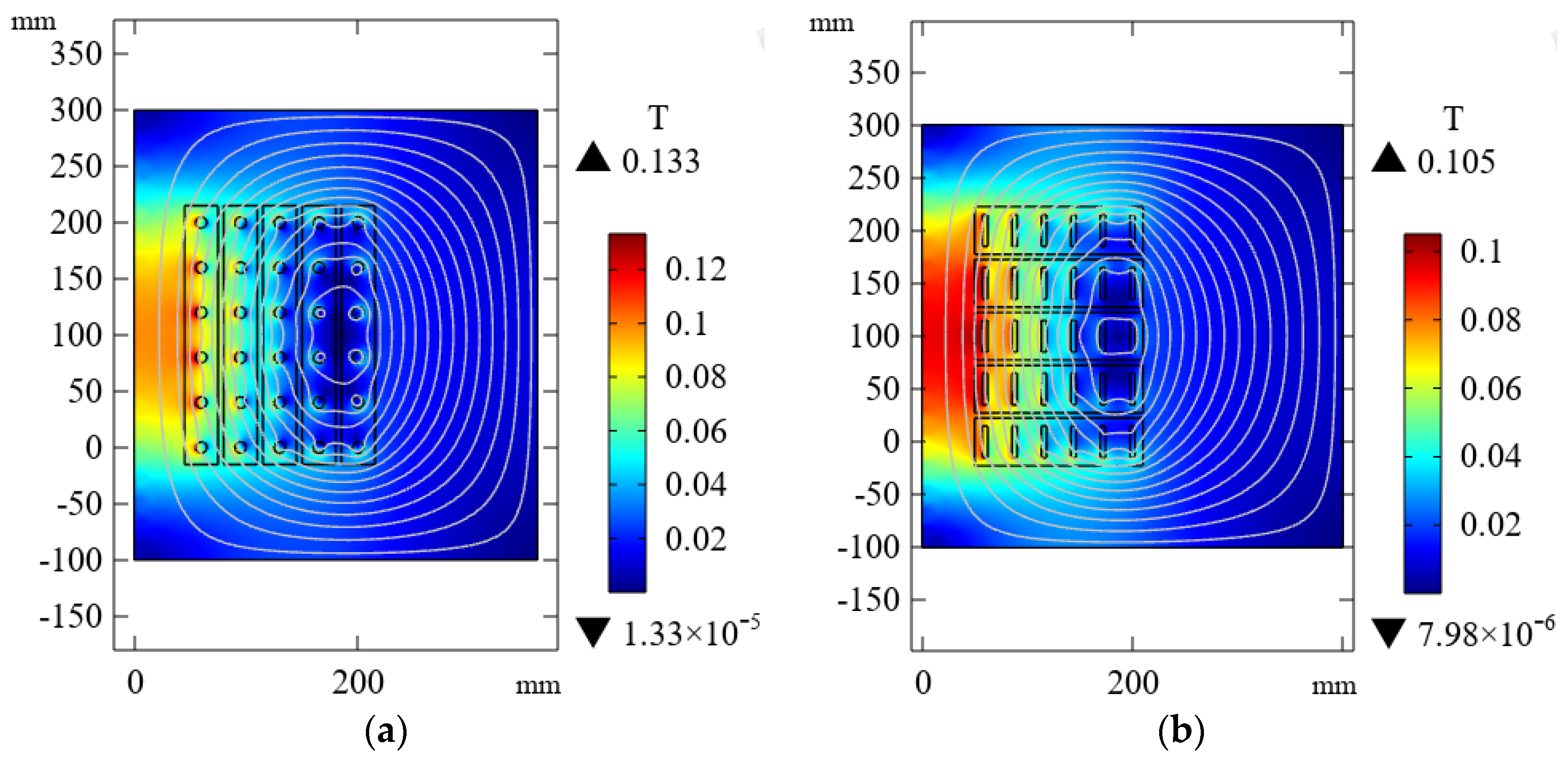
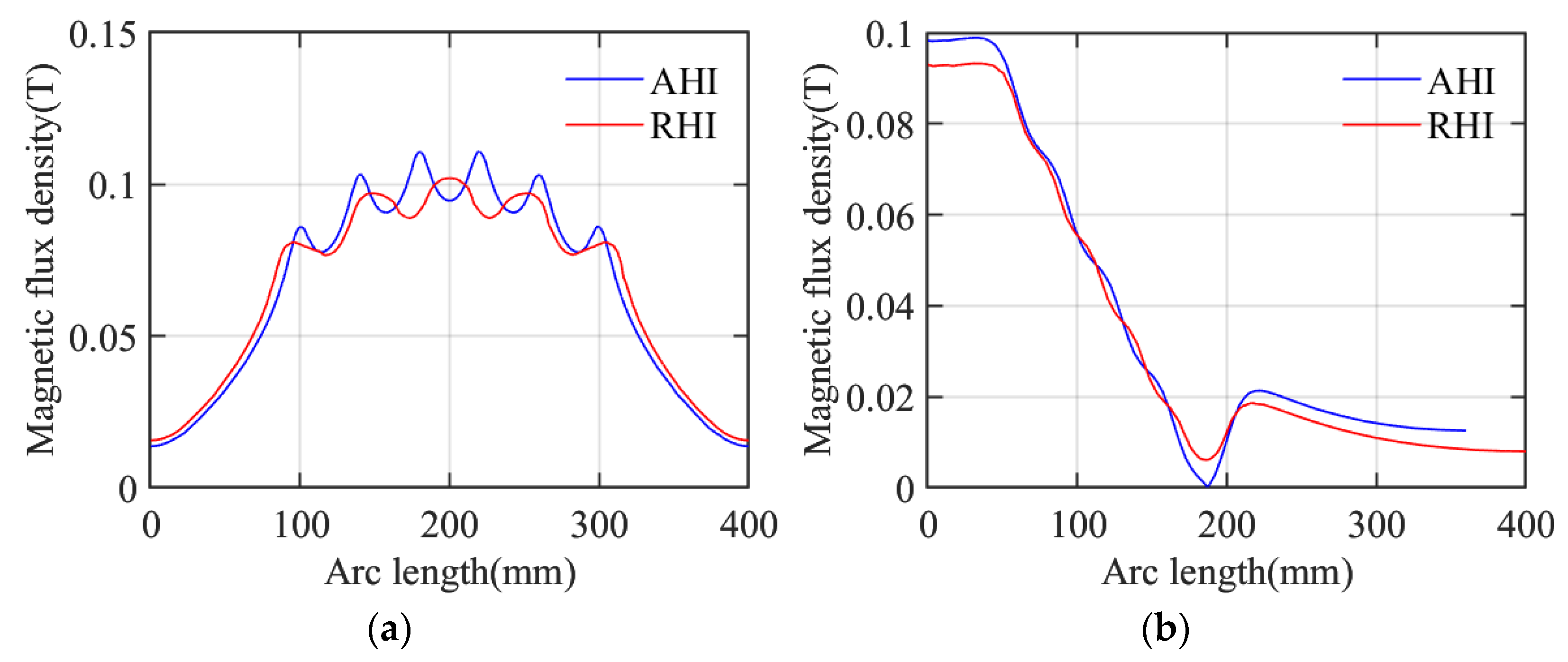
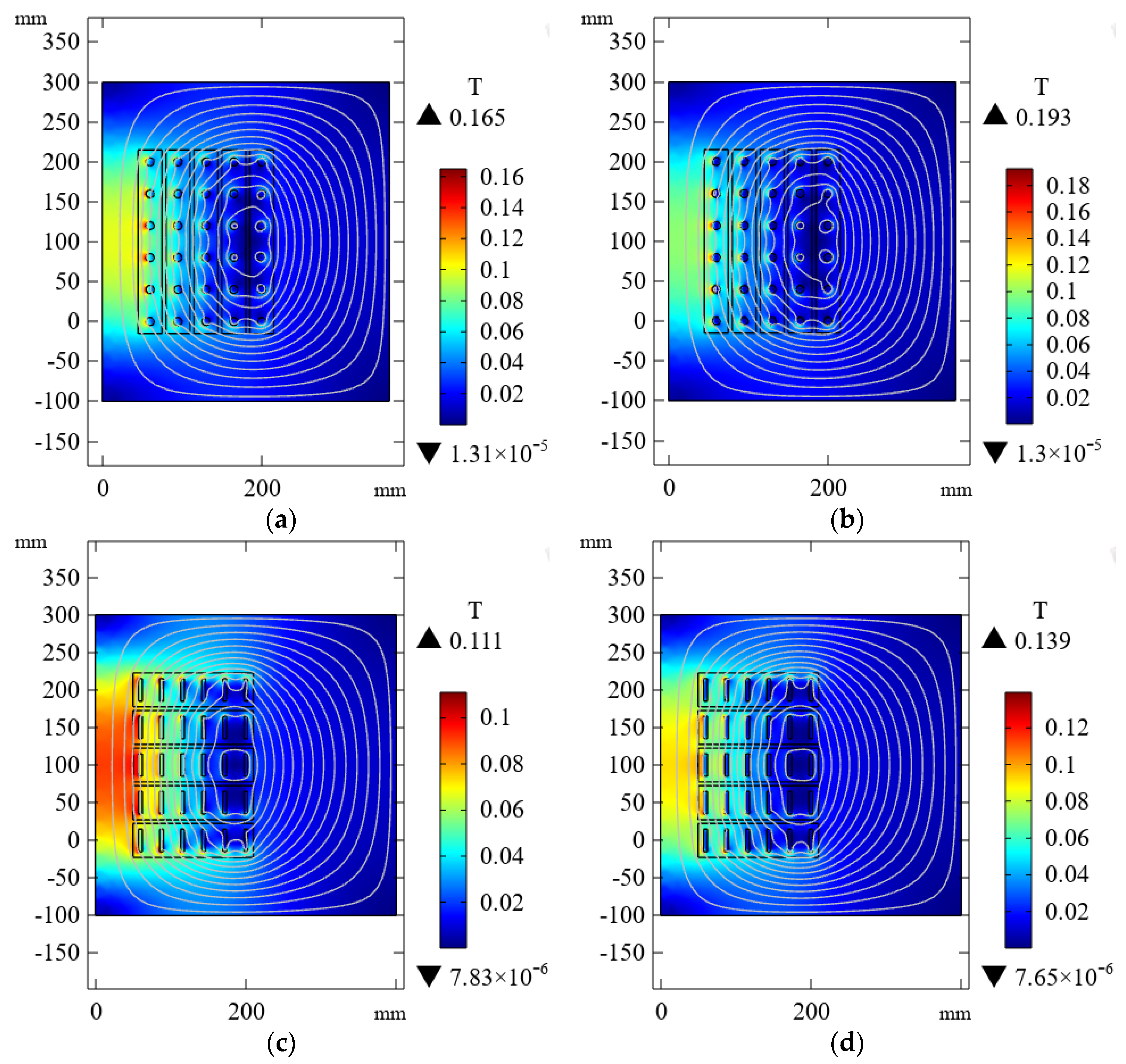
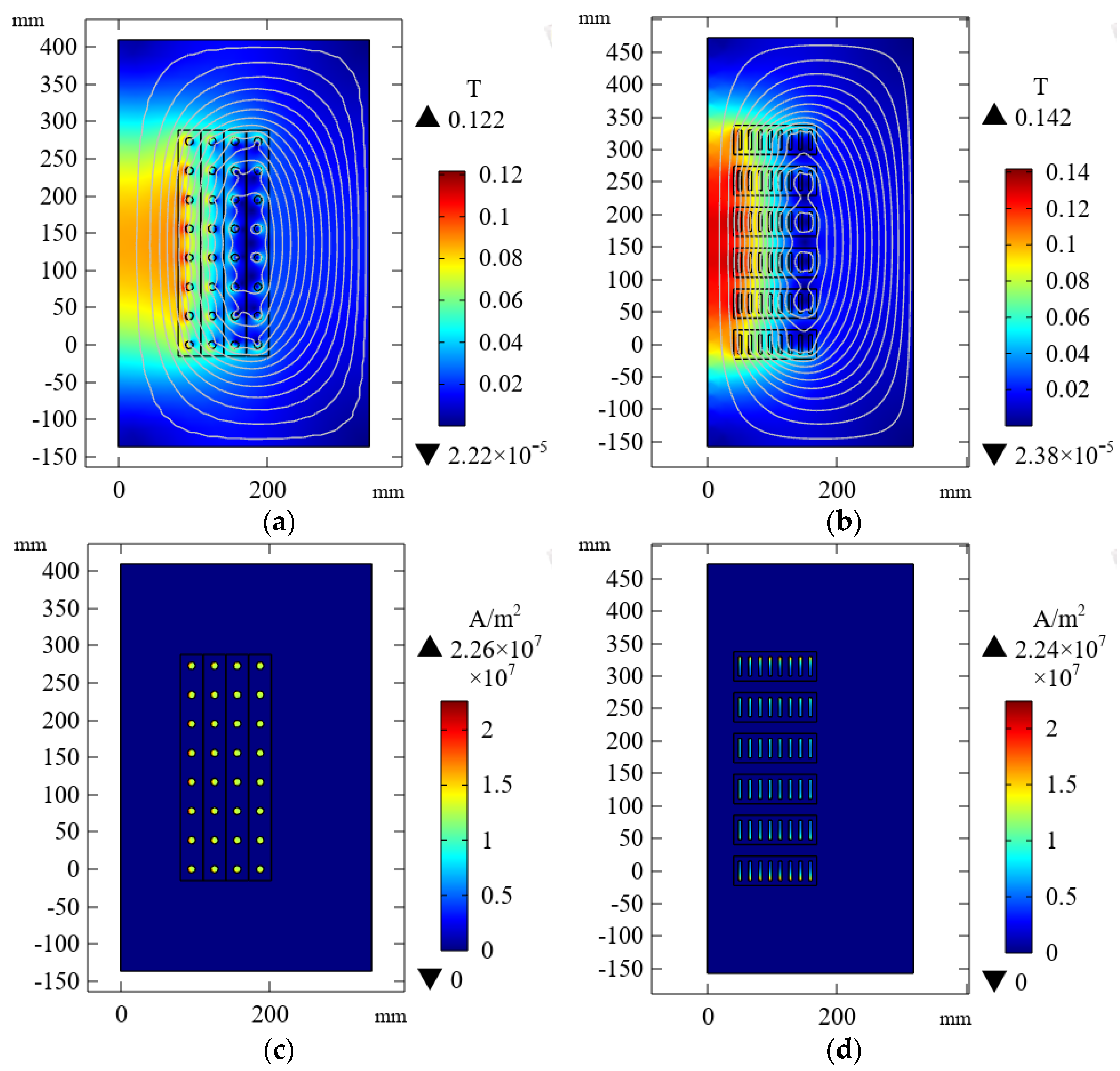
2.3. Spatial Magnetic Field Distribution Characteristics of Inductors
3. Generation of Training Data and Modeling of BP Neural Network
3.1. Monte Carlo Sampling
3.2. Modeling of BP Neural Network
4. Analysis of Factors Affecting the Inductance Value of Inductors
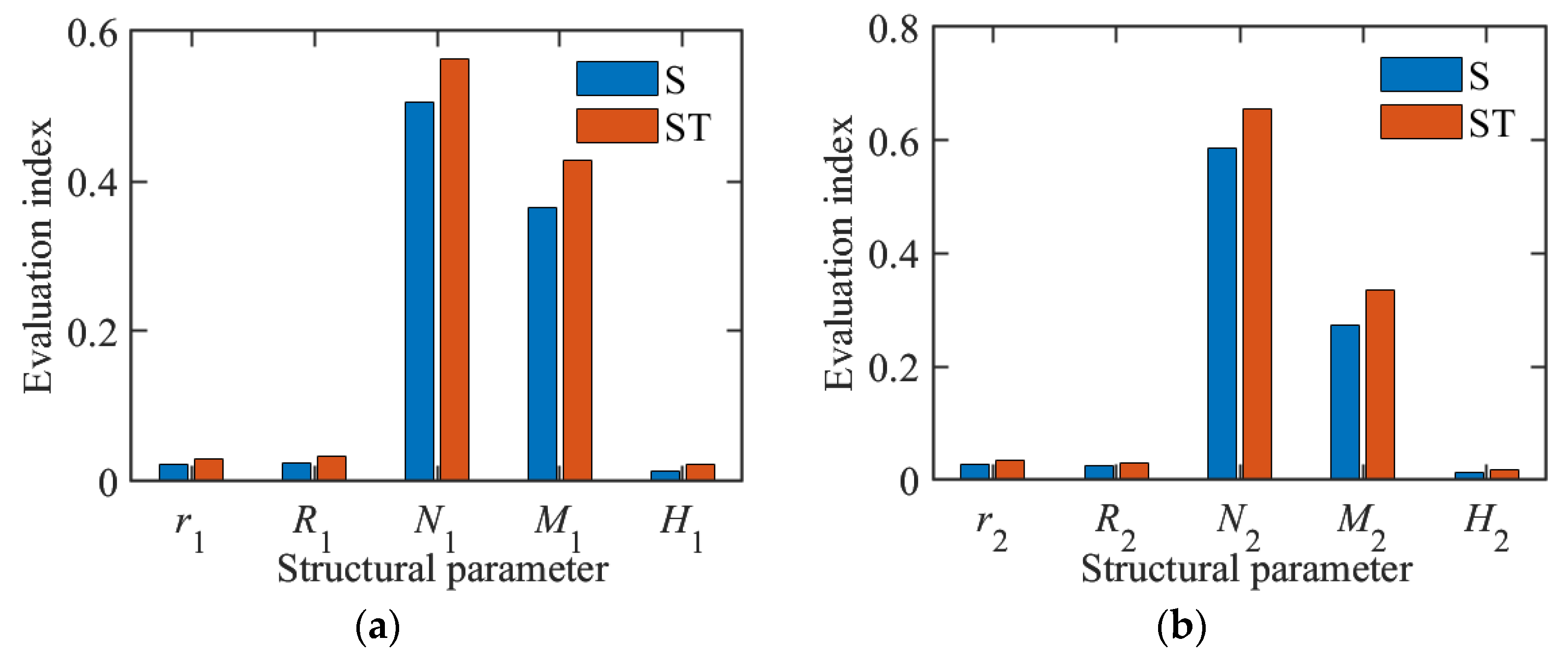
4.1. Sensitivity Analysis of Structural Parameters
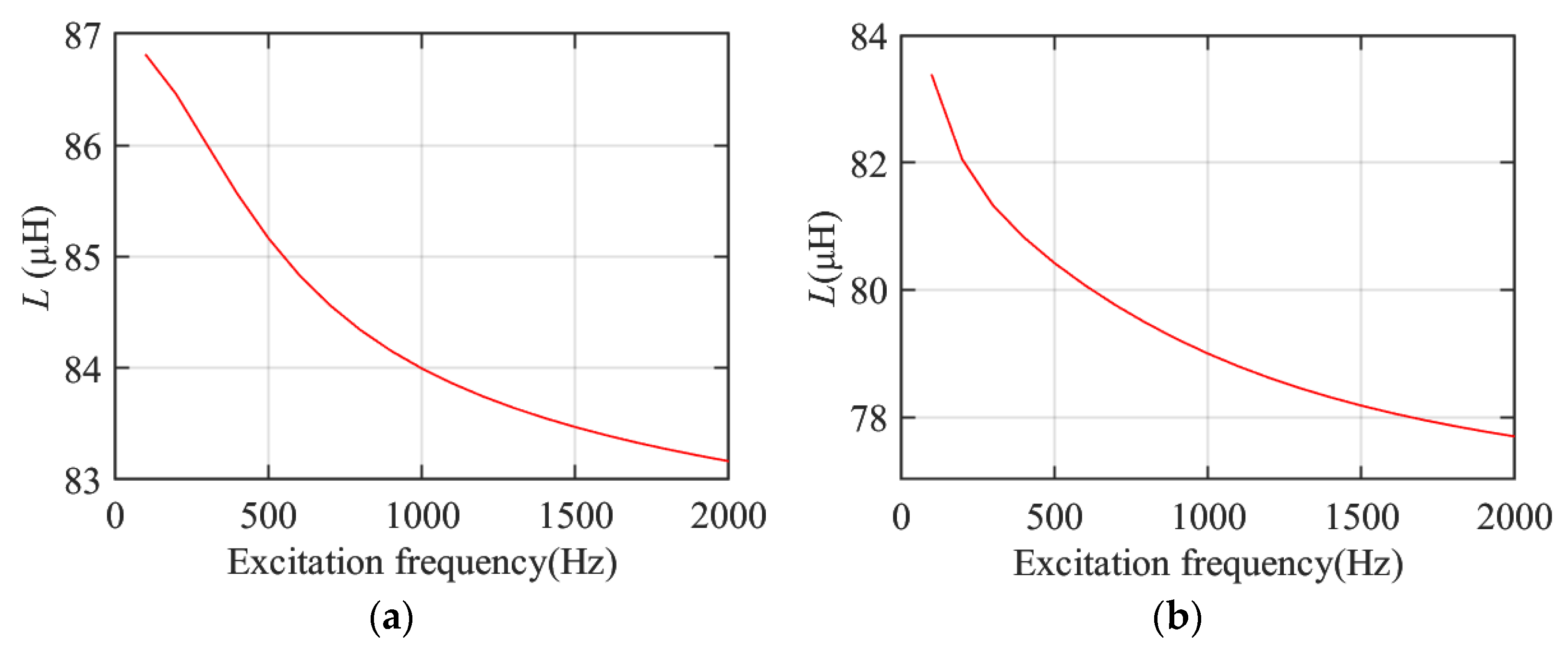
4.2. The Effect of Excitation Frequency
5. Optimization of Inductor Structural Parameters Based on BP-GA Algorithm
5.1. Mathematical Model for the Structural Optimization of Inductors
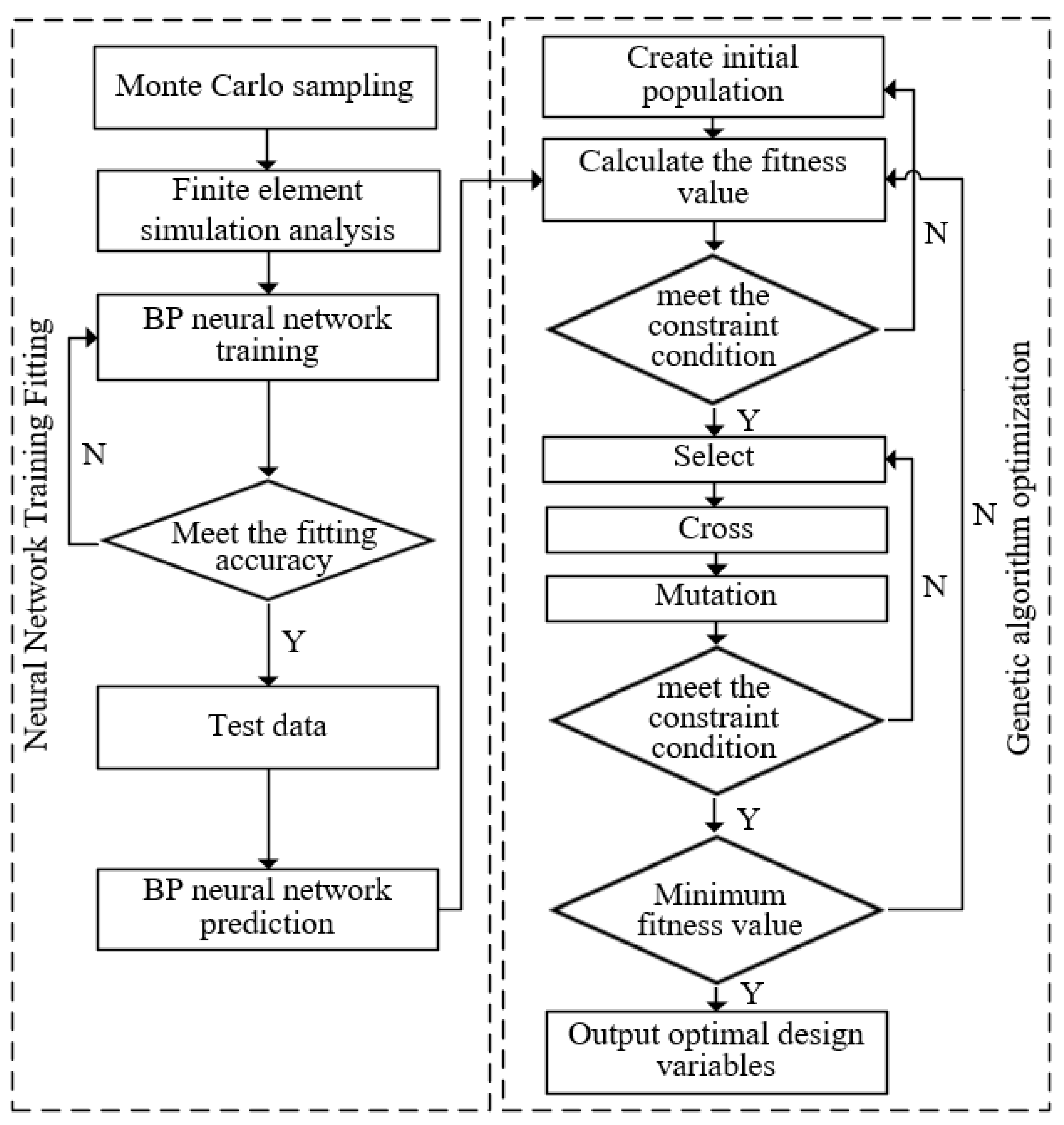
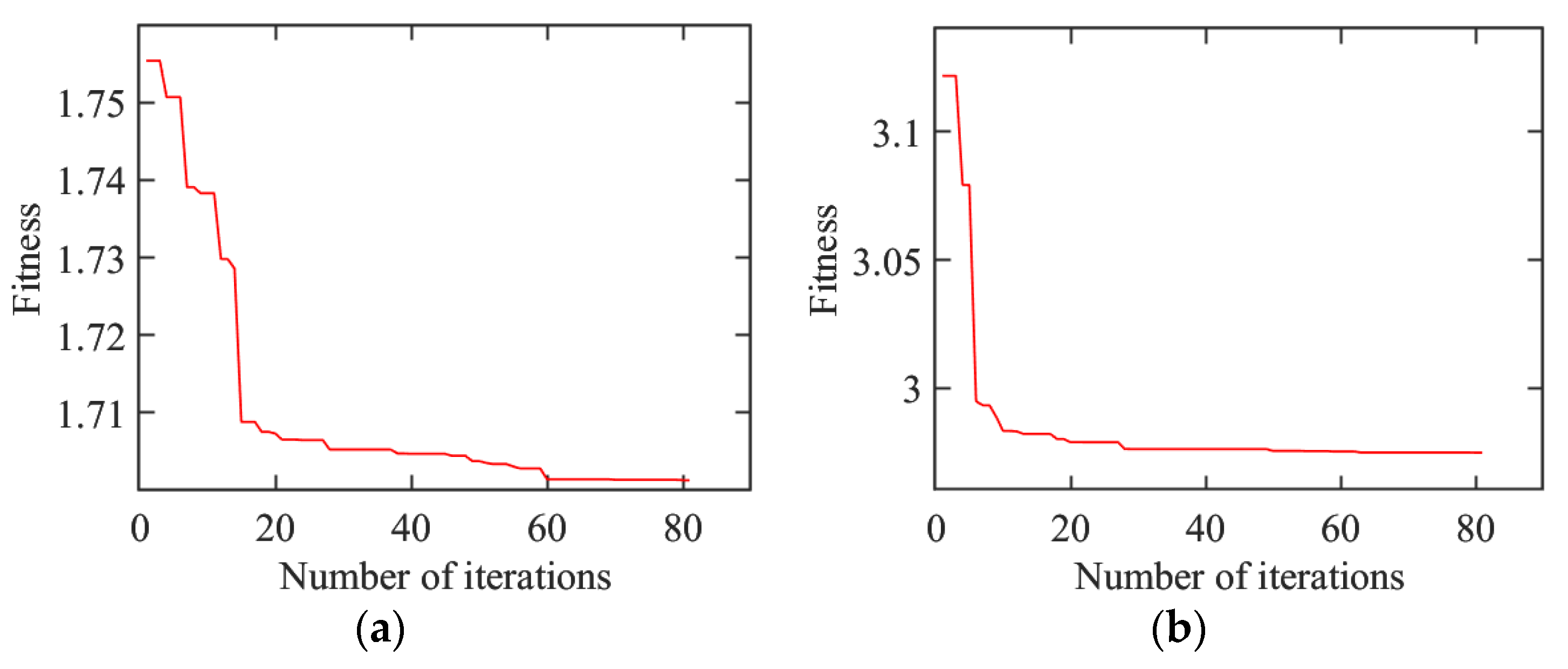
5.2. Optimization by BP-GA Joint Algorithm
5.3. Finite Element Validation
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Tian, M.; Wang, T.; Zhang, H.; Yi, L. Review and prospect of controllable inductors. J. Jilin Univ. Eng. Technol. Ed. 2023, 53, 328–345. [Google Scholar]
- Zhang, Y.; Zhao, J.; Qin, C.; Zhang, R.; Li, S. Analysis of turn-to-turn short circuit magnetic field of dry-type air-core inductor. In Proceedings of the 2023 3rd New Energy and Energy Storage System Control Summit Forum (NEESSC), Mianyang, China, 26–28 September 2023. [Google Scholar]
- Bai, G.; Gu, C.; Lai, L. Electromagnetic analysis of an air-core HTS transformer. IEEE Trans. Appl. Supercond. 2019, 29, 1–3. [Google Scholar] [CrossRef]
- Jin, L.; Zhu, D.; Yang, Q.; Zhang, J.; Gong, D. Grey-box model and optimization for inductance calculation of EHV inductors. Trans. China Electrotech. Soc. 2022, 37, 6093–6103. [Google Scholar]
- Wang, T.; Tian, M.; Zhang, H.; Zhang, Y. Unified study on electromagnetic characteristics of controllable inductors based on transformer models. Power Syst. Technol. 2023, 47, 2947–2956. [Google Scholar]
- Yuan, F.; Lv, K.; Liu, J.; Zhou, B.; Tang, B. Optimization method for coil structure of iron-core inductors based on electromagnetic-thermal-structural multi-physics coupling. Trans. China Electrotech. Soc. 2022, 37, 6431–6441. [Google Scholar]
- Hao, S.; Li, Z.; Ma, F.; Li, B. Characteristic analysis of inductor in pulsed power supply changing with shape ratio. In Proceedings of the 2020 Spring International Conference on Defence Technology (ICDT Spring), Nanjing, China, 20–24 April 2020. [Google Scholar]
- Liu, X.; Yu, X.; Li, Z. Inductance calculation and energy density optimization of the tightly coupled inductors used in inductive pulsed power supplies. IEEE Trans. Plasma Sci. 2017, 45, 1026–1031. [Google Scholar] [CrossRef]
- Jiang, Z.; Zhou, H.; Song, J.; Yu, Y.; Weng, X. Calculation and experimental analysis of temperature field in dry-type air-core inductor. Trans. China Electrotech. Soc. 2017, 32, 218–224. [Google Scholar]
- Shetty, C.; Kandeel, Y.; Ye, L.; O’Driscoll, S.; McCloskey, p.; Duffy, M.; Mathúna, C.Ó. Analytical expressions for inductances of 3-D air-core inductors for integrated power supply. IEEE J. Emerg. Sel. Top. Power Electron. 2022, 10, 1363–1383. [Google Scholar] [CrossRef]
- Liu, Z.; Wang, J.; Geng, Y.; Shi, C. Calculation and analysis of magnetic field and inductance of dry-type air-core inductor. High Volt. Appar. 2003, 39, 7–11. [Google Scholar]
- Gan, Y.; Bai, R.; Zhang, Q. Steady-state electromagnetic field and electromotive force analysis of dry-type air-core inductor based on field-circuit coupling. Power Syst. Prot. Control. 2019, 47, 144–149. [Google Scholar]
- Lin, Q. Magnetic field analysis of dry-type air-core inductor. Transformer 2019, 56, 29–33. [Google Scholar]
- Ye, C.; Yu, K.; Zhang, G.; Pan, Y. The windings inductance calculation of an air-core compulsator. IEEE Trans. Magn. 2009, 45, 522–524. [Google Scholar]
- Tan, W.; Zhou, L.; Gong, X.; Wu, W.; Ou, Q. Research on structural optimization design of controllable inductor with taps. Transformer 2019, 56, 9–14. [Google Scholar]
- Li, S.; Lu, J.; Cheng, L.; Zhu, B. Stress analysis and structural design of pulsed inductor for electromagnetic launch. J. Natl. Univ. Def. Technol. 2019, 41, 39–45. [Google Scholar]
- Sun, H.; Yu, X.; Li, Z.; Li, B.; He, H. Inductance calculation and structural optimization of toroidal circular disk-type inductors in IPPS. IEEE Trans. Plasma Sci. 2021, 49, 2247–2255. [Google Scholar] [CrossRef]
- Li, Z.; Yu, X.; Ma, S.; Sha, Y. Structural parameter optimization of inductors used in inductive pulse power supply. IEEE Trans. Plasma Sci. 2015, 43, 1456–1461. [Google Scholar]
- Li, Y.; Zhang, Z.; Zhu, L.; Jiang, M. Calculation and Design of Dry-Type Hollow Inductors. Transformer 2013, 50, 1–6. [Google Scholar]
- Hung, Y.C. A review of Monte Carlo and quasi-Monte Carlo sampling techniques. Wiley Interdiscip. Rev. Comput. Stat. 2023, 16, e1637. [Google Scholar] [CrossRef]
- Qi, S.; Lu, X.; Liu, H.; Zhu, L.; Wang, F. Application of BP Neural Network Optimized by Genetic Algorithm in Fault Diagnosis of Distribution Network. Electr. Power Sci. Technol. 2023, 38, 182–187. [Google Scholar]
- Wang, Y.; Liu, L.; Zhang, M.; Zhang, W.; Li, P. Review of Turn-to-Turn Insulation Detection for Dry-Tors. Electr. Power Capacit. React. Power Compens. 2018, 39, 91–95. [Google Scholar]



| Inductor Type | Structural Design Variables | Lower Design Limit | Upper Design Limit |
|---|---|---|---|
| AHI | r1 (mm) | 50 | 100 |
| R1 (mm) | 150 | 250 | |
| N1 | 5 | 14 | |
| M1 | 3 | 7 | |
| H1 (mm) | 200 | 400 | |
| RHI | r2 (mm) | 50 | 100 |
| R2 (mm) | 150 | 250 | |
| N2 | 5 | 14 | |
| M2 | 5 | 9 | |
| H2 (mm) | 200 | 400 |
| Inductor Type | Evaluation Index | L | L/V | Wj | |
|---|---|---|---|---|---|
| AHI | Training samples | R2 | 0.9987 | 0.9985 | 0.9992 |
| RRMSE | 0.0033 | 0.0027 | 0.0006 | ||
| Testing samples | R2 | 0.9963 | 0.9965 | 0.9984 | |
| RRMSE | 0.0078 | 0.0063 | 0.0011 | ||
| RHI | Training samples | R2 | 0.9982 | 0.9984 | 0.9990 |
| RRMSE | 0.0037 | 0.0026 | 0.0005 | ||
| Testing samples | R2 | 0.9903 | 0.9938 | 0.9960 | |
| RRMSE | 0.0092 | 0.0055 | 0.0013 | ||
| Inductor Type | Structural Design Variables | Optimal Parameter |
|---|---|---|
| AHI | r1 (mm) | 95.15 |
| R1 (mm) | 186.70 | |
| N1 | 8 | |
| M1 | 4 | |
| H1 (mm) | 272.89 | |
| RHI | r2 (mm) | 50.34 |
| R2 (mm) | 158.72 | |
| N2 | 8 | |
| M2 | 6 | |
| H2 (mm) | 315.03 |
| Inductor Type | L (μH) | L/V (μH/m3) | Wj | |
|---|---|---|---|---|
| AHI | Sample of optimal L/V | 486.0346 | 8459.9692 | 2.8657 |
| Sample of optimal Wj | 116.7442 | 3531.5769 | 1.7934 | |
| post-optimization | 114.6565 | 3510.6846 | 1.7115 | |
| RHI | Sample of optimal L/V | 803.1687 | 13330.8319 | 3.9640 |
| Sample of optimal Wj | 114.9423 | 4591.9504 | 3.0388 | |
| post-optimization | 127.8841 | 4539.2142 | 2.8768 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, J.; Zhang, Y.; Yang, B.; Li, S.; Song, H. Electromagnetic Fields Calculation and Optimization of Structural Parameters for Axial and Radial Helical Air-Core Inductors. Electronics 2024, 13, 3463. https://doi.org/10.3390/electronics13173463
Wu J, Zhang Y, Yang B, Li S, Song H. Electromagnetic Fields Calculation and Optimization of Structural Parameters for Axial and Radial Helical Air-Core Inductors. Electronics. 2024; 13(17):3463. https://doi.org/10.3390/electronics13173463
Chicago/Turabian StyleWu, Jinguo, Yujie Zhang, Bin Yang, Sihan Li, and Haipeng Song. 2024. "Electromagnetic Fields Calculation and Optimization of Structural Parameters for Axial and Radial Helical Air-Core Inductors" Electronics 13, no. 17: 3463. https://doi.org/10.3390/electronics13173463






