An Analog Integrated Multiloop LDO: From Analysis to Design
Abstract
:1. Introduction
- In the literature, there are different publications in which a multiloop compensation technique is analyzed for a variety of operational amplifiers, while in this work, an LDO which employs this technique is proposed.
- A low-voltage, low-power and area-efficient NMOS LDO is introduced for efficient power management and high performance.
- A fully mathematical analysis for stability and noise performance is conducted, which presents the trade-off between the circuit’s parameters and performance. This can be used as a promising tool for optimal pre-simulation (design) parameter selection.
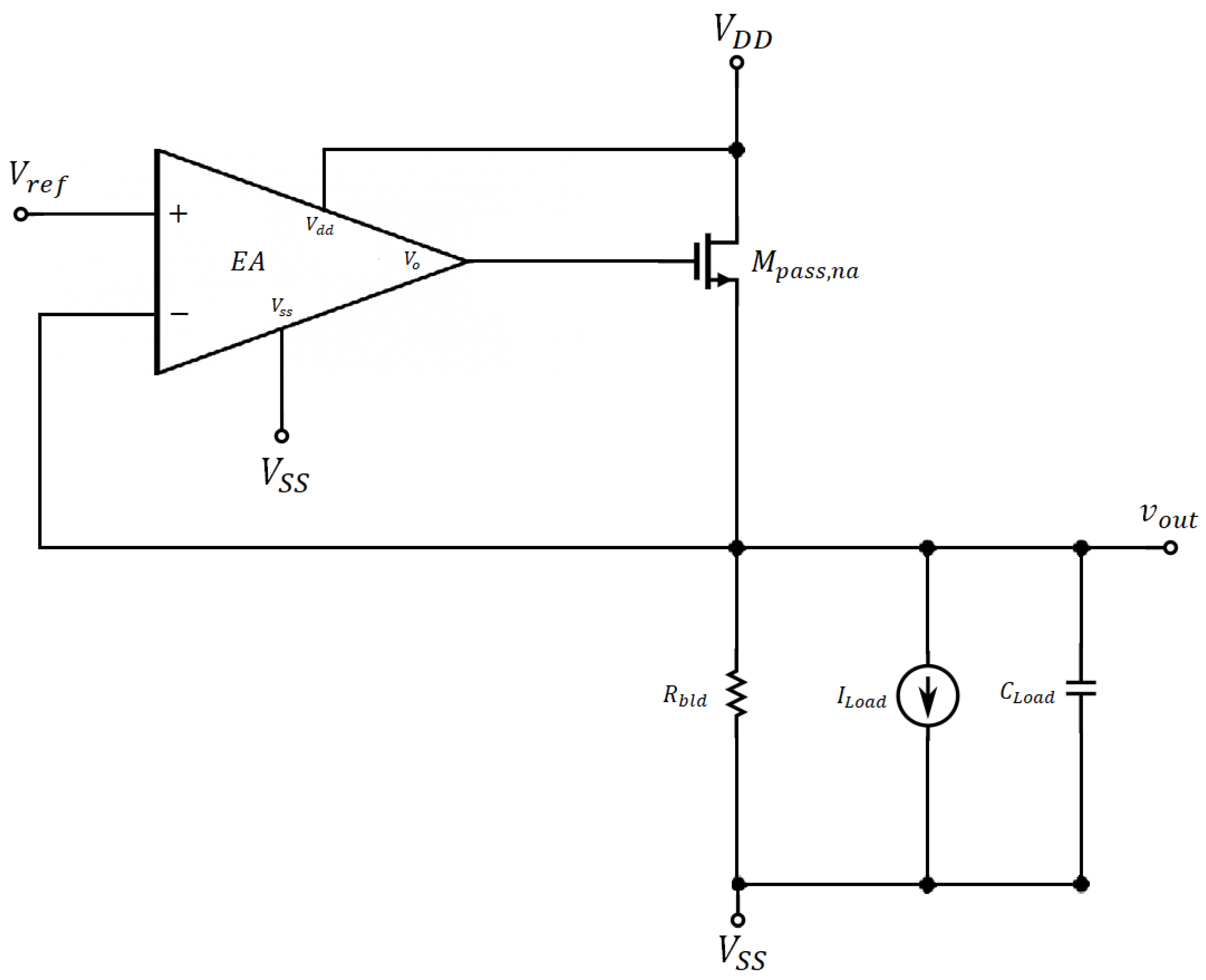
2. LDO Architecture
2.1. Typical LDO Architecture
2.2. High-Level Architecture
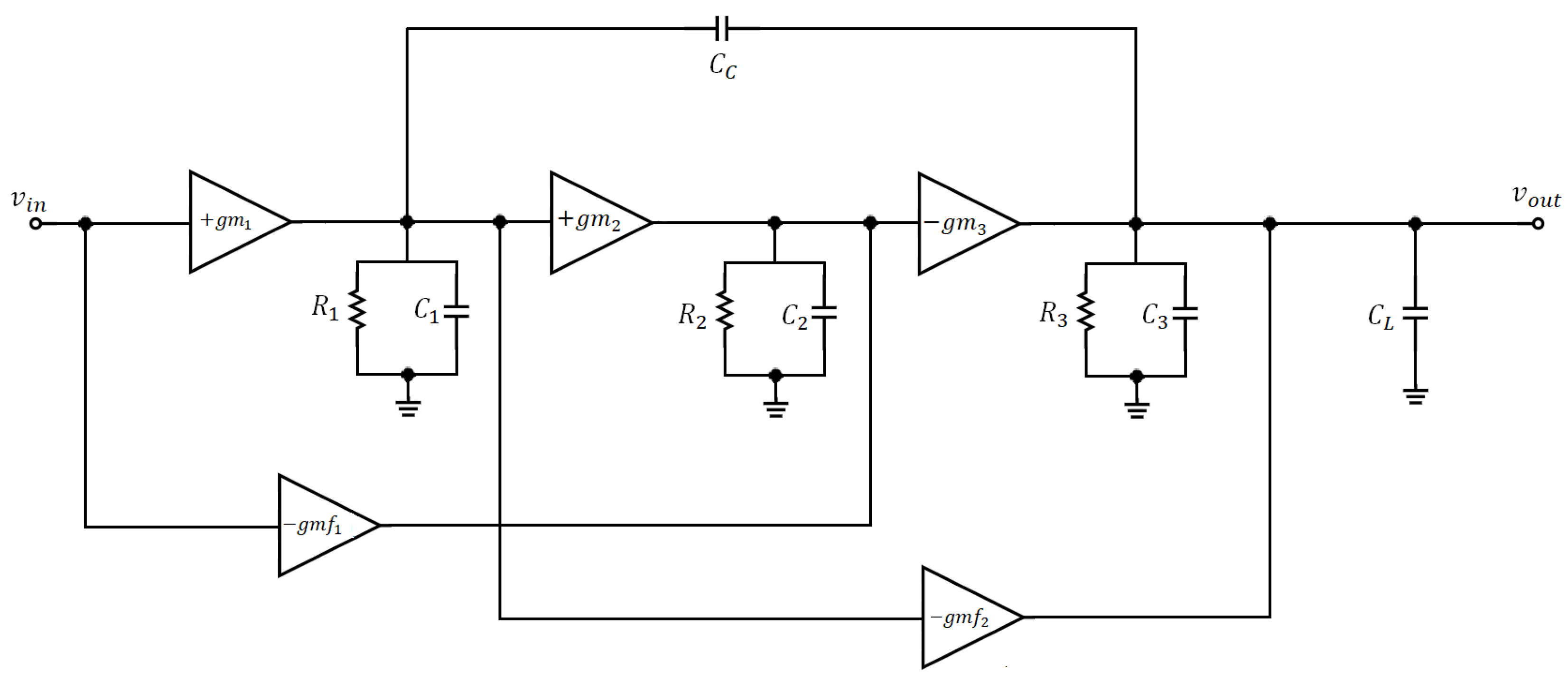
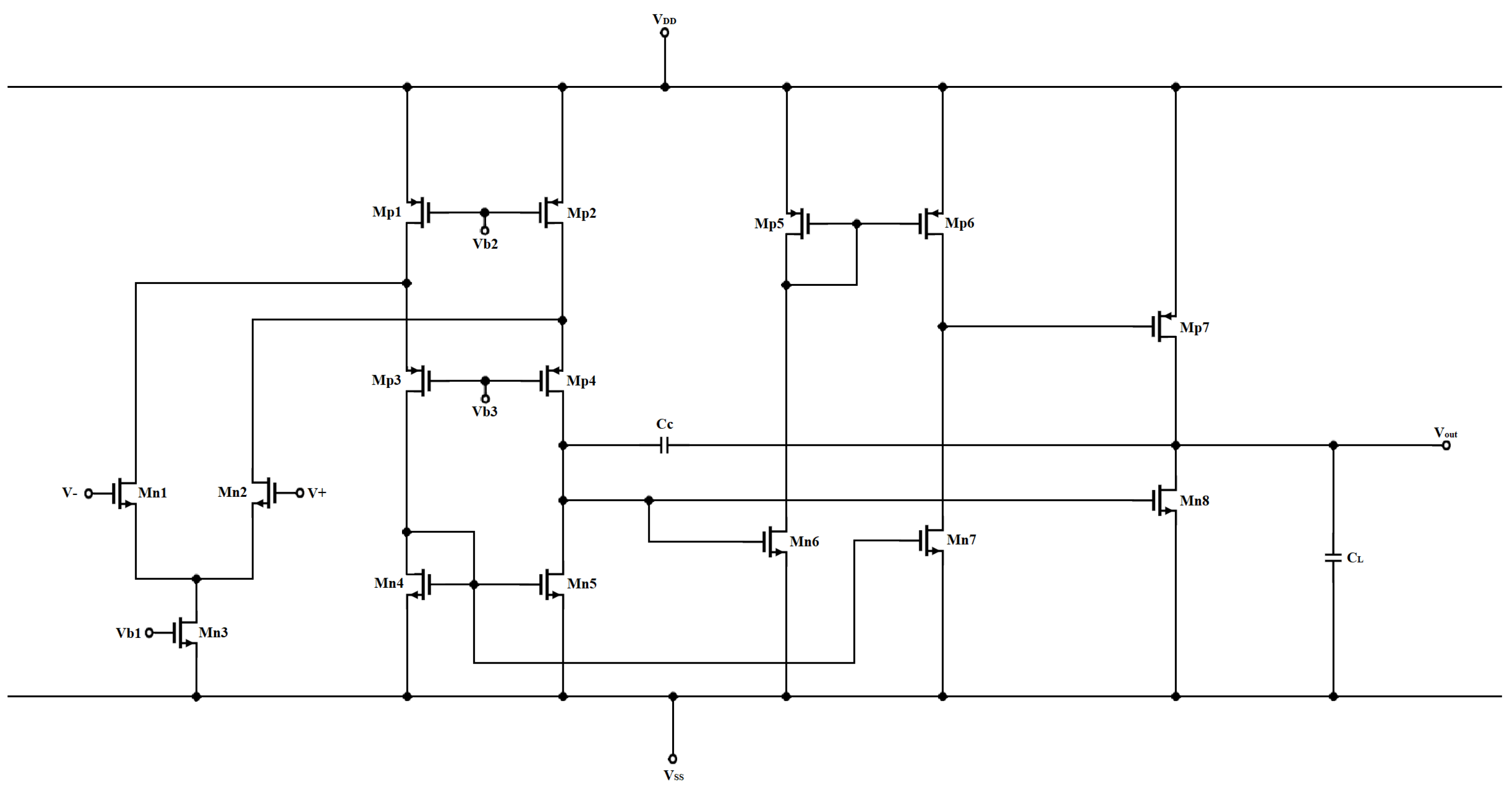
2.3. Multiloop Amplifier
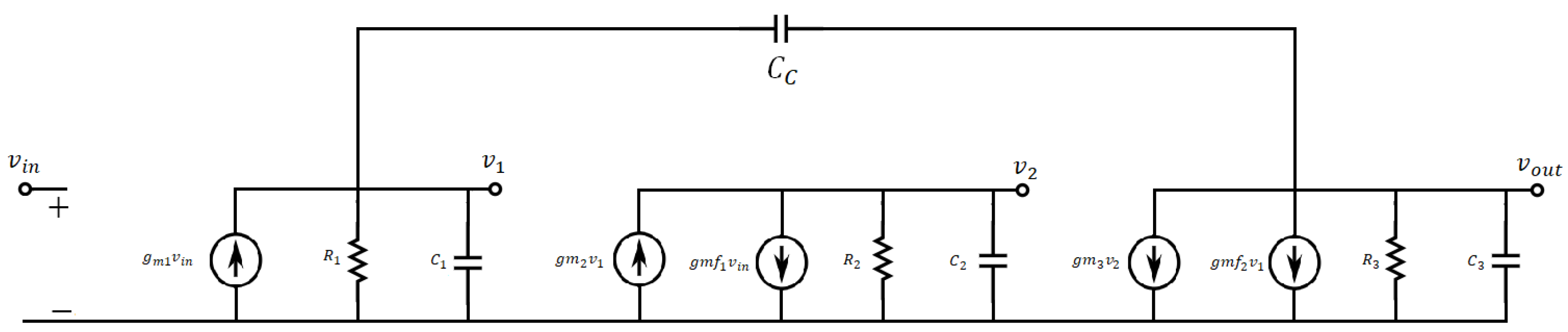
3. LDO Analysis and Modeling
3.1. Stability Analysis
3.2. Noise Analysis
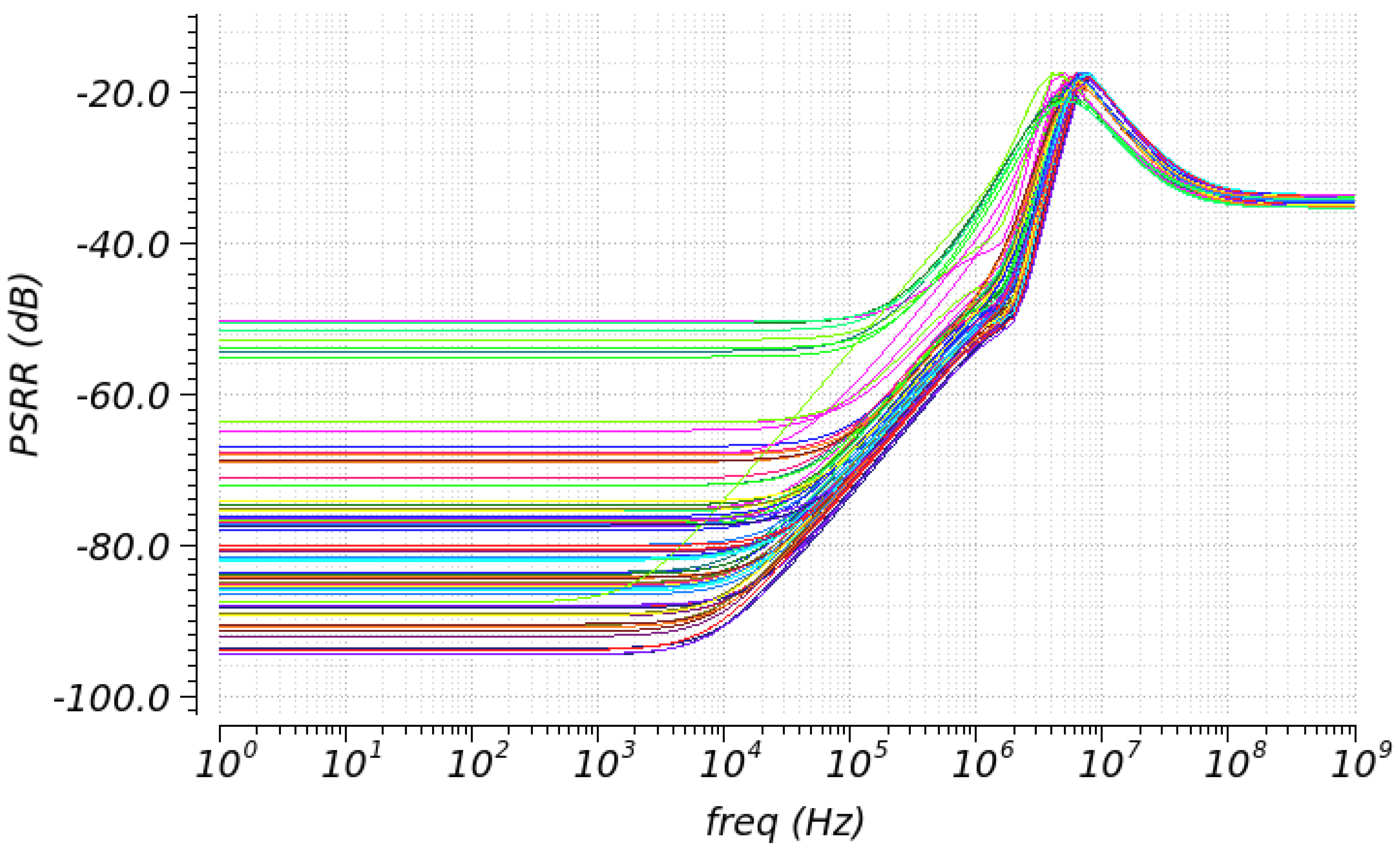
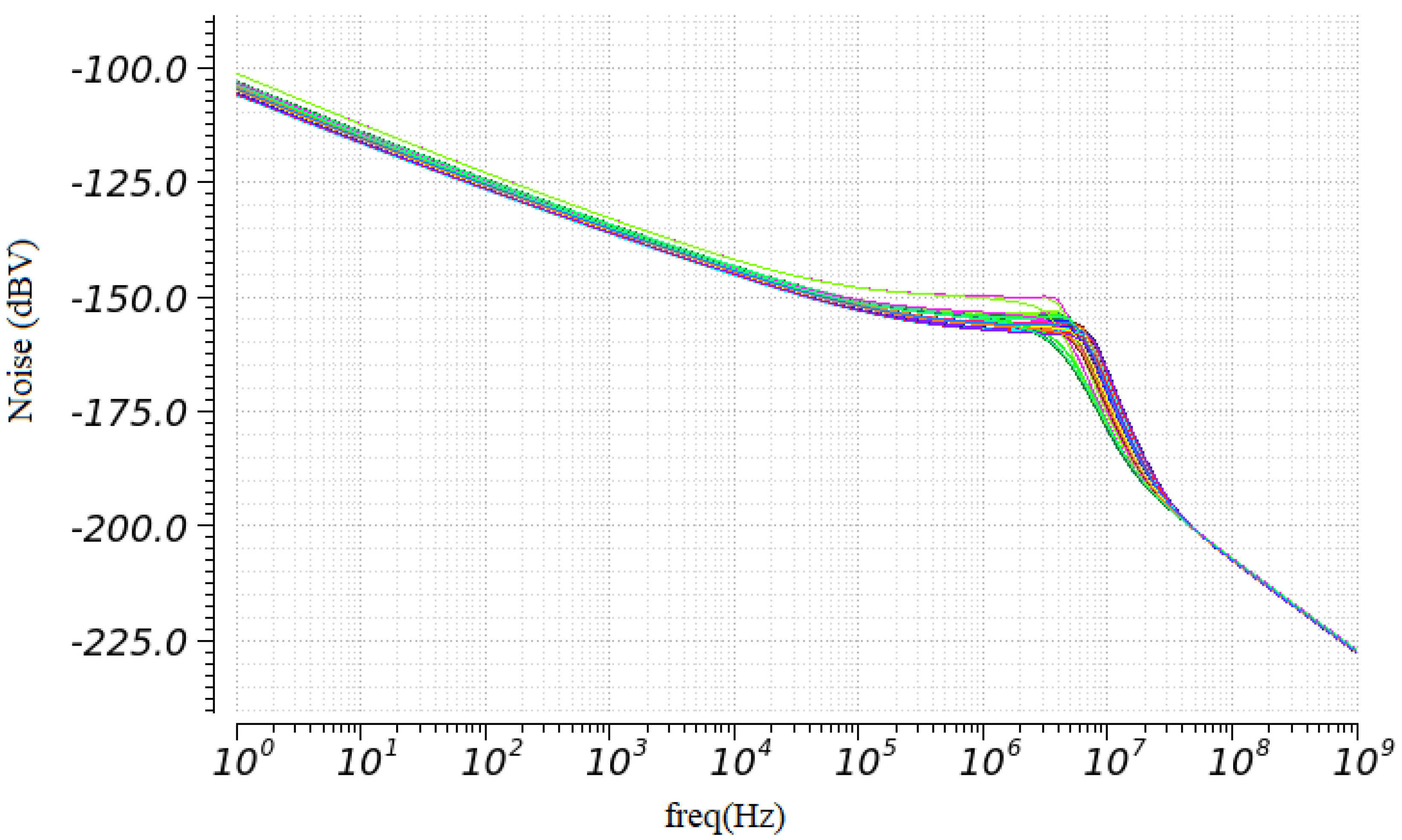
4. Simulation Results
5. Comparison and Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Kassakian, J.G.; Jahns, T.M. Evolving and emerging applications of power electronics in systems. IEEE J. Emerg. Sel. Top. Power Electron. 2013, 1, 47–58. [Google Scholar] [CrossRef]
- Shearer, F. Power Management in Mobile Devices; Elsevier: Amsterdam, The Netherlands, 2011. [Google Scholar]
- Katiraei, F.; Iravani, M.R. Power management strategies for a microgrid with multiple distributed generation units. IEEE Trans. Power Syst. 2006, 21, 1821–1831. [Google Scholar] [CrossRef]
- Sobhan Bhuiyan, M.A.; Hossain, M.R.; Minhad, K.N.; Haque, F.; Hemel, M.S.K.; Md Dawi, O.; Ibne Reaz, M.B.; Ooi, K.J. CMOS low-dropout voltage regulator design trends: An overview. Electronics 2022, 11, 193. [Google Scholar] [CrossRef]
- Chyan, T.Y.; Ramiah, H.; Hatta, S.W.M.; Lai, N.S.; Lim, C.C.; Chen, Y.; Mak, P.I.; Martins, R.P. Evaluation and perspective of analog low-dropout voltage regulators: A review. IEEE Access 2022, 10, 114469–114489. [Google Scholar] [CrossRef]
- Lai, L.F.; Ramiah, H.; Tan, Y.C.; Lai, N.S.; Lim, C.C.; Chen, Y.; Mak, P.I.; Martins, R.P. Design Trends and Perspectives of Digital Low Dropout Voltage Regulators for Low Voltage Mobile Applications: A Review. IEEE Access 2023, 11, 85237–85258. [Google Scholar] [CrossRef]
- Kularatna, N. Review of Fundamentals Related to DC Power Supply Design and Linear Regulators. In DC Power Supplies; CRC Press: Boca Raton, FL, USA, 2018; p. 1. [Google Scholar]
- Hsia, S.C.; Sheu, M.H.; Wu, S.H. Wide operation range high-voltage linear regulator chip design. Electr. Eng. 2024, 106, 2197–2208. [Google Scholar] [CrossRef]
- Kampus, V.; Rang, T. A smart capless voltage regulator for very high bandwidth A/D and D/A converters in a standard 28 nm CMOS process. In Proceedings of the 2016 15th Biennial Baltic Electronics Conference (BEC), Tallinn, Estonia, 3–5 October 2016; pp. 43–46. [Google Scholar]
- Eleftheriou, N.P.; Ntasiou, O.; Alimisis, V.; Sotiriadis, P.P. A Low-Power Temperature and Process Insensitive CMOS Power Management Unit. In Proceedings of the 2024 Panhellenic Conference on Electronics & Telecommunications (PACET), Thessaloniki, Greece, 28–29 March 2024; pp. 1–4. [Google Scholar]
- Carreon-Bautista, S.; Huang, L.; Sanchez-Sinencio, E. An autonomous energy harvesting power management unit with digital regulation for IoT applications. IEEE J. Solid-State Circuits 2016, 51, 1457–1474. [Google Scholar] [CrossRef]
- Hu, J.; Ismail, M. CMOS High Efficiency On-Chip Power Management; Springer Science & Business Media: Cham, Switzerland, 2011. [Google Scholar]
- Marasco, K. How to successfully apply low-dropout regulators. Analog Dialogue 2009, 43. [Google Scholar]
- Torres, J.; El-Nozahi, M.; Amer, A.; Gopalraju, S.; Abdullah, R.; Entesari, K.; Sanchez-Sinencio, E. Low drop-out voltage regulators: Capacitor-less architecture comparison. IEEE Circuits Syst. Mag. 2014, 14, 6–26. [Google Scholar] [CrossRef]
- Silva-Martinez, J.; Liu, X.; Zhou, D. Recent advances on linear low-dropout regulators. IEEE Trans. Circuits Syst. II Express Briefs 2020, 68, 568–573. [Google Scholar] [CrossRef]
- Haid, J.; Kargl, W.; Leutgeb, T.; Scheiblhofer, D. Power management for RF-powered vs. battery-powered devices. In Proceedings of the Workshop on Wearable and Pervasive Computing, Graz, Austria, 8–9 March 2005. [Google Scholar]
- Joshi, K. Mixed-Mode Adaptive Ripple Canceller for Switching Regulators; Arizona State University: Tempe, AZ, USA, 2016. [Google Scholar]
- Xiu, Y.; Rosenbaum, E. Analysis and Design of Integrated Voltage Regulators for Supply Noise Rejection During System-Level ESD. IEEE Trans. Circuits Syst. I Regul. Pap. 2020, 67, 4199–4210. [Google Scholar] [CrossRef]
- Wang, L. High Performance Distributed On-Chip Voltage Regulation for Modern Integrated Systems; University of South Florida: Tampa, FL, USA, 2018. [Google Scholar]
- Li, K. Design and Realization of Low Dropout Voltage Regulators in PMIC for Portable Applications. Ph.D. Thesis, Nanyang Technological University, Singapore, 2020. [Google Scholar]
- Choe, Y.J.; Nam, H.; Park, J.D. A Low-Dropout Regulator with PSRR Enhancement through Feed-Forward Ripple Cancellation Technique in 65 nm CMOS Process. Electronics 2020, 9, 146. [Google Scholar] [CrossRef]
- Jang, H.J.; Roh, Y.S.; Moon, Y.J.; Park, J.P.; Yoo, C.S. Low drop-out (ldo) voltage regulator with improved power supply rejection. JSTS J. Semicond. Technol. Sci. 2012, 12, 313–319. [Google Scholar] [CrossRef]
- Morita, G. Noise Sources in Low Dropout (LDO) Regulators; One Technology Way: Norwood, MA, USA, 2011; pp. 1–12. [Google Scholar]
- Teel, J.C. Understanding Noise in Linear Regulators; Texas Instruments Incorporated: Dallas, TX, USA, 2005. [Google Scholar]
- Gabriel, A. Rincon-Mora, Member, I.; Phillip E. Allen, Fellow, I. A Low-Voltage, Low Quiescent Current, Low Drop-Out Regulator. IEEE J. Solid-State Circuits 1998, 33, 36–44. [Google Scholar]
- Kim, Y.I.; Lee, S.S. A Capacitorless LDO Regulator with Fast Feedback Technique and Low-Quiescent Current Error Amplifier. IEEE Trans. Circuits Syst. 2013, 60, 326–330. [Google Scholar] [CrossRef]
- Tan, X.L.; Chong, S.S.; Chan, P.K.; Dasgupta, U. A LDO regulator with weighted current feedback technique for 0.47 nF–10 nF capacitive load. IEEE J. Solid-State Circuits 2014, 49, 2658–2672. [Google Scholar] [CrossRef]
- Irianto, S.A.; Prasetyo, W.E.; Dyah, N.; Kurniawan, H.R. A 4 V, 100 MA Low Dropout Voltage Regulator (LDO) for Mobile Phone Solar Charger Application. ICIC Int. 2021, 13, 553. [Google Scholar]
- Ziadi, Y.; Qjidaa, H. A High Efficiency Li-Ion Battery LDO-Based Charger for Portable Application. Hindawi Publ. Corp. Act. Passiv. Electron. Compon. 2015, 2015, 591986. [Google Scholar] [CrossRef]
- Banba, H.; Shiga, H.; Umezawa, A.; Miyaba, T.; Tanzawa, T.; Atsumi, S.; Sakui, K. A CMOS bandgap reference circuit with sub-1-V operation. IEEE J. Solid-State Circuits 1999, 34, 670–674. [Google Scholar] [CrossRef]
- Johns, D.A.; Martin, K. Analog Integrated Circuit Design; John Wiley & Sons: Hoboken, NJ, USA, 2008. [Google Scholar]
- Alimisis, V.; Arnaoutoglou, D.G.; Serlis, E.A.; Kamperi, A.; Metaxas, K.; Kyriacou, G.A.; Sotiriadis, P.P. A radar-based system for detection of human fall utilizing analog hardware architectures of decision tree model. IEEE Open J. Circuits Syst. 2024, 5, 224–242. [Google Scholar] [CrossRef]
- Khateb, F.; Kulej, T.; Akbari, M.; Steffan, P. 0.3-V bulk-driven nanopower OTA-C integrator in 0.18 μm CMOS. Circuits Syst. Signal Process. 2019, 38, 1333–1341. [Google Scholar] [CrossRef]
- Alimisis, V.; Dimas, C.; Pappas, G.; Sotiriadis, P.P. Analog realization of fractional-order skin-electrode model for tetrapolar bio-impedance measurements. Technologies 2020, 8, 61. [Google Scholar] [CrossRef]
- Charitos, P.; Alimisis, V.; Eleftheriou, N.P.; Sotiriadis, P.P. A General Purpose 2 MHz 68 μW Temperature Compensated Reference Clock Oscillator. In Proceedings of the 2024 Panhellenic Conference on Electronics & Telecommunications (PACET), Thessaloniki, Greece, 28–29 March 2024; pp. 1–4. [Google Scholar]
- Hanson, S.; Sylvester, D. A 0.45–0.7 V sub-microwatt CMOS image sensor for ultra-low power applications. In Proceedings of the 2009 Symposium on VLSI Circuits, Kyoto, Japan, 16–18 June 2009; pp. 176–177. [Google Scholar]
- Koniavitis, K.; Alimisis, V.; Eleftheriou, N.P.; Kamperi, A.; Sotiriadis, P.P. A Multistage Nested-Loops Stabilized Operational Amplifier. In Proceedings of the 2024 Panhellenic Conference on Electronics & Telecommunications (PACET), Thessaloniki, Greece, 28–29 March 2024; pp. 1–4. [Google Scholar]
- Chong, S.S.; Chan, P.K. Cross feedforward cascode compensation for low-power three-stage amplifier with large capacitive load. IEEE J. Solid-State Circuits 2012, 47, 2227–2234. [Google Scholar] [CrossRef]
- Gray, P.R.; Hurst, P.J.; Lewis, S.H.; Meyer, R.G. Analysis and Design of Analog Integrated Circuits; John Wiley & Sons: Hoboken, NJ, USA, 2024. [Google Scholar]
- El-Nozahi, M.; Amer, A.; Torres, J.; Entesari, K.; Sánchez-Sinencio, E. High PSR low drop-out regulator with feed-forward ripple cancellation technique. IEEE J. Solid-State Circuits 2010, 45, 565–577. [Google Scholar] [CrossRef]
- Lim, Y.; Lee, J.; Park, S.; Jo, Y.; Choi, J. An external capacitorless low-dropout regulator with high PSR at all frequencies from 10 kHz to 1 GHz using an adaptive supply-ripple cancellation technique. IEEE J. Solid-State Circuits 2018, 53, 2675–2685. [Google Scholar] [CrossRef]
- Park, C.J.; Onabajo, M.; Silva-Martinez, J. External capacitor-less low drop-out regulator with 25 dB superior power supply rejection in the 0.4–4 MHz range. IEEE J. Solid-State Circuits 2013, 49, 486–501. [Google Scholar] [CrossRef]

| Transistor | W/L (m/m) |
|---|---|
| Parameter | Min | Typ | Max |
|---|---|---|---|
| Supply voltage (V) | 1 | ||
| Regulated output voltage (mV) | 600 | ||
| PSRR@DC (dB) | |||
| PSRR@100kHz (dB) | |||
| PSRR@1MHz (dB) | |||
| Worst PSRR (dB) | |||
| Output noise@1Hz (dBV/) | |||
| Output noise@1kHz (dBV/) | |||
| Output noise@10kHz (dBV/) | |||
| Output noise@100kHz (dBV/) | |||
| Output noise@1MHz (dBV/) | |||
| DC gain (dB) | |||
| Phase margin | |||
| Unity gain frequency (MHz) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Koniavitis, K.; Alimisis, V.; Uzunoglu, N.; Sotiriadis, P.P. An Analog Integrated Multiloop LDO: From Analysis to Design. Electronics 2024, 13, 3602. https://doi.org/10.3390/electronics13183602
Koniavitis K, Alimisis V, Uzunoglu N, Sotiriadis PP. An Analog Integrated Multiloop LDO: From Analysis to Design. Electronics. 2024; 13(18):3602. https://doi.org/10.3390/electronics13183602
Chicago/Turabian StyleKoniavitis, Konstantinos, Vassilis Alimisis, Nikolaos Uzunoglu, and Paul P. Sotiriadis. 2024. "An Analog Integrated Multiloop LDO: From Analysis to Design" Electronics 13, no. 18: 3602. https://doi.org/10.3390/electronics13183602
APA StyleKoniavitis, K., Alimisis, V., Uzunoglu, N., & Sotiriadis, P. P. (2024). An Analog Integrated Multiloop LDO: From Analysis to Design. Electronics, 13(18), 3602. https://doi.org/10.3390/electronics13183602








