Online Joint Optimization of Virtual Network Function Deployment and Trajectory Planning for Virtualized Service Provision in Multiple-Unmanned-Aerial-Vehicle Mobile-Edge Networks
Abstract
:1. Introduction
- We studied joint VNF deployment and UAV trajectory planning optimization in multi-UAV mobile-edge networks with the aim of maximizing the number of accepted GU requests under a given period T while minimizing both the energy consumption and the cost of accepting the requests for all UAVs with the constraints on their resources and the latency requirement of real-time requests. To the best of our knowledge, we are the first to jointly optimize VNF deployment and UAV trajectory planning based on emphasizing the coupling effect of the two processes to maximize the accepted number of requests under a given period T while minimizing both energy consumption and the cost, where the number of accepted requests is related to two process decisions, energy consumption is decided by UAV trajectories, and the cost is mainly related to VNF deployment.
- We formulated the proposed online joint problem as a nonconvex mixed integer nonlinear programming problem, and we designed an online DRL based on jointly optimizing discrete and continuous actions. The proposed algorithm can be used to solve real-time online joint problems of discrete and continuous variables that are coupled.
- We performed numerous simulations to verify algorithm performance. We compared the proposed algorithm with some baseline algorithms through simulations to verify that our algorithm is promising.
2. Related Studies
2.1. VNF Deployment in Mobile-Edge Networks with Terrestrial Fixed-Edge Servers
2.2. VNF Deployment on Mobile-Edge Networks with Movable-Edge Servers
2.3. Joint Optimization of Resource Allocation and UAV Trajectory Planning in Multi-UAV MEC Networks
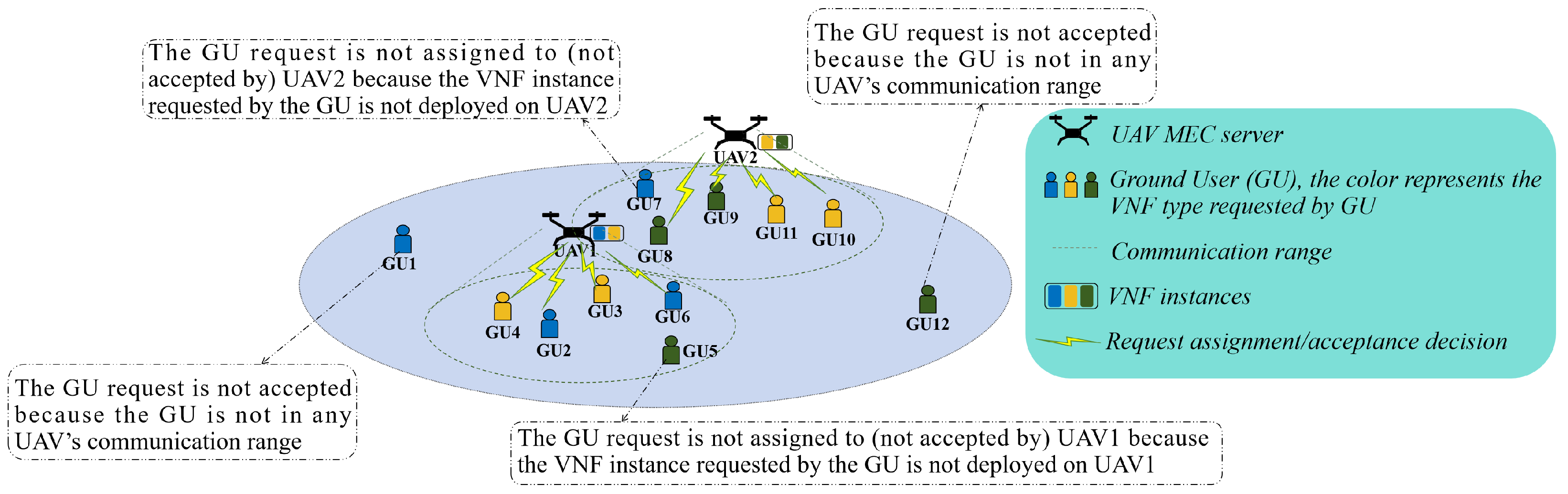
3. Problem Description
3.1. Network Architecture Model
3.2. GU and UAV Mobility Model
3.2.1. GU Mobility Model
3.2.2. UAV Mobility Model
3.3. Request Admission Model
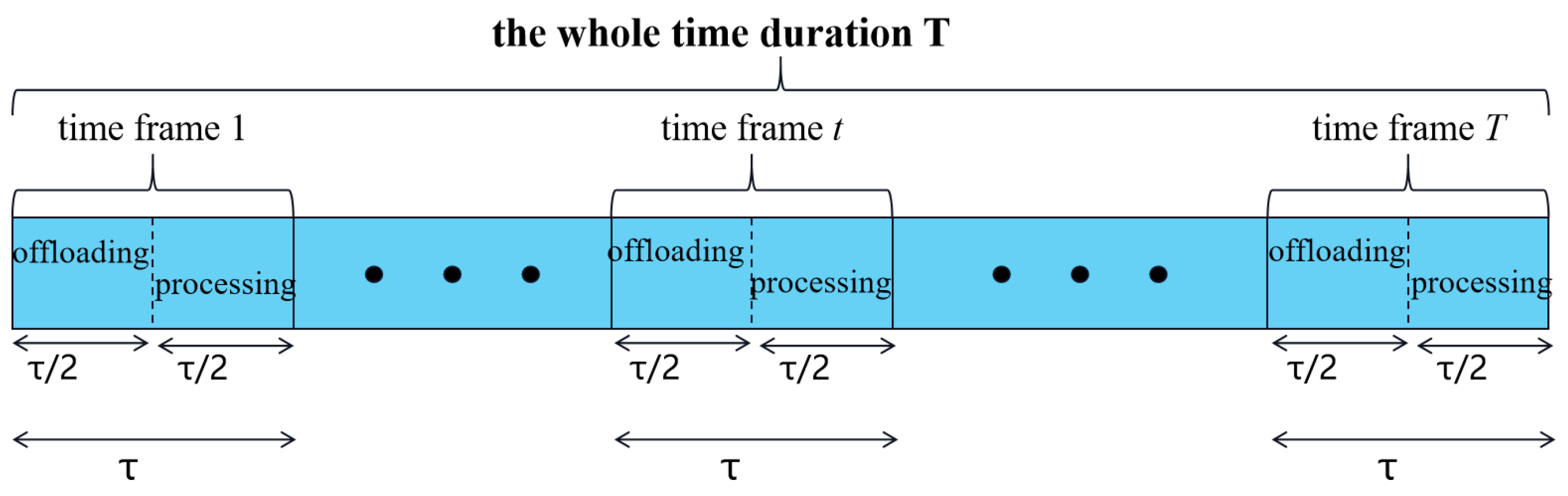
3.3.1. Request Offloading
3.3.2. Request Processing
3.4. UAV Energy Consumption Model
3.4.1. Computing Energy Consumption
3.4.2. Flight Propulsion Energy Consumption
3.5. Cost of UAVs’ Model for Accepting Requests
3.5.1. Instantiation Cost
3.5.2. Computing Cost
3.6. Problem Formulation
4. Problem Solution
4.1. The Key Idea of the Proposed Algorithm
4.2. Environment State
4.3. Reward
4.4. The Single-Agent Case in Centralized Scenario
4.4.1. Neural Network
- Online-VNF-Qnetwork: This neural network is used to obtain discrete actions (VNF deployment in the current time frame). Its input State_DA and its output DA_ID/DA are as follows: (a) State_DA includes state information ➁–➄, where the information about GUs is sorted by ➅. (b) DA_ID/DA: DA_ID is an integer representing a discrete action (DA, VNF deployment). Note that (1) DA_ID ∈ {0, 1, …, 1}, where is the number of all VNF deployments (DA) on all UAVs that satisfy computing resource constraint C1; (2) all VNF deployments (DA) in all UAVs that satisfy computing resource constraint C1 and are obtained via preprocessing.
- UAVs-Trajectories Actor Network: This neural network is used to obtain continuous actions (CAs, the UAV flying action). Its input State_CA and its output CA are as follows: (a) State_CA includes the new VNF deployment obtained by using DA to change ➁, state information ➂–➄, where the information about GUs is sorted using ➅. (b) CA includes 2 · M continuous variables. These continuous variables and the DA together determine the next location of the UAVs, which is described in detail in the Action Selection and Execution Process Section.
- Critic Network: This neural network is used in the training process to evaluate the quality of the continuous action. Its input State_Cri and its output Q_Cri are as follows: (a) State_Cri includes state information ➁–➄, where the information about GUs is sorted by ➅, the DA and the CA. (b) Q_Cri is a a real number used to evaluate the continuous action’s quality.
4.4.2. Action Selection and Execution Process
4.4.3. Training Process
| Algorithm 1 The algorithm for the training of the single-agent case. |
|
4.4.4. Computational Complexity for Generating Actions/Q-Value
4.5. The Multi-Agent Case in a Decentralized Scenario
4.5.1. Neural Network
- Online-VNF-Qnetwork m: This neural network is used to obtain the discrete action (VNF deployment in the current time frame) of UAV m. Its input and its output are as follows: (a) includes state information ➁–➄ (except for the location of UAV m), where the information on GUs is sorted via ➅. Additionally, when inputting GUs, other UAVs, and locations, the location of UAV m is the relative origin. (b) is an integer representing a discrete action (DA, VNF deployment) of UAV m. Note that (1) each UAV’s DA is the same; (2) ∈ {0, 1, …, 1}, where is the number of all VNF deployments for UAV m that satisfy computing resource constraint C1; and (3) all VNF deployments on UAV m that satisfy computing resource constraint C1 and are obtained via preprocessing.
- UAVs-Trajectories Actor Network m: This neural network is used to obtain continuous actions (CAs, the UAV’s flying action) of UAV m. Its input and its output are as follows: (a) includes state information ➁–➄ (except for the location of UAV m), , where the information on GUs is sorted via ➅. When inputting GUs, other UAVs, and locations, the location of UAV m is the relative origin. (b) includes two continuous variables to guide the trajectory of UAV m. These continuous variables and together determine the next locations of the UAVs, which is similar to the description in the Action Selection and Execution Process Section in the single-agent centralized scenario.
- Critic Network m: This neural network is used in the training process to evaluate the quality of the continuous action . Its input and its output are as follows: (a) : it includes state information ➁–➄ (except for the location of UAV m), the and the , where the information about GUs is sorted via ➅. (b) is a real number that is used to evaluate the quality of .
4.5.2. Action Selection and Execution Process
4.5.3. Training Process
| Algorithm 2 Pseudo-code of the training process for the multi-agent case. |
|
4.5.4. Computational Complexity of an Agent Generating Actions/Q-Value
5. Performance Evaluation
- (1)
- Greedy target minimization traverse VNF deployment and discretized UAV trajectories (GTMTVT): In each time frame, traverse VNF deployment (this was mentioned in the Neural Network section) and combinations of all mobile UAVs (this was mentioned in the Action-Selection and -Execution Process section). Next, calculate the target value in the current time frame for each combination of VNF deployments and UAV mobility combinations. Then, choose the combination of VNF deployment and UAV mobility with the maximum target value as the solution in the current time frame. This baseline was used to compare the performance of the proposed algorithms in the single- and multi-agent cases.
- (2)
- Greedy cost minimization traverse VNF deployment and discretized UAV trajectories (GCMTVT): In each time frame, perform traverse VNF deployment and combinations of all mobile UAVs. Next, calculate the number of accepted requests and the cost of accepting requests for each combination of VNF deployments and UAV mobility. Then, choose the combination of VNF deployment and UAV mobility with the minimum cost under the condition that the accepted number of requests is the maximum as per the solution in the current time frame. Because cost is closely related to VNF deployment, only focusing on cost means considering VNF deployment only. Thus, this baseline was used to verify the importance of jointly optimizing VNF deployment and trajectory planning.
- (3)
- Greedy energy minimization traverse VNF deployment and discretized UAV trajectories (GEMTVT): In each time frame, perform traverse VNF deployment and combinations of all mobile UAV. Next, calculate the accepted number of requests and the UAV energy consumption for each combination of VNF deployments and mobile UAVs. Then, choose the combination of VNF deployment and mobile UAV with the minimum energy consumption under the condition that the accepted number of requests is the maximum as per the solution in the current time frame. Because energy consumption is closely related to UAVs’ trajectories, only focusg on energy consumption means considering UAV trajectories only. This baseline was used to verify the importance of jointly optimizing VNF deployment and trajectory planning.
- (4)
- Environment state VNF deployment obtained using Online-VNF-Qnetwork and UAV trajectories obtained randomly (EVQTR): To achieve the target, in each state, the online VNF deployment is chosen by the trained Online-VNF-Qnetwork (the single-agent case), and the UAV trajectories are randomly generated. This baseline was used to test the necessity and effectiveness of training the Trajectory Actor Network in the single-agent case to choose continuous actions.
- (5)
- DDPG: To achieve the target, the DDPG method was used to obtain VNF deployment and UAV trajectories. Because DDPG is suitable for continuous actions and VNF deployment is a discrete action, the discrete action (VNF deployment) was converted into a continuous action as follows: (1) The VNF deployment of each UAV was decided using a continuous variable (e.g., for two UAVs, there are two continuous variables representing the two UAVs’ VNF deployment action). (2) We assumed that the value range of the continuous variables representing the VNF deployment action was the same, which was [,], and was the number of all VNF deployments in one UAV that satisfies computing resource constraint C1, and was obtained via preprocessing. Thus, the value range was evenly divided into subsegments, with each representing a discrete action (e.g., the value range of the continuous variables representing VNF deployment action was [0, 3]. Three VNF deployments were deployed on one UAV that satisfied computing resource constraint C1, which were named VNF deployment 1, VNF deployment 2, and VNF deployment 3. Thus, if the value ranged from 0 to 1, VNF deployment 1 was selected; if the value ranged from 1 to 2, VNF deployment 2 was selected; and if the value ranged from 2 to 3, VNF deployment 3 was selected. Additionally, when using this method, constraints C2–C16 were also satisfied in a manner similar to our proposed algorithms.In the DDPG, unless otherwise stated, the hidden layers of its actor network had [32, 16, 8] neurons, and the hidden layers of its critic network had [32, 8, 2] neurons. The learning rates of its actor and critic networks were , and the discount factor was 0.99. Additionally, the Adam optimizer was used to update all neural networks; the activation function Rule was used.
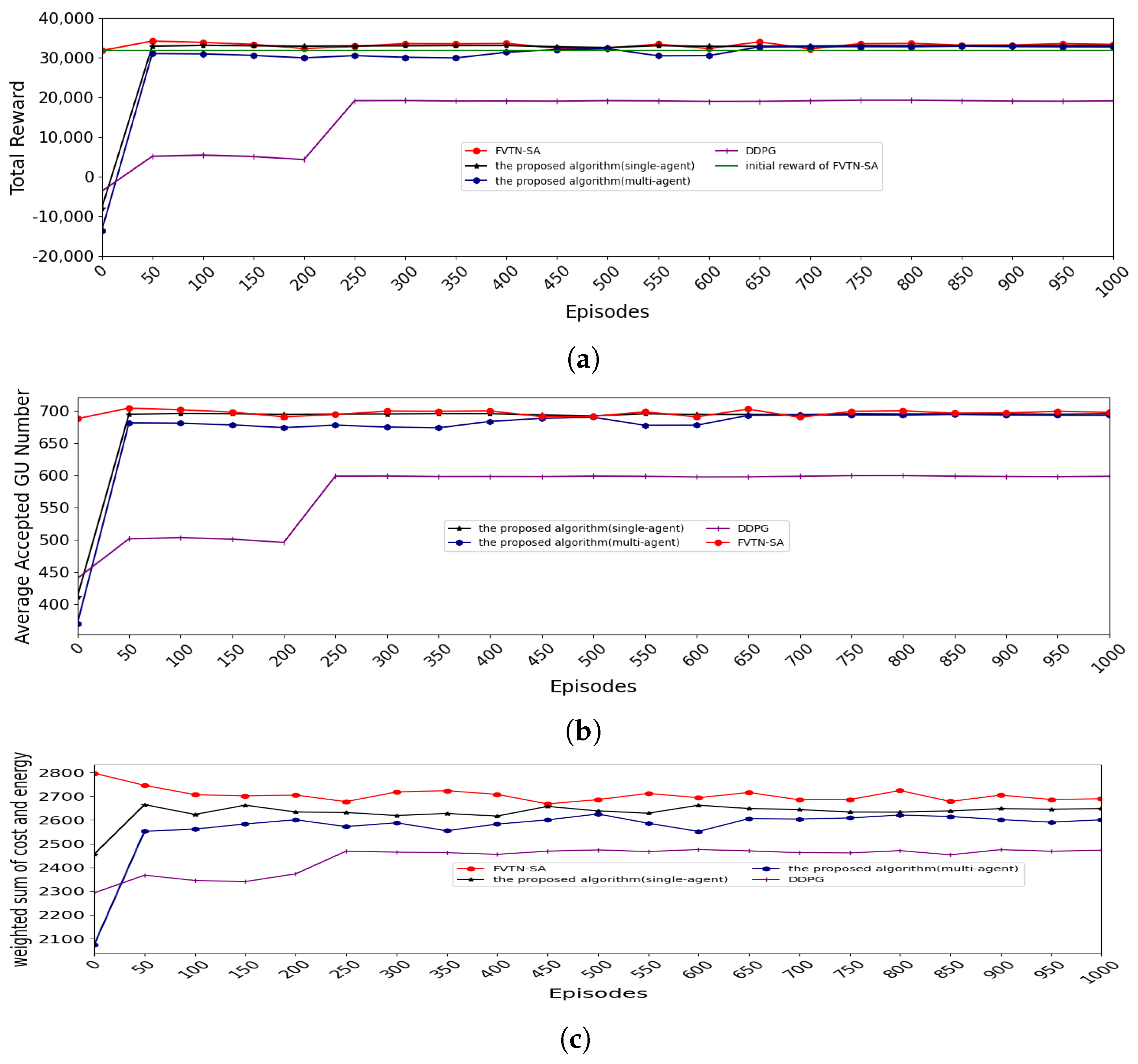
5.1. Convergence of Training Neural Networks
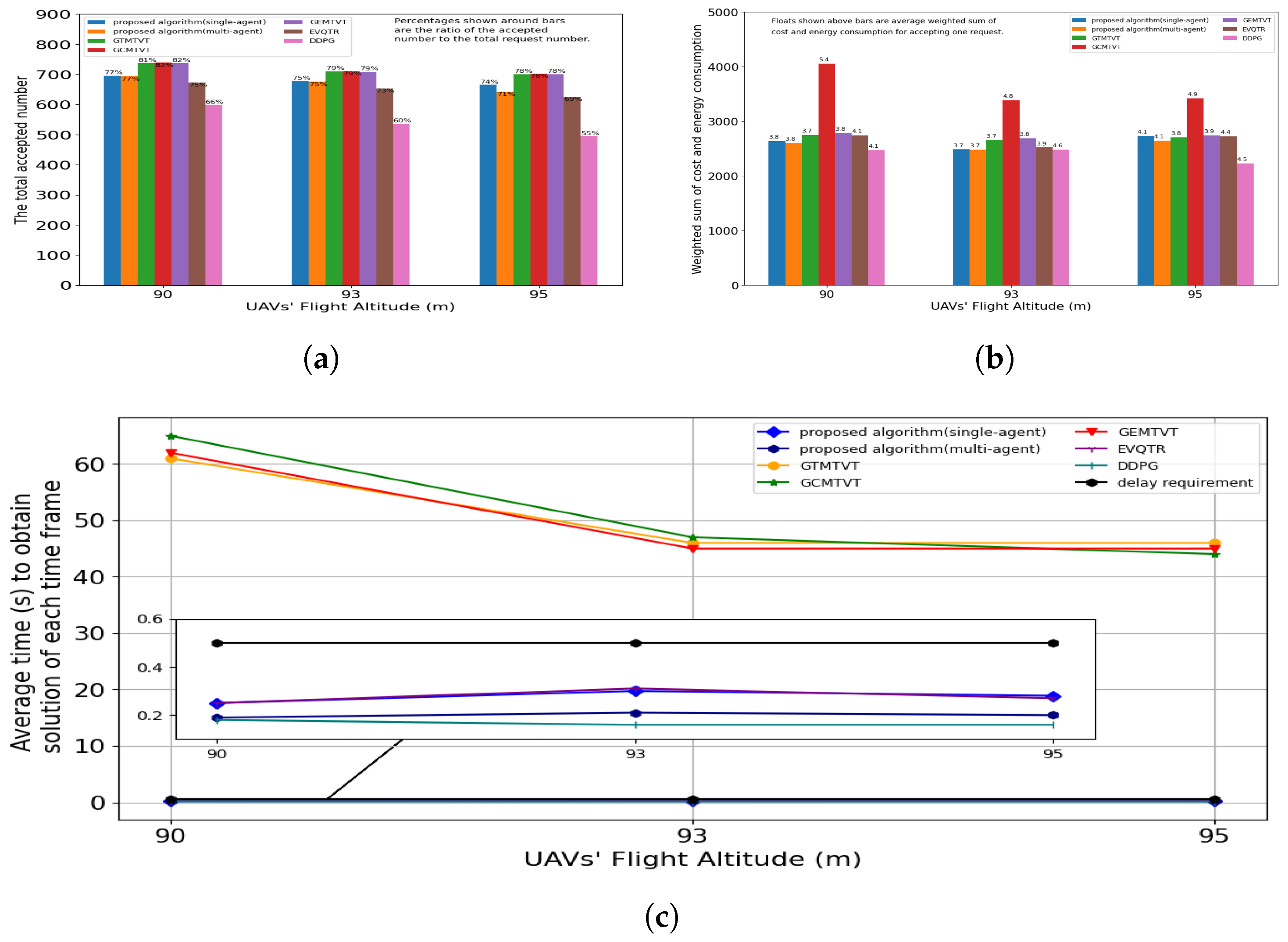
5.2. The Influence of UAV Flight Altitude
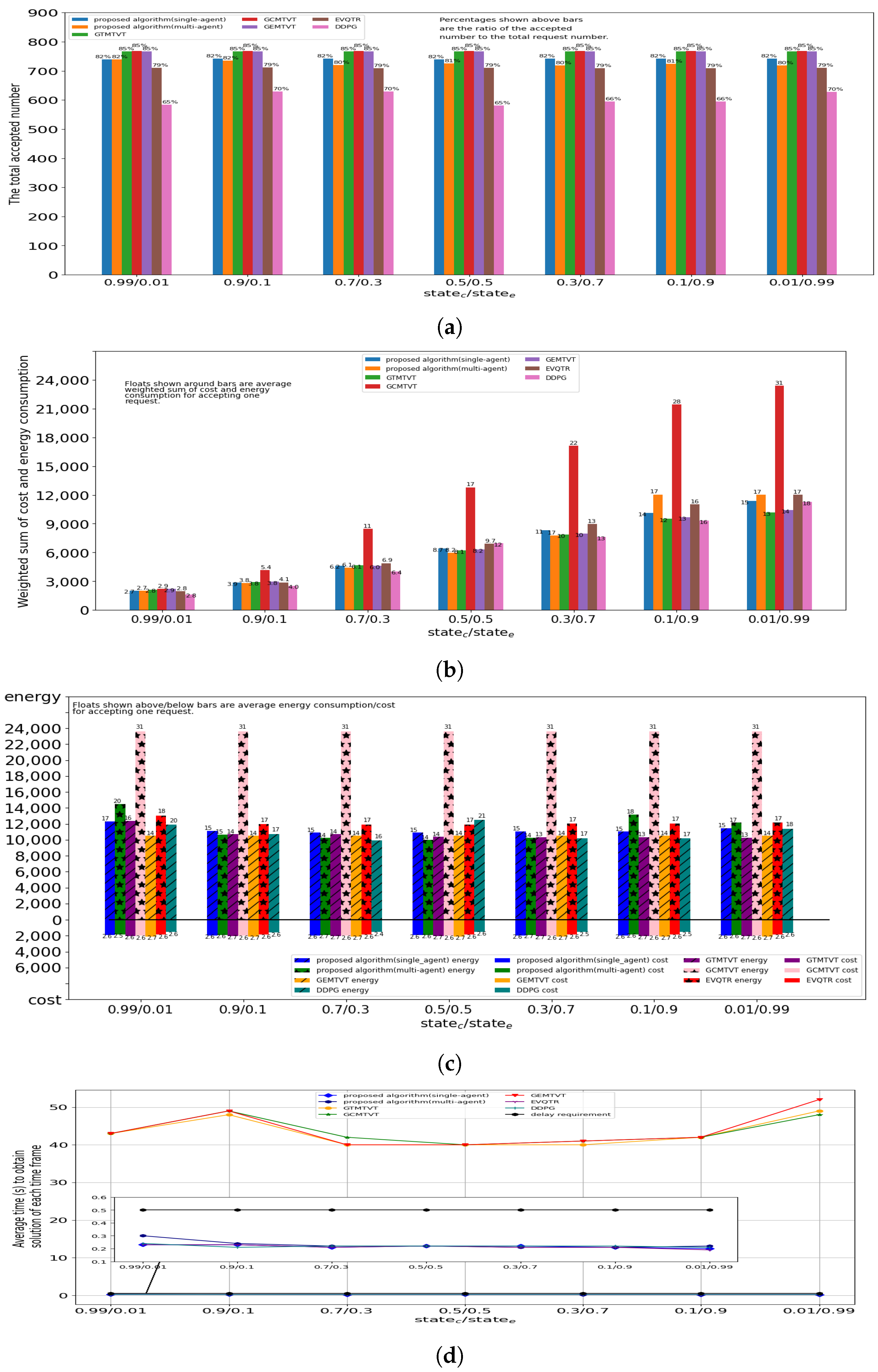
5.3. The Influences of and
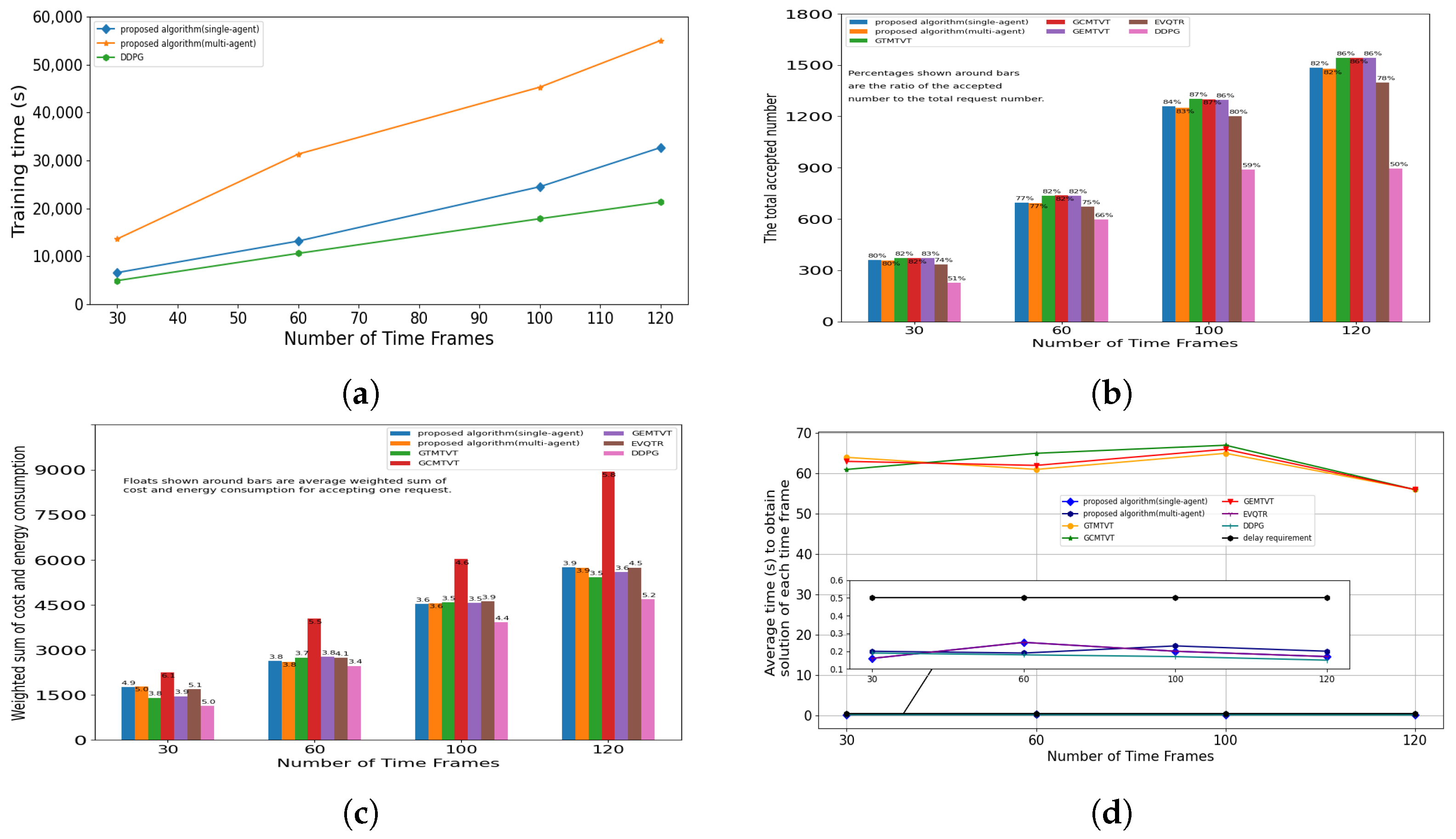
5.4. The Influence of the Number of Time Frames
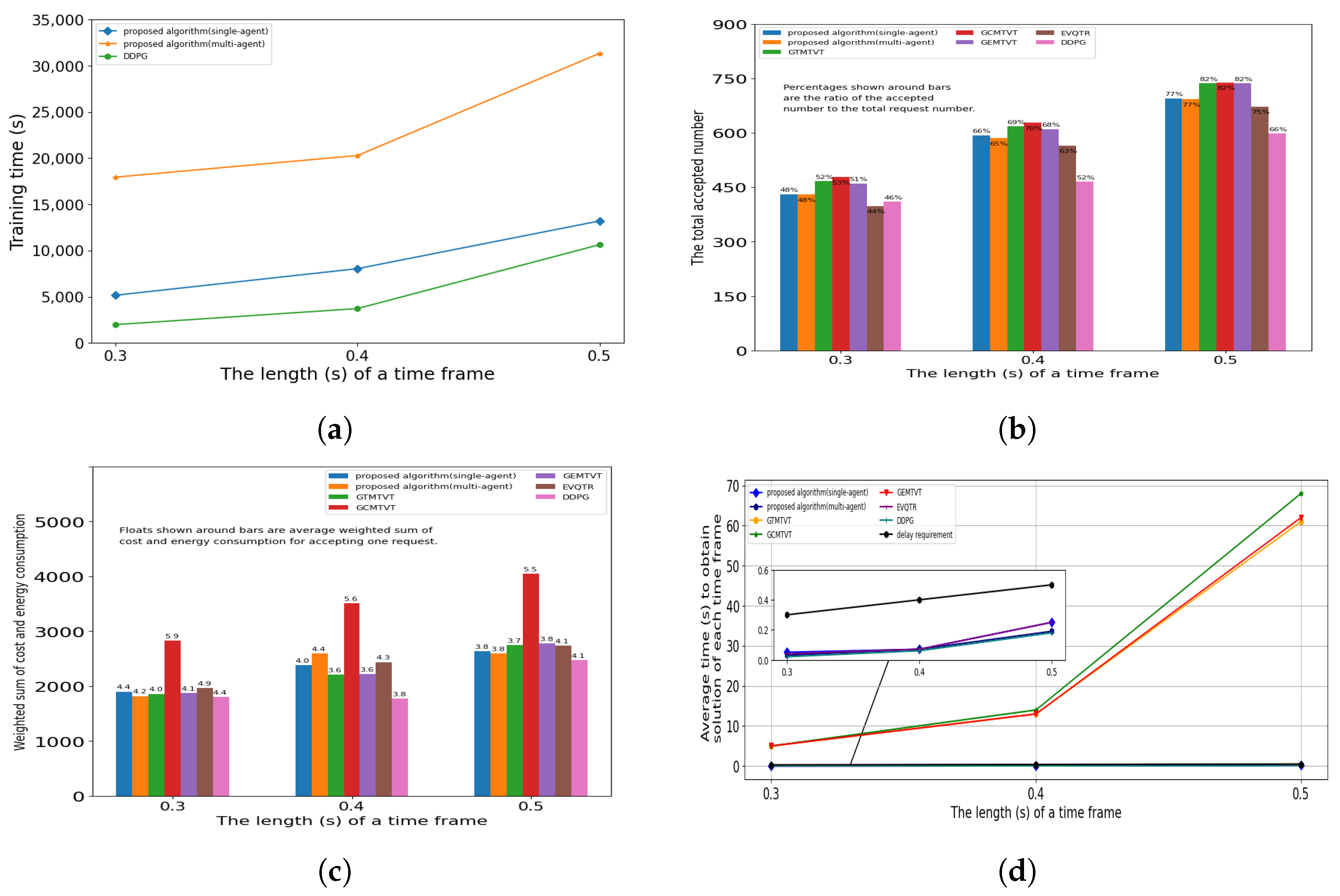
5.5. The Influence of Time Frame Length
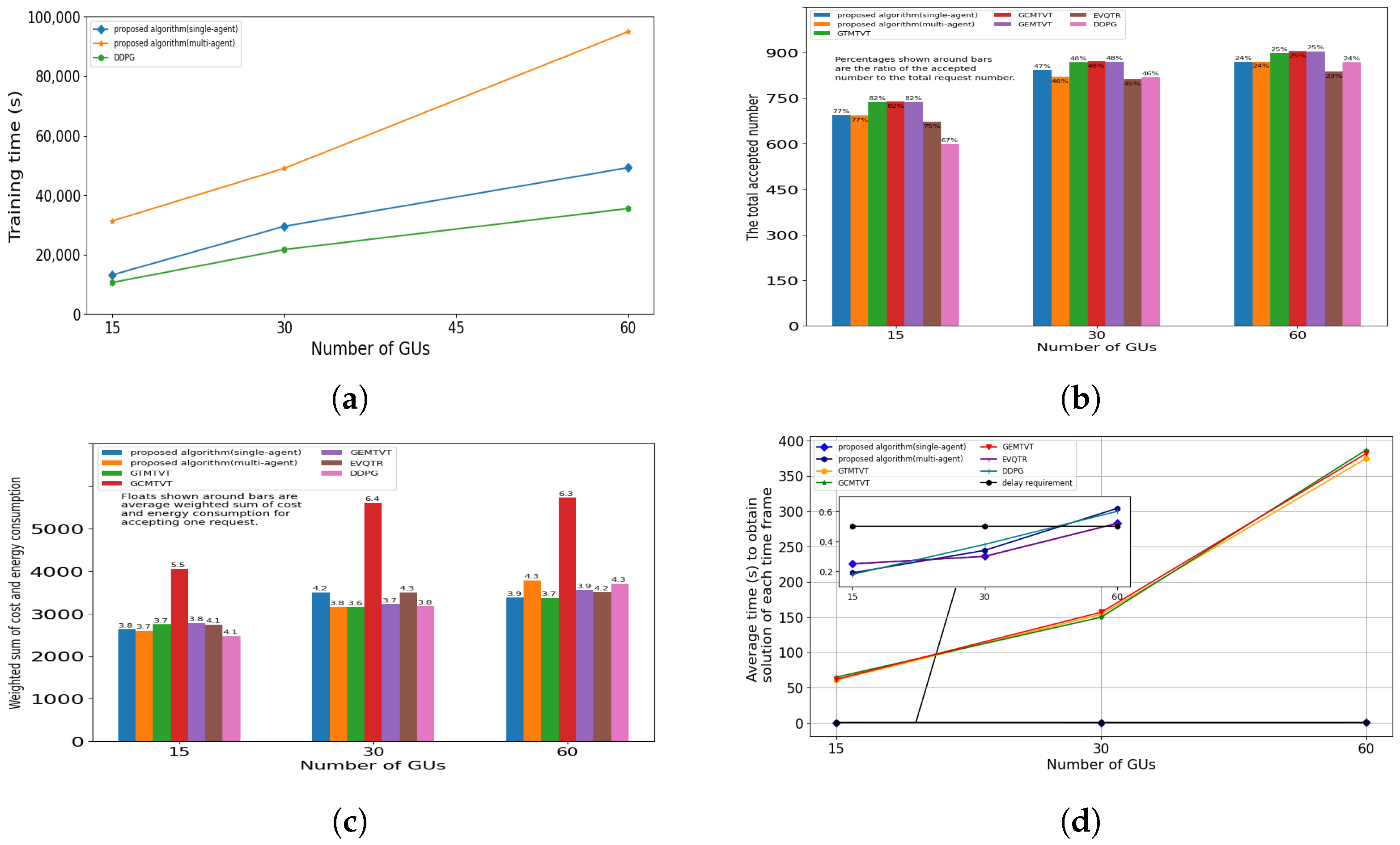
5.6. The Influence of GU Number
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| UAV | Unmanned Aerial Vehicle |
| VNF | Virtual Network Function |
| GU | Ground User |
| DRL | Deep Reinforcement Learning |
References
- Zhou, F.; Hu, R.Q.; Li, Z.; Wang, Y. Mobile Edge Computing in Unmanned Aerial Vehicle Networks. IEEE Wirel. Commun. 2020, 27, 140–146. [Google Scholar] [CrossRef]
- Le, L.; Nguyen, T.N.; Suo, K.; He, J.S. 5G network slicing and drone-assisted applications: A deep reinforcement learning approach. In Proceedings of the 5th International ACM Mobicom Workshop on Drone Assisted Wireless Communications for 5G and Beyond, DroneCom 2022, Sydney, NSW, Australia, 17 October 2022; ACM: New York, NY, USA, 2022; pp. 109–114. [Google Scholar] [CrossRef]
- Nogales, B.; Vidal, I.; Sanchez-Aguero, V.; Valera, F.; Gonzalez, L.; Azcorra, A. OSM PoC 10 Automated Deployment of an IP Telephony Service on UAVs using OSM. In Proceedings of the ETSI-OSM PoC 10, Remote, 30 November–4 December; 2020. Available online: https://dspace.networks.imdea.org/handle/20.500.12761/911 (accessed on 18 January 2024).
- Quang, P.T.A.; Bradai, A.; Singh, K.D.; Hadjadj-Aoul, Y. Multi-domain non-cooperative VNF-FG embedding: A deep reinforcement learning approach. In Proceedings of the IEEE INFOCOM 2019—IEEE Conference on Computer Communications Workshops (INFOCOM WKSHPS), Paris, France, 29 April–2 May 2019; pp. 886–891. [Google Scholar] [CrossRef]
- Xu, Z.; Gong, W.; Xia, Q.; Liang, W.; Rana, O.F.; Wu, G. NFV-Enabled IoT Service Provisioning in Mobile Edge Clouds. IEEE Trans. Mob. Comput. 2021, 20, 1892–1906. [Google Scholar] [CrossRef]
- Ma, Y.; Liang, W.; Li, J.; Jia, X.; Guo, S. Mobility-Aware and Delay-Sensitive Service Provisioning in Mobile Edge-Cloud Networks. IEEE Trans. Mob. Comput. 2022, 21, 196–210. [Google Scholar] [CrossRef]
- Ma, Y.; Liang, W.; Huang, M.; Xu, W.; Guo, S. Virtual Network Function Service Provisioning in MEC Via Trading Off the Usages Between Computing and Communication Resources. IEEE Trans. Cloud Comput. 2022, 10, 2949–2963. [Google Scholar] [CrossRef]
- Ren, H.; Xu, Z.; Liang, W.; Xia, Q.; Zhou, P.; Rana, O.F.; Galis, A.; Wu, G. Efficient Algorithms for Delay-Aware NFV-Enabled Multicasting in Mobile Edge Clouds With Resource Sharing. IEEE Trans. Parallel Distrib. Syst. 2020, 31, 2050–2066. [Google Scholar] [CrossRef]
- Huang, M.; Liang, W.; Shen, X.; Ma, Y.; Kan, H. Reliability-Aware Virtualized Network Function Services Provisioning in Mobile Edge Computing. IEEE Trans. Mob. Comput. 2020, 19, 2699–2713. [Google Scholar] [CrossRef]
- Yang, S.; Li, F.; Trajanovski, S.; Chen, X.; Wang, Y.; Fu, X. Delay-Aware Virtual Network Function Placement and Routing in Edge Clouds. IEEE Trans. Mob. Comput. 2021, 20, 445–459. [Google Scholar] [CrossRef]
- Qiu, Y.; Liang, J.; Leung, V.C.M.; Wu, X.; Deng, X. Online Reliability-Enhanced Virtual Network Services Provisioning in Fault-Prone Mobile Edge Cloud. IEEE Trans. Wirel. Commun. 2022, 21, 7299–7313. [Google Scholar] [CrossRef]
- Li, J.; Liang, W.; Xu, W.; Xu, Z.; Jia, X.; Zomaya, A.Y.; Guo, S. Budget-Aware User Satisfaction Maximization on Service Provisioning in Mobile Edge Computing. IEEE Trans. Mob. Comput. 2022, 22, 7057–7069. [Google Scholar] [CrossRef]
- Li, J.; Guo, S.; Liang, W.; Chen, Q.; Xu, Z.; Xu, W.; Zomaya, A.Y. Digital Twin-Assisted, SFC-Enabled Service Provisioning in Mobile Edge Computing. IEEE Trans. Mob. Comput. 2022, 23, 393–408. [Google Scholar] [CrossRef]
- Liang, W.; Ma, Y.; Xu, W.; Xu, Z.; Jia, X.; Zhou, W. Request Reliability Augmentation With Service Function Chain Requirements in Mobile Edge Computing. IEEE Trans. Mob. Comput. 2022, 21, 4541–4554. [Google Scholar] [CrossRef]
- Tian, F.; Liang, J.; Liu, J. Joint VNF Parallelization and Deployment in Mobile Edge Networks. IEEE Trans. Wirel. Commun. 2023, 22, 8185–8199. [Google Scholar] [CrossRef]
- Liang, J.; Tian, F. An Online Algorithm for Virtualized Network Function Placement in Mobile Edge Industrial Internet of Things. IEEE Trans. Ind. Inform. 2023, 19, 2496–2507. [Google Scholar] [CrossRef]
- Wang, X.; Xing, H.; Song, F.; Luo, S.; Dai, P.; Zhao, B. On Jointly Optimizing Partial Offloading and SFC Mapping: A Cooperative Dual-Agent Deep Reinforcement Learning Approach. IEEE Trans. Parallel Distrib. Syst. 2023, 34, 2479–2497. [Google Scholar] [CrossRef]
- Bai, J.; Chang, X.; Rodríguez, R.J.; Trivedi, K.S.; Li, S. Towards UAV-Based MEC Service Chain Resilience Evaluation: A Quantitative Modeling Approach. IEEE Trans. Veh. Technol. 2023, 72, 5181–5194. [Google Scholar] [CrossRef]
- Zhang, P.; Zhang, Y.; Kumar, N.; Guizani, M.; Barnawi, A.; Zhang, W. Energy-Aware Positioning Service Provisioning for Cloud-Edge-Vehicle Collaborative Network Based on DRL and Service Function Chain. IEEE Trans. Mob. Comput. 2023. Early Access. [Google Scholar] [CrossRef]
- Bao, L.; Luo, J.; Bao, H.; Hao, Y.; Zhao, M. Cooperative Computation and Cache Scheduling for UAV-Enabled MEC Networks. IEEE Trans. Green Commun. Netw. 2022, 6, 965–978. [Google Scholar] [CrossRef]
- Zhou, R.; Wu, X.; Tan, H.; Zhang, R. Two Time-Scale Joint Service Caching and Task Offloading for UAV-assisted Mobile Edge Computing. In Proceedings of the IEEE INFOCOM 2022—IEEE Conference on Computer Communications, London, UK, 2–5 May 2022; pp. 1189–1198. [Google Scholar] [CrossRef]
- Shen, L. User Experience Oriented Task Computation for UAV-Assisted MEC System. In Proceedings of the IEEE INFOCOM 2022—IEEE Conference on Computer Communications, London, UK, 2–5 May 2022; pp. 1549–1558. [Google Scholar] [CrossRef]
- Sharma, L.; Budhiraja, I.; Consul, P.; Kumar, N.; Garg, D.; Zhao, L.; Liu, L. Federated learning based energy efficient scheme for MEC with NOMA underlaying UAV. In Proceedings of the 5th International ACM Mobicom Workshop on Drone Assisted Wireless Communications for 5G and Beyond, DroneCom 2022, Sydney, NSW, Australia, 17 October 2022; ACM: New York, NY, USA, 2022; pp. 73–78. [Google Scholar] [CrossRef]
- Ju, Y.; Tu, Y.; Zheng, T.X.; Liu, L.; Pei, Q.; Bhardwaj, A.; Yu, K. Joint design of beamforming and trajectory for integrated sensing and communication drone networks. In Proceedings of the 5th International ACM Mobicom Workshop on Drone Assisted Wireless Communications for 5G and Beyond, DroneCom 2022, Sydney, NSW, Australia, 17 October 2022; ACM: New York, NY, USA; pp. 55–60. [Google Scholar] [CrossRef]
- Wang, C.; Zhang, R.; Cao, H.; Song, J.; Zhang, W. Joint optimization for latency minimization in UAV-assisted MEC networks. In Proceedings of the 5th International ACM Mobicom Workshop on Drone Assisted Wireless Communications for 5G and Beyond, DroneCom 2022, Sydney, NSW, Australia, 17 October 2022; ACM: New York, NY, USA, 2022; pp. 19–24. [Google Scholar] [CrossRef]
- Liu, Y.; Yan, J.; Zhao, X. Deep Reinforcement Learning Based Latency Minimization for Mobile Edge Computing with Virtualization in Maritime UAV Communication Network. IEEE Trans. Veh. Technol. 2022, 71, 4225–4236. [Google Scholar] [CrossRef]
- Lu, W.; Mo, Y.; Feng, Y.; Gao, Y.; Zhao, N.; Wu, Y.; Nallanathan, A. Secure Transmission for Multi-UAV-Assisted Mobile Edge Computing Based on Reinforcement Learning. IEEE Trans. Netw. Sci. Eng. 2023, 10, 1270–1282. [Google Scholar] [CrossRef]
- Asim, M.; ELAffendi, M.; El-Latif, A.A.A. Multi-IRS and Multi-UAV-Assisted MEC System for 5G/6G Networks: Efficient Joint Trajectory Optimization and Passive Beamforming Framework. IEEE Trans. Intell. Transp. Syst. 2023, 24, 4553–4564. [Google Scholar] [CrossRef]
- Asim, M.; Abd El-Latif, A.A.; ELAffendi, M.; Mashwani, W.K. Energy Consumption and Sustainable Services in Intelligent Reflecting Surface and Unmanned Aerial Vehicles-Assisted MEC System for Large-Scale Internet of Things Devices. IEEE Trans. Green Commun. Netw. 2022, 6, 1396–1407. [Google Scholar] [CrossRef]
- Wang, Z.; Rong, H.; Jiang, H.; Xiao, Z.; Zeng, F. A Load-Balanced and Energy-Efficient Navigation Scheme for UAV-Mounted Mobile Edge Computing. IEEE Trans. Netw. Sci. Eng. 2022, 9, 3659–3674. [Google Scholar] [CrossRef]
- Qi, X.; Chong, J.; Zhang, Q.; Yang, Z. Collaborative Computation Offloading in the Multi-UAV Fleeted Mobile Edge Computing Network via Connected Dominating Set. IEEE Trans. Veh. Technol. 2022, 71, 10832–10848. [Google Scholar] [CrossRef]
- Tang, Q.; Fei, Z.; Zheng, J.; Li, B.; Guo, L.; Wang, J. Secure Aerial Computing: Convergence of Mobile Edge Computing and Blockchain for UAV Networks. IEEE Trans. Veh. Technol. 2022, 71, 12073–12087. [Google Scholar] [CrossRef]
- Miao, Y.; Hwang, K.; Wu, D.; Hao, Y.; Chen, M. Drone Swarm Path Planning for Mobile Edge Computing in Industrial Internet of Things. IEEE Trans. Ind. Inform. 2022, 19, 6836–6848. [Google Scholar] [CrossRef]
- Tripathi, S.; Pandey, O.J.; Cenkeramaddi, L.R.; Hegde, R.M. A Socially-Aware Radio Map Framework for Improving QoS of UAV-Assisted MEC Networks. IEEE Trans. Netw. Serv. Manag. 2023, 20, 342–356. [Google Scholar] [CrossRef]
- Liao, Y.; Chen, X.; Xia, S.; Ai, Q.; Liu, Q. Energy Minimization for UAV Swarm-Enabled Wireless Inland Ship MEC Network with Time Windows. IEEE Trans. Green Commun. Netw. 2022, 7, 594–608. [Google Scholar] [CrossRef]
- Qin, Z.; Wei, Z.; Qu, Y.; Zhou, F.; Wang, H.; Ng, D.W.K.; Chae, C.B. AoI-Aware Scheduling for Air-Ground Collaborative Mobile Edge Computing. IEEE Trans. Wirel. Commun. 2023, 22, 2989–3005. [Google Scholar] [CrossRef]
- Hou, Q.; Cai, Y.; Hu, Q.; Lee, M.; Yu, G. Joint Resource Allocation and Trajectory Design for Multi-UAV Systems With Moving Users: Pointer Network and Unfolding. IEEE Trans. Wirel. Commun. 2023, 22, 3310–3323. [Google Scholar] [CrossRef]
- Sun, L.; Wan, L.; Wang, J.; Lin, L.; Gen, M. Joint Resource Scheduling for UAV-Enabled Mobile Edge Computing System in Internet of Vehicles. IEEE Trans. Intell. Transp. Syst. 2022, 24, 15624–15632. [Google Scholar] [CrossRef]
- Chen, J.; Cao, X.; Yang, P.; Xiao, M.; Ren, S.; Zhao, Z.; Wu, D.O. Deep Reinforcement Learning Based Resource Allocation in Multi-UAV-Aided MEC Networks. IEEE Trans. Commun. 2023, 71, 296–309. [Google Scholar] [CrossRef]
- Goudarzi, S.; Soleymani, S.A.; Wang, W.; Xiao, P. UAV-Enabled Mobile Edge Computing for Resource Allocation Using Cooperative Evolutionary Computation. IEEE Trans. Aerosp. Electron. Syst. 2023, 59, 5134–5147. [Google Scholar] [CrossRef]
- Qin, Y.; Zhang, Z.; Li, X.; Huangfu, W.; Zhang, H. Deep Reinforcement Learning Based Resource Allocation and Trajectory Planning in Integrated Sensing and Communications UAV Network. IEEE Trans. Wirel. Commun. 2023, 22, 8158–8169. [Google Scholar] [CrossRef]
- Zhang, R.; Xiong, K.; Lu, Y.; Fan, P.; Ng, D.W.K.; Letaief, K.B. Energy Efficiency Maximization in RIS-Assisted SWIPT Networks With RSMA: A PPO-Based Approach. IEEE J. Sel. Areas Commun. 2023, 41, 1413–1430. [Google Scholar] [CrossRef]
- Liu, C.H.; Chen, Z.; Tang, J.; Xu, J.; Piao, C. Energy-Efficient UAV Control for Effective and Fair Communication Coverage: A Deep Reinforcement Learning Approach. IEEE J. Sel. Areas Commun. 2018, 36, 2059–2070. [Google Scholar] [CrossRef]
- Chen, Z.; Cheng, N.; Yin, Z.; He, J.; Lu, N. Service-Oriented Topology Reconfiguration of UAV Networks with Deep Reinforcement Learning. In Proceedings of the 2022 14th International Conference on Wireless Communications and Signal Processing (WCSP), Nanjing, China, 1–3 November 2022; pp. 753–758. [Google Scholar] [CrossRef]
- Pourghasemian, M.; Abedi, M.R.; Hosseini, S.S.; Mokari, N.; Javan, M.R.; Jorswieck, E.A. AI-Based Mobility-Aware Energy Efficient Resource Allocation and Trajectory Design for NFV Enabled Aerial Networks. IEEE Trans. Green Commun. Netw. 2023, 7, 281–297. [Google Scholar] [CrossRef]
- Zeng, Y.; Xu, J.; Zhang, R. Energy Minimization for Wireless Communication With Rotary-Wing UAV. IEEE Trans. Wirel. Commun. 2019, 18, 2329–2345. [Google Scholar] [CrossRef]
- Lillicrap, T.P.; Hunt, J.J.; Pritzel, A.; Heess, N.; Erez, T.; Tassa, Y.; Silver, D.; Wierstra, D. Continuous control with deep reinforcement learning. arXiv 2015, arXiv:1509.02971. [Google Scholar]
- Li, J.; Liang, W.; Ma, Y. Robust Service Provisioning With Service Function Chain Requirements in Mobile Edge Computing. IEEE Trans. Netw. Serv. Manag. 2021, 18, 2138–2153. [Google Scholar] [CrossRef]



| Parameter | Value | Parameter | Value | Parameter | Value |
|---|---|---|---|---|---|
| ,m∈ | 1.5 GHz (32 bits) | 100 m | K | 15 | |
| 0.5 | H | 90 m | T | 60 | |
| W | 10 MHz | 50 m/s | 1 m | ||
| 102 m | 9.5 J/cycle | 79.856 W | |||
| 88.628 W | 300 | 120 | |||
| 4.029 | s | 0.05 | 0.6 | ||
| 0.503 | 1.225 | ||||
| −174 dBm/Hz | 5 m | 1 m/s | |||
| 0.9 | 0.1 | 1 W |
| Time Frame | GTMTVT | GCMTVT | GEMTVT | |||
|---|---|---|---|---|---|---|
| Cost | Energy | Cost | Energy | Cost | Energy | |
| 1 | 24.137 | 135.174 | 23.975 | 552.144 | 24.137 | 135.174 |
| 2 | 36.176 | 849.687 | 35.258 | 235.078 | 36.176 | 849.687 |
| 3 | 34.879 | 431.842 | 34.879 | 431.842 | 34.879 | 431.842 |
| 4 | 32.585 | 105.844 | 30.761 | 248.601 | 32.585 | 105.844 |
| 5 | 30.434 | 105.858 | 28.051 | 321.329 | 30.434 | 105.858 |
| 6 | 37.77 | 111.725 | 36.04 | 692.163 | 37.77 | 111.725 |
| 7 | 36.054 | 105.862 | 35.629 | 205.579 | 36.054 | 105.862 |
| 8 | 41.046 | 278.293 | 35.647 | 105.895 | 41.046 | 278.293 |
| 9 | 33.567 | 105.891 | 36.235 | 523.825 | 33.567 | 105.891 |
| 10 | 34.992 | 211.455 | 34.992 | 250.411 | 34.992 | 211.455 |
| 11 | 36.128 | 105.925 | 35.592 | 647.442 | 40.56 | 105.887 |
| 12 | 34.517 | 105.93 | 33.595 | 820.811 | 35.441 | 105.908 |
| 13 | 37.946 | 105.974 | 37.946 | 105.974 | 38.865 | 105.974 |
| 14 | 30.729 | 105.886 | 35.092 | 461.745 | 35.092 | 211.418 |
| 15 | 29.339 | 105.895 | 29.82 | 523.491 | 31.302 | 105.868 |
| 16 | 34.434 | 105.966 | 32.412 | 552.579 | 35.443 | 141.444 |
| 17 | 34.372 | 321.456 | 32.307 | 531.635 | 34.372 | 226.539 |
| 18 | 34.807 | 105.928 | 33.15 | 105.9 | 35.236 | 105.899 |
| 19 | 40.634 | 105.934 | 37.478 | 150.738 | 40.634 | 105.934 |
| 20 | 30.341 | 111.768 | 29.477 | 692.16 | 30.341 | 111.768 |
| 21 | 37.73 | 105.933 | 36.812 | 105.933 | 37.73 | 105.933 |
| 22 | 35.437 | 105.964 | 32.465 | 529.671 | 35.437 | 105.964 |
| 23 | 34.641 | 105.927 | 33.086 | 461.745 | 34.641 | 105.927 |
| 24 | 42.589 | 180.398 | 41.877 | 351.109 | 45.19 | 180.396 |
| 25 | 33.813 | 644.433 | 33.813 | 321.477 | 33.813 | 644.433 |
| 26 | 33.481 | 105.905 | 33.481 | 226.5 | 34.394 | 105.862 |
| 27 | 36.197 | 105.902 | 34.95 | 182.539 | 37.301 | 105.902 |
| 28 | 32.211 | 211.412 | 29.52 | 205.611 | 32.471 | 211.424 |
| 29 | 34.606 | 135.475 | 29.19 | 205.458 | 31.218 | 105.836 |
| 30 | 36.462 | 105.948 | 36.513 | 736.994 | 38.484 | 105.948 |
| Time Frame | Proposed Algorithm (Single-Agent) | Proposed Algorithm (Multi-Agent) | EVQTR | |||
|---|---|---|---|---|---|---|
| Cost | Energy | Cost | Energy | Cost | Energy | |
| 1 | 24.53 | 252.85 | 20.96 | 549.29 | 23.84 | 282.43 |
| 2 | 27.98 | 785.8 | 29.08 | 550.13 | 25.66 | 652.17 |
| 3 | 32.08 | 633.47 | 32.06 | 621.75 | 30.92 | 414.01 |
| 4 | 30.97 | 468.07 | 30.73 | 443.12 | 28.84 | 510.56 |
| 5 | 32.76 | 147.67 | 33.09 | 117.75 | 30.7 | 245.18 |
| 6 | 36.51 | 423.64 | 37.46 | 449.6 | 32.69 | 266.49 |
| 7 | 32.85 | 280.99 | 32.4 | 221.53 | 32.63 | 266.35 |
| 8 | 38.02 | 426.19 | 38.63 | 461.57 | 32.02 | 316.94 |
| 9 | 32.78 | 608.22 | 32.95 | 716.55 | 30.9 | 409.1 |
| 10 | 35.37 | 196.54 | 35.03 | 210.32 | 32.23 | 235.8 |
| 11 | 32.29 | 425.12 | 32.37 | 397.17 | 30.2 | 438.39 |
| 12 | 33.27 | 214.26 | 33.34 | 238.74 | 32.3 | 317.13 |
| 13 | 35.04 | 139.68 | 34.85 | 149.16 | 32.33 | 160.84 |
| 14 | 33.99 | 116.48 | 33.99 | 116.16 | 31.88 | 200.15 |
| 15 | 31.69 | 282.69 | 31.52 | 259.51 | 29.68 | 245.5 |
| 16 | 32.19 | 107.81 | 32.23 | 108.37 | 29.98 | 118.15 |
| 17 | 30.7 | 166.63 | 30.52 | 131.62 | 30.38 | 196.0 |
| 18 | 34.2 | 450.28 | 34.4 | 512.75 | 31.97 | 378.7 |
| 19 | 36.8 | 144.01 | 36.79 | 147.74 | 35.15 | 170.51 |
| 20 | 31.67 | 152.83 | 31.54 | 154.16 | 29.01 | 187.53 |
| 21 | 32.03 | 161.32 | 32.02 | 169.25 | 29.58 | 270.04 |
| 22 | 32.51 | 122.1 | 32.49 | 129.18 | 30.79 | 256.44 |
| 23 | 28.54 | 556.23 | 28.52 | 544.3 | 26.11 | 385.01 |
| 24 | 33.82 | 251.33 | 33.79 | 283.2 | 32.14 | 230.87 |
| 25 | 31.01 | 125.78 | 30.82 | 131.34 | 29.49 | 133.21 |
| 26 | 34.25 | 192.43 | 34.47 | 157.7 | 31.97 | 414.36 |
| 27 | 30.79 | 107.21 | 30.44 | 107.21 | 30.08 | 161.38 |
| 28 | 31.19 | 166.53 | 31.16 | 233.18 | 28.38 | 216.46 |
| 29 | 30.97 | 527.64 | 31.14 | 572.12 | 29.27 | 314.18 |
| 30 | 35.42 | 240.78 | 35.52 | 236.78 | 33.86 | 377.48 |
| Proposed Algorithm (Single Agent) | Proposed Algorithm (Multi-Agent) | DDPG | |||||
|---|---|---|---|---|---|---|---|
| K= 30 | K= 60 | K= 30 | K= 60 | K= 30 | K= 60 | ||
| Accepted request number | max | 849 | 879 | 825 | 883 | 823 | 875 |
| min | 831 | 846 | 814 | 860 | 815 | 856 | |
| avg | 842.88 | 870.28 | 819.62 | 870.78 | 819.72 | 868.32 | |
| std | 30.55 | 32.31 | 14.89 | 32.78 | 14.36 | 24.14 | |
| Weighted sum of cost and energy consumption | max | 3771.29 | 3822.59 | 3344.37 | 4376.71 | 3457.33 | 4019.02 |
| min | 3215.33 | 3075.34 | 2980.52 | 3515.32 | 2934.55 | 3317.69 | |
| avg | 3489.75 | 3348.85 | 3147.99 | 3808.39 | 3170.55 | 3741.01 | |
| std | 910.55 | 1307.24 | 541.13 | 1171.01 | 785.85 | 1009.55 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
He, Q.; Liang, J. Online Joint Optimization of Virtual Network Function Deployment and Trajectory Planning for Virtualized Service Provision in Multiple-Unmanned-Aerial-Vehicle Mobile-Edge Networks. Electronics 2024, 13, 938. https://doi.org/10.3390/electronics13050938
He Q, Liang J. Online Joint Optimization of Virtual Network Function Deployment and Trajectory Planning for Virtualized Service Provision in Multiple-Unmanned-Aerial-Vehicle Mobile-Edge Networks. Electronics. 2024; 13(5):938. https://doi.org/10.3390/electronics13050938
Chicago/Turabian StyleHe, Qiao, and Junbin Liang. 2024. "Online Joint Optimization of Virtual Network Function Deployment and Trajectory Planning for Virtualized Service Provision in Multiple-Unmanned-Aerial-Vehicle Mobile-Edge Networks" Electronics 13, no. 5: 938. https://doi.org/10.3390/electronics13050938
APA StyleHe, Q., & Liang, J. (2024). Online Joint Optimization of Virtual Network Function Deployment and Trajectory Planning for Virtualized Service Provision in Multiple-Unmanned-Aerial-Vehicle Mobile-Edge Networks. Electronics, 13(5), 938. https://doi.org/10.3390/electronics13050938






