A Novel Single-Phase Five-Level Current-Source Inverter Topology
Abstract
:1. Introduction
2. Materials and Methods
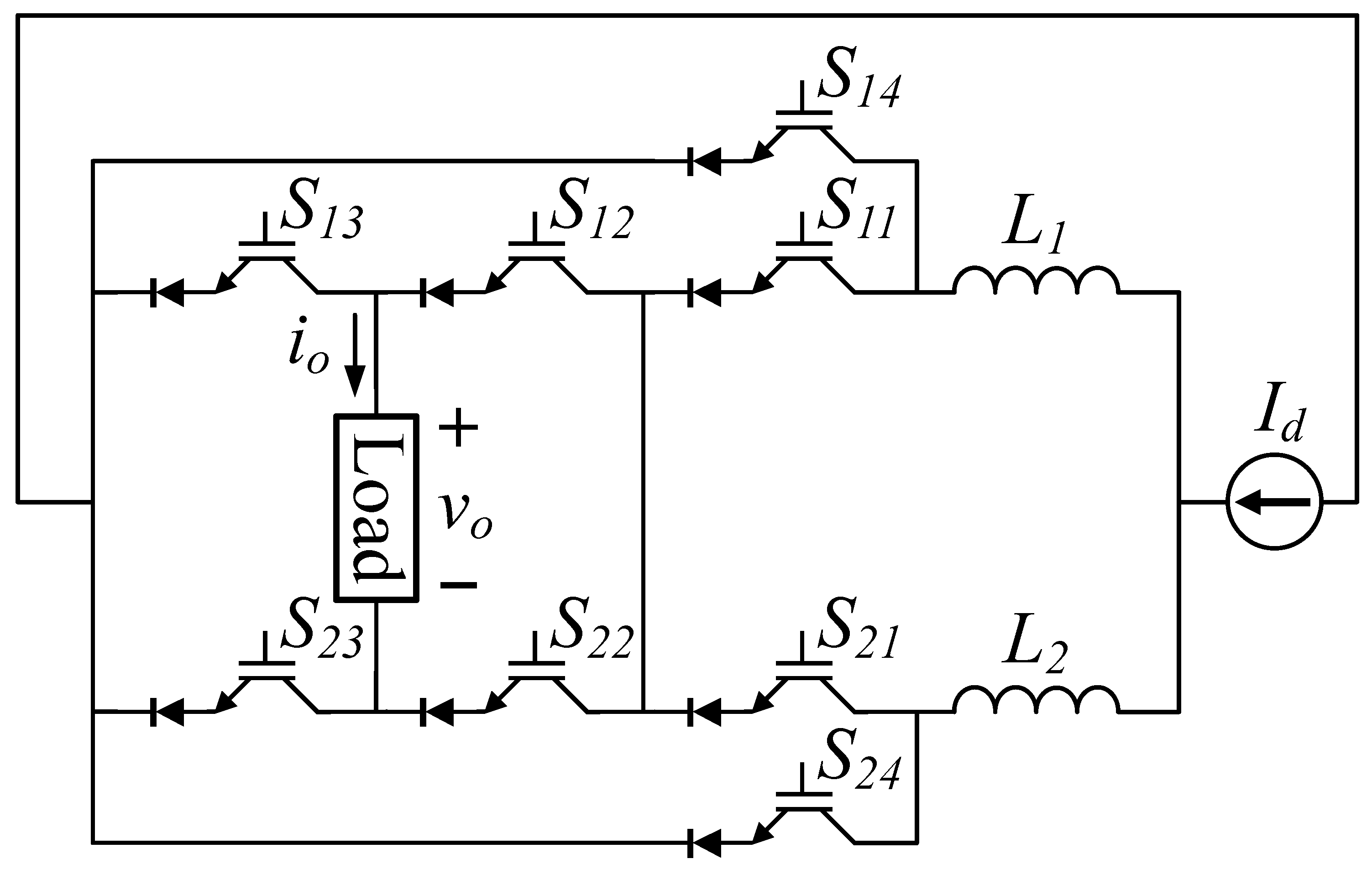
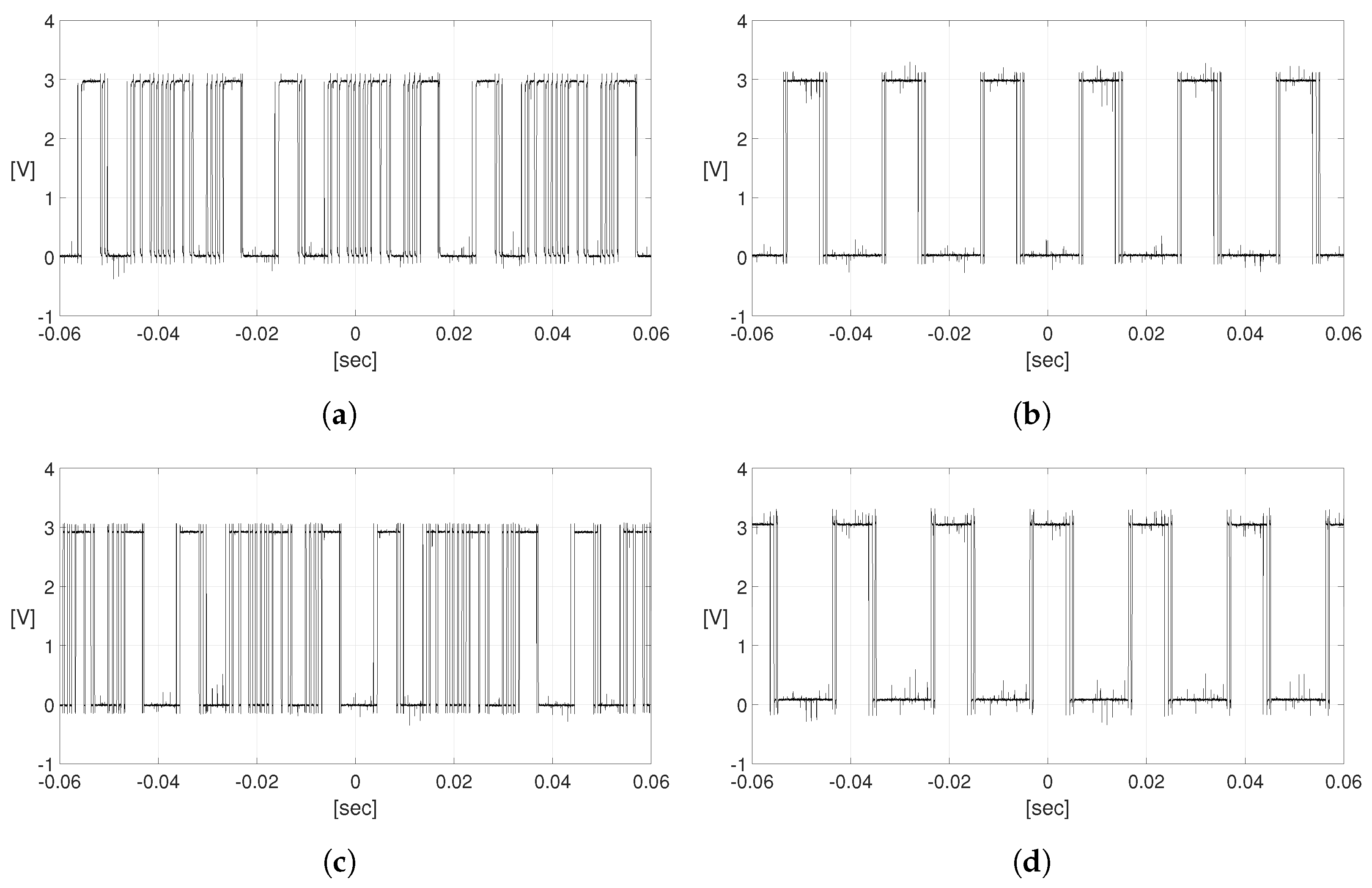
2.1. Inverter Switching States
2.2. Inductor Current Balancing
2.3. Sizing Considerations
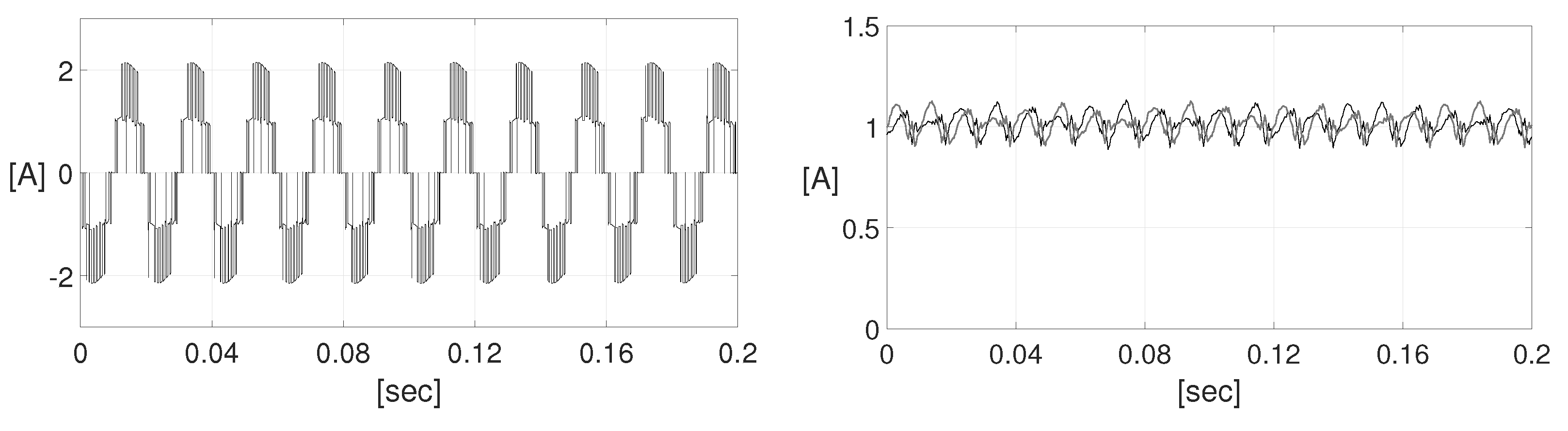
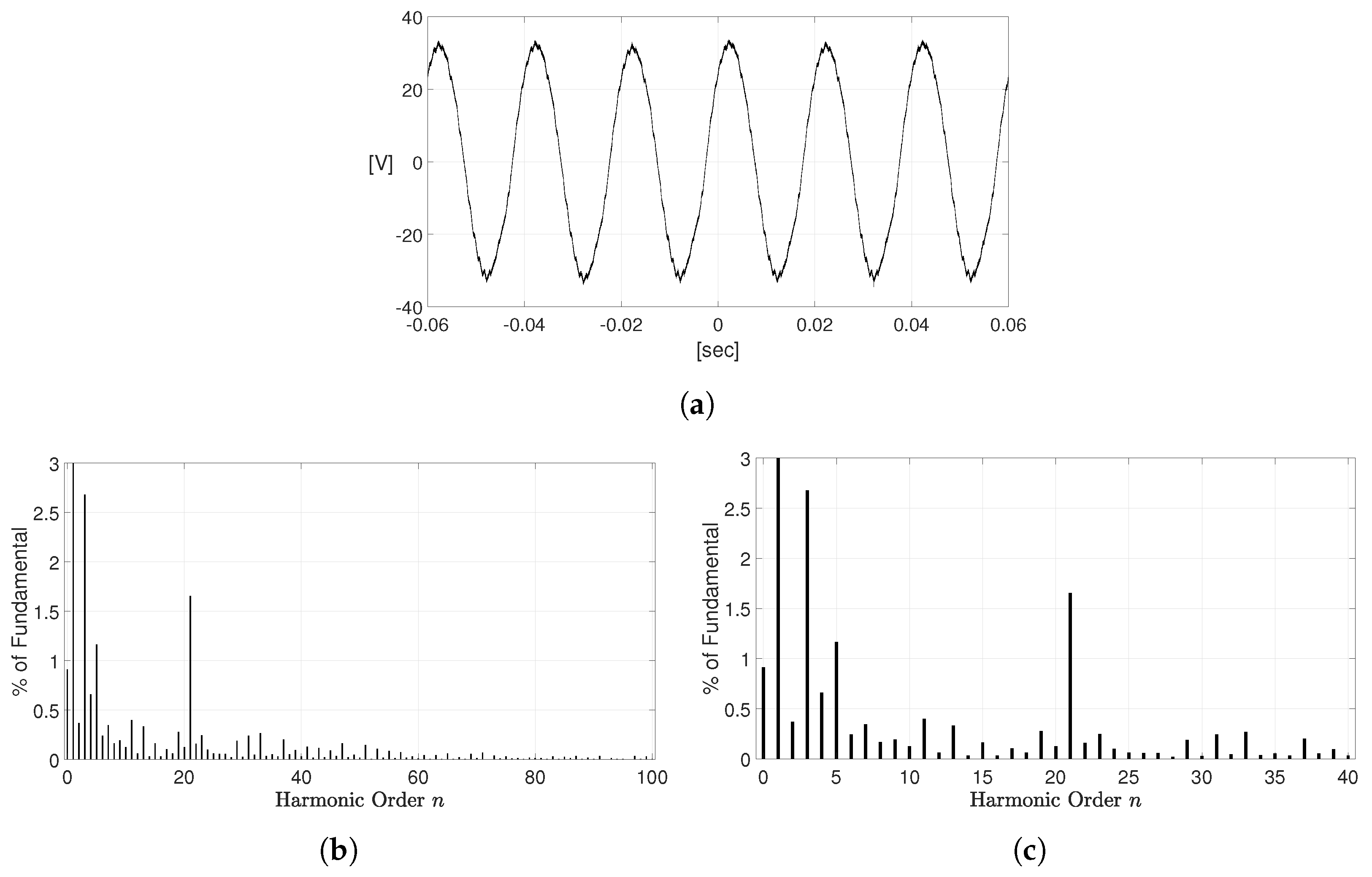
3. Simulation Verification
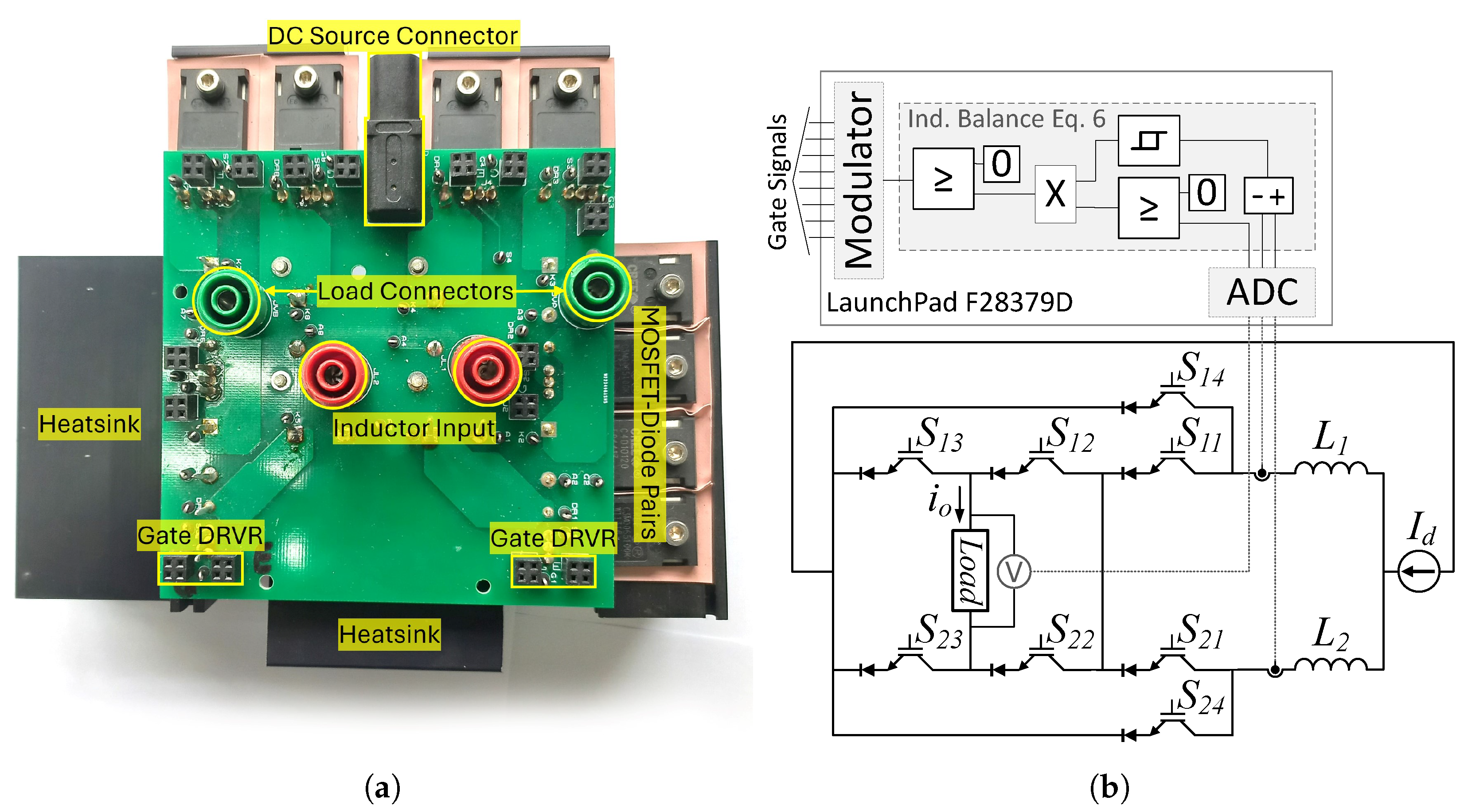
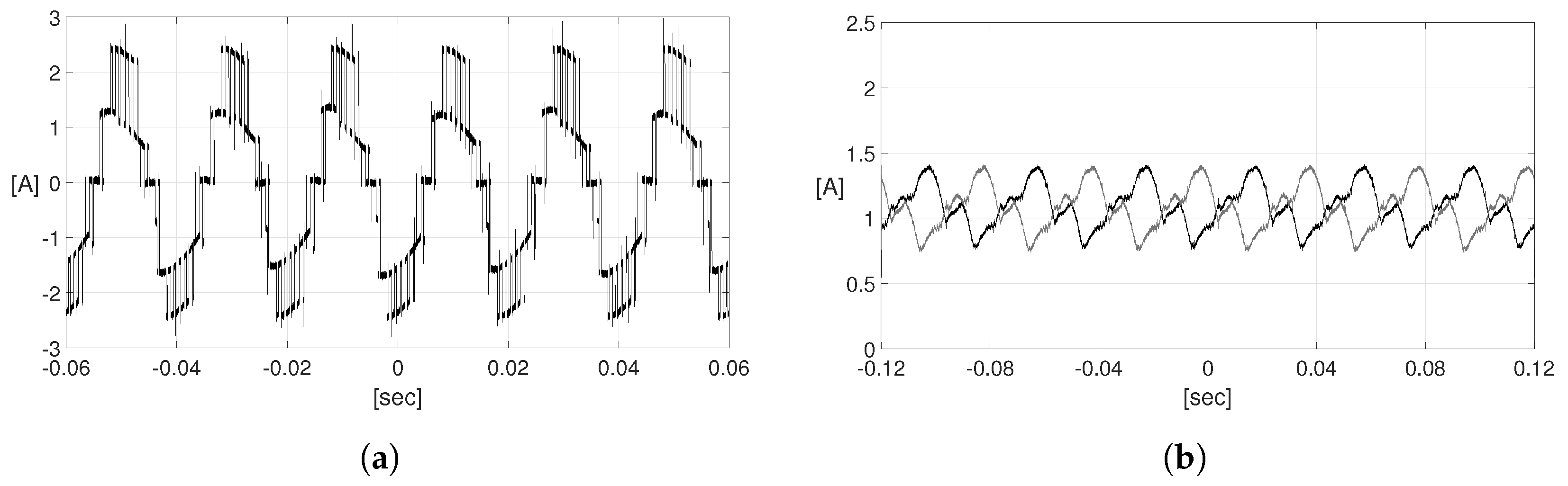
4. Experimental Verification
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| AEC | Aluminium electrolytic capacitor |
| CSI | Current-source inverter |
| EM | Electric machine |
| EV | Electric vehicle |
| HB | H-bridge |
| MEA | More electric aircraft |
| MII | Module-integrated inverter |
| MPPT | Maximum power point tracking |
| PV | Photovoltaic |
| RB | Reverse blocking |
| ROI | Return on investment |
| THD | Total harmonic distortion |
| VSI | Voltage-source inverter |
| WBG | Wide bandgap |
References
- Akbar, F.; Cha, H.; Do, D.T. CSI7: Novel Three-Phase Current-Source Inverter With Improved Reliability. IEEE Trans. Power Electron. 2021, 36, 9170–9182. [Google Scholar] [CrossRef]
- Estévez-Bén, A.A.; López Tapia, H.J.C.; Carrillo-Serrano, R.V.; Rodríguez-Reséndiz, J.; Vázquez Nava, N. A New Predictive Control Strategy for Multilevel Current-Source Inverter Grid-Connected. Electronics 2019, 8, 902. [Google Scholar] [CrossRef]
- Guo, X.; Bai, Y.; Wang, B. A Programmable Single-Phase Multilevel Current Source Inverter. IEEE Access 2019, 7, 102417–102426. [Google Scholar] [CrossRef]
- Nguyen, T.T.; Cha, H. Five-Level Current Source Inverter With Inductor Cell Using Switching-Cell Structure. IEEE Trans. Ind. Electron. 2022, 69, 6859–6869. [Google Scholar] [CrossRef]
- Fidone, G.L.; Migliazza, G.; Carfagna, E.; Benatti, D.; Immovilli, F.; Buticchi, G.; Lorenzani, E. Common Architectures and Devices for Current Source Inverter in Motor-Drive Applications: A Comprehensive Review. Energies 2023, 16, 5645. [Google Scholar] [CrossRef]
- Senthilnathan, K.; Annapoorani, I. Multi-Port Current Source Inverter for Smart Microgrid Applications: A Cyber Physical Paradigm. Electronics 2019, 8, 1. [Google Scholar] [CrossRef]
- Dai, H.; Torres, R.A.; Gossmann, J.; Lee, W.; Jahns, T.M.; Sarlioglu, B. A Seven-Switch Current-Source Inverter Using Wide Bandgap Dual-Gate Bidirectional Switches. IEEE Trans. Ind. Appl. 2022, 58, 3721–3737. [Google Scholar] [CrossRef]
- He, J.; Lyu, Y.; Han, J.; Wang, C. An SVM Approach for Five-Phase Current Source Converters Output Current Harmonics and Common-Mode Voltage Mitigation. IEEE Trans. Ind. Electron. 2020, 67, 5232–5245. [Google Scholar] [CrossRef]
- Torres, R.A.; Dai, H.; Lee, W.; Sarlioglu, B.; Jahns, T. Current-Source Inverter Integrated Motor Drives Using Dual-Gate Four-Quadrant Wide-Bandgap Power Switches. IEEE Trans. Ind. Appl. 2021, 57, 5183–5198. [Google Scholar] [CrossRef]
- Migliazza, G.; Buticchi, G.; Carfagna, E.; Lorenzani, E.; Madonna, V.; Giangrande, P.; Galea, M. DC Current Control for a Single-Stage Current Source Inverter in Motor Drive Application. IEEE Trans. Power Electron. 2021, 36, 3367–3376. [Google Scholar] [CrossRef]
- Song, Y.; Luo, Y.; Xiong, X.; Blaabjerg, F.; Wang, W. An Improved Submodule Topology of MMC With Fault Blocking Capability Based On Reverse-Blocking Insulated Gate Bipolar Transistor. IEEE Trans. Power Deliv. 2022, 37, 1559–1568. [Google Scholar] [CrossRef]
- Kanale, A.; Agarwal, A.; Baliga, B.J.; Bhattacharya, S. Monolithic Reverse Blocking 1.2 kV 4H-SiC Power Transistor: A Novel, Single-Chip, Three-Terminal Device for Current Source Inverter Applications. IEEE Trans. Power Electron. 2022, 37, 10112–10116. [Google Scholar] [CrossRef]
- Wang, H.; Mao, W.; Zhao, S.; Du, M.; Zhang, Y.; Zheng, X.; Wang, C.; Zhang, C.; Zhang, J.; Hao, Y. 1.3 kV Reverse-Blocking AlGaN/GaN MISHEMT With Ultralow Turn-On Voltage 0.25 V. IEEE J. Electron Devices Soc. 2021, 9, 125–129. [Google Scholar] [CrossRef]
- Madonna, V.; Migliazza, G.; Giangrande, P.; Lorenzani, E.; Buticchi, G.; Galea, M. The Rebirth of the Current Source Inverter: Advantages for Aerospace Motor Design. IEEE Ind. Electron. Mag. 2019, 13, 65–76. [Google Scholar] [CrossRef]
- Lazaroiu, A.C.; Gmal Osman, M.; Strejoiu, C.-V.; Lazaroiu, G. A Comprehensive Overview of Photovoltaic Technologies and Their Efficiency for Climate Neutrality. Sustainability 2023, 15, 16297. [Google Scholar] [CrossRef]
- Anand, S.; Gundlapalli, S.K.; Fernandes, B.G. Transformer-Less Grid Feeding Current Source Inverter for Solar Photovoltaic System. IEEE Trans. Ind. Electron. 2014, 61, 5334–5344. [Google Scholar] [CrossRef]
- Kjaer, S.B.; Pedersen, J.K.; Blaabjerg, F. A review of single-phase grid-connected inverters for photovoltaic modules. IEEE Trans. Ind. Appl. 2005, 41, 1292–1306. [Google Scholar] [CrossRef]
- Liu, Y.-F.; Meyer, E.; Liu, X. Recent Developments in Digital Control Strategies for DC/DC Switching Power Converters. IEEE Trans. Power Electron. 2009, 24, 2567–2577. [Google Scholar]
- Dai, H.; Jahns, T.M.; Torres, R.A.; Han, D.; Sarlioglu, B. Comparative Evaluation of Conducted Common-Mode EMI in Voltage-Source and Current-Source Inverters using Wide-Bandgap Switches. In Proceedings of the 2018 IEEE Transportation Electrification Conference and Expo (ITEC), Long Beach, CA, USA, 13–15 June 2018; pp. 788–794. [Google Scholar]
- Dunlop, E.D.; Halton, D.; Ossenbrink, H.A. 20 years of life and more: Where is the end of life of a PV module? In Proceedings of the Conference Record of the Thirty-first IEEE Photovoltaic Specialists Conference, Lake Buena Vista, FL, USA, 3–7 January 2005; pp. 1593–1596. [Google Scholar] [CrossRef]
- Harb, S.; Balog, R.S. Reliability of Candidate Photovoltaic Module-Integrated-Inverter (PV-MII) Topologies—A Usage Model Approach. IEEE Trans. Power Electron. 2013, 28, 3019–3027. [Google Scholar] [CrossRef]
- Quan, L.; Wolfs, P. A review of the single phase photovoltaic module integrated converter topologies with three different DC link configurations. IEEE Trans. Power Electron. 2008, 23, 1320–1333. [Google Scholar] [CrossRef]
- Castillo, S.J.; Balog, R.S.; Enjeti, P. Predicting capacitor reliability in a module-integrated photovoltaic inverter using stress factors from an environmental usage model. In North American Power Symposium 2010; IEEE: New York, NY, USA, 2010; pp. 1–6. [Google Scholar]
- Bazzi, A.M.; Kim, K.A.; Johnson, B.B.; Krein, P.T.; Dominguez-Garcıa, A. Fault impacts on solar power unit reliability. In Proceedings of the 2011 Twenty-Sixth Annual IEEE Applied Power Electronics Conference and Exposition (APEC), Fort Worth, TX, USA, 6–11 March 2011; pp. 1223–1231. [Google Scholar]
- Lorenzani, E.; Immovilli, F.; Migliazza, G.; Frigieri, M.; Bianchini, C.; Davoli, M. CSI7: A Modified Three-Phase Current-Source Inverter for Modular Photovoltaic Applications. IEEE Trans. Ind. Electron. 2017, 64, 5449–5459. [Google Scholar] [CrossRef]
- De Brito, M.A.G.; Galotto, L.; Sampaio, L.P.; Melo, G.D.A.E.; Canesin, C.A. Evaluation of the Main MPPT Techniques for Photovoltaic Applications. IEEE IEEE Trans. Ind. Electron. 2013, 60, 1156–1167. [Google Scholar] [CrossRef]
- Chen, Y.; Smedley, K. Three-Phase Boost-Type Grid-Connected Inverter. IEEE Trans. Power Electron. 2008, 23, 2301–2309. [Google Scholar] [CrossRef]
- Singh, A.; Mirafzal, B. An Efficient Grid-Connected Three-Phase Single-Stage Boost Current Source Inverter. IEEE Power Energy Technol. Syst. J. 2019, 6, 142–151. [Google Scholar] [CrossRef]
- Mirafzal, B.; Saghaleini, M.; Kaviani, A.K. An SVPWM-Based Switching Pattern for Stand-Alone and Grid-Connected Three-Phase Single-Stage Boost Inverters. IEEE Trans. Power Electron. 2011, 26, 1102–1111. [Google Scholar] [CrossRef]
- Guo, X.; Wang, N.; Zhang, J.; Wang, B.; Nguyen, M.K. A Novel Transformerless Current Source Inverter for Leakage Current Reduction. IEEE Access 2019, 7, 50681–50690. [Google Scholar] [CrossRef]
- Bai, Z.; Zhang, Z.; Ruan, X. A Natural Soft-Commutation PWM Scheme for Current Source Converter and Its Logic Implementation. IEEE Trans. Ind. Electron. 2011, 58, 2772–2779. [Google Scholar] [CrossRef]
- Wang, Z.; Wu, B.; Xu, D.; Cheng, M.; Xu, L. DC-Link Current Ripple Mitigation for Current-Source Grid-Connected Converters Under Unbalanced Grid Conditions. IEEE Trans. Ind. Electron. 2016, 63, 4967–4977. [Google Scholar] [CrossRef]
- Sarlioglu, B.; Morris, C.T. More Electric Aircraft: Review, Challenges, and Opportunities for Commercial Transport Aircraft. IEEE Trans. Transp. Electrif. 2015, 1, 54–64. [Google Scholar] [CrossRef]
- Mazzanti, G.; Diban, B.; Chiodo, E.; De Falco, P.; Noia, L.P.D. Forecasting the Reliability of Components Subjected to Harmonics Generated by Power Electronic Converters. Electronics 2020, 9, 1266. [Google Scholar] [CrossRef]
- Melfi, M.; Sung, A.M.J.; Bell, S.; Skibinski, G.L. Effect of surge voltage risetime on the insulation of low-voltage machines fed by PWM converters. IEEE Trans. Ind. Appl. 1998, 34, 766–775. [Google Scholar] [CrossRef]
- Dai, J.; Xu, D.; Wu, B. A Novel Control Scheme for Current-Source-Converter-Based PMSG Wind Energy Conversion Systems. IEEE Trans. Power Electron. 2009, 24, 963–972. [Google Scholar] [CrossRef]
- Zhang, J.; Ding, H.; Wang, B.; Guo, X.; Padmanaban, S. Active Power Decoupling for Current Source Converters: An Overview Scenario. Electronics 2019, 8, 197. [Google Scholar] [CrossRef]
- Iglesias, I.J.; Acero, J.; Bautista, A. Comparative study and simulation of optimal converter topologies for SMES systems. IEEE Trans. Appl. Supercond. 1995, 5, 254–257. [Google Scholar] [CrossRef]
- Wang, Z.; Zheng, Y.; Cheng, M.; Fan, S. Unified Control for a Wind Turbine-Superconducting Magnetic Energy Storage Hybrid System Based on Current Source Converters. IEEE Trans. Magn. 2012, 48, 3973–3976. [Google Scholar] [CrossRef]
- Shen, D.; Lehn, P.W. Modeling, analysis, and control of a current source inverter-based STATCOM. IEEE Trans. Power Deliv. 2002, 17, 248–253. [Google Scholar] [CrossRef]
- Marignetti, F.; Stefano, R.L.D.; Rubino, G.; Giacomobono, R. Current Source Inverter (CSI) Power Converters in Photovoltaic Systems: A Comprehensive Review of Performance, Control, and Integration. Energies 2023, 16, 7319. [Google Scholar] [CrossRef]
- Rodríguez-Benítez, O.M.; Aqui-Tapia, J.A.; Ortega-Velázquez, I.; Espinosa-Pérez, G. Current Source Topologies for Photovoltaic Applications: An Overview. Electronics 2022, 11, 2953. [Google Scholar] [CrossRef]
- Wang, Z.; Zou, Z.; Zheng, Y. Design and Control of a Photovoltaic Energy and SMES Hybrid System With Current-Source Grid Inverter. IEEE Trans. Appl. Supercond. 2013, 23, 505–509. [Google Scholar]
- Xu, J.; Yang, X.; Zhao, H.; Qiu, J.; Liu, K. An Inductor-Based and Capacitor-Free Bipolar Pulse Converter with Overvoltage Protection. World Electr. Veh. J. 2022, 13, 91. [Google Scholar] [CrossRef]
- Yang, X.; Zhao, Z.; Wang, C.; Xu, J.; Liu, K.; Qiu, J. Analysis and Parameter Design of SiC-Based Current Source Inverter (CSI). World Electr. Veh. J. 2022, 13, 187. [Google Scholar] [CrossRef]
- Cardoso, J.; Vazquez, N.; Hernandez, C.; Vaquero, J. A Transformerless Single-Phase Current Source Inverter Topology and Control for Photovoltaic Applications. Energies 2018, 11, 2011. [Google Scholar] [CrossRef]
- Dagan, K.J.; Zuckerberger, A.; Rabinovici, R. Fourth-Arm Common-Mode Voltage Mitigation. IEEE Trans. Power Electron. 2016, 31, 1401–1407. [Google Scholar] [CrossRef]
- Migliazza, G.; Lorenzani, E.; Immovilli, F.; Buticchi, G. Single-Phase Current Source Inverter with Reduced Ground Leakage Current for Photovoltaic Applications. Electronics 2020, 9, 1618. [Google Scholar] [CrossRef]
- Braga, H.A.C.; Barbi, I. A new technique for parallel connection of commutation cells: Analysis, design, and experimentation. IEEE Trans. Power Electron. 1997, 12, 387–395. [Google Scholar] [CrossRef]
- Bai, Z.; Zhang, Z. Conformation of Multilevel Current Source Converter Topologies Using the Duality Principle. IEEE Trans. Power Electron. 2008, 23, 2260–2267. [Google Scholar] [CrossRef]
- Antunes, F.L.M.; Braga, H.A.C.; Barbi, I. Application of a generalized current multilevel cell to current-source inverters. IEEE Trans. Ind. Electron. 1999, 46, 31–38. [Google Scholar] [CrossRef]
- Xiong, Y.; Chen, D.; Yang, X.; Hu, C.; Zhang, Z. Analysis and experimentation of a new three-phase multilevel current-source inverter. In Proceedings of the 2004 IEEE 35th Annual Power Electronics Specialists Conference (IEEE Cat. No.04CH37551), Aachen, Germany, 20–25 June 2004; Volume 1, pp. 548–551. [Google Scholar] [CrossRef]
- Bai, Z.-H.; Zhang, Z.-C. Research on topology and PWM method of a single-phase multilevel current-source inverter. Proc. CSEE 2007, 27, 73–77. [Google Scholar]


| 1 | 1 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | |
| 1 | 1 | 0 | 0 | 0 | 0 | 1 | 1 | ||
| 0 | 1 | 0 | 1 | 1 | 0 | 1 | 0 | ||
| 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 |
| 0 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | ||
| 1 | 0 | 1 | 0 | 0 | 1 | 0 | 1 | ||
| 1 | 0 | 1 | 0 | 1 | 1 | 0 | 0 | 0 |
| Switches | Maximum Current | Switching Frequency | Role |
|---|---|---|---|
| HB | |||
| non-HB |
| Parameter | Value | Units | Comments |
|---|---|---|---|
| 50 | Hz | Fundamental frequency | |
| 1050 | Hz | Carrier frequency | |
| 15 | Source voltage | ||
| 100 | mH | Source inductance | |
| Load resistance | |||
| 140 | uF | Filter capacitor |
| Parameter | Value | Units | Comments |
|---|---|---|---|
| 50 | Hz | Fundamental frequency | |
| 1050 | Hz | Carrier frequency | |
| us | Off-delay | ||
| 15 | Source voltage | ||
| 100 | mH | Source and coil inductances | |
| Load resistance | |||
| 140 | uF | Filter capacitor | |
| Wolfspeed | |||
| Keysight | |||
| Keysight | |||
| C2000 Delfino MCU | |||
| Wolfspeed | |||
| LEM | |||
| LEM |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Aldin, M.F.; Dagan, K.J. A Novel Single-Phase Five-Level Current-Source Inverter Topology. Electronics 2024, 13, 1213. https://doi.org/10.3390/electronics13071213
Aldin MF, Dagan KJ. A Novel Single-Phase Five-Level Current-Source Inverter Topology. Electronics. 2024; 13(7):1213. https://doi.org/10.3390/electronics13071213
Chicago/Turabian StyleAldin, Mayas Fakher, and Kfir Jack Dagan. 2024. "A Novel Single-Phase Five-Level Current-Source Inverter Topology" Electronics 13, no. 7: 1213. https://doi.org/10.3390/electronics13071213
APA StyleAldin, M. F., & Dagan, K. J. (2024). A Novel Single-Phase Five-Level Current-Source Inverter Topology. Electronics, 13(7), 1213. https://doi.org/10.3390/electronics13071213






