Material Point Method-Based Simulation Techniques for Medical Applications
Abstract
:1. Introduction
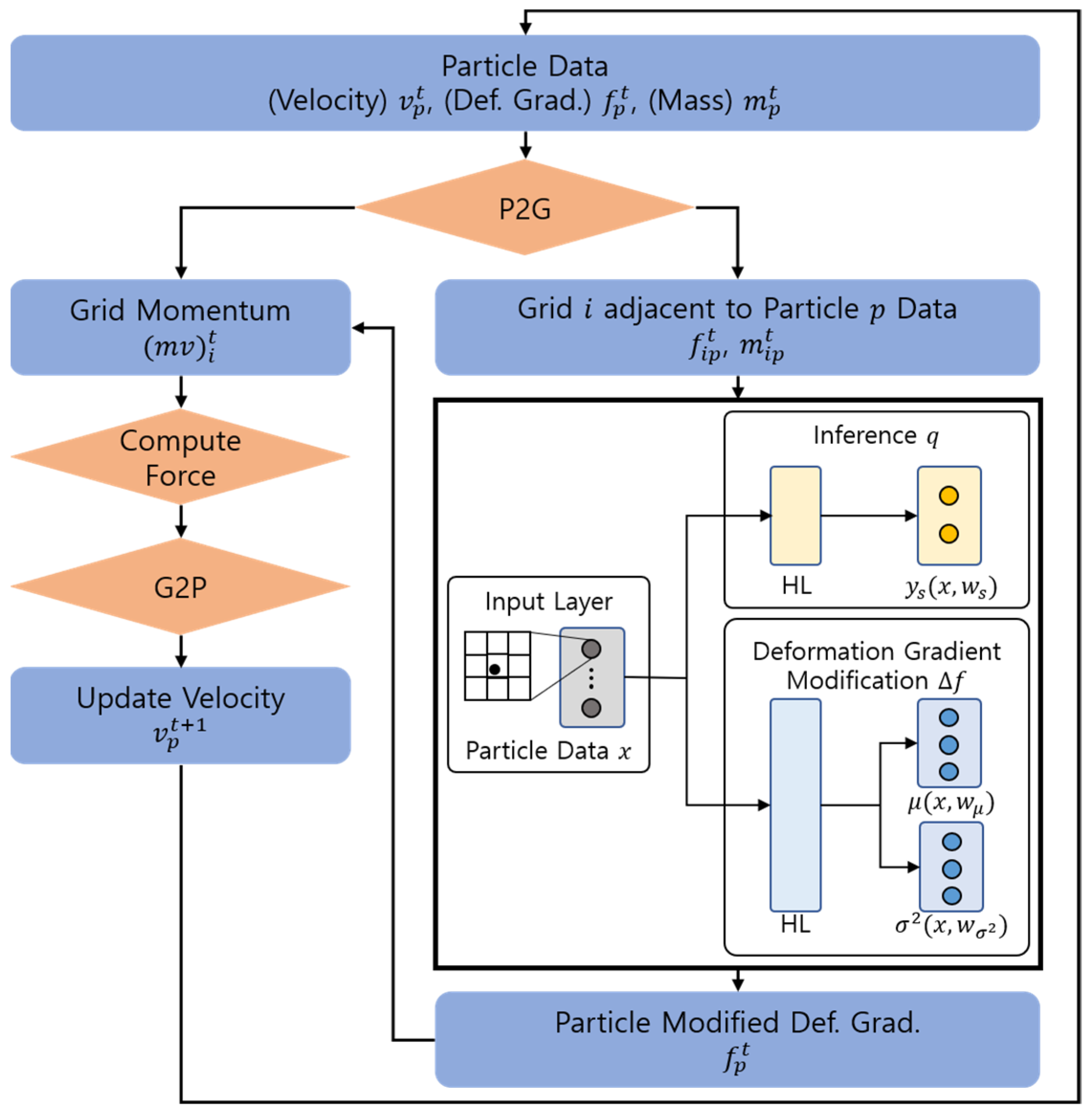
- To accurately simulate the tearing process of a force-impacted elastic object, we utilize a hybrid approach using both particles and a grid-based method known as the MPM technique.
- We propose a DL-based fracture generation method that learns the fractures occurring during elastic object tearing. This approach allows for the effective simulation of the destruction process even at low resolutions.
2. Materials and Methods
2.1. Elastic Object Simulation Based on Constraints Using MPM
2.2. Fragment Detection Algorithm
| Algorithm 1: Fragment detection algorithm |
| 1: procedure searchFragmentParticles(): 2: Init grid G 3: for each particle Pi: 4: Hash Table T ← (Pi, G index) 5: SetGroupNumber(T) 6: if number of G includes the min fragment =< Pi < max fragment 7: Fragment = Pi 8: end for 9: end procedure |
3. Experimental Results
3.1. Fragment Movement during Elastic Object Tearing
3.2. Algorithm Execution Time Comparison
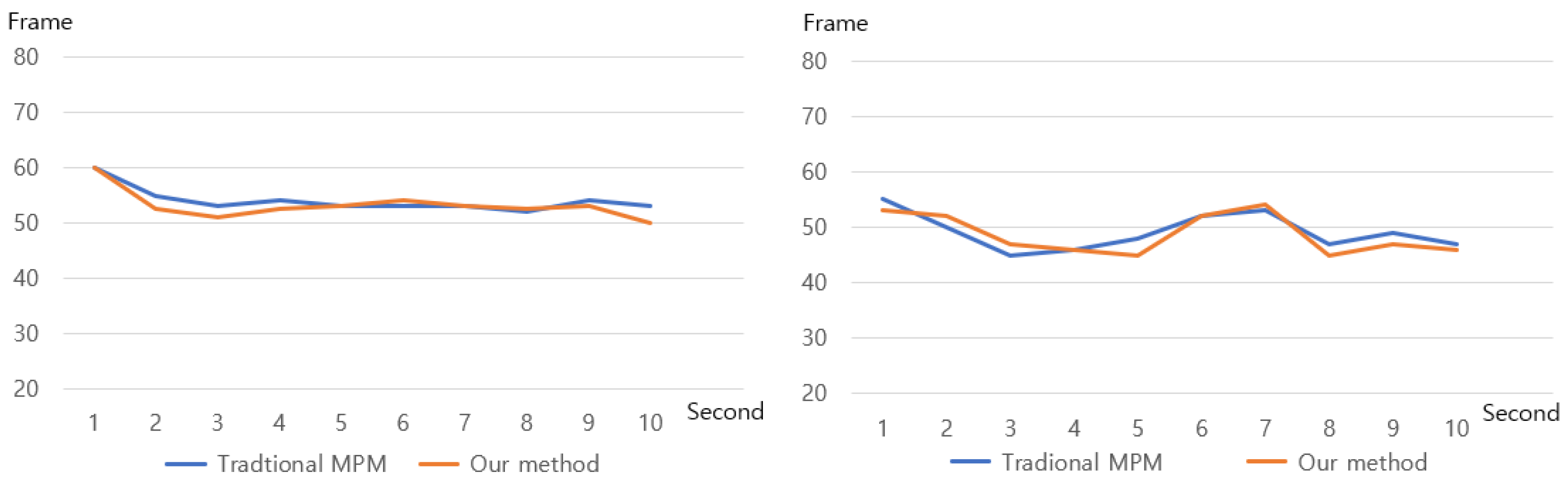
3.3. Simulation Time
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Gibson, S.F.F.; Mirtich, B. A Survey of Deformable Modeling in Computer Graphics; Mitsubishi Electric Research Laboratories: Cambridge, MA, USA, 1997. [Google Scholar]
- Selle, A.; Lentine, M.; Fedkiw, R. A Mass Spring Model for Hair Simulation. In ACM SIGGRAPH 2008 Papers; Association for Computing Machinery: New York, NY, USA, 2008; pp. 1–11. [Google Scholar]
- Choi, K.-J.; Ko, H.-S. Stable but Responsive Cloth. In ACM SIGGRAPH 2005 Courses; Association for Computing Machinery: New York, NY, USA, 2005; pp. 604–611. [Google Scholar]
- Nealen, A.; Müller, M.; Keiser, R.; Boxerman, E.; Carlson, M. Physically Based Deformable Models in Computer Graphics. Comput. Graph. Forum 2006, 25, 809–836. [Google Scholar] [CrossRef]
- Bro-Nielsen, M.; Cotin, S. Real-Time Volumetric Deformable Models for Surgery Simulation Using Finite Elements and Condensation. Comput. Graph. Forum 1996, 15, 57–66. [Google Scholar] [CrossRef]
- Lee, B.; Popescu, D.C.; Joshi, B.; Ourselin, S. Efficient Topology Modification and Deformation for Finite Element Models Using Condensation. Stud. Health Technol. Inf. 2006, 119, 299–304. [Google Scholar]
- Felippa, C. A Systematic Approach to the Element-Independent Corotational Dynamics of Finite Elements; University of Colorado, CO, USA, 2000.
- Taylor, Z.A.; Comas, O.; Cheng, M.; Passenger, J.; Hawkes, D.J.; Atkinson, D.; Ourselin, S. Modelling Anisotropic Viscoelasticity for Real-Time Soft Tissue Simulation. In Medical Image Computing and Computer-Assisted Intervention–MICCAI 2008: 11th International Conference, New York, NY, USA, 6–10 September 2008; Metaxas, D., Axel, L., Fichtinger, G., Székely, G., Eds.; Springer: Berlin/Heidelberg, Germany, 2008; pp. 703–710. [Google Scholar]
- Asareh, I.; Song, J.-H.; Mullen, R.L.; Qian, Y. A general mass lumping scheme for the variants of the extended finite element method. Int. J. Numer. Methods Eng. 2020, 121, 2262–2284. [Google Scholar] [CrossRef]
- Zhang, W.; Zhong, Z.; Peng, C.; Yuan, W.; Wu, W. GPU-Accelerated Smoothed Particle Finite Element Method for Large Deformation Analysis in Geomechanics. Comput. Geotech. 2021, 129, 103856. [Google Scholar] [CrossRef]
- Joldes, G.R.; Wittek, A.; Couton, M.; Warfield, S.K.; Miller, K. Real-Time Prediction of Brain Shift Using Nonlinear Finite Element Algorithms. In Medical Image Computing and Computer-Assisted Intervention–MICCAI 2009: 12th International Conference, London, UK, 20–24 September 2009; Yang, G.-Z., Hawkes, D., Rueckert, D., Noble, A., Taylor, C., Eds.; Springer: Berlin/Heidelberg, Germany, 2009; pp. 300–307. [Google Scholar]
- Brackbill, J.U.; Ruppel, H.M. FLIP: A Method for Adaptively Zoned, Particle-in-Cell Calculations of Fluid Flows in Two Dimensions. J. Comput. Phys. 1986, 65, 314–343. [Google Scholar] [CrossRef]
- Zhu, Y.; Bridson, R. Animating Sand as a Fluid. ACM Trans. Graph. 2005, 24, 965–972. [Google Scholar] [CrossRef]
- Stomakhin, A.; Schroeder, C.; Chai, L.; Teran, J.; Selle, A. A Material Point Method for Snow Simulation. ACM Trans. Graph. 2013, 32, 1–10. [Google Scholar] [CrossRef]
- Daviet, G.; Bertails-Descoubes, F. A Semi-Implicit Material Point Method for the Continuum Simulation of Granular Materials. ACM Trans. Graph. 2016, 35, 1–13. [Google Scholar] [CrossRef]
- Klar, G.; Gast, T.; Pradhana, A.; Fu, C.; Schroeder, C.; Jiang, C.; Teran, J. Drucker-Prager Elastoplasticity for Sand Animation. ACM Trans. Graph. 2016, 35, 1–12. [Google Scholar] [CrossRef]
- Ram, D.; Gast, T.; Jiang, C.; Schroeder, C.; Stomakhin, A.; Teran, J.; Kavehpour, P. A Material Point Method for Viscoelastic Fluids, Foams and Sponges. In Proceedings of the 14th ACM SIGGRAPH/Eurographics Symposium on Computer Animation, Los Angeles, CA, USA, 7–9 August 2015; Association for Computing Machinery: New York, NY, USA, 2015; pp. 157–163. [Google Scholar]
- Yue, Y.; Smith, B.; Batty, C.; Zheng, C.; Grinspun, E. Continuum Foam: A Material Point Method for Shear-Dependent Flows. ACM Trans. Graph. 2015, 34, 1–20. [Google Scholar] [CrossRef]
- Jiang, C.; Gast, T.; Teran, J. Anisotropic Elastoplasticity for Cloth, Knit and Hair Frictional Contact. ACM Trans. Graph. 2017, 36, 1–14. [Google Scholar] [CrossRef]
- Stomakhin, A.; Schroeder, C.; Jiang, C.; Chai, L.; Teran, J.; Selle, A. Augmented MPM for Phase-Change and Varied Materials. ACM Trans. Graph. 2014, 33, 1–11. [Google Scholar] [CrossRef]
- Tampubolon, A.P.; Gast, T.; Klár, G.; Fu, C.; Teran, J.; Jiang, C.; Museth, K. Multi-Species Simulation of Porous Sand and Water Mixtures. ACM Trans. Graph. 2017, 36, 1–11. [Google Scholar] [CrossRef]
- Wretborn, J.; Armiento, R.; Museth, K. Animation of Crack Propagation by Means of an Extended Multi-Body Solver for the Material Point Method. Comput. Graph. 2017, 69, 131–139. [Google Scholar] [CrossRef]
- Cherepanov, G.P. Crack propagation in a continuum. Prikl. Mat. Mekh. (USSR) 1967, 31, 476–488. [Google Scholar]
- Terashima, H.; Tryggvason, G. A front-tracking/ghost-fluid method for fluid interfaces in compressible flows. J. Comput. Phys. 2009, 228, 4012–4037. [Google Scholar] [CrossRef]
- Wolper, J.; Fang, Y.; Li, M.; Lu, J.; Gao, M.; Jiang, C. CD-MPM: Continuum damage material point methods for dynamic fracture animation. ACM Trans. Graph. 2019, 38, 1–15. [Google Scholar] [CrossRef]
- Xiong, P.-Y.; Almarashi, A.; Dhahad, H.A.; Alawee, W.H.; Issakhov, A.; Chu, Y.-M. Nanoparticles for Phase Change Process of Water Utilizing FEM. J. Mol. Liq. 2021, 334, 1–11. [Google Scholar] [CrossRef]
- Gao, M.; Tampubolon, A.P.; Jiang, C.; Sifakis, E. An Adaptive Generalized Interpolation Material Point Method for Simulating Elastoplastic Materials. ACM Trans. Graph. 2017, 36, 1–12. [Google Scholar] [CrossRef]
- Moutsanidis, G.; Kamensky, D.; Chen, J.S.; Bazilevs, Y. Hyperbolic Phase Field Modeling of Brittle Fracture: Part II—Immersed IGA–RKPM Coupling for Air-Blast–Structure Interaction. J. Mech. Phys. Solids 2018, 121, 114–132. [Google Scholar] [CrossRef]
- Moutsanidis, G.; Long, C.C.; Bazilevs, Y. IGA-MPM: The Isogeometric Material Point Method. Comput. Methods Appl. Mech. Eng. 2020, 372, 113346. [Google Scholar] [CrossRef]
- Li, X.; Fang, Y.; Li, M.; Jiang, C. BFEMP: Interpenetration-Free MPM–FEM Coupling with Barrier Contact. Comput. Methods Appl. Mech. Eng. 2022, 390, 114350. [Google Scholar] [CrossRef]
- Tang, J.; Azevedo, V.C.; Cordonnier, G.; Solenthaler, B. Neural Green’s Function for Laplacian Systems. Comput. Graph. 2022, 107, 186–196. [Google Scholar] [CrossRef]
- Yang, C.; Yang, X.; Xiao, X. Data-Driven Projection Method in Fluid Simulation. Comput. Animat. Virtual Worlds 2016, 27, 415–424. [Google Scholar] [CrossRef]
- Gao, Y.; Zhang, Q.; Li, S.; Hao, A.; Qin, H. Accelerating liquid simulation with an improved data-driven method. Comput. Graph. Forum 2020, 39, 180–191. [Google Scholar] [CrossRef]
- Xiao, X.; Zhou, Y.; Wang, H.; Yang, X. A novel CNN-based Poisson solver for fluid simulation. IEEE Trans. Vis. Comput. Graph. 2020, 26, 1454–1465. [Google Scholar] [CrossRef] [PubMed]
- Tompson, J.; Schlachter, K.; Sprechmann, P.; Perlin, K. Accelerating Eulerian Fluid Simulation with Convolutional Networks. In Proceedings of the 34th International Conference on Machine Learning, Sydney, Australia, 6–11 August 2017; pp. 3424–3433. [Google Scholar]
- Kim, B.; Azevedo, V.C.; Thuerey, N.; Kim, T.; Gross, M.; Solenthaler, B. Deep fluids: A generative network for parameterized fluid simulations. Comput. Graph. Forum 2019, 38, 59–70. [Google Scholar] [CrossRef]
- Wiewel, S.; Kim, B.; Azevedo, V.C.; Solenthaler, B.; Thuerey, N. Latent space subdivision: Stable and controllable time predictions for fluid flow. Comput. Graph. Forum 2020, 39, 15–25. [Google Scholar] [CrossRef]
- Um, K.; Brand, R.; Fei, Y.R.; Holl, P.; Thuerey, N. Solver-in-the-Loop: Learning from Differentiable Physics to Interact with Iterative PDE-Solvers. Adv. Neural Inf. Process. Syst. 2020, 33, 6111–6122. [Google Scholar]
- Chu, M.; Thuerey, N. Data-Driven Synthesis of Smoke Flows with CNN-Based Feature Descriptors. ACM Trans. Graph. 2017, 36, 1–14. [Google Scholar] [CrossRef]
- Xie, Y.; Franz, E.; Chu, M.; Thuerey, N. TempoGAN: A temporally coherent, volumetric GAN for super-resolution fluid flow. ACM Trans. Graph. 2018, 37, 1–15. [Google Scholar] [CrossRef]
- Xiao, X.; Wang, H.; Yang, X. A CNN-based flow correction method for fast preview. Comput. Graph. Forum 2019, 38, 431–440. [Google Scholar] [CrossRef]
- Li, C.; Qiu, S.; Wang, C.; Qin, H. Learning physical parameters and detail enhancement for gaseous scene design based on data guidance. IEEE Trans. Vis. Comput. Graph. 2020, 27, 3867–3880. [Google Scholar] [CrossRef] [PubMed]
- Gasteiger, J.; Giri, S.; Margraf, J.T.; Günnemann, S. Fast and Uncertainty-Aware Directional Message Passing for Non-Equilibrium Molecules. arXiv 2020, arXiv:2011.14115. [Google Scholar]
- Khosravi, A.; Nahavandi, S.; Creighton, D.; Atiya, A.F. Comprehensive Review of Neural Network-Based Prediction Intervals and New Advances. IEEE Trans. Neural Netw. 2011, 22, 1341–1356. [Google Scholar] [CrossRef] [PubMed]
- Hao, L.; Wang, Y.; Bai, Y.; Zhou, Q. Energy Management Strategy on a Parallel Mild Hybrid Electric Vehicle Based on Breadth First Search Algorithm. Energy Convers. Manag. 2021, 243, 114408. [Google Scholar] [CrossRef]
- Lessley, B.; Childs, H. Data-Parallel Hashing Techniques for GPU Architectures. IEEE Trans. Parallel Distrib. Syst. 2020, 31, 237–250. [Google Scholar] [CrossRef]

| Algorithm | Execution Time (FPS) | Training Data Generation Time (FPS) |
|---|---|---|
| BFS | 794 | 8.10 |
| Hash Table | 1695 | 17.30 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sung, S.-K.; Kim, J.-H.; Shin, B.-S. Material Point Method-Based Simulation Techniques for Medical Applications. Electronics 2024, 13, 1340. https://doi.org/10.3390/electronics13071340
Sung S-K, Kim J-H, Shin B-S. Material Point Method-Based Simulation Techniques for Medical Applications. Electronics. 2024; 13(7):1340. https://doi.org/10.3390/electronics13071340
Chicago/Turabian StyleSung, Su-Kyung, Jae-Hyeong Kim, and Byeong-Seok Shin. 2024. "Material Point Method-Based Simulation Techniques for Medical Applications" Electronics 13, no. 7: 1340. https://doi.org/10.3390/electronics13071340
APA StyleSung, S.-K., Kim, J.-H., & Shin, B.-S. (2024). Material Point Method-Based Simulation Techniques for Medical Applications. Electronics, 13(7), 1340. https://doi.org/10.3390/electronics13071340








