Application of a Centroid Frequency-Based Back Propagation Neural Network Fault Location Method for a Distribution Network Considering Renewable Energy Assessment
Abstract
:1. Introduction
1.1. Background
1.2. Status of the Study
1.3. Algorithms for Fault Location
1.4. Main Work
2. Fault Characterization Analysis
2.1. Overview
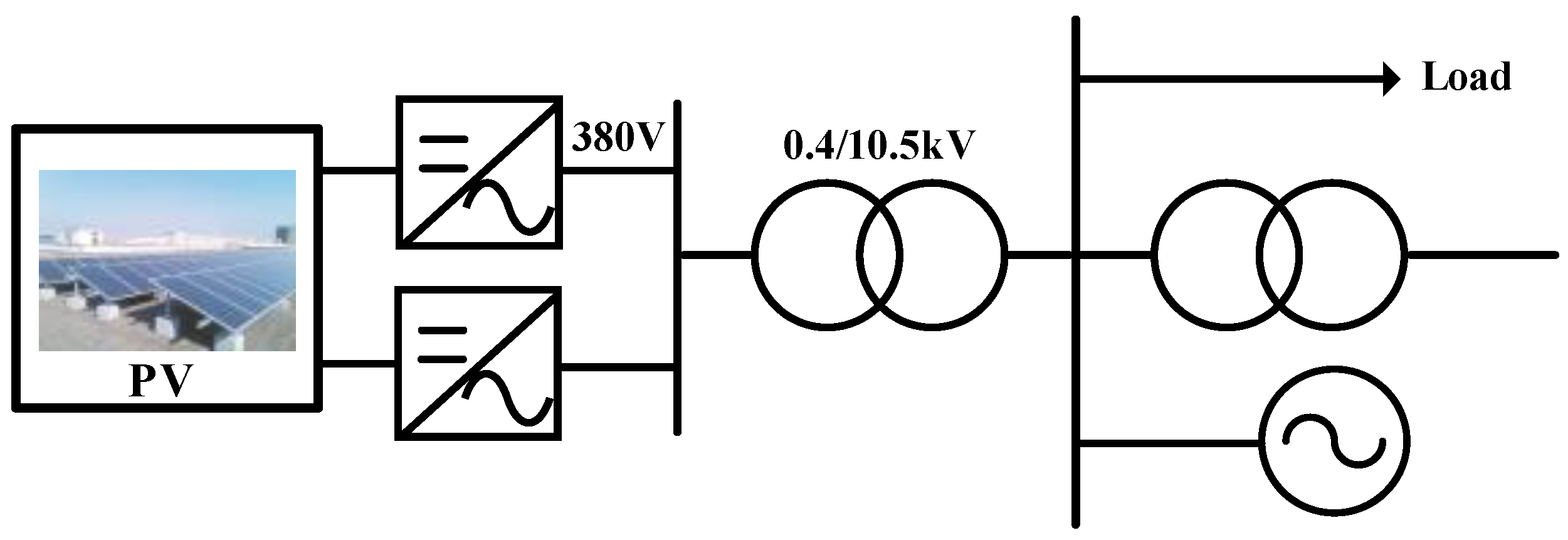
2.1.1. Distributed Generator
2.1.2. Photovoltaic Power Generation
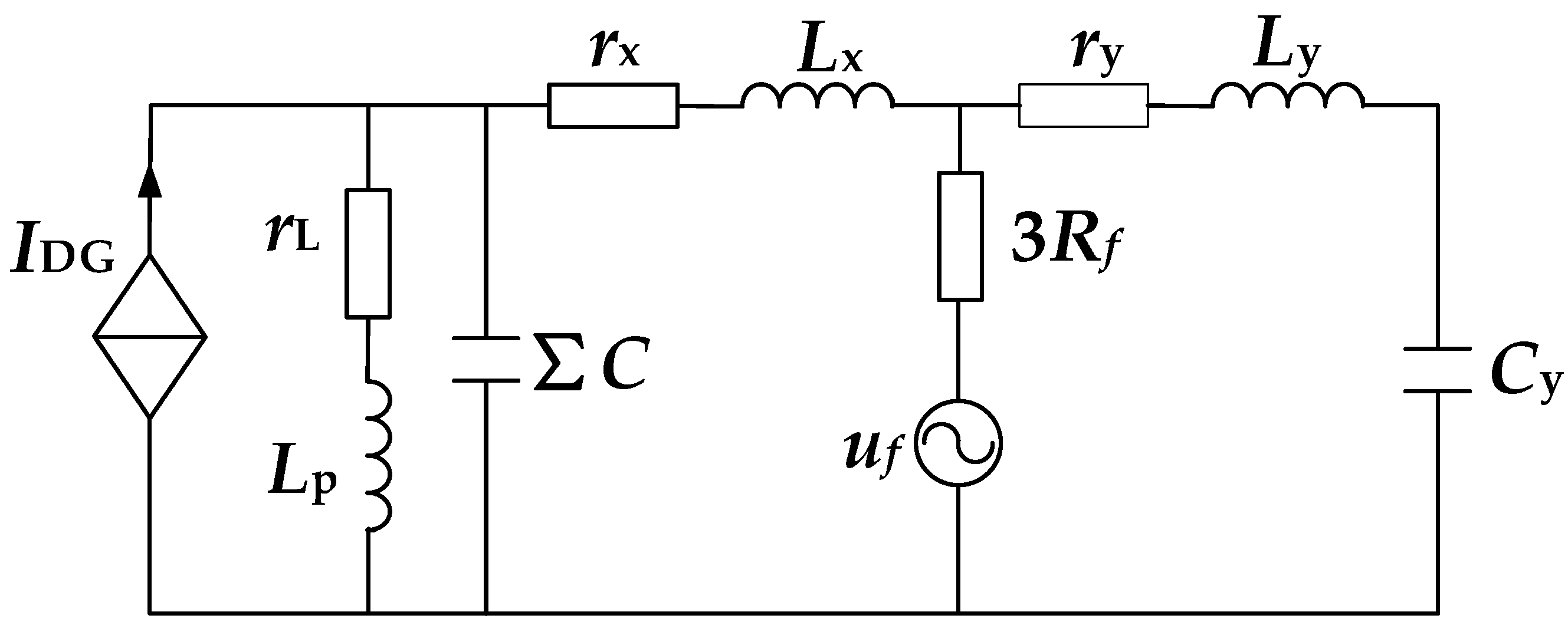
2.2. Analysis of Asymmetrical Fault
3. Location Method Based on Centroid Frequency
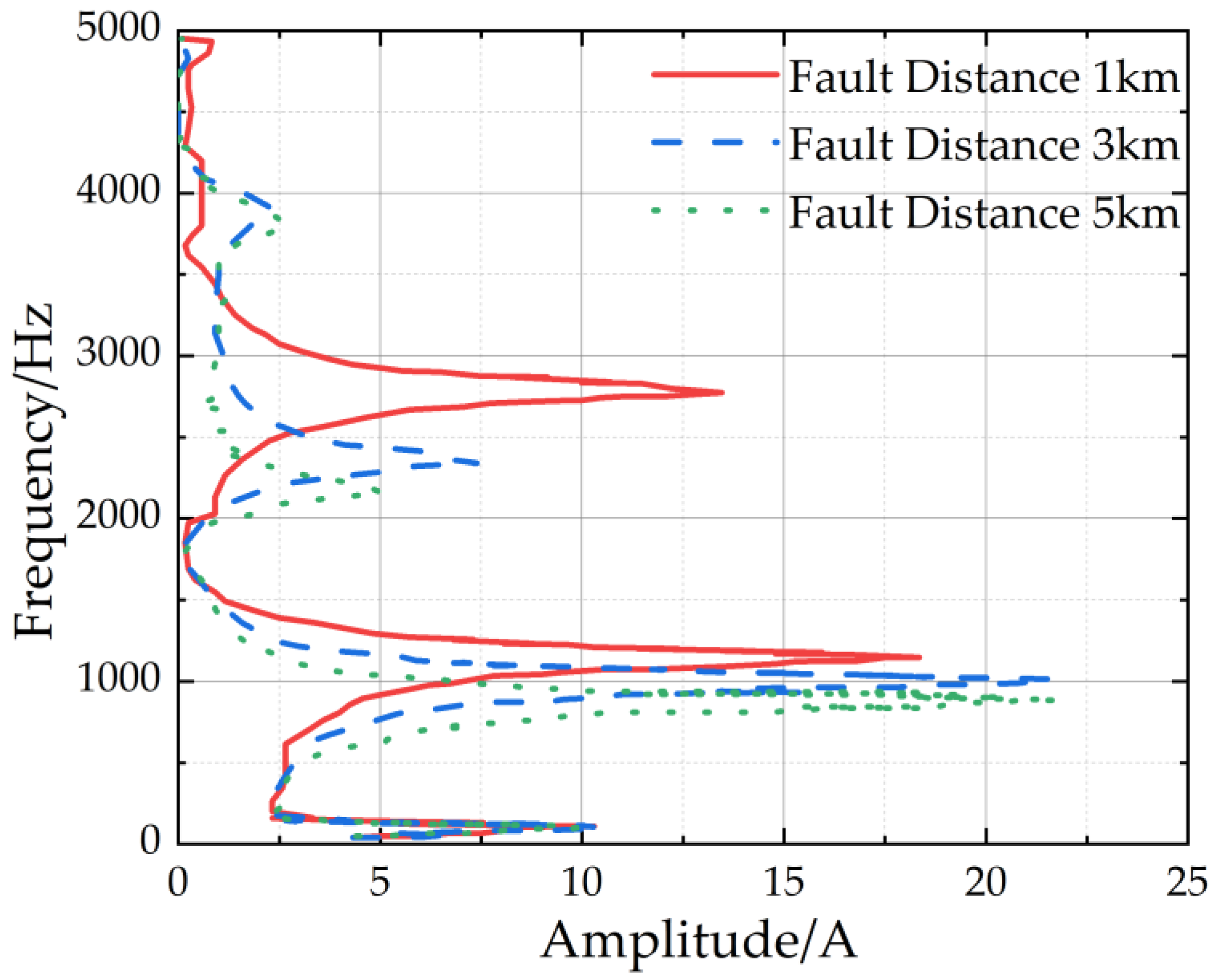
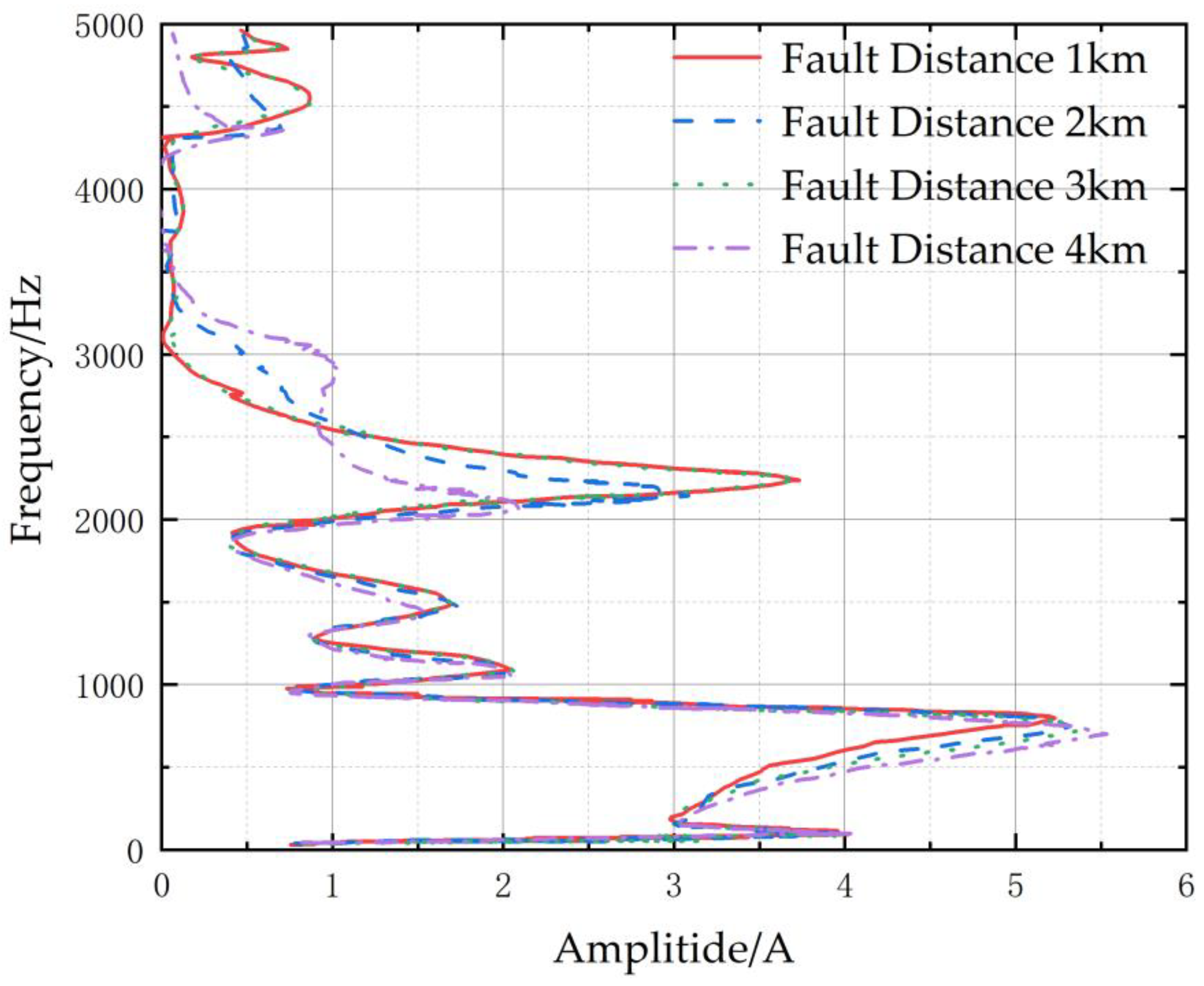
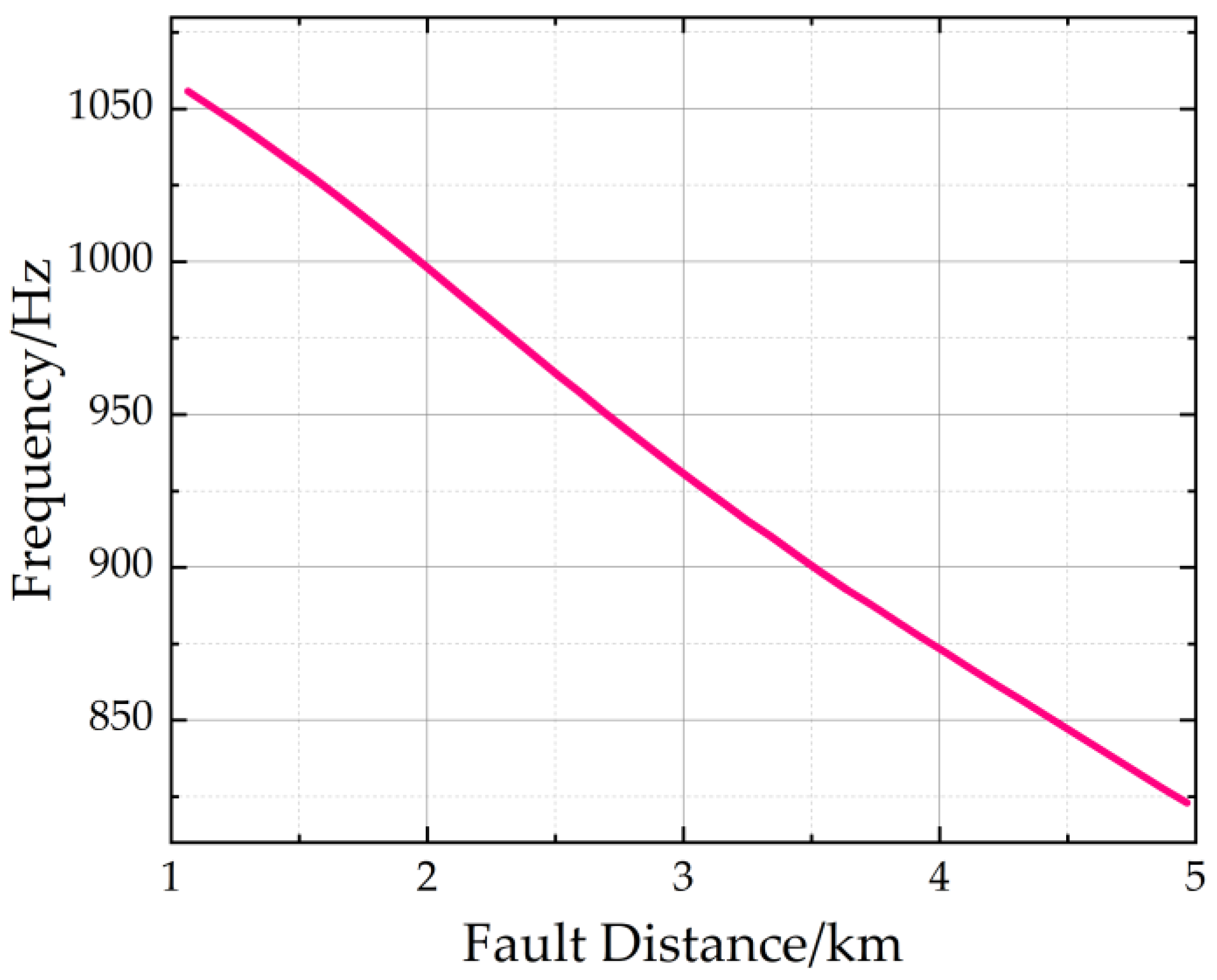
3.1. Centroid Frequency
3.2. Location Principle
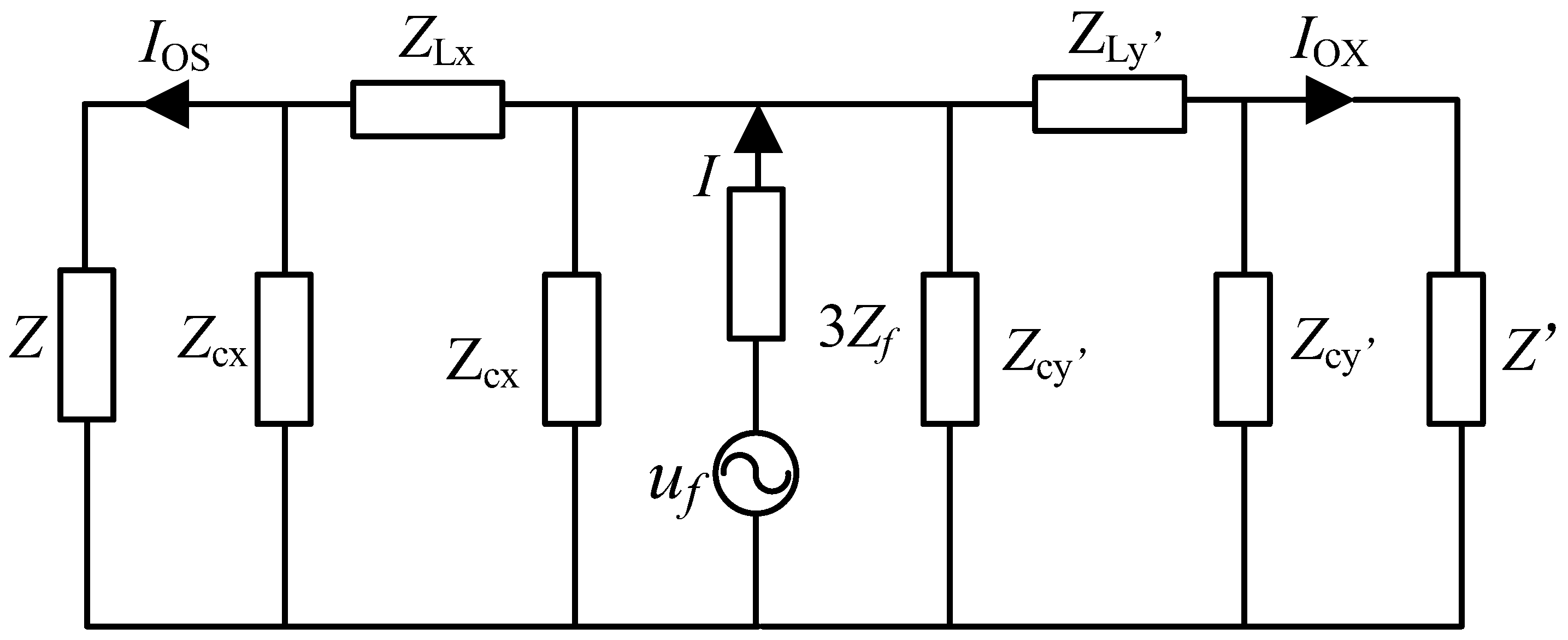
3.2.1. Fundamentals
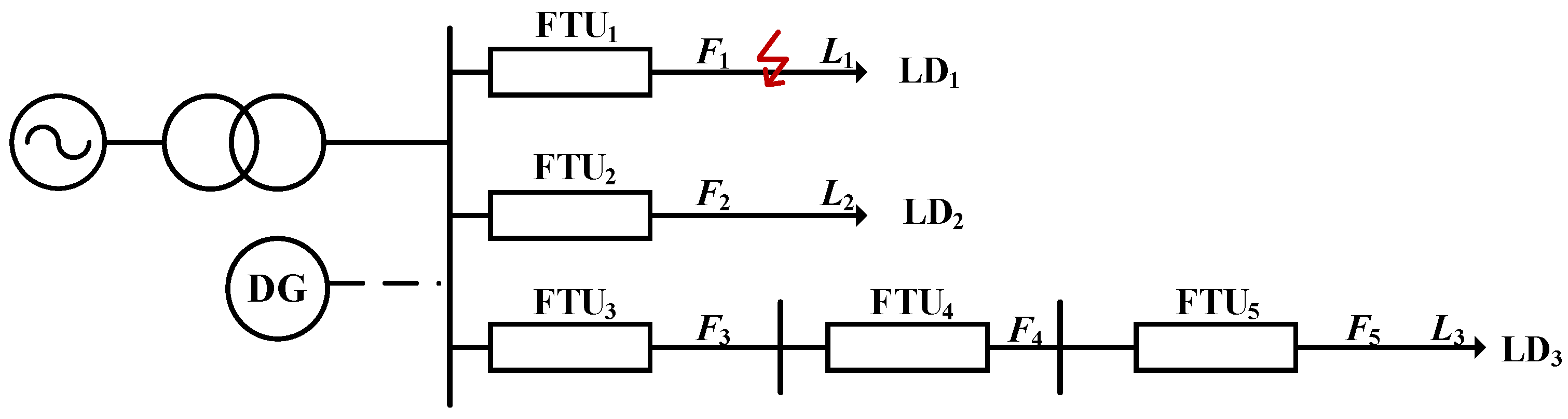
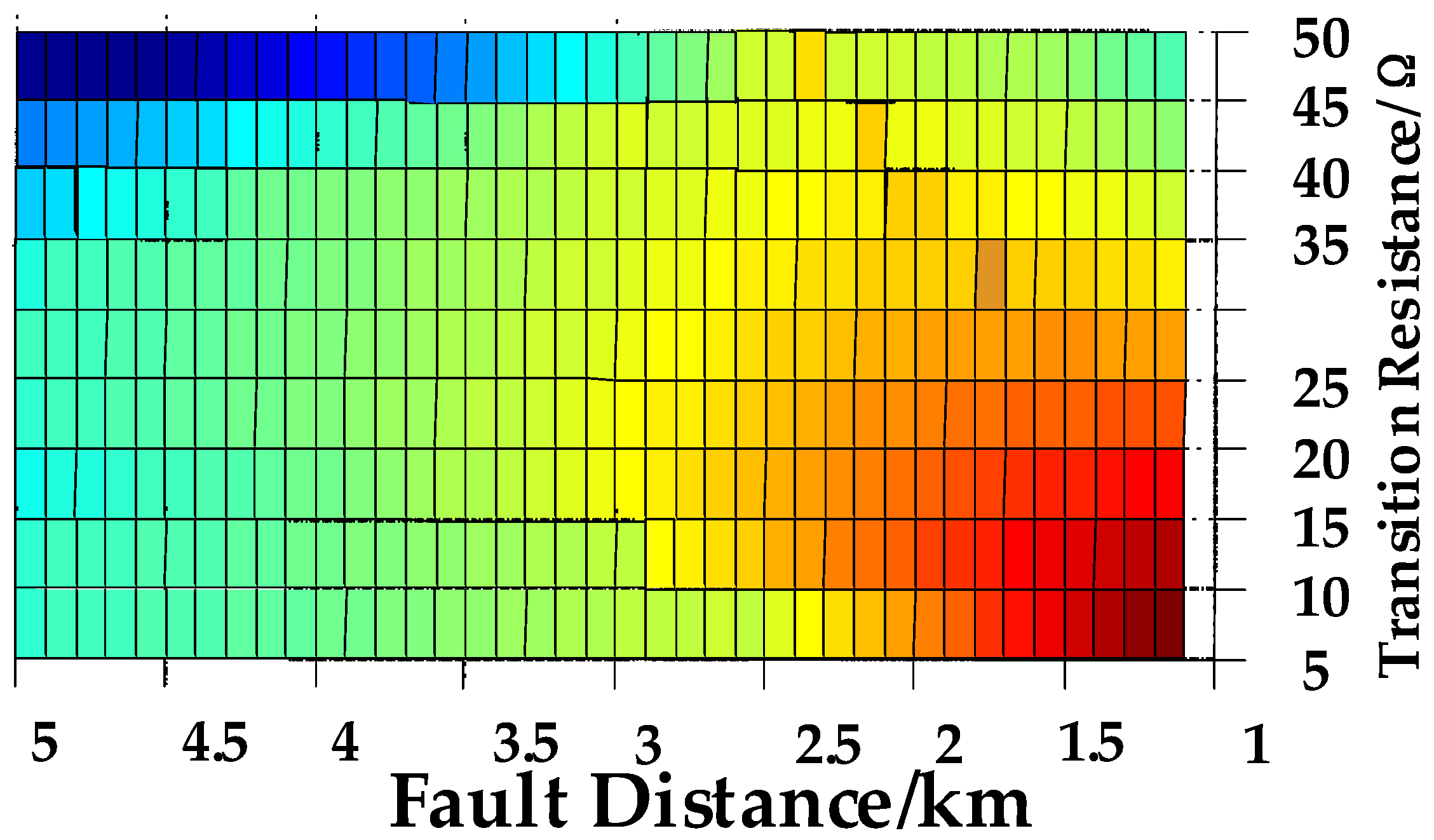
3.2.2. Determination of Fault Location
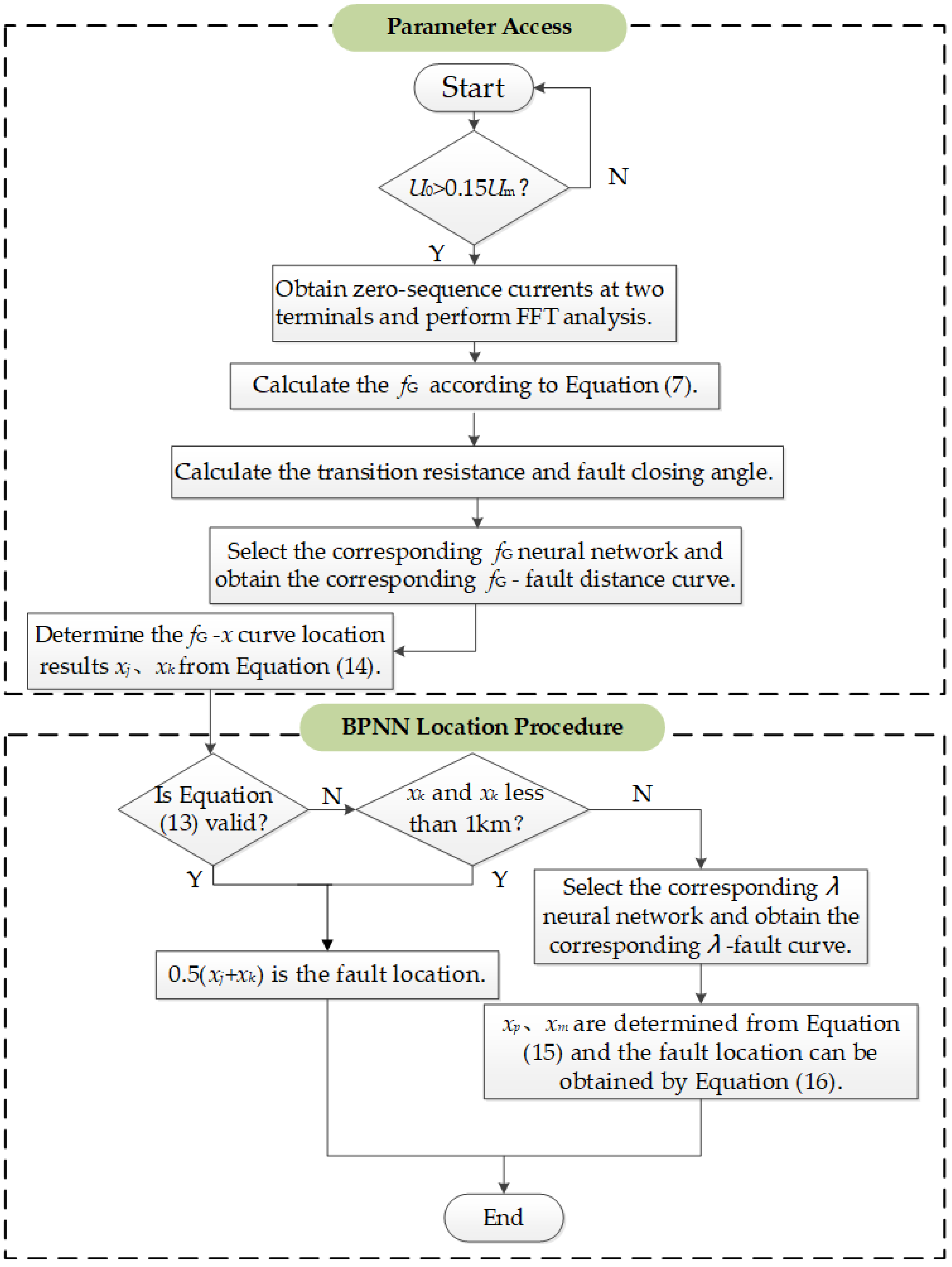
3.3. Procedure
3.4. Simulation
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
| Variable | Definition |
|---|---|
| rx | Upstream resistance from the fault point. |
| Lx | Upstream inductance from the fault point. |
| ry | Downstream resistance from the fault point. |
| Ly | Downstream inductance from the fault point. |
| rL | Grounding resistance. |
| Lp | Grounding inductance. |
| Rf | Transition resistance. |
| Pout, Qout | The instantaneous output active power and reactive power of DG |
| uP,q | q-axis component of instantaneous output active power. |
| uP* | PCC voltage standard unit value. |
| K1, K2, Kmax | Voltage support factor, reactive current peak factor, and overload current multiple. |
| IDGR | Rated current. |
| Zos | Equivalent impedance. |
| Yos | Equivalent admittance. |
| fG | Centroid frequency. |
| Hi | Spectral amplitude. |
| L0k | Zero-sequence inductance per unit. |
| C0k | Zero-sequence capacitance per unit. |
| lk | Length per unit. |
| Z | Equivalent impedance of the sound line |
| uf | fault voltage. |
| Ios | Zero-sequence current at the bus of the fault line. |
| Iox | Zero-sequence current at the end of the line at 0.5 km. |
| λ | The ratio of the same frequency component of the current at the starting and ending ends of the faulted line circuit. |
| Zcx, Zcy’, ZLx, ZLy | Parameters in the π equivalent circuit of single-phase earth fault. |
References
- Abeysinghe, S.; Abeysekera, M.; Wu, J. Electrical properties of medium voltage electricity distribution networks. CSEE J. Power Energy Syst. 2020, 7, 497–509. [Google Scholar]
- Dashti, R.; Daisy, M.; Mirshekali, H. A survey of fault prediction and location methods in electrical energy distribution networks. Measurement 2021, 184, 109947. [Google Scholar] [CrossRef]
- Hussain, S.; Razi, F.; Hewage, k. The perspective of energy poverty and 1st energy crisis of green transition. Energy 2023, 275, 127487. [Google Scholar] [CrossRef]
- Guo, K.; Luan, L.; Cai, X. Energy trade stability of China: Policy options with increasing climate risks. Energy Policy 2024, 184, 113858. [Google Scholar] [CrossRef]
- Ahmad, F.; Iqbal, A.; Ashraf, I. Optimal location of electric vehicle charging station and its impact on distribution network: A review. Energy Rep. 2022, 8, 2314–2333. [Google Scholar] [CrossRef]
- Yang, W.; Yin, X.; Tao, J. Fault current constrained impedance-based method for high resistance ground fault location in distribution grid. Electr. Power Syst. Res. 2024, 227, 109998. [Google Scholar] [CrossRef]
- Boštjan, P.; Matej, P.; Janez, R.; Miran, R.; Gorazd, Š. Parametrization of ground-fault relays in MV distribution networks with resonant grounding. Int. J. Electr. Power Energy Syst. 2022, 143, 108449. [Google Scholar]
- Cao, L.; Fang, R.; Zhang, Y. Analysis of the impact of distributed power access in distribution networks. Power Energy 2023, 44, 622–624. [Google Scholar]
- Wang, Q.; Xiao, Y.; Dampage, U. An effective fault section location method based three-line defense scheme considering distribution systems resilience. Energy Rep. 2022, 8, 10937–10949. [Google Scholar] [CrossRef]
- Moisés, J.; Davi, M.; Felipe, V. An impedance-multi-method-based fault location methodology for transmission lines connected to inverter-based resources. Int. J. Electr. Power Energy Syst. 2023, 154, 109466. [Google Scholar]
- García-Ceballos, C.; Pérez-Londoño, S.; Mora-Flórez, J. Compensated fault impedance estimation for distance-based protection in active distribution networks. Int. J. Electr. Power Energy Syst. 2023, 151, 109114. [Google Scholar] [CrossRef]
- Sayed, H.; Mohammad, E. Fault location observability rules for impedance-based fault location algorithms. Electr. Power Syst. Res. 2023, 224, 109771. [Google Scholar]
- da Silva Pessoa, A.L.; Oleskovicz, M. Fault location algorithm for distribution systems with distributed generation based on impedance and metaheuristic methods. Electr. Power Syst. Res. 2023, 225, 109871. [Google Scholar] [CrossRef]
- Reyhaneh, T.; Mahdiyeh, E.; Yaser, D. A current-based algorithm for one-end fault location in series capacitor compensated double-circuit transmission lines. Comput. Electr. Eng. 2023, 106, 108618. [Google Scholar]
- Tian, X.; Liu, Z.; Shan, J. Identification of overhead line fault traveling wave and interference clutter based on convolution neural network and random forest fusion. Energy Rep. 2023, 9, 1531–1545. [Google Scholar] [CrossRef]
- Zhao, J.; Hou, H.; Gao, Y. Single-phase ground fault location method for distribution network based on traveling wave time-frequency characteristics. Electr. Power Syst. Res. 2020, 186, 106401. [Google Scholar]
- Davod, R.; Mehdi, G.; Farzad, P. A single-ended traveling-wave-based fault location for a hybrid transmission line using detected arrival times and TW’s polarity. Electr. Power Syst. Res. 2022, 210, 108058. [Google Scholar]
- Alberto, J.; Guillen, D.; Tapia-Olvera, R.; Escobar, G. An improved algorithm for fault detection and location in multi-terminal transmission lines based on wavelet correlation modes. Electr. Power Syst. Res. 2021, 192, 106953. [Google Scholar]
- Zhang, Y.; Cong, W. An improved single-ended frequency-domain-based fault detection scheme for MMC-HVDC transmission lines. Int. J. Electr. Power Energy Syst. 2021, 125, 106463. [Google Scholar] [CrossRef]
- Bertoletti, A.; Cardoso, G.; de Peres, A. Ground and phase fault classification for half-wavelength transmission lines relaying purposes. Int. J. Electr. Power Energy Syst. 2023, 148, 108966. [Google Scholar] [CrossRef]
- Pirmani, S.; Mahmud, A. Advances on fault detection techniques for resonant grounded power distribution networks in bushfire prone areas: Identification of faulty feeders, faulty phases, faulty sections, and fault locations. Electr. Power Syst. Res. 2023, 220, 109265. [Google Scholar] [CrossRef]
- Peng, N.; Zhang, P.; Liang, R.; Guo, Z.; Hu, Y. Fault location of three-core power distribution cables based on lump-parameter model considering conductor couplings. Int. J. Electr. Power Energy Syst. 2021, 130, 106953. [Google Scholar] [CrossRef]
- Treider, T.; Høidalen, H. Estimating distance to transient and restriking earth faults in high-impedance grounded, ring-operated distribution networks using current ratios. Electr. Power Syst. Res. 2023, 224, 109765. [Google Scholar] [CrossRef]
- Penaloza, J.; Borghetti, A.; Napolitano, F.; Tossani, F. Performance analysis of a transient-based earth fault protection system for unearthed and compensated radial distribution networks. Electr. Power Syst. Res. 2021, 197, 107306. [Google Scholar] [CrossRef]
- Ghorbani, A.; Mehrjerdi, H. Accurate fault location algorithm for shunt-compensated double circuit transmission lines using single end data. Int. J. Electr. Power Energy Syst. 2020, 116, 105515. [Google Scholar] [CrossRef]
- Hossam, A.; Soliman, I.; Ahmed, E. Generalized wide-area fault detection and location algorithm for transmission system based on optimal PMUs allocation. Int. J. Electr. Power Energy Syst. 2024, 155, 109634. [Google Scholar]
- Li, C.; Wu, H.; Zhang, L.; Shan, H. Two-stage fault section location for distribution networks based on compressed sensing with estimated voltage measurements. Electr. Power Syst. Res. 2023, 223, 109702. [Google Scholar] [CrossRef]
- Liang, Y.; He, A.; Yuan, J. An accurate fault location method for distribution lines based on data fusion of outcomes from multiple algorithms. Int. J. Electr. Power Energy Syst. 2023, 153, 109290. [Google Scholar] [CrossRef]
- Mohammad, F.; Mahmood, J.; Alireza, S.; Mehdi, M. A single-ended traveling wave-based fault location method using DWT in hybrid parallel HVAC/HVDC overhead transmission lines on the same power. Electr. Power Syst. Res. 2023, 220, 109302. [Google Scholar]
- Bai, H. Single-phase grounding fault line selection method based on zero-sequence current increment. Energy Rep. 2022, 8, 305–312. [Google Scholar]
- Xu, D. A New Efficient Bidirectional T-Source Circuit Breaker for Flexible DC Distribution Networks. IEEE J. Emerg. Sel. Top. Power Electron. 2020, 9, 7056–7065. [Google Scholar]
- Xu, R.; Song, G.; Chang, Z. A ground fault section location method based on active detection approach for non-effectively grounded DC distribution networks. Int. J. Electr. Power Energy Syst. 2023, 152, 109174. [Google Scholar] [CrossRef]
- Wang, Z.; Leng, Y.; Qiu, X. Reconfigurable bandpass filter with flexible tuning of both center frequency and bandwidth. Int. J. Electron. Commun. 2024, 173, 155027. [Google Scholar] [CrossRef]
- Sergio, U.; Molina-Pineda, A. A center-of-gravity-based framework for small- and large-signal frequency analysis of interconnected power systems. Electr. Power Syst. Res. 2023, 223, 109677. [Google Scholar]
- Hussain, M.; Dhimish, M.; Titarenko, S. Artificial neural network based photovoltaic fault detection algorithm integrating two bi-directional input parameters. Renew. Energy 2020, 155, 1272–1292. [Google Scholar] [CrossRef]
- Guo, J.; Wang, X.; Ooi, B. Online purely data-driven estimation of inertia and center-of-inertia frequency for power systems with VSC-interfaced energy sources. Int. J. Electr. Power Energy Syst. 2022, 137, 107643. [Google Scholar] [CrossRef]
- Siddique, M.; Shafiullah, M.; Mekhilef, S. Fault classification and location of a PMU-equipped active distribution network using deep convolution neural network (CNN). Electr. Power Syst. Res. 2024, 229, 110178. [Google Scholar] [CrossRef]
- Mirshekali, H.; Dashti, R.; Keshavarz, A. A novel fault location methodology for smart distribution networks. IEEE Trans. Smart Grid 2020, 12, 1277–1288. [Google Scholar] [CrossRef]
- Mohammad, D.; Rahman, D.; Hamid, R. Fault location in power grids using substation voltage magnitude differences: A comprehensive technique for transmission lines, distribution networks, and AC/DC microgrids. Measurement 2023, 220, 113403. [Google Scholar]
- Vishal, K.; Bhavesh, R.; Ahmed, S. New ground fault location method for three-terminal transmission line using unsynchronized current measurements. Int. J. Electr. Power Energy Syst. 2022, 135, 107513. [Google Scholar]
- Tesfaye, A.; Thomas, T.; Lars, B. Two novel current-based methods for locating earth faults in unearthed ring operating MV networks. Electr. Power Syst. Res. 2022, 213, 108774. [Google Scholar]
- Ghaemi, A.; Safari, A.; Afsharirad, H. Accuracy enhance of fault classification and location in a smart distribution network based on stacked ensemble learning. Electr. Power Syst. Res. 2022, 205, 107766. [Google Scholar] [CrossRef]
- David, T.; Matti, L.; Petr, T. An earth fault location method based on negative sequence voltage changes at low voltage side of distribution transformers. Int. J. Electr. Power Energy Syst. 2020, 118, 105768. [Google Scholar]
- Askari, Q.; Saeed, M.; Younas, I. Heap-based optimizer inspired by corporate rank hierarchy for global optimization. ESA 2020, 161, 113702. [Google Scholar] [CrossRef]
- El-Rifaie, A.M.; Shaheen, A.M.; Tolba M, A. Modified Gradient-Based Algorithm for Distributed Generation and Capacitors Integration in Radial Distribution Networks. IEEE Access 2023, 11, 120899–120917. [Google Scholar] [CrossRef]


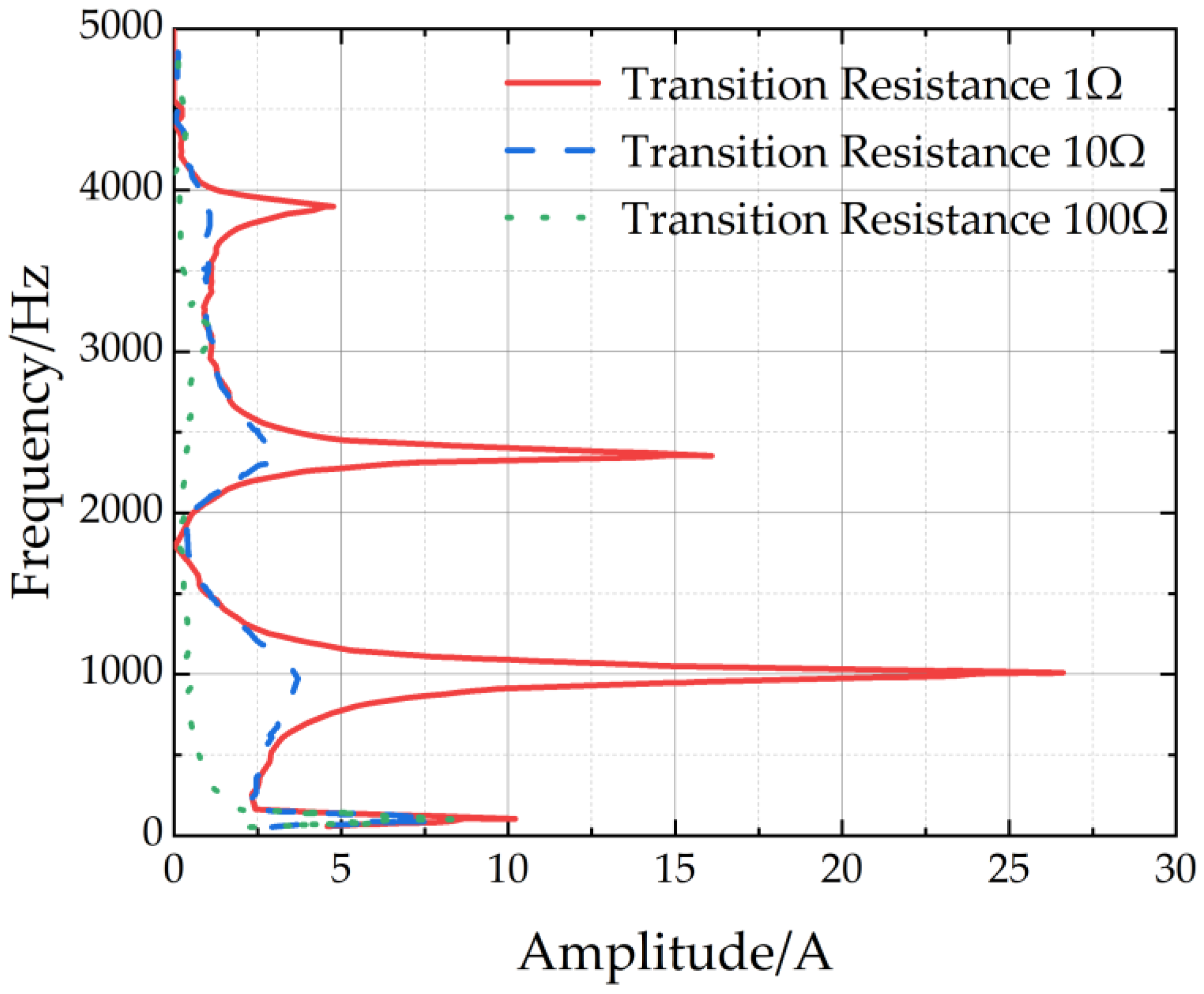
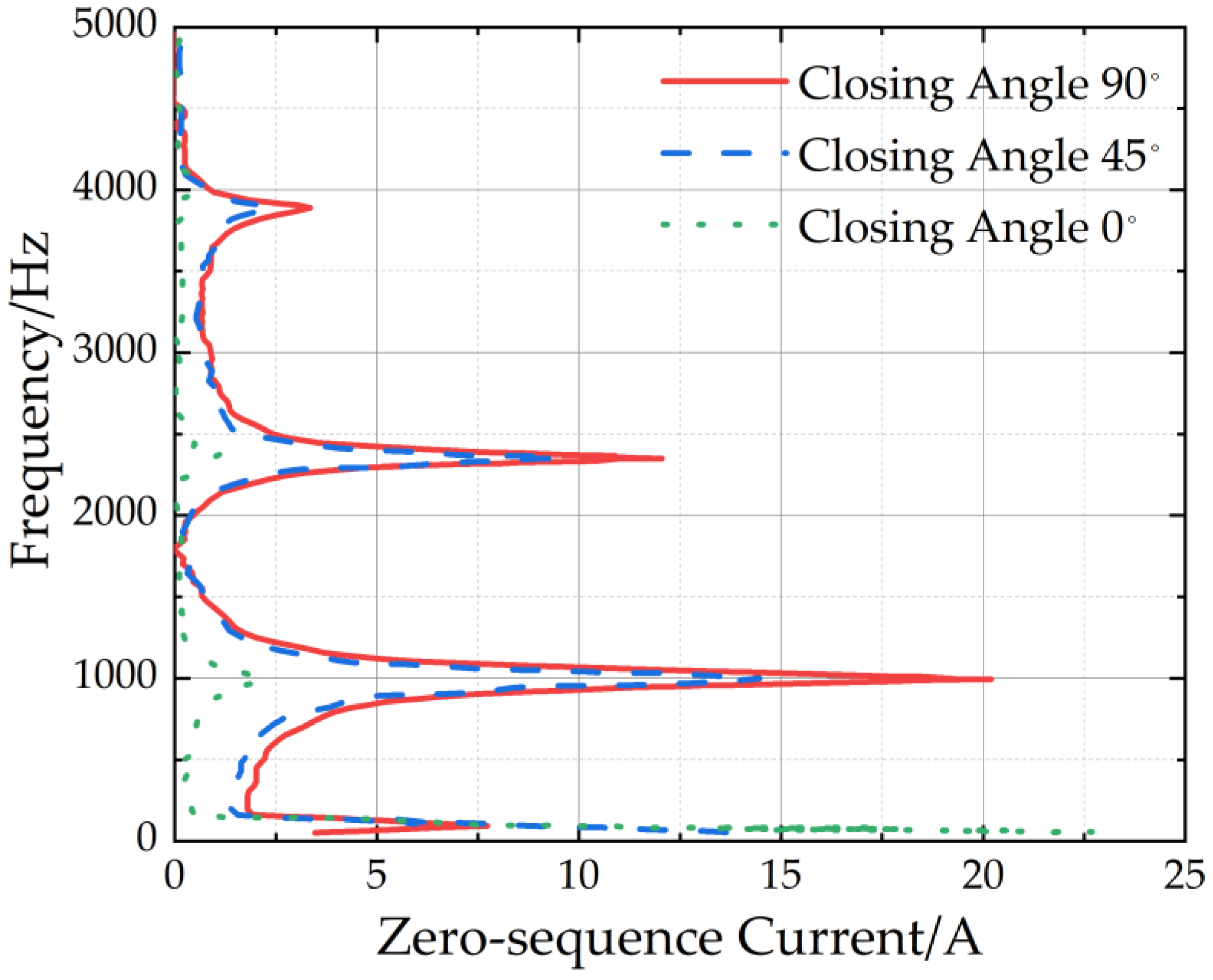

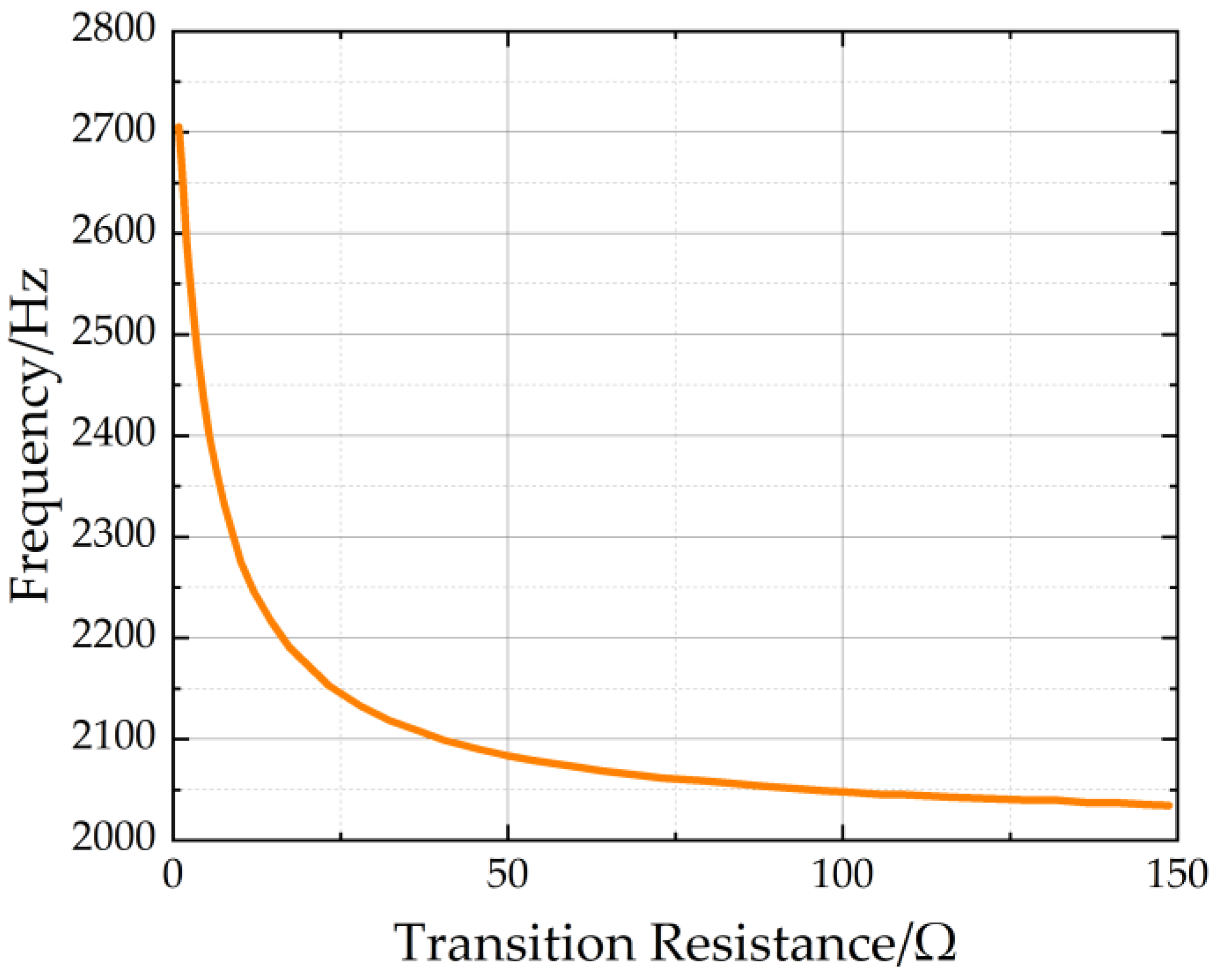



| Fault Condition | fG Results | λ Results | Results |
|---|---|---|---|
| Line 2, 2 km, 10 Ω, 90° | 2.03 km, 2.02 km | No | 2.025 km |
| Line 2, 3 km, 10 Ω, 90° | 3.02 km, 3.01 km | No | 3.015 km |
| Line 2, 1.5 km, 50 Ω, 90° | 1.53 km, 2.8 km | 1.44 km, 3.41 km | 1.485 km |
| Line 2, 2 km, 50 Ω, 90° | 1.87 km, 2.2 km | No | 2.035 km |
| Line 2, 4 km, 50 Ω, 90° | 3.96 km, 3.97 km | No | 3.965 km |
| Line 5, 1.5 km, 45 Ω, 90° | 1.48 km, 1.49 km | No | 1.485 km |
| Line 3, 6 km, 25 Ω, 90° | 6.01 km, 6.02 km | No | 6.015 km |
| Line 1, 2.5 km, 10 Ω, 60° | 2.54 km, 2.51 km | No | 2.525 km |
| Line 1, 6.4 km, 10 Ω, 60° | 6.35 km, 6.37 km | No | 6.36 km |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, R.; Lu, J.; Chen, Q.; Zhou, N.; Liu, H. Application of a Centroid Frequency-Based Back Propagation Neural Network Fault Location Method for a Distribution Network Considering Renewable Energy Assessment. Electronics 2024, 13, 1491. https://doi.org/10.3390/electronics13081491
Zhao R, Lu J, Chen Q, Zhou N, Liu H. Application of a Centroid Frequency-Based Back Propagation Neural Network Fault Location Method for a Distribution Network Considering Renewable Energy Assessment. Electronics. 2024; 13(8):1491. https://doi.org/10.3390/electronics13081491
Chicago/Turabian StyleZhao, Ruifeng, Jiangang Lu, Qizhan Chen, Niancheng Zhou, and Haoyu Liu. 2024. "Application of a Centroid Frequency-Based Back Propagation Neural Network Fault Location Method for a Distribution Network Considering Renewable Energy Assessment" Electronics 13, no. 8: 1491. https://doi.org/10.3390/electronics13081491
APA StyleZhao, R., Lu, J., Chen, Q., Zhou, N., & Liu, H. (2024). Application of a Centroid Frequency-Based Back Propagation Neural Network Fault Location Method for a Distribution Network Considering Renewable Energy Assessment. Electronics, 13(8), 1491. https://doi.org/10.3390/electronics13081491





