A Nonlinear Subspace Predictive Control Approach Based on Locally Weighted Projection Regression
Abstract
:1. Introduction
- (1)
- Seamless integration of LWPR and SPC: The LWPR algorithm and the SPC method are seamlessly integrated for industrial process control. By projecting the input space into localized regions, constructing precise local models, and aggregating them through weighted summation, the proposed approach effectively addresses the complex nonlinear relationships in industrial processes.
- (2)
- Enhanced adaptability and efficiency: The proposed approach constructs the controller from the trained regression model. This implies that it can adapt the control strategy using online process data and local model parameters. In addition, it removes the necessity for storing offline process data. These advancements highlight improvements in both adaptability and efficiency.
- (3)
- Improved predictive and tracking performance: The proposed approach shows improvements in both predictive and tracking performance. It creates an accurate predictive model by capturing the dynamic characteristics of the system from input/output (I/O) data. This boosts the accuracy of the predictive controller, especially during transitions from nonlinear to steady-state processes. The increased prediction accuracy also greatly enhances the tracking performance of the predictive controller. In situations where the expected output of the nonlinear process changes, the controlled system adjusts smoothly to match the projected output path, ensuring consistent and smooth tracking.
2. Preliminaries
2.1. Subspace Predictor
2.2. LWPR Learning Scheme
3. Locally Weighted Projection Regression-Based Subspace Predictive Control
3.1. Controller Design
| Algorithm 1 The proposed NSPC-LWPR approach. |
|
3.2. Parameters Determination Criteria
3.2.1. and
3.2.2. and
3.2.3. and
3.3. Theoretical Analysis
4. Benchmark Study on Continuous Stirred Tank Heater
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Dong, Y.; Lang, Z.Q.; Zhao, J.; Wang, W.; Lan, Z. A Novel Data-Driven Approach to Analysis and Optimal Design of Forced Periodic Operation of Chemical Reactions. IEEE Trans. Ind. Electron. 2023, 70, 8365–8376. [Google Scholar] [CrossRef]
- Wen, S.; Guo, G. Distributed Trajectory Optimization and Sliding Mode Control of Heterogenous Vehicular Platoons. IEEE Trans. Intell. Transp. Syst. 2022, 23, 7096–7111. [Google Scholar] [CrossRef]
- Du, S.; Wu, M.; Chen, X.; Cao, W. An Intelligent Control Strategy for Iron Ore Sintering Ignition Process Based on the Prediction of Ignition Temperature. IEEE Trans. Ind. Electron. 2020, 67, 1233–1241. [Google Scholar] [CrossRef]
- Li, S.; Zheng, Y.; Li, S.; Huang, M. Data-Driven Modeling and Operation Optimization with Inherent Feature Extraction for Complex Industrial Processes. IEEE Trans. Autom. Sci. Eng. 2023, 21, 1092–1106. [Google Scholar] [CrossRef]
- Zhou, P.; Zhang, S.; Wen, L.; Fu, J.; Chai, T.; Wang, H. Kalman Filter-Based Data-Driven Robust Model-Free Adaptive Predictive Control of a Complicated Industrial Process. IEEE Trans. Autom. Sci. Eng. 2022, 19, 788–803. [Google Scholar] [CrossRef]
- Ren, L.; Meng, Z.; Wang, X.; Zhang, L.; Yang, L.T. A Data-Driven Approach of Product Quality Prediction for Complex Production Systems. IEEE Trans. Ind. Inform. 2021, 17, 6457–6465. [Google Scholar] [CrossRef]
- Harbaoui, H.; Khalfallah, S. An Effective Optimization Approach to Minimize Waste in a Complex Industrial System. IEEE Access 2022, 10, 13997–14012. [Google Scholar] [CrossRef]
- Mehrtash, M.; Capitanescu, F.; Heiselberg, P.K.; Gibon, T. A New Bi-Objective Approach for Optimal Sizing of Electrical and Thermal Devices in Zero Energy Buildings Considering Environmental Impacts. IEEE Trans. Sustain. Energy 2021, 12, 886–896. [Google Scholar] [CrossRef]
- Zhang, F.; Kodituwakku, H.A.D.E.; Hines, J.W.; Coble, J. Multilayer Data-Driven Cyber-Attack Detection System for Industrial Control Systems Based on Network, System, and Process Data. IEEE Trans. Ind. Inform. 2019, 15, 4362–4369. [Google Scholar] [CrossRef]
- Kang, E.; Qiao, H.; Chen, Z.; Gao, J. Tracking of Uncertain Robotic Manipulators Using Event-Triggered Model Predictive Control With Learning Terminal Cost. IEEE Trans. Autom. Sci. Eng. 2022, 19, 2801–2815. [Google Scholar] [CrossRef]
- Choi, W.Y.; Lee, S.H.; Chung, C.C. Horizonwise Model-Predictive Control With Application to Autonomous Driving Vehicle. IEEE Trans. Ind. Inform. 2022, 18, 6940–6949. [Google Scholar] [CrossRef]
- Oshnoei, A.; Kheradmandi, M.; Khezri, R.; Mahmoudi, A. Robust Model Predictive Control of Gate-Controlled Series Capacitor for LFC of Power Systems. IEEE Trans. Ind. Inform. 2021, 17, 4766–4776. [Google Scholar] [CrossRef]
- Shang, C.; You, F. A data-driven robust optimization approach to scenario-based stochastic model predictive control. J. Process Control 2019, 75, 24–39. [Google Scholar] [CrossRef]
- Yao, L.; Shao, W.; Ge, Z. Hierarchical Quality Monitoring for Large-Scale Industrial Plants With Big Process Data. IEEE Trans. Neural Netw. Learn. Syst. 2021, 32, 3330–3341. [Google Scholar] [CrossRef] [PubMed]
- Han, H.; Fu, S.; Sun, H.; Qiao, J. Data-Driven Multimodel Predictive Control for Multirate Sampled-Data Nonlinear Systems. IEEE Trans. Autom. Sci. Eng. 2023, 20, 2182–2194. [Google Scholar] [CrossRef]
- Habib, M.; Wang, Z.; Qiu, S.; Zhao, H.; Murthy, A.S. Machine Learning Based Healthcare System for Investigating the Association Between Depression and Quality of Life. IEEE J. Biomed. Health Inform. 2022, 26, 2008–2019. [Google Scholar] [CrossRef]
- Sun, Q.; Ge, Z. A Survey on Deep Learning for Data-Driven Soft Sensors. IEEE Trans. Ind. Inform. 2021, 17, 5853–5866. [Google Scholar] [CrossRef]
- Xue, W.; Fan, J.; Lopez, V.G.; Li, J.; Jiang, Y.; Chai, T.; Lewis, F.L. New Methods for Optimal Operational Control of Industrial Processes Using Reinforcement Learning on Two Time Scales. IEEE Trans. Ind. Inform. 2020, 16, 3085–3099. [Google Scholar] [CrossRef]
- Kadali, R.; Huang, B.; Rossiter, A. A data driven subspace approach to predictive controller design. Control Eng. Pract. 2003, 11, 261–278. [Google Scholar] [CrossRef]
- Li, Z.; Wang, H.; Fang, Q.; Wang, Y. A data-driven subspace predictive control method for air-cooled data center thermal modelling and optimization. J. Frankl. Inst. 2023, 360, 3657–3676. [Google Scholar] [CrossRef]
- Navalkar, S.T.; van Solingen, E.; van Wingerden, J.W. Wind Tunnel Testing of Subspace Predictive Repetitive Control for Variable Pitch Wind Turbines. IEEE Trans. Control Syst. Technol. 2015, 23, 2101–2116. [Google Scholar] [CrossRef]
- Zhang, X.; Zhang, L.; Zhang, Y. Model Predictive Current Control for PMSM Drives With Parameter Robustness Improvement. IEEE Trans. Power Electron. 2019, 34, 1645–1657. [Google Scholar] [CrossRef]
- Wahab, N.A.; Katebi, R.; Balderud, J.; Rahmat, M.F. Data-driven adaptive model-based predictive control with application in wastewater systems. Control Theory Appl. IET 2010, 5, 803–812. [Google Scholar] [CrossRef]
- Vajpayee, V.; Mukhopadhyay, S.; Tiwari, A.P. Data-Driven Subspace Predictive Control of a Nuclear Reactor. IEEE Trans. Nucl. Sci. 2018, 65, 666–679. [Google Scholar] [CrossRef]
- Hallouzi, R.; Verhaegen, M. Fault-Tolerant Subspace Predictive Control Applied to a Boeing 747 Model. J. Guid. Control Dyn. 2008, 31, 873–883. [Google Scholar] [CrossRef]
- Zhou, P.; Zhang, S.; Dai, P. Recursive Learning-Based Bilinear Subspace Identification for Online Modeling and Predictive Control of a Complicated Industrial Process. IEEE Access 2020, 8, 62531–62541. [Google Scholar] [CrossRef]
- Zhou, P.; Song, H.; Wang, H.; Chai, T. Data-Driven Nonlinear Subspace Modeling for Prediction and Control of Molten Iron Quality Indices in Blast Furnace Ironmaking. IEEE Trans. Control Syst. Technol. 2017, 25, 1761–1774. [Google Scholar] [CrossRef]
- Luo, X.S.; Song, Y.D. Data-driven predictive control of Hammerstein–Wiener systems based on subspace identification. Inf. Sci. 2018, 422, 447–461. [Google Scholar] [CrossRef]
- Vijayakumar, S.; D’Souza, A.; Schaal, S. Incremental Online Learning in High Dimensions. Neural Comput. 2006, 17, 2602–2634. [Google Scholar] [CrossRef]
- Ferranti, F.; Rolain, Y. A local identification method for linear parameter-varying systems based on interpolation of state-space matrices and least-squares approximation. Mech. Syst. Signal Process. 2017, 82, 478–489. [Google Scholar] [CrossRef]
- De Caigny, J.; Camino, J.F.; Swevers, J. Interpolating model identification for SISO linear parameter-varying systems. Mech. Syst. Signal Process. 2009, 23, 2395–2417. [Google Scholar] [CrossRef]
- Felici, F.; van Wingerden, J.W.; Verhaegen, M. Subspace identification of MIMO LPV systems using a periodic scheduling sequence. Automatica 2007, 43, 1684–1697. [Google Scholar] [CrossRef]
- Favoreel, W.; Moor, B.D.; Gevers, M. SPC: Subspace Predictive Control. IFAC Proc. Vol. 1999, 32, 4004–4009. [Google Scholar] [CrossRef]
- Atkeson, C.G.; Schaal, M.S. Locally Weighted Learning. Artif. Intell. Rev. 1997, 11, 11–73. [Google Scholar] [CrossRef]
- Thornhill, N.F.; Patwardhan, S.C.; Shah, S.L. A continuous stirred tank heater simulation model with applications. J. Process Control 2008, 18, 347–360. [Google Scholar] [CrossRef]
- Johansson, R. Numerical Python: Scientific Computing and Data Science Applications with Numpy, SciPy and Matplotlib; Apress: New York, NY, USA, 2019. [Google Scholar]
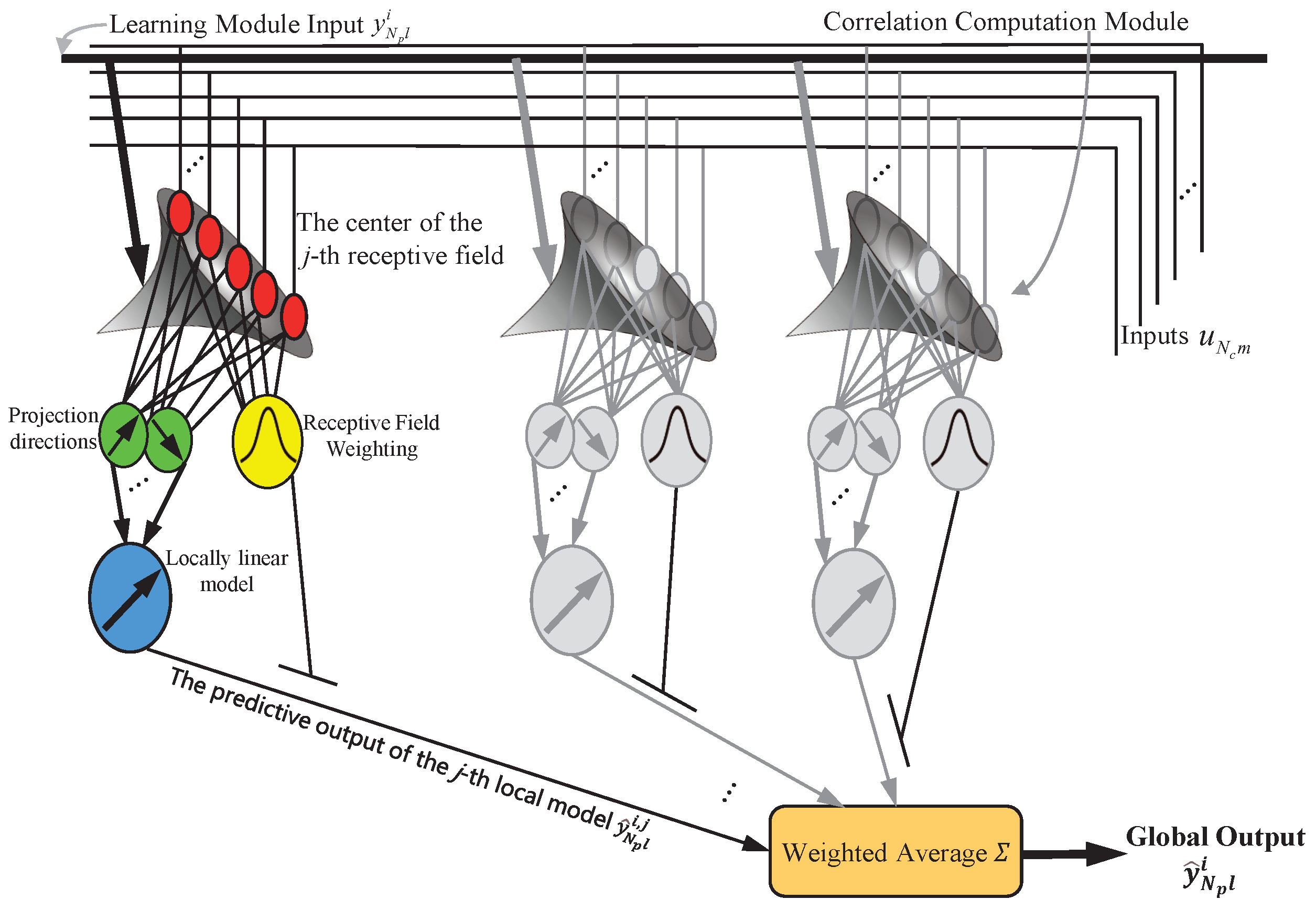

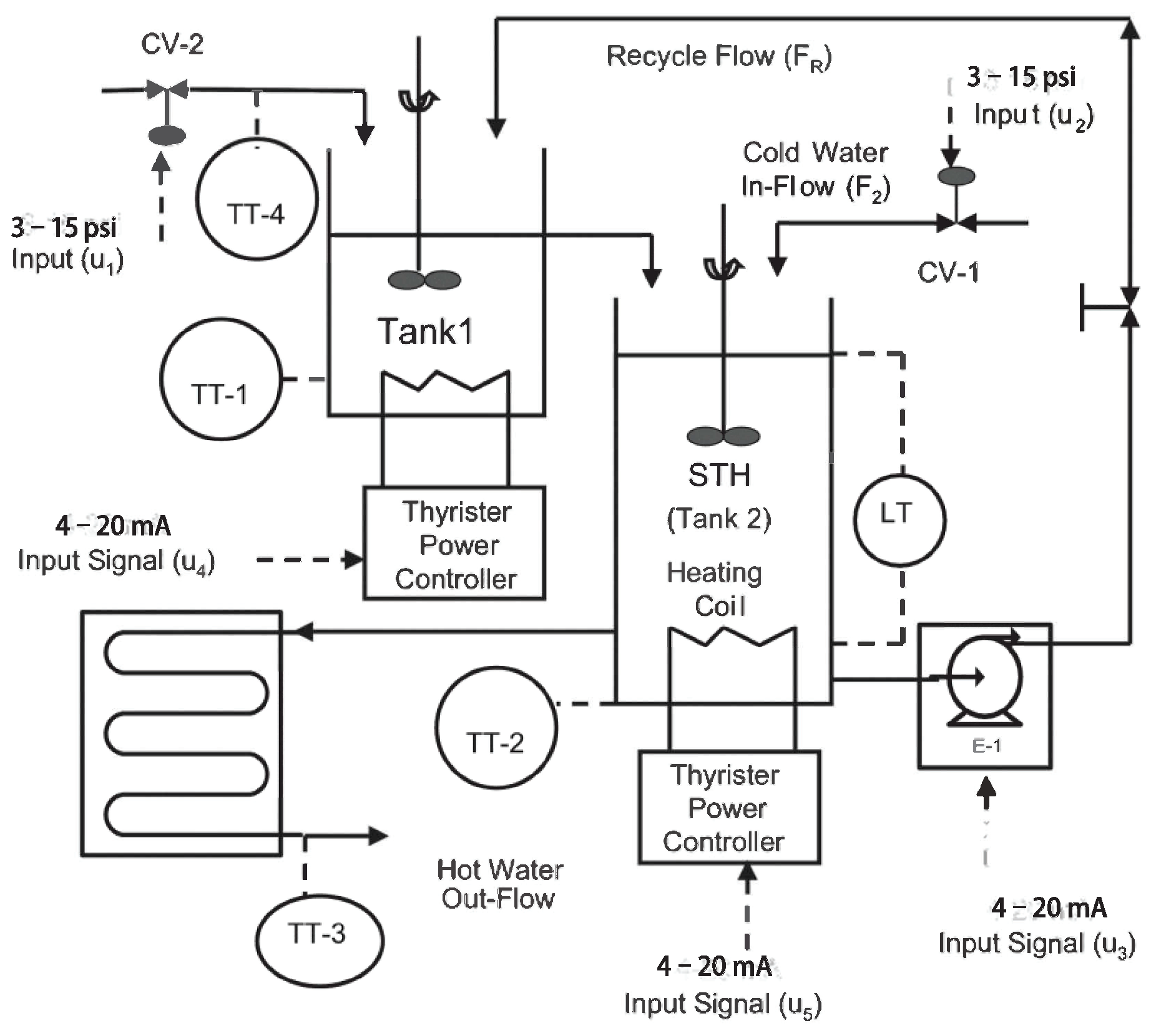
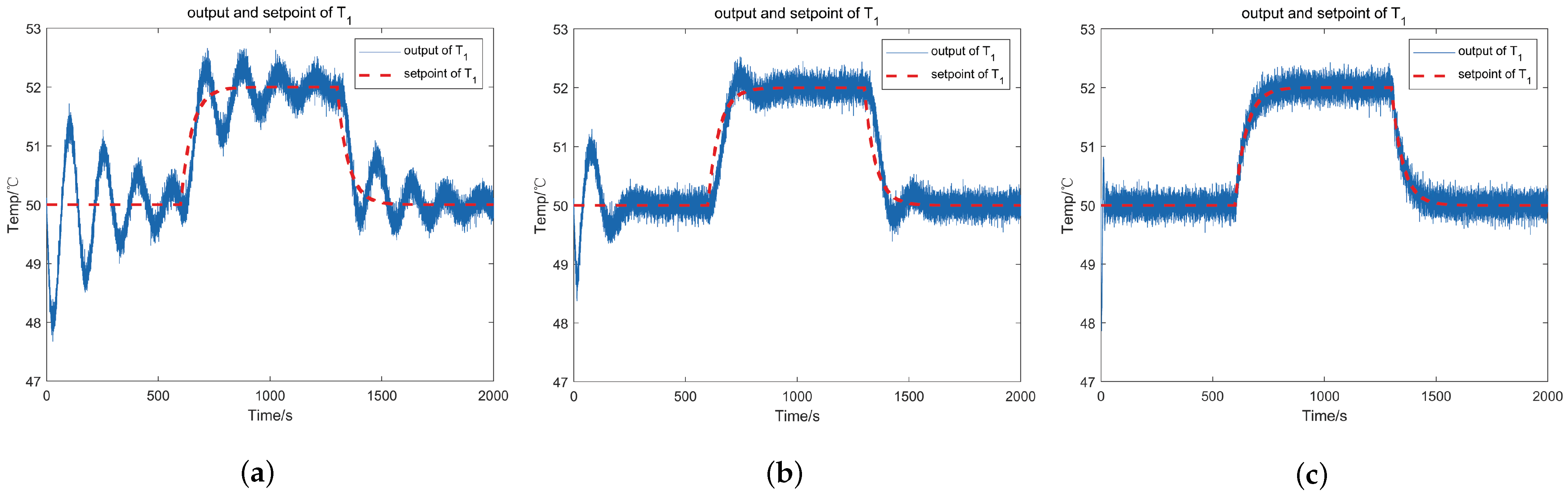
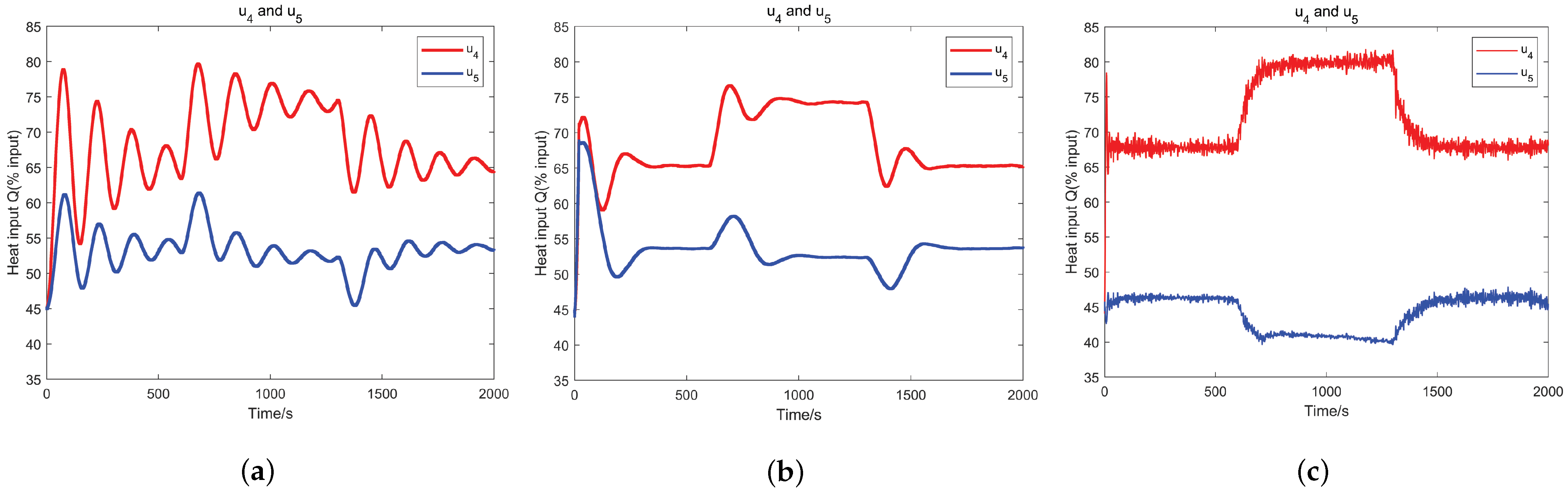

| 1. Initialization: (number of training samples seen ) |
| 2. Incorporating new data: Given training point(x,y) |
| 2a. Compute activation and update the means |
| 1. |
| 2.; |
| 2b. Compute the current prediction error |
| Repeat for (projections) |
| 2c. Update the local model |
| Repeat for (projections) |
| 2c.1 Update the local regression and compute residuals |
| 2c.2 Update the projection directions |
| Notation | Description |
|---|---|
| N | Number of training data points |
| M | Number of local models |
| R | Number of local projections |
| rth element of the lower-dimensional projection of input data x | |
| rth projection direction | |
| Regressed input space to be subtracted to maintain orthogonality of projection directions | |
| W | Diagonal weight matrix representing the activation due to all samples |
| rth component of slope of the local linear model | |
| Forgetting factor used to exclude data and accelerate the learning process | |
| Mean square error of the nth sample in the rth projection | |
| Sufficient statistics for incremental computation of rth dimension of variable var after seeing n data points |
| Method | MPC | SPC | ASPC | NSPC-LWPR |
|---|---|---|---|---|
| Approach Type | model-based | data-driven | data-driven | data-driven |
| Prior Knowledge | model information | off-line process data | no need | no need |
| Dynamic Ability | able | unable | able | able |
| Controller Type | fixed; linear | fixed; linear | unfixed; linear | unfixed; nonlinear |
| Parameter | Description | Value |
|---|---|---|
| Volume of tank 1 | ||
| Cross sectional area of tank 2 | ||
| Radius of tank 2 | m | |
| U | Heat transfer coefficient | W/K |
| Cooling water temperature | 30 °C | |
| Atmospheric temperature | 25 °C | |
| Flow (% Input) | ||
| Flow (% Input) | ||
| Flow (% Input) | ||
| Heat input (% Input) | ||
| Heat input (% Input) | ||
| Steady state temperature (tank 1) | 49.77 °C | |
| Steady state temperature (tank 2) | 52.92 °C | |
| Steady state level | m |
| Parameter | |||||||
|---|---|---|---|---|---|---|---|
| Value | 1 | 2 | 10 | 5 | 3 | 4 | 10 Hz |
| Control Methods | |||||
|---|---|---|---|---|---|
| SPC | 1.5429 | 1.2649 | 1.0923 | 0.9732 | 0.8983 |
| ASPC | 0.1321 | 0.1147 | 0.1026 | 0.0934 | 0.0896 |
| NSPC-LWPR | 0.0946 | 0.0845 | 0.0740 | 0.0711 | 0.0661 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, X.; Yang, X. A Nonlinear Subspace Predictive Control Approach Based on Locally Weighted Projection Regression. Electronics 2024, 13, 1670. https://doi.org/10.3390/electronics13091670
Wu X, Yang X. A Nonlinear Subspace Predictive Control Approach Based on Locally Weighted Projection Regression. Electronics. 2024; 13(9):1670. https://doi.org/10.3390/electronics13091670
Chicago/Turabian StyleWu, Xinwei, and Xuebo Yang. 2024. "A Nonlinear Subspace Predictive Control Approach Based on Locally Weighted Projection Regression" Electronics 13, no. 9: 1670. https://doi.org/10.3390/electronics13091670
APA StyleWu, X., & Yang, X. (2024). A Nonlinear Subspace Predictive Control Approach Based on Locally Weighted Projection Regression. Electronics, 13(9), 1670. https://doi.org/10.3390/electronics13091670






