Virtual Inertia Methods for Supporting Frequency Stabilisation in Autonomous AC/DC Microgrids
Abstract
1. Introduction
2. The Proposed Structure of the Microgrid
3. VSC Network Connection Power Model
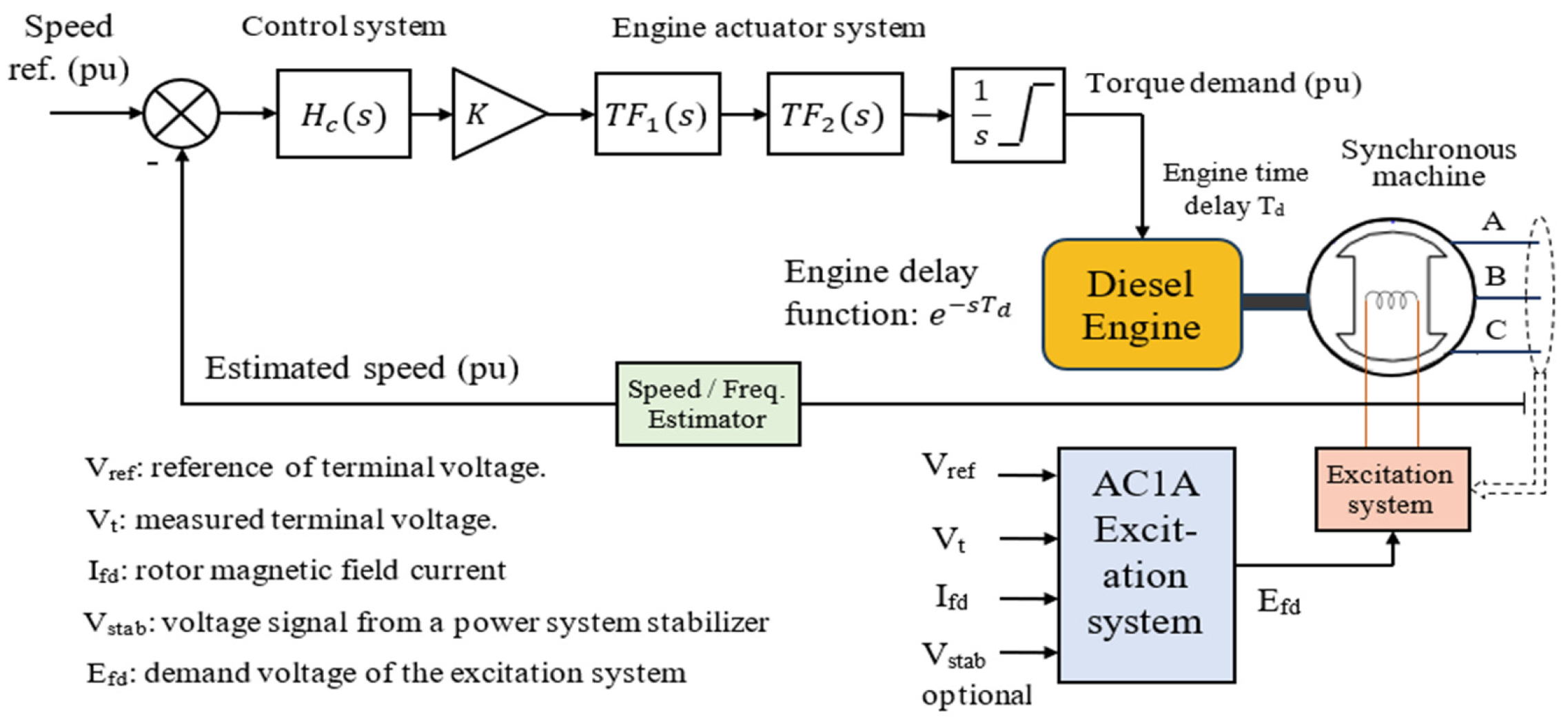
4. The Electromechanical Power-Speed Model
5. Model Linearisation and System Analysis
6. The Proposed Methods for Frequency Support
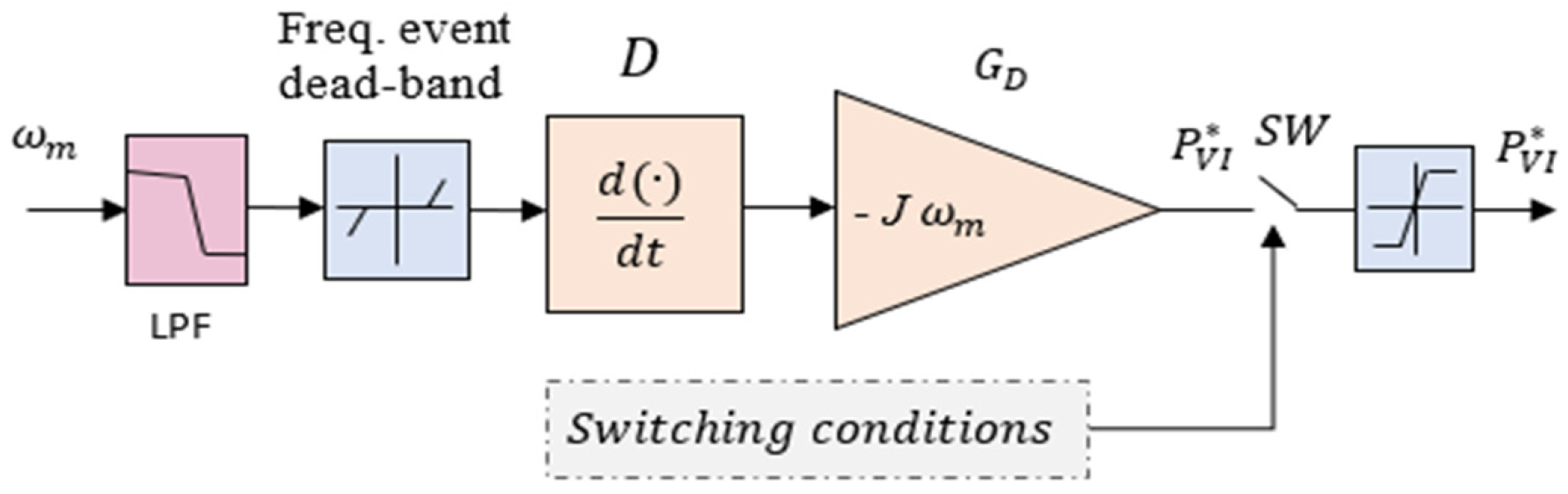
6.1. The Model-Based Virtual Inertia Method
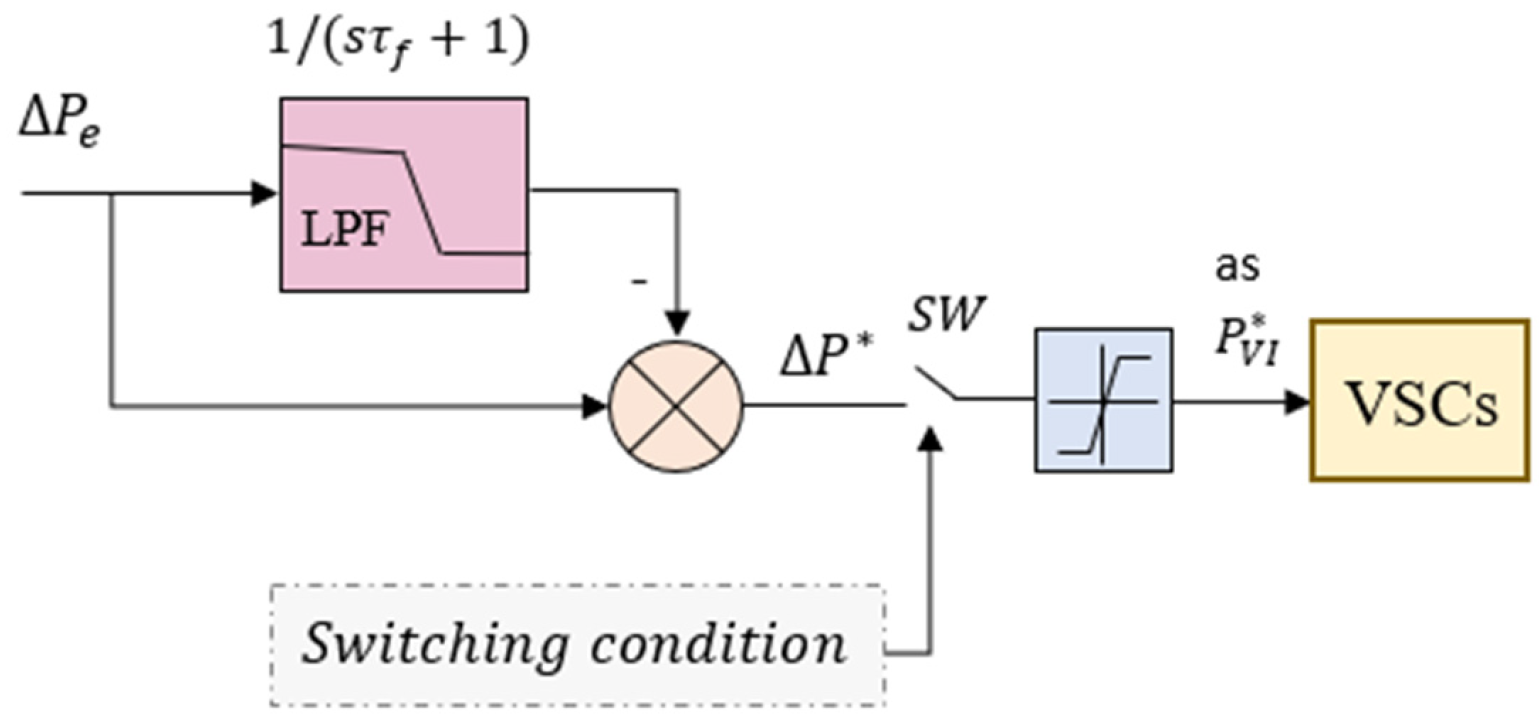
6.2. The Filter-Based Virtual Inertia Method
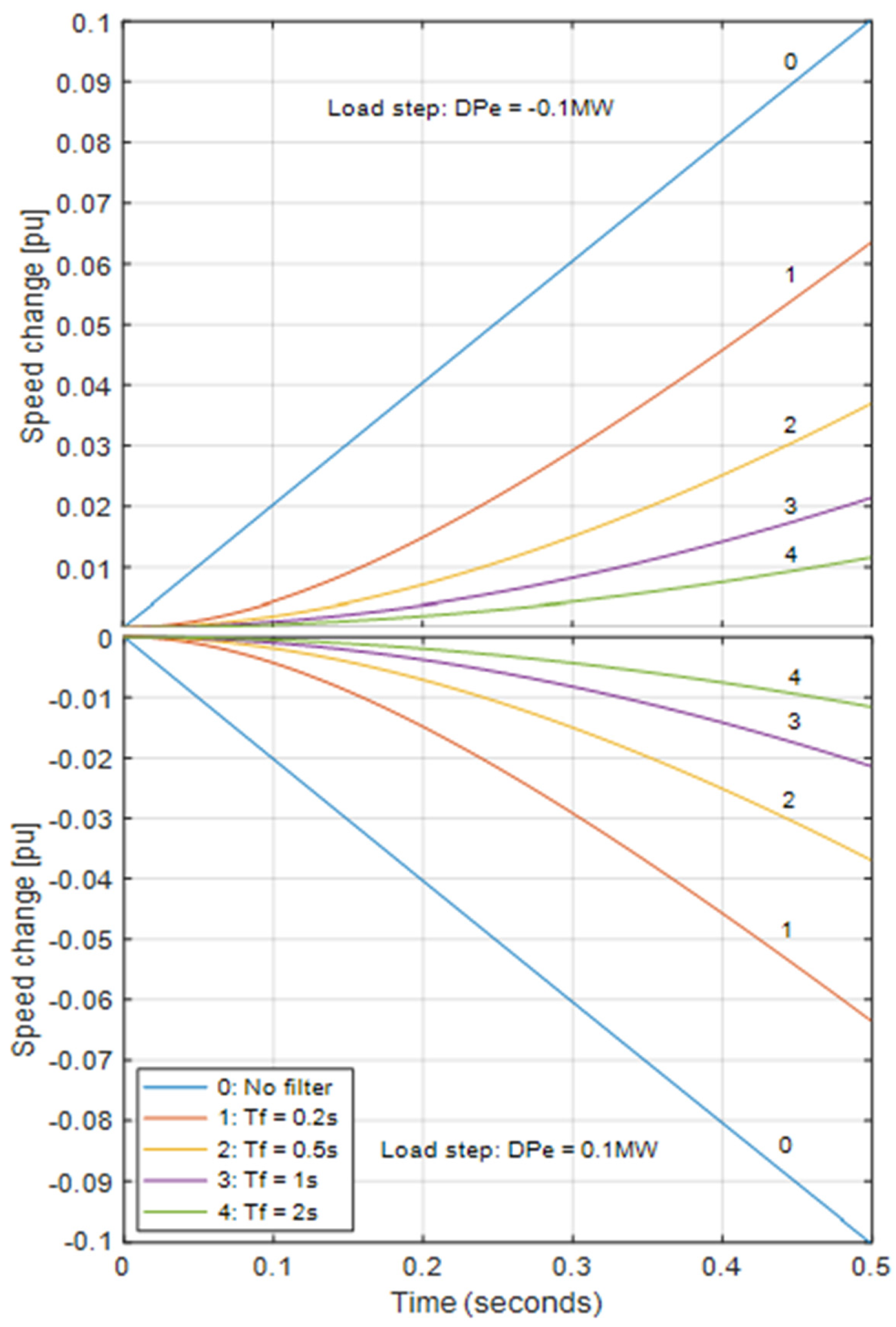
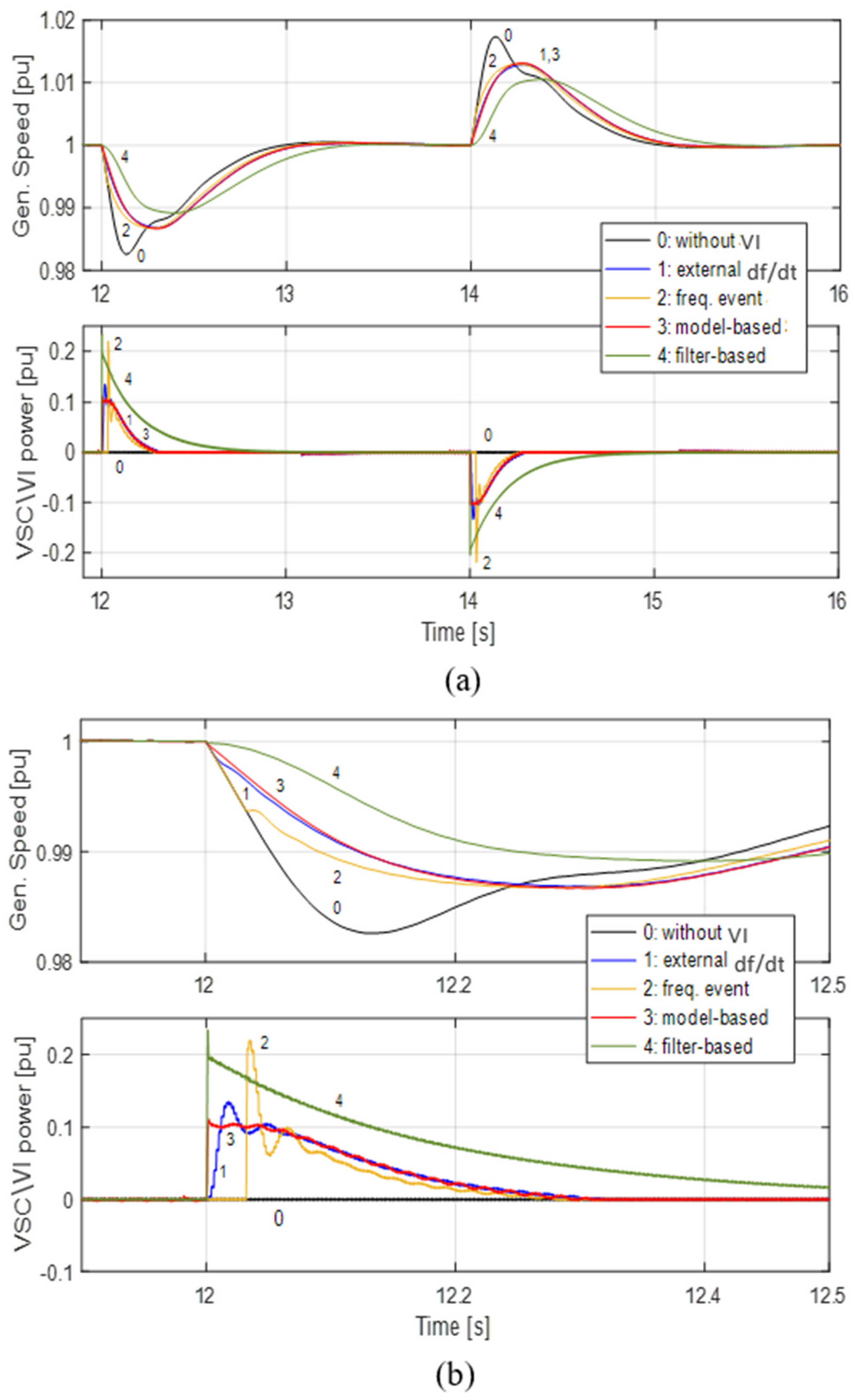
7. System Simulation and Test Results
8. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| BESS | Battery energy storage system |
| DEG | Diesel engine generator |
| DER | Distributed energy resource |
| ESS | Energy storage system |
| IGBT | Integrated gate bipolar transistor |
| LPF | Low pass filter |
| NPC | Neutral point clamping |
| OP | Operating point |
| PCC | Point of common coupling |
| PE | Power electronic |
| PV | Photovoltaic |
| PWM | Pulse width modulation |
| RES | Renewable energy source |
| SI | Synthetic inertia |
| VI | Virtual inertia |
| VSC | Voltage source converter |
| Generator inertia constant [s] | |
| DEG moment of inertia [kg.m2] | |
| Connection circuit inductance [Henry] | |
| Equivalent VSC connection inductance [Henry] | |
| DEG pole pair number | |
| VSC active power [W] | |
| Generator accelerating power [W] | |
| Load electrical power [W] | |
| Power losses of the generators [W] | |
| Mechanical power of the generator engines [W] | |
| VSC reactive power [VAr] | |
| Connection circuit resistance [Ohm] | |
| Equivalent VSC connection resistance [Ohm] | |
| Apparent total power vector of the VSCs [VA] | |
| DEG rated power [VA] | |
| Filter time constant [s] | |
| Per-phase voltage magnitude at the PCC [V] | |
| d- and q-axis voltage components at the PCC [V] | |
| Equivalent time constant of the connected VSCs [s] | |
| Microgrid/system angular frequency [rad/s] | |
| Speed of the DEG [rad/s] |
Appendix A
- The per-unit (PU) base system
- Base diesel genset power: 1 MVA
- Base VSC power: 500 kVA
- Base DC-link voltage Vdc: 1 kV
- Base network phase voltage: 240 V
- Base network phase current: 1380 A
- Base genset speed: 50·π rad/s
- Voltage Source Converter (VSC)
- Type: three-phase, three-level, neutral point clamping
- DC voltage bus: 1000 V
- Nominal line voltage: 415 V
- Total nominal power: 0.5 MVA
- Switching frequency Fc: 2250 Hz
- Equivalent connection inductance
- Equivalent connection resistance
- Diesel genset unit
- Nominal line voltage: 415 V
- Speed: 1500 rpm
- Nominal frequency: 50 Hz
- Nominal power: 0.5 MVA
- Generator Inertia Constant H: 0.247 s
- Mechanical moment of inertia J: 10 kg/m2
- Considered average power losses Pls: 10 kW.
- Generator constant
- Speed governor control functions and parameters:
- ,
- ,
- ,
- ,
- .
Appendix B
- Calculation for RLC components of network single-tuned shunt-filter
- Tuning frequency: ,
- Filter quality factor: ,
- Filter frequency bandwidth: ,
- Generated reactive power at fundamental (grid) frequency : where and is the nominal applied voltage to the filter terminals.
- Filter designed at equivalent to four times of the converter switching frequency :
- Given per-phase (Y connected three-phase filter), , , , and considering , gives: , ; reduced impedance at a frequency equivalent to four times the converter switching frequency due to parallel connection of four interleaved converters.
References
- Hatziargyriou, N.; Asano, H.; Iravani, R.; Marnay, C. Microgrids. IEEE Power Energy Mag. 2007, 5, 78–94. [Google Scholar] [CrossRef]
- Hirsch, A.; Parag, Y.; Guerrero, J. Microgrids: A review of technologies, key drivers, and outstanding issues. Renew. Sustain. Energy Rev. 2018, 90, 402–411. [Google Scholar] [CrossRef]
- AbdelHady, R. Modeling and simulation of a micro grid-connected solar PV system. Water Sci. 2017, 31, 1–10. [Google Scholar] [CrossRef]
- Yukita, K. AC/DC microgrids. In Integration of Distributed Energy Resources in Power Systems: Implementation, Operation and Control; Funabashi, T., Ed.; Academic Press: Cambridge, MA, USA, 2016; pp. 236–260. [Google Scholar]
- Jiang, Q.; Xue, M.; Geng, G. Energy Management of Microgrid in Grid-Connected and Stand-Alone Modes. IEEE Trans Power Syst. 2013, 28, 3380–3389. [Google Scholar] [CrossRef]
- Ortiz, L.; Orizondo, R.; Águila, A.; González, J.W.; López, G.J.; Isaac, I. Hybrid AC/DC microgrid test system simulation: Grid-connected mode. Heliyon 2019, 5, e02862. [Google Scholar] [CrossRef] [PubMed]
- Navarro-Rodríguez, Á.; García, P.; Gómez-Aleixandre, C.; Blanco, C. Cooperative Primary Control of a Hybrid AC/DC Microgrid Based on AC/DC Virtual Generators. IEEE Trans. Energy Convers. 2022, 37, 2837–2850. [Google Scholar] [CrossRef]
- Hu, J.; Shan, Y.; Xu, Y.; Guerrero, J.M. A coordinated control of hybrid ac/dc microgrids with PV-wind-Battery under variable generation and load conditions. Int. J. Electr. Power Energy Syst. 2019, 104, 583–592. [Google Scholar] [CrossRef]
- Mahmoud, M. (Ed.) MICROGRID—Advanced Control Methods and Renewable Energy System Integration, 1st ed.; Butterworth-Heinemann: Oxford, UK, 2016; ISBN 9780081017531. [Google Scholar]
- Chen, Y.; Zhao, S.; Li, Z.; Wei, X.; Kang, Y. Modeling and Control of the Isolated DC–DC Modular Multilevel Converter for Electric Ship Medium Voltage Direct Current Power System. IEEE J. Emerg. Sel. Top. Power Electron. 2017, 5, 124–139. [Google Scholar] [CrossRef]
- Eajal, A.A.; Shaaban, M.F.; Ponnambalam, K.; El-Saadany, E.F. Stochastic Centralized Dispatch Scheme for AC/DC Hybrid Smart Distribution Systems. IEEE Trans. Sustain. Energy 2016, 7, 1046–1059. [Google Scholar] [CrossRef]
- Khatibi, M.; Ahmed, S. Impact of Distributed Energy Resources on Frequency Regulation of the Bulk Power System. In Proceedings of the IEEE Conference on Power Electronics and Renewable Energy (CPERE), Aswan, Egypt, 23–25 October 2019. [Google Scholar] [CrossRef]
- Bose, U.; Chattopadhyay, S.K.; Chakraborty, C.; Pal, B. A Novel Method of Frequency Regulation in Microgrid. IEEE Trans. Ind. Appl. 2019, 55, 111–121. [Google Scholar] [CrossRef]
- Zhang, Y.; Sun, Q.; Zhou, J.; Li, L.; Wang, P.; Guerrero, J.M. Coordinated Control of Networked AC/DC Microgrids With Adaptive Virtual Inertia and Governor-Gain for Stability Enhancement. IEEE Trans. Energy Convers. 2021, 36, 95–110. [Google Scholar] [CrossRef]
- Rapizza, M.R.; Canevese, S.M. Fast frequency regulation and synthetic inertia in a power system with high penetration of renewable energy sources: Optimal design of the required quantities. Sustain. Energy Grids Netw. 2020, 24, 100407. [Google Scholar] [CrossRef]
- Skiparev, V.; Machlev, R.; Chowdhury, N.R.; Levron, Y.; Petlenkov, E.; Belikov, J. Virtual Inertia Control Methods in Islanded Microgrids. Energies 2021, 14, 1562. [Google Scholar] [CrossRef]
- Mandal, R.; Chatterjee, K. Virtual inertia emulation and RoCoF control of a microgrid with high renewable power penetration. Electr. Power Syst. Res. 2021, 194, 107093. [Google Scholar] [CrossRef]
- Kerdphol, T.; Rahman, F.S.; Watanabe, M.; Mitani, Y. Robust Virtual Inertia Control of a Low Inertia Microgrid Considering Frequency Measurement Effects. IEEE Access 2019, 7, 57550–57560. [Google Scholar] [CrossRef]
- Ali, H.; Magdy, G.; Li, B.; Shabib, G.; Elbaset, A.A.; Xu, D.; Mitani, Y. A New Frequency Control Strategy in an Islanded Microgrid Using Virtual Inertia Control-Based Coefficient Diagram Method. IEEE Access 2019, 7, 16979–16990. [Google Scholar] [CrossRef]
- Fini, M.H.; Hamedani Golshan, M.E. Determining optimal virtual inertia and frequency control parameters to preserve the frequency stability in islanded microgrids with high penetration of renewables. Electr. Power Syst. Res. 2018, 154, 13–22. [Google Scholar] [CrossRef]
- Farmer, W.J.; Rix, A.J. Optimising Power System Frequency Stability Using Virtual Inertia from Inverter-based Renewable Energy Generation. IET Renew. Power Gener. 2020, 14, 2820–2829. [Google Scholar] [CrossRef]
- Michael, N.E.; Hasan, S.; Mishra, S. Virtual inertia provision through data centre and electric vehicle for ancillary services support in microgrid. IET Renew. Power Gener. 2020, 14, 3792–3801. [Google Scholar] [CrossRef]
- Marchgraber, J.; Alács, C.; Guo, Y.; Gawlik, W.; Anta, A.; Stimmer, A.; Lenz, M.; Froschauer, M.; Leonhardt, M. Comparison of Control Strategies to Realize Synthetic Inertia in Converters. Energies 2020, 13, 3491. [Google Scholar] [CrossRef]
- Zhang, Y.; Melin, A.M.; Djouadi, S.M.; Olama, M.M.; Tomsovic, K. Provision for Guaranteed Inertial Response in Diesel-Wind Systems via Model Reference Control. IEEE Trans. Power Syst. 2018, 33, 6557–6568. [Google Scholar] [CrossRef]
- Lerch, K.S.; Kerdphol, T.; Mitani, Y.; Turschner, D. Frequency Stability Assessment on Virtual Inertia Control Strategy in Connected and Islanded Multi-Area Power Systems. In Proceedings of the IEEE International Conference on Environment and Electrical Engineering and IEEE Industrial and Commercial Power Systems Europe (EEEIC/I&CPS Europe), Madrid, Spain, 9–12 June 2020. [Google Scholar] [CrossRef]
- Kerdphol, T.; Rahman, F.; Mitani, Y.; Hongesombut, K.; Küfeoğlu, S. Virtual Inertia Control-Based Model Predictive Control for Microgrid Frequency Stabilization Considering High Renewable Energy Integration. Sustainability 2017, 9, 773. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, C.; Xu, L.; Meng, J.; Hei, Y. Adjustable Inertial Response from the Converter With Adaptive Droop Control in DC Grids. IEEE Trans. Smart Grid 2019, 10, 3198–3209. [Google Scholar] [CrossRef]
- Samanta, S.; Prakash Mishra, J.; Krishna Roy, B. Implementation of a virtual inertia control for inertia enhancement of a DC microgrid under both grid connected and isolated operation. Comput. Electr. Eng. 2019, 76, 283–298. [Google Scholar] [CrossRef]
- Brisebois, J.; Aubut, N. Wind Farm Inertia Emulation to Fulfil Hydro-Quebec’s Specific Need. In Proceedings of the 2011 IEEE Power and Energy Society General Meeting, Detroit, MI, USA, 24–28 July 2011. [Google Scholar] [CrossRef]
- Hardan, F.; Norman, R. Balancing loads of rotating generators utilizing VSC direct power controllers in a ship AC/DC smartgrid. Electr. Power Syst. Res. 2020, 182, 106200. [Google Scholar] [CrossRef]
- Duckwitz, D.; Fischer, B. Modeling and Design of df/dt-Based Inertia Control for Power Converters. IEEE J. Emerg. Sel. Top. Power Electron. 2017, 5, 1553–1564. [Google Scholar] [CrossRef]
- Liu, H.; Chen, Z. Contribution of VSC-HVDC to frequency regulation of power systems with offshore wind generation. IEEE Trans. Energy Convers. 2015, 30, 918–926. [Google Scholar] [CrossRef]
- Gloe, A.; Jauch, C.; Cracium, B.; Winkelmann, J. Continuous provision of synthetic inertia with wind turbines: Implications for the wind turbine and for the grid. IET Renew. Power Gener. 2019, 13, 668–675. [Google Scholar] [CrossRef]
- Rodriguez, J.; Lai, J.S.; Peng, F.Z. Multilevel inverters: A survey of topologies, controls, and applications. IEEE Trans. Ind. Electron. 2002, 49, 724–738. [Google Scholar] [CrossRef]
- Bloemink, J.M.; Green, T.C. Reducing passive filter sizes with tuned traps for distribution level power electronics. In Proceedings of the 14th European Conference on Power Electronics and Applications, Birmingham, UK, 30 August–1 September 2011. [Google Scholar]
- Rashid, M.H. Power Electronics: Devices, Circuits, and Applications, International Edition, 4th ed.; Pearson Education Limited: Essex, UK, 2014. [Google Scholar]
- Glover, J.D.; Sarma, M.S.; Overbye, T.J. Transient Stability. In Power System Analysis and Design, 5th ed.; Stamford, C.T., Ed.; Cengage Learning: Boston, MA, USA, 2012. [Google Scholar]
- Hardan, F.; Bleijs, J.A.M.; Jones, R.; Bromley, P. Bi-directional power control for flywheel energy storage system with vector-controlled induction machine drive. In Proceedings of the Seventh International Conference on Power Electronics and Variable Speed Drives (IEE Conf. Publ. No. 456), London, UK, 21–23 September 1998. [Google Scholar] [CrossRef]
- Jin, Z.; Meng, L.; Guerrero, J.M.; Han, R. Hierarchical Control Design for a Shipboard Power System with DC Distribution and Energy Storage Aboard Future More-Electric Ships. IEEE Trans. Ind. Inform. 2018, 14, 703–714. [Google Scholar] [CrossRef]
- Xiao, Z.; Li, H.; Fang, H.; Guan, Y.; Liu, T.; Hou, L.; Guerrero, J.M. Operation Control for Improving Energy Efficiency of Shipboard Microgrid Including Bow Thrusters and Hybrid Energy Storages. IEEE Trans. Transp. Electrif. 2020, 6, 856–868. [Google Scholar] [CrossRef]
- Song, Q.; Grigoriadis, K.M. Diesel engine speed regulation using linear parameter varying control. In Proceedings of the American Control Conference, Denver, CO, USA, 4–6 June 2003. [Google Scholar] [CrossRef]
- 421.5-2016; IEEE Recommended Practice for Excitation System Models for Power System Stability Studies. (Revision of IEEE 521.5-1992). IEEE Standard: Piscataway, NJ, USA, 2005; Volume 421.


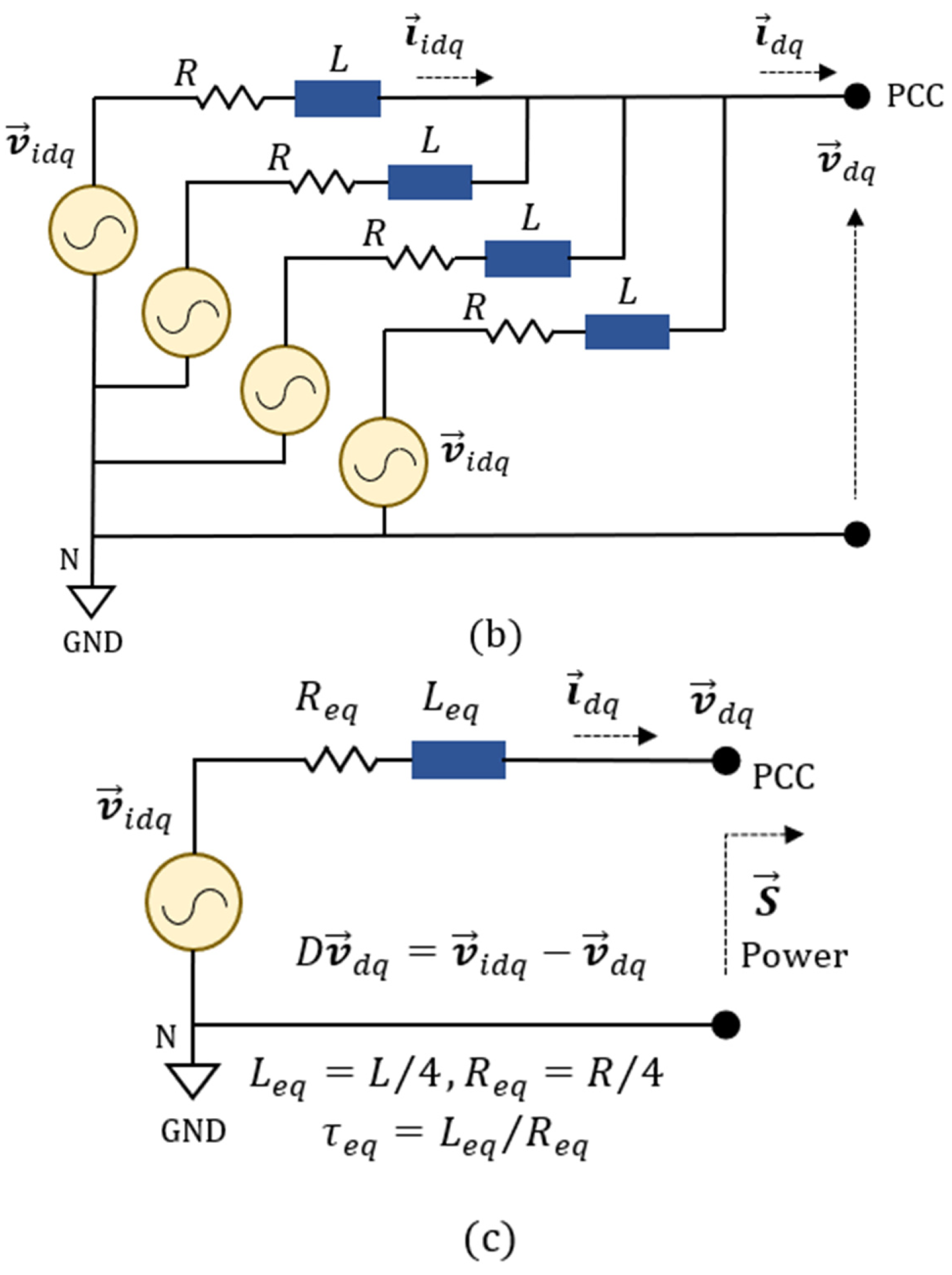
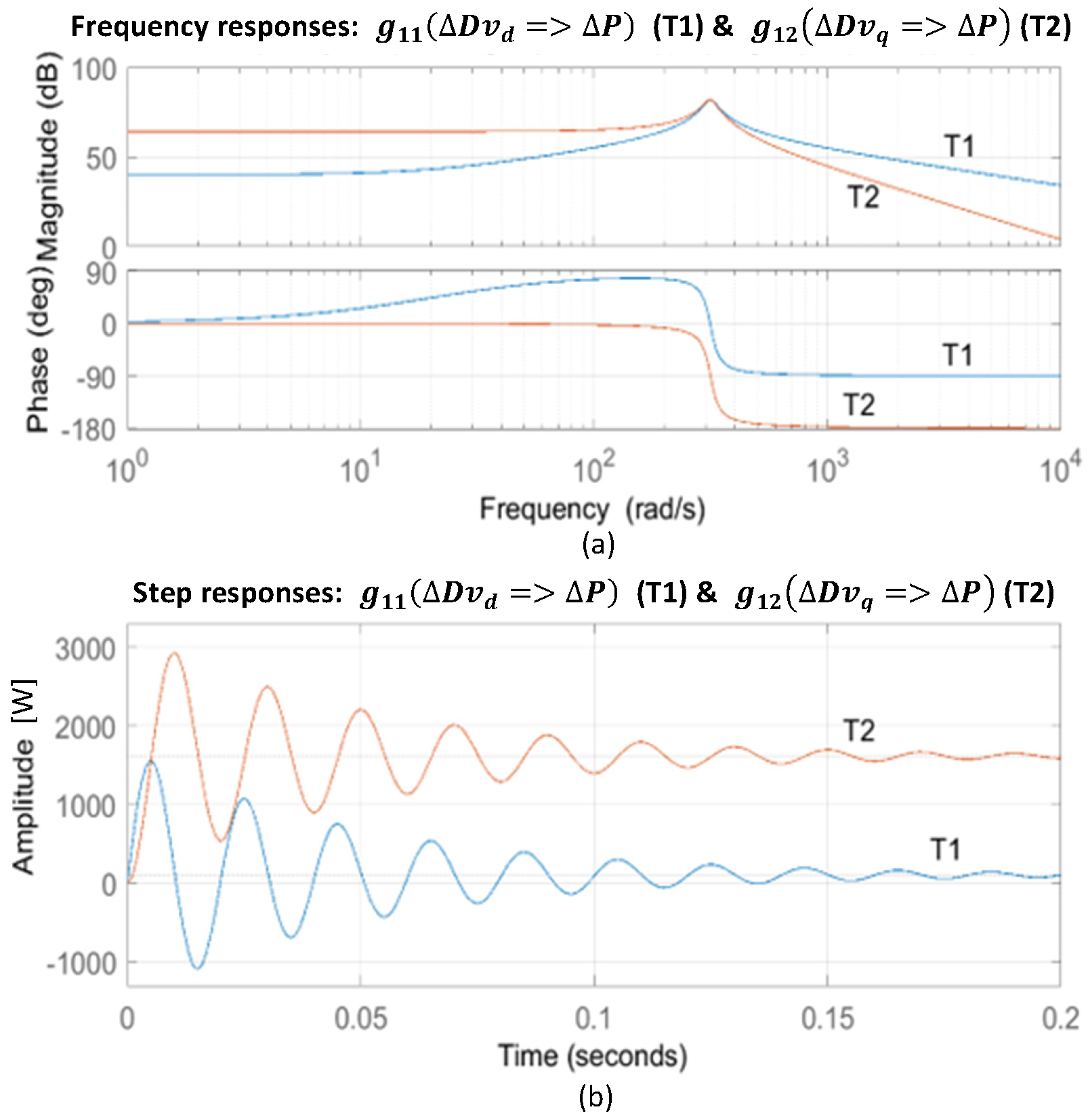
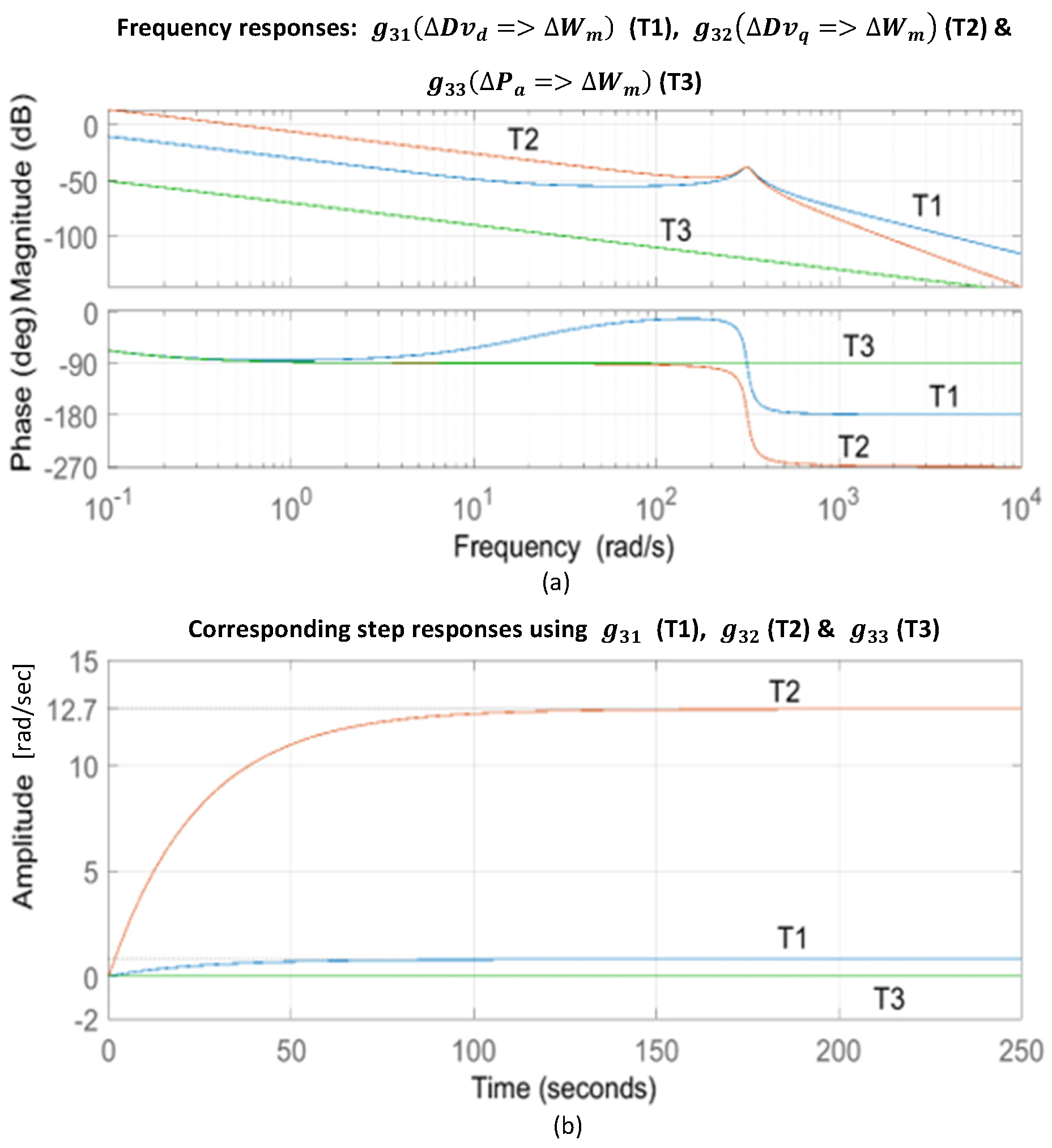
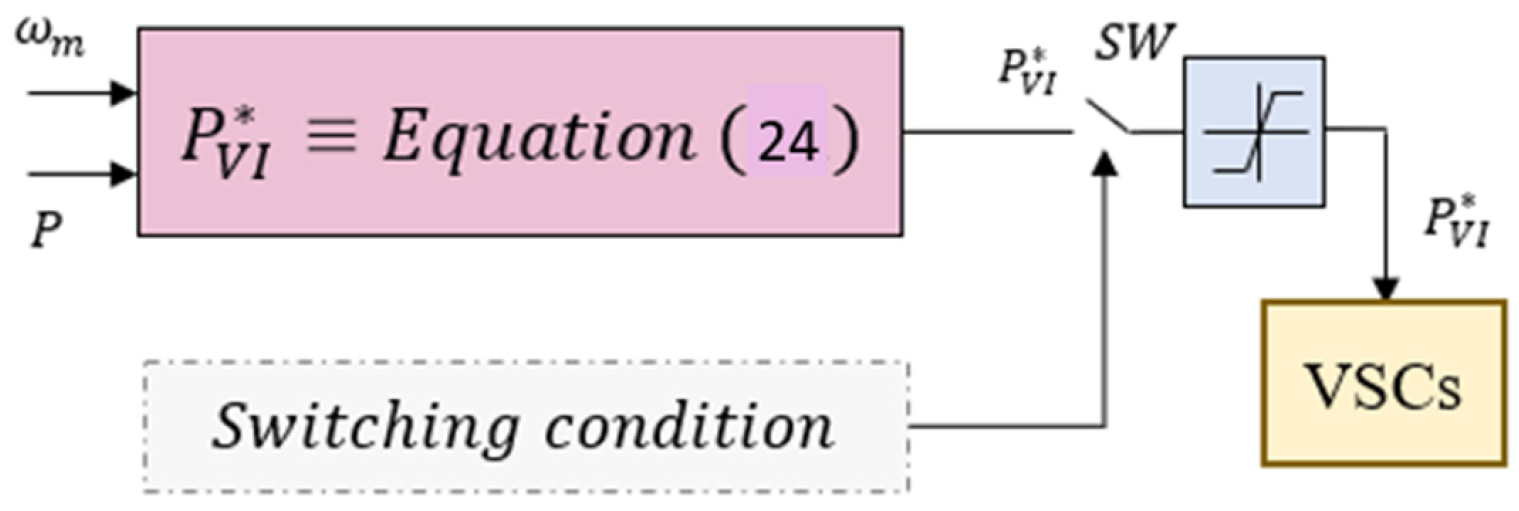


| Function | Gain Margin | Freq. [rad/s] | Phase Margin | Freq. [rad/s] |
|---|---|---|---|---|
| inf. (1) | n/a (2) | 90 | 500 K | |
| inf. | inf. | 0.18 | 13 K | |
| 0.0006 | 0 | −180 | 13 K | |
| inf. | inf. | inf. | n/a | |
| 78 | 314.8 | 94.5 | 0.51 | |
| inf. | n/a | inf. | n/a |
| [s] | Filter-Based | Model-Based | Frequency Event | |
|---|---|---|---|---|
| 0.2 | 0.01953 | 0.007 | 0.007 | 0.005 |
| 0.5 | 0.04813 | |||
| 1.0 | 0.08508 | |||
| 2.0 | 0.12477 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hardan, F.; Norman, R.; Tricoli, P. Virtual Inertia Methods for Supporting Frequency Stabilisation in Autonomous AC/DC Microgrids. Electronics 2025, 14, 91. https://doi.org/10.3390/electronics14010091
Hardan F, Norman R, Tricoli P. Virtual Inertia Methods for Supporting Frequency Stabilisation in Autonomous AC/DC Microgrids. Electronics. 2025; 14(1):91. https://doi.org/10.3390/electronics14010091
Chicago/Turabian StyleHardan, Faysal, Rosemary Norman, and Pietro Tricoli. 2025. "Virtual Inertia Methods for Supporting Frequency Stabilisation in Autonomous AC/DC Microgrids" Electronics 14, no. 1: 91. https://doi.org/10.3390/electronics14010091
APA StyleHardan, F., Norman, R., & Tricoli, P. (2025). Virtual Inertia Methods for Supporting Frequency Stabilisation in Autonomous AC/DC Microgrids. Electronics, 14(1), 91. https://doi.org/10.3390/electronics14010091








