Utilization of MCU and Real-Time Simulator for Identifying Beatless Control for Six-Step Operation of Three-Phase Inverter
Abstract
1. Introduction
2. Beat Phenomenon in Six-Step Operation
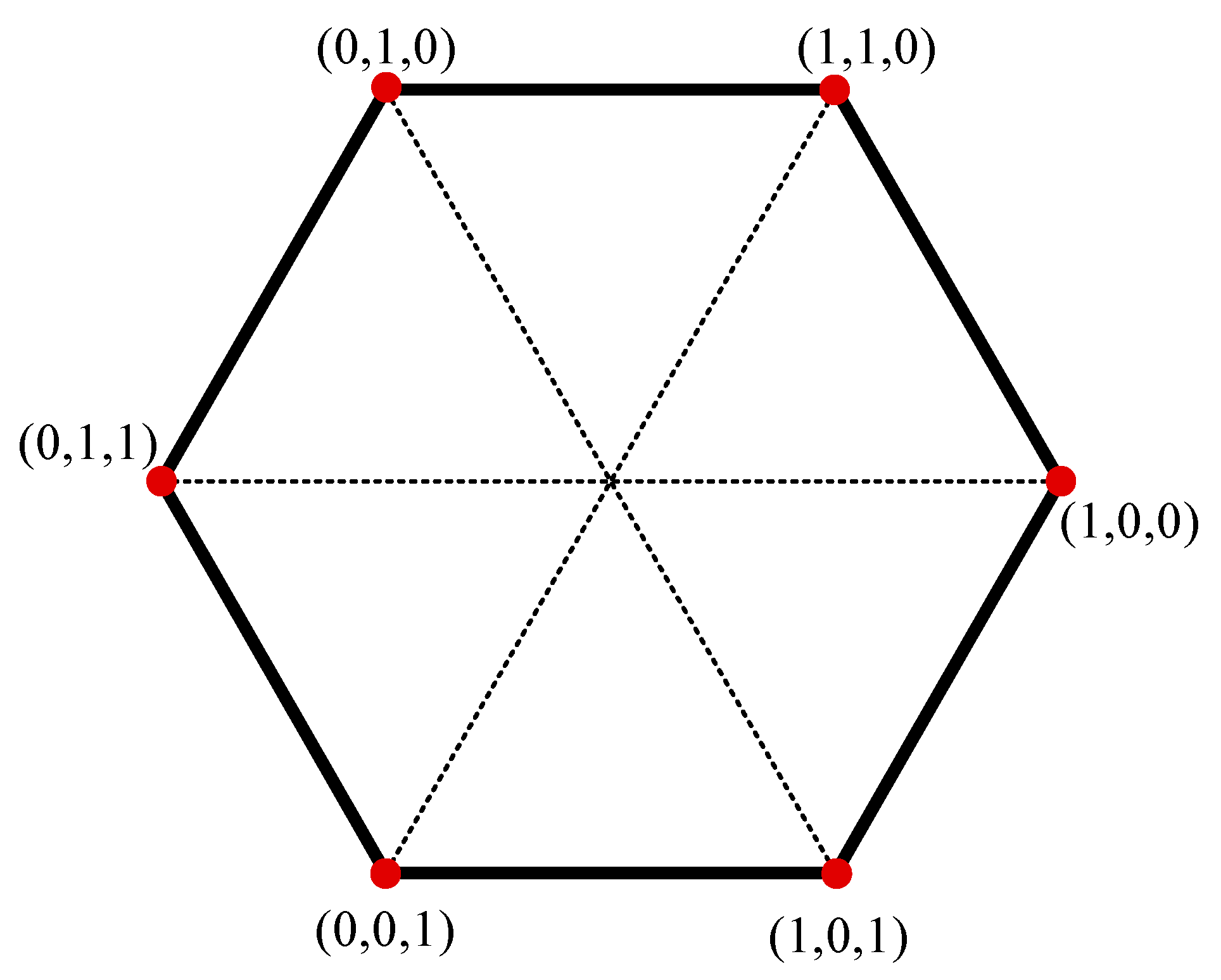
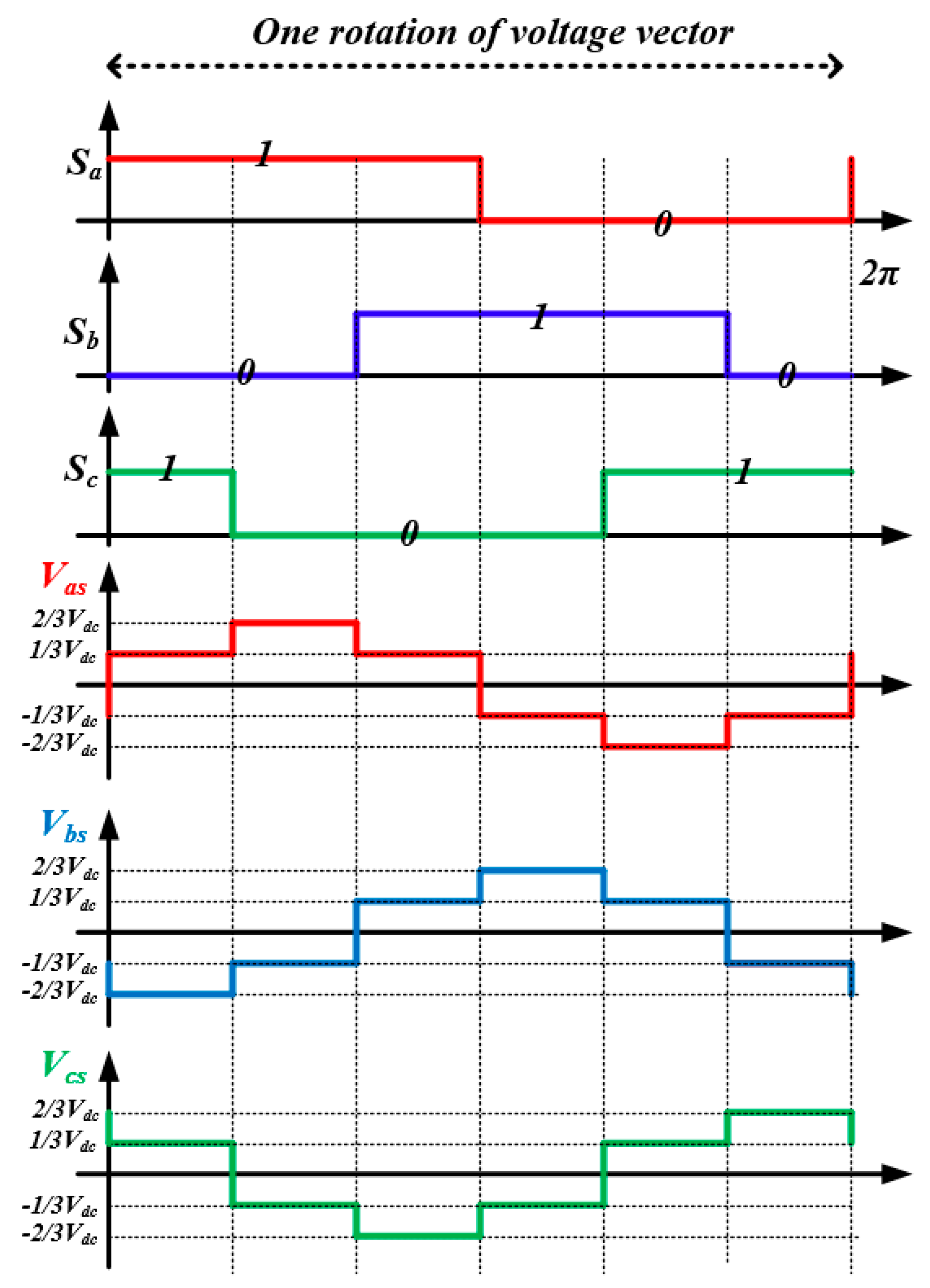
2.1. Ideal Voltage Output in Six-Step Operation
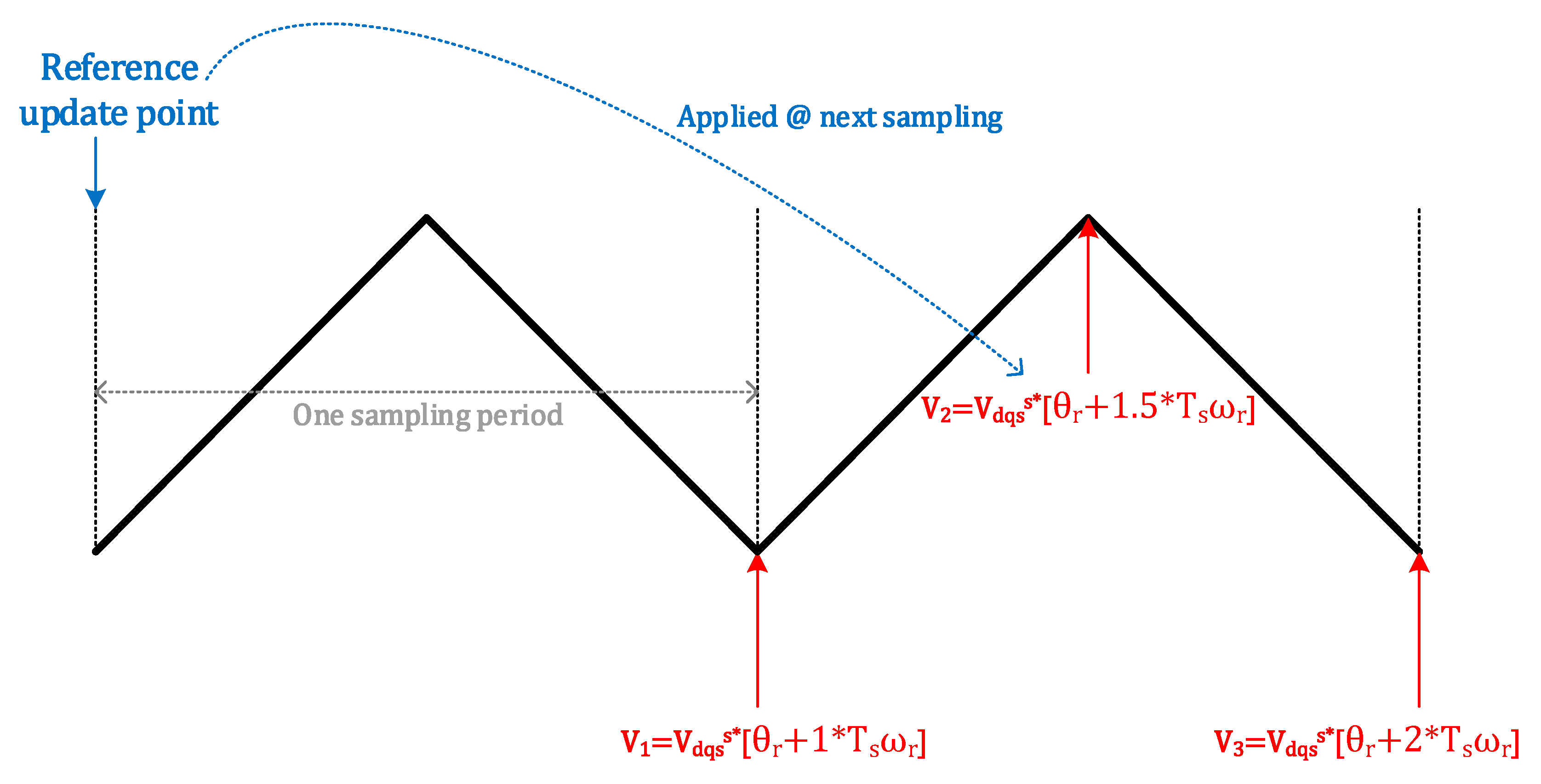
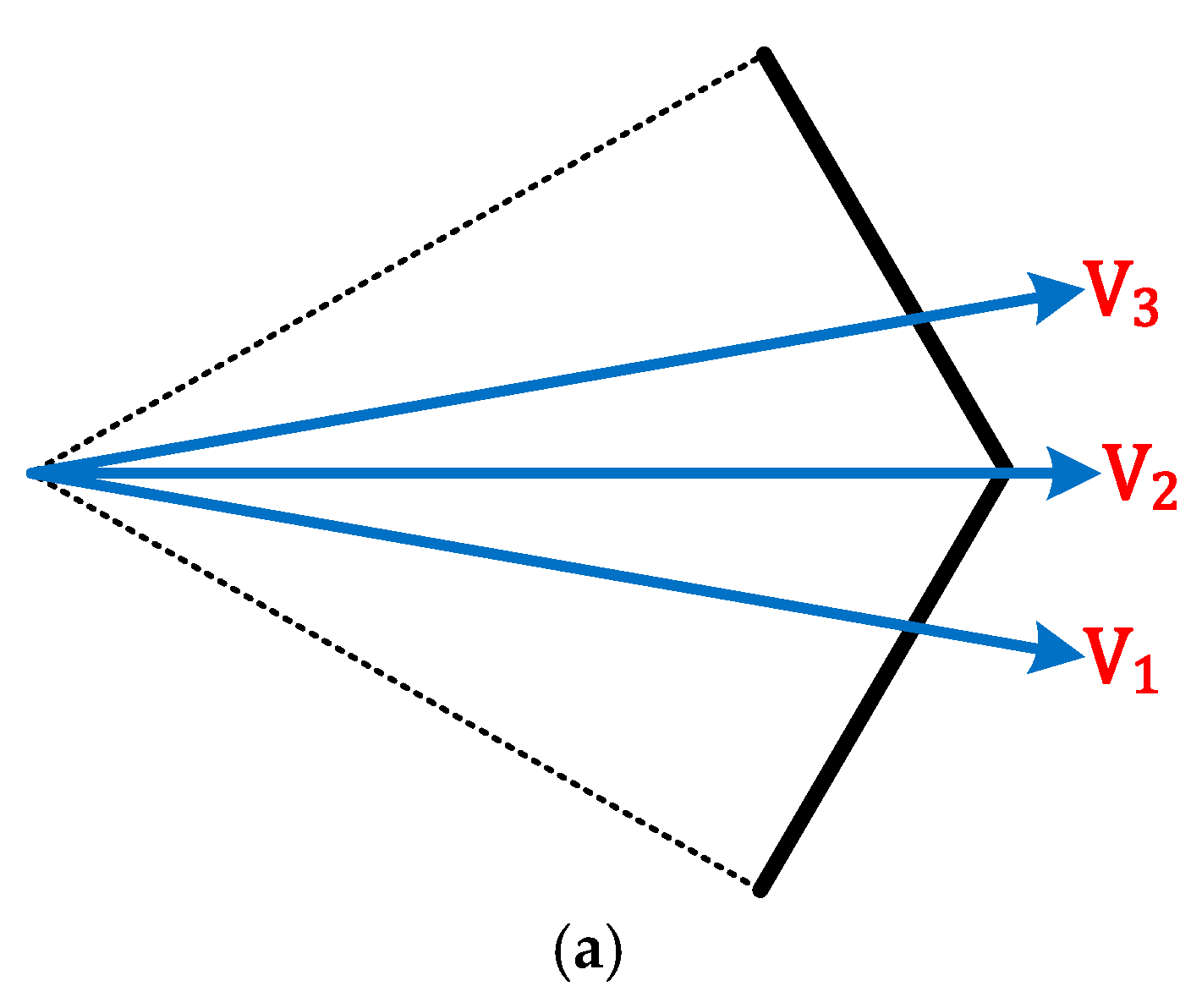
2.2. Beat Phenomenon Due to Fixed Sampling Frequency in Six-Step Operation
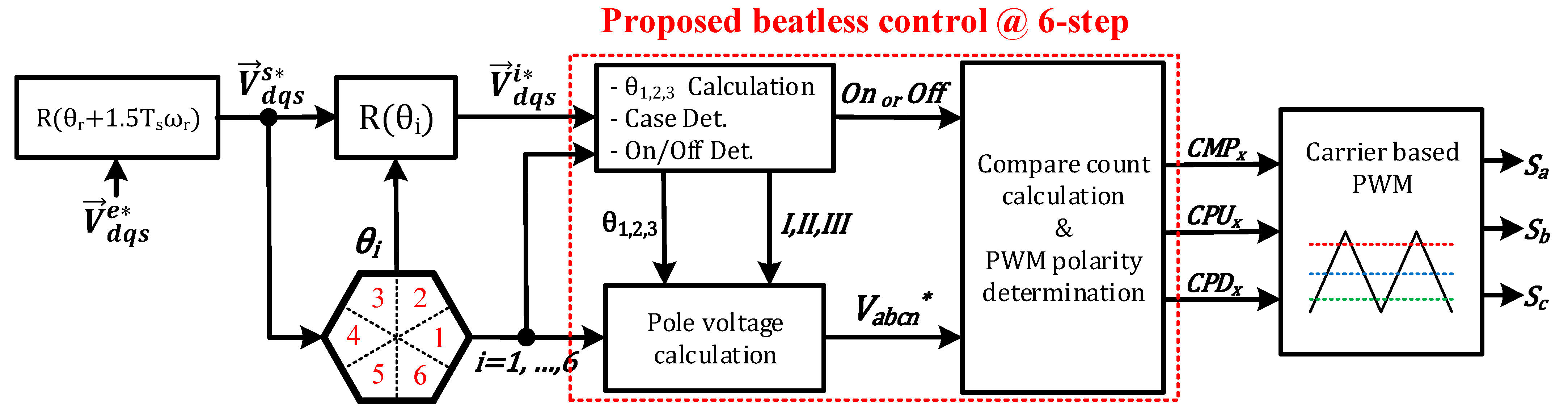
3. Proposed Beatless Operation and Its Implementation in MCU Timer Module
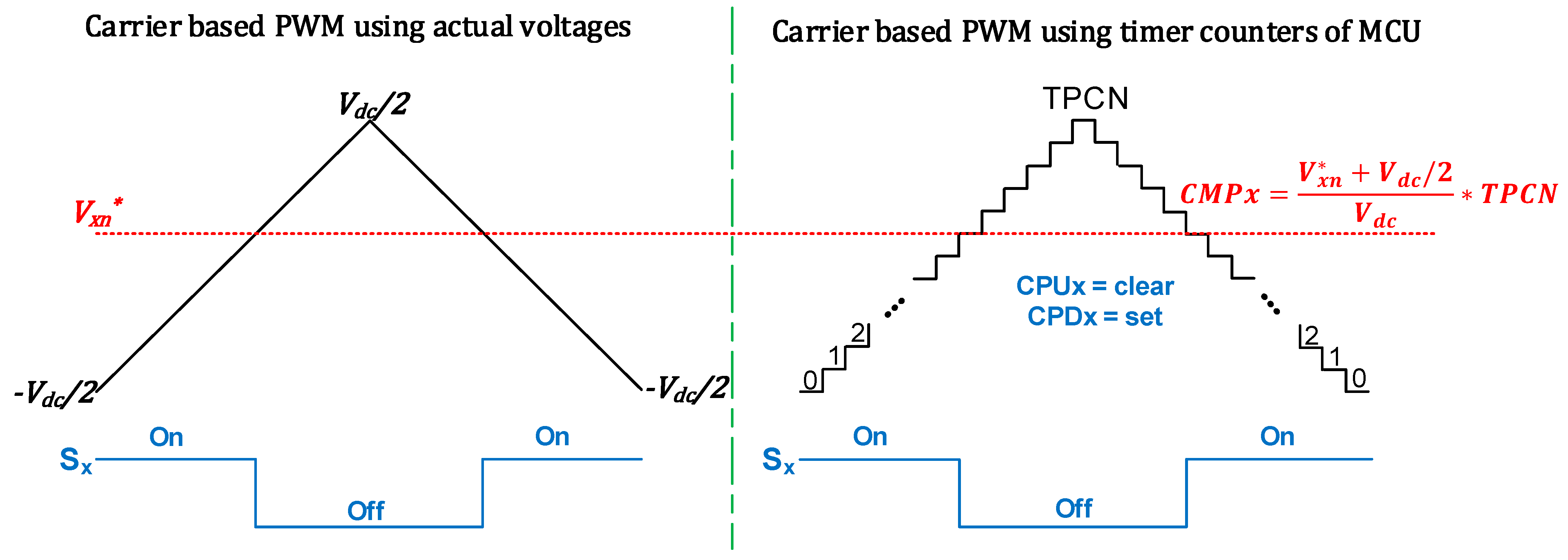
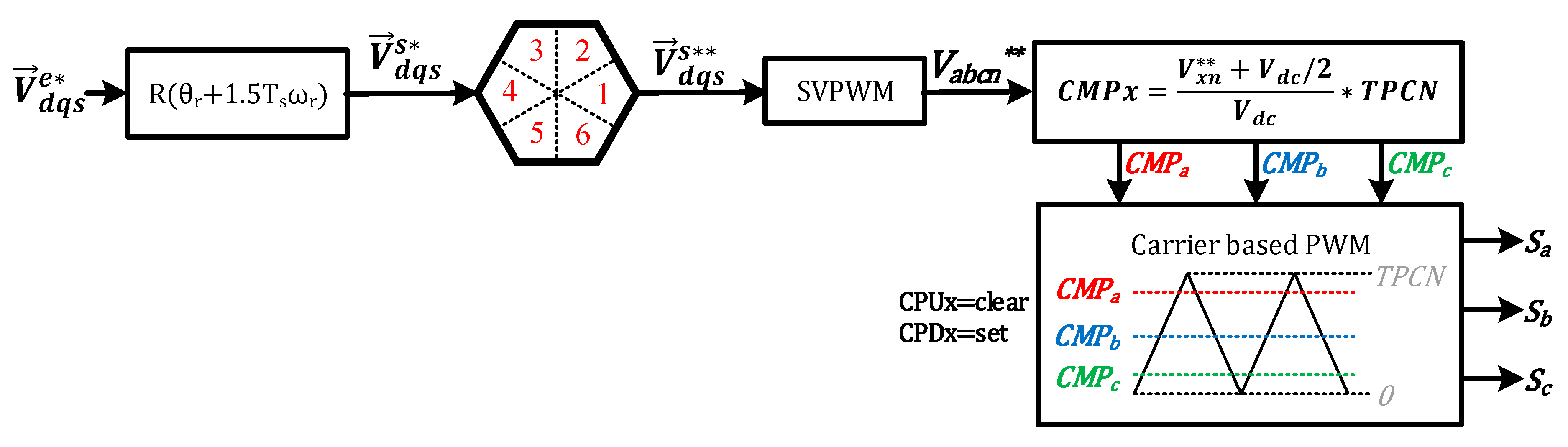
3.1. Register Configuration of MCU Timer Module for Carrier-Based PWM
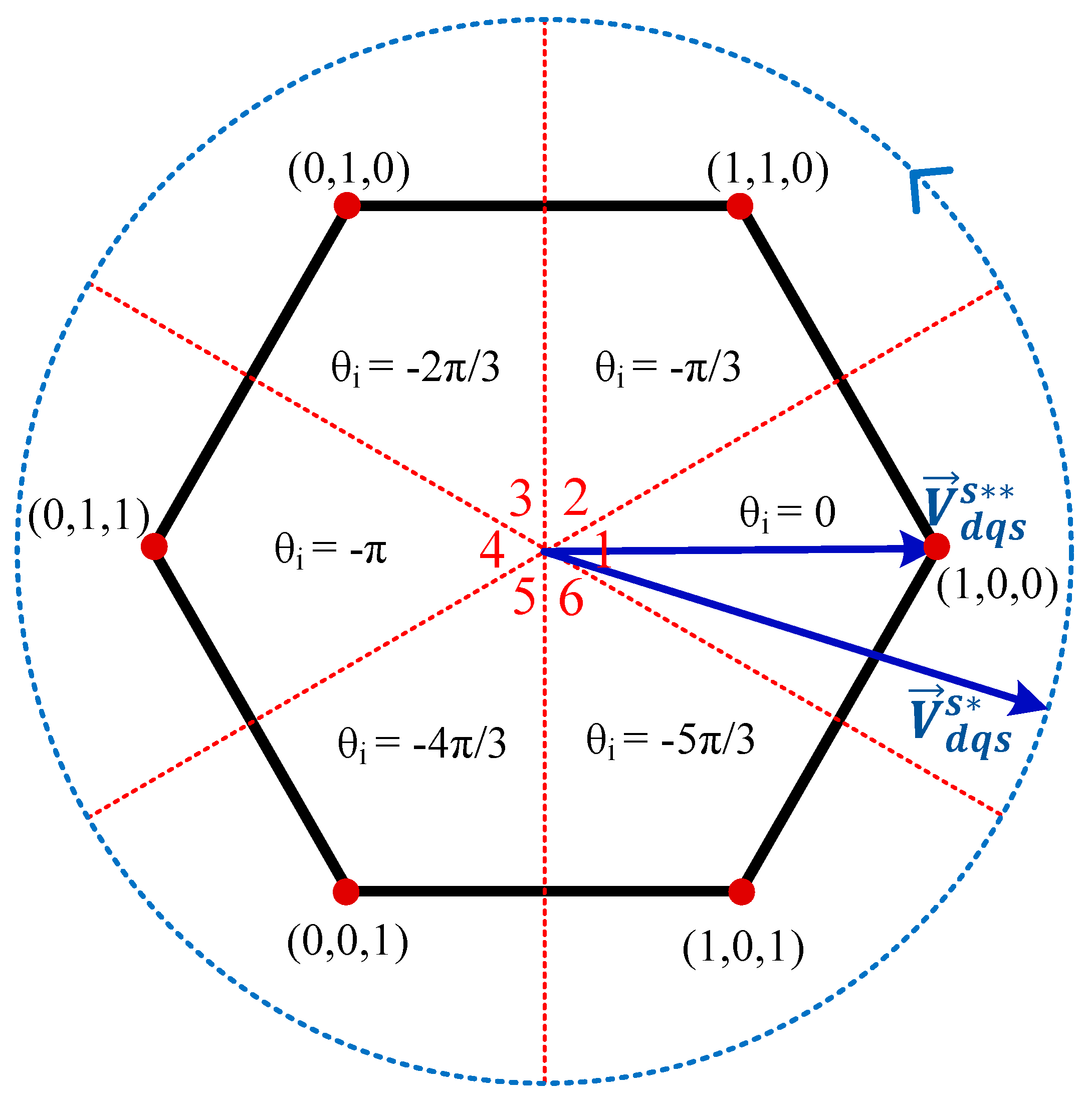
3.2. Voltage Command Modification Method for 6-Step Operation
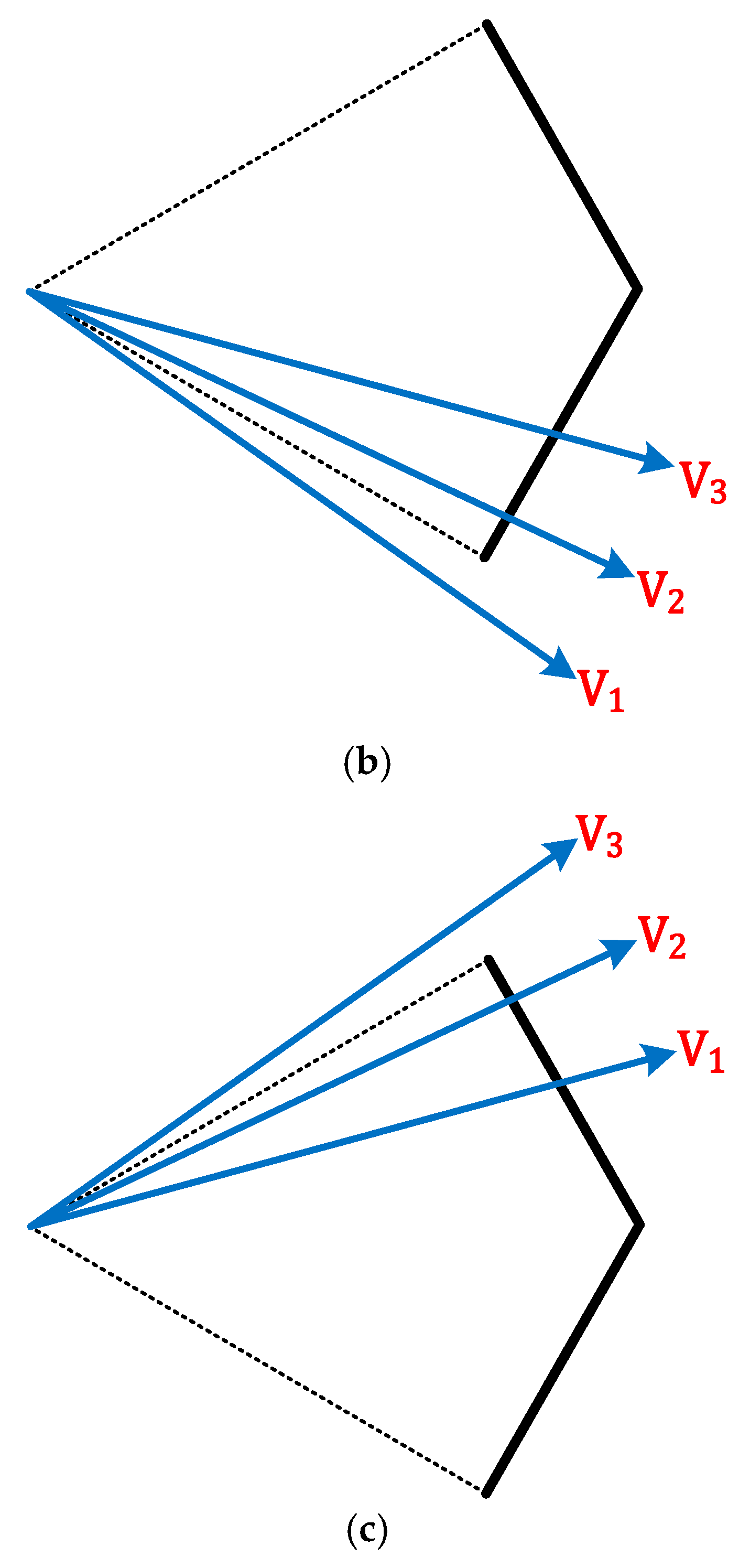
3.3. Method for Determining Pole Voltage Considering Beatless
3.4. Proposed Beatless Control Method Based on Fixed Switching Frequency
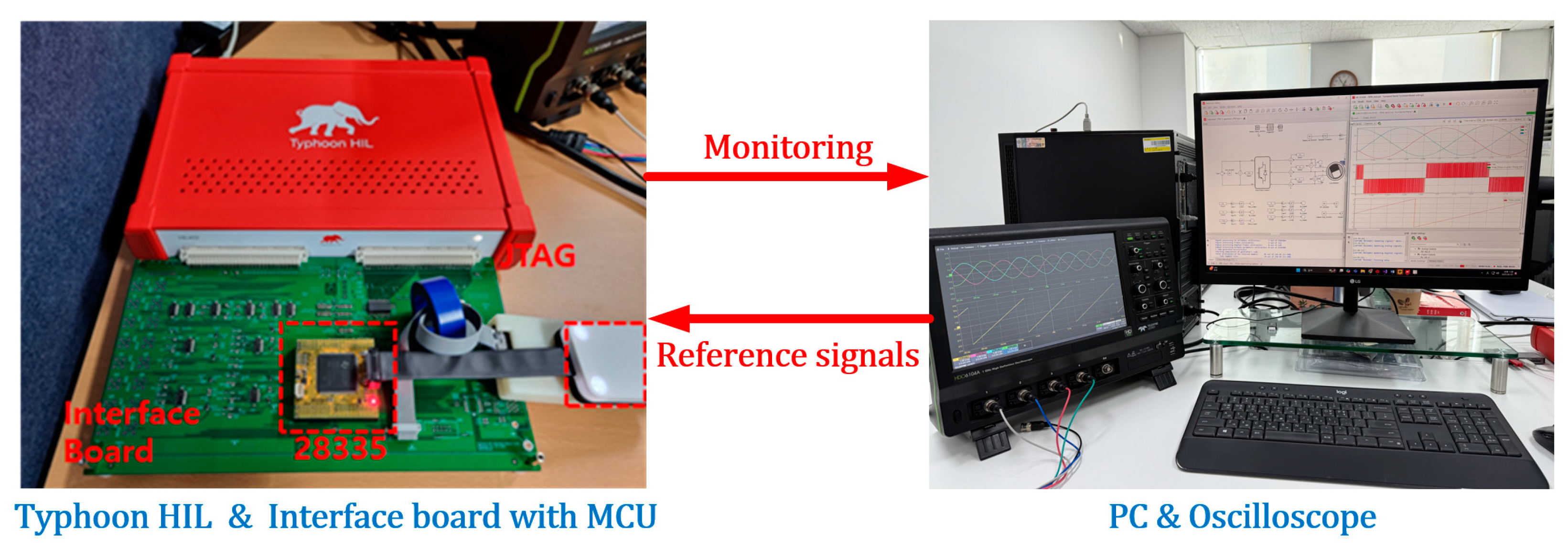
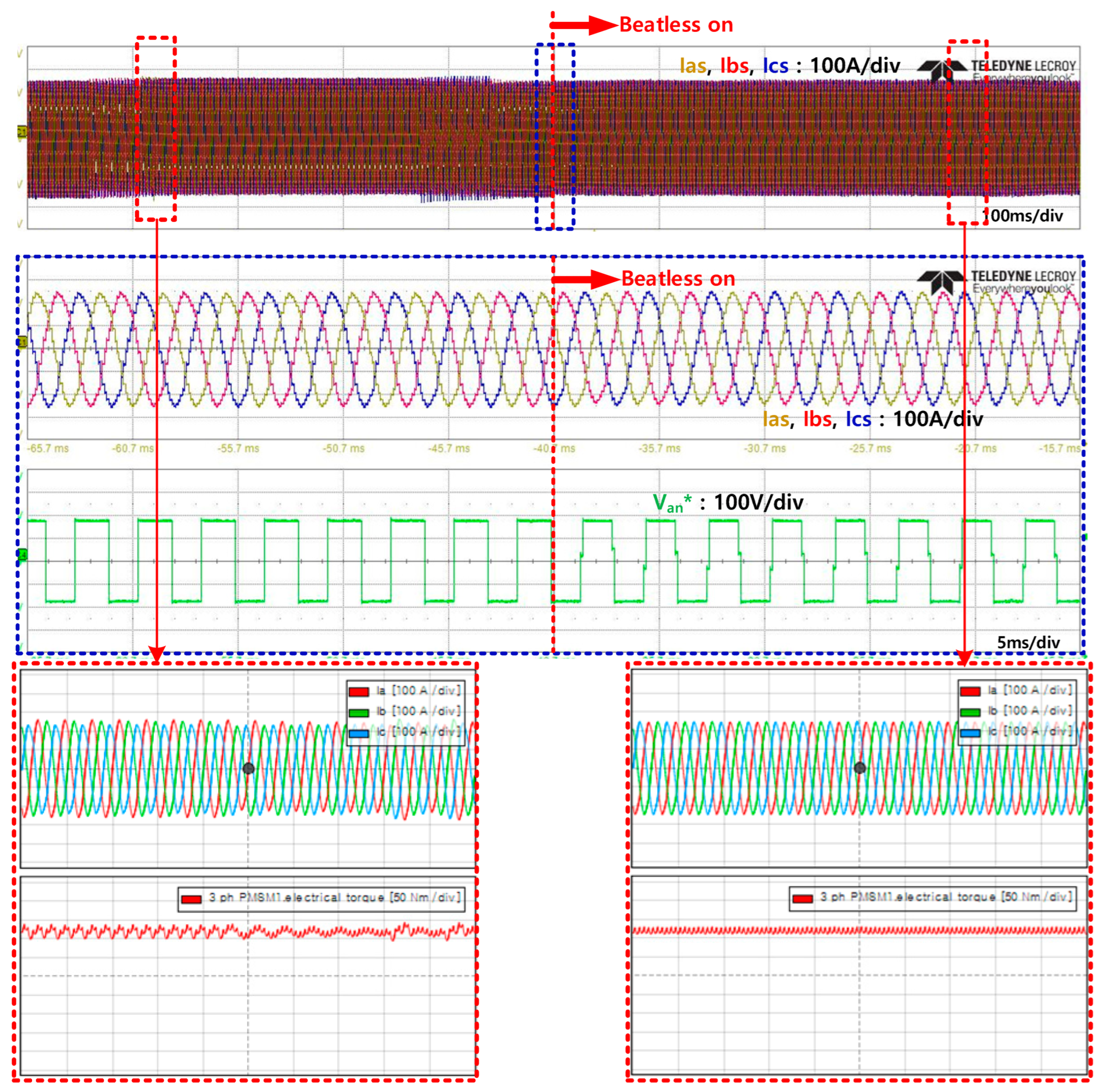
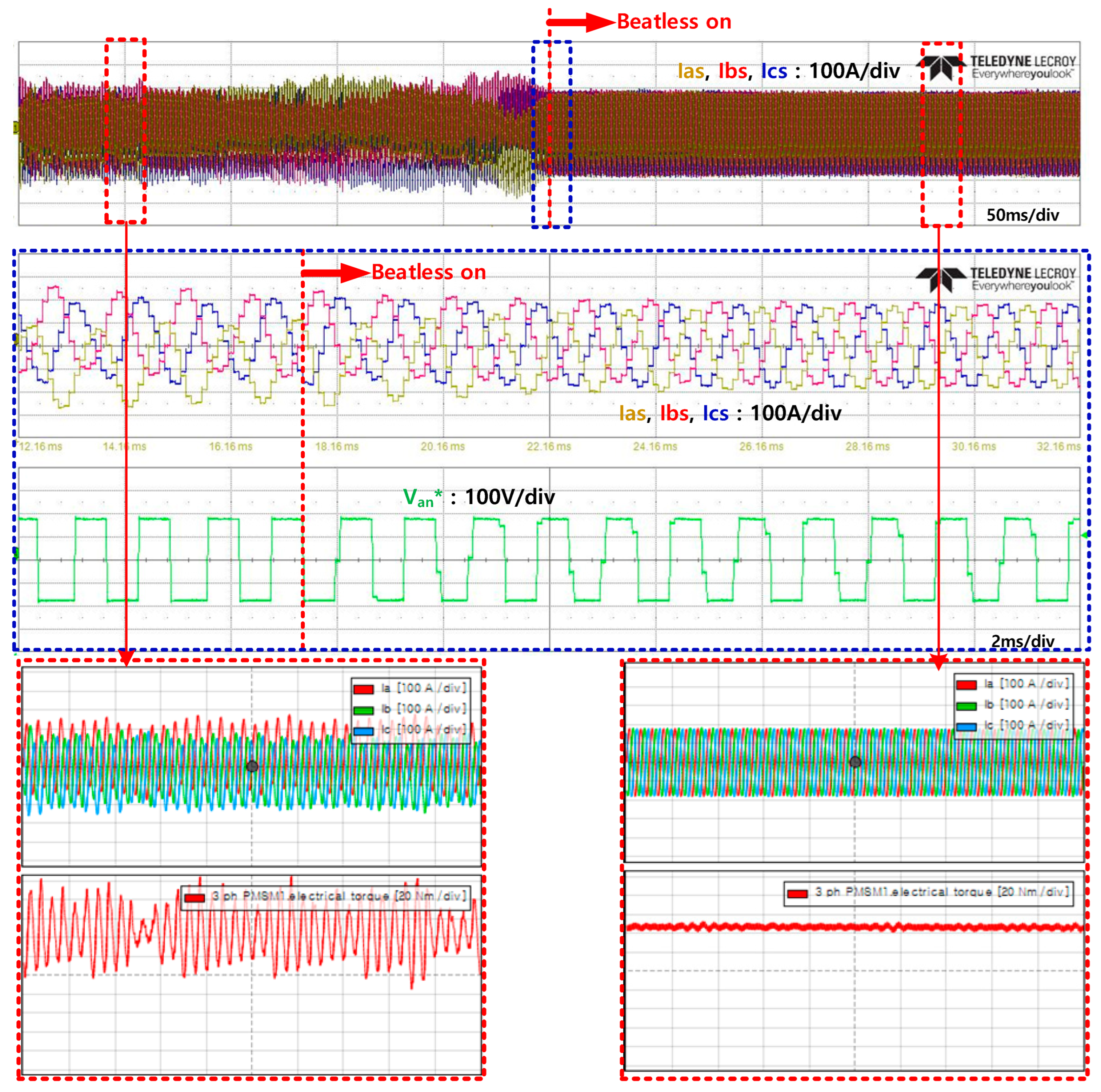
4. Verification of the Proposed Beatless Control Through the Real-Time Simulator
5. Conclusions
Funding
Data Availability Statement
Conflicts of Interest
References
- Atanalian, S.; Sebaaly, F.; Zgheib, R.; AL-Haddad, K. Real-Time Implementation of Three-Phase Z Packed U-Cell Modualr Multilevel Grid-Connected Converter Using CPU and FPGA. Electronics 2024, 13, 2186. [Google Scholar] [CrossRef]
- Sang, Z.; Li, S.; Huang, Y.; Gao, X.; Qiao, R. Indirect Matrix Converter Hardware-in-the Loop Semi-Physical Simulation Based on Latency-Free Decoupling. Electronics 2023, 12, 4802. [Google Scholar] [CrossRef]
- Shanyeghan, M.; Benedetto, M.D.; Lidozzi, A.; Solero, L. HIL-Based Fault-Tolerant Vector Space Decomposition Control for a Six-Phase PMSM Fed by a Five-Level CHB Converter. Energies 2025, 18, 507. [Google Scholar] [CrossRef]
- Sonzanski, K. Low-Cost Hardware Analog and Digital Real-Time Circuit Simulators for Developing Power Electronics Control Circuits. Energies 2024, 17, 6359. [Google Scholar] [CrossRef]
- Holtz, J.; Lotzkat, W.; Khambadkone, A.M. On continuous control of PWM inverters in the overmodulation range including the six-step mode. IEEE Trans. Power Electron. 1993, 8, 546–553. [Google Scholar] [CrossRef]
- Lee, K.; Han, Y. PWM strategy in OVM and Six-Step Regions for Open-End Winding PMSM Fed by a Dual Inverter with a Common DC Bus. IEEE Trans. Power Electron. 2024, 39, 13696–13707. [Google Scholar] [CrossRef]
- Wang, B.; Wang, L.; Yu, Y.; Xu, D. Adaptive Overmodulation Strategy for PMSM Field-Weakening Control Based on Working Quadrant. IEEE Trans. Ind. Electron. 2023, 70, 9959–9970. [Google Scholar] [CrossRef]
- Jung, B.; Lee, T.; Nam, K. Overmodulation Strategy for Voltage Source Inverter With a Single DC-Link Current Sensor. IEEE Trans. Ind. Appl. 2022, 58, 531–540. [Google Scholar] [CrossRef]
- Chen, Z.; Mao, H.; Yang, X.; Wang, Z. A study on pulse width errors of digitized naturally sampled PWM. In Proceedings of the 2008 IEEE Power Electronics Specialists Conference, Rhodes, Greece, 15–19 June 2008; pp. 592–597. [Google Scholar] [CrossRef]
- Stumpf, P.; Jardan, R.K.; Nagy, I. Comparison of naturally sampled PWM techniques in ultrahigh speed drives. In Proceedings of the 2012 IEEE International Symposium on Industrial Electronics, Hangzhou, China, 28–31 May 2012; pp. 246–251. [Google Scholar] [CrossRef]
- Stumpf, P.; Jardan, R.K.; Nagy, I. Subharmonics generated by space vector modulation in ultrahigh speed drives. IEEE Trans. Ind. Electron. 2012, 59, 1029–1037. [Google Scholar] [CrossRef]
- Halasz, S. DC components and subharmonics of carrier-based PWM. In Proceedings of the 2012 15th International Power Electronics and Motion Control Conference (EPE/PEMC), Novi Sad, Serbia, 4–6 September 2012. [Google Scholar] [CrossRef]
- Jardan, R.K.; Stumpf, P.; Bartal, P.; Varga, Z.; Nagy, I. A novel approach in studying the effects of subharmonics on ultrahigh-speed AC motor drives. IEEE Trans. Ind. Electron. 2011, 58, 1274–1281. [Google Scholar] [CrossRef]
- Ke, Z.; Zhang, J.; Raich, R. Low-Frequency Current Oscillation Reduction for Six-Step Operation of Three-Phase Inverters. IEEE Trans. Power Electron. 2017, 32, 2948–2956. [Google Scholar] [CrossRef]
- Hara, T.; Taniguchi, S.; Ajima, T.; Sawahata, M.; Hori, M.; Tsukagoshi, T. Synchronous PWM Control with Carrier Wave Phase Shifts for Permanent Magnet Synchronous Motor. IEEE Trans. Ind. Appl. 2022, 58, 5650–5658. [Google Scholar] [CrossRef]
- Hara, T.; Taniguchi, S.; Ajima, T.; Sawahata, M.; Hori, M.; Tsukagoshi, T. Vibration and Loss Reduction of Permanent Magnet Synchronous Motor Driven by Synchronous PWM Control with Carrier Wave Phase Shifts. In Proceedings of the 2021 IEEE Energy Conversion Congress and Exposition (ECCE), Vancouver, BC, Canada, 10–14 October 2021. [Google Scholar] [CrossRef]
- Tommaso, A.; Miceli, R.; Nevoloso, C.; Marsala, S. Practical Implementation of a Synchronous PWM Strategy for Low Switching Frequency FOC of IM Drives with ATSAM3X8E Microcontroller. In Proceedings of the 2021 Sixteenth International Conference on Ecological Vehicles and Renewable Energies (EVER), Monte-Carlo, Monaco, 5–7 May 2021. [Google Scholar] [CrossRef]
- Lin, H.; Cai, C.; Chen, J.; Gao, Y.; Vazquez, S.; Li, Y. Modulation and Control Independent Dead-Zone Compensation for H-Bridge Converters: A Simplified Digital Logic Scheme. IEEE Trans. Ind. Electron. 2024, 71, 15239–15244. [Google Scholar] [CrossRef]
- Wang, H.; Xu, J.; Ye, J.; Li, B.; Huang, S.; Huang, Y.; Liu, D.; Shen, A. Harmonic spectra analysis of digital SPWM in VSI with DC bus ripple and dead-time effects. IEEE Trans. Power Electron. 2023, 38, 9494–9513. [Google Scholar] [CrossRef]
- Lin, Y.; Lai, Y. Dead-time elimination of PWM-Controlled inverter/converter without separate power sources for current polarity detection circuit. IEEE Trans. Ind. Electron. 2009, 56, 2121–2127. [Google Scholar]
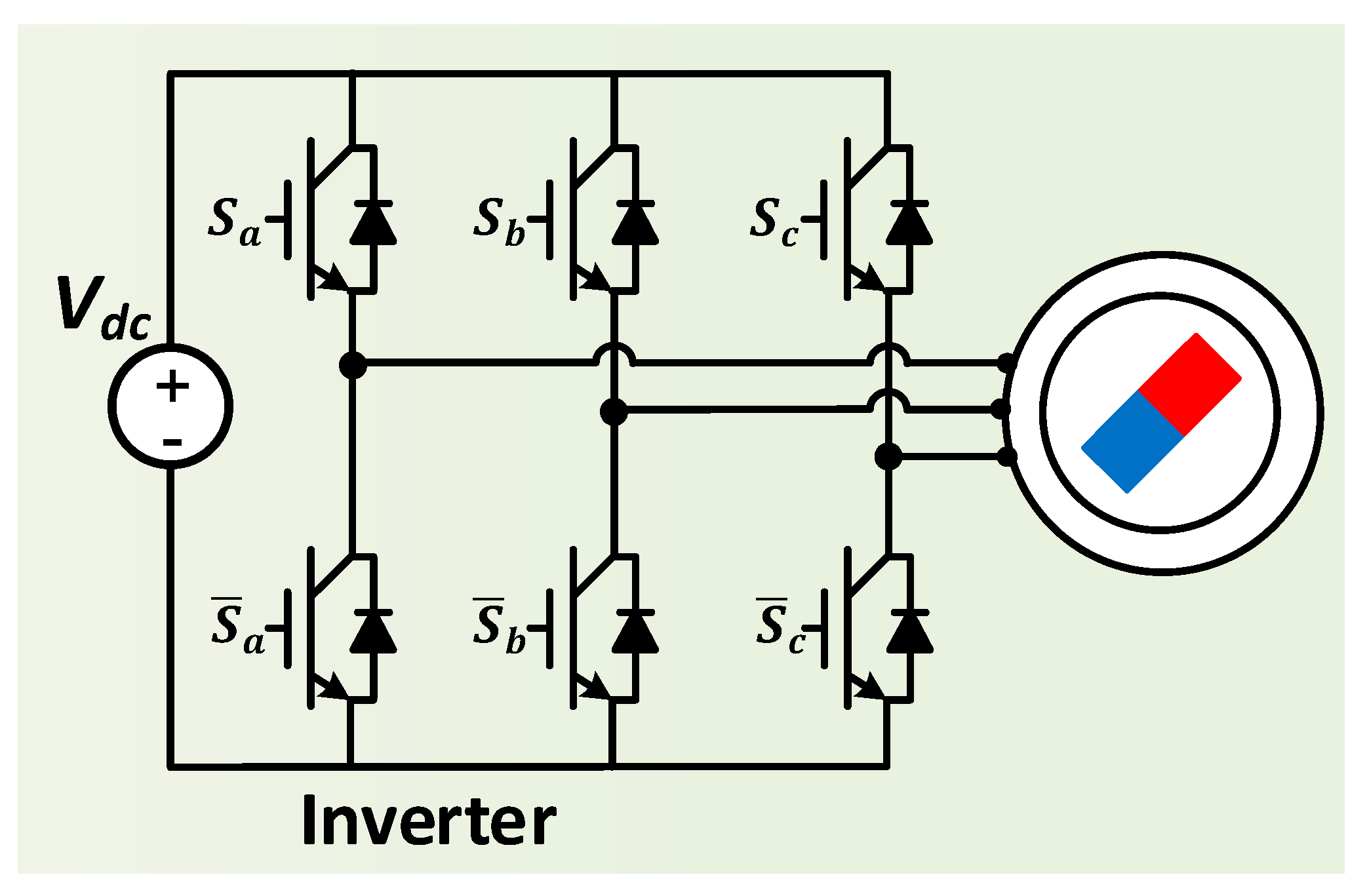



| Parameters of Inverter and Motors | |
|---|---|
| Motor Type | Permanent Magnet Synchronous Motor |
| DC Link Voltage | 300 [V] |
| Switching Frequency | 10 [kHz] |
| Rated Current | 350 [Arms] |
| Rated/Max Speed | 2500/10,000 [r/min] |
| Rated Torque | 180 [Nm] |
| Phase Resistance | 0.05 [Ω] |
| d-Axis Inductance | 0.45 [mH] |
| q-Axis Inductance | 0.65 [mH] |
| Register Name | Operation Description |
|---|---|
| TPCN (Timer-Peak-Counter) | Peak point value of the timer counter (carrier)
|
| CMPx (Compare-Counter) | Comparison-match value for the switching point
|
| CPUx (Carrier-Polarity-Up-sequence) | When the carrier rises, if the counter value is equal to the comparison match value (CMPx), the PWM output polarity is set as follows.
|
| CPDx (Carrier-Polarity-Down-sequence) | When the carrier falls, if the counter value is equal to the comparison match value (CMPx), the PWM output polarity is set as follows.
|
| Case II | Case III | ||
|---|---|---|---|
| b ON: (100) ➔ (110) | b ON: (100) ➔ (110) | ||
| a OFF: (110) ➔ (010) | a OFF: (110) ➔ (010) | ||
| c ON: (010) ➔ (011) | c ON: (010) ➔ (011) | ||
| b OFF: (011) ➔ (001) | b OFF: (011) ➔ (001) | ||
| a ON: (001) ➔ (101) | a ON: (001) ➔ (101) | ||
| c OFF: (101) ➔ (100) | c OFF: (101) ➔ (100) | ||
| Vxn* > 0 | Vxn* < 0 | |
|---|---|---|
| 0 ➔ 1 (On) | 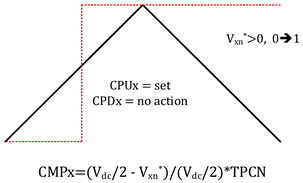 |  |
| 1 ➔ 0 (Off) | 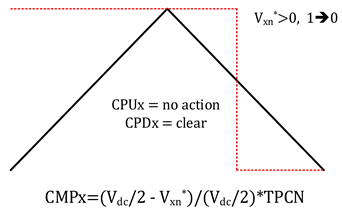 |  |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Han, Y. Utilization of MCU and Real-Time Simulator for Identifying Beatless Control for Six-Step Operation of Three-Phase Inverter. Electronics 2025, 14, 1030. https://doi.org/10.3390/electronics14051030
Han Y. Utilization of MCU and Real-Time Simulator for Identifying Beatless Control for Six-Step Operation of Three-Phase Inverter. Electronics. 2025; 14(5):1030. https://doi.org/10.3390/electronics14051030
Chicago/Turabian StyleHan, Yongsu. 2025. "Utilization of MCU and Real-Time Simulator for Identifying Beatless Control for Six-Step Operation of Three-Phase Inverter" Electronics 14, no. 5: 1030. https://doi.org/10.3390/electronics14051030
APA StyleHan, Y. (2025). Utilization of MCU and Real-Time Simulator for Identifying Beatless Control for Six-Step Operation of Three-Phase Inverter. Electronics, 14(5), 1030. https://doi.org/10.3390/electronics14051030









