Realization and Inverse Design of Multifunctional Steerable Transflective Linear-to-Circular Polarization Converter Empowered by Machine Learning

Abstract

The development of polarization converters is crucial for various applications, such as communication and sensing technologies. However, traditional polarization converters often encounter challenges in optimizing performance due to the complexity of multiparameter structures. In this study, we propose a novel multiparameter linear-to-circular polarization (LCP) converter design that addresses the difficulties of comprehensive optimization, where balancing multiple structural parameters is key to maximizing device performance. To solve this issue, we employ a machine learning (ML)-guided approach that effectively navigates the complexities of parameter interactions and optimizes the design. By utilizing the XGBoost model, we analyze a dataset of over 1.3 million parameter combinations and successfully predict high-performing designs. The results highlight that key parameters, such as the graphene Fermi level, square frame size, and VO₂ conductivity, play a dominant role in determining the performance of the LCP converter. This approach not only provides new insights into the design of LCP converters but also offers a practical solution to the complex challenge of multiparameter optimization in device engineering.

1. Introduction

The polarization state is a fundamental property of electromagnetic (EM) waves, describing the vibration direction of the electric-field (E-field) vector and its relationship to frequency and phase. This property conveys valuable information and is critical in diverse applications. Circularly polarized (CP) waves, in particular, are extensively used in satellite communications and navigation due to their high interference immunity, in molecular detection due to their unique interactions with chiral molecules, and in advanced optical sensing and imaging for their additional information acquisition capabilities [1,2,3,4]. Despite their significance, producing CP waves remains challenging due to the predominance of linearly polarized light sources and the inherent limitations of natural optical materials.

To address these challenges, metamaterials, artificially engineered structures with tailored subwavelength components, have emerged as promising solutions for manipulating EM wave polarization states. These materials leverage phenomena such as Fano resonances, plasmonic resonances, and plasmon-induced transparency [5,6,7]. Consequently, significant research efforts have focused on developing linear-to-circular polarization (LCP) converters to meet the diverse requirements of these applications [8,9,10]. Typically, these designs employ patterns that decompose an incident wave into orthogonal components, subsequently synthesizing circular polarization.

Among various design approaches, self-complementary structures stand out for their exceptional ability to achieve polarization conversion. These structures utilize the Babinet principle to separate incident waves into orthogonal components at a 90° angle on both transmission and reflection sides, independent of frequency. Numerous studies have demonstrated the superior LCP performance of self-complementary metamaterial designs [11,12,13]. However, these structures often suffer from the limitation of having a single functionality, which restricts their broader applicability. Addressing this constraint necessitates the development of multifunctional devices with enhanced versatility.

Two main strategies are commonly employed to achieve multifunctionality. The first involves introducing electrically tunable materials to the structure. Materials such as graphene, with properties tunable via external stimuli [14,15,16], VO₂ (vanadium dioxide), which transitions from insulating to metallic states at temperatures above 68 °C [17,18,19], and phosphorene, noted for its well-balanced attributes [20], enable dynamic control over optical and EM responses. By integrating such materials into devices, researchers have developed tunable and multifunctional designs while maintaining LCP conversion functionality. Despite the excellent performance achieved with single tunable materials, there is limited exploration of combining multiple tunable materials with self-complementary structures to enhance multifunctionality. This study addresses this gap by proposing novel combinations of materials and structures.

The second approach combines tunable materials with specialized EM structures incorporating components like varactor or PIN diodes [21,22,23], semiconductor elements [24], or liquid crystals [25]. While effective, these designs often result in increased structural complexity, presenting challenges in multiparameter optimization and performance enhancement.

The growing complexity of multifunctional devices necessitates sophisticated optimization techniques. Traditional optimization methods often struggle to manage the increasing number of parameters and their varying influence on device performance. Artificial intelligence (AI), particularly machine learning (ML), has emerged as a transformative tool in addressing these challenges. With steady advancements in algorithms and computational power, AI enables the efficient exploration of new material properties, device designs, and parameter optimizations [14,15,16,26,27]. ML’s ability to establish connections between diverse parameters and functional outcomes through inverse design makes it an invaluable asset for developing innovative devices [28].

Building on this background, we propose an innovative LCP converter design that combines a wire grid structure with a self-complementary architecture. This design introduces VO₂ and graphene as the foundational tunable materials for their respective components, leveraging their unique properties to achieve adjustable transflective switching control. Utilizing ML tools, we optimize multiparameter device design by treating structural parameters as the feature set and performance metrics as the label set. Forward analysis reveals the mechanisms of and parameter weight on LCP conversion, while reverse prediction identifies the optimal parameter combination to achieve superior performance.

This study demonstrates the validity and feasibility of combining self-complementary structures with tunable materials (graphene and VO₂) within a wire grid polarizer (WGP) framework. Under ML-guided optimization, the proposed device achieves excellent circular polarization performance (attenuation < 3 dB) within a broad 100 GHz frequency range and exhibits dynamic switching capabilities through VO₂ phase transition adjustments. Furthermore, this work provides a valuable reference for developing multifunctional EM devices by integrating advanced materials and computational tools.

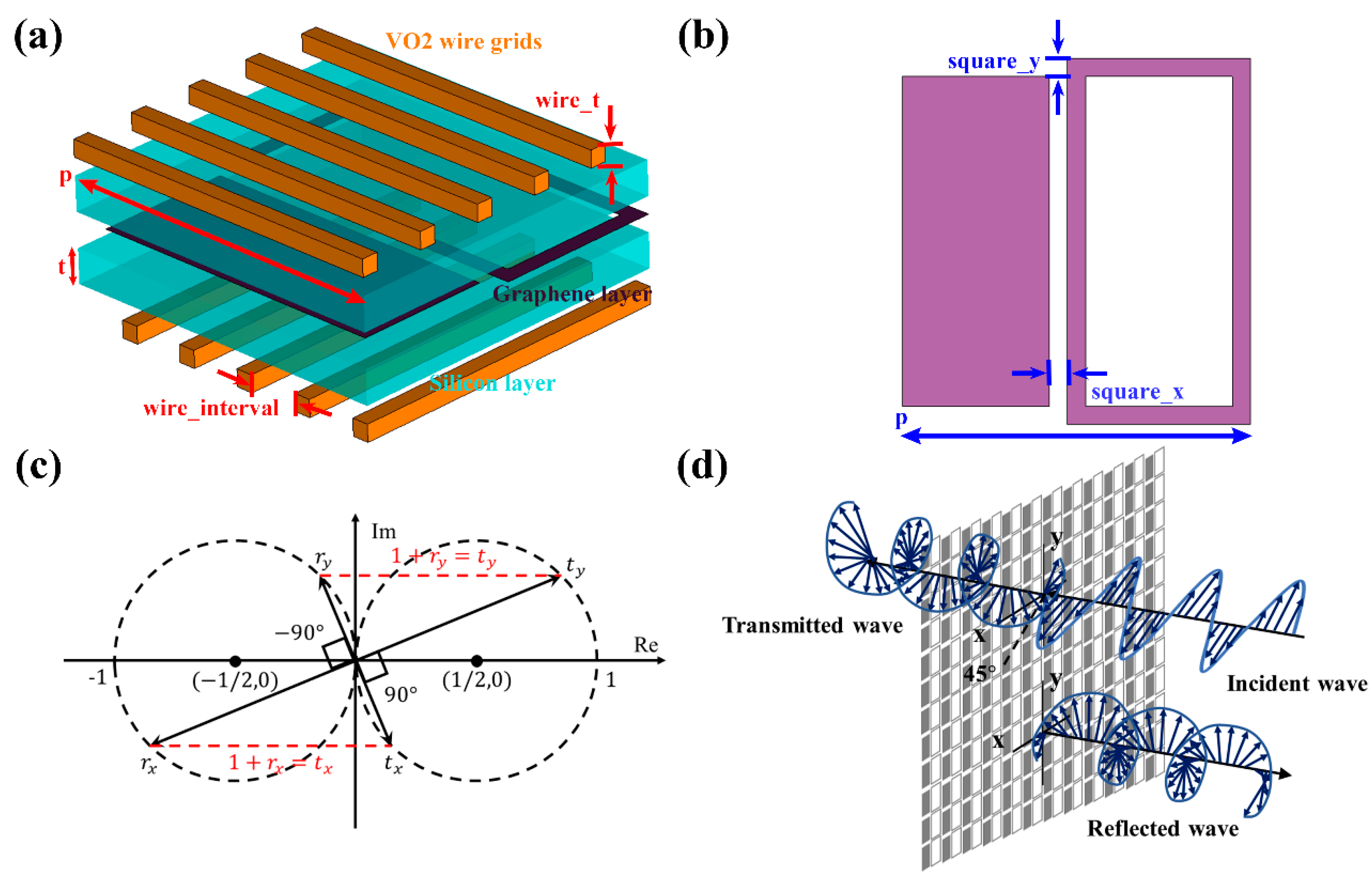
2. Theoretical Analysis and Design

2.1. Influence of Graphene Layer Number on Device Performance

The number of graphene layers in the proposed linear-to-circular polarization (LCP) converter can influence its performance. Graphene’s electronic and optical properties are highly dependent on its layer thickness, which affects its conductivity, Fermi level tunability, and interaction with electromagnetic (EM) waves [29]. In the current design, a single layer of graphene is used due to its optimal balance between conductivity and tunability.

Single-layer graphene exhibits a linear dispersion relation near the Dirac point, resulting in unique electronic properties such as high carrier mobility and tunable conductivity [30]. These characteristics make it ideal for applications requiring precise control over EM wave interactions, such as polarization conversions [31].

Few-layer graphene (2–10 layers) can exhibit higher conductivity compared to single-layer graphene, which may enhance the device’s ability to modulate EM waves [32]. However, the increased thickness can also introduce additional optical losses, potentially reducing the overall efficiency of polarization conversion [33].

Therefore, single-layer graphene is currently the preferred choice for the proposed LCP converter due to its optimal balance of tunability and low loss.

2.2. Theoretical Analysis and Fundamental Principles of LCP Device

The design of the LCP converter was performed in CST Microwave Studio, and the detailed configuration is shown in Figure 1a. Material-wise, VO₂ was used for WGP layers due to its phase transition capability, while graphene forms the core self-complementary layer for EM property modulation. The structural parameters (units in μm) were configured: graphene plays a crucial role in the proposed linear-to-circular polarization (LCP) converter due to its unique electronic and optical properties. As a two-dimensional material, graphene exhibits high electrical conductivity, a tunable Fermi level, and strong interaction with electromagnetic (EM) waves, particularly in the terahertz frequency range [34]. The Fermi level of graphene can be dynamically adjusted via external bias, allowing for precise control over its conductivity and optical response [29]. This tunability is essential for achieving efficient polarization conversion, as it enables the modulation of the phase and amplitude of the transmitted and reflected EM waves.

In the proposed design, graphene forms the core self-complementary layer, which is responsible for mediating LCP conversion. The ability to tune the graphene’s Fermi level allows the device to achieve optimal performance across a wide frequency range, particularly in the 500–750 GHz band. The high conductivity and low loss of graphene at these frequencies make it an ideal material for enhancing polarization conversion efficiency [30].

While graphene is a key component in the current design, it is worth exploring whether other carbon-based materials, such as carbon nanotubes (CNTs) or carbon nanofibers (CNFs), could be used as alternatives. CNTs and CNFs share some similarities with graphene, such as high electrical conductivity and mechanical strength, but they also exhibit distinct properties that may influence their performance in polarization conversion devices.

CNTs are one-dimensional materials with excellent electrical conductivity and mechanical properties [31]. They can be metallic or semiconducting depending on their chirality, which may offer additional degrees of freedom in tuning the EM response. However, CNTs typically exhibit anisotropic properties, which could complicate the design of polarization converters that require uniform EM wave interaction across all directions [35]. Additionally, the fabrication of large-area CNT films with consistent properties remains a challenge [36].

CNFs are another class of carbon-based materials with high surface area and good electrical conductivity [37]. They are often used in composite materials and could potentially be integrated into EM devices. However, CNFs generally have lower conductivity compared to graphene and CNTs, which may limit their effectiveness in high-frequency applications such as terahertz polarization conversion [18].

While CNTs and CNFs offer interesting possibilities, their use in the proposed LCP converter would require significant modifications to the design and optimization process. The anisotropic nature of CNTs and the lower conductivity of CNFs may necessitate additional structural adjustments to achieve comparable performance to graphene [17]. Furthermore, the tunability of these materials via external stimuli (e.g., bias voltage) may not be as straightforward as with graphene, potentially limiting their applicability in dynamically tunable devices [19].

The parameters of the device components are as follows: middle self-complementary layer—graphene monolayer (thickness = 0.334 nm); SiO₂ layers—thickness (t) = 10 μm, length (p) = 100 μm; WGP—wire thickness (wire_t) = 1 μm, width (wire_width) = 5 μm, interval (wire_interval) = 20 μm. The Babinet principle schematic (Figure 1b) explains how the self-complementary graphene structure mediates LCP conversion. The square dimensions of the self-complementary pattern are set as square_x = 5 μm and spuare_y = 5 μm.

2.3. The Principle of the Self-Complementary Transflective Polarization Converter

The self-complementary structure is a planar design comprising two fully complementary regions: open and solid. As shown in Figure 1b, it supports bidirectional EM wave propagation: incident waves ($E_1^{+}$, $E_2^{+}$) are the forward-propagating waves, and the escaping waves represent the waves exiting the metasurface. The scattering matrix is defined as

$$\left(\begin{array}{c}{E}_1^{-}\\ E_2^{-}\end{array}\right)=\left(\begin{array}{cc}{S}_{11}& S_{12}\\ S_{21}& S_{22}\end{array}\right)·\left(\begin{array}{c}{E}_1^{+}\\ E_2^{+}\end{array}\right)$$

(1)

During wave propagation through the metasurface, the E-field decomposes into orthogonal components (x- and y-polarized). Energy conservation ensures that

$${\left|r_x\right|}^2+{\left|t_x\right|}^2=1$$

(2)

$${\left|r_y\right|}^2+{\left|t_y\right|}^2=1$$

(3)

where r_x, r_y and t_x, t_y are reflection and transmission coefficients, respectively. Phase delay differences between these orthogonal components lead to a consistent 90° phase shift:

$$arg\left(r_y\right)-arg\left(r_x\right)=-\left(arg\right(t_y)-arg(t_x\left)\right)=\pm 90°$$

(4)

This ensures that the self-complementary layer induces LCP conversion [38], as depicted in Figure 1d.

To better evaluate the performance of the LCP converter, circular polarization parameters can be derived from the co-polarization and cross-polarization coefficients under linear excitation. Linearly polarized waves propagating along the x- and y-directions are assumed to impinge perpendicularly upon the device along the z-direction. The critical parameters, including the polarization azimuth rotation angle (α), ellipticity (β), and axial ratio (AR), can be expressed as follows:

$$\alpha ={\displaystyle \frac{1}{2}}{tan}^{-1}{\displaystyle \frac{2\left|t_{yy}\right|·{|t}_{xy}\left|cos\right({\phi }_{xy}-{\phi }_{yy})}{{{|t}_{yy}|}^2-{\left|t_{xy}\right|}^2}}$$

(5)

$$\beta ={\displaystyle \frac{1}{2}}{sin}^{-1}{\displaystyle \frac{2\left|t_{yy}\right|·{|t}_{xy}\left|sin\right({\phi }_{xy}-{\phi }_{yy})}{{{|t}_{yy}|}^2+{\left|t_{xy}\right|}^2}}$$

(6)

$$AR=10·{log}_{10}\left(tan\beta \right)$$

(7)

where t_yy and t_xy are the magnitude components of the transmission coefficients for the respective polarization directions; φ_yy and φ_xy represent the phase components of the corresponding transmission coefficients; and tan⁻¹ and sin⁻¹ denote the inverse trigonometric functions.

These parameters provide a detailed characterization of the device’s LCP conversion performance, serving as a vital reference for analyzing and optimizing the designed polarization converter.

2.4. The Materials with Tunable Properties

The functionality of the device relies on the tunable properties of graphene and VO₂, each playing a distinct role: graphene adjusts its EM properties through bias voltage, forming the core LCP layer; VO₂ achieves transreflective control through its temperature-dependent phase transition (insulator to metal).

Graphene conductivity is approximated using the Kubo formula, valid under high frequencies ($\mathrm{\hslash }\omega \ll E_f$ and $K_{B}T\ll E_f$):

$${\sigma }_{intra}\approx {\displaystyle \frac{e^2{E}_f}{\pi \hslash }}{\displaystyle \frac{i}{\omega +i{\tau }^{-1}}}$$

(8)

where Ef is the Fermi level, and τ is relaxation time determined by mobility and Fermi velocity.

VO₂ is modeled by the Drude model:

$$\epsilon (\omega )={\epsilon }_{\infty }-{\displaystyle \frac{{\omega }_p^2\left(\sigma \right)}{{\omega }^2+i{\rm Y}\omega }}$$

(9)

where ε_∞ = 12, ${\rm Y}$ = 5.75 × 1013 Rad/s, and ωp varies with conductivity. VO₂ exhibits phase-dependent conductivity, ranging from 20 S/m (at 298 K) to 2 × 105 S/m (at 358 K).

The Fermi level of graphene was modulated from 0 to 5 eV, and conductivity changes in VO₂ were validated across this range, ensuring flexibility in transreflective LCP performance [29,39].

3. Results and Discussion

As shown in Figure 2a, critical structural parameters and material properties were determined based on EM wave interactions and prior research [40]. Five structural parameters were selected as key inputs: the self-complementary square frame dimensions (square_x and square_y, in μm), wire grid width (wire_w, in μm), wire grid thickness (wire_t, in μm), substrate thickness (t, in μm), and square substrate size (p, in μm). Table S1 (Supplementary Materials) provides a comprehensive overview of these features.

To explore optimal designs, 183 simulations combining material properties (graphene, VO₂) and device structures were conducted. Details of the prepared dataset are listed in Table S2 (Supplementary Materials). Among the simulations, for reflection mode, 20 simulations demonstrated successful LCP performance (AR < 3 dB), while 163 simulations failed (AR > 3 dB). For transmission mode, 28 simulations succeeded, while 155 failed. A binary classification framework was developed, categorizing “Design success” as the positive class and “Design failure” as the negative class.

Given the variability in the effectiveness of different algorithms across various scenarios, it was crucial to identify the most suitable model for this specific problem, considering factors such as feature number, noise levels, and data value forms [41]. Four widely used ML models were trained and validated with 10-fold nested cross-validation (Figure 2b,c). Among the models, XGBoost delivered the best performance for optimizing designs in both reflection and transmission modes. Training performance and learning curves for XGBoost are presented in Figures S1 and S2 (Supplementary Materials).

XGBoost is an optimized gradient boosting algorithm derived from Gradient Boosting Decision Tree (GBDT). It excels at modeling complex relationships using an ensemble of decision trees, balancing accuracy and regularization to prevent overfitting. This approach is particularly effective for small datasets. This model works by selecting from an ensemble of M estimators w_j, j = 1,…, M:

$$\widehat{y_i}={\sum }_{j=1}^M{w}_j\left(x_i\right),$$

(10)

Mathematically, given N training data ${\{x_i,y_i\}}_{i=1}^N$, the objective of XGBoost is minimized:

$$obj(\theta )={\sum }_{i=1}^{N}l(y_i,\widehat{y_i})+{\sum }_{j=1}^M\mathsf{\Omega }\left(w_j\right)$$

(11)

where the loss term ${\sum }_{i=1}^{N}l(y_i,\widehat{y_i})$ measures prediction errors, and the regularization term ${\sum }_{j=1}^M\mathsf{\Omega }(w_j)$ penalizes model complexity. The additive training strategy adds one new tree at a time, by choosing the tree that optimizes the objective at step t, and a sequential additive strategy optimizes the model by iteratively building trees:

$${\widehat{y_i}}^t={\sum }_{j=1}^t{w}_j\left(x_i\right)={\widehat{y_i}}^{t-1}+w_t(x_i)$$

(12)

After the integration of useful structure–performance relationships (Figure 2a) and successive ML-based optimization, we identified essential parameters and an optimal model capable of reducing the AR below 3 dB across 500–750 GHz, as shown in Figure 2d.

The performance of the selected XGBoost model was assessed using the receiver operating characteristic (ROC) curve, shown in Figure 3a. The area under the ROC (AUROC) is a key metric for evaluating a model’s ability to discriminate between two classes at varying decision thresholds. An AUROC of 1.0 indicates perfect classification, while an AUROC of 0.5 (marked by the dashed line) represents random guessing. The XGBoost model achieved exceptional AUROC values of 0.98 for reflection and 0.95 for transmission, demonstrating its superior capability to distinguish between the “Design success” and “Design failure” categories in both directions. This high AUROC also implies that the model consistently identifies patterns and relationships between input parameters and design outcomes.

To optimize the multiparameter LCP converter and ensure effective LCP conversion with an AR below 3 dB in both the transmission and reflection directions (as outlined in Figure 1d), feature importance was analyzed based on the trained XGBoost model. The results, depicted in Figure 3b,c, reveal that the graphene Fermi level exerts the most significant influence on the LCP converter design. Following this, the horizontal and vertical square frame size (square_x and square_y) and VO₂ conductivity emerge as critical features. Conversely, the thickness and width of the wire grids (wire_t and wire_w) play relatively minor roles, consistent with previously reported findings [32]. This prioritization highlights the dominant role of certain parameters in achieving optimal LCP performance and informs the targeted adjustment of key features during the design process.

Using the input feature ranges detailed in Table S3 (Supplementary Materials), the XGBoost model predicted the “Design success” probabilities for the 1,358,280 combinations.

The results of these predictions were further analyzed to understand the effect of each feature on the model’s output. As illustrated in Figure 3d,e, which represent the reflection and transmission directions, respectively, a threshold probability of 0.5 (denoted by the black dotted line) was used to classify combinations as successful or not. The data show that features such as the Fermi level, VO₂ conductivity, and square frame sizes (square_x and square_y) strongly influence the clustering of successful designs (probability > 0.5). This observation is consistent with the importance rankings in Figure 3b,c, emphasizing the critical impact of these parameters on the design’s success probability.

Beyond numerical evaluation, the results also suggest underlying physical mechanisms that govern LCP performance. The prominence of the graphene Fermi level may be attributed to its direct impact on the material’s conductivity and tunability in response to EM waves. Similarly, square frame sizes and VO₂ conductivity likely affect polarization conversion efficiency by modulating resonance conditions and material properties. Features like wire_t and wire_w, while less influential, still contribute to fine-tuning overall device performance, potentially by minimizing parasitic effects and optimizing structural stability.

The combined analysis of both feature importance and predicted probabilities provides comprehensive guidance for the design optimization of LCP converters. By focusing on the key parameters identified, the design process can efficiently converge on configurations that maximize performance, paving the way for practical implementations of high-efficiency polarization conversion devices.

Among the numerous transmission and reflection combinations predicted by the trained ML model, 12 combinations with the highest success probability in both directions were selected for simulation to validate the predictions. The results confirmed that all these combinations yielded positive outcomes, with at least some frequency points achieving an AR < 3 dB within the 500–750 GHz range. This consistent agreement between predictions and experimental observations highlights the efficacy of the multiparameter LCP converter design framework guided by the ML model. Figure 4 presents the results for the optimal combination among the 12 combinations, showcasing its detailed parameter configuration and performance. For this configuration, the substrate thickness t is 10 μm, the square substrate size p is 100 μm, the graphene Fermi level is 0.5 eV, wire_t and wire_w are both 5 μm, and the square frame dimensions (square_x and square_y) are also 5 μm. These parameters collectively lead to a device capable of achieving high-performance LCP conversion in both the transmission and reflection directions under distinct VO₂ conductivity states.

In the transmission direction, the LCP converter demonstrates excellent performance, maintaining an AR < 3 dB across a bandwidth of approximately 0.1 THz when the VO₂ conductivity of the wire grids is 20 S/m. This value represents the insulating state of VO₂, wherein the material’s dielectric properties contribute to the efficient control of polarization rotation without significant energy loss. In the reflection direction, similar high-performance LCP conversion is observed when VO₂ conductivity transitions to 200,000 S/m, representing its metallic state. This transition underscores the material’s tunability and its capacity to modulate polarization conversion by altering electrical conductivity.

The superior performance achieved with the optimal combination not only validates the robustness of the trained ML model but also provides deeper insights into the underlying design principles. For instance, the relatively high Fermi level of graphene (0.5 eV) plays a crucial role in enhancing the tunability and reconfigurability of the device, particularly in the terahertz frequency range where graphene exhibits unique electro-optical properties. The dimensions of the square frame and the wire grid components contribute to achieving precise resonance conditions that enhance polarization conversion efficiency, highlighting the importance of structural parameters in guiding the LCP converter’s behavior. Furthermore, this analysis exemplifies the potential for fine-tuning device performance across diverse operating conditions by leveraging the programmable conductivity of VO₂. The dual functionality of the device in the transmission and reflection directions, regulated by different VO₂ conductivity states, offers significant practical advantages for developing versatile LCP converters. These findings provide a pathway for extending the design methodology to other frequency ranges and device applications, reinforcing the role of ML-driven optimization in advancing the field of tunable metamaterials.

In summary, the configuration highlighted in Figure 4 underscores the success of combining ML with parameter-specific optimization to design high-performance LCP converters. The validation of predictive results and the identified design mechanisms pave the way for the future exploration and implementation of reconfigurable devices in advanced communication and sensing systems.

To further elucidate information embedded in the predicted combinations, a new metric—the “Design success” ratio—was defined and calculated. This ratio represents the proportion of “Design success” conditions for each feature at specific values, relative to the total number of 1,135,280 combinations. The results are visualized in Figure 5, with subplots illustrating the “Design success” ratios for the reflection direction (Figure 5a) and the transmission direction (Figure 5b).

The analysis of Figure 5 enables the determination of optimal parameter ranges that yield high success probabilities for designing an excellent LCP converter:

• Fermi level: The optimal ranges are < 3 eV for reflection and approximately 0.5 eV for transmission. These values highlight the role of graphene’s tunable Fermi energy in influencing polarization conversion and enabling precise resonant behavior in different directions.
• Wire grid thickness (wire_t): Success ratios peak for thickness values between 1 and 5 μm in the reflection direction and at exactly 5 μm in the transmission direction. This confirms the importance of fine-tuning grid dimensions to achieve effective impedance matching.
• Wire grid width (wire_w): The optimal width range spans 2–10 μm for both directions, excluding 4 μm in the transmission case. The slight variation suggests nuanced interplay between the grid’s geometrical properties and the underlying field distribution.
• Square frame size (square_x, square_y): For reflection, the preferred ranges are 5–30 μm (square_x) and 8–30 μm (square_y). For transmission, optimal sizes are fixed at 5 μm (square_x) and within 5–7 μm (square_y). This indicates that smaller, symmetric frame dimensions perform better in the transmission direction due to their contribution to uniform field enhancement.
• VO₂ conductivity: The model identifies distinct optimal values for VO₂: 20 S/m (insulating state) and 200,000 S/m (metallic state) for reflection, and primarily 20 S/m for transmission. These findings validate VO₂’s critical role in modulating the dual-direction functionality of the device.
• Square substrate size (p): The preferred size ranges are 40–100 μm for reflection and, specifically, 90–100 μm for transmission. The observed trend underscores the role of substrate dimensions in achieving resonance and minimizing energy losses.

Notably, the identified parameter ranges align closely with the optimal combination highlighted in earlier analyses, thereby reinforcing the predictive accuracy and reliability of the ML-guided design approach. These results also exhibit strong consistency with experimental data, confirming the ability of the ML model to navigate a complex, high-dimensional design space and isolate configurations that achieve superior LCP conversion performance.

The machine learning (ML)-guided optimization approach presented in this study offers several advantages over traditional design methods, particularly in terms of speed, cost, and accuracy. Traditional design methods for electromagnetic (EM) devices, such as linear-to-circular polarization (LCP) converters, often rely on iterative trial-and-error processes, which can be time-consuming and resource-intensive [41]. These methods typically involve manual parameter tuning and extensive simulations, which may not efficiently explore the vast design space of multiparameter devices. In contrast, ML-based optimization provides a more systematic and efficient approach to navigating complex parameter interactions, leading to faster and more cost-effective design processes.

Traditional design methods often require numerous iterations and simulations to identify optimal parameter combinations, which can take weeks or even months depending on the complexity of the device [27]. In contrast, ML algorithms, such as the XGBoost model used in this study, can analyze large datasets of parameter combinations and predict high-performing designs in a matter of hours or days [26]. This significant reduction in design time is particularly beneficial for complex devices with multiple tunable materials and intricate parameter interactions.

The computational cost of traditional design methods can be high due to the need for extensive simulations and experimental validations [15]. ML-based optimization reduces these costs by leveraging pre-trained models and efficient algorithms to predict optimal designs without the need for exhaustive simulations. Additionally, the ability of ML to identify high-performing designs early in the design process can reduce the need for costly experimental iterations [14].

Traditional design methods often struggle to achieve high accuracy in multiparameter optimization due to the complexity of parameter interactions and the limitations of manual tuning [38]. ML algorithms, on the other hand, can establish complex relationships between input parameters and device performance, leading to more accurate predictions of optimal designs. In this study, the XGBoost model achieved high accuracy, with area under the receiver operating characteristic (AUROC) values of 0.98 for reflection and 0.95 for transmission, demonstrating its superior ability to distinguish between successful and unsuccessful designs [28].

This study further exemplifies the capability of ML-driven frameworks to offer actionable insights into metamaterial design. By translating predictive outputs into interpretable metrics such as success ratios, the method enables the precise identification of key parameter regimes, thereby simplifying the optimization process. The observed agreement between simulations, experiments, and the optimal predicted ranges solidifies the foundation for leveraging ML in future metamaterial and device design endeavors.

The machine learning (ML)-guided optimization approach presented in this study is not limited to linear-to-circular polarization (LCP) converters. The methodology can be extended to other types of polarization converters and electromagnetic (EM) devices, offering a versatile framework for multiparameter optimization. For instance, ML techniques have been successfully applied in the design of broadband linear-to-linear polarization converters [9], circular-to-linear polarization converters [8], and even multifunctional chiral metamaterials [17]. These studies demonstrate the potential of ML in optimizing complex EM structures, particularly when dealing with multiple tunable materials and intricate parameter interactions.

Moreover, the integration of ML with tunable materials such as graphene and VO₂ can be adapted for other EM devices, including tunable absorbers [22], reconfigurable metasurfaces [28], and frequency-selective surfaces [21]. The ability of ML to navigate high-dimensional design spaces and identify optimal parameter combinations makes it a powerful tool for advancing the field of tunable metamaterials and EM devices. For example, recent work has shown that ML can be used to optimize the performance of terahertz modulators [24] and dynamically tunable antennas [23], further highlighting the broad applicability of this approach.

By leveraging the insights gained from this study, future research can explore the application of ML-guided optimization in other frequency ranges and device configurations, potentially leading to the development of novel EM devices with enhanced performance and functionality.

The performance of the proposed linear-to-circular polarization (LCP) converter under various environmental conditions, such as temperature changes, physical stress, and the presence of interfering signals, is an important consideration for practical applications. The device’s design incorporates tunable materials like graphene and vanadium dioxide (VO₂), which are sensitive to environmental factors, making it essential to evaluate its robustness in real-world scenarios.

For the temperature sensitivity, the phase transition property of VO₂, which changes from an insulating to metallic state at temperatures above 68 °C, plays a critical role in the device’s functionality [19]. While this property enables dynamic switching between reflective and transmissive modes, it also means that the device’s performance may be affected by ambient temperature fluctuations. However, the ML-guided optimization process ensures that the device operates efficiently within a specified temperature range, as demonstrated by the successful performance in both insulating (20 S/m) and metallic (200,000 S/m) states of VO₂ [18]. Future work could explore the integration of temperature compensation mechanisms to enhance the device’s stability under varying thermal conditions [17].

Additionally, the structural integrity of the device under physical stress, such as mechanical deformation or vibration, is another important consideration. The use of graphene, known for its exceptional mechanical strength and flexibility, provides some resilience against physical stress [29]. However, the rigid components of the wire grid polarizer (WGP) and substrate may be more susceptible to damage under extreme conditions. To address this, future designs could incorporate flexible substrates or protective coatings to improve the device’s durability [37].

In practical applications, the presence of interfering signals from other EM sources could also impact the device’s performance. The self-complementary structure of the LCP converter, combined with the tunable properties of graphene and VO₂, provides a degree of immunity to interference by allowing the dynamic adjustment of the device’s response [9]. Additionally, the ML-guided optimization process ensures that the device operates efficiently within a broad frequency range (500–750 GHz), reducing the likelihood of interference from signals outside this band [8]. Further studies could explore the use of advanced filtering techniques or adaptive algorithms to enhance the device’s resistance to interference [23].

4. Conclusions

This study successfully demonstrates the application of machine learning (ML) in guiding the multiparameter design of a novel LCP converter. The device, comprising two wire grid structures with a Babinet LCP converter structure, achieves excellent performance in both the transmission and reflection directions within the 500–750 GHz frequency range, with an AR (reflection loss) less than 3 dB. The high AUROC values of 0.98 for reflection and 0.95 for transmission indicate the excellent performance of the well-trained XGBoost model. We compare the performance of our proposed linear-to-circular polarization (LCP) converter with previous similar studies in Table S4.

Through the model’s feature importance analysis, we identified that the graphene Fermi level, wire grid thickness, and VO₂ conductivity are the most critical parameters influencing the converter’s performance, consistent with the fact that material properties govern EM wave interactions. By optimizing the structural parameters, we achieved high “Design success” probabilities, and simulation verifications confirmed the strong correlation between the square size and LCP conversion performance.

Our work not only showcases the potential of ML for optimizing complex design parameters but also highlights the successful integration of ML into the multiparameter design of multifunctional EM devices. The developed device structure offers a new design framework for high-performance, tunable, and multifunctional LCP converters with steerable functions. The integration of ML into the design process marks a significant advancement in accelerating the development of metamaterial-based devices and offers a foundation for future studies aimed at enhancing their functionalities.