Application of Highly Spatially Resolved Area Array Velocity Measurement in the Cracking Behavior of Materials
Abstract
1. Introduction
2. Materials and Methods
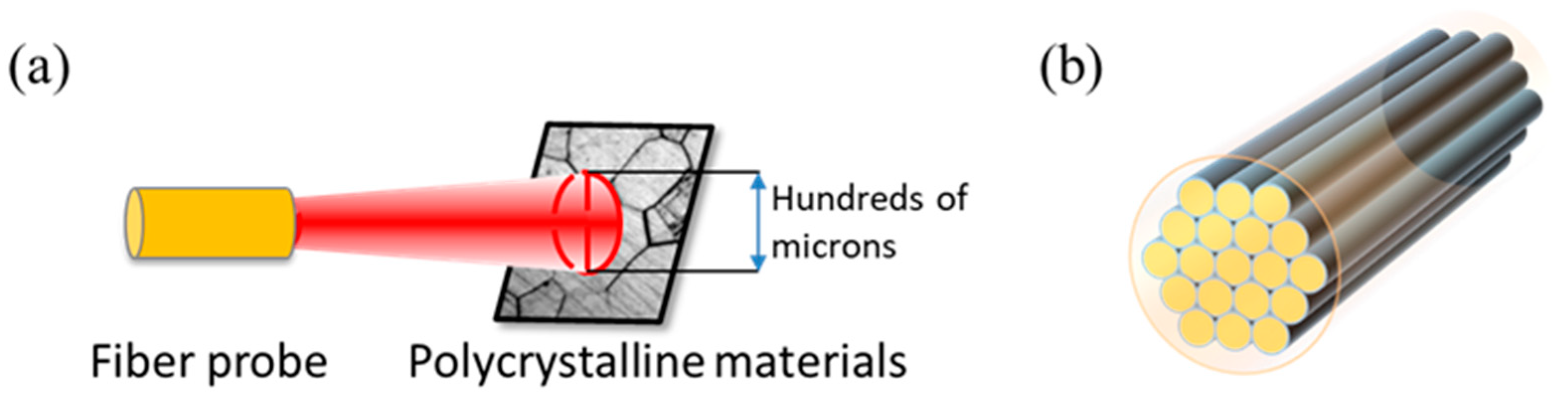
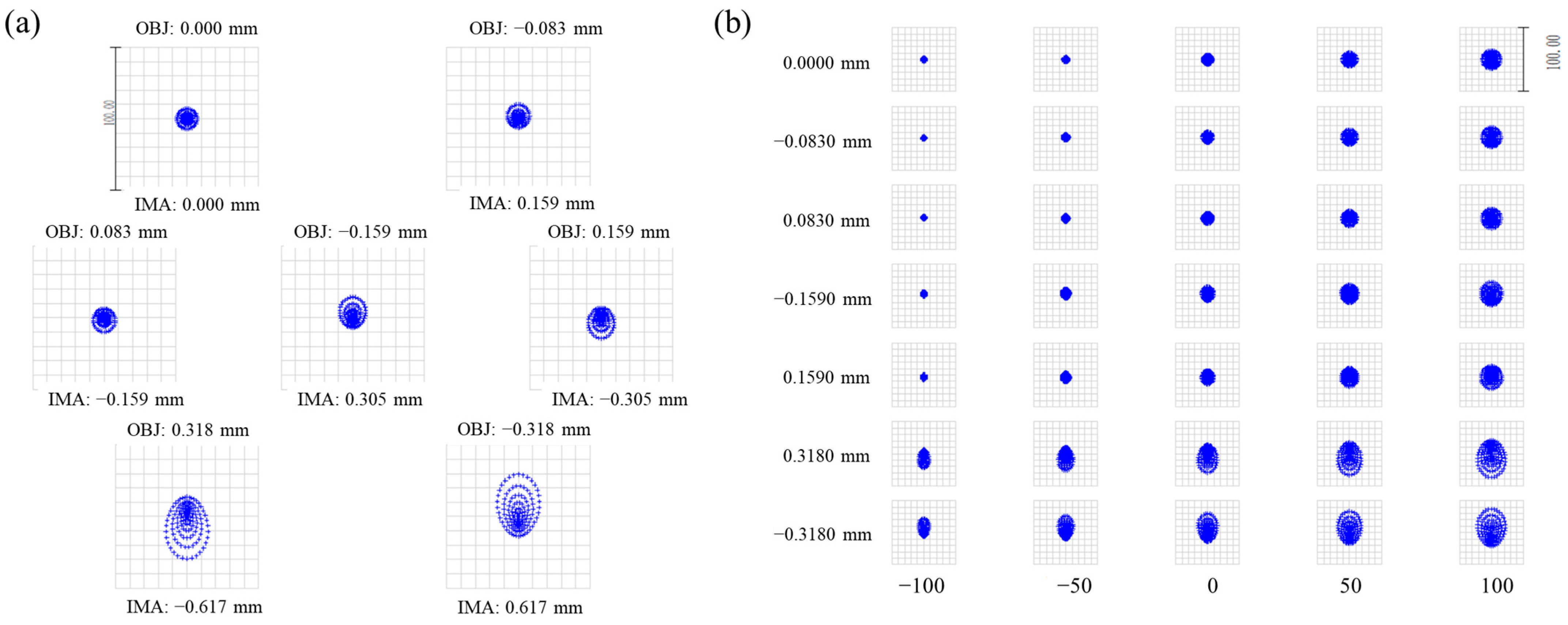
2.1. Area Array Fiber Optic Probes
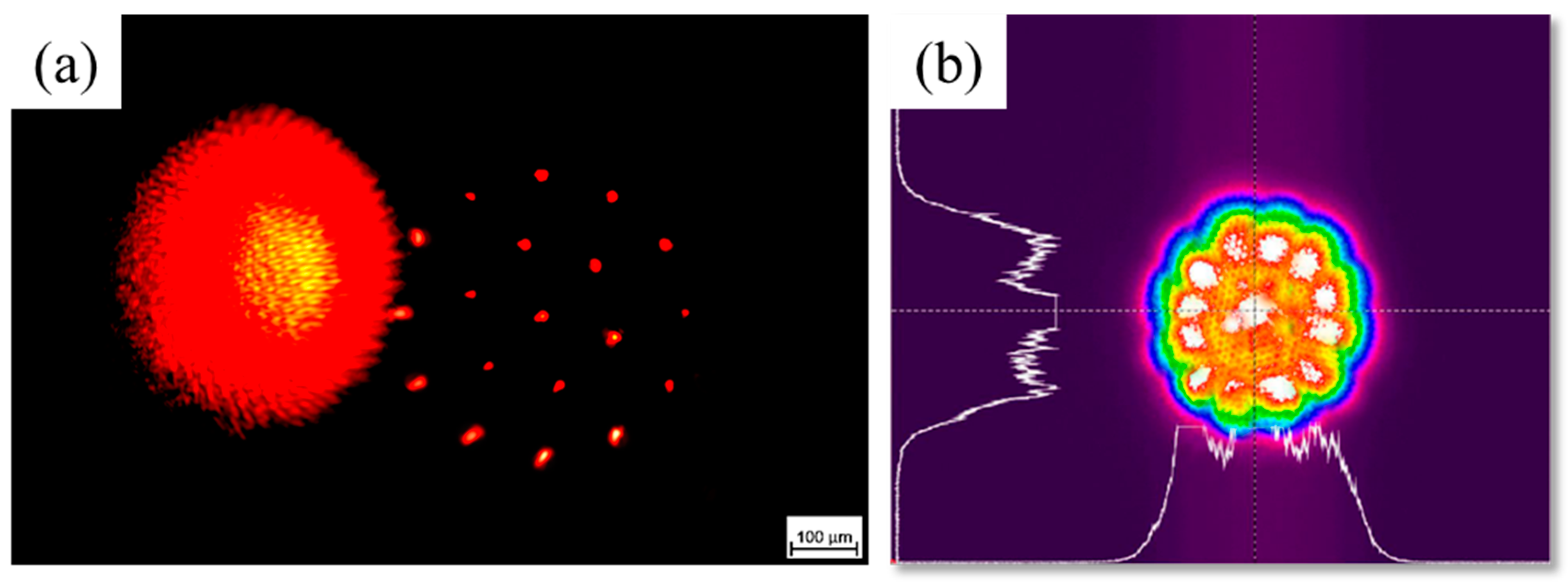
2.2. Experimental System
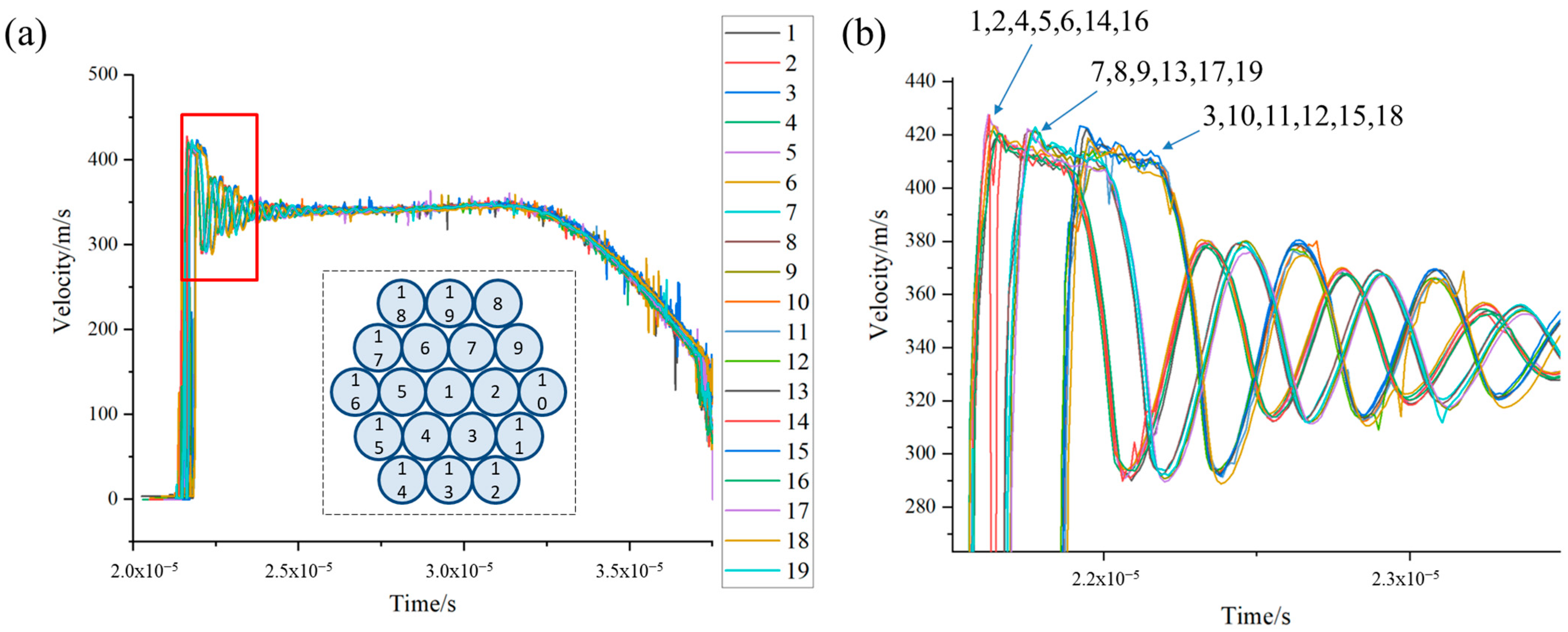
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Huang, J.Y.; E, J.C.; Huang, J.W.; Sun, T.; Fezzaa, K.; Xu, S.L.; Luo, S.N. Dynamic deformation and fracture of single crystal silicon: Fracture modes, damage laws, and anisotropy. Acta Mater. 2016, 114, 136–145. [Google Scholar] [CrossRef]
- Williams, C.L.; Kale, C.; Turnage, S.A.; Shannahan, L.S.; Solanki, K.N.; Becker, R.; Hufnagel, T.C.; Ramesh, K.T. Real-time observation of twinning-detwinning in shock-compressed magnesium via time-resolved in situ synchrotron XRD experiments. Phys. Rev. Mater. 2020, 4, 083603. [Google Scholar] [CrossRef]
- Menshykov, O.V.; Menshykova, M.V.; Guz, I.A. Effects of crack closure and friction for linear crack under normal impact. Eng. Anal. Bound. Elem. 2020, 115, 1–9. [Google Scholar] [CrossRef]
- Nissim, N.; Greenberg, E.; Werdiger, M.; Horowitz, Y.; Bakshi, L.; Ferber, Y.; Glam, B.; Fedotov-Gefen, A.; Perelmutter, L.; Eliezer, S. Free-surface velocity measurements of opaque materials in laser-driven shock-wave experiments using photonic Doppler velocimetry. Matter Radiat. Extrem. 2021, 6, 046902. [Google Scholar] [CrossRef]
- Weng, J.D.; Tan, H.; Wang, X.; Ma, Y.; Hu, S.L.; Wang, X.S. Optical-fiber interferometer for velocity measurements with picosecond resolution. Appl. Phys. Lett. 2006, 89, 111101. [Google Scholar] [CrossRef]
- Whiteman, G.; Owen, G.D.; De, J.; Chapman, D.; Eakins, D.; Turner, J.; Millett, J. Spatially resolved measurements of grain size effects on the shock and spall response of quasi-Taylor wave loaded pure copper. J. Appl. Phys. 2017, 122, 035106. [Google Scholar] [CrossRef]
- Vogler, T.J.; Trott, W.M.; Reinhart, W.D.; Alexander, C.S.; Furnish, M.D.; Furnish, M.D.; Chhabildas, L.C. Using the line-VISAR to study multi-dimensional and mesoscale impact phenomena. Int. J. Impact Eng. 2008, 35, 1844–1852. [Google Scholar] [CrossRef]
- Mikhaylyuk, A.V.; Koshkin, D.S.; Gubskii, K.L.; Kuznetsov, A.P. Line-imaging VISAR for laser-driven equations of state experiments. J. Phys. Conf. Ser. 2016, 774, 012057. [Google Scholar] [CrossRef]
- Zhou, K.; Huang, Y.P.; Chen, E.; Yuan, R.; Zhang, Z. Real-Time Detection and Spatial Segmentation of Difference Image Motion Changes. IEEE Access 2020, 8, 144931–144944. [Google Scholar] [CrossRef]
- Sheng, B.; Huang, J.C.; Ji, H.F.; Huang, Z.Y. A New Contactless Cross-Correlation Velocity Measurement System for Gas—Liquid Two-Phase Flow. Sensors 2023, 23, 4886. [Google Scholar] [CrossRef]
- Rocha, D.M.; Kanizawa, F.T.; Hayashi, K.; Hosokawa, K.; Tomiyama, A.; Ribatski, G. Velocity field characterization of single-phase flows across a tube bundle through spatial filter velocimetry. Exp. Therm. Fluid Sci. 2023, 147, 110947. [Google Scholar] [CrossRef]
- Chi, Z.P.; Yang, H.; Li, R.; Sun, Q.C. Measurements of unconfined fresh concrete flow on a slope using spatial filtering velocimetry. Powder Technol. 2021, 393, 349–356. [Google Scholar] [CrossRef]
- Schaeper, M.; Damaschke, N. Fourier-based layout for grating function structure in spatial filtering velocimetry. Meas. Sci. Technol. 2017, 28, 055008. [Google Scholar] [CrossRef]
- Celliers, P.M.; Bradley, D.K.; Collins, G.W.; Hicks, D.G.; Boehly, T.R.; Armstrong, W.J. Line-imaging velocimeter for shock diagnostics at the OMEGA laser facility. Rev. Sci. Instrum. 2004, 75, 4916. [Google Scholar] [CrossRef]
- Fratanduono, D.E.; Eggert, J.H.; Boehly, T.R.; Barrios, M.A.; Collins, G.W. Internal target reflections and line-imaging velocimetry. High Energy Density Phys. 2014, 11, 26–29. [Google Scholar] [CrossRef]
- Glinsky, M.E.; Weis, M.R.; Pollock, B.; Moody, J.; Strozzi, D.J.; Beckwith, K.; Thompson, A.J. Line VISAR measurements of energy deposition for next generation MagLIF laser preheat at NIF. In Proceedings of the IEEE International Conference on Plasma Science (ICOPS), Lake Tahoe, NV, USA, 12–16 September 2021. [Google Scholar]
- Darbon, S.; Duval, A.; Masclet-Gobin, I.; Marchet, B.; Brygoo, S.; Courtois, C.; Debras, G.; Patissou, L.; Parreault, R.; Lobios, O.; et al. VISAR diagnostic at LIL facility. EPJ Web Conf. 2013, 59, 13001. [Google Scholar] [CrossRef]
- Pawlicki, J.; Stanik, Z.; Płachta, A.; Kubik, A. A New Method of Testing the Dynamic Deformation of Metals. Materials 2021, 14, 3317. [Google Scholar] [CrossRef]
- Eksergian, C.L. The Plastic Behavior of Metal in Drawing. J. Fluids Eng. 2023, 48, 609. [Google Scholar] [CrossRef]
- Deluigi, O.; Amigo, N.; Valencia, F.J.; Aquistapace, F.; Tramontina, D.R.; Tramontina, R.I.; Tramontina, E.M. Plastic behavior of a nanoporous high-entropy alloy under compression. Comput. Mater. Sci. 2023, 226, 112241. [Google Scholar] [CrossRef]
- Chatterjee, K.; Arumuru, V.; Patil, D.; Jha, R. Multipoint monitoring of amplitude, frequency, and phase of vibrations using concatenated modal interferometers. Sci. Rep. 2022, 12, 3798. [Google Scholar] [CrossRef]
- Van Acoleyen, K.; Rogier, H.; Baets, R. Two-dimensional optical phased array antenna on silicon-on-insulator. Opt. Express 2010, 18, 13655–13660. [Google Scholar] [CrossRef] [PubMed]
- Das, U.; Mishra, H.; Mallick, Z.; Gupta, V.; Dehingia, A.; Roy, A.; Manda, D. Insight of the high switching window and data retention in lead-free 2D layered double perovskite resistive memory device. Appl. Phys. Lett. 2023, 123, 203505. [Google Scholar] [CrossRef]
- Liu, X.S.; Li, R.Z.; Chen, G.H.; Liu, J.; Tian, J.H.; Meng, J.H.; Peng, Q.X.; Yuan, S.Y. Demonstration of High Resolution Line-Imaging VISAR Application in Detonation Physics. Chin. J. High Press. Phys. 2014, 28, 307–312. [Google Scholar]
- Park, S.J.; Heogh, W.; Yang, J.; Kang, S.; Jeong, W.; Lee, H.; Jang, T.S.; Jung, H.D.; Jahazi, M.; Han, S.C.; et al. Meta-structure of amorphous-inspired 65.1Co28.2Cr5.3Mo lattices augmented by artificial intelligence. Adv. Compos. Hybrid Mater. 2024, 7, 224. [Google Scholar] [CrossRef]
- Hintsala, E.D.; Hangen, U.; Stauffer, D.D. High-Throughput Nanoindentation for Statistical and Spatial Property Determination. J. Miner. Met. Mater. Soc. 2018, 70, 494–503. [Google Scholar] [CrossRef]



| Parameter | DISAR | VISAR | Comparative Analysis |
|---|---|---|---|
| temporal resolution | 50 ps (single-channel) | 20 ps (streak camera recording) | DISAR achieves picosecond-level resolution via fiber dispersion compensation; VISAR relies on hardware limits of high-speed cameras. |
| spatial resolution | 80 nm (axial) | 4 μm (lateral) | DISAR’s axial resolution reaches nanometer scale, ideal for micro-zone damage analysis; VISAR excels in lateral resolution for full-field observation. |
| velocity range | 0.1 m/s–10 km/s | 4–50 km/s (high-energy laser loading) | VISAR is mature for ultra-high velocities (>20 km/s), while DISAR offers higher accuracy at low velocities (<1 km/s). |
| relative velocity error | <1% (full range) | 1–3% (depends on fringe contrast) | DISAR’s error stems from photodetector noise (<0.5%); VISAR’s error arises from fringe-counting ambiguity. |
| multi-channel capability | 1–16 channels (synchronous) | Single-point or line array (requires multiple cameras) | DISAR’s fiber arrays enable distributed damage monitoring; VISAR’s scalability is limited by optical system complexity. |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, L.; Tang, L.; Ma, H.; Gu, W.; Liu, C.; Jia, X.; Tao, T.; Liu, S.; Chen, Y.; Wang, X.; et al. Application of Highly Spatially Resolved Area Array Velocity Measurement in the Cracking Behavior of Materials. Electronics 2025, 14, 1732. https://doi.org/10.3390/electronics14091732
Chen L, Tang L, Ma H, Gu W, Liu C, Jia X, Tao T, Liu S, Chen Y, Wang X, et al. Application of Highly Spatially Resolved Area Array Velocity Measurement in the Cracking Behavior of Materials. Electronics. 2025; 14(9):1732. https://doi.org/10.3390/electronics14091732
Chicago/Turabian StyleChen, Long, Longhuang Tang, Heli Ma, Wei Gu, Cangli Liu, Xing Jia, Tianjiong Tao, Shenggang Liu, Yongchao Chen, Xiang Wang, and et al. 2025. "Application of Highly Spatially Resolved Area Array Velocity Measurement in the Cracking Behavior of Materials" Electronics 14, no. 9: 1732. https://doi.org/10.3390/electronics14091732
APA StyleChen, L., Tang, L., Ma, H., Gu, W., Liu, C., Jia, X., Tao, T., Liu, S., Chen, Y., Wang, X., Wu, J., Li, C., & Weng, J. (2025). Application of Highly Spatially Resolved Area Array Velocity Measurement in the Cracking Behavior of Materials. Electronics, 14(9), 1732. https://doi.org/10.3390/electronics14091732







