Energy Efficiency Based Control Strategy of a Three-Level Interleaved DC-DC Buck Converter Supplying a Proton Exchange Membrane Electrolyzer
Abstract
1. Introduction
2. Presentation and Benefits of the Three-Level Interleaved DC-DC Buck Converter
- Enhanced overall converter efficiency due to the interleaved architecture and zero-current-transition (ZCT) feature.
- A higher step-down conversion ratio needed for multi-source systems based on DC grid configuration.
- Minimized output current ripples which allow enhancing performance of the EL.
- Improved system availability following power switch failures and increase the converter power rating by paralleling phases.
- Decreased both voltage and current ratings of power switches and diodes.
- Reduced volume of passive components.
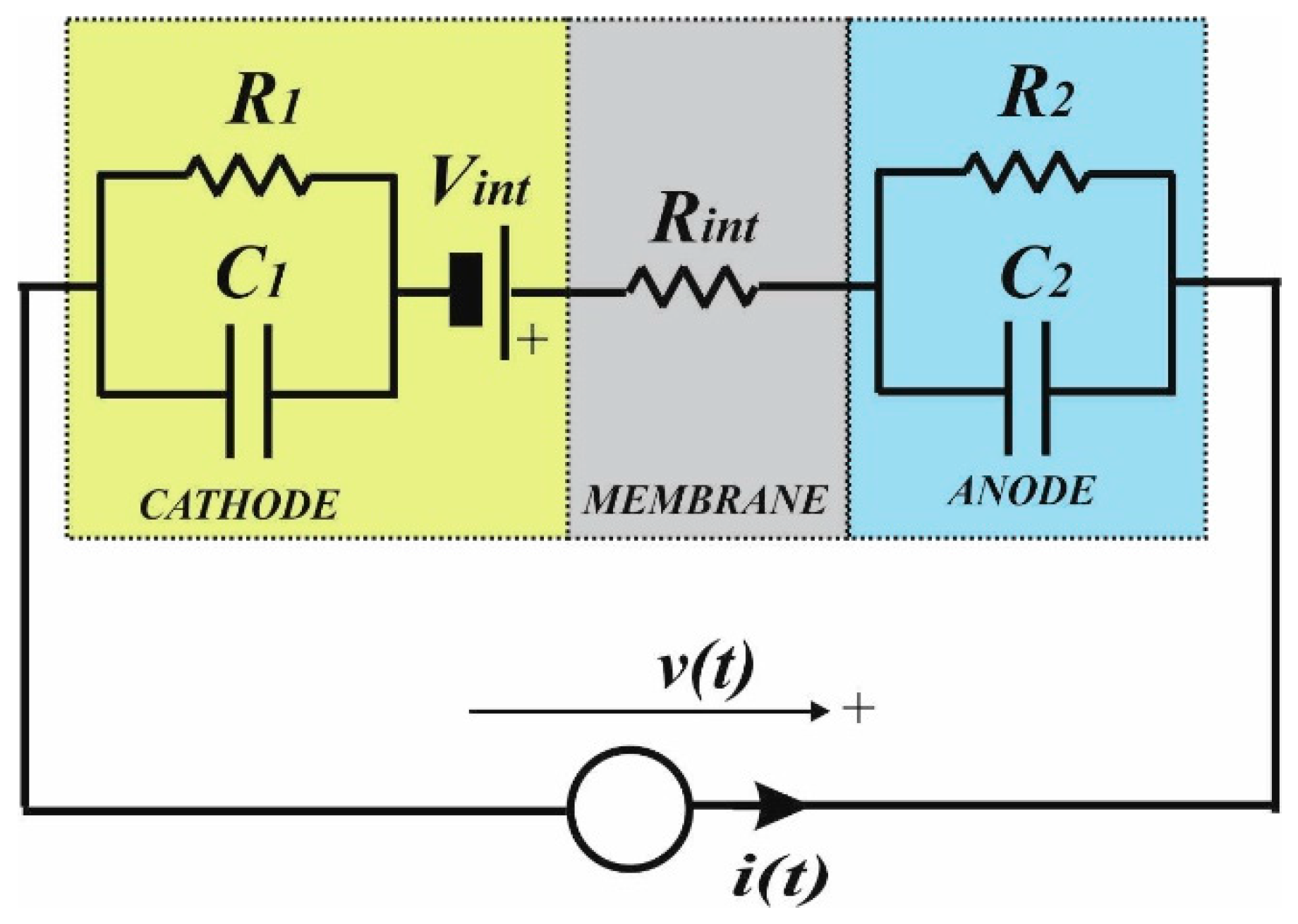
- Rtot: sum of the resistance in the equivalent model, taking into consideration activation losses both at the anode and cathode and membrane losses. The total resistance value is equal to 0.441 Ω.
- Vint: reversible voltage of the PEM EL, which is equal to 4.38 V.
3. Objective, Energy Efficiency Investigation and Design of Control Laws
3.1. Objective of the Control
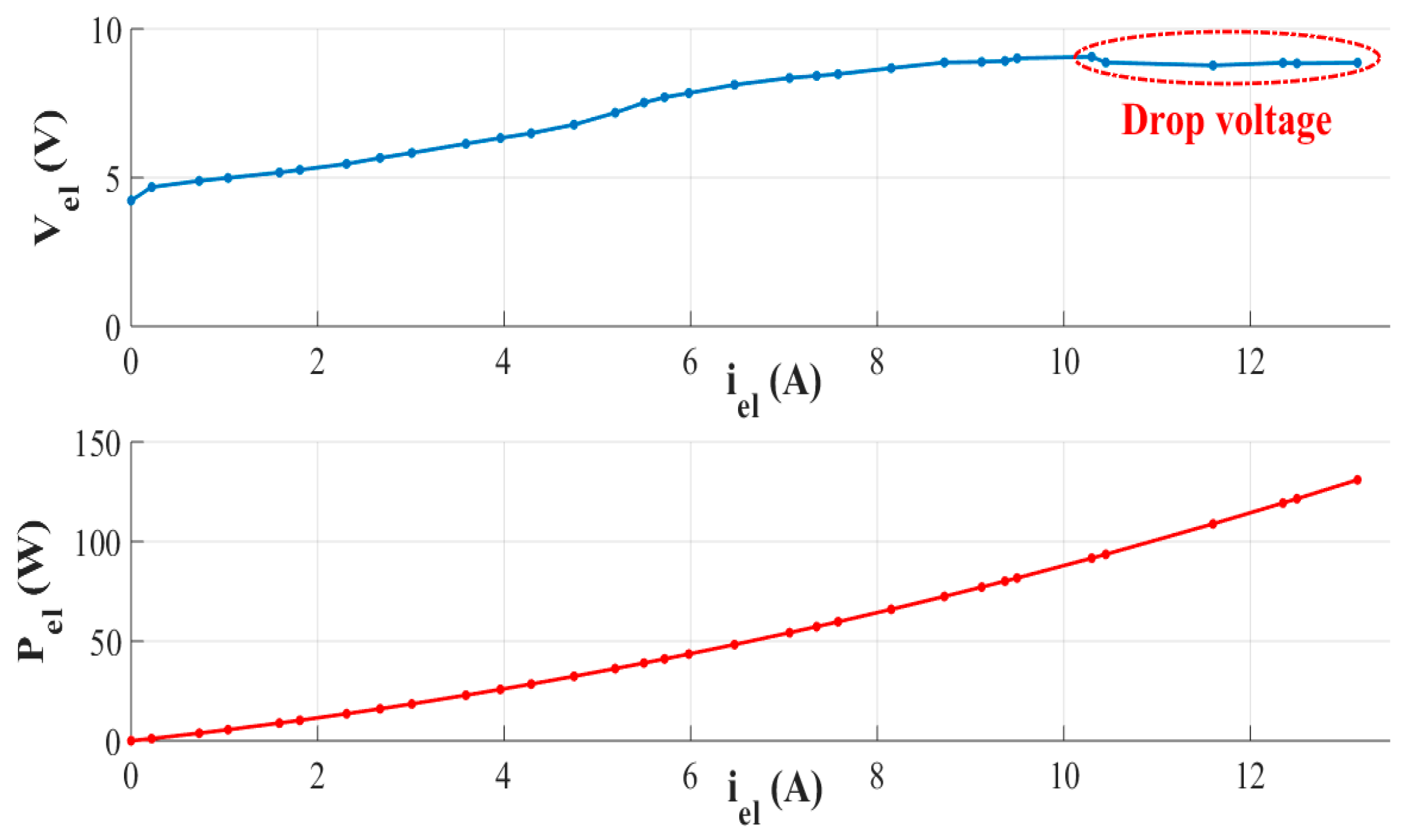
3.2. Specific energy consumption and hydrogen flow rate investigation
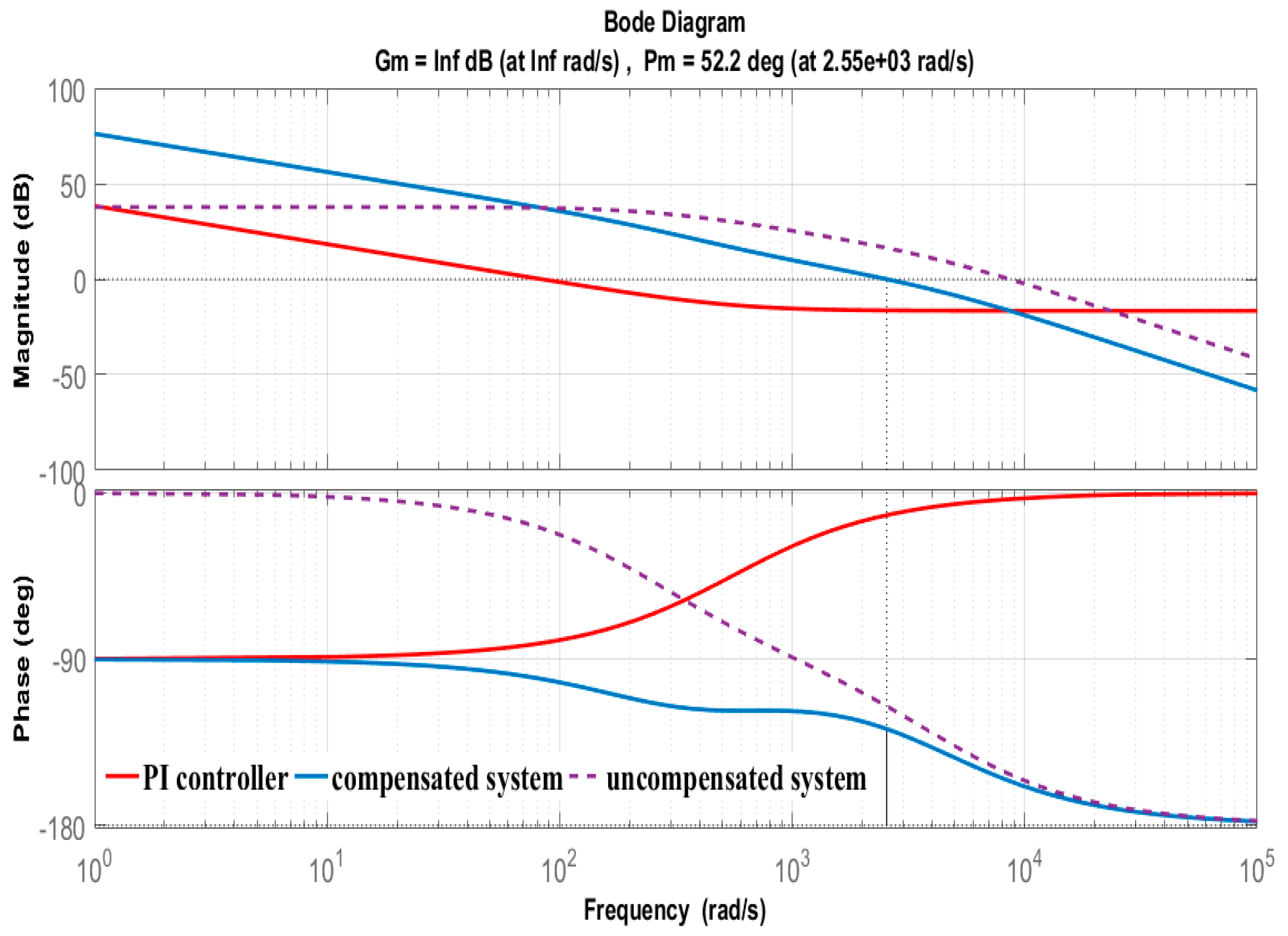
3.3. Design of the EL Voltage Control
4. Presentation of the Experimental Setup and Results
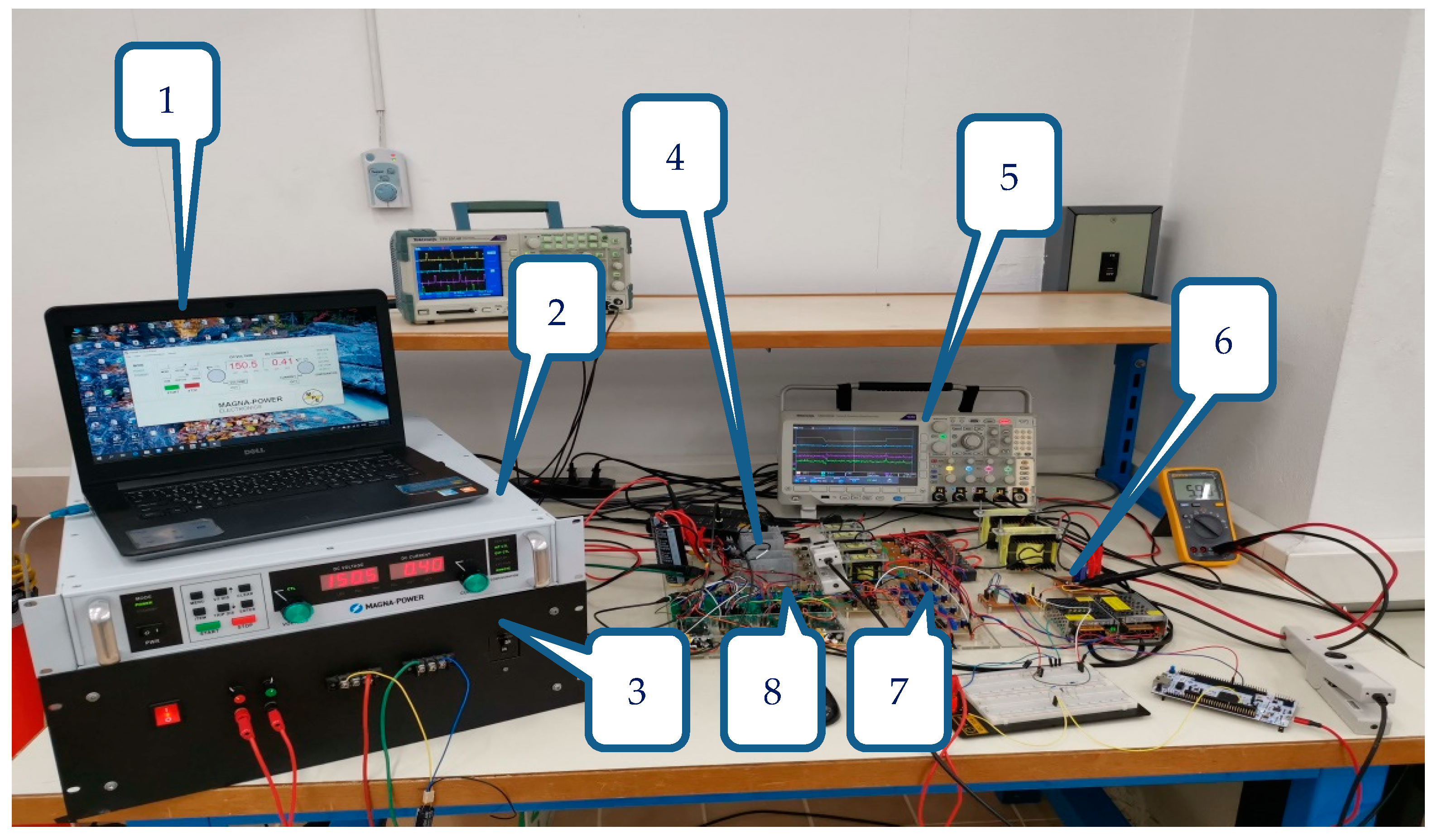
4.1. Realization of the Experimental Setup
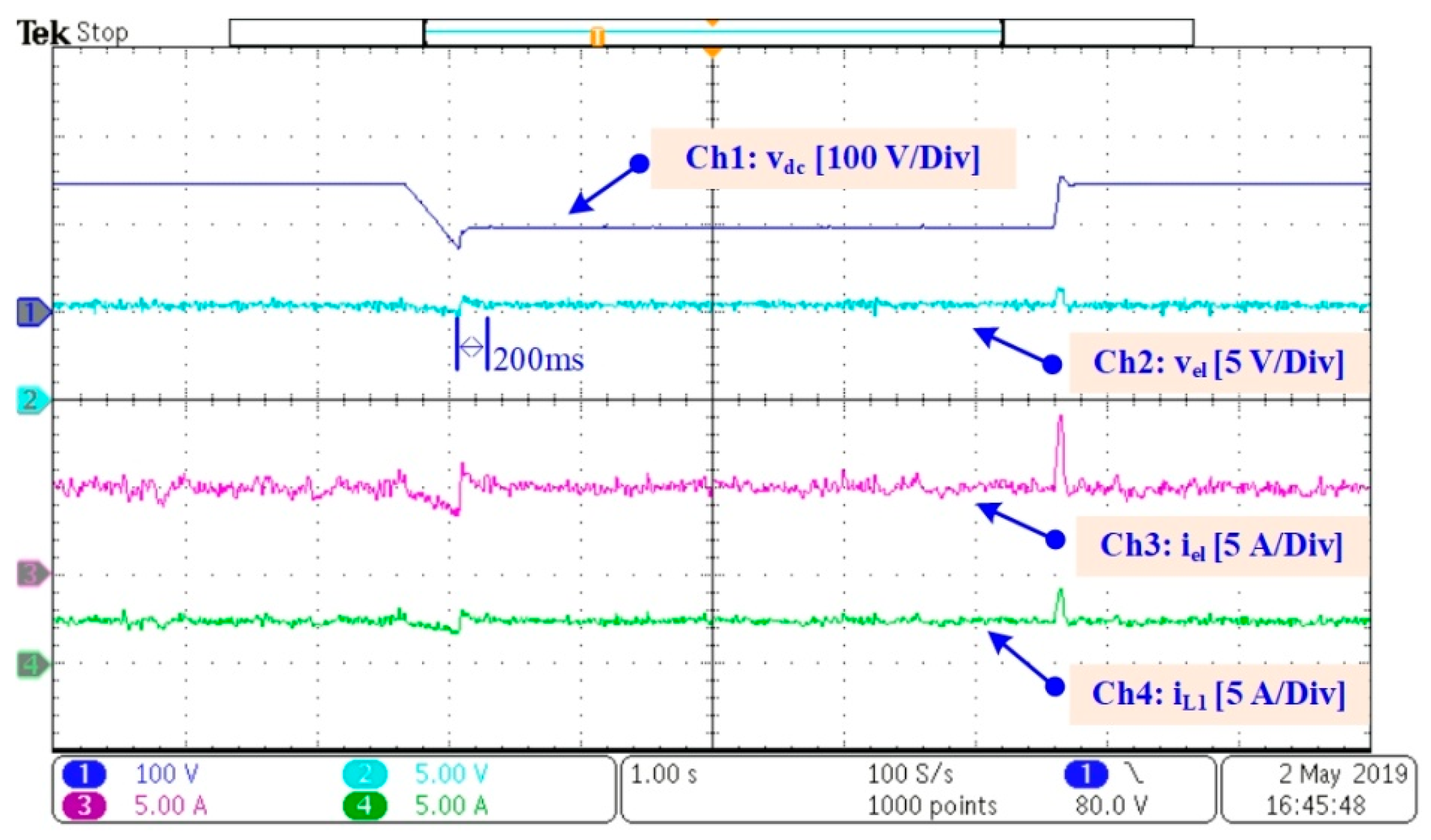
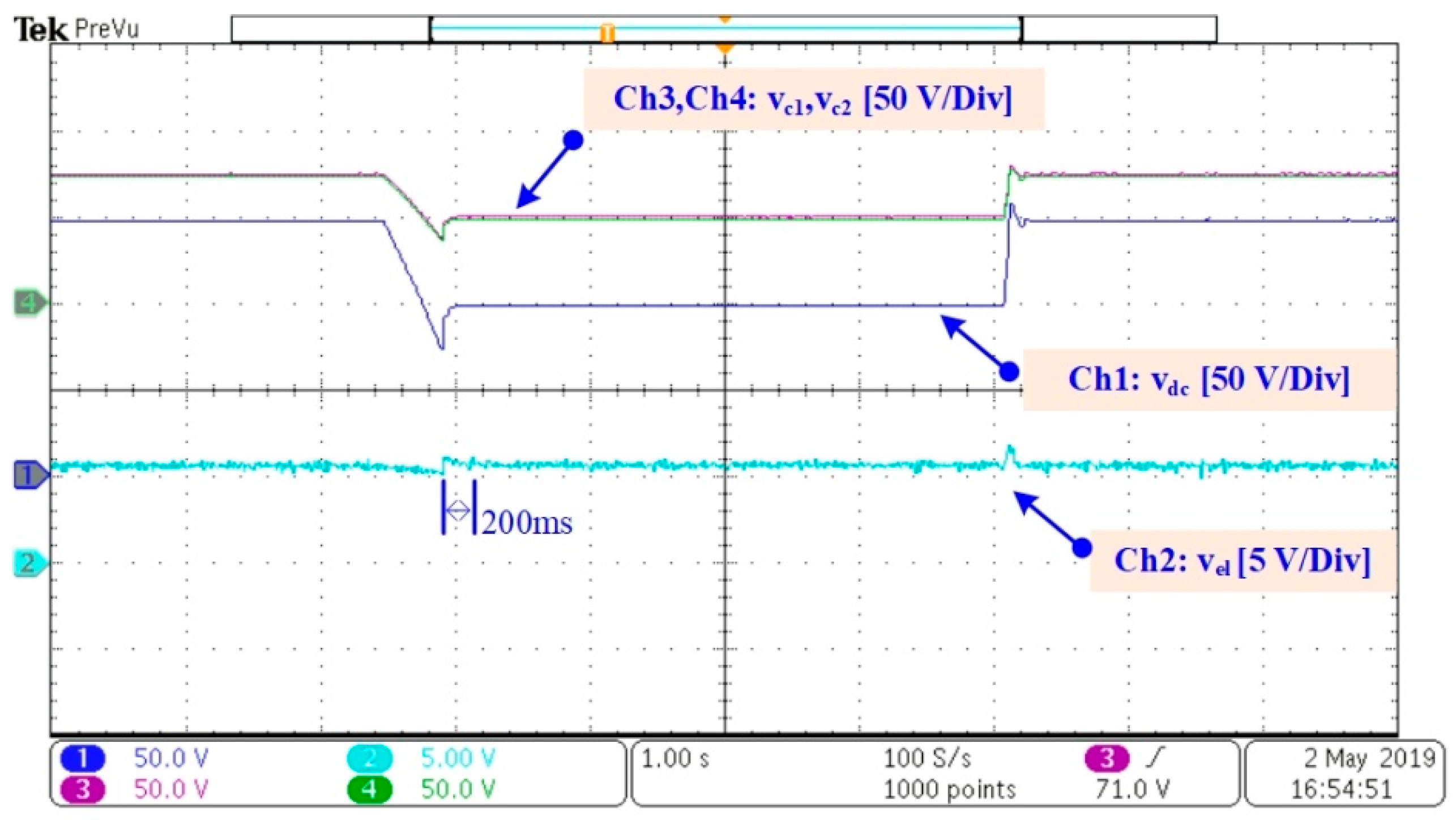
4.2. Obtained Results
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Kim, J.-Y.; Kim, H.-S.; Baek, J.-W.; Jeong, D.-K. Analysis of Effective Three-Level Neutral Point Clamped Converter System for the Bipolar LVDC Distribution. Electronics 2019, 8, 691. [Google Scholar] [CrossRef]
- Rouzbehi, K.; Miranian, A.; Escaño, J.M.; Rakhshani, E.; Shariati, N.; Pouresmaeil, E. A Data-Driven Based Voltage Control Strategy for DC-DC Converters: Application to DC Microgrid. Electronics 2019, 8, 493. [Google Scholar] [CrossRef]
- Vivas, F.; Heras, A.D.L.; Segura, F.; Andújar, J. A review of energy management strategies for renewable hybrid energy systems with hydrogen backup. Renew. Sustain. Energy Rev. 2018, 82, 126–155. [Google Scholar] [CrossRef]
- Guilbert, D.; Collura, S.M.; Scipioni, A. DC/DC converter topologies for electrolyzers: State-of-the-art and remaining key issues. Int. J. Hydrogen Energy 2017, 42, 23966–23985. [Google Scholar] [CrossRef]
- Andrijanovitš, A.; Vinnikov, D.; Roasto, I.; Blinov, A. Three-Level Half-Bridge ZVS DC/DC Converter for Electrolyzer Integration with Renewable Energy Systems. In Proceedings of the 10th IEEE International Conference on Environment and Electrical Engineering (EEEIC), Rome, Italy, 8–11 May 2011; pp. 1–4. [Google Scholar]
- Andrijanovitsh, A.; Steiks, I.; Zakis, J.; Vinnikov, D. Analysis of State-of-the-Art Converter Topologies for Interfacing of Hydrogen Buffer with Renewable Energy Systems. Sci. J. Riga Tech. Univ. Power Electr. Eng. 2011, 29, 87–94. [Google Scholar] [CrossRef]
- Blinov, A.; Andrijanovits, A. New DC/DC Converter for Electrolyser Interfacing with Stand-Alone Renewable Energy System. Electr. Control. Commun. Eng. 2012, 1, 24–29. [Google Scholar] [CrossRef]
- Chandrasekhar, P.; Rama Reddy, S. Performance of Soft-Switched DC-DC Resonant converter for Electrolyzer. In Proceedings of the 4th IEEE International Symposium on Resilient Control Systems (ISRCS), Boise, ID, USA, 9–11 August 2011; pp. 95–100. [Google Scholar]
- Viswamohan, K.; Jayakrishna, G. Soft-Switching Techniques for DC-to-DC Converters in Electrolyzer Application. Int. J. Adv. Technol. Innovative Res. 2014, 6, 1021–1026. [Google Scholar]
- Gautam, D.S.; Bhat, A.K.S. A Comparison of Soft-Switched DC-to-DC Converters for Electrolyzer Application. IEEE Trans. Power Electron. 2013, 28, 54–63. [Google Scholar] [CrossRef]
- Rajesh babu, R.S.; Henry, J. A comparative Analysis of DC-DC Converters for Renewable Energy System. In Proceedings of the International MultiConference of Engineers and Computer Scientists (IMECS), Hong Kong, China, 14–16 March 2012; pp. 1–6. [Google Scholar]
- Pittini, R.; Zhang, Z.; Andersen, M.A.E. Isolated full-bridge boost DC-DC converter designed for bidrectional operation of fuel cells/electrolyzer cells in grid-tie applications. In Proceedings of the 15th European Conference on Power Electronics and Applications (EPE), Lille, France, 2–6 September 2013; pp. 1–10. [Google Scholar]
- Cavallaro, C.; Chimento, F.; Musumeci, S.; Sapuppo, C.; Santonocito, C. Electrolyser in H2 Self-Producing Systems Connected to DC Link with Dedicated Phase Shift Converter. In Proceedings of the IEEE International Conference on Clean Electrical Power (ICCEP), Capri, Italy, 21–23 May 2007; pp. 632–638. [Google Scholar]
- Chandrasekhar, P.; Rama Reddy, S. Design of LCL Resonant Converter for Electrolyser. Ann. “Dunarea de Jos” Univ. Galati 2010, 33, 5–11. [Google Scholar]
- Guida, V.; Guilbert, D.; Douine, B. Literature Survey of Interleaved DC-DC Step-Down Converters for Proton Exchange Membrane Electrolyzer Applications. Trans. Environ. Electr. Eng. 2019, 3, 33–43. [Google Scholar] [CrossRef]
- Ilic, M.; Hesterman, B.; Maksimovic, D. Interleaved zero current transition three-level buck converter. In Proceedings of the Twenty-First Annual IEEE Applied Power Electronics Conference and Exposition, Dallas, TX, USA, 19–23 March 2006; pp. 72–78. [Google Scholar]
- Ilic, M.; Maksimovic, D. Interleaved Zero-Current-Transition Buck Converter. IEEE Trans. Ind. Appl. 2007, 43, 1619–1627. [Google Scholar] [CrossRef]
- Mohanpurkar, M.; Luo, Y.; Terlip, D.; Dias, F.; Harrison, K.; Eichman, J.; Hovsapian, R.; Kurtz, J. Electrolyzers Enhancing Flexibility in Electric Grids. Energies 2017, 10, 1836. [Google Scholar] [CrossRef]
- Carmo, M.; Fritz, D.L.; Mergel, J.; Stolten, D. A comprehensive review on PEM water electrolysis. Int. J. Hydrogen Energy 2013, 38, 4901–4934. [Google Scholar] [CrossRef]
- Guilbert, D.; Vitale, G. Dynamic Emulation of a PEM Electrolyzer by Time Constant Based Exponential Model. Energies 2019, 12, 750. [Google Scholar] [CrossRef]
- Arunkumari, T.; Indragandhi, V. An overview of high voltage conversion ratio DC-DC converter configurations used in DC micro-grid architectures. Renew. Sustain. Energy Rev. 2017, 77, 670–687. [Google Scholar] [CrossRef]
- Şahin, M.E.; Okumuş, H.I.; Aydemir, M.T. Implementation of an electrolysis system with DC/DC synchronous buck converter. Int. J. Hydrogen Energy 2014, 39, 6802–6812. [Google Scholar] [CrossRef]
- Sarrias-Mena, R.; Fernández-Ramírez, L.M.; García-Vásquez, C.A.; Jurado, F. Electrolyzer models for hydrogen production from wind energy systems. Int. J. Hydrogen Energy 2015, 40, 2927–2938. [Google Scholar] [CrossRef]
- Zhou, T.; François, B. Modeling and control design of hydrogen production process for an active hydrogen/wind hybrid power system. Int. J. Hydrogen Energy 2009, 34, 21–30. [Google Scholar] [CrossRef]
- Fuel Cell Store. Available online: https://www.fuelcellstore.com/ (accessed on 24 August 2019).
- Kolli, A.; Gaillard, A.; De Bernardinis, A.; Bethoux, O.; Hissel, D.; Khatir, Z. A review on DC/DC converter architectures for power fuel cell applications. Energy Convers. Manage. 2015, 105, 716–730. [Google Scholar] [CrossRef]
- Kabalo, M.; Blunier, B.; Bouquain, D.; Miraoui, A. State-of-the-Art of DC/DC converters for fuel cell vehicles. In Proceedings of the IEEE Vehicle Power and Propulsion Conference (VPPC’10), Lille, France, 1–3 September 2010; pp. 1–6. [Google Scholar]
- Ulleberg, O. Stand-alone power systems for the future: optimal design, operation, & control of solar-hydrogen energy systems. Ph.D. Thesis, Norwegian University of science and Technology, Trondheim, Norway, December 1998. [Google Scholar]
- Khalilnejad, A.; Sundararajan, D.; Sarwat, A.I. Optimal design of hybrid wind/photovoltaic electrolyzer for maximum hydrogen production using imperialist competitive algorithm. J. Mod. Power Syst. Clean Energy 2018, 6, 40–49. [Google Scholar] [CrossRef]
- Rashid, M.; Al Mesfer, M.K.; Naseem, H.; Danish, M. Hydrogen Production by Water Electrolysis: A Review of Alkaline Water Electrolysis, PEM Water Electrolysis and High Temperature Water Electrolysis. Int. J. Eng. Adv. Technol. 2015, 4, 1–14. [Google Scholar]
- Ulleberg, Ø. Modeling of advanced alkaline electrolyzers: a system simulation approach. Int. J. Hydrogen Energy 2003, 28, 21–33. [Google Scholar] [CrossRef]
- Tijani, A.S.; Yusup, N.A.B.; Rahim, A.A. Mathematical Modelling and Simulation Analysis of Advanced Alkaline Electrolyzer System for Hydrogen Production. Procedia Technol. 2014, 15, 798–806. [Google Scholar] [CrossRef]
- Tijani, A.S.; Rahim, A.A. Numerical Modeling the Effect of Operating Variables on Faraday Efficiency in PEM Electrolyzer. Procedia Technol. 2016, 26, 419–427. [Google Scholar] [CrossRef]
- Tjarks, G.; Gibelhaus, A.; Lanzerath, F.; Müller, M.; Bardow, A.; Stolten, D. Energetically-optimal PEM electrolyzer pressure in power-to-gas plants. Appl. Energy 2018, 218, 192–198. [Google Scholar] [CrossRef]
- Schalenbach, M.; Carmo, M.; Fritz, D.L.; Mergel, J.; Stolten, D. Pressurized PEM water electrolysis: Efficiency and gas crossover. Int. J. Hydrogen Energy 2013, 38, 14921–14933. [Google Scholar] [CrossRef]
- Guilbert, D.; Gaillard, A.; Mohammadi, A.; N’Diaye, A.; Djerdir, A. Investigation of the interactions between proton exchange membrane fuel cell and interleaved DC/DC boost converter in case of power switch faults. Int. J. Hydrogen Energy 2015, 40, 519–537. [Google Scholar] [CrossRef]
- Koponen, J.; Kosonen, A.; Huoman, K.; Ahola, J.; Ahonen, T.; and Ruuskanen, V. Specific energy consumption of PEM water electrolysers in atmospheric and pressurised conditions. In Proceedings of the 18th European Conf. on Power Electron. and Applicat. (EPE ‘16–ECCE Europe), Karlsruhe, Germany, 5–9 September 2016. [Google Scholar]
- Bacha, S.; Munteanu, I.; Bratcu, A.I. Power Electronics Converters Modeling and Control; Springer: London, England, 2014. [Google Scholar]
- Dobo, Z.; Bence Palotas, Á.; Toth, P. The effect of power supply ripple on dc water electrolysis efficiency. Mater. Sci. Eng. 2016, 41, 23–31. [Google Scholar]
- Ursúa, A.; Marroyo, L.; Gubía, E.; Gandia, L.M.; Dieguez, P.M.; Sanchis, P. Influence of the power supply on the energy efficiency of an alkaline water electrolyser. Int. J. Hydrogen Energy 2009, 34, 3221–3233. [Google Scholar] [CrossRef]
- Ruuskanen, V.; Koponen, J.; Huoman, K.; Kosonen, A.; Niemelä, M.; Ahola, J. PEM water electrolyzer model for a power-hardware-in-loop simulator. Int. J. Hydrogen Energy 2017, 42, 10775–10784. [Google Scholar] [CrossRef]
- Pevere, A.; Petrella, R.; Mi, C.C.; Zhou, S. Novel interleaved multiphase proposal for a three level neutral point clamped buck converter. In Proceedings of the 2015 IEEE Applied Power Electronics Conference and Exposition (APEC), Charlotte, NC, USA, 15–19 March 2015; pp. 927–934. [Google Scholar]






| Parameters | Value | Unit |
|---|---|---|
| Rated electrical power | 120 | W |
| Stack operating voltage range | 7.5–8 | V |
| Stack current range | 0–15 | A |
| Delivery output pressure | 0.1–10.5 | bar |
| Cells number | 3 | - |
| Active area Section | 50 | cm2 |
| Hydrogen flow rate at STP (Standard Temperature and Pressure, 20 °C and 1 bar) | 0.3 | slpm |
| Vel (V) | Iel (A) | Pel (W) | VH2 (slpm) | QH2 (kg·h−1) | Eel (kWh·kg−1) | ηs (%) |
|---|---|---|---|---|---|---|
| 4.7 | 1.4 | 6.6 | 0.028 | 0.0002 | 39.5 | 69 |
| 5.48 | 3.55 | 19.5 | 0.071 | 0.0004 | 46 | 71 |
| 6 | 5 | 30 | 0.1 | 0.0006 | 50.45 | 72 |
| 6.2 | 6.1 | 37.8 | 0.122 | 0.0007 | 52.1 | 68 |
| 6.5 | 7 | 45.5 | 0.14 | 0.008 | 54.65 | 63 |
| 7.42 | 9.6 | 71.2 | 0.192 | 0.0011 | 62.4 | 45 |
| 8.25 | 10.64 | 87.8 | 0.213 | 0.0013 | 69.4 | 36 |
| Components | Parameters |
|---|---|
| Vdc (Input voltage) | 75–150 V |
| L1,2,3,4 (phase inductors) | 200 μH |
| L0 (auxiliary inductor) | 1.1 mH |
| C1,2 (input capacitors) | 4.9 mF |
| C0 (output capacitor) | 3.3 mF |
| r (parasitic resistance of L) | 0.7 Ω |
| Re | 4.7 Ω |
| (equivalent load) [20] | 1.63 Ω |
| Vel (EL voltage) | 6 V |
| Switching frequency | 10 kHz |
| VDC (V) | Phase margin, PM (°) | Cutoff frequency (rad·s−1) | DC gain (dB) | Pole (×1000) |
|---|---|---|---|---|
| 75 | 38.6 | 5770 | 38.7 | −4.2042 −0.2541 |
| 100 | 33.7 | 6850 | 51.6 | −4.2042 −0.2541 |
| 125 | 30.3 | 7780 | 64.5 | −4.2042 −0.2541 |
| 150 | 27.7 | 8620 | 77.4 | −4.2042 −0.2541 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yodwong, B.; Guilbert, D.; Kaewmanee, W.; Phattanasak, M. Energy Efficiency Based Control Strategy of a Three-Level Interleaved DC-DC Buck Converter Supplying a Proton Exchange Membrane Electrolyzer. Electronics 2019, 8, 933. https://doi.org/10.3390/electronics8090933
Yodwong B, Guilbert D, Kaewmanee W, Phattanasak M. Energy Efficiency Based Control Strategy of a Three-Level Interleaved DC-DC Buck Converter Supplying a Proton Exchange Membrane Electrolyzer. Electronics. 2019; 8(9):933. https://doi.org/10.3390/electronics8090933
Chicago/Turabian StyleYodwong, Burin, Damien Guilbert, Wattana Kaewmanee, and Matheepot Phattanasak. 2019. "Energy Efficiency Based Control Strategy of a Three-Level Interleaved DC-DC Buck Converter Supplying a Proton Exchange Membrane Electrolyzer" Electronics 8, no. 9: 933. https://doi.org/10.3390/electronics8090933
APA StyleYodwong, B., Guilbert, D., Kaewmanee, W., & Phattanasak, M. (2019). Energy Efficiency Based Control Strategy of a Three-Level Interleaved DC-DC Buck Converter Supplying a Proton Exchange Membrane Electrolyzer. Electronics, 8(9), 933. https://doi.org/10.3390/electronics8090933








