Transceiver Design for GFDM with Hexagonal Time–Frequency Allocation Using the Polyphase Decomposition
Abstract
:1. Introduction
1.1. Contributions
- (1)
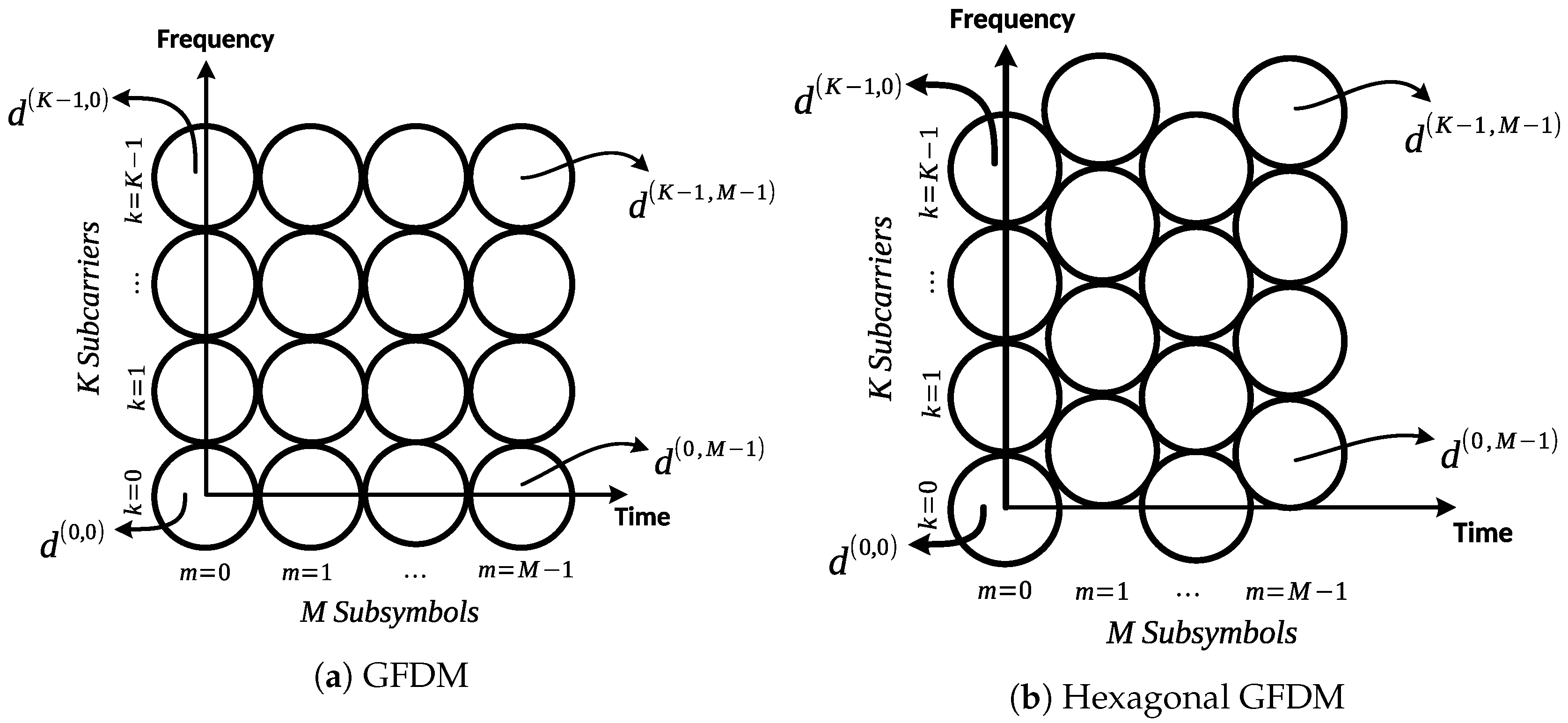
- To decrease symbol duration and also latency, we combine hexagonal time-frequency lattice structure with the GFDM, which is referred to as the hexagonal GFDM. The hexagonal lattice structure is a more optimal time-frequency allocation way than the rectangular structure. The symbol duration and thus latency is decreased by using proposed hexagonal GFDM.
- (2)
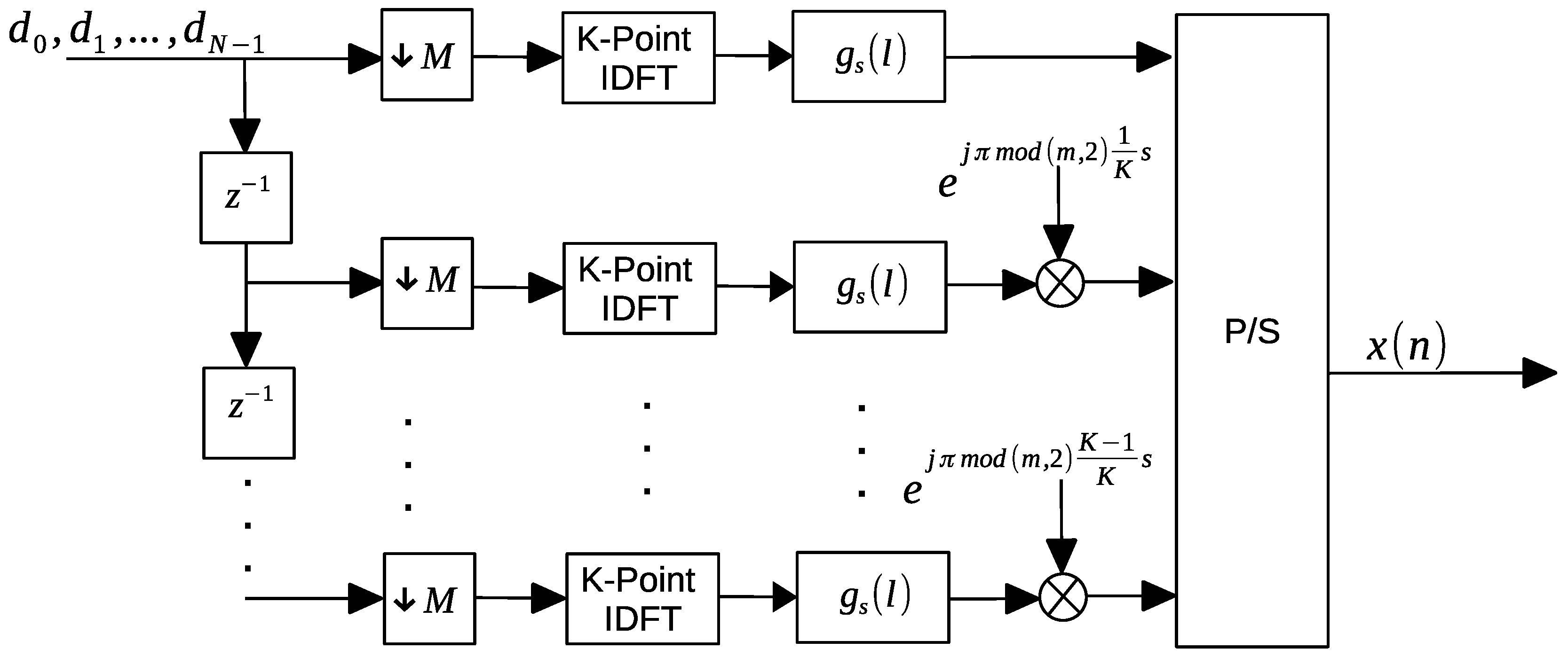
- To induce computational complexity, we use the polyphase decomposition of the prototype filter. Thus, the computational complexity is reduced by using parallel processing techniques of polyphase decomposition.
- (3)
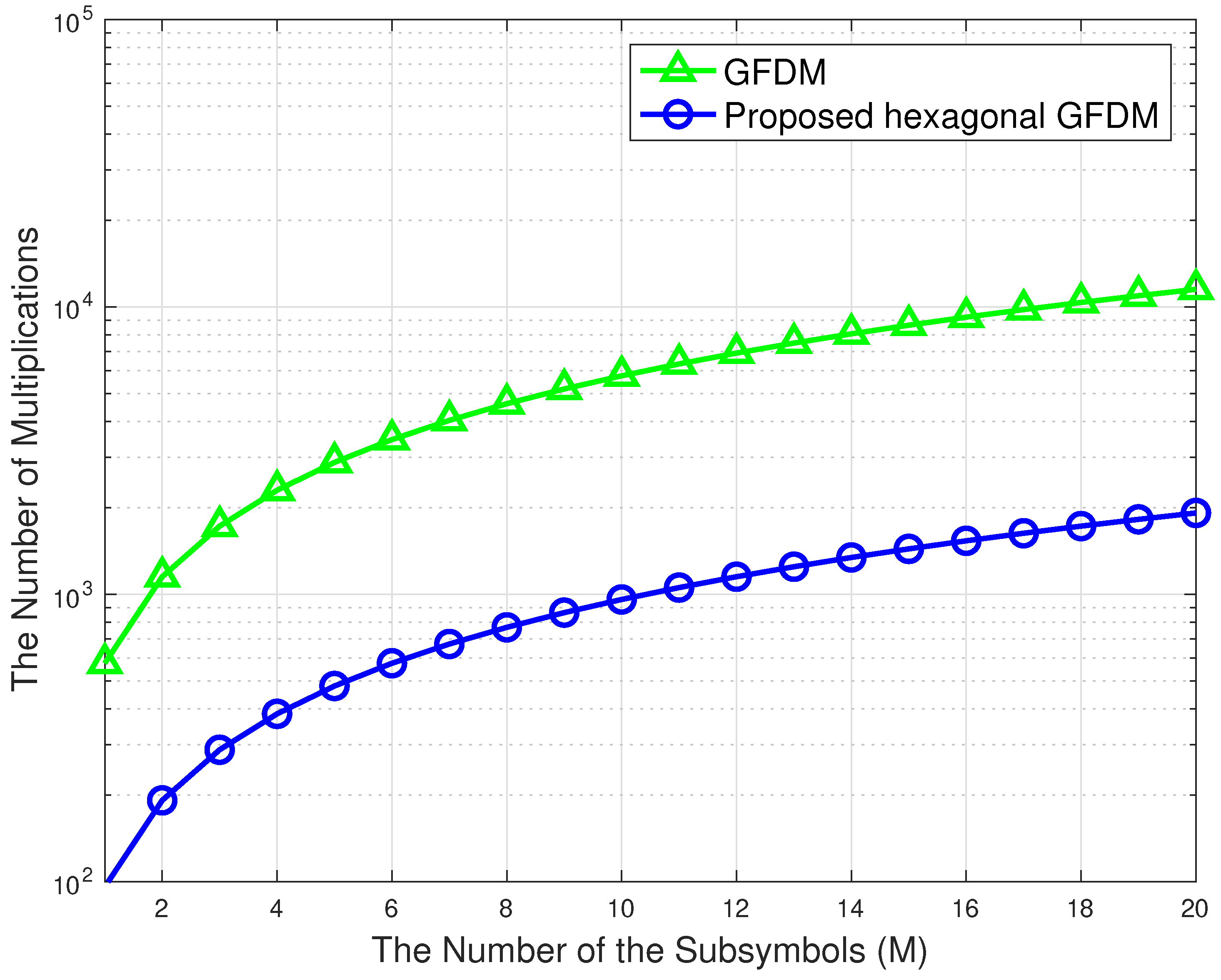
- We distinguish the proposed model and the traditional GFDM model and show that the symbol duration and computational complexity are decreased. The number of symbols on the same time and frequency interval is risen by using the hexagonal GFDM model.
1.2. Organization
2. Preliminaries
2.1. GFDM
2.2. Polyphase Decomposition
3. System Model
Proposed Hexagonal GFDM Model
4. Performance Evaluation
4.1. Complexity Analysis
- (i)
- M times of K-point IDFT transformations for
- (ii)
- times multiplication with length of the filter
4.2. Transmission Time Analysis
4.3. BER Performances of the Proposed Hexagonal GFDM
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Wunder, G.; Jung, P.; Kasparick, M.; Wild, T.; Schaich, F.; Chen, Y.; Brink, S.T.; Gaspar, I.; Michailow, N.; Festag, A.; et al. 5GNOW: Non-orthogonal, asynchronous waveforms for future mobile applications. IEEE Commun. Mag. 2014, 52, 97–105. [Google Scholar] [CrossRef]
- Andrews, J.G.; Buzzi, S.; Choi, W.; Hanly, S.V.; Lozano, A.; Soong, A.C.; Zhang, J.C. What will 5G be? IEEE J. Sel. Areas Commun. 2014, 32, 1065–1082. [Google Scholar] [CrossRef]
- Akyildiz, I.F.; Gutierrez-Estevez, D.M.; Balakrishnan, R.; Chavarria-Reyes, E. LTE-Advanced and the evolution to Beyond 4G (B4G) systems. Phys. Commun. 2014, 10, 31–60. [Google Scholar] [CrossRef]
- Çatak, E.; Tekçe, F.; Dizdar, O.; Durak-Ata, L. Multi-user shared access in massive machine-type communication systems via superimposed waveforms. Phys. Commun. 2019, 37, 100896. [Google Scholar] [CrossRef]
- Shariatmadari, H.; Ratasuk, R.; Iraji, S.; Laya, A.; Taleb, T.; Jäntti, R.; Ghosh, A. Machine-type communications: Current status and future perspectives toward 5G systems. IEEE Commun. Mag. 2015, 53, 10–17. [Google Scholar] [CrossRef] [Green Version]
- Palattella, M.R.; Dohler, M.; Grieco, A.; Rizzo, G.; Torsner, J.; Engel, T.; Ladid, L. Internet of Things in the 5G Era: Enablers, Architecture, and Business Models. IEEE J. Sel. Areas Commun. 2016, 34, 510–527. [Google Scholar] [CrossRef] [Green Version]
- Farhang-Boroujeny, B. Filter bank multicarrier modulation: A waveform candidate for 5G and beyond. Adv. Electr. Eng. 2014, 2014, 25. [Google Scholar] [CrossRef] [Green Version]
- Çatak, E.; Durak-Ata, L. Adaptive filterbank-based multi-carrier waveform design for flexible data rates. Comput. Electr. Eng. 2017, 61, 184–194. [Google Scholar] [CrossRef]
- Khelouani, I.; Elbahhar, F.; Elassali, R.; Idboufker, N. Performance Analysis of LDS Multi Access Technique and New 5G Waveforms for V2X Communication. Electronics 2020, 9, 1094. [Google Scholar] [CrossRef]
- Vakilian, V.; Wild, T.; Schaich, F.; ten Brink, S.; Frigon, J.F. Universal-filtered multi-carrier technique for wireless systems beyond LTE. In Proceedings of the 2013 IEEE Globecom Workshops (GC Wkshps), Atlanta, GA, USA, 9–13 December 2013; pp. 223–228. [Google Scholar] [CrossRef]
- Schaich, F.; Wild, T. Waveform contenders for 5G-OFDM vs. FBMC vs. UFMC. In Proceedings of the IEEE International Symposium on Communications, Control and Signal Processing (ISCCSP), Athens, Greece, 21–23 May 2014; pp. 457–460. [Google Scholar]
- Matthé, M.; Mendes, L.L.; Fettweis, G. Asynchronous multi-user uplink transmission with generalized frequency division multiplexing. In Proceedings of the 2015 IEEE International Conference on Communication Workshop (ICCW), London, UK, 8–12 June 2015; pp. 2269–2275. [Google Scholar]
- Jiang, L.; Zhang, H.; Cheng, S.; Lv, H.; Li, P. An Overview of FIR Filter Design in Future Multicarrier Communication Systems. Electronics 2020, 9, 599. [Google Scholar] [CrossRef] [Green Version]
- Han, F.; Zhang, X. Hexagonal Multicarrier Modulation: A Robust Transmission Scheme for Time-Frequency Dispersive Channels. IEEE Trans. Signal Process. 2007, 55, 1955–1961. [Google Scholar] [CrossRef]
- Xu, K.; Xu, Y.; Ma, W.; Xie, W.; Zhang, D. Time and Frequency Synchronization for Multicarrier Transmission on Hexagonal Time-Frequency Lattice. IEEE Trans. Signal Process. 2013, 61, 6204–6219. [Google Scholar] [CrossRef] [Green Version]
- Strohmer, T.; Beaver, S. Optimal OFDM system design through optimal sphere coverings. In Proceedings of the 2001 IEEE International Conference on Acoustics, Speech, and Signal Processing, Salt Lake City, UT, USA, 7–11 May 2001; Volume 4, pp. 2373–2376. [Google Scholar] [CrossRef] [Green Version]
- Ayadi, R.; Kammoun, I.; Siala, M. Efficient Offline Waveform Design Using Quincunx/Hexagonal Time-Frequency Lattices. Wireless Commun. Mob. Comput. 2017, 2017, 9207108. [Google Scholar] [CrossRef] [Green Version]
- Korevaar, C.W.; Kokkeler, A.B.J.; Boer, P.; Smit, G.J.M. Spectrum Efficient, Localized, Orthogonal Waveforms: Closing the Gap With the Balian-Low Theorem. IEEE Trans. Commun. 2016, 64, 2155–2165. [Google Scholar] [CrossRef]
- Senay, S.; Durak, L.; Chaparro, L.F. A time-frequency division multiplexing communications system with hexagonal lattice structure. In Proceedings of the 2009 17th European Signal Processing Conference, Glasgow, UK, 24–28 August 2009; pp. 1186–1189. [Google Scholar]
- Han, F.; Zhang, X. Asymptotic Equivalence of Two Multicarrier Transmission Schemes in Terms of Robustness Against Time—Frequency Dispersive Channels. IEEE Trans. Veh. Technol. 2010, 59, 682–691. [Google Scholar]
- Çatak, E.; Durak-Ata, L. An efficient transceiver design for superimposed waveforms with orthogonal polynomials. In Proceedings of the 2017 IEEE International Black Sea Conference on Communications and Networking (BlackSeaCom), Istanbul, Turkey, 5–8 June 2017; pp. 1–5. [Google Scholar]
- Cherubini, G.; Eleftheriou, E.; Olcer, S. Filtered multitone modulation for very high-speed digital subscriber lines. IEEE J. Sel. Areas Commun. 2002, 20, 1016–1028. [Google Scholar] [CrossRef]
- Michailow, N.; Gaspar, I.; Krone, S.; Lentmaier, M.; Fettweis, G. Generalized frequency division multiplexing: Analysis of an alternative multi-carrier technique for next generation cellular systems. In Proceedings of the 2012 International Symposium on Wireless Communication Systems (ISWCS), Paris, France, 28–31 August 2012; pp. 171–175. [Google Scholar] [CrossRef] [Green Version]
- Farhang, A.; Marchetti, N.; Doyle, L.E. Low-Complexity Modem Design for GFDM. IEEE Trans. Signal Process. 2016, 64, 1507–1518. [Google Scholar] [CrossRef] [Green Version]
- Alves, B.M.; Mendes, L.L.; Guimarães, D.A.; Gaspar, I. Performance of GFDM over frequency selective channels. In Proceedings of the 2013 INATEL International Workshop on Telecommunications (IWT), Minas Gerais, Brazil, 6–9 May 2013; pp. 1–6. [Google Scholar]
- Harris, F.; Chen, X.; Venosa, E. Chapter 6—Filter Banks for Software-Defined Radio. In Orthogonal Waveforms and Filter Banks for Future Communication Systems; Renfors, M., Mestre, X., Kofidis, E., Bader, F., Eds.; Academic Press: Cambridge, MA, USA, 2017; pp. 105–127. [Google Scholar] [CrossRef]
- Xu, K.; Zhu, L.; Zhang, D.; Xu, Y.; Ma, W.; Xie, W. Synchronization approach for dynamic hexagonal time–frequency lattice MCM system. Digit. Signal Process. 2014, 25, 72–83. [Google Scholar] [CrossRef]
- Peng, S.; Liu, A.; Pan, X.; Wang, H. Hexagonal Multicarrier Faster-Than-Nyquist Signaling. IEEE Access 2017, 5, 3332–3339. [Google Scholar] [CrossRef]
- Astely, D.; Dahlman, E.; Furuskär, A.; Jading, Y.; Lindström, M.; Parkvall, S. LTE: The evolution of mobile broadband. IEEE Commun. Mag. 2009, 47, 44–51. [Google Scholar] [CrossRef]
- Gaspar, I.; Michailow, N.; Navarro, A.; Ohlmer, E.; Krone, S.; Fettweis, G. Low Complexity GFDM Receiver Based on Sparse Frequency Domain Processing. In Proceedings of the 2013 IEEE 77th Vehicular Technology Conference (VTC Spring), Dresden, Germany, 2–5 June 2013; pp. 1–6. [Google Scholar] [CrossRef]
- Michailow, N.; Matthé, M.; Gaspar, I.S.; Caldevilla, A.N.; Mendes, L.L.; Festag, A.; Fettweis, G. Generalized Frequency Division Multiplexing for 5th Generation Cellular Networks. IEEE Trans. Commun. 2014, 62, 3045–3061. [Google Scholar] [CrossRef]



| Model | The Number of Multiplications |
|---|---|
| GFDM [23,24] | |
| Proposed Hexagonal GFDM |
| Time-Frequency Allocation | Frame Duration | The Number of the Symbols for 1 ms |
|---|---|---|
| Rectangular allocation on LTE standard [29] | 1 ms | 14 or 12 symbols |
| Hexagonal allocation | ms | 16 or 14 symbols |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Catak, E.; Moldsvor, A.; Derawi, M. Transceiver Design for GFDM with Hexagonal Time–Frequency Allocation Using the Polyphase Decomposition. Electronics 2020, 9, 1862. https://doi.org/10.3390/electronics9111862
Catak E, Moldsvor A, Derawi M. Transceiver Design for GFDM with Hexagonal Time–Frequency Allocation Using the Polyphase Decomposition. Electronics. 2020; 9(11):1862. https://doi.org/10.3390/electronics9111862
Chicago/Turabian StyleCatak, Evren, Arild Moldsvor, and Mohammad Derawi. 2020. "Transceiver Design for GFDM with Hexagonal Time–Frequency Allocation Using the Polyphase Decomposition" Electronics 9, no. 11: 1862. https://doi.org/10.3390/electronics9111862
APA StyleCatak, E., Moldsvor, A., & Derawi, M. (2020). Transceiver Design for GFDM with Hexagonal Time–Frequency Allocation Using the Polyphase Decomposition. Electronics, 9(11), 1862. https://doi.org/10.3390/electronics9111862






