Review and Comparison of Genetic Algorithm and Particle Swarm Optimization in the Optimal Power Flow Problem
Abstract
:1. Introduction
1.1. Motivation
1.2. Similar Works & Contribution
- To perform a comprehensive literature review of the most prominent GA and PSO OPF works.
- To pinpoint the best practices from the reviewed works, and, where possible, corroborate them with literature from other domains.
- To perform a cross-comparison among the reviewed GA and PSO OPF implementations (where possible) by analyzing the reported results.
- To propose promising research directions for the standardization of GA and PSO OPF algorithms.
2. The Optimal Power Flow Problem
3. Optimal Power Flow Using the Genetic Algorithm
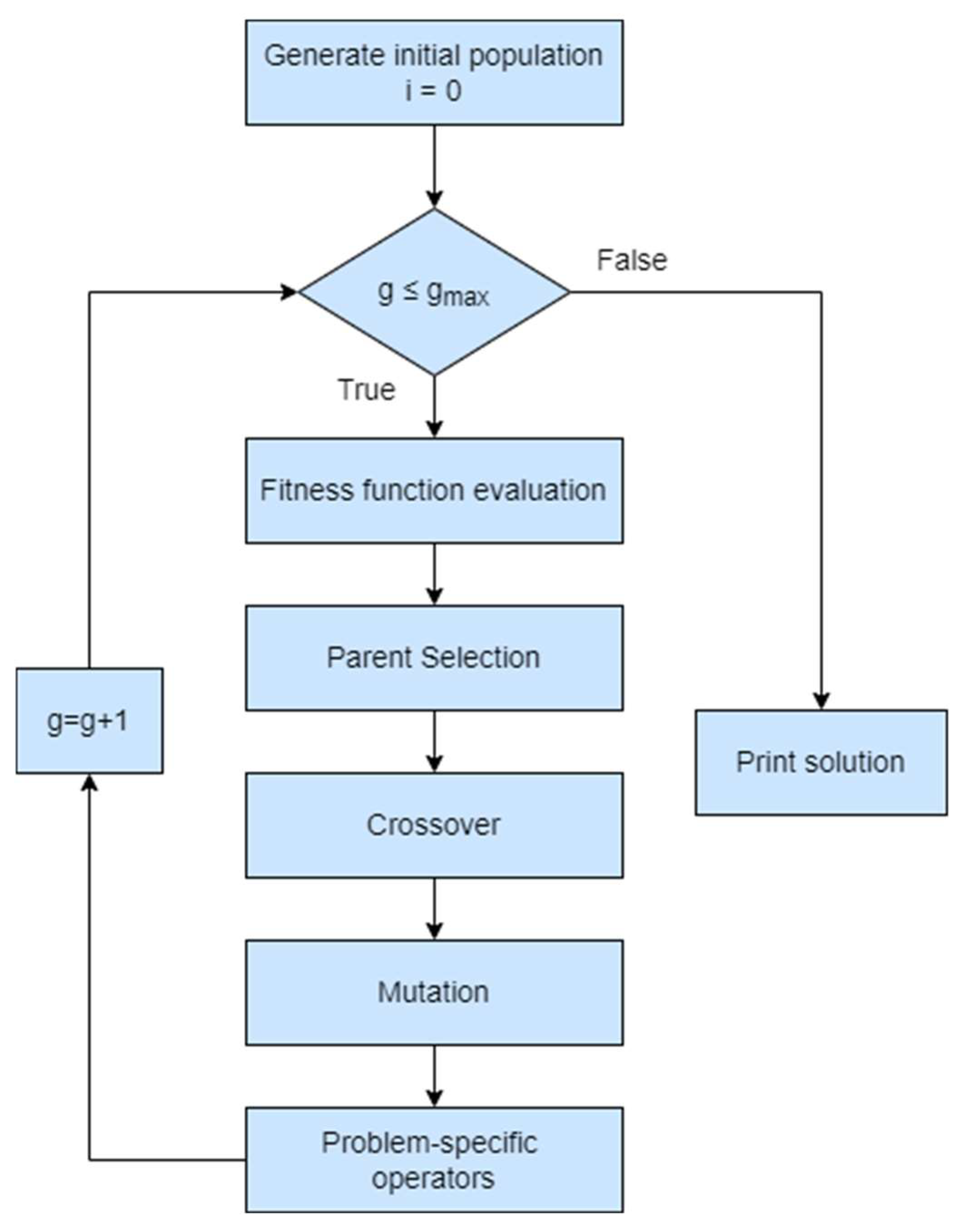
3.1. The Genetic Algorithm
3.2. Genetic Algorithm Optimal Power Flow
3.3. Discussion on GA OPF
- Encoding: The choice of encoding is an important factor in GA applications. Most early works use binary encoding, as it lowers the memory requirements. More recent works usually adopt real encoding, as it circumvents the encoding-decoding steps of the GA, increasing the overall efficiency.
- Parent selection: Almost all works use roulette wheel selection, as it is easy to implement and leads to good results. A few exceptions also exist, e.g., [37] which uses tournament selection. According to [16], tournament selection allows for better exploration of the search space, but it leads to slower convergence. It should be noted that using roulette wheel selection requires special transformations, in case particles with negative fitness values exist amongst the population.
- Crossover: Single-point crossover is the most popular choice amongst the reviewed papers, as it is one of the first and easiest ways to implement crossover methods. The uniform crossover has also been used, which is considered suitable for large-scale problems [16]. Other crossover methods, such as blend and dispersed crossing, have also been explored in the context of GA OPF.
- Adaptiveness: In this work, adaptiveness is defined as the dynamic tuning of coefficients over the generations. Many works adaptively change mutation and crossover probabilities, using each generation’s population statistics, to keep the diversity within the population and allow for better exploration. Other works dynamically change coefficients for the penalization of constraint violations. These coefficients are usually small during the first generation (i.e., violations are not heavily penalized), which allows for better explorations of the edges of the search space. In later generations, violations are heavily penalized, to keep the population within the search space. Some works omit the use of adaptive coefficients and rely on static values.
- Power flow formulation: To calculate the FF for each member of the population, a PF analysis must be executed. Due to the volume of the required calculations, this is the most time-consuming step of the GA OPF. Most works use a full PF, i.e., no approximations are used and the PF is solved, e.g., with the Newton-Raphson method. Other methods used to solve the required PFs include FDLF, DQLF, and the method introduced in [41]. While these methods can ease the computational burden, they can lead to some loss of accuracy and pose some limitations to the applicability of each algorithm (e.g., FDLF is not accurate in the distribution network due to its line characteristics).
- Objective functions: As presented in Table 2, many different objectives can be applied to OPF. While cost minimization is the most popular amongst the reviewed works, a wide array of other objectives has also been used, which is a testament to the versatility of the GA OPF.
- Constraint violation penalties: As earlier discussed, to include the constraints in the GA OPF, penalties for the violation of each constraint are added to the FF. Most works use quadratic penalties to penalize the violations. Quadratic penalties penalize heavily large deviations from the search space limits and lightly smaller deviations. This way, they allow for better exploration of the search space, as points close to the bounds of the search space are not penalized too much, but points far off are. On the contrary, linear penalties place the same weight on smaller and larger violations of constraints.
4. Optimal Power Flow Using Particle Swarm Optimization
4.1. The Particle Swarm Optimization Algorithm
4.2. Particle Swarm Optimization Optimal Power Flow
4.3. Discussion on PSO OPF
- Adaptiveness: Similar to the GA OPF analysis, adaptiveness is defined as the dynamic tuning of parameters as time elapses. Most reviewed inertia weights adapt dynamically, as time elapses. The simplest form of adaptation is to linearly reduce the weights as time elapses. However, more sophisticated techniques have also been proposed, such as the GLbest and WI algorithms (in [64,65] respectively) or fuzzy rules [68]. According to all researchers, the use of adaptive weights allows for a more uniform search of the search space. Apart from inertia weights, penalty coefficients are also commonly adapted dynamically. These works use small penalty coefficients at the beginning of the process, to allow for better exploration of the search space. Penalty coefficients are subsequently increased in the latter stages, to confine the swarm within the feasible search space. An interesting concept is presented in [66], where the leader’s leading power was dynamically adapted.
- Maximum velocity: Many works use an upper limit on the velocity of each particle for each dimension. The use of such a limit can enhance the local character of the search, and better resembles the incremental process of the human learning process [54].
- Objective functions: The PSO OPF has been applied for many different objective functions, showcasing its versatility.
- Constraint violation penalties: Similar to the GA OPF analysis, quadratic penalties penalize heavily large deviations from the search space limits and lightly smaller deviations. This way, they allow for better exploration of the search space, as points close to the bounds of the search space are not penalized too much, but points far off are. On the contrary, linear penalties place the same weight on smaller and larger violations of constraints.
5. Cross-Comparison of GA OPF and PSO OPF
6. Conclusions
- The development of frameworks for the systematic tuning of the hyperparameters of GA and PSO OPF. This could entail providing generic rules for the tuning of the hyper-parameters depending on the parameters of each specific OPF (e.g., size of the problem, number of constraints, desired accuracy, etc.).
- Future works should provide more transparent details regarding their implementation (e.g., reporting of the values of all hyper-parameters should be done explicitly). This would allow easier comparison of different methodologies and the replication of the work by other researchers.
- The results reported in each work should also be standardized. Apart from the values of objective functions in each case, a useful metric that should be reported is the NFFEs. As discussed in this work, the NFFE metric allows the extraction of useful conclusions regarding the computational efficiency of each method.
- Finally, standardization is also desired in the topologies used for benchmarking the proposed methods. The IEEE 30-bus network is a good benchmark for proof-of-concept experimentation. However, since practical networks are much larger, and as the scalability of GA and PSO OPF has not been extensively researched, larger benchmark networks should also be introduced and used. Additionally, future works should use distribution network topologies to benchmark the proposed methodology, as the application of GA or PSO OPF in the distribution network has not yet been adequately researched.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Carpentier, J. Contribution to the economic dispatch problem. Bull. De La Soc. Fr. Des Electr. 1962, 3, 431–447. [Google Scholar]
- Frank, S.; Steponavice, I.; Rebennack, S. Optimal power flow: A bibliographic survey I: Formulations and deterministic methods. Energy Syst. 2012, 3, 221–258. [Google Scholar] [CrossRef]
- Biskas, P.N.; Ziogos, N.; Tellidou, A.; Zoumas, C.; Bakirtzis, A.; Petridis, V.; Tsakoumis, A.L. Comparison of Two Metaheuristics with Mathematical Programming Methods for the Solution of OPF. In Proceedings of the 13th International Conference on Intelligent Systems Application to Power Systems, Arlington, VA, USA, 6–10 November 2005; pp. 510–515. [Google Scholar] [CrossRef]
- Tong, X.; Wu, F.F.; Zhang, Y.; Yan, Z.; Ni, Y. A semismooth Newton method for solving optimal power flow. J. Ind. Manag. Optim. 2007, 3, 553–567. [Google Scholar] [CrossRef]
- Qiu, Z.; Deconinck, G.; Belmans, R. A literature survey of Optimal Power Flow problems in the electricity market context. In Proceedings of the 2009 IEEE/PES Power Systems Conference and Exposition, Seattle, WA, USA, 15–18 March 2009; pp. 1–6. [Google Scholar] [CrossRef]
- Chatzigiannis, D.I.; Dourbois, G.; Biskas, P.; Bakirtzis, A.G. European day-ahead electricity market clearing model. Electr. Power Syst. Res. 2016, 140, 225–239. [Google Scholar] [CrossRef]
- Papazoglou, G.K.; Forouli, A.; Bakirtzis, E.; Biskas, P.; Bakirtzis, A.G. Day-ahead local flexibility market for active and reactive power with linearized network constraints. Electr. Power Syst. Res. 2022, 212, 108317. [Google Scholar] [CrossRef]
- Forouli, A.; Bakirtzis, E.; Papazoglou, G.; Oureilidis, K.; Gkountis, V.; Candido, L.; Ferrer, E.; Biskas, P. Assessment of Demand Side Flexibility in European Electricity Markets: A Country Level Review. Energies 2021, 14, 2324. [Google Scholar] [CrossRef]
- Frank, S.; Steponavice, I.; Rebennack, S. Optimal power flow: A bibliographic survey II: Non-deterministic and hybrid methods. Energy Syst. 2012, 3, 259–289. [Google Scholar] [CrossRef]
- Momoh, J.A.; Adapa, R.; El-Hawary, M.E. A review of selected optimal power flow literature to 1993. I. Nonlinear and quadratic programming approaches. IEEE Trans. Power Syst. 1999, 14, 96–104. [Google Scholar] [CrossRef]
- Momoh, J.A.; Adapa, R.; El-Hawary, M.E. A review of selected optimal power flow literature to 1993. II. Newton, linear programming and interior point methods. IEEE Trans. Power Syst. 1999, 14, 105–111. [Google Scholar] [CrossRef]
- Ebeed, M.; Kamel, S.; Jurado, F. Optimal Power Flow Using Recent Optimization Techniques. In Classical and Recent Aspects of Power System Optimization; Elsevier: Amsterdam, The Netherlands, 2018; pp. 157–183. [Google Scholar] [CrossRef]
- Lin, M.-H.; Tsai, J.-F.; Yu, C.-S. A Review of Deterministic Optimization Methods in Engineering and Management. Math. Probl. Eng. 2012, 2012, 756023. [Google Scholar] [CrossRef] [Green Version]
- Papadimitrakis, M.; Giamarelos, N.; Stogiannos, M.; Zois, E.; Livanos, N.-I.; Alexandridis, A. Metaheuristic search in smart grid: A review with emphasis on planning, scheduling and power flow optimization applications. Renew. Sustain. Energy Rev. 2021, 145, 111072. [Google Scholar] [CrossRef]
- Banks, A.; Vincent, J.; Anyakoha, C. A review of particle swarm optimization. Part II: Hybridisation, combinatorial, multicriteria and constrained optimization, and indicative applications. Nat. Comput. 2008, 7, 109–124. [Google Scholar] [CrossRef]
- Katoch, S.; Chauhan, S.; Kumar, V. A review on genetic algorithm: Past, present, and future. Multimed. Tools Appl. 2021, 80, 8091–8126. [Google Scholar] [CrossRef] [PubMed]
- Dashtdar, M.; Najafi, M.; Esmaeilbeig, M. Calculating the locational marginal price and solving optimal power flow problem based on congestion management using GA-GSF algorithm. Electr. Eng. 2020, 102, 1549–1566. [Google Scholar] [CrossRef]
- Shabir, S. A Comparative Study of Genetic Algorithm and the Particle Swarm Optimization. Int. J. Electr. Eng. 2016, 9, 215–223. [Google Scholar]
- Hassanat, A.; Almohammadi, K.; Alkafaween, E.; Abunawas, E.; Hammouri, A.; Prasath, V.B.S. Choosing Mutation and Crossover Ratios for Genetic Algorithms—A Review with a New Dynamic Approach. Information 2019, 10, 390. [Google Scholar] [CrossRef] [Green Version]
- Kumari, M.S.; Priyanka, G.; Sydulu, M. Comparison of Genetic Algorithms and Particle Swarm Optimization for Optimal Power Flow Including FACTS devices. In Proceedings of the 2007 IEEE Lausanne Power Tech, Lausanne, Switzerland, 1–5 July 2007; pp. 1105–1110. [Google Scholar] [CrossRef]
- Wood, A.J.; Wollenberg, B.; Sheblé, G.B. Power Generation, Operation, and Control; John Wiley & Sons: New York, NY, USA, 2013. [Google Scholar]
- Frank, S.; Rebennack, S. An introduction to optimal power flow: Theory, formulation, and examples. IIE Trans. 2016, 48, 1172–1197. [Google Scholar] [CrossRef]
- Zheng, X.; Xu, Y.; LI, Z.; Chen, H. Co-optimisation and settlement of power-gas coupled system in day-ahead market under multiple uncertainties. IET Renew. Power Gener. 2021, 15, 1632–1647. [Google Scholar] [CrossRef]
- Gomez, T.; Perez-Arriaga, I.; Lumbreras, J.; Parra, V.M. A security-constrained decomposition approach to optimal reactive power planning. IEEE Trans. Power Syst. 1991, 6, 1069–1076. [Google Scholar] [CrossRef] [Green Version]
- Bakirtzis, A.G.; Biskas, P.; Zoumas, C.; Petridis, V. Optimal Power Flow by Enhanced Genetic Algorithm. IEEE Trans. Power Syst. 2002, 17, 8. [Google Scholar] [CrossRef]
- Jiang, Q.; Han, Z. Solvability identification and feasibility restoring of divergent optimal power flow problems. Sci. China Ser. E-Technol. Sci. 2009, 52, 944–954. [Google Scholar] [CrossRef]
- Papazoglou, G.K.; Bakirtzis, E.; Forouli, A.; Biskas, P.; Bakirtzis, A.G. A two-stage market-based TSO-DSO coordination framework. In Proceedings of the 2022 2nd International Conference on Energy Transition in the Mediterranean Area (SyNERGY MED), Thessaloniki, Greece, 17–19 October 2022; pp. 1–6. [Google Scholar] [CrossRef]
- Yang, Z.; Zhong, H.; Xia, Q.; Bose, A.; Kang, C. Optimal power flow based on successive linear approximation of power flow equations. IET Gener. Transm. Amp. Distrib. 2016, 10, 3654–3662. [Google Scholar] [CrossRef]
- Dommel, H.W.; Tinney, W.F. Optimal Power Flow Solutions. IEEE Trans. Power Appar. Syst. 1968, PAS-87, 1866–1876. [Google Scholar] [CrossRef]
- Burchett, R.C.; Happ, H.; Vierath, D.R. Quadratically Convergent Optimal Power Flow. IEEE Trans. Power Appar. Syst. 1984, PAS-103, 3267–3275. [Google Scholar] [CrossRef]
- Sun, D.I.; Ashley, B.; Brewer, B.; Hughes, A.; Tinney, W.F. Optimal Power Flow By Newton Approach. IEEE Trans. Power Appar. Syst. 1984, PAS–103, 2864–2880. [Google Scholar] [CrossRef]
- Holland, J.H. Genetic Algorithms-Computer programs that ‘evolve’ in ways that resemble natural selection can solve complex problems even their creators do not fully understand. Sci. Am. 2005, 267, 1992. [Google Scholar]
- Goldberg, D.E. Genetic Algorithms in Search, Optimization and Machine Learning, 13th ed.; Addison-Wesley Professional: Boston, MA, USA, 1989. [Google Scholar]
- Lai, L.L.; Ma, J.T. Improved genetic algorithms for optimal power flow under both normal and contigent operation states. Electr. PowerEnergy Syst. 1996, 19, 287–292. [Google Scholar] [CrossRef]
- Osman, M.S.; Abo-Sinna, M.; Mousa, A.A. A solution to the optimal power flow using genetic algorithm. Appl. Math. Comput. 2004, 155, 391–405. [Google Scholar] [CrossRef]
- Attia, A.-F.; Al-Turki, Y.; Abusorrah, A.M. Optimal Power Flow Using Adapted Genetic Algorithm with Adjusting Population Size. Electr. Power Compon. Syst. 2012, 40, 1285–1299. [Google Scholar] [CrossRef]
- Devaraj, D.; Yegnanarayana, B. Genetic-algorithm-based optimal power flow for security enhancement. IEE Proc. Gener. Transm. Distrib. 2005, 152, 899. [Google Scholar] [CrossRef]
- Paranjothi, S.R.; Anburaja, K. Optimal Power Flow Using Refined Genetic Algorithm. Electr. Power Compon. Syst. 2002, 30, 1055–1063. [Google Scholar] [CrossRef]
- Kumari, M.S.; Maheswarapu, S. Enhanced Genetic Algorithm based computation technique for multi-objective Optimal Power Flow solution. Int. J. Electr. Power Energy Syst. 2010, 32, 736–742. [Google Scholar] [CrossRef]
- Todorovski, M.; Rajicic, D. An Initialization Procedure in Solving Optimal Power Flow by Genetic Algorithm. IEEE Trans. Power Syst. 2006, 21, 480–487. [Google Scholar] [CrossRef]
- Todorovski, M.; RajiCiC, D. A Power Flow Method Suitable for Solving OPF Problems Using Genetic Algorithms. In Proceedings of the IEEE Region 8 EUROCON 2003. Computer as a Tool, Ljubljana, Slovenia, 22–24 September; 2003; p. 1248186. [Google Scholar]
- Szuvovivski, I.; Fernandes, T.; Aoki, A.R. Simultaneous allocation of capacitors and voltage regulators at distribution networks using Genetic Algorithms and Optimal Power Flow. Int. J. Electr. Power Energy Syst. 2012, 40, 62–69. [Google Scholar] [CrossRef]
- Forouli, A.A.; Papazoglou, G.; Bakirtzis, E.; Biskas, P.; Bakirtzis, A.G. AC-feasible Local Flexibility Market with Continuous Trading. In Proceedings of the 11th Bulk Power Systems Dynamics and Control Symposium-IREP 2022, Banff, AB, Canada, 25–30 July 2022; p. 9. [Google Scholar] [CrossRef]
- Biswas, P.; Pal, B. A fuzzy goal programming method to solve congestion management problem using genetic algorithm. Decis. Mak. Appl. Manag. Eng. 2019, 2, 36–53. [Google Scholar] [CrossRef]
- Li, S.; Gong, W.; Wang, L.; Gu, Q. Multi-objective optimal power flow with stochastic wind and solar power. Appl. Soft Comput. 2022, 114, 108045. [Google Scholar] [CrossRef]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T. A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Trans. Evol. Computat. 2002, 6, 182–197. [Google Scholar] [CrossRef]
- Maaranen, H.; Miettinen, K.; Penttinen, A. On initial populations of a genetic algorithm for continuous optimization problems. J. Glob. Optim. 2007, 37, 405–436. [Google Scholar] [CrossRef]
- Vrajitoru, D. Large Population or Many Generations for Genetic Algorithms? Implications in Information Retrieval. In Soft Computing in Information Retrieval; Crestani, F., Pasi, G., Eds.; Physica-Verlag Heidelberg: Heidelber, Germany, 2000; Volume 50, pp. 199–222. [Google Scholar] [CrossRef]
- Alander, J.T. On optimal population size of genetic algorithms. In Proceedings of the CompEuro 1992 Proceedings Computer Systems and Software Engineering, Hague, The Netherlands, 4–8 May 1992. [Google Scholar] [CrossRef]
- Eiben, A.E.; Marchiori, E.; Valkó, V.A. Evolutionary Algorithms with On-the-Fly Population Size Adjustment. In Parallel Problem Solving from Nature-PPSN VIII; Yao, X., Burke, E., Lozano, J., Smith, J., Merelo-Guervós, J., Bullinaria, J., Rowe, J., Tiňo, P., Kabán, A., Schwefel, H.-P., Eds.; Springer: Berlin/Heidelberg, Germany, 2004; Volume 3242, pp. 41–50. [Google Scholar] [CrossRef] [Green Version]
- Kennedy, J.; Eberhart, R. Particle Swarm Optimization. In Proceedings of the ICNN’95-International Conference on Neural Networks, Perth, WA, Australia, 27 November–1 December 1995; p. 7. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R.C. A discrete binary version of the particle swarm algorithm. In Proceedings of the 1997 IEEE International Conference on Systems, Man, and Cybernetics. Computational Cybernetics and Simulation, Orlando, FL, USA, 12–15 October 1997; Volume 5, pp. 4104–4108. [Google Scholar] [CrossRef]
- Laskari, E.C.; Parsopoulos, K.; Vrahatis, M.N. Particle swarm optimization for integer programming. In Proceedings of the 2002 Congress on Evolutionary Computation. CEC’02 (Cat. No.02TH8600), Honolulu, HI, USA, 12–17 May 2002; Volume 2, pp. 1582–1587. [Google Scholar] [CrossRef]
- Abido, M.A. Optimal power Flow using particle swarm optimization. Int. J. Electr. Power Energy Syst. 2002, 24, 563–571. [Google Scholar] [CrossRef]
- Wang, C.-R.; Yuan, H.-J.; Huang, Z.-Q.; Zhang, J.-W.; Sun, C.-J. A modified particle swarm optimization algorithm and its application in optimal power flow problem. In Proceedings of the 2005 International Conference on Machine Learning and Cybernetics, Guangzhou, China, 18–21 August 2005; Volume 5, pp. 2885–2889. [Google Scholar] [CrossRef]
- Zhao, B.; Guo, C.; Cao, Y.J. Improved particle swam optimization algorithm for OPF problems. In Proceedings of the IEEE PES Power Systems Conference and Exposition, New York, NY, USA, 10–13 October 2004; pp. 933–938. [Google Scholar] [CrossRef]
- Zhao, B.; Guo, C.; Cao, Y.J. An improved particle swarm optimization algorithm for optimal reactive power dispatch. In Proceedings of the IEEE Power Engineering Society General Meeting, San Francisco, CA, USA, 16 June 2005; pp. 403–410. [Google Scholar] [CrossRef]
- Vlachogiannis, J.G.; Lee, K.Y. A Comparative Study on Particle Swarm Optimization for Optimal Steady-State Performance of Power Systems. IEEE Trans. Power Syst. 2006, 21, 1718–1728. [Google Scholar] [CrossRef] [Green Version]
- Vlachogiannis, J.G.; Lee, K.Y. Coordinated aggregation particle swarm optimization applied in reactive power and voltage control. In Proceedings of the 2006 IEEE Power Engineering Society General Meeting, Montreal, QC, Canada, 18–22 June 2006; p. 6. [Google Scholar] [CrossRef]
- He, S.; Wen, J.; Prempain, E.; Wu, Q.; Fitch, J.; Mann, S. An improved particle swarm optimization for optimal power flow. In Proceedings of the 2004 International Conference on Power System Technology, Singapore, 21–24 November 2004. [Google Scholar] [CrossRef]
- Yumbla, P.E.O.; Ramirez, J.; Coello, C.A.C. Optimal Power Flow Subject to Security Constraints Solved With a Particle Swarm Optimizer. IEEE Trans. Power Syst. 2008, 23, 33–40. [Google Scholar] [CrossRef]
- Gaing, Z.-L. Constrained optimal power flow by mixed-integer particle swarm optimization. In Proceedings of the IEEE Power Engineering Society General Meeting, San Francisco, CA, USA, 16 June 2005; pp. 290–297. [Google Scholar] [CrossRef]
- Swarup, K.S. Swarm intelligence approach to the solution of optimal power flow. J. Indian Inst. Sci. 2006, 86, 439. [Google Scholar]
- Umapathy, P.; Venkataseshaiah, C.; Arumugam, M.S. Particle Swarm Optimization with Various Inertia Weight Variants for Optimal Power Flow Solution. Discret. Dyn. Nat. Soc. 2010, 2010, 462145. [Google Scholar] [CrossRef] [Green Version]
- Vu, P.; Le, D.; Vo, N.; Tlusty, J. A novel weight-improved particle swarm optimization algorithm for optimal power flow and economic load dispatch problems. In Proceedings of the IEEE PES T&D 2010, New Orleans, LA, USA, 19–22 April 2010; pp. 1–7. [Google Scholar] [CrossRef]
- Singh, R.P.; Mukherjee, V.; Ghoshal, S.P. Particle swarm optimization with an aging leader and challengers algorithm for the solution of optimal power flow problem. Appl. Soft Comput. 2016, 40, 161–177. [Google Scholar] [CrossRef]
- Singh, R.P.; Mukherjee, V.; Ghoshal, S.P. Particle swarm optimization with an aging leader and challengers algorithm for optimal power flow problem with FACTS devices. Int. J. Electr. Power Energy Syst. 2015, 64, 1185–1196. [Google Scholar] [CrossRef]
- Naderi, E.; Pourakbari-Kasmaei, M.; Abdi, H. An efficient particle swarm optimization algorithm to solve optimal power flow problem integrated with FACTS devices. Appl. Soft Comput. 2019, 80, 243–262. [Google Scholar] [CrossRef]
- Sarstedt, M.; Kluß, L.; Gerster, J.; Meldau, T.; Hofmann, L. Survey and Comparison of Optimization-Based Aggregation Methods for the Determination of the Flexibility Potentials at Vertical System Interconnections. Energies 2021, 14, 687. [Google Scholar] [CrossRef]
- Zaro, F.R.; Abido, M.A. Multi-objective particle swarm optimization for optimal power flow in a deregulated environment of power systems. In Proceedings of the 2011 11th International Conference on Intelligent Systems Design and Applications, Cordoba, Spain, 22–24 November 2011; pp. 1122–1127. [Google Scholar] [CrossRef]
- Niknam, T.; Narimani, M.; Aghaei, J.; Azizipanah-Abarghooee, R. Improved particle swarm optimisation for multi-objective optimal power flow considering the cost, loss, emission and voltage stability index. IET Gener. Transm. Distrib. 2012, 6, 515. [Google Scholar] [CrossRef]
- Clerc, M. The swarm and the queen: Towards a deterministic and adaptive particle swarm optimization. In Proceedings of the 1999 Congress on Evolutionary Computation-CEC99 (Cat. No. 99TH8406), Washington, DC, USA, 6–9 July 1999; pp. 1951–1957. [Google Scholar] [CrossRef]
- Bonyadi, M.R.; Michalewicz, Z. Particle Swarm Optimization for Single Objective Continuous Space Problems: A Review. Evol. Comput. 2017, 25, 1–54. [Google Scholar] [CrossRef]
- Parrish, J.K.; Hamner, W.M. Animal Groups in Three Dimensions: How Species Aggregate, 1st ed.; Cambridge University Press: Cambridge, UK, 1997. [Google Scholar]
- He, S.; Wu, Q.; Wen, J.; Saunders, J.; Paton, R.C. A particle swarm optimizer with passive congregation. Biosystems 2004, 78, 135–147. [Google Scholar] [CrossRef]
- Rosendo, M.; Pozo, A. Applying a Discrete Particle Swarm Optimization Algorithm to Combinatorial Problems. In Proceedings of the 2010 11th Brazilian Symposium on Neural Networks, Sao Paulo, Brazil, 23–28 October 2010; pp. 235–240. [Google Scholar] [CrossRef]
- ECampana, F.; Fasano, G.; Pinto, A. Dynamic analysis for the selection of parameters and initial population, in particle swarm optimization. J. Glob. Optim. 2010, 48, 347–397. [Google Scholar] [CrossRef]
- Chen, D.; Zhao, C. Particle swarm optimization with adaptive population size and its application. Appl. Soft Comput. 2009, 9, 39–48. [Google Scholar] [CrossRef]
- Piotrowski, A.P.; Napiorkowski, J.; Piotrowska, A.E. Population size in Particle Swarm Optimization. Swarm Evol. Comput. 2020, 58, 100718. [Google Scholar] [CrossRef]
- Papazoglou, G.; Biskas, P. Review of Methodologies for the Assessment of Feasible Operating Regions at the TSO–DSO Interface. Energies 2022, 15, 5147. [Google Scholar] [CrossRef]


| Reference | Literature Review Extent | Literature Review Focus | Analysis of Reviewed GA and PSO OPF Characteristics | Comparison of GA and PSO OPF | Date Published |
|---|---|---|---|---|---|
| [3] | Limited | PSO and GA | Yes (limited) | Yes (limited) | 2005 |
| [9] | Extensive | Metaheuristics | No | No | 2012 |
| [12] | Extensive | Metaheuristics | No | No | 2018 |
| [14] | Extensive | Metaheuristics | No | Yes (limited) | 2021 |
| [20] | Limited | PSO and GA | Yes (limited) | Yes (limited) | 2007 |
| This work | Extensive | PSO and GA | Yes (extensive) | Yes (extensive) | 2023 |
| Objective Function | Abbreviation | Example |
|---|---|---|
| (Linear/Quadratic) Generation Cost Minimization | (L/Q)GCM | Fuel cost minimization |
| Welfare Maximization | WM | Market-based applications |
| Losses Minimization | LM | Minimization of active power losses |
| Reactive Power Dispatch Optimization | RPDO | Minimization of reactive power dispatch |
| Investment Cost Minimization | ICM | Minimization of cost of capacitor banks |
| Post-Contingency Security Maximization | PCSM | Minimization of post-contingency loading |
| Minimization of Voltage Deviation | MVD | Voltage profile improvement |
| Minimization of Environmental Impact | MEI | Minimization of emissions |
| Congestion Minimization | CM | Overload alleviation |
| Ref. | Encoding | Parent Selection | Crossover | Adaptiveness | Power Flow Formulation | Objective Functions * | Constraint Violation Penalties |
|---|---|---|---|---|---|---|---|
| [25] | Binary | Roulette wheel | Single-point | Mutation, crossover probabilities | FDLF | QGCM | Linear |
| [34] | Binary | Roulette wheel | Uniform | Static | Full PF | QGCM | Quadratic |
| [35] | Binary | Roulette wheel | Single-point | Constraint violation penalties | Full PF | QGCM | Quadratic |
| [36] | Binary | Roulette wheel | N/A | Mutation, crossover probabilities, population size | Full PF | LGCM, QGCM, MVD | N/A |
| [37] | Real | Tournament | Blend | Static | Full PF | PCSM | Quadratic |
| [38] | Binary | Roulette wheel | Uniform | Mutation, crossover probabilities (exponential variation) | FDLF | QGCM | Quadratic |
| [39] | Binary | Roulette wheel | Single-point | Mutation, crossover probabilities | DQLF | QGCM, LM, MVD | Quadratic |
| [40] | Real | Roulette wheel | Single-point | Constraint violation penalties increase | FDFL, [41] | QGCM | Quadratic |
| [42] | Binary | Roulette wheel | Dispersed crossing | Static | Full PF | LM, MVD, ICM | Quadratic |
| [17] | Real | N/A | N/A | Static | Full PF | QGCM | Linear |
| [44] | Real | Roulette wheel | Single-point | Static | Full PF | CM, QGCM, LM | N/A |
| [45] | Real | N/A | N/A | Crossover, mutation, probabilities | Full PF | QGCM, LM, MVD, MEI | N/A |
| Ref. | Adaptiveness of Inertia Weights | Maximum Velocity | Objective Functions * | Constraint Violation Penalties |
|---|---|---|---|---|
| [54] | Annealing to reduce inertia weights | Yes | LGCM, QGCM, MVD | Quadratic |
| [55] | Dynamic inertia weights adjustment | N/A | LGCM | Linear |
| [56,57] | Dynamic penalty coefficients | Yes | LCGM, RPDO | Linear |
| [58,59] | Dynamic inertia weights adjustment | Yes | LM, MVD | Linear |
| [60] | No | Yes | GCM | Quadratic |
| [61] | Dynamic penalty coefficients, inertia weights adjustment | N/A | GCM | Quadratic |
| [62] | Dynamic inertia weights adjustment | Yes | GCM, MVD | Linear |
| [63] | Dynamic inertia weights adjustment | Yes | GCM | Quadratic |
| [64] | Dynamic inertia weights adjustment (GLbest algorithm) | N/A | GCM | N/A |
| [65] | Dynamic inertia weights adjustment (WI algorithm) | N/A | GCM | N/A |
| [66,67] | Dynamic adjustment of leader’s leading power | N/A | GCM, LM, MEI | Linear |
| [68] | Dynamic inertia weights adjustment (Mamdani-type fuzzy rules) | Yes | GCM | Quadratic |
| [69] | Dynamic penalty coefficients | Yes | FOR estimation | Linear |
| [70] | No | N/A | GCM, wheeling cost minimization | N/A |
| [71] | Dynamic inertia weights adjustment (chaotic formula), influence of the personal and global bests (self-adaptive) | N/A | GCM, LM, MEI | N/A |
| Ref. | Number of Generations | Population Size | NFFEs | Crossover Probability | Mutation Probability | Cost [$] |
|---|---|---|---|---|---|---|
| [25] | 200 | 80 | 16,000 | 0.9 (initial) | 0.001/bit (initial) | 802.06 |
| [36] | 50 | 400 (initial) | ~17,000 | dynamic | dynamic | 799.84 |
| [34] | 200 | 50 | 10,000 | 0.9 | 1 (initial), 0.005 (final) | 801.49 |
| [40] | 500 | 200 | 12,000 | 0.9 | 0.01 | 801.05 |
| [17] | - | - | - | 0.85 | - | 796.22 |
| Ref. | Number of Epochs | Population Size | NFFEs | Cognitive Coef. | Social Coef. | Inertia Weight | Cost [$] |
|---|---|---|---|---|---|---|---|
| [54] | 500 | 50 | 25,000 | 2 | 2 | - | 800.41 |
| [60] | 500 | 50 | 25,000 | 0.5 | 0.5 | 0.9 (initial), 0.4 (final) | 802.04 |
| [56] | 100 | 50 | 5000 | 2.05 | 2.05 | - | 4389 * |
| [63] | 150 | 20 | 3000 | 2.1 | 2.1 | 1 (initial) | 800.74 |
| [66] | - | 60 | 5000 | 2.05 | 2.05 | 0.9 (initial), 0.4 (final) | 825.89 * |
| [67] | 797.14 | ||||||
| [68] | 50 | 200 | 10,000 | - | - | 0.9 (initial), 0.4 (final) | 800.4 |
| [64] | 20 | 200 | 4000 | 2 | 2 | - | 801.84 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Papazoglou, G.; Biskas, P. Review and Comparison of Genetic Algorithm and Particle Swarm Optimization in the Optimal Power Flow Problem. Energies 2023, 16, 1152. https://doi.org/10.3390/en16031152
Papazoglou G, Biskas P. Review and Comparison of Genetic Algorithm and Particle Swarm Optimization in the Optimal Power Flow Problem. Energies. 2023; 16(3):1152. https://doi.org/10.3390/en16031152
Chicago/Turabian StylePapazoglou, Georgios, and Pandelis Biskas. 2023. "Review and Comparison of Genetic Algorithm and Particle Swarm Optimization in the Optimal Power Flow Problem" Energies 16, no. 3: 1152. https://doi.org/10.3390/en16031152
APA StylePapazoglou, G., & Biskas, P. (2023). Review and Comparison of Genetic Algorithm and Particle Swarm Optimization in the Optimal Power Flow Problem. Energies, 16(3), 1152. https://doi.org/10.3390/en16031152








