Temperature and Thermal Stress Analysis of a Hot Blast Stove with an Internal Combustion Chamber
Abstract
:1. Introduction
2. Numerical Modelling
2.1. CFD Analysis of a Hot Blast Stove
2.1.1. Fluid Flow Model
2.1.2. Species Transport and Chemical Reaction Models
2.1.3. Radiation Model
2.1.4. Porous Media Model
2.1.5. Boundary Conditions
2.2. Thermal Boundary Conditions of the Structure
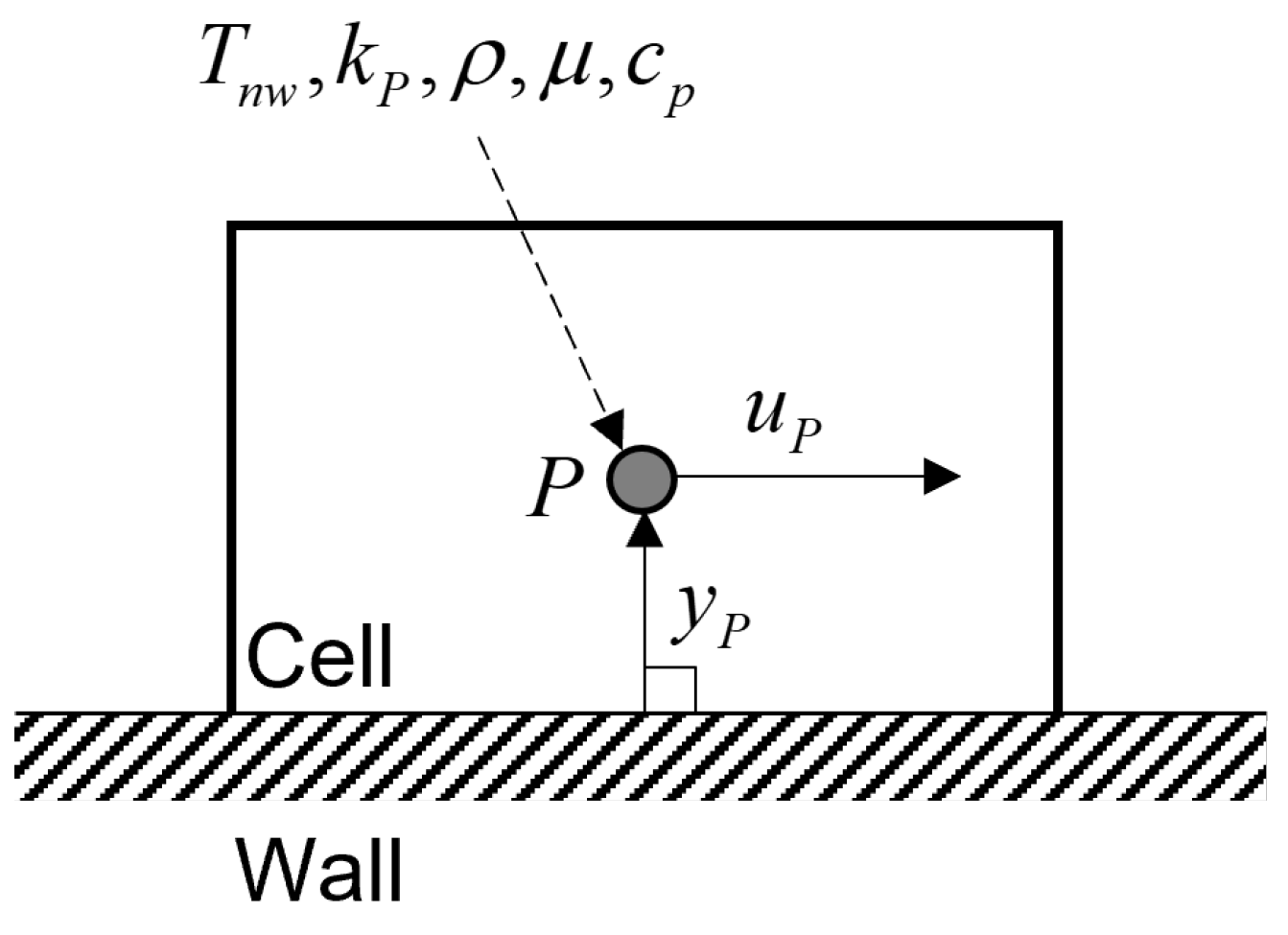
2.2.1. Convective Heat Transfer
2.2.2. Radiation Heat Transfer
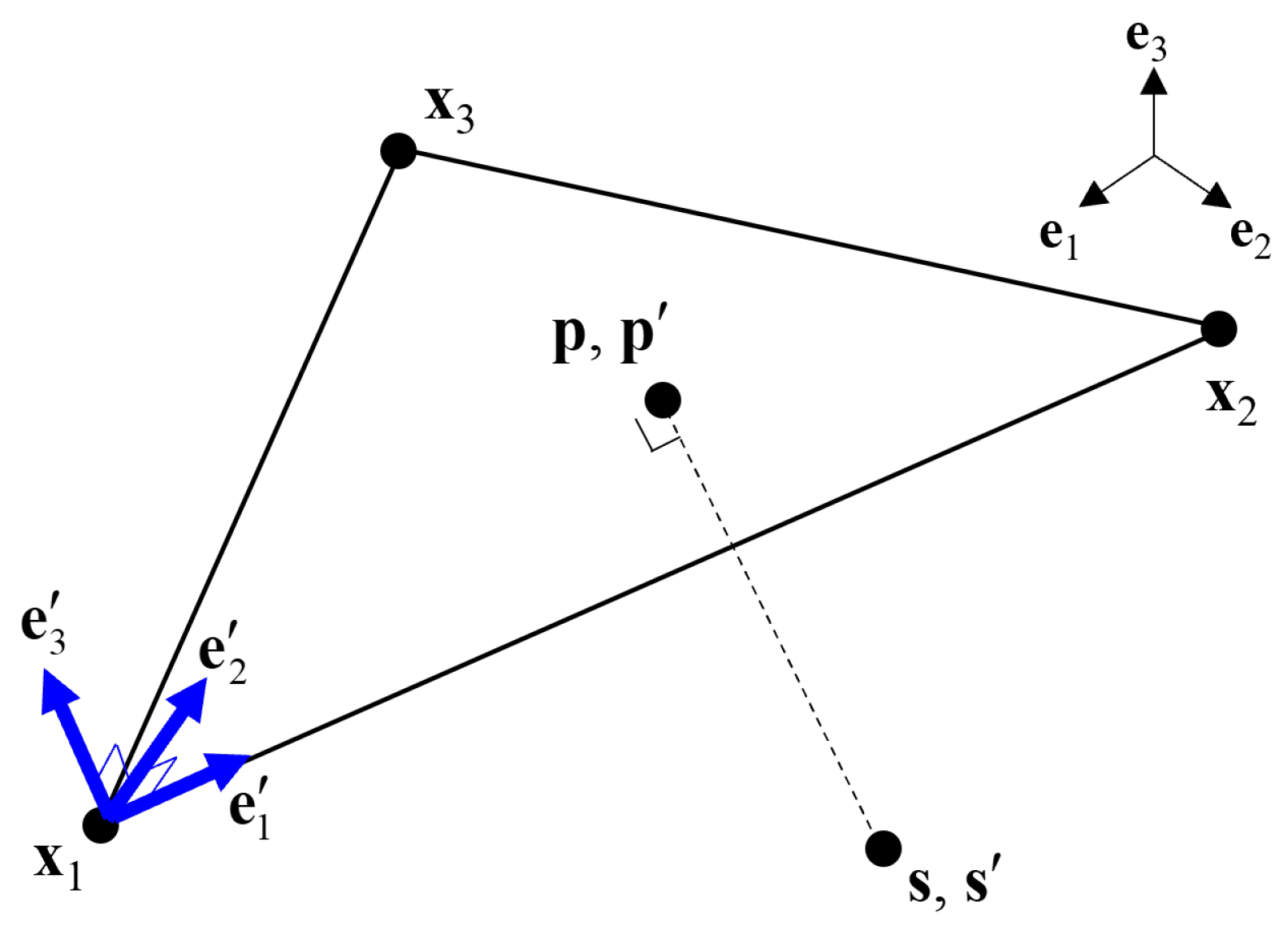
2.3. Mapping of the Thermal Boundary Conditions
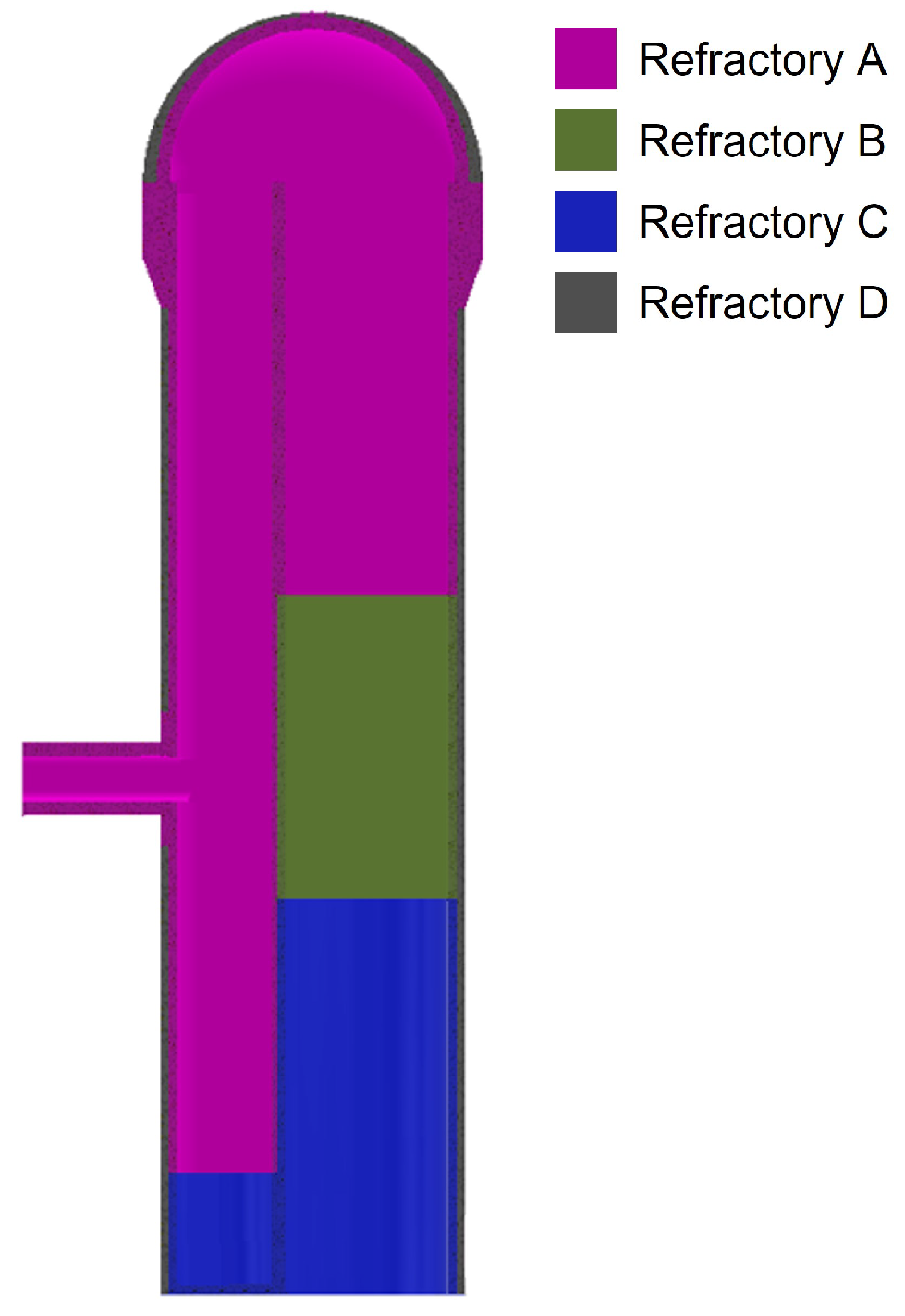
2.4. Material Properties of the Refractory Linings and Shell
2.5. Computational Conditions
3. Results and Discussion
4. Conclusions
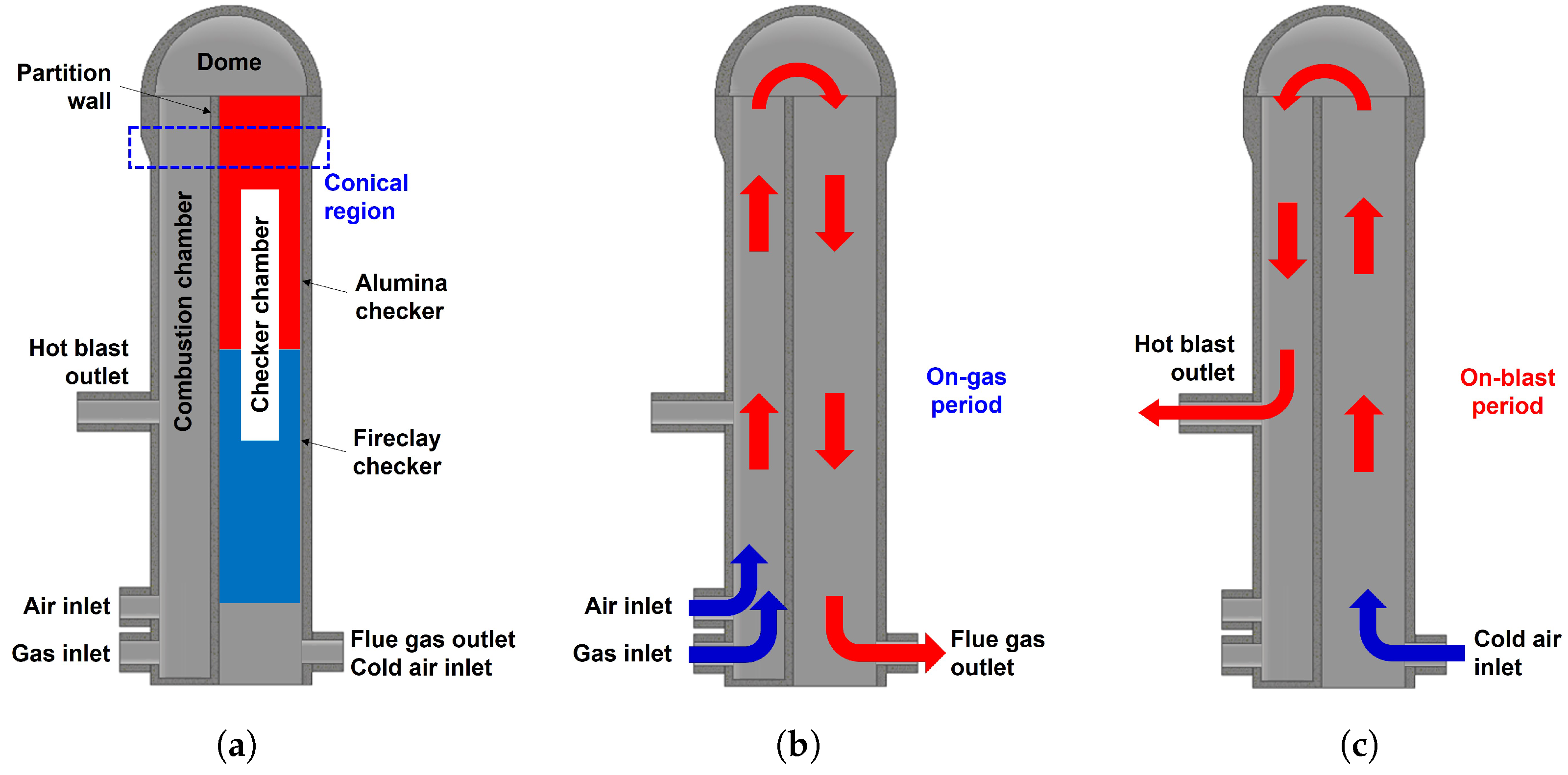
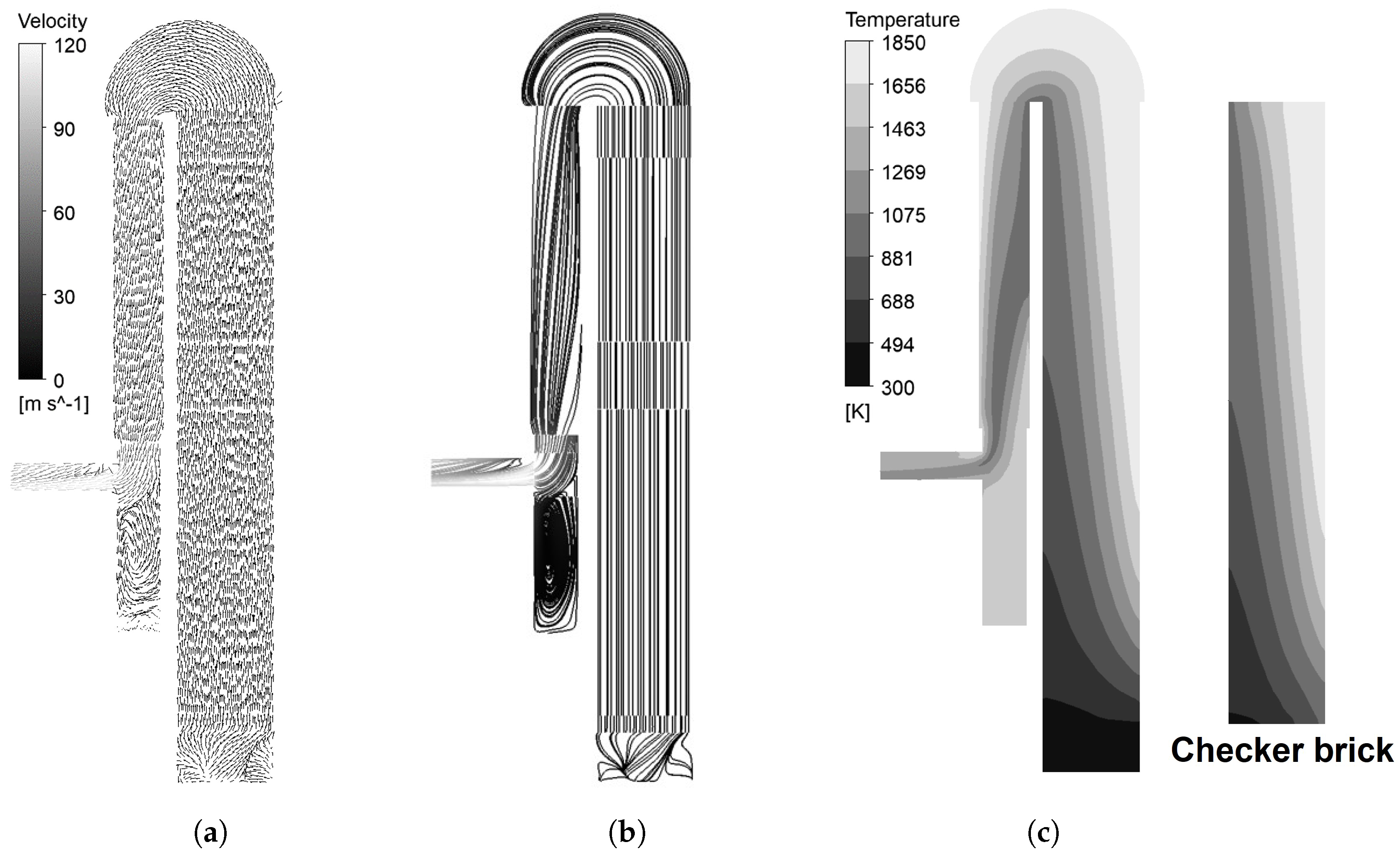
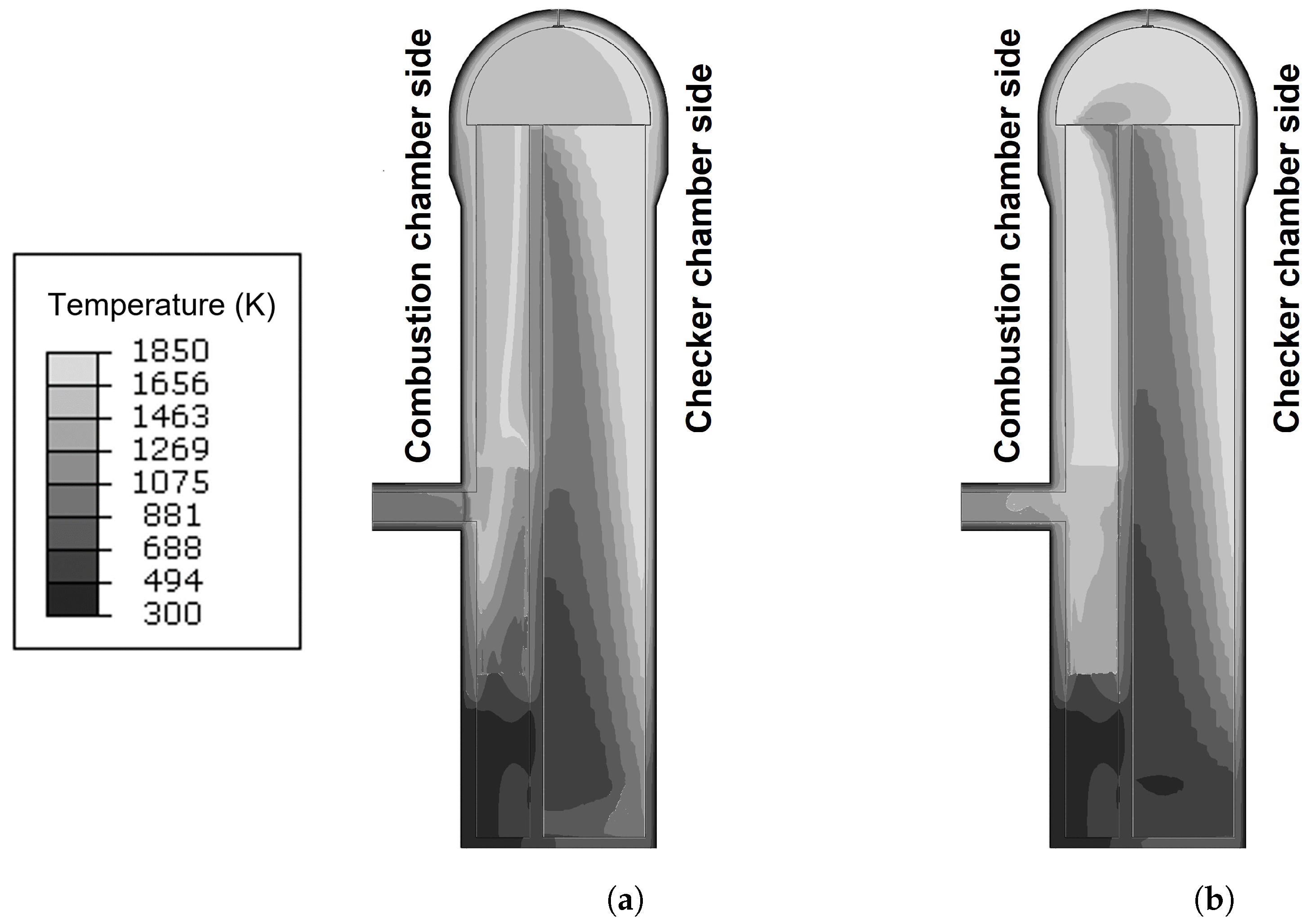
- In the on-gas period, a vortex was generated above the partition wall while the main flow passed through the outer region of the dome. The inner region of the checker chamber could not absorb the heat from the flue gas due to a lack of flow, even though the vortex temperature was high enough;
- The average temperature of the hot blast reached 1345 K in the on-blast period. There was no vortex generation, and the velocity distribution was considerably even compared to the on-gas period. The temperature distribution had the elevated temperature region at the outer region of the hot blast stove;
- The refractory linings in the outer side of the checker chamber and the dome region near the outer side of the checker chamber were continuously exposed to a high temperature. These regions would be a significant area of interest in managing the deterioration of the refractory linings;
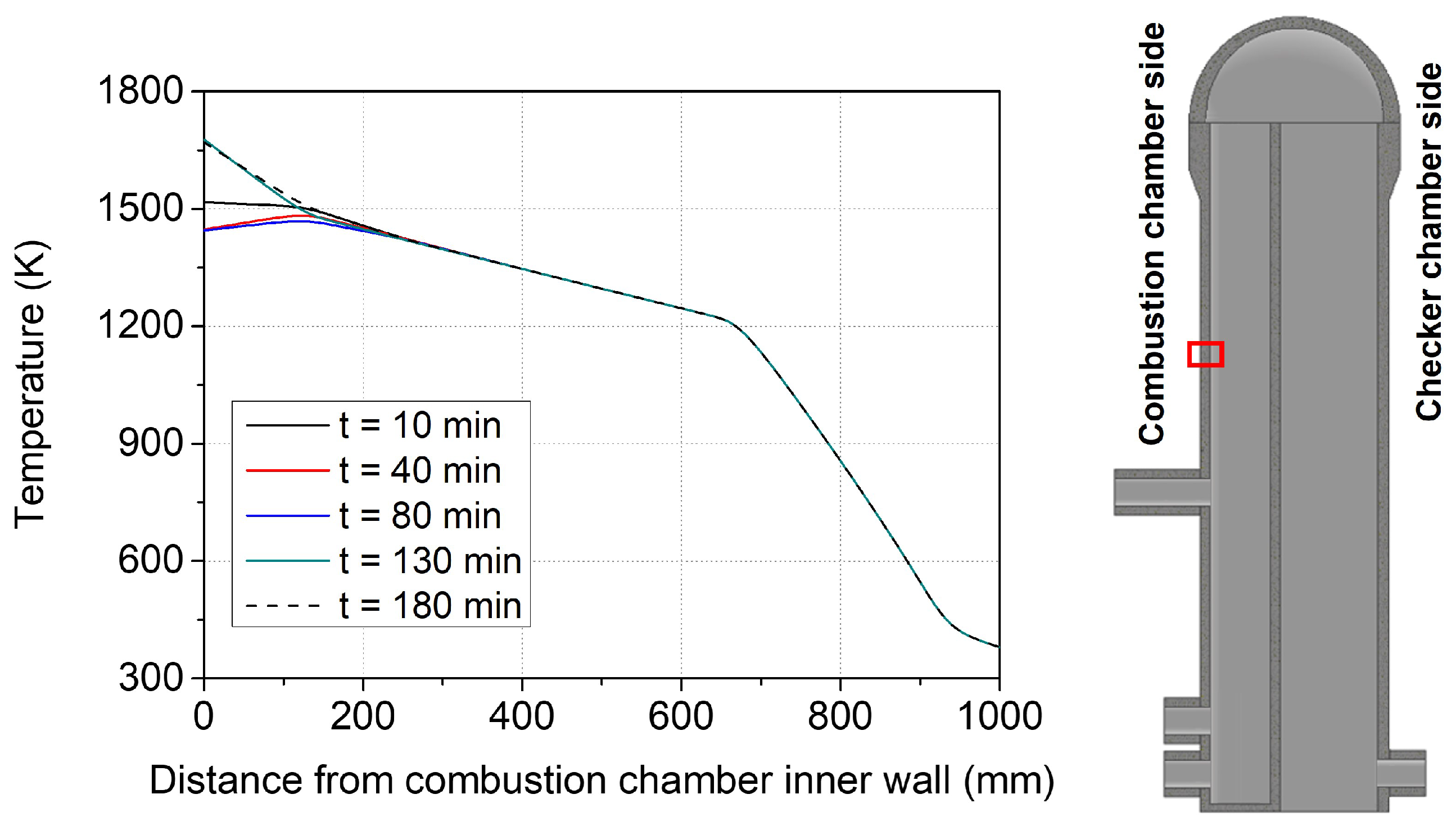
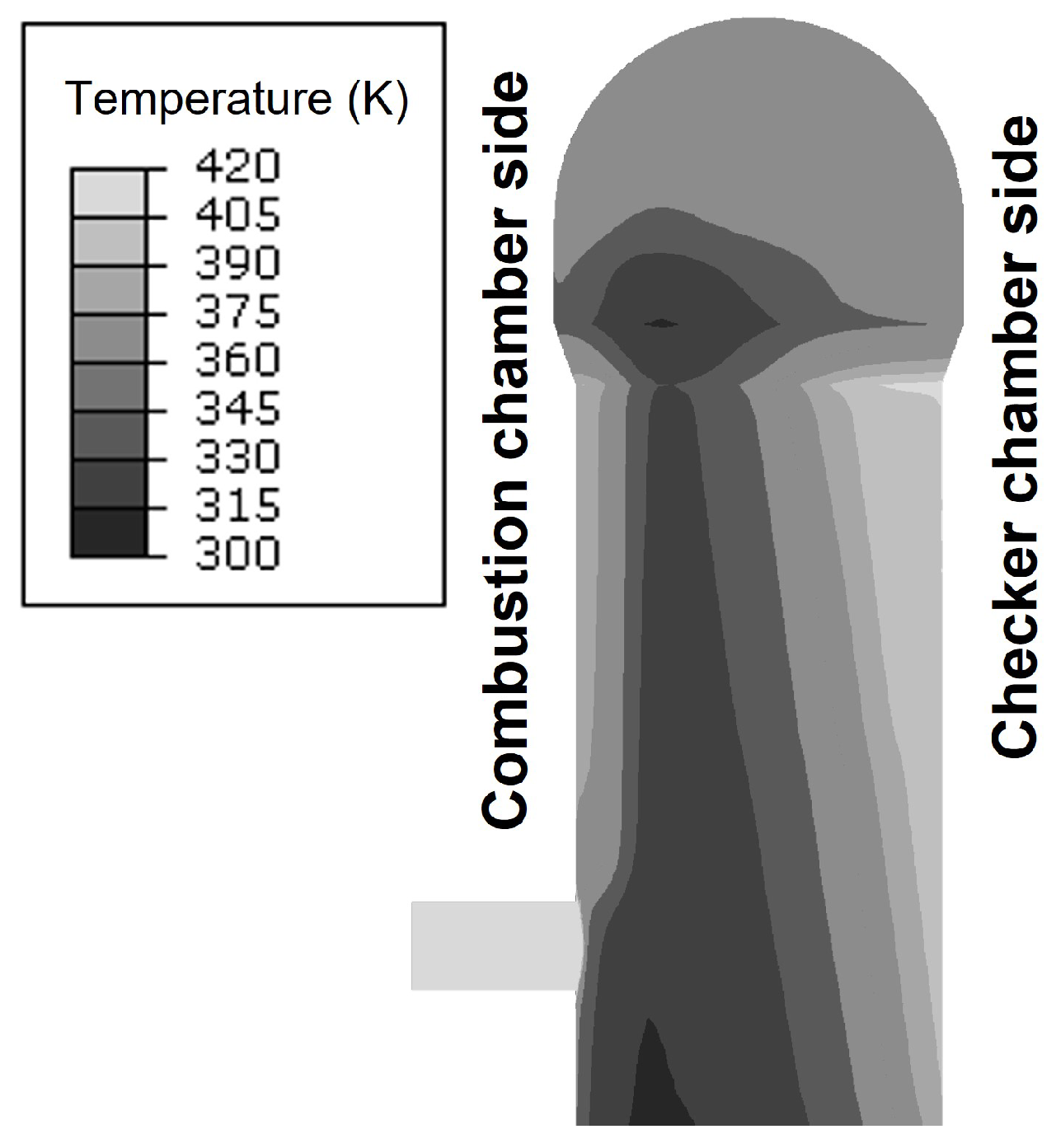
- Although the inner surface of the refractory lining temperature changed from 1441 K to 1659 K, the temperature change from 250 mm location into the thickness direction significantly decreased. The shell temperature did not change during the operation thanks to the low thermal diffusivity of the refractories;
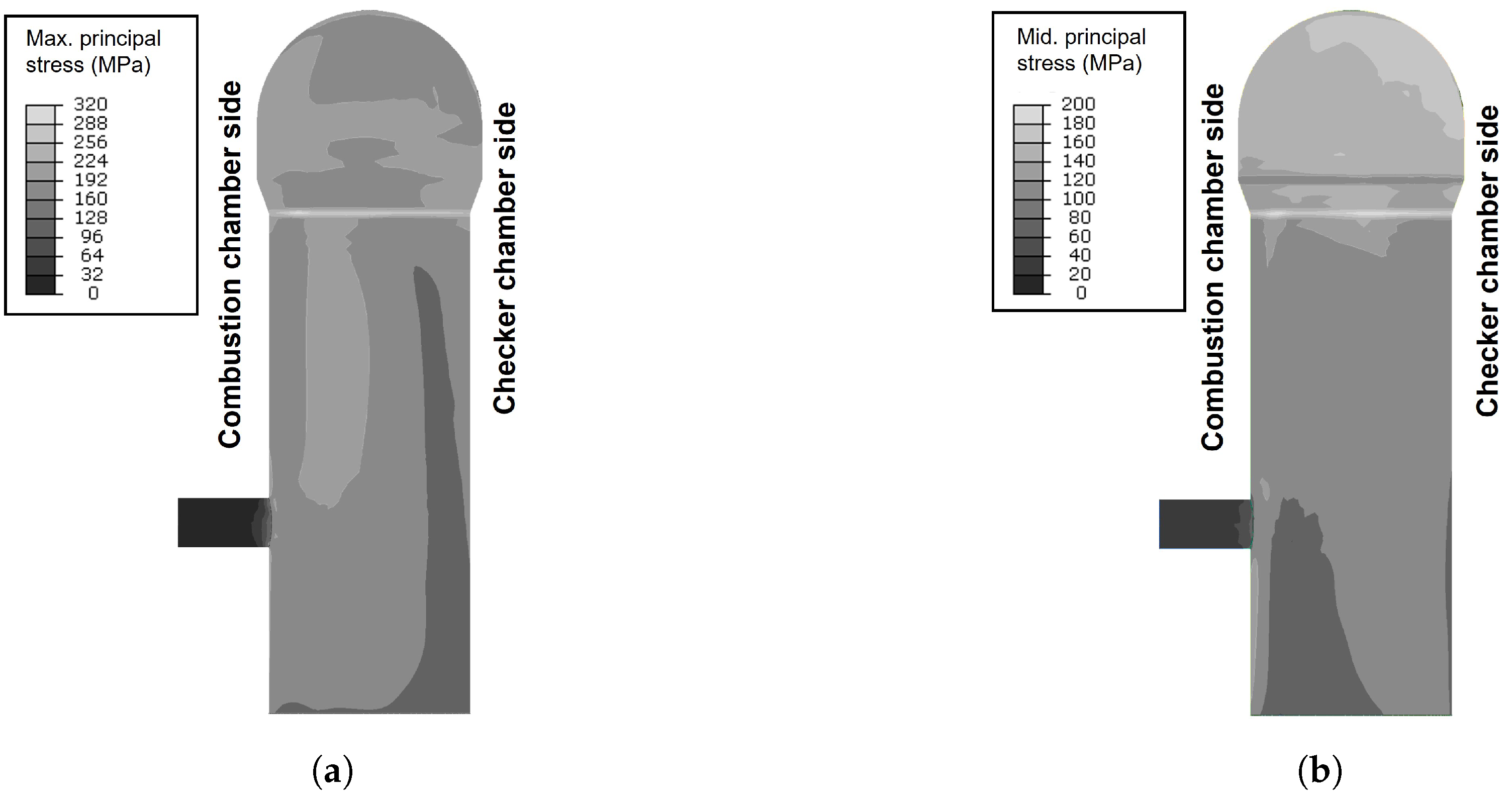
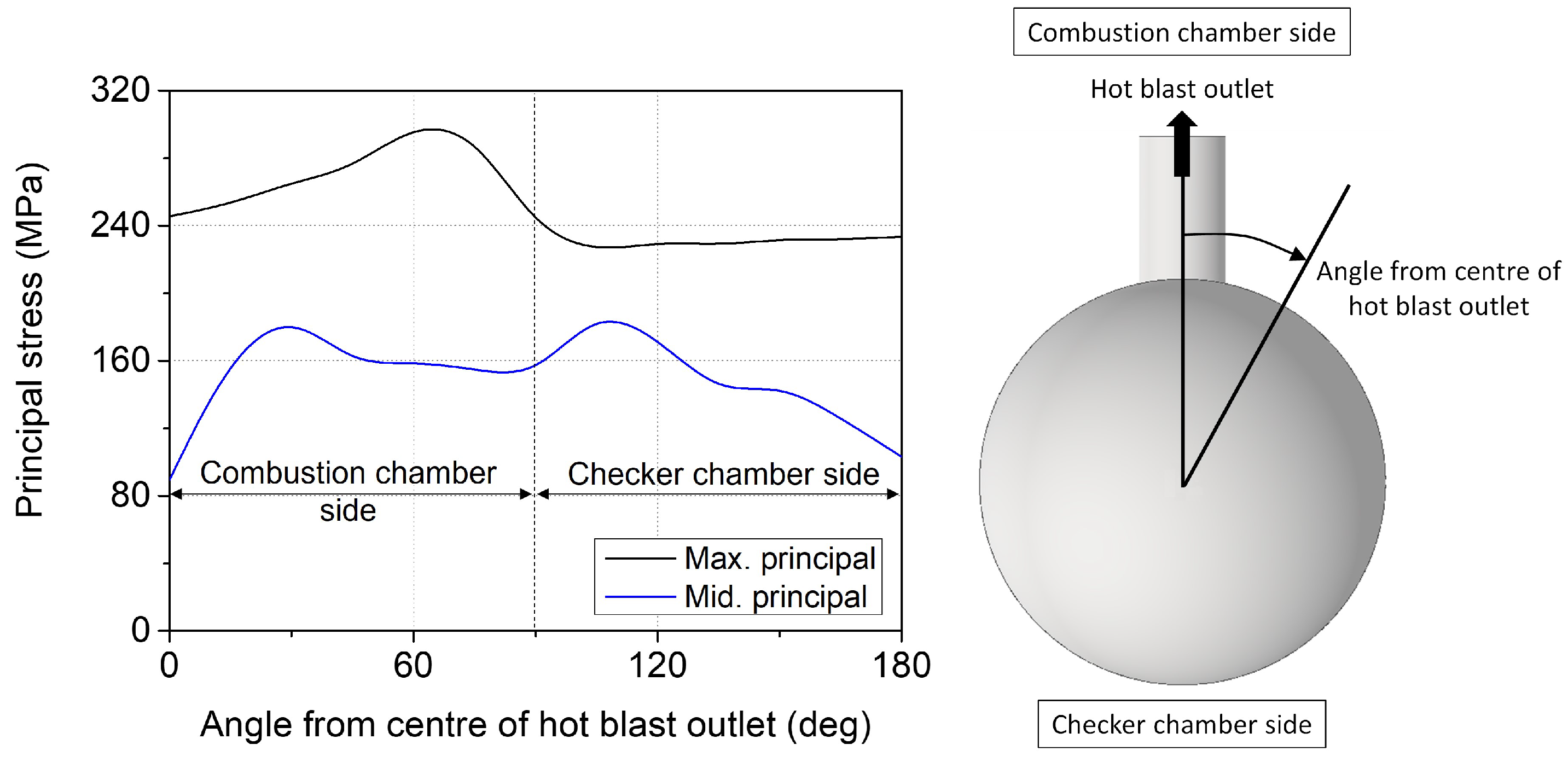
- The conical region of the shell was found to have high maximum and middle principal thermal stresses. The maximum and middle principal stresses were calculated as 300.6 MPa and 192.0 MPa, respectively. The thermal stress is induced due to the high-temperature gradient near the conical region, and the geometric characteristic of the conical region made the thermal stress much higher. The thermal stress analysis result indicates that the conical region would be a significant area of interest.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Dwivedi, S.K.; Vishwakarma, M.; Soni, A. Advances and researches on non destructive testing: A review. Mater. Today Proc. 2018, 5, 3690–3698. [Google Scholar] [CrossRef]
- Gol’dfarb, E.; Gres, L.; Lebedev, V.; Kazimirova, I.; Tsukanov, P. Character of fracture of the shell metal of blast-furnace stoves. Metallurgist 1979, 23, 469–472. [Google Scholar] [CrossRef]
- Van Ikelen, J.; Nugteren, B. Intercrystalline Stress Corrosion-A Creeping Threat. IRON Steel Technol. 2006, 3, 202. [Google Scholar]
- Zhang, F.M.; Mao, Q.W.; Mei, C.H.; Xin, L.; Hu, Z.R. Dome combustion hot blast stove for huge blast furnace. J. Iron Steel Res. Int. 2012, 19, 1–7. [Google Scholar] [CrossRef]
- Rieger, J.; Weiss, C.; Rummer, B. Modelling and control of pollutant formation in blast stoves. J. Clean. Prod. 2015, 88, 254–261. [Google Scholar] [CrossRef]
- Guo, H.; Yan, B.; Zhang, J.; Liu, F.; Pei, Y. Optimization of the number of burner nozzles in a hot blast stove by the way of simulation. JOM 2014, 66, 1241–1252. [Google Scholar] [CrossRef]
- Qi, F.; Liu, Z.; Yao, C.; Li, B. Numerical study and structural optimization of a top combustion hot blast stove. Adv. Mech. Eng. 2015, 7, 709675. [Google Scholar] [CrossRef]
- Zetterholm, J.; Ji, X.; Sundelin, B.; Martin, P.M.; Wang, C. Dynamic modelling for the hot blast stove. Appl. Energy 2017, 185, 2142–2150. [Google Scholar] [CrossRef]
- Zhang, Q.; Chen, L.; Zhao, C. Numerical simulation of combustion and air supply process and optimal design of traditional top combustion hot blast stoves. Steel Res. Int. 2021, 92, 2000311. [Google Scholar] [CrossRef]
- Yan, K.; Cheng, S. Stress and deformation analysis of top combustion hot blast stove shell. In Characterization of Minerals, Metals, and Materials 2017; Springer: Berlin/Heidelberg, Germany, 2017; pp. 757–765. [Google Scholar]
- Hwang, Y.M.; Lee, Y.M. Thermal stress analysis of refractory linings in a hot blast stove. J. Phys. Conf. Ser. 2020, 1633, 012075. [Google Scholar] [CrossRef]
- Gan, Y.F.; Jang, J.Y.; Wu, T.Y. 3D dynamic thermal and thermomechanical stress analysis of a hot blast stove. Ironmak. Steelmak. 2020, 47, 959–972. [Google Scholar] [CrossRef]
- van Straaten, V.; de Graaff, B.; Engel, E. Hot Blast System Development: Technology, Operations, Campaign Management. BHM Berg-und Hüttenmännische Monatshefte 2019, 164, 452–460. [Google Scholar] [CrossRef]
- Rajić, M.N.; Banić, M.S.; Živković, D.S.; Tomić, M.M.; Mančić, M.V. Construction optimization of hot water fire-tube boiler using thermomechanical finite element analysis. Therm. Sci. 2018, 22, 1511–1523. [Google Scholar] [CrossRef]
- Jaremkiewicz, M.; Taler, D.; Dzierwa, P.; Taler, J. Determination of transient fluid temperature and thermal stresses in pressure thick-walled elements using a new design thermometer. Energies 2019, 12, 222. [Google Scholar] [CrossRef] [Green Version]
- Taler, J.; Dzierwa, P.; Jaremkiewicz, M.; Taler, D.; Kaczmarski, K.; Trojan, M.; Sobota, T. Thermal stress monitoring in thick walled pressure components of steam boilers. Energy 2019, 175, 645–666. [Google Scholar] [CrossRef]
- Hoseinzadeh, S.; Heyns, P.S. Thermo-structural fatigue and lifetime analysis of a heat exchanger as a feedwater heater in power plant. Eng. Fail. Anal. 2020, 113, 104548. [Google Scholar] [CrossRef]
- Rajić, M.; Zivković, D.; Banić, M.; Mančić, M.; Maneski, T.; Milošević, M.; Mitrović, N. Experimental and numerical stress and strain analysis of the boiler reversing chamber tube plate. Therm. Sci. 2022, 26, 2135–2145. [Google Scholar] [CrossRef]
- Yıldırım, A.; Yarımpabuç, D.; Arikan, V.; Eker, M.; Celebi, K. Nonlinear thermal stress analysis of functionally graded spherical pressure vessels. Int. J. Press. Vessel. Pip. 2022, 200, 104830. [Google Scholar] [CrossRef]
- Jeong, S.H.; Chung, K.S.; Ma, W.J.; Yang, J.S.; Choi, J.B.; Kim, M.K. Thermal stress intensity factor solutions for reactor pressure vessel nozzles. Nucl. Eng. Technol. 2022, 54, 2188–2197. [Google Scholar] [CrossRef]
- Karamavruc, A. Obtaining bulk flow based heat transfer coefficients for thermal evaluation of turbochargers. In Proceedings of the IMechE Conference, C6231-110, London, UK, 17–18 May 2016. [Google Scholar]
- Hochstein, J.I.; Gerhart, A.L. Young, Munson and Okiishi’s A Brief Introduction to Fluid Mechanics; John Wiley & Sons: Hoboken, NJ, USA, 2021. [Google Scholar]
- Kimura, Y.; Takatani, K.; Otsu, N. Three-dimensional mathematical modeling and designing of hot stove. ISIJ Int. 2010, 50, 1040–1047. [Google Scholar] [CrossRef] [Green Version]
- Amirshaghaghi, H.; Zamaniyan, A.; Ebrahimi, H.; Zarkesh, M. Numerical simulation of methane partial oxidation in the burner and combustion chamber of autothermal reformer. Appl. Math. Model. 2010, 34, 2312–2322. [Google Scholar] [CrossRef]
- Mollamahdi, M.; Hashemi, S.A. The effects of porous wall as a novel flame stabilization method on flame characteristics in a premixed burner for CH4/air mixture by numerical simulation. Proc. Inst. Mech. Eng. Part A J. Power Energy 2020, 234, 211–225. [Google Scholar] [CrossRef]
- Rieger, J.; Drózd-Ryś, M.; Weiss, C.; Harmuth, H. Thermochemical wear of refractory linings associated with gas firing in metallurgical plants. Steel Res. Int. 2014, 85, 527–536. [Google Scholar] [CrossRef]
- Jia, Z.; Ye, Q.; Wang, H.; Li, H.; Shi, S. Numerical simulation of a new porous medium burner with two sections and double decks. Processes 2018, 6, 185. [Google Scholar] [CrossRef] [Green Version]
- Launder, B.E. Lectures in Mathematical Models of Turbulence; Academic Press: Cambridge, MA, USA, 1972. [Google Scholar]
- Versteeg, H.K.; Malalasekera, W. An Introduction to Computational Fluid Dynamics: The Finite Volume Method; Pearson Education: Upper Saddle River, NJ, USA, 2007. [Google Scholar]
- Magnussen, B.F.; Hjertager, B.H. On mathematical modeling of turbulent combustion with special emphasis on soot formation and combustion. Symp. (Int.) Combust. 1977, 16, 719–729. [Google Scholar] [CrossRef]
- Coelho, P.J. Numerical simulation of the interaction between turbulence and radiation in reactive flows. Prog. Energy Combust. Sci. 2007, 33, 311–383. [Google Scholar] [CrossRef]
- Coelho, P.J. Advances in the discrete ordinates and finite volume methods for the solution of radiative heat transfer problems in participating media. J. Quant. Spectrosc. Radiat. Transf. 2014, 145, 121–146. [Google Scholar] [CrossRef]
- Sakami, M.; Charette, A. A new differencing scheme for the discrete-ordinates method in complex geometries. Revue Générale de Thermique 1998, 37, 440–449. [Google Scholar] [CrossRef]
- Joseph, D.; Coelho, P.J.; Cuenot, B.; El Hafi, M. Application of the discrete ordinates method to grey media in complex geometries using unstructured meshes. Eurotherm Comput. Therm. Radiat. Particip. Media 2003, 11, 97–106. [Google Scholar]
- Fiveland, W. Discrete-ordinates solutions of the radiative transport equation for rectangular enclosures. J. Heat Transfer. 1984, 106, 699–706. [Google Scholar] [CrossRef]
- Fluent, A. Ansys Fluent Theory Guide; Ansys Inc.: Canonsburg, PA, USA, 2011; Volume 15317, pp. 724–746. [Google Scholar]
- Haaland, S.E. Simple and explicit formulas for the friction factor in turbulent pipe flow. J. Fluids Eng. 1983, 105, 89–90. [Google Scholar] [CrossRef]
- Gnielinski, V. New equations for heat and mass transfer in turbulent pipe and channel flow. Int. Chem. Eng. 1976, 16, 359–368. [Google Scholar]
- Carnigila, S.C.; Barna, G.L. Handbook of Industrial Refractories Technology; Elsevier: Amsterdam, The Netherlands, 1991. [Google Scholar]
- uczyński, P.; Giesen, M.; Gier, T.S.; Wirsum, M. Uncoupled CFD-FEA methods for the Thermo-structural analysis of turbochargers. Int. J. Turbomachinery Propuls. Power 2019, 4, 39. [Google Scholar] [CrossRef] [Green Version]
- Launder, B.E.; Spalding, D.B. The numerical computation of turbulent flows. In Numerical Prediction of Flow, Heat Transfer, Turbulence and Combustion; Elsevier: Amsterdam, The Netherlands, 1983; pp. 96–116. [Google Scholar]
- Kader, B. Temperature and concentration profiles in fully turbulent boundary layers. Int. J. Heat Mass Transf. 1981, 24, 1541–1544. [Google Scholar] [CrossRef]
- Incropera, F.P.; DeWitt, D.P.; Bergman, T.L.; Lavine, A.S. Fundamentals of Heat and Mass Transfer; Wiley: New York, NY, USA, 1996; Volume 6. [Google Scholar]
- Bordbar, M.H.; Węcel, G.; Hyppänen, T. A line by line based weighted sum of gray gases model for inhomogeneous CO2–H2O mixture in oxy-fired combustion. Combust. Flame 2014, 161, 2435–2445. [Google Scholar] [CrossRef]
- Schacht, C. Refractories Handbook; CRC Press: Boca Raton, FL, USA, 2004. [Google Scholar]
- Sarkar, R. Refractory Technology: Fundamentals and Applications; CRC Press: Boca Raton, FL, USA, 2016. [Google Scholar]

| Component | CO2 | O2 | CO | H2 | H2O | N2 |
|---|---|---|---|---|---|---|
| Composition (%) | 18.1 | 0.1 | 24.5 | 0.3 | 0.2 | 56.8 |
| Checker Type | Density (kg/m3) | Thermal Conductivity (W/m·K) | Specific Heat Capacity (J/kg·K) | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Temperature (K) | Temperature (K) | ||||||||
| 300 | 1000 | 2000 | 300 | 500 | 1000 | 1500 | 2000 | ||
| Alumina | 2.57 | 1.70 | 1.78 | 1.96 | 823 | 994 | 1171 | 1249 | 1284 |
| Fireclay | 2.29 | 1.36 | 1.48 | 1.55 | 799 | 965 | 1138 | 1214 | 1248 |
| Material | Density (g/cm3) | Thermal Conductivity (W/m·K) | Thermal Expansion Coefficient ( K) | |
|---|---|---|---|---|
| at 500 °C | at 1000 °C | |||
| Refractory A | 2.56 | 1.77 | 1.79 | 64 |
| Refractory B | 2.24 | 1.75 | 1.79 | 62 |
| Refractory C | 2.11 | 1.75 | 1.78 | 59 |
| Refractory D | 0.78 | 0.24 | 0.39 | 55 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Park, D.; Guo, F.; Choi, J.; Park, J.-H.; Kim, N. Temperature and Thermal Stress Analysis of a Hot Blast Stove with an Internal Combustion Chamber. Processes 2023, 11, 707. https://doi.org/10.3390/pr11030707
Park D, Guo F, Choi J, Park J-H, Kim N. Temperature and Thermal Stress Analysis of a Hot Blast Stove with an Internal Combustion Chamber. Processes. 2023; 11(3):707. https://doi.org/10.3390/pr11030707
Chicago/Turabian StylePark, Donghwi, Feng Guo, Jongrak Choi, Joo-Hyoung Park, and Naksoo Kim. 2023. "Temperature and Thermal Stress Analysis of a Hot Blast Stove with an Internal Combustion Chamber" Processes 11, no. 3: 707. https://doi.org/10.3390/pr11030707
APA StylePark, D., Guo, F., Choi, J., Park, J.-H., & Kim, N. (2023). Temperature and Thermal Stress Analysis of a Hot Blast Stove with an Internal Combustion Chamber. Processes, 11(3), 707. https://doi.org/10.3390/pr11030707









