Quantitative Comparison of Statistical Methods for Analyzing Human Metabolomics Data
Abstract
:1. Introduction
2. Results
2.1. Statistical Analyses of Simulated Metabolomics Data
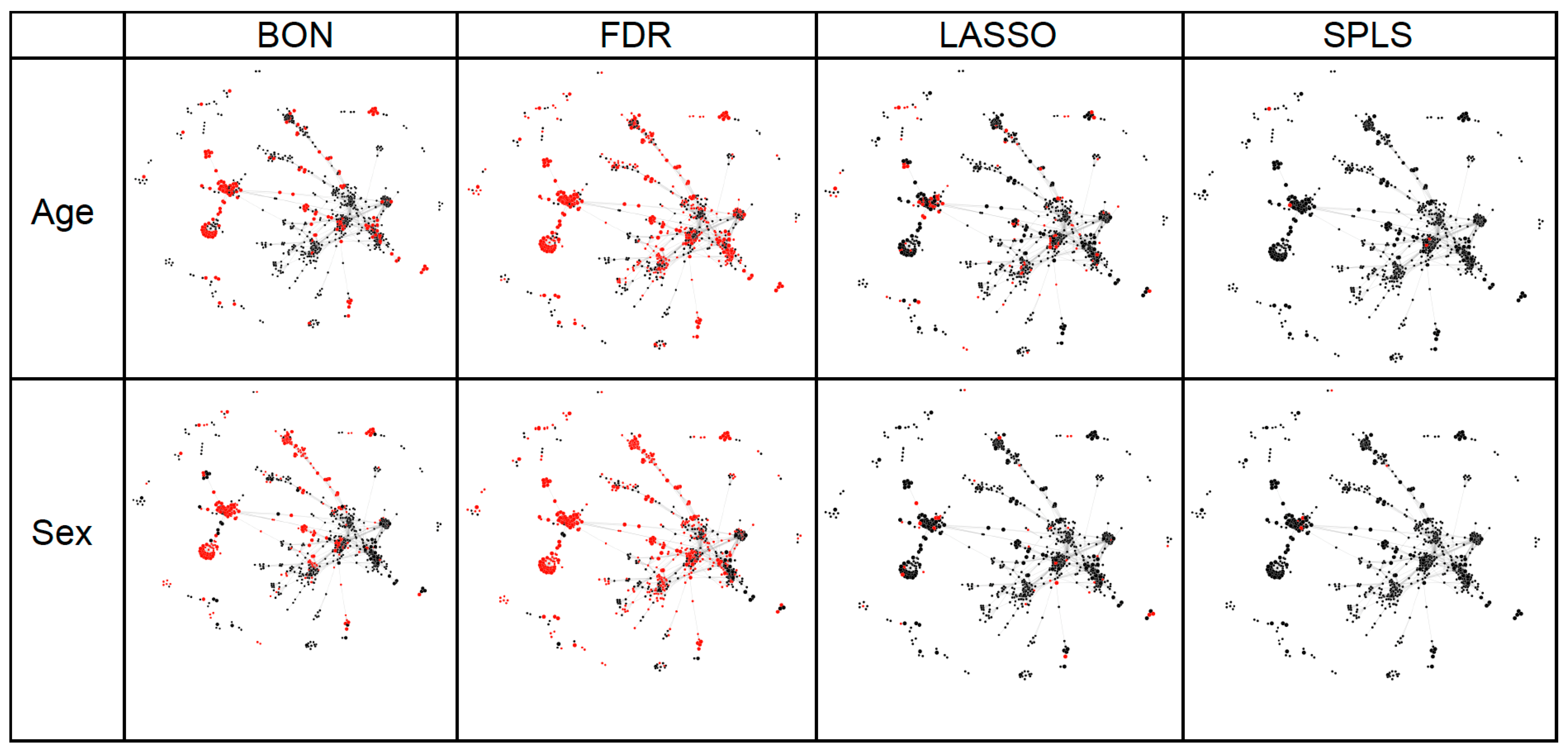
2.2. Statistical Analyses of Experimentally Derived Metabolomics Data
2.3. Results from Both Simulated and Experimentally Derived Data
3. Discussion
4. Materials and Methods
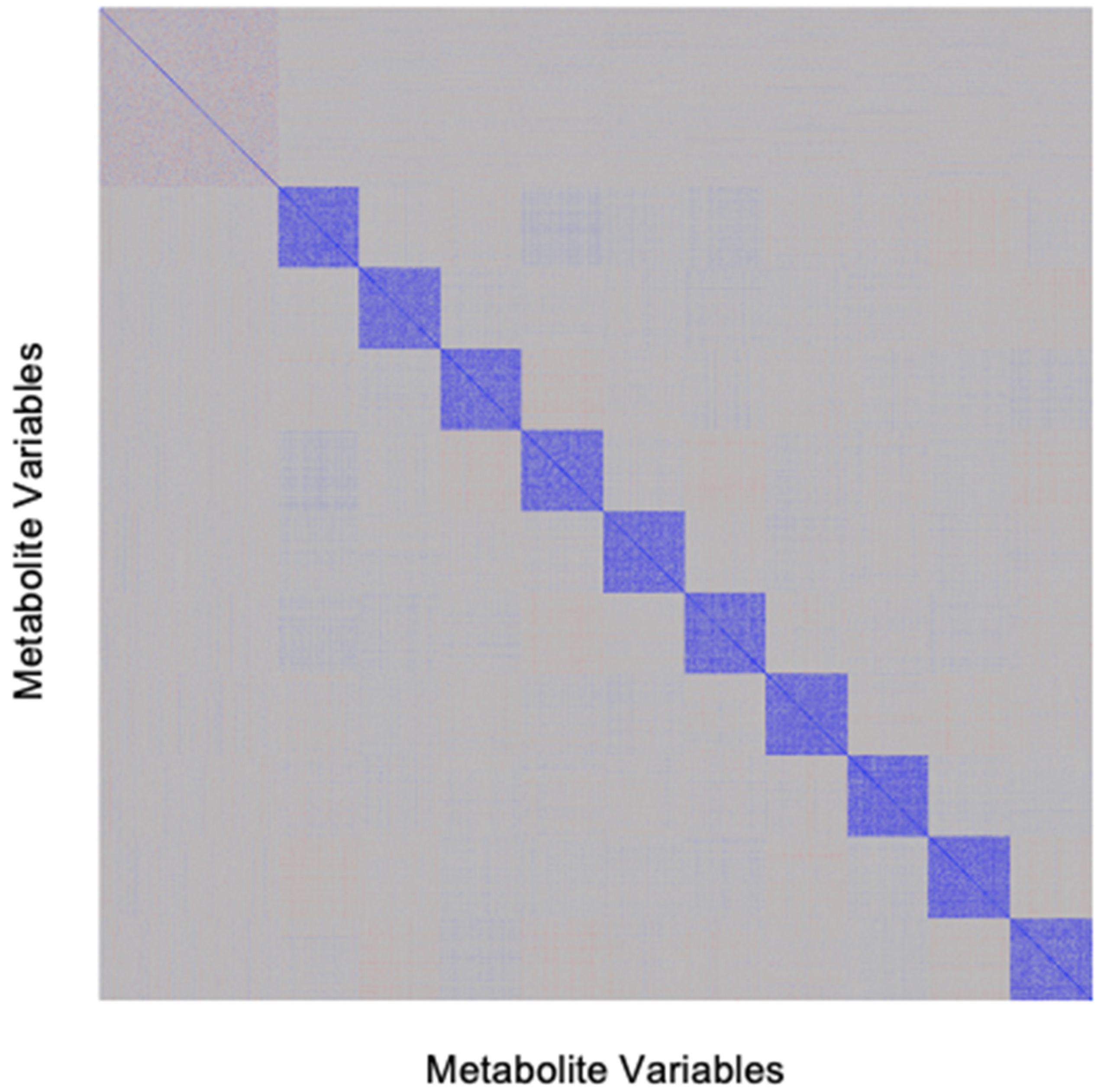
4.1. Development of Simulated Metabolomics Dataset
4.2. Statistical Approaches for Analyzing Metabolomics Data
4.3. Experimental Human Metabolomics Data
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Nicholson, J.K.; Holmes, E.; Kinross, J.M.; Darzi, A.W.; Takats, Z.; Lindon, J.C. Metabolic phenotyping in clinical and surgical environments. Nature 2012, 491, 384–392. [Google Scholar] [CrossRef]
- van der Greef, J.; van Wietmarschen, H.; van Ommen, B.; Verheij, E. Looking back into the future: 30 years of metabolomics at TNO. Mass Spectrom. Rev. 2013, 32, 399–415. [Google Scholar] [CrossRef]
- Ala-Korpela, M.; Davey Smith, G. Metabolic profiling-multitude of technologies with great research potential, but (when) will translation emerge? Int. J. Epidemiol. 2016, 45, 1311–1318. [Google Scholar] [CrossRef] [Green Version]
- Barnes, S.; Benton, H.P.; Casazza, K.; Cooper, S.J.; Cui, X.; Du, X.; Engler, J.; Kabarowski, J.H.; Li, S.; Pathmasiri, W.; et al. Training in metabolomics research. II. Processing and statistical analysis of metabolomics data, metabolite identification, pathway analysis, applications of metabolomics and its future. J. Mass Spectrom. 2016, 51, 535–548. [Google Scholar] [CrossRef] [Green Version]
- Sugimoto, M.; Kawakami, M.; Robert, M.; Soga, T.; Tomita, M. Bioinformatics Tools for Mass Spectroscopy-Based Metabolomic Data Processing and Analysis. Curr. Bioinform. 2012, 7, 96–108. [Google Scholar] [CrossRef]
- Barber, R.F.; Candes, E.J. Controlling the false discovery rate via knockoffs. Ann. Stat. 2015, 43, 2055–2085. [Google Scholar] [CrossRef] [Green Version]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef] [Green Version]
- Chun, H.; Keles, S. Sparse partial least squares regression for simultaneous dimension reduction and variable selection. J. R. Stat. Soc. Ser. B Stat. Methodol. 2010, 72, 3–25. [Google Scholar] [CrossRef] [Green Version]
- Le Cao, K.A.; Boitard, S.; Besse, P. Sparse PLS discriminant analysis: Biologically relevant feature selection and graphical displays for multiclass problems. BMC Bioinform. 2011, 12, 253. [Google Scholar] [CrossRef] [Green Version]
- Le Cao, K.A.; Rossouw, D.; Robert-Granie, C.; Besse, P. A sparse PLS for variable selection when integrating omics data. Stat. Appl. Genet. Mol. Biol. 2008, 7, 35. [Google Scholar] [CrossRef]
- Tibshirani, R. Regression shrinkage and selection via the lasso. J. R. Stat. Soc. Ser. B Stat. Methodol. 1996, 58, 267–288. [Google Scholar] [CrossRef]
- Jiang, M.; Wang, C.; Zhang, Y.; Feng, Y.; Wang, Y.; Zhu, Y. Sparse partial-least-squares discriminant analysis for different geographical origins of Salvia miltiorrhiza by (1) H-NMR-based metabolomics. Phytochem. Anal. 2014, 25, 50–58. [Google Scholar] [CrossRef] [PubMed]
- Waldron, L.; Pintilie, M.; Tsao, M.S.; Shepherd, F.A.; Huttenhower, C.; Jurisica, I. Optimized application of penalized regression methods to diverse genomic data. Bioinformatics 2011, 27, 3399–3406. [Google Scholar] [CrossRef] [Green Version]
- Friedman, J.; Hastie, T.; Tibshirani, R. Regularization Paths for Generalized Linear Models via Coordinate Descent. J. Stat. Softw. 2010, 33, 1–22. [Google Scholar] [CrossRef] [Green Version]
- Alonso, A.; Marsal, S.; Julia, A. Analytical methods in untargeted metabolomics: State of the art in 2015. Front. Bioeng. Biotechnol. 2015, 3, 23. [Google Scholar] [CrossRef] [Green Version]
- Bovelstad, H.M.; Nygard, S.; Storvold, H.L.; Aldrin, M.; Borgan, O.; Frigessi, A.; Lingjaerde, O.C. Predicting survival from microarray data--a comparative study. Bioinformatics 2007, 23, 2080–2087. [Google Scholar] [CrossRef] [Green Version]
- Carvalho, C.M.; Chang, J.; Lucas, J.E.; Nevins, J.R.; Wang, Q.; West, M. High-Dimensional Sparse Factor Modeling: Applications in Gene Expression Genomics. J. Am. Stat. Assoc. 2008, 103, 1438–1456. [Google Scholar] [CrossRef] [Green Version]
- Dobra, A.; Hans, C.; Jones, B.; Nevins, J.R.; Yao, G.; West, M. Sparse graphical models for exploring gene expression data. J. Multivar. Anal. 2004, 90, 196–212. [Google Scholar] [CrossRef]
- Xing, E.P.; Jordan, M.I.; Karp, R.M. Feature selection for high-dimensional genomic microarray data. In Proceedings of the Eighteenth International Conference on Machine Learning, San Francisco, CA, USA, 28 June–1 July 2001; pp. 601–608. [Google Scholar]
- Maertens, A.; Bouhifd, M.; Zhao, L.; Odwin-DaCosta, S.; Kleensang, A.; Yager, J.D.; Hartung, T. Metabolomic network analysis of estrogen-stimulated MCF-7 cells: A comparison of overrepresentation analysis, quantitative enrichment analysis and pathway analysis versus metabolite network analysis. Arch. Toxicol. 2017, 91, 217–230. [Google Scholar] [CrossRef] [Green Version]
- Xie, Y.; Pan, W.; Khodursky, A.B. A note on using permutation-based false discovery rate estimates to compare different analysis methods for microarray data. Bioinformatics 2005, 21, 4280–4288. [Google Scholar] [CrossRef] [Green Version]
- Benjamini, Y.; Yekutieli, D. The control of the false discovery rate in multiple testing under dependency. Ann. Stat. 2001, 29, 1165–1188. [Google Scholar] [CrossRef]
- Mahieu, N.G.; Patti, G.J. Systems-Level Annotation of a Metabolomics Data Set Reduces 25 000 Features to Fewer than 1000 Unique Metabolites. Anal. Chem. 2017, 89, 10397–10406. [Google Scholar] [CrossRef]
- Han, W.; Li, L. Evaluating and minimizing batch effects in metabolomics. Mass Spectrom. Rev. 2022, 41, 421–442. [Google Scholar] [CrossRef]
- Cala, M.P.; Agulló-Ortuño, M.T.; Prieto-García, E.; González-Riano, C.; Parrilla-Rubio, L.; Barbas, C.; Díaz-García, C.V.; García, A.; Pernaut, C.; Adeva, J.; et al. Multiplatform plasma fingerprinting in cancer cachexia: A pilot observational and translational study. J. Cachexia Sarcopenia Muscle 2018, 9, 348–357. [Google Scholar] [CrossRef]
- Miller, J.; Alshehri, A.; Ramage, M.I.; Stephens, N.A.; Mullen, A.B.; Boyd, M.; Ross, J.A.; Wigmore, S.J.; Watson, D.G.; Skipworth, R.J.E. Plasma Metabolomics Identifies Lipid and Amino Acid Markers of Weight Loss in Patients with Upper Gastrointestinal Cancer. Cancers 2019, 11, 1594. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Pang, Z.; Zhou, G.; Chong, J.; Xia, J. Comprehensive Meta-Analysis of COVID-19 Global Metabolomics Datasets. Metabolites 2021, 11, 44. [Google Scholar] [CrossRef]
- Benjamini, Y.; Hochberg, Y. Controlling the false discovery rate: A practical and powerful approach to multiple testing. J. R. Stat. Soc. Ser. B Stat. Methodol. 1995, 57, 289–300. [Google Scholar] [CrossRef]
- Jolliffe, I.T. A note on the use of principal components in regression. Appl. Stat. 1982, 31, 300–303. [Google Scholar] [CrossRef]
- Massy, W.F. Principal components regression in exploratory statistical research. J. Am. Stat. Assoc. 1965, 60, 234–256. [Google Scholar] [CrossRef]
- Mayers, J.R.; Wu, C.; Clish, C.B.; Kraft, P.; Torrence, M.E.; Fiske, B.P.; Yuan, C.; Bao, Y.; Townsend, M.K.; Tworoger, S.S.; et al. Elevation of circulating branched-chain amino acids is an early event in human pancreatic adenocarcinoma development. Nat. Med. 2014, 20, 1193–1198. [Google Scholar] [CrossRef]
- Scholtens, D.M.; Bain, J.R.; Reisetter, A.C.; Muehlbauer, M.J.; Nodzenski, M.; Stevens, R.D.; Ilkayeva, O.; Lowe, L.P.; Metzger, B.E.; Newgard, C.B.; et al. Metabolic Networks and Metabolites Underlie Associations Between Maternal Glucose During Pregnancy and Newborn Size at Birth. Diabetes 2016, 65, 2039–2050. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wang, T.J.; Larson, M.G.; Vasan, R.S.; Cheng, S.; Rhee, E.P.; McCabe, E.; Lewis, G.D.; Fox, C.S.; Jacques, P.F.; Fernandez, C.; et al. Metabolite profiles and the risk of developing diabetes. Nat. Med. 2011, 17, 448–453. [Google Scholar] [CrossRef] [PubMed]
- Barker, M.; Rayens, W. Partial least squares for discrimination. J. Chemometr. 2003, 17, 166–173. [Google Scholar] [CrossRef]
- Mehmood, T.; Martens, H.; Saebo, S.; Warringer, J.; Snipen, L. A Partial Least Squares based algorithm for parsimonious variable selection. Algorithms Mol. Biol. 2011, 6, 27. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Roy, P.P.; Roy, K. On Some Aspects of Variable Selection for Partial Least Squares Regression Models. QSAR Comb. Sci. 2008, 27, 302–313. [Google Scholar] [CrossRef]
- Bostock, M. Force-Directed Graph. 2018. Available online: https://bl.ocks.org/mbostock/4062045 (accessed on 3 February 2022).
- Fontes, J.D.; Yamamoto, J.F.; Larson, M.G.; Wang, N.; Dallmeier, D.; Rienstra, M.; Schnabel, R.B.; Vasan, R.S.; Keaney, J.F., Jr.; Benjamin, E.J. Clinical correlates of change in inflammatory biomarkers: The Framingham Heart Study. Atherosclerosis 2013, 228, 217–223. [Google Scholar] [CrossRef] [Green Version]
- Watrous, J.D.; Henglin, M.; Claggett, B.; Lehmann, K.A.; Larson, M.G.; Cheng, S.; Jain, M. Visualization, Quantification, and Alignment of Spectral Drift in Population Scale Untargeted Metabolomics Data. Anal. Chem. 2017, 89, 1399–1404. [Google Scholar] [CrossRef] [Green Version]
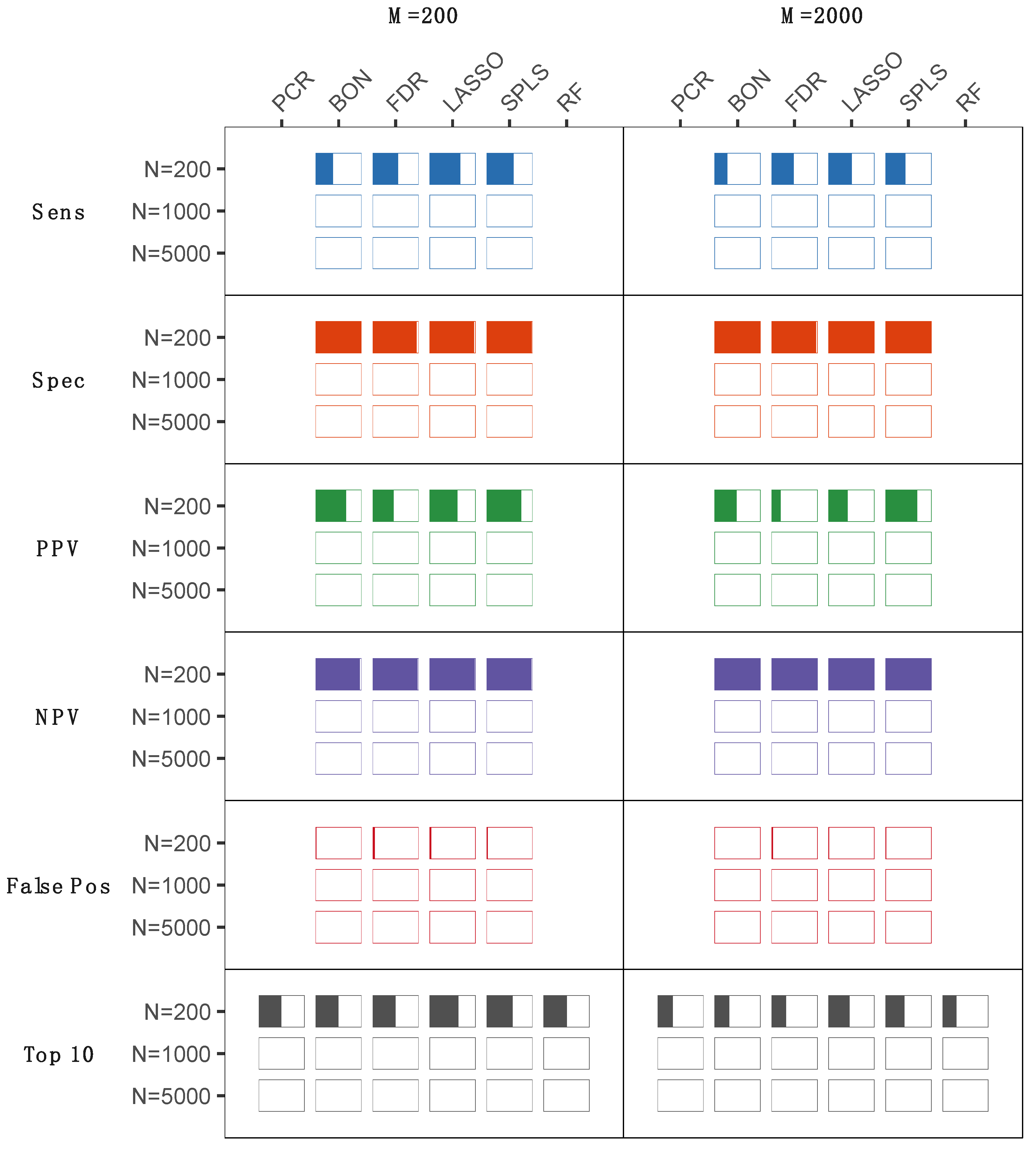
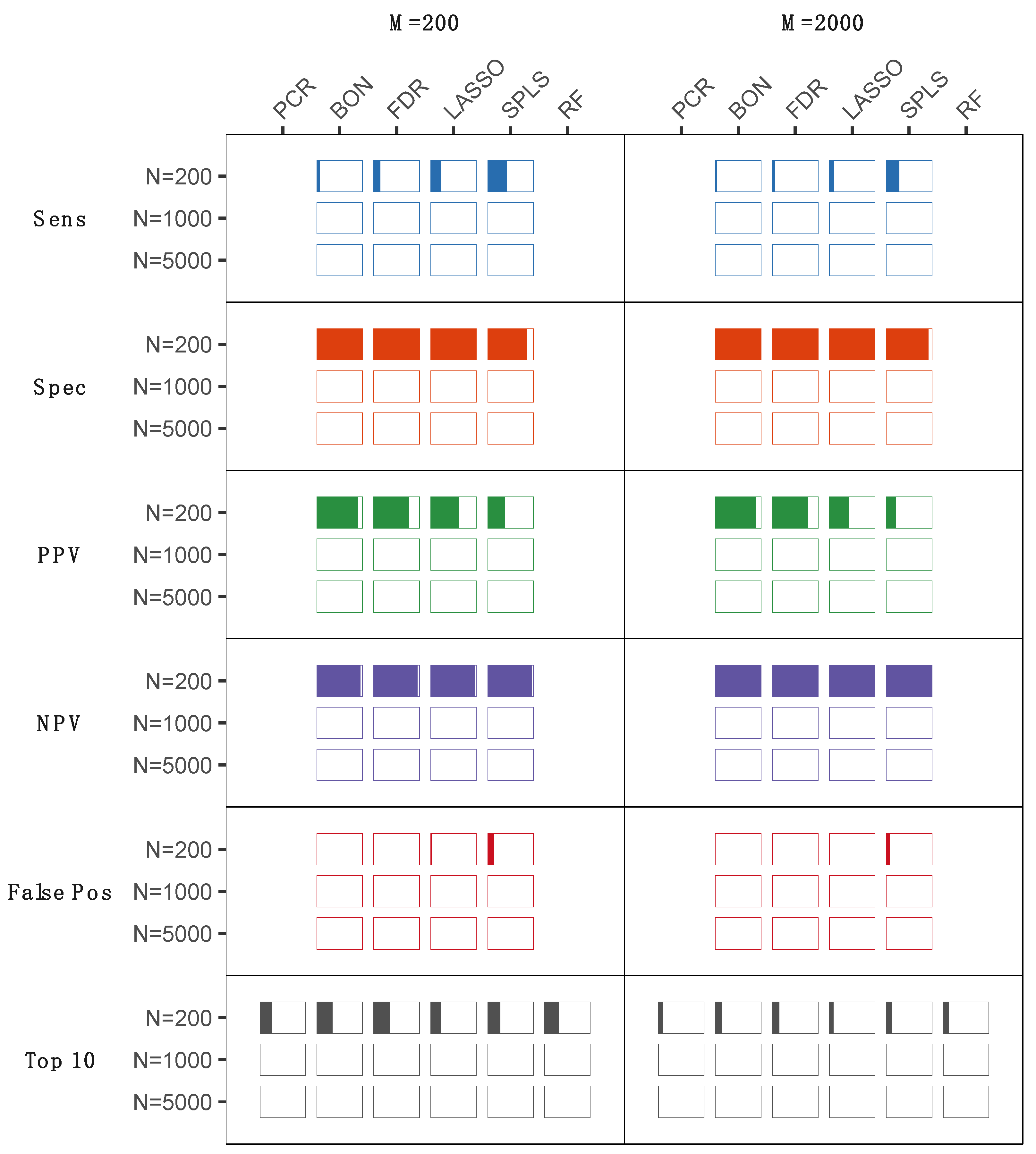

| Dataset | Outcome Characteristics | No. of Metabolites | No. of Observations (i.e., No. of Persons) |
|---|---|---|---|
| 1 | Continuous | 200 | 200 |
| 2 | Continuous | 200 | 1000 |
| 3 | Continuous | 200 | 5000 |
| 4 | Continuous | 2000 | 200 |
| 5 | Continuous | 2000 | 1000 |
| 6 | Continuous | 2000 | 5000 |
| 7 | Binary: 20% frequency | 200 | 200 |
| 8 | Binary: 50% frequency | 200 | 1000 |
| 9 | Binary: 50% frequency | 200 | 5000 |
| 10 | Binary: 20% frequency | 2000 | 200 |
| 11 | Binary: 50% frequency | 2000 | 1000 |
| 12 | Binary: 50% frequency | 2000 | 5000 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Henglin, M.; Claggett, B.L.; Antonelli, J.; Alotaibi, M.; Magalang, G.A.; Watrous, J.D.; Lagerborg, K.A.; Ovsak, G.; Musso, G.; Demler, O.V.; et al. Quantitative Comparison of Statistical Methods for Analyzing Human Metabolomics Data. Metabolites 2022, 12, 519. https://doi.org/10.3390/metabo12060519
Henglin M, Claggett BL, Antonelli J, Alotaibi M, Magalang GA, Watrous JD, Lagerborg KA, Ovsak G, Musso G, Demler OV, et al. Quantitative Comparison of Statistical Methods for Analyzing Human Metabolomics Data. Metabolites. 2022; 12(6):519. https://doi.org/10.3390/metabo12060519
Chicago/Turabian StyleHenglin, Mir, Brian L. Claggett, Joseph Antonelli, Mona Alotaibi, Gino Alberto Magalang, Jeramie D. Watrous, Kim A. Lagerborg, Gavin Ovsak, Gabriel Musso, Olga V. Demler, and et al. 2022. "Quantitative Comparison of Statistical Methods for Analyzing Human Metabolomics Data" Metabolites 12, no. 6: 519. https://doi.org/10.3390/metabo12060519
APA StyleHenglin, M., Claggett, B. L., Antonelli, J., Alotaibi, M., Magalang, G. A., Watrous, J. D., Lagerborg, K. A., Ovsak, G., Musso, G., Demler, O. V., Vasan, R. S., Larson, M. G., Jain, M., & Cheng, S. (2022). Quantitative Comparison of Statistical Methods for Analyzing Human Metabolomics Data. Metabolites, 12(6), 519. https://doi.org/10.3390/metabo12060519







