Epicyclic Oscillations and Circular Orbits in Hairy Black Holes: Testing by High-Frequency Quasi-Periodic Oscillations Observed in Microquasars

Abstract

Recently, Ovalle and his collaborators proposed an exact solution to Einstein’s equations. In this study, we investigate the main characteristics of the spherically symmetric spacetime determined by the hair parameter l, with a specific focus on circular orbits, particularly the innermost circular orbits (ISCOs), and the epicyclic oscillatory motion along these orbits. To assess the validity of this novel geometry, we employ the frequencies derived from the epicyclic resonance model of high-frequency quasi-periodic oscillations (HF QPOs) observed in microquasars, as well as the ISCOs. By analyzing the observed data from three selected microquasars, we establish constraints on the parameter l. Our findings suggest that this geometric framework can encompass the phenomena associated with HF QPOs and offer a partial explanation for the observed shift in the ISCOs, which is commonly attributed to the rotation of the black hole.

1. Introduction

Recently, a novel solution of Einstein’s equations has been presented by J. Ovalle and his colleagues [1]. It gives us an excellent opportunity to explain unsolved problems and phenomena. However, such new geometry also has to fit on already known and explained phenomena. This leads us to the main goal of this paper which is to map this new geometry, compared to the already known Schwarzchild one, and to compare predictions based on this background with observational data.

Ovalle introduced the so-called minimal geometric deformation method developed by himself [2,3]. This method is the first simple, systematic and direct method of decoupling gravitational sources in general relativity. Initially, it was proposed [4] in the context of the Randall–Sundrum braneworld model [5,6]. The notable feature of the minimal geometric deformation method is that it preserves the spherical symmetry, as well as the physical acceptability, and thus opens up a new window to study physically plausible anisotropic solutions. It is important to mention that this procedure does not use action formalism to produce the new solution to Einstein’s equations. This solution describes how spherically symmetric fluid modifies the Schwarzschild vacuum solution when there is no exchange of energy-momentum between the fluid and the central source of the Schwarzschild metric.

The phenomena observed in the X-ray spectrum, the so-called quasi-periodic oscillations [7] coming from the vicinity of compact objects, are not yet a completely clarified question. These phenomena are attributed to resonances in the motion of particles in the accretion disk and described by a geodesic model of twin high-frequency quasiperiodic oscillations [8,9]. However, observations and theoretical predictions are consistent only for microquasars [10]; for supermassive active galactic nuclei [11], an explanation is still pending, and the influence of external factors such as magnetic field [12], the presence of dark matter [13] or the presence of a wormhole [14] is assumed. Therefore, for the assumption of microquasars, we can use these phenomena as a test of new geometry.

The structure of this paper is as follows. The second section describes the new black hole solution and its horizon. In the third section, the motion of massive test particles, as well as their effective potentials and circular orbits including the innermost stable circular orbit (ISCO), are examined. The fourth and fifth sections are focused on the astrophysical application of mimicking the rotation of a Kerr black hole and HF QPOs observed in microquasars, respectively. The last section summarizes the results of our research.

Throughout this paper, we use a space-like signature $(-,+,+,+)$, a system of units in which $G=c=1$, and we restore them when we need to compare our results with observational data. Greek indices run from 0 to 3, and Latin indices from 1 to 3.

2. Hairy Spherically Symmetric Spacetime and Horizon

Here, we briefly introduce this new solution and examine its horizon.

2.1. Hairy Spherically Symmetric Spacetime

The metric for the hairy spherically symmetric spacetime in standard Schwarzschild coordinates is given by [1]

$$\begin{array}{c}\hfill \mathrm{d}{s}^2=-f\left(r\right)\mathrm{d}{t}^2+f{\left(r\right)}^{-1}\mathrm{d}{r}^2+r^2\mathrm{d}{\theta }^2+r^2{sin}^2\theta \mathrm{d}{\varphi }^2,\end{array}$$

(1)

where

$$f\left(r\right)=\left(1-\frac{2M}{r}+\alpha e^{-\frac{r}{M-\frac{\alpha l}{2}}}\right),$$

(2)

and M is the mass of the central object. The parameter $\alpha$ represents the power of the new effect. We will treat it through our paper as a switcher, which means that we merely activate the hairy effect or deactivate it, without altering it in any way by parameter $\alpha$. If $\alpha =0$, this corresponds to the effect being switched off—the metric transitions to the standard Schwarzschild metric for any value of l. If $\alpha =1$, this corresponds to the effect being switched on and we deal with a hairy metric (note that $$ must be positive, as indicated in [1]). From now on, whenever we discuss a hairy spacetime, we will assume $\alpha =1$.

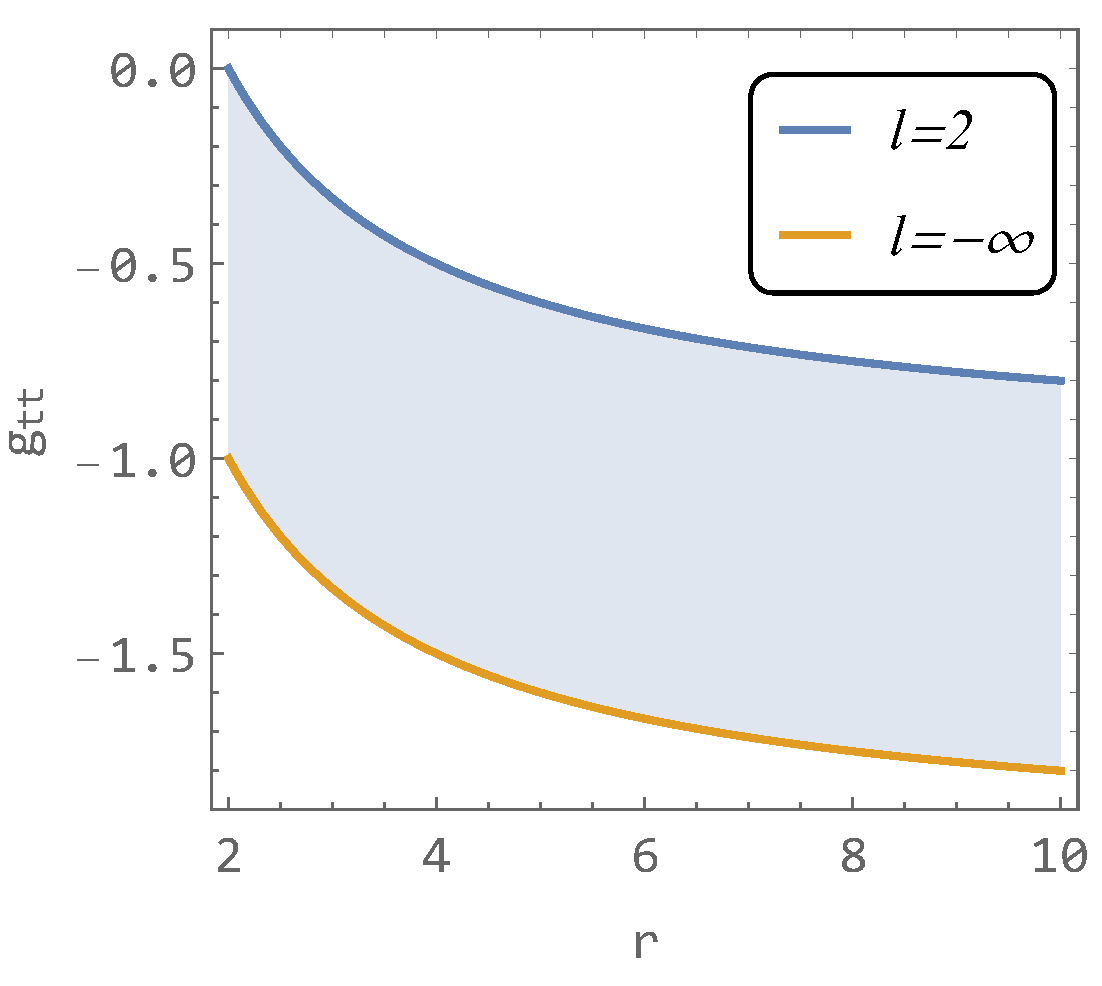
The new effect is determined by the parameter l (proportional to $\alpha$) with dimensions of length. The upper limit for this parameter is given by $l\le \frac{2M}{\alpha }$, and when $l=\frac{2M}{\alpha }$, the metric recovers the Schwarzschild solution (the extra term in (2) disappears). However, the lower limit is minus infinity [1]. The value corresponding to minus infinity serves as the lower bound for physical solutions. Solutions for $l=-\infty$ represent the first non-physical solutions. Despite being the first non-physical solution (lower bound), we can still use it to illustrate the constraint on the employed functions, where the lower bounding function is no longer physical (the example is given in Figure 1). Here, we present the limiting case for the hairy metric coefficient $g_{tt}$ ($\alpha =1$):

$$\begin{array}{c}\hfill \underset{l\to -\infty }{lim}{g}_{tt}=-\left(2-\frac{2M}{r}\right).\end{array}$$

(3)

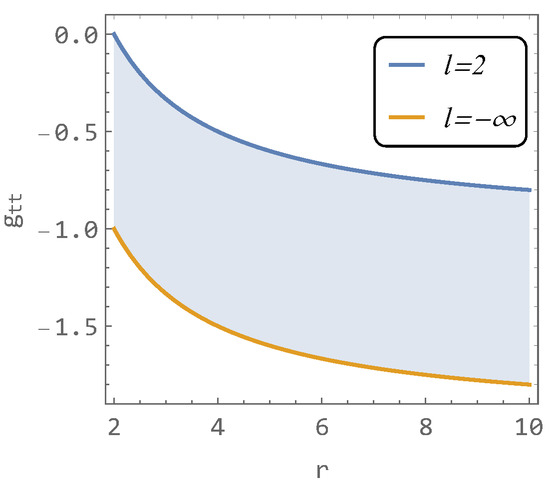
Figure 1. The restricting functions (blue and orange curves) of $g_{tt}$ metric function. The shaded area gives a place for all physical $g_{tt}$ with $l\in ($−$\infty ,2⟩$. Here, we set $\alpha =M=1$.

Figure 1 indicates that the function $g_{tt}$ can vary only between the curve $g_{tt}(r;l=2)$ (Schwarzschild case) and the curve $g_{tt}(r;l=-\infty )$—the shaded region—where the curve $g_{tt}(r;l=-\infty )$ represents the first non-physical solution.

Due to the potentially infinite range of the parameter l, we will focus exclusively on examining l in the order of units around $l=0$ with an upper limit of $l=\frac{2M}{\alpha }$, unless stated otherwise.

For simplification, we introduce a dimensionless hairy parameter and radial coordinate by the transformations

$$l\to \frac{l}{M}\mathrm{and}r\to \frac{r}{M}.$$

(4)

2.2. Hairy Black Hole Horizon

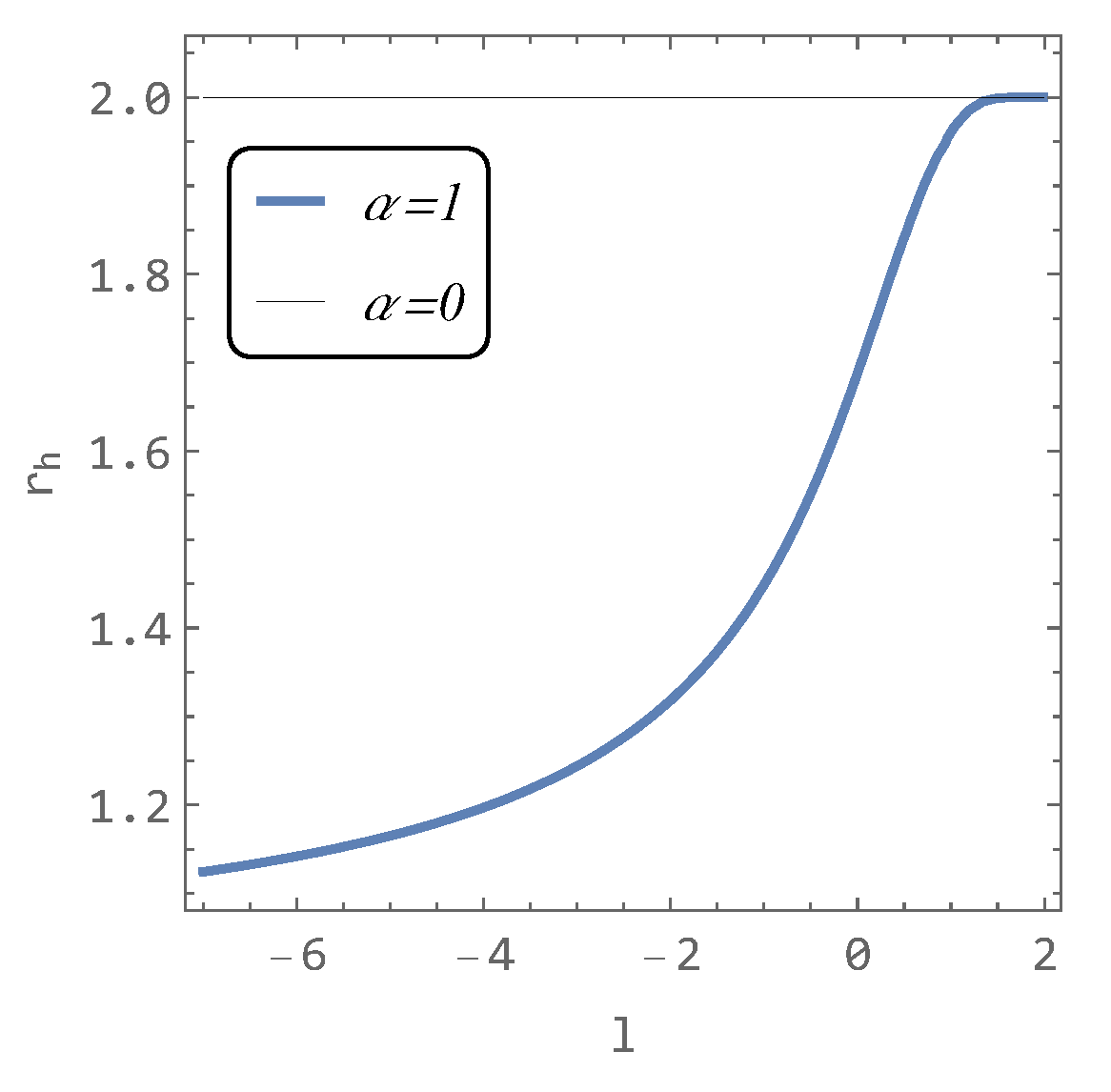
Now we explore the behavior of the horizon of the hairy black hole ($\alpha =1$). The horizon is defined by $g_{tt}=0$, which yields

$$\begin{array}{c}\hfill e^{\frac{2r}{l-2}}+1=\frac{2}{r}.\end{array}$$

(5)

The limiting case hairy $r_{\mathrm{hl}}$ ($\alpha =1$) when $l\to$ −∞ is

$$\begin{array}{c}\hfill \underset{l\to -\infty }{lim}{r}_{\mathrm{h}}=r_{\mathrm{hl}}=1.\end{array}$$

(6)

The position of the horizon decreases as the parameter l decreases, reaching the limit given by (6). For $\alpha =1$, the limiting case is $r_{\mathrm{hl}}=1$, as shown in Figure 2.

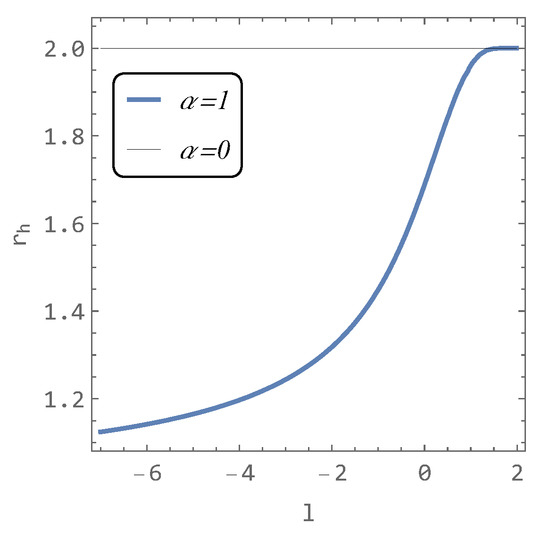
Figure 2. The location of the horizon in the hairy black hole spacetime as a function of the parameter l for $\alpha =0$ (Schwarzschild) and $\alpha =1$.

3. Test Particle Motion in Hairy Spherically Symmetric Spacetime

Circular orbits around black holes are the most important in the astrophysical context; therefore, we will investigate here the effective potentials leading to finding the circular orbits, with a primary focus on the location of the nearest stable circular orbit from the center of the black hole, which holds significant specific importance in the observations.

3.1. Effective Potential of Massive Test Particles

The effective potential governing the motion of a test particle can be obtained by employing the following normalization condition:

$$g_{\mu \nu }{u}^{\mu }{u}^{\nu }=-m^2,$$

(7)

where m denotes the mass of the test particle. By exploiting the symmetries of the spacetime, we introduce the conserved quantities, specifically the particle’s energy (E) and angular momentum (L), which are measured at infinity

$$\begin{array}{c}\hfill E=-g_{tt}{u}^t\mathrm{and}L=g_{\varphi \varphi }{u}^{\varphi }.\end{array}$$

(8)

Hereafter, we focus on circular geodesics, which can be studied by examining the effective potential. The motion is confined to the central plane, which can be chosen as the equatorial plane ($\theta =\pi /2$). The radial motion is determined by

$$\begin{array}{c}\hfill {\left(\frac{dr}{d\tau }\right)}^2=-\frac{1}{g_{rr}{g}_{tt}}\left[E^2-V_{\mathrm{eff}}\right],\end{array}$$

(9)

where $\tau$ represents the particle’s proper time. The effective potential corresponds to the square of the energy, and we will define it this way. This choice does not affect the qualitative properties of the function (the position of the maximum, minimum, or inflection point). The effective potential is a function of r and the angular momentum L and can be expressed as

$$V_{\mathrm{eff}}(r,L)=-g_{tt}\left(r\right)\left(\frac{L^2}{r^2}+m^2\right).$$

(10)

To simplify the problem, we introduce the transformations $L/m\to L$ and $E/m\to E$, leading to the effective potential

$$V_{\mathrm{eff}}=\frac{\left(L^2+r^2\right)\left(\alpha e^{\frac{2r}{\alpha l-2}}+1-2/r\right)}{2r^2}.$$

(11)

In the limiting case $l\to -\infty$, the hairy effective potential ($\alpha =1$) becomes

$$\begin{array}{c}\hfill \underset{l\to -\infty }{lim}{V}_{\mathrm{eff}}=V_{\mathrm{effl}}=\frac{\left(L^2+r^2\right)(1+r-2/r)}{2r^2}.\end{array}$$

(12)

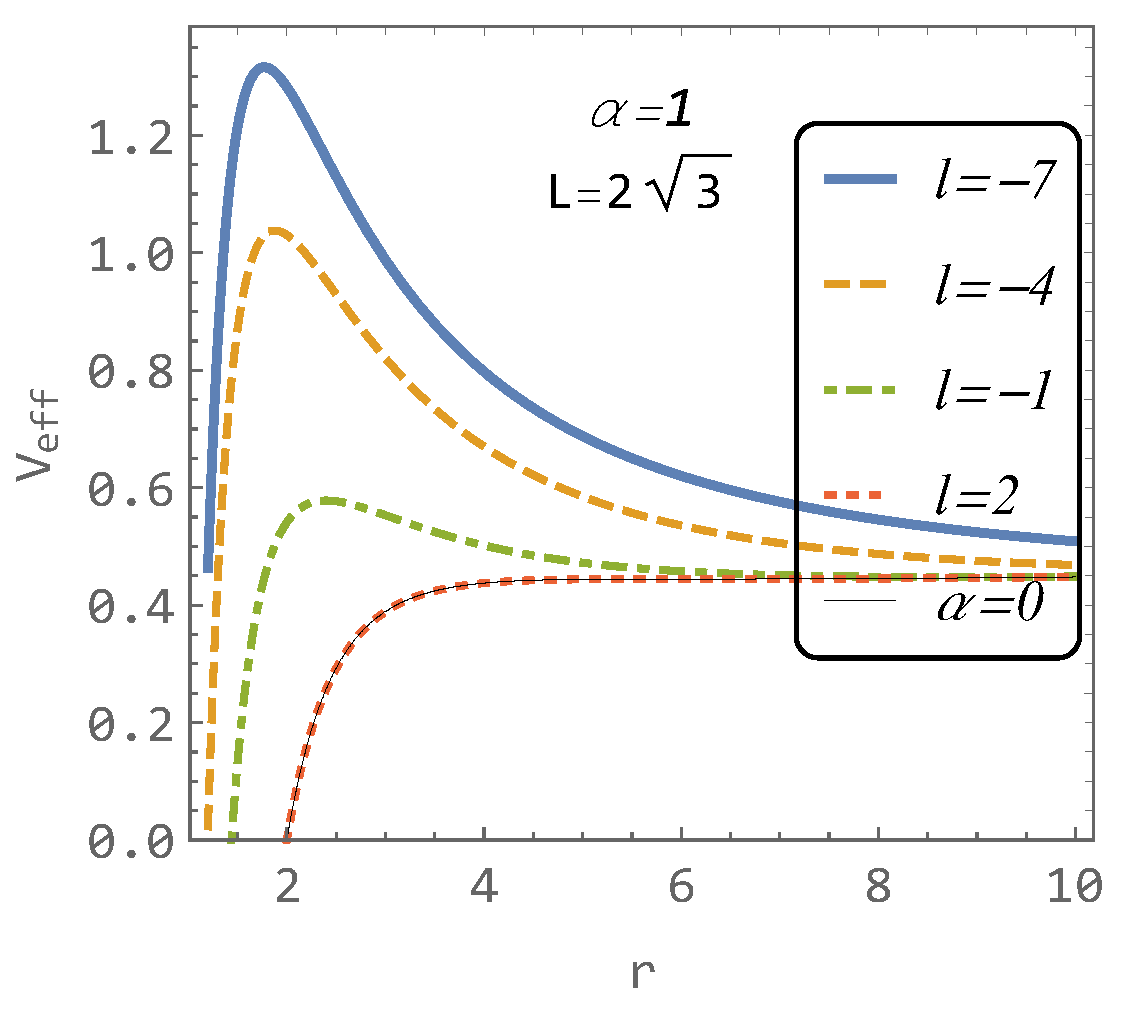
In the context of our study, it is important to note that the Schwarzschild effective potential possesses an inflection point for $L=2\sqrt{3}$ located at $r=6$. This critical point plays a pivotal role in our analysis and corresponds to the ISCO. It is used in Figure 3 to illustrate the hairy effective potentials for various values of the parameter l in comparison with the Schwarzschild effective potential (represented by the thin black line) for the same value $L=2\sqrt{3}$.

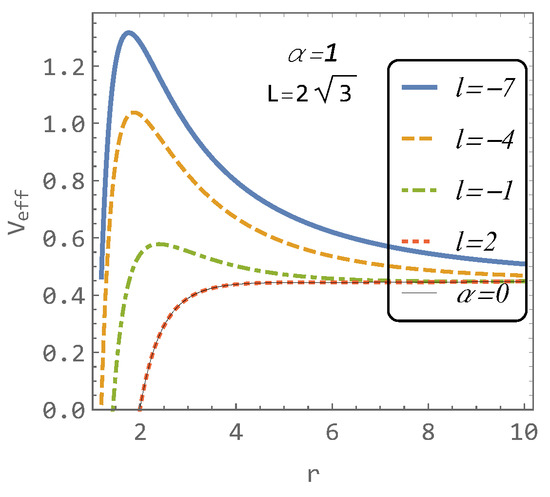
Figure 3. The effective potentials for various parameter l and angular momentum $L=2\sqrt{3}$ compared to the Schwarzschild effective potential (thin black line).

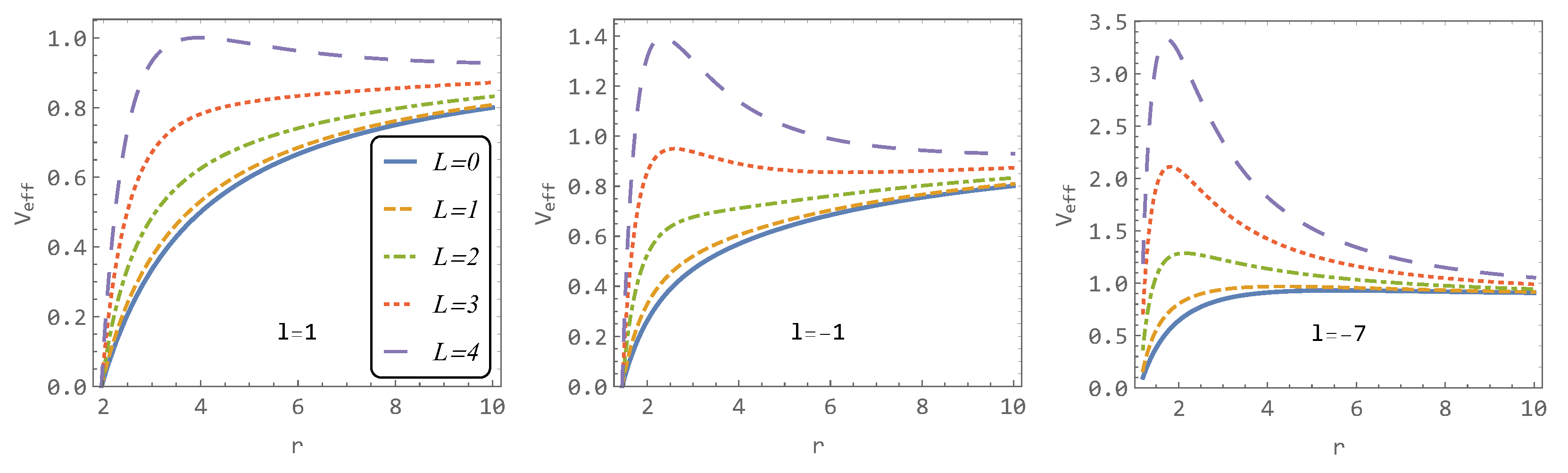
Figure 4 shows the effective potentials for different values of angular momentum L and the parameter l. As observed, a lower value of l emphasizes the maxima and minima of the effective potential (or conversely, the effective potential becomes more flattened for higher values of l). The parameter l exhibits a similar effect on the effective potential as the angular momentum L (see Figure 3).

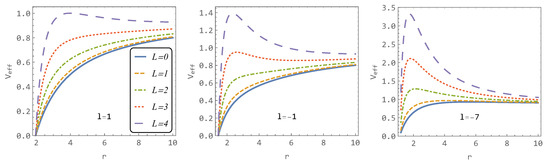
Figure 4. The effective potential for various parameter l and angular momentum L.

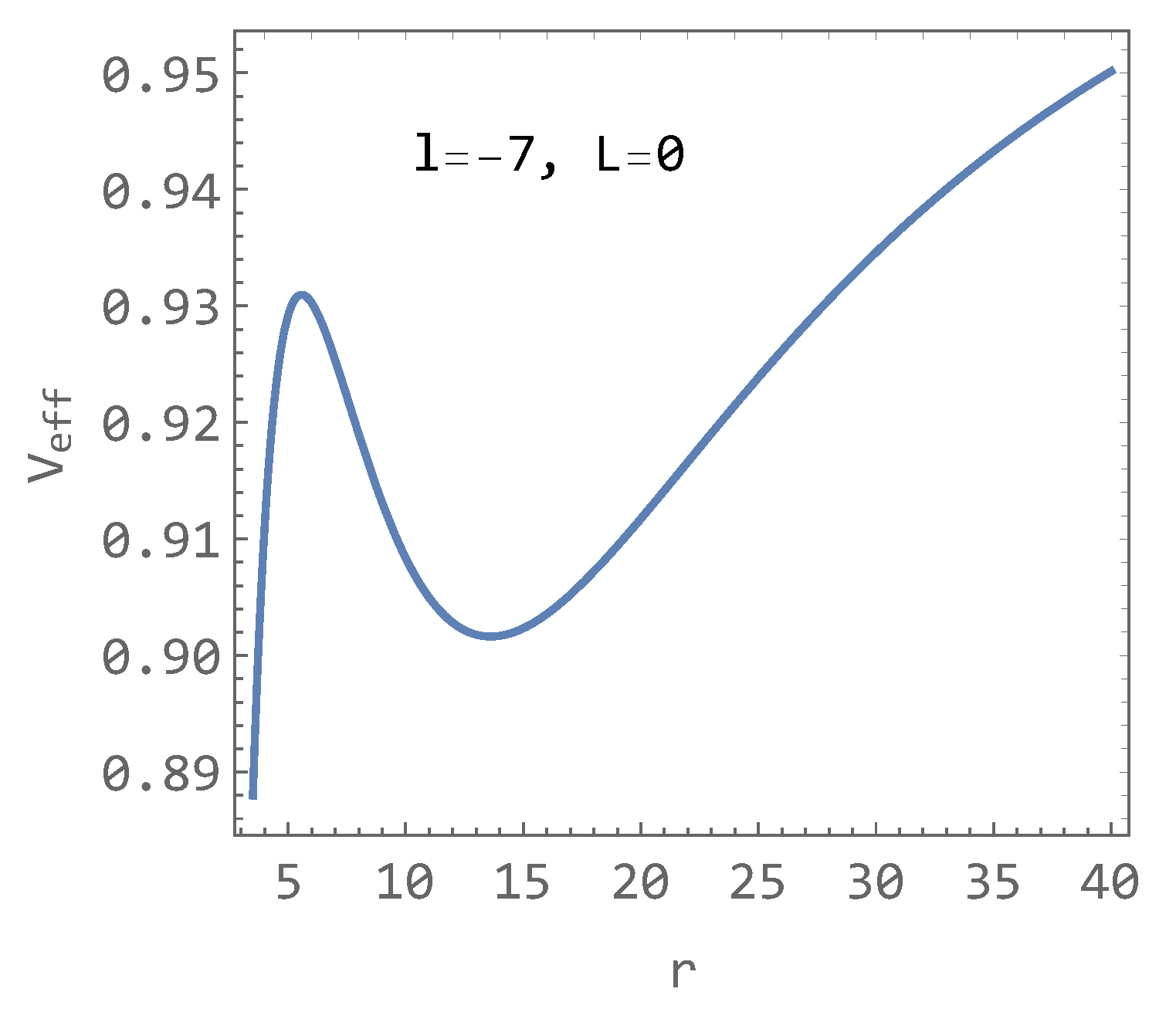
The manifestations of the parameter l on the behavior of the effective potential are globally intricate and lack uniform rules. Decreasing the parameter l below the value of $l\doteq$$-5.39$ (explained below), the effective potential always possesses a maximum and a minimum, even for $L=0$ (see Figure 5), which leads to the disappearance of the ISCO position as conventionally known. This characteristic vanishes around the value of $l\approx -80$ (explained below).

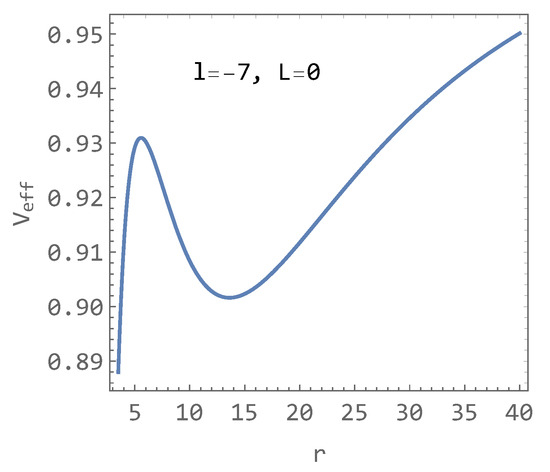
Figure 5. The effective potential for $l=$$-7$ and $L=0$ demonstrating the existence of two extremes in effective potential function.

3.2. Photon Sphere

Although the primary goal of this work is the study of the motion of massive particles in a hairy spacetime, we will here examine a fundamental property describing the motion of massless particles, focusing in particular on the location of unstable circular photon orbit (photon sphere—$r_{\mathrm{ph}}$) and how they are influenced by the parameter l.

To determine the position of the photon sphere of hairy spacetime, we can utilize the effective potential (10), substituting $m=0$,

$$\begin{array}{c}\hfill V_{\mathrm{Peff}}=\frac{L^2\left(r{e}^{\frac{2r}{l-2}}+r-2\right)}{r^3}.\end{array}$$

(13)

The limiting function of the effective potential for massless particles as l goes to infinity is

$$\begin{array}{c}\hfill \underset{l\to -\infty }{lim}{V}_{\mathrm{Peff}}=V_{\mathrm{Peffl}}=\frac{2L^2(r-1)}{r^3}.\end{array}$$

(14)

The derivative $\mathrm{d}{V}_{\mathrm{Peff}}/\mathrm{d}r$ of this photon effective potential yields

$$\begin{array}{c}\hfill d{V}_{\mathrm{Peff}}=\frac{2L^2}{r^4}\left[\frac{r{e}^{\frac{2r}{l-2}}(l-r-2)}{2-l}-(r-3)\right].\end{array}$$

(15)

The limit of the derivative of the photon effective potential as l approaches infinity yields

$$\begin{array}{c}\hfill \underset{l\to -\infty }{lim}\mathrm{d}{V}_{\mathrm{Peff}}=\mathrm{d}{V}_{\mathrm{Peffl}}=\left[2L^2(3-2r)\right]/r^4.\end{array}$$

(16)

Now, we will find general circular orbits by solving the equation $\mathrm{d}{V}_{\mathrm{Peff}}/\mathrm{d}r=0$ given by

$$\begin{array}{c}\hfill \frac{r{e}^{\frac{2r}{l-2}}(l-r-2)}{2-l}-(r-3)=0.\end{array}$$

(17)

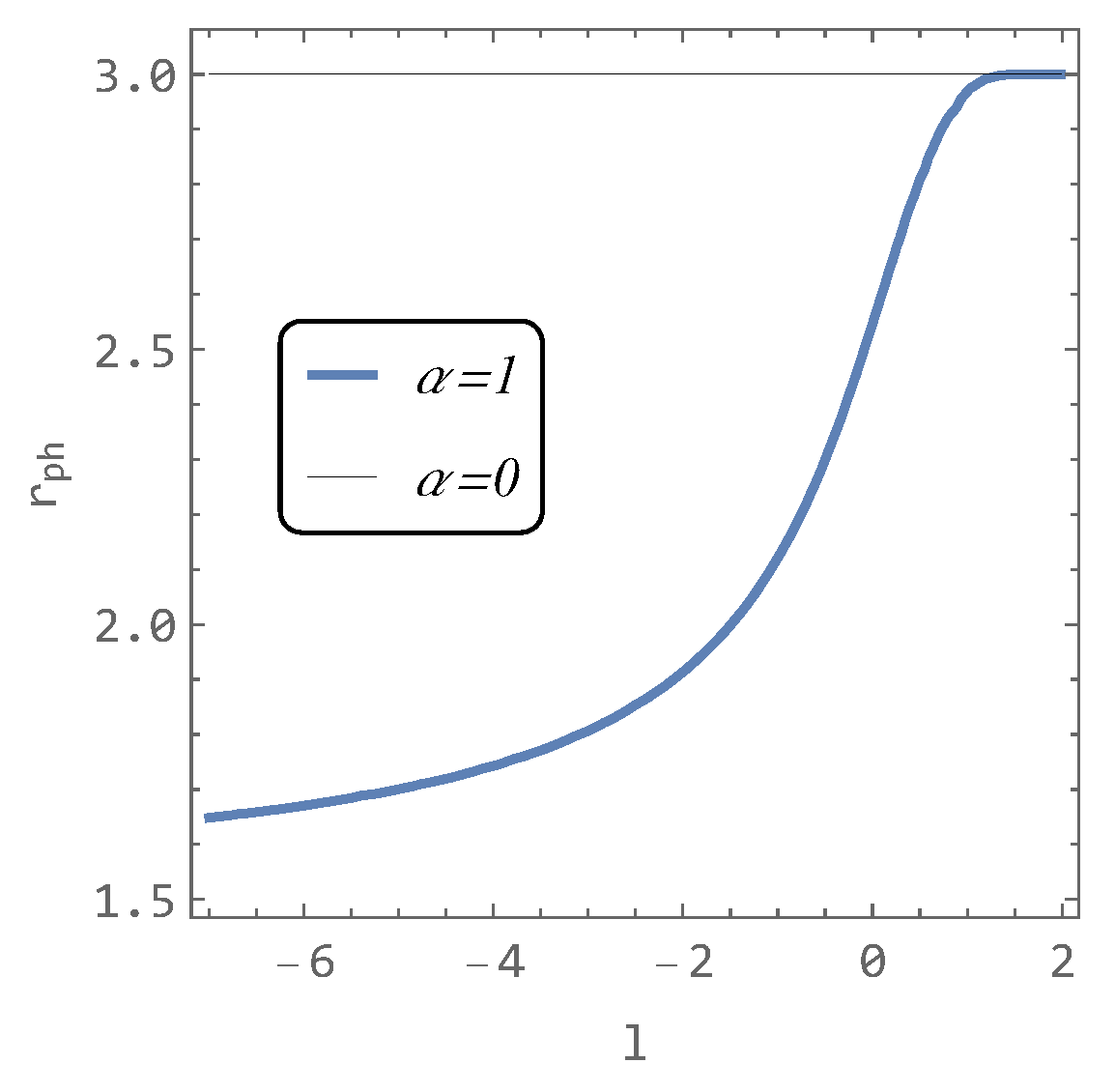
In Figure 6, one can see the results of the numerical solution of Equation (17). It is evident that as the parameter l decreases, the photon sphere approaches its limiting value of $r_{\mathrm{phl}}=3/2$.

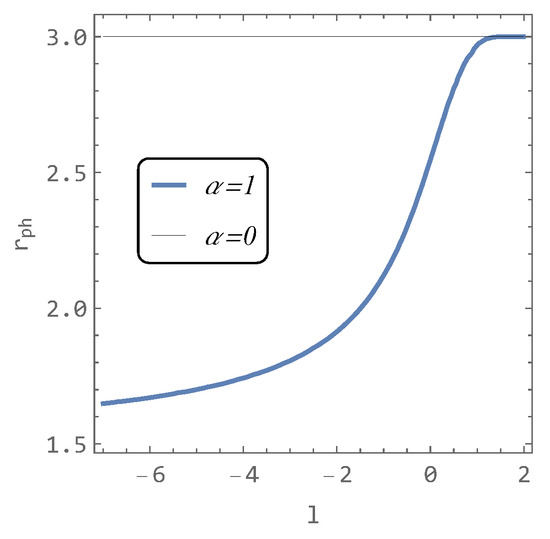
Figure 6. The location of the photon sphere in the hairy black hole spacetime as a function of the parameter l.

3.3. Circular Orbits of Massive Test Particles

Since some physically interesting phenomena occur only at very low values of the parameter l, this chapter will address them as well.

Circular orbits are determined by local extrema of the effective potential, coming from solution $\mathrm{d}{V}_{\mathrm{eff}}/\mathrm{d}r=0$

$$L^2\left[3\alpha l+\alpha r^2{e}^{\frac{2r}{\alpha l-2}}-r(\alpha l-2)\left(\alpha e^{\frac{2r}{\alpha l-2}}+1\right)-6\right]=r^2\left[2-\alpha \left(r^2{e}^{\frac{2r}{\alpha l-2}}+l\right)\right].$$

(18)

The dependence of the circular orbit $r_{\mathrm{c}}$ on $L_{\mathrm{c}}$ for various values of parameter l is illustrated in Figure 7. It is noteworthy that the curve corresponding to $l=-10$ lacks a minimum, signifying the absence of ISCO. In contrast, the curve associated with $l=-200$ exhibits the presence of two extremes (as commented later).

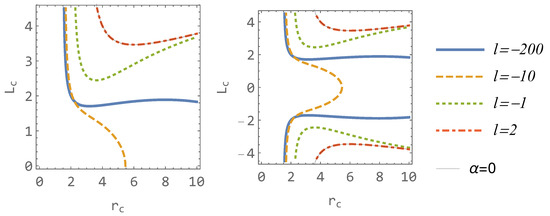
Figure 7. The location of the circular orbit $r_{\mathrm{c}}$ (both stable or unstable) for various l. Schwarzschild case is depicted by the black thin curve (coinciding with $l=2$ curve).

Due to the fact that the situation regarding the nearest stable circular orbit to the center in a hairy spacetime is slightly more complex, we will first define the terms that we will subsequently use:

IPEP: Inflex point of effective potential, given by simultaneous satisfying $\mathrm{d}{V}_{\mathrm{eff}}/\mathrm{d}r=0$ and ${\mathrm{d}}^2{V}_{\mathrm{eff}}/\mathrm{d}{r}^2=0$ (or alternatively in the minimum of the function $L\left(r_{\mathrm{c}}\right)$). It is possible to have more such points.

ISCO: The specific situation, when only one IPEP exists.

LSCO: Last stable circular orbit given in a situation when the effective potential is not monotonic (has a maximum and a minimum) even for $L=0$, i.e., it gives the location of such minimum.

The condition ${\mathrm{d}}^2{V}_{\mathrm{eff}}/\mathrm{d}{r}^2=0$ can be written in the form

$$\frac{\alpha r{e}^{\frac{2r}{\alpha l-2}}\left\{L^2\left[3{(\alpha l-2)}^2+r(8-4\alpha l)+2r^2\right]+2r^4\right\}}{{(\alpha l-2)}^2}+3L^2(r-4)-2r^2=0.$$

(19)

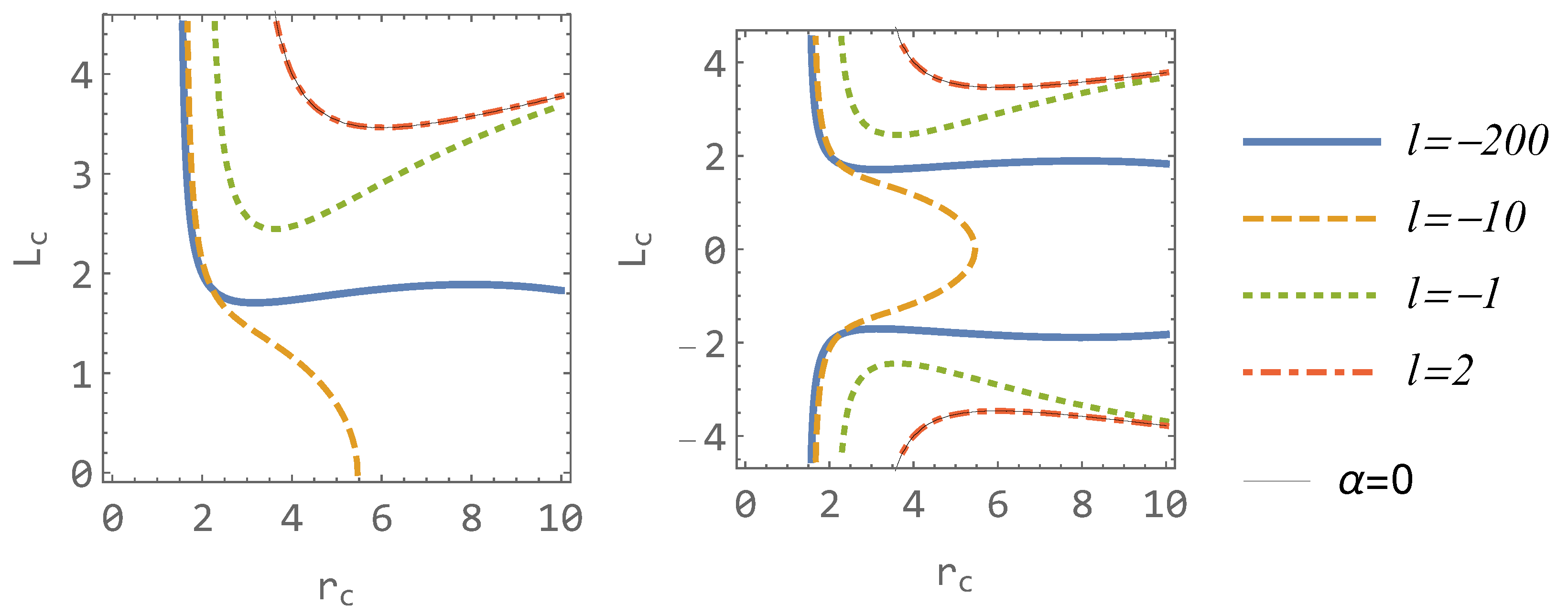
We can observe from Figure 7 that, for a certain range of the parameter l, there are no minima in the function $L_{\mathrm{c}}\left(r\right)$ (ISCO); for values of $l=2,-1$, a minimum exists, for $l=-10$ it does not exist, and for $l=-200$, there is both a minimum and a maximum. Let us denote the interval where is no minimum of $L_{\mathrm{c}}\left(r\right)$ as $⟨l_{\mathrm{t}},l_{\mathrm{c}}⟩$ and notice that the standard ISCO (known, for example, from Schwarzschid spacetime) does not exist there because there is no real solution of Equations (18) and (19). These boundary values can be calculated numerically: $l_{\mathrm{c}}\doteq -5.39$ and $l_{\mathrm{t}}\doteq -78.55$. We therefore have three distinct families of behavior dependent on parameter l:

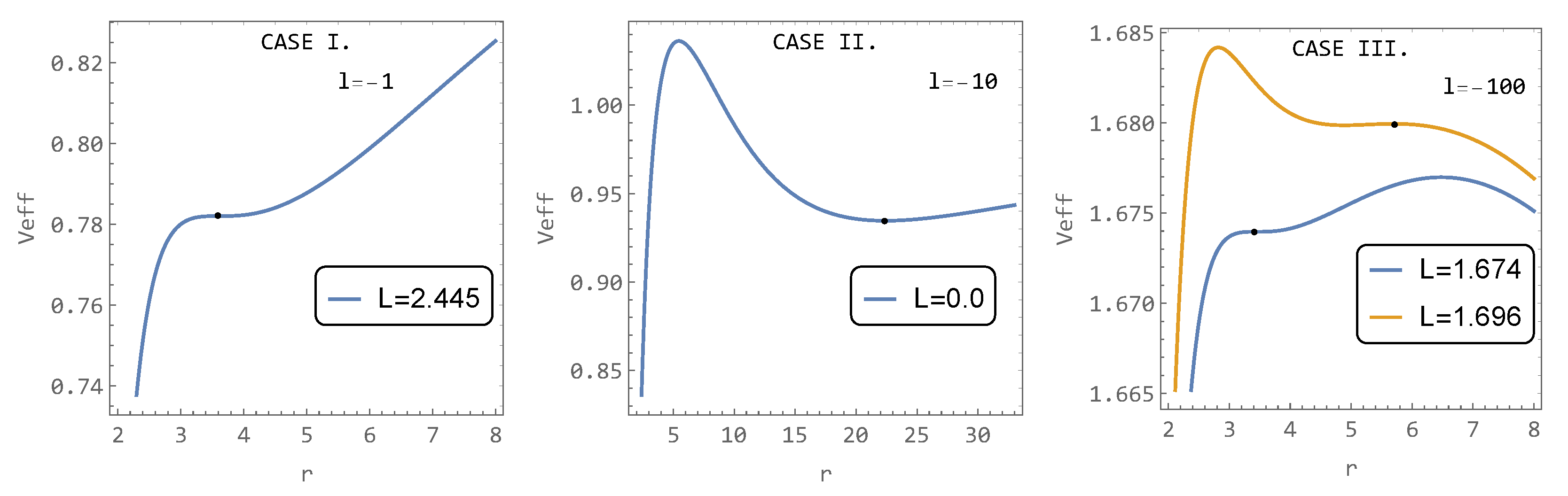
Case I. (${\mathit{l}}_{\mathbf{c}}<\mathit{l}<\mathbf{2}$): The standard behavior known, for example, from Schwarzschid spacetime, in which the effective potential can be monotonically increasing (for sufficiently small positive L, no circular orbit), it can have a maximum and minimum (for sufficiently large positive L, stable circular orbits at a minimum and unstable circular orbit at maximum), and for one specific value of L that separates these cases, the effective potential has an inflection point at the ISCO (stable circular orbit).

Case II. (${\mathit{l}}_{\mathbf{t}}<\mathbf{l}<{\mathit{l}}_{\mathbf{c}}$): The effective potential always poses a maximum and minimum (even for $L=0$). Therefore, there is no chance of finding an inflection point, but we will always find a stable circular orbit in the minimum of the hairy effective potential.

Case III. ($\mathit{l}<{\mathit{l}}_{\mathbf{t}}$): The behavior of the effective potential is more complex, and one can find two inflection points for two different values of L where stable circular orbits are located. Additional stable circular orbits are found in the minimum of the effective potential. All three cases and their specifics connected to the nearest stable circular orbit to the center or inflex points are presented in Figure 8.

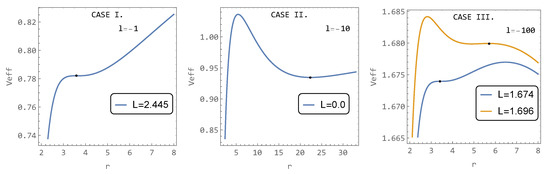
Figure 8. Overview of three possible cases of behavior of effective potential of hairy spacetime.

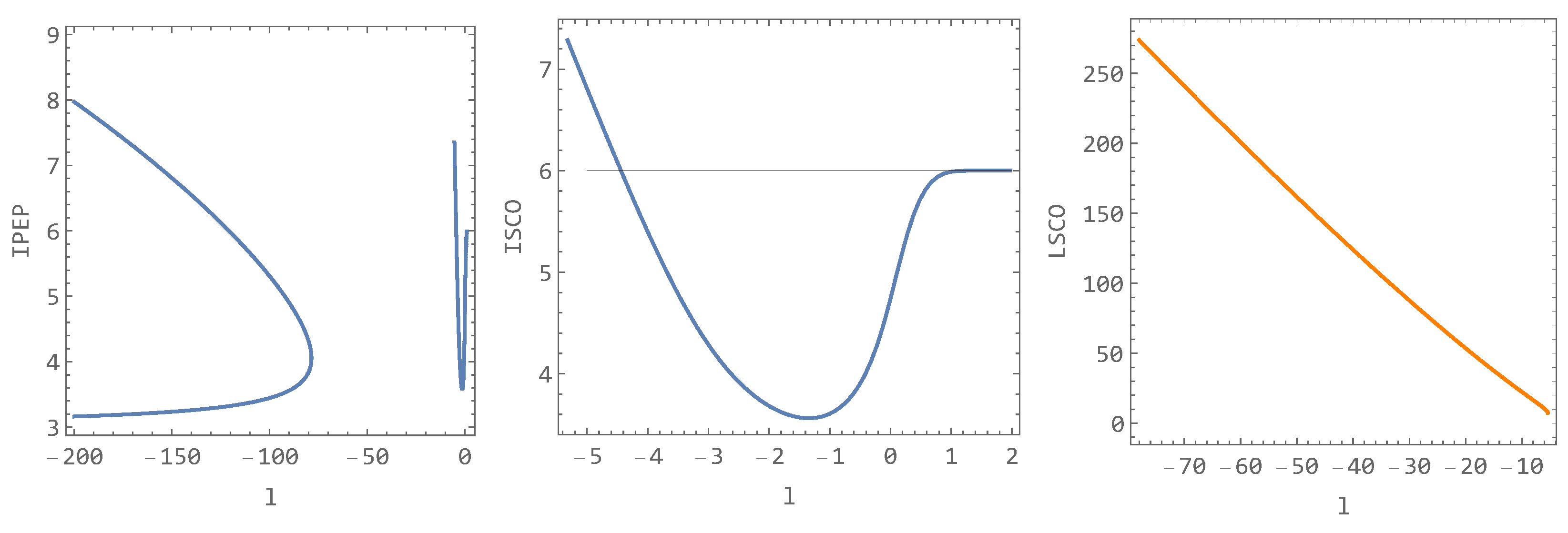
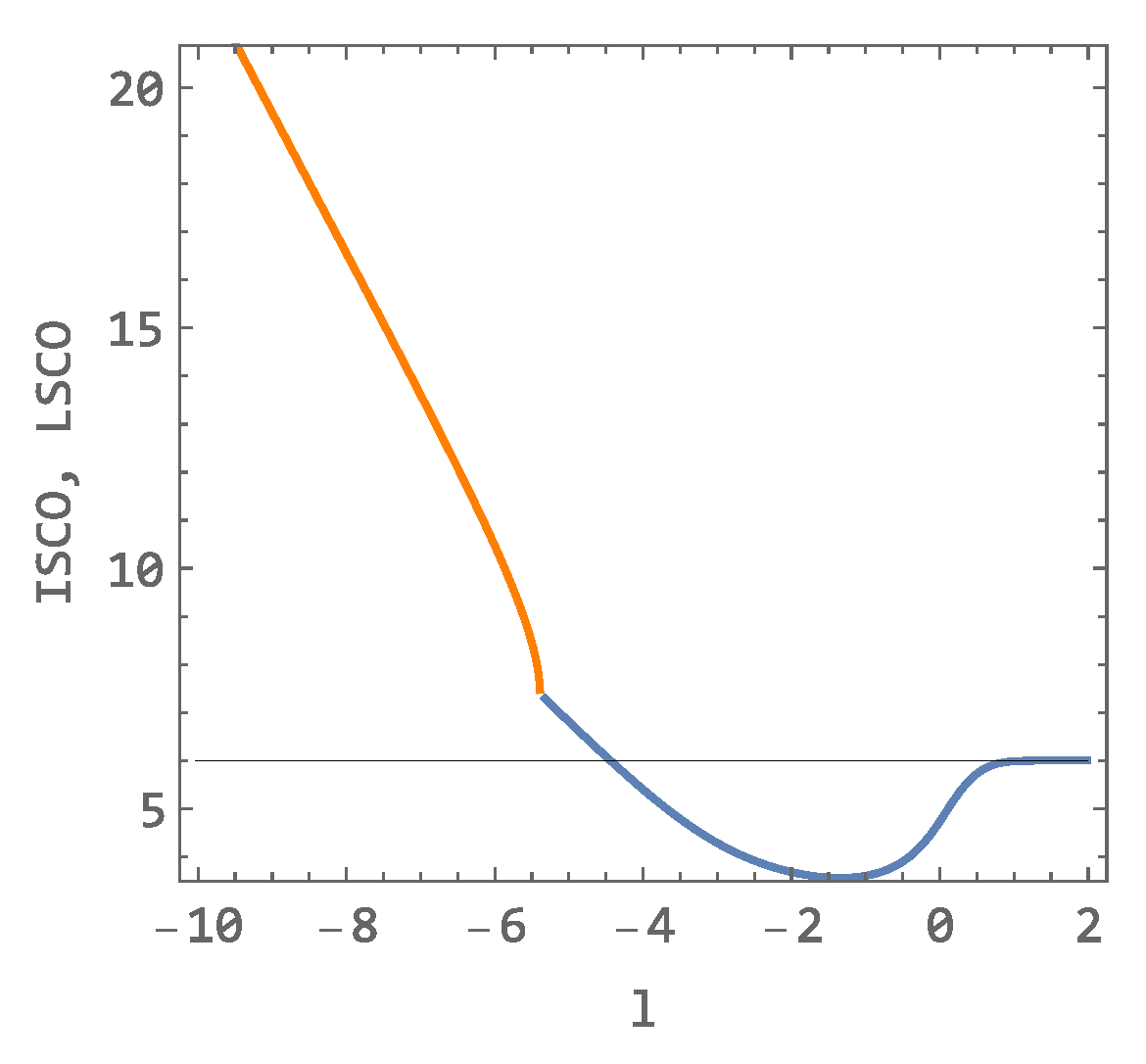
The dependence of ISCO on the parameter l ($l>l_{\mathrm{c}}$) is not monotonic and is presented in the central panel of Figure 9. On the left panel are plotted all IPEPs as a functions of the parameter l. Notice that the squeezed curve in the right part of the left (IPEP) panel is enlarged in the central (ISCO) panel. On the right, we observe a monotonically increasing distance of the LSCO. The LSCO curve continues from the end of the ISCO, as seen in Figure 10. Practically, this means that, as the parameter l is reduced approaching $l_{\mathrm{c}}$, the angular momentum L required to reach the inflection point of the effective potential gradually approaches zero. The last inflection point of the effective potential arises at $l\doteq l_{\mathrm{c}}$ and $L=0$. Further reduction in the parameter l then leads to the creation of a maximum and minimum from the inflection point. This characteristic persists until $l>l_{\mathrm{t}}$.

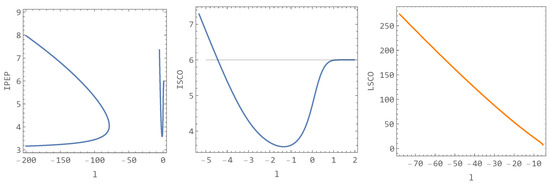
Figure 9. In the left panel one sees the position of IPEP dependent on parameter l. In the middle panel is standard ISCO (also corresponding to IPEP, enlarged right part of the left panel) dependent on parameter l and Schwarzschild ISCO at $r=6$ (black line). In the right panel is presented LSCO dependent on the parameter l.

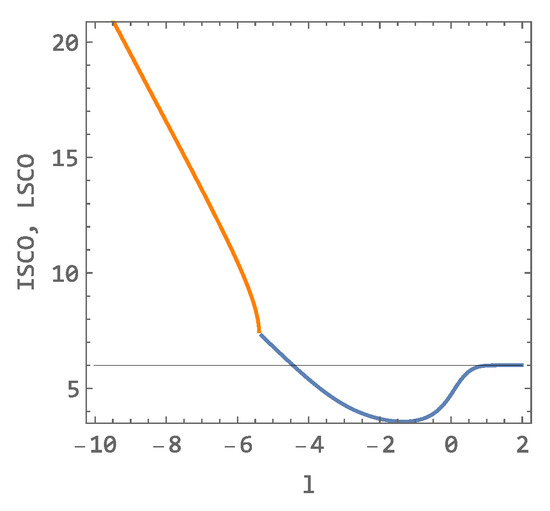
Figure 10. The standard ISCO dependent on parameter l (blue curve) and LSCO dependent on parameter l (orange curve) presented at the location of the transition of both curves. Black line indicates Schwarzschild ISCO.

4. Hairy Black Holes as a Mimicker of the Kerr Black Hole

Many astrophysical observations aimed at estimating the spin of black holes rely on investigating the edge of the accretion disk and identifying the ISCO [15,16]. If the ISCO of hairy black holes varies with the parameter “l”, this raises the question of whether and to what extent hairy black holes can mimic Kerr black holes. It should be noted that the shift in the ISCO could be caused by the presence of a magnetic or electric field [17,18], alternative tidal charge [19] or other black hole parameters.

For most values of the parameter l where the standard ISCO exists ($l\in ⟨l_{\mathrm{c}},2⟩$), it places the ISCO below $r=6$, which is the ISCO in Schwarzschild spacetime.

In Kerr geometry [20], the ISCO is affected by the rotation of the black hole, and it monotonically decreases with the increasing rotation parameter a for co-rotating matter [21].

We introduce a new parameter $l_{\mathrm{p}}\left(l\right)$ defined as

$$l_{\mathrm{p}}=\frac{l-2}{l_{\mathrm{c}}-2},$$

(20)

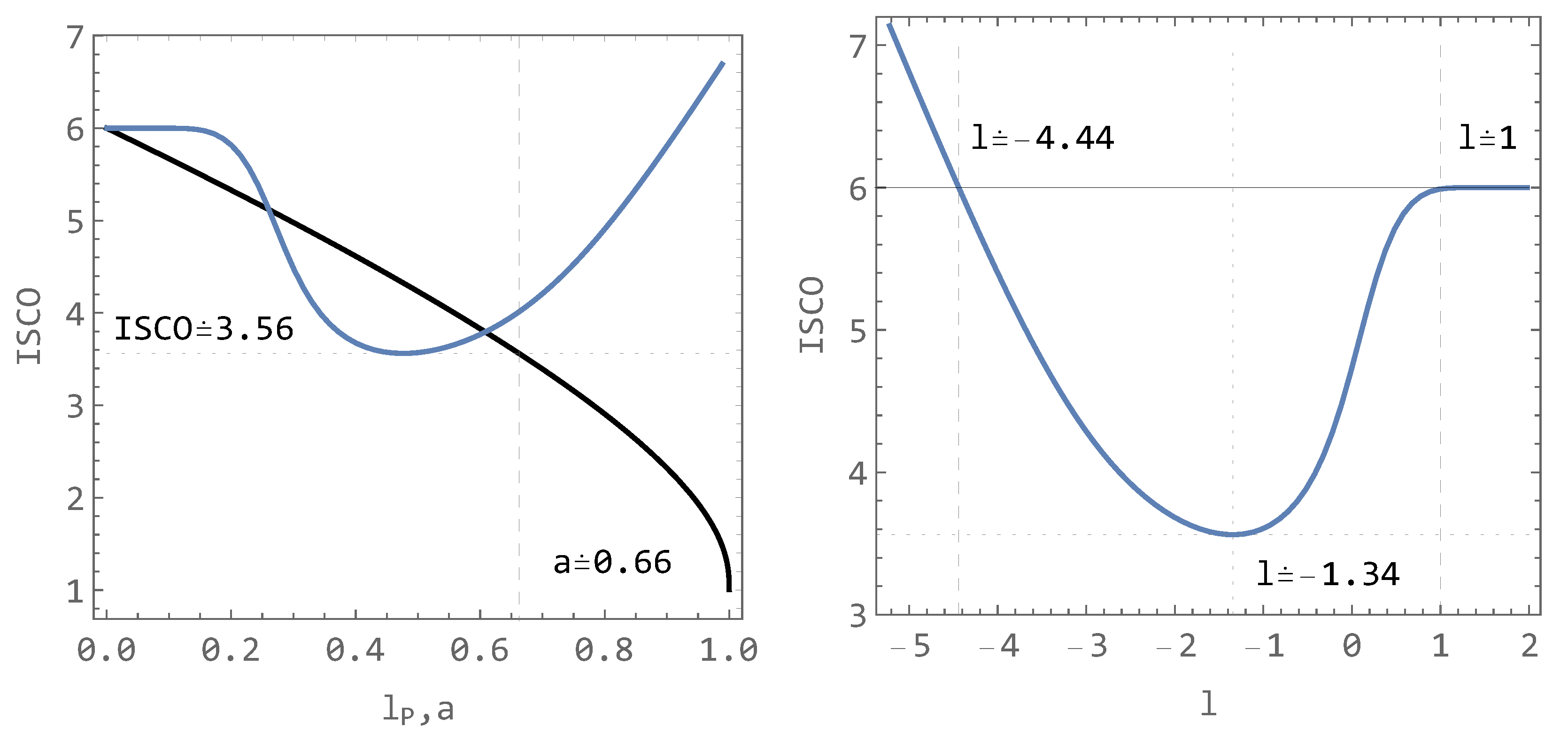
which transforms the parameter l such that the interval $(l_{\mathrm{c}},2)$ is squeezed into $(0,1)$, where $l_{\mathrm{p}}=0$ corresponds to $l=2$ (i.e., the Schwarzschild case), and $l_{\mathrm{p}}=1$ corresponds to $l=l_{\mathrm{c}}$. The reason for this transformation is to have both parameters (l and rotating a) in the same range. The comparison of the effects of l and a on the ISCO is presented in the left panel of Figure 11. The right panel of the same figure suggests that the mimicry can occur only for l in the range approximately $l\in (-4.44,1)$.

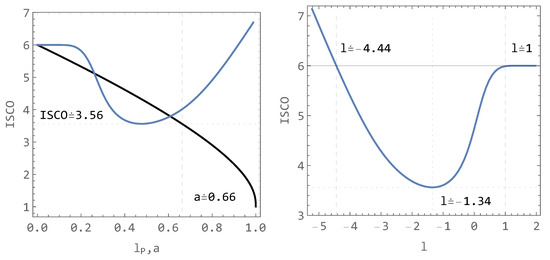
Figure 11. Comparison of the effect of the parameter $l_{\mathrm{p}}\left(l\right)$ of Ovalle spacetime and the parameter a of Kerr spacetime on the position of ISCO (left panel). Dependence of ISCO on the original parameter l with the marked range where l can mimic Kerr’s spin parameter a (right panel).

As seen in Figure 11, the minimum ISCO in our hairy spacetime is located at approximately $r\doteq 3.56$. This leads to potential mimicry of the spin parameter a of the Kerr black hole up to $a\doteq 0.66$. The mimicry of the highest rotation ($a\doteq 0.66$) occurs at $l\doteq -1.34$ (see the right panel of Figure 11).

5. Epicyclic Frequencies and HF QPOs in the Field of Ovalle Spacetime Applied to Microquasars Observation

This section investigates the epicyclic motion of massive test particles that orbit stable circular orbits (discussed in Section 3) and explores the phenomenon of high-frequency quasi-periodic oscillations observed in several microquasars.

HF QPOs are predominantly explained by models that rely on the resonance between orbital and epicyclic frequencies, or combinations thereof, with a ratio of the Upper frequency to the Lower frequency given by $f_{\mathrm{U}}:f_{\mathrm{L}}=3:2$. In this study, we specifically focus on the epicyclic resonance model, where $f_{\mathrm{U}}={\omega }_{\theta }$ and $f_{\mathrm{L}}={\omega }_r$.

5.1. Frequencies of Epicyclic Motion

If the particle is displaced from its equilibrium position at the stable circular orbit, it initiates an epicyclic motion around this position. The displacement coordinates (for small perturbations) $r=r_{\mathrm{c}}+\delta r$ and $\theta =\pi /2+\delta \theta$ are governed by equations for linear harmonic oscillations in the radial and latitudinal directions:

$$\begin{array}{c}\hfill \ddot{\delta r}+{\omega }_r^2\delta r=0,\ddot{\delta \theta }+{\omega }_{\theta }^2\delta \theta =0,\end{array}$$

(21)

where the dot denotes the derivative with respect to the proper time of the particle $\tau$, and ${\omega }_r$ and ${\omega }_{\theta }$ are the frequencies of the epicyclic oscillation measured by a local observer. The last frequency, ${\omega }_{\varphi }$, corresponds to the frequency of the orbital motion and is obtained from (8).

The dynamics are described by the Hamiltonian formalism [12] with the Hamiltonian H in the form1:

$$\begin{array}{c}\hfill H=\frac{1}{2}{g}^{\alpha \beta }{p}_{\alpha }{p}_{\beta }+\frac{1}{2}.\end{array}$$

(22)

Here, $p_{\alpha }$ represents the four-momentum of the test particle. The Hamiltonian (22) can be split into a potential and a dynamical part:

$$\begin{array}{c}\hfill H=H_{\mathrm{dyn}}+H_{\mathrm{pot}},\end{array}$$

(23)

where

$$\begin{array}{ccc}\hfill H_{\mathrm{dyn}}& =& \frac{1}{2}\left(g^{rr}{p}_r^2+g^{\theta \theta }{p}_{\theta }^2\right),\hfill \end{array}$$

(24)

$$\begin{array}{ccc}\hfill H_{\mathrm{pot}}& =& \frac{m^2}{2}\left(g^{tt}{E}^2+g^{\varphi \varphi }{L}^2+1\right).\hfill \end{array}$$

(25)

The relations for the epicyclic frequencies are given by

$$\begin{array}{ccc}\hfill {\omega }_r^2& =& \frac{1}{g_{rr}}\frac{{\partial }^2{H}_{\mathrm{pot}}}{\partial r^2},{\omega }_{\theta }^2=\frac{1}{g_{\theta \theta }}\frac{{\partial }^2{H}_{\mathrm{pot}}}{\partial {\theta }^2},\hfill \\ \hfill {\omega }_{\varphi }& =& \frac{L}{g_{\varphi \varphi }},\hfill \end{array}$$

(26)

By using (25) in (26), we obtain

$$\begin{array}{ccc}\hfill & & {\omega }_{\varphi }={\omega }_{\theta }=\frac{L}{r^2},\hfill \end{array}$$

(27)

$$\begin{array}{ccc}& & {\omega }_r=\sqrt{\frac{3L^2{(\alpha l-2)}^2{\left(\alpha r{e}^{\frac{2r}{\alpha l-2}}+r-2\right)}^3}{r^5{(\alpha l-2)}^2{\left(\alpha r{e}^{\frac{2r}{\alpha l-2}}+r-2\right)}^2}}\hfill \\ & & +\sqrt{\frac{2e^2\left\{{\alpha }^2{r}^3\left(-e^{\frac{4r}{\alpha l-2}}\right)+\alpha e^{\frac{2r}{\alpha l-2}}\left[r(8-4\alpha l)+r^3-2r^2-{(\alpha l-2)}^2\right]-{(\alpha l-2)}^2\right\}}{r{(\alpha l-2)}^2{\left(\alpha r{e}^{\frac{2r}{\alpha l-2}}+r-2\right)}^2}}.\hfill \end{array}$$

(28)

To obtain the epicyclic frequencies that can be measured by a distant observer (at infinity) and in standard unit (Hz), one must rescale (27) by the factor $-c^3/2\pi GM{g}^{tt}E$.

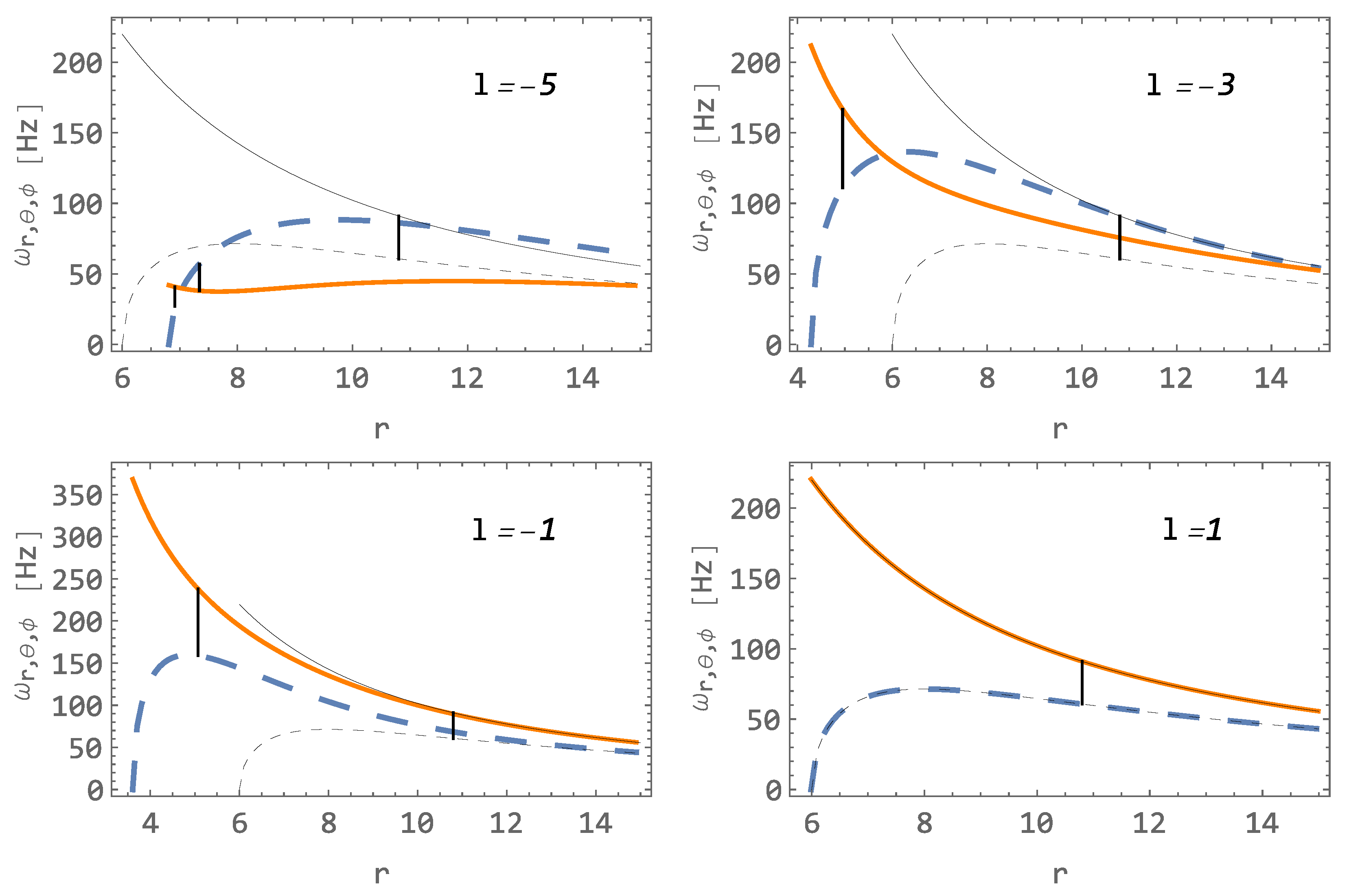
The frequencies (27) and (29), with an emphasis on the position of the ratio $f_{\mathrm{U}}:f_{\mathrm{L}}=3:2$, compared with those in Schwarzschild spacetime, are presented in Figure 12. The epicyclic frequencies do not change significantly from their Schwarzschild frequencies if the hair parameter l is positive. However, as the parameter l becomes negative and decreases further, all frequencies decrease, but not evenly. The latitudinal (orbital) frequency decreases much faster with l than the radial frequency, as seen in Figure 12.

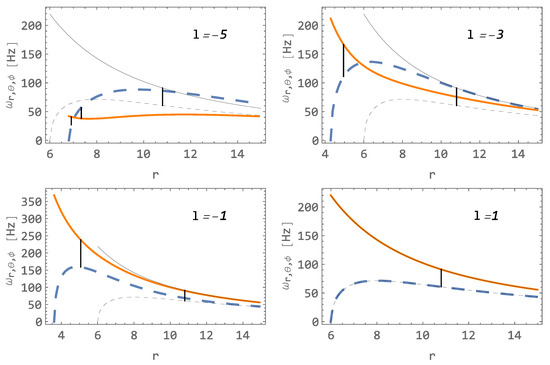
Figure 12. The epicyclic frequencies of a hairy black hole ${\omega }_r$ (dashed blue), ${\omega }_{\theta }$, and ${\omega }_{\varphi }$ (the same orange curves) and for the Schwarzschild case ${\omega }_r$ (dashed black), ${\omega }_{\theta }$, and ${\omega }_{\varphi }$ (the same solid black curves) for a central object with $M=10M_{\odot }$. Vertical lines indicate 3:2 frequency ratios.

5.2. Hairy Black Hole Test by HF QPOs Observed in Microquasars

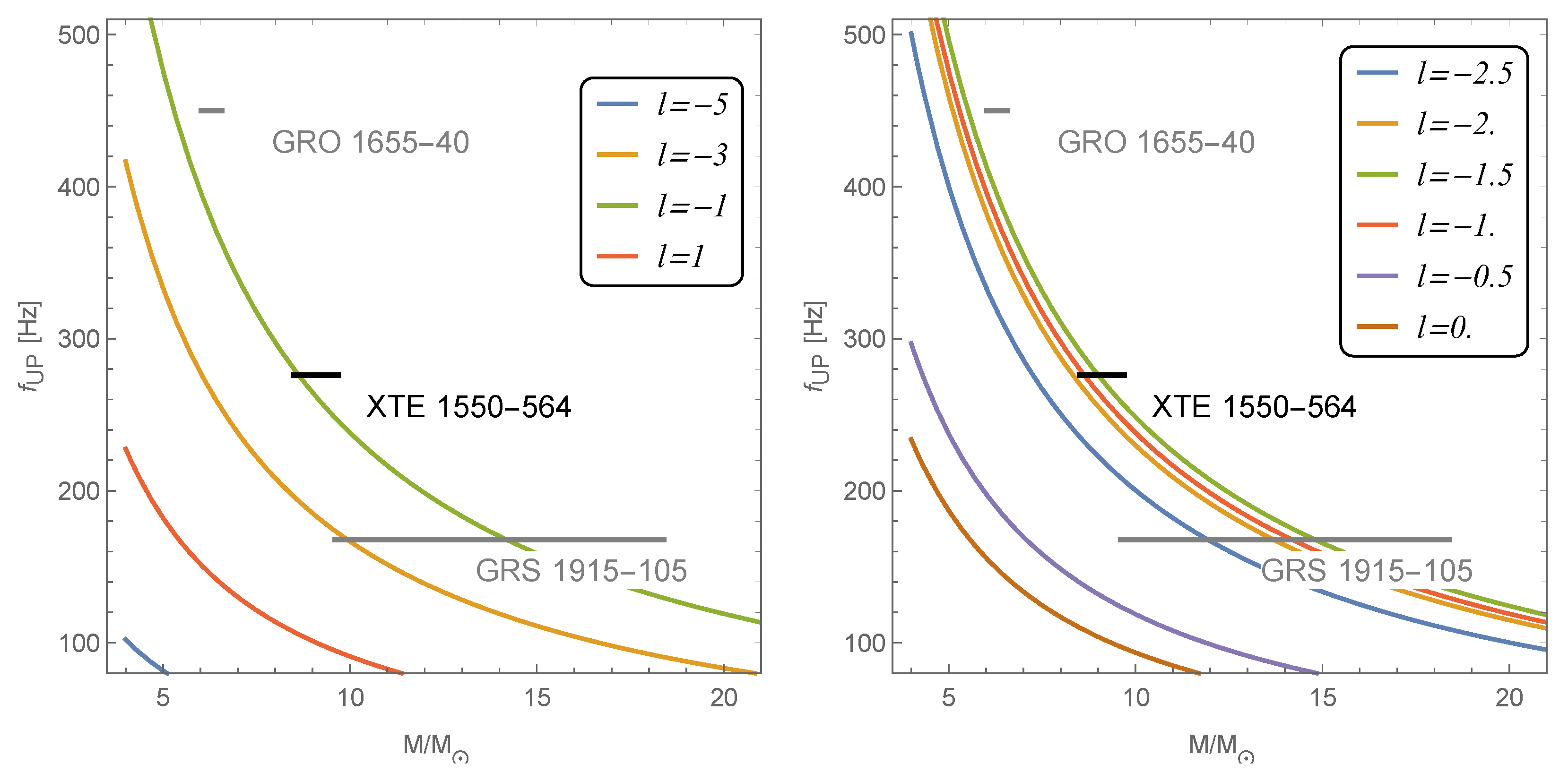
In this study, we utilize the HF QPOs observed in three selected microquasars [22,23] as a means to test the Ovalle hairy spacetime. Our objective is to investigate the applicability of this spacetime to explain the phenomenon of HF QPOs and to determine potential constraints on the parameter l that would best fit these observed signals. We employ an epicyclic resonant model of HF QPOs for this purpose. The obtained results are presented in the form of the upper frequency–mass relation for the epicyclic resonance model. These theoretical curves, corresponding to different values of the parameter l, are compared with the observed data from selected microquasars.

Figure 13 shows the observational data of three microquasars along with the theoretical curves based on the epicyclic resonance model, considering a hairy black hole as the central object, for various values of the parameter l.

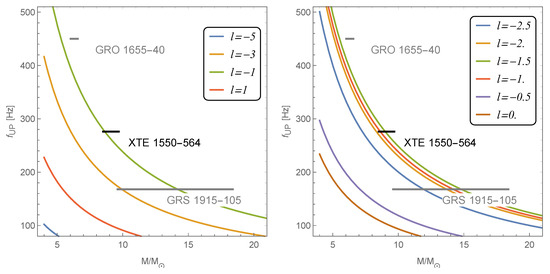
Figure 13. The upper frequency–mass relations (resonance 3:2 of $f_{\mathrm{U}}$:$f_{\mathrm{L}}$) for various values of the parameter l.

It is noteworthy that the shifting of the curves is not monotonous with an increasing parameter l. For instance, in the left panel of Figure 13, the curve with $l=1$ lies below the curves with $l=-1$ and $l=-3$, but above the curve with $l=-5$ simultaneously. A rough estimation of the constraints on the parameter l for our selected microquasars, based on fitting within the framework of Ovalle spacetime, yields $l=⟨-3,-0.7⟩$.

Table 1 presents the list of selected microquasars, their spin values, and the constraints on the parameter l obtained from QPO fits; $l_{\mathrm{QPO}}$ comes from comparing astrophysical data with presented results, as seen in Figure 13, and the position of the innermost stable circular orbit (ISCO); $l_{\mathrm{ISCO}}$ comes from comparing astrophysical data with presented results, as seen in Figure 11. However, despite the promising results, none of the three selected sources match both restrictions for the parameter l.

Table 1. Selected microquasars with spin [22] and constraints on the hairy parameter l from ISCO position ($l_{\mathrm{ISCO}}$) and QPO fitting ($l_{\mathrm{QPO}}$) given by numerical comparison of astrophysical data and presented results.

Source	Spin a	${\mathit{l}}_{\mathbf{ISCO}}$	${\mathit{l}}_{\mathbf{QPO}}$
GRS 1915+105	>$0.98$	-	$⟨-3,-0.7⟩$
GRO J1655–40	$0.70\pm 0.05$	$⟨-1.93,-0.85⟩$	-
XTE J1550–564	$0.{34}_{-0.28}^{+0.20}$	$⟨-4.3,-2.73⟩\cup ⟨-0.35,0.57⟩$	$⟨-1.8,-0.7⟩$

6. Conclusions

We conducted a study on the motion of massive particles in the gravitational field of spherically symmetric hairy black holes [1]. This metric has two free parameters, l and $\alpha$; however, $\alpha$ can only be considered as an amplification of the effect caused by the parameter l, whose effects are being studied here, and we set $\alpha =1$ during the investigation (if $\alpha =0$, the metric transitions to Schwarzschild). Our investigation primarily focused on circular orbits, particularly the innermost stable circular orbit (ISCO), as well as the frequencies associated with orbital and related epicyclic oscillations around stable circular orbits. The ISCO served as a means to assess the possibility of the hairy black hole mimicking the rotation of a Kerr black hole, while the epicyclic frequencies were employed to analyze the twin high-frequency quasi-periodic oscillations [24] observed in microquasars.

Our findings indicate that, through appropriate scaling of the parameter l, hairy black holes could potentially emulate rotating Kerr black holes for spin parameters up to $a\doteq 0.66$.

Furthermore, we demonstrated that hairy black holes have the potential to explain the observed HF QPOs in microquasars using a simple epicyclic resonance model. Additionally, our results yielded constraints on the parameter l based on observational data from three selected microquasars. The resulting constraints derived from QPO fits and the ISCO are presented in Table 1.

However, it is noteworthy that the constraints obtained from both QPO fits and the ISCO position did not overlap for any of the selected sources when assuming the hairy parameter l as the only factor modifying the ISCO. There are a few possible explanations:

I. The chosen sources do not exhibit the characteristics of hairy black holes.

II. The chosen epicyclic resonant model is not suitable for the description of these HF QPOs.

III. The inclusion of rotation in our simple spherically symmetric model of hairy black holes should be considered.

IV. Other effects play a significant role (electric or magnetic fields, dark matter…).

All this has to be investigated in the future.