Leveraging the Interplanetary Superhighway for Propellant–Optimal Orbit Insertion into Saturn–Titan System
Abstract
:1. Introduction
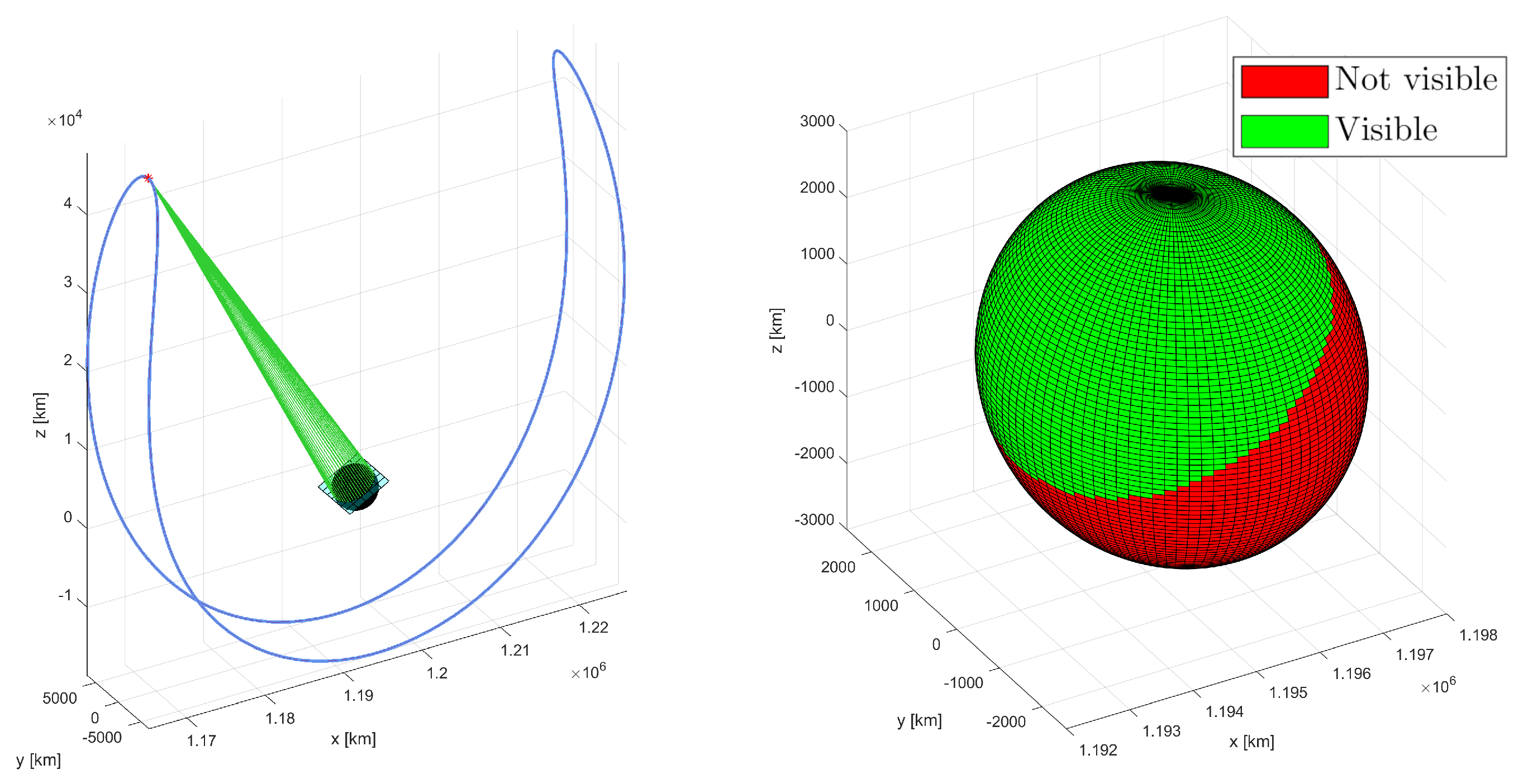
2. Titan
3. Background Theory
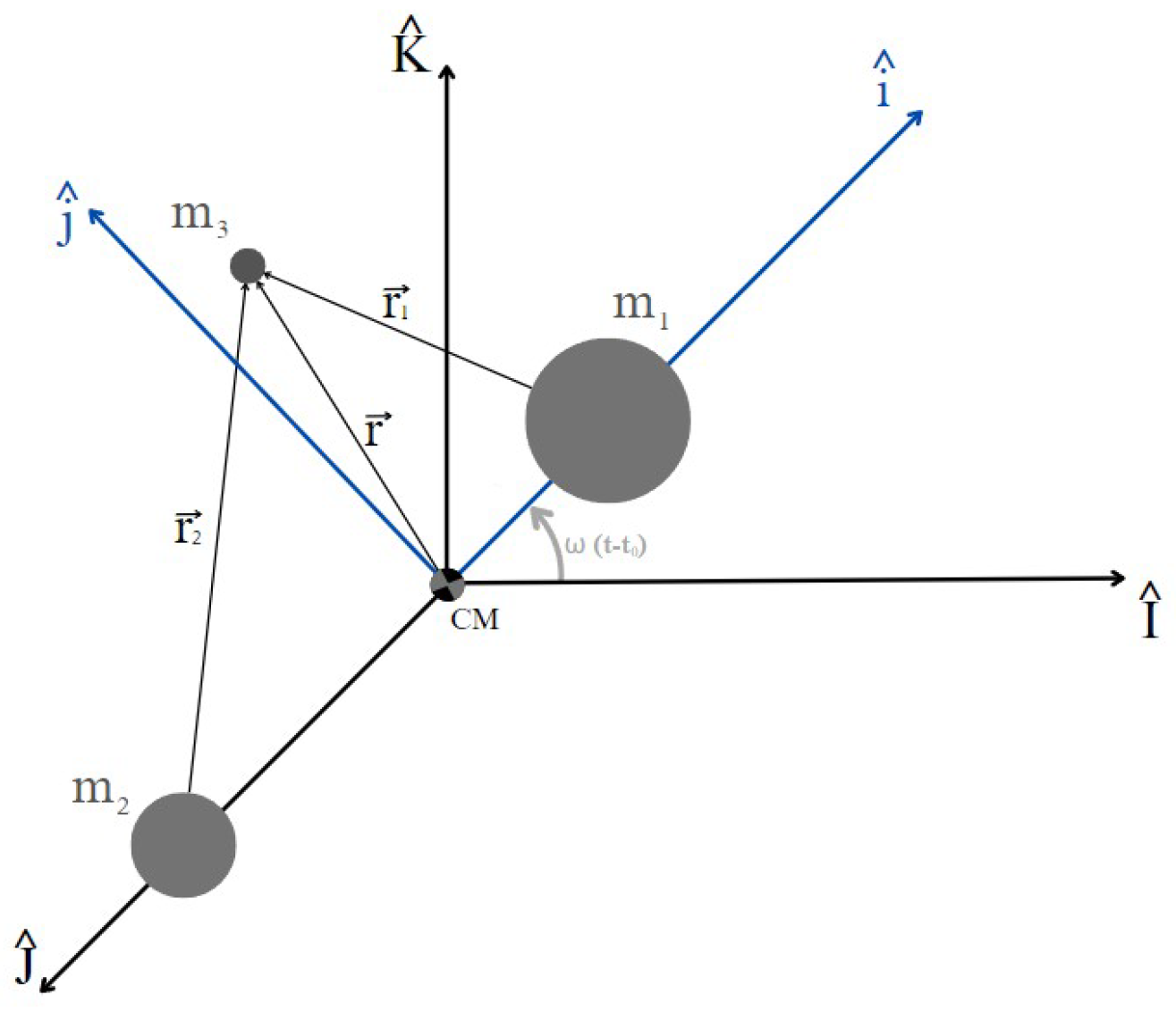
3.1. Circular Restricted Three−Body Problem
- The CR3BP considers three bodies, m1, m2 and m3, such that the third mass is much smaller than the two main ones, termed primaries:
- The third body m3 has no gravitational influence on the motion of m1 and m2;
- The two primaries m1 and m2 orbit in circular orbits relative to their center of mass (CM).
3.2. Lagrange Points
- Equilateral points. Setting , we can find two of the five solutions of Equation (4):Solving for x and using the non−dimensionalized equation to substitute in y, the equilateral points can be found:These two points are called and .
- Collinear points. Noting that is a solution of the second equation of Equation (3), one can compute the values from the first equation. In particular, one can use the fact that and , both of which must be positive quantities, since they represent physical distances, and substitute them into the equation. This yields the following:This algebraic equation has three real roots for x that correspond to the coordinates of the collinear points , , and , which are all unstable for any value of . On the other hand, and are stable for all Sun−planet and planet−moon combinations, except for the Pluto−Charon system ().
3.3. Dynamical Systems Theory
- Invariant manifolds are mathematical structures that play a crucial role in trajectory optimization for interplanetary missions. Invariant manifolds help define regions in space that remain unchanged under the influence of gravitational forces, providing stable paths for spacecrafts. Understanding and utilizing these manifolds contribute to the optimization of trajectories, allowing for more efficient and fuel−effective interplanetary orbit insertion maneuvers.
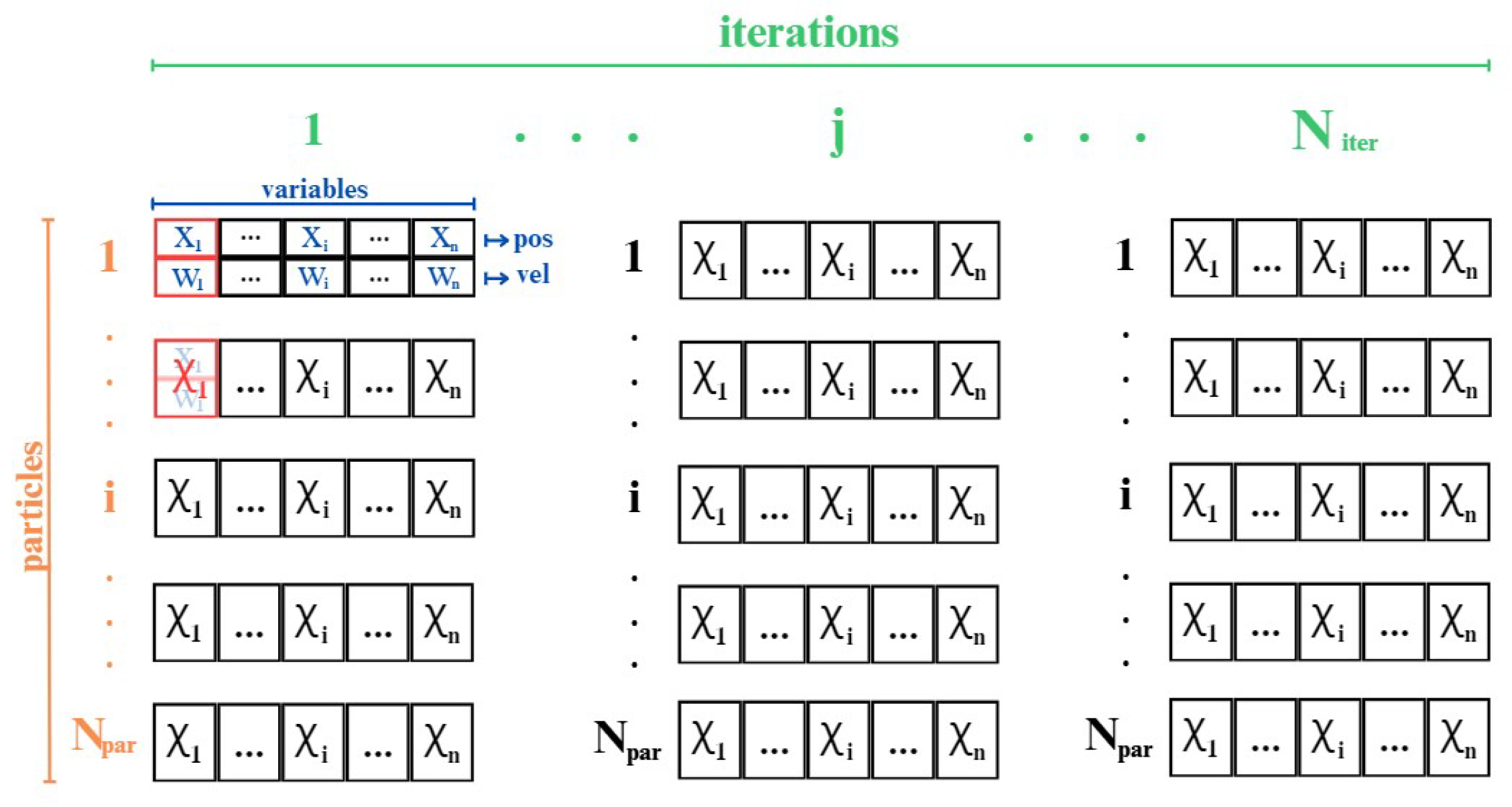
3.4. Particle Swarm Optimization
- PSO algorithm: The idea of applying PSO is to minimize a certain objective function related to a dynamic system during its temporal evolution.
- For i = 1, …, Npar
- (a)
- Evaluate the objective function for the i−th particle:
- (b)
- Define the best position visited by the i−th particle up to the current j−th iteration:
- Define the global best position ever visited by the entire swarm up to the current j−th iteration:
- Update the velocity w for each particle i and each component :The inertial, cognitive, and social weights have the following expressions [21]:where , and represent three independent random numbers between 0 and 1.
- (a)
- If
- (b)
- If
- Update the position x for each particle i and each component :
- (a)
- If and
- (b)
- If and
- The first term, , is referred to as the inertial term, and for each particle, it is proportional to the particle’s velocity in the previous iteration.
- The second term, , represents the cognitive term and is proportionate to the distance between the current position of the particle and the best position the particle has achieved up to the j−th iteration.
- The third term, , is the social term, and in this case, it is proportional to the difference between the current position of the particle and the best position encountered among all particles up to the j−th iteration.
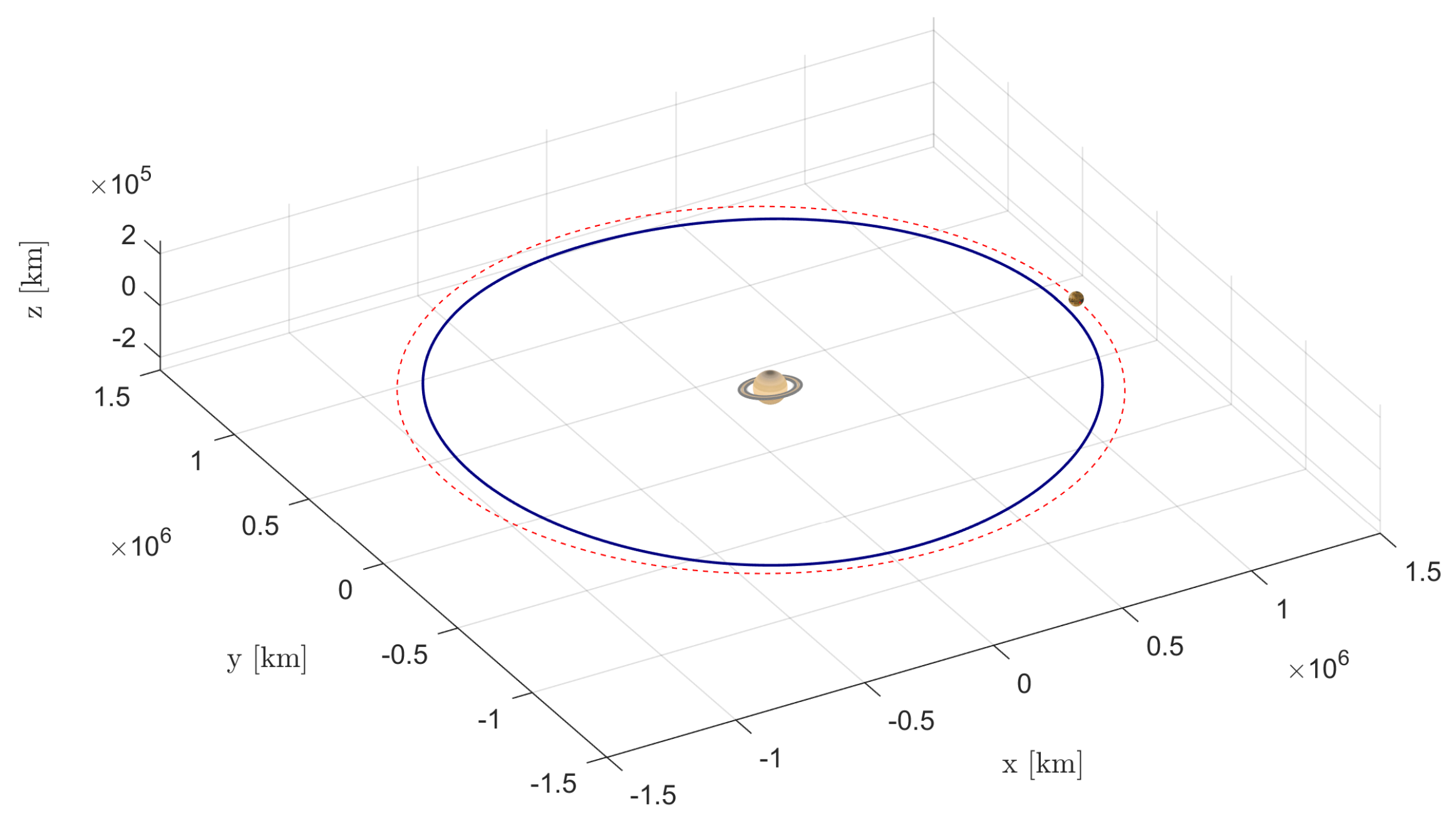
4. A Trade−Off Analysis of CR3BP Orbits
Orbit Selection
5. Trajectory Optimization
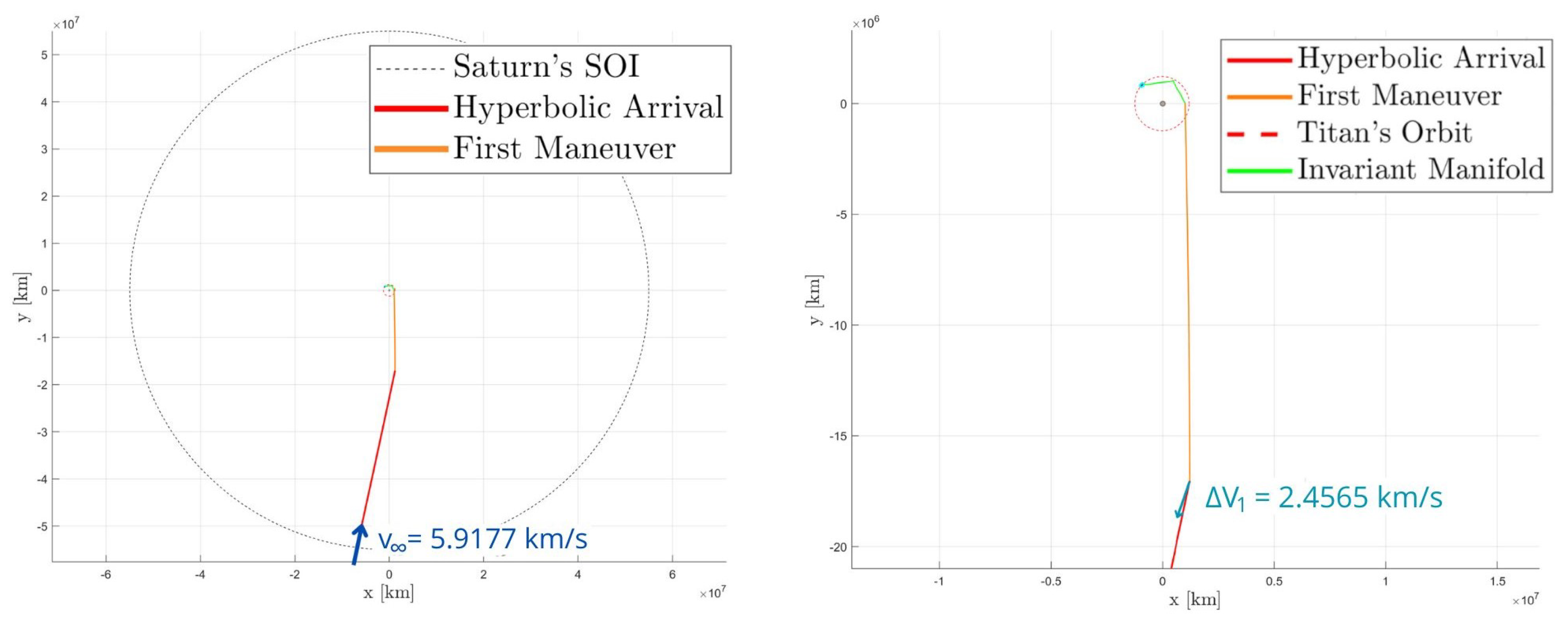
5.1. Direct Arrival to Titan
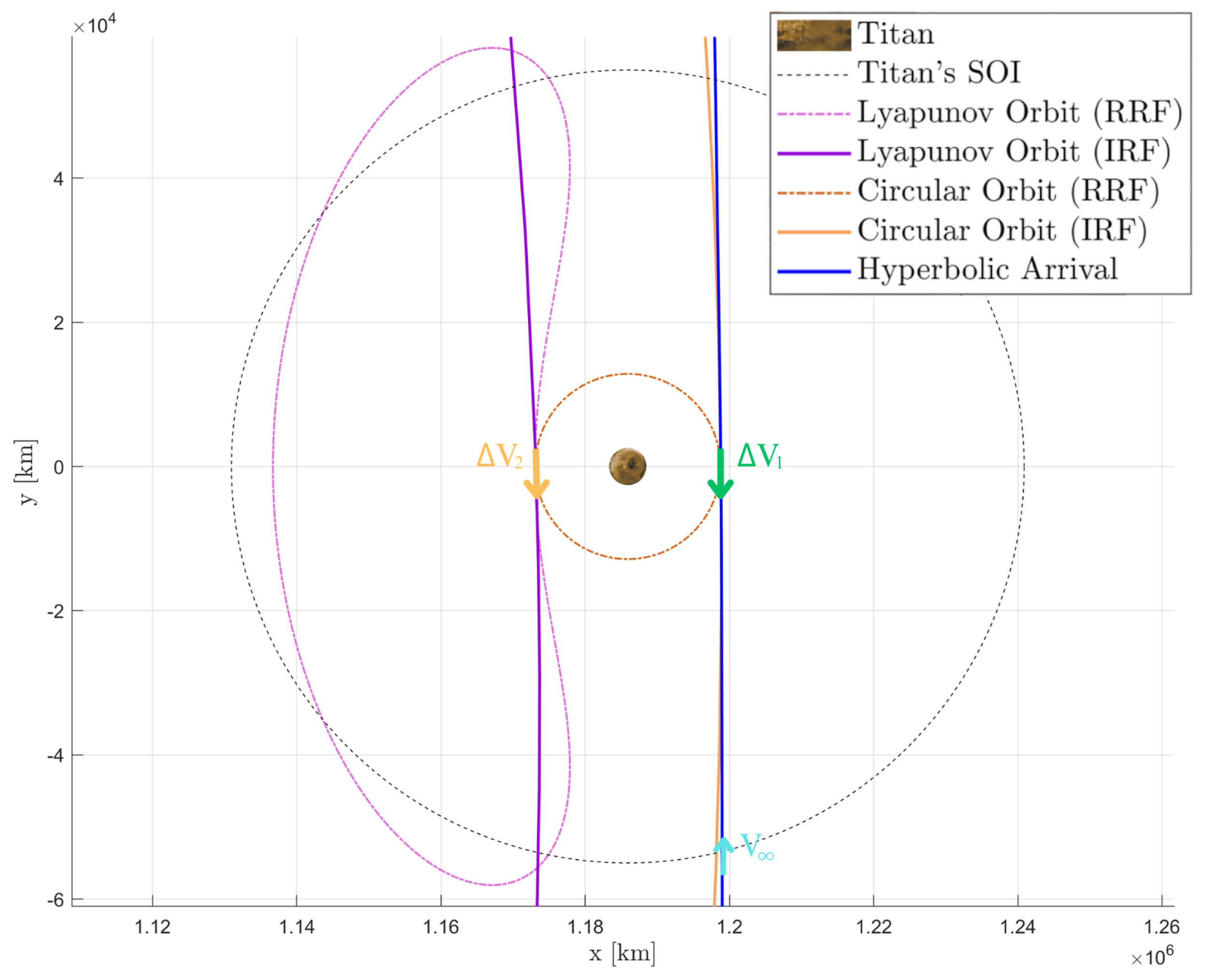
5.2. Hyperbolic Arrival in Invariant Manifolds
5.2.1. PSO Structure Applied to Trajectory Optimization
- The i−th trajectory of the invariant manifold; hence, the velocity required for the spacecraft to enter that trajectory. Indirectly, this parameter provides .
- The , indicating the retrograde change in velocity required.
- The position on the arrival hyperbolic trajectory where the first maneuver described by will occur. This parameter will be evaluated based on the angle between Saturn and the considered point of the hyperbola.
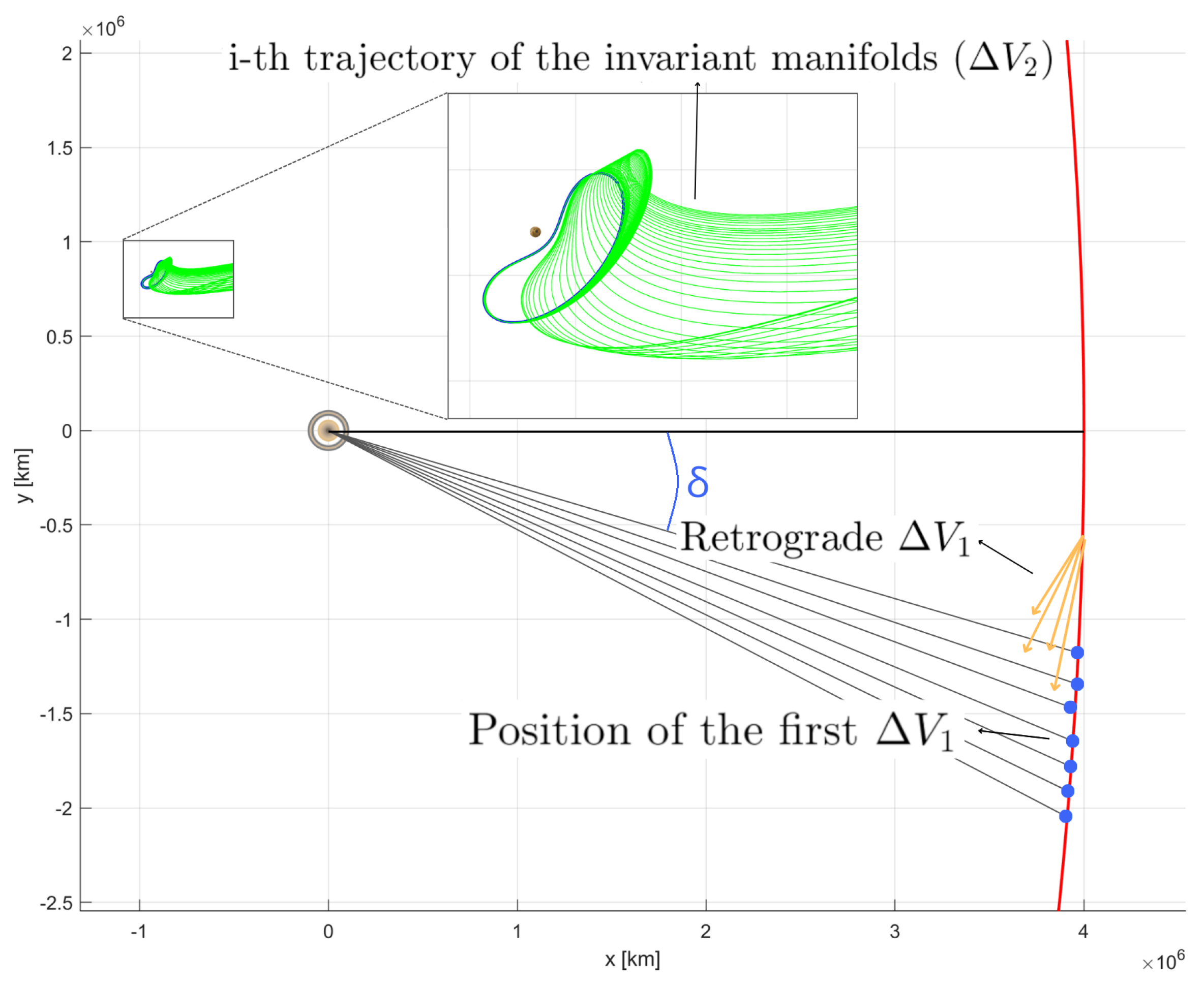
5.2.2. Benefits of Reduced
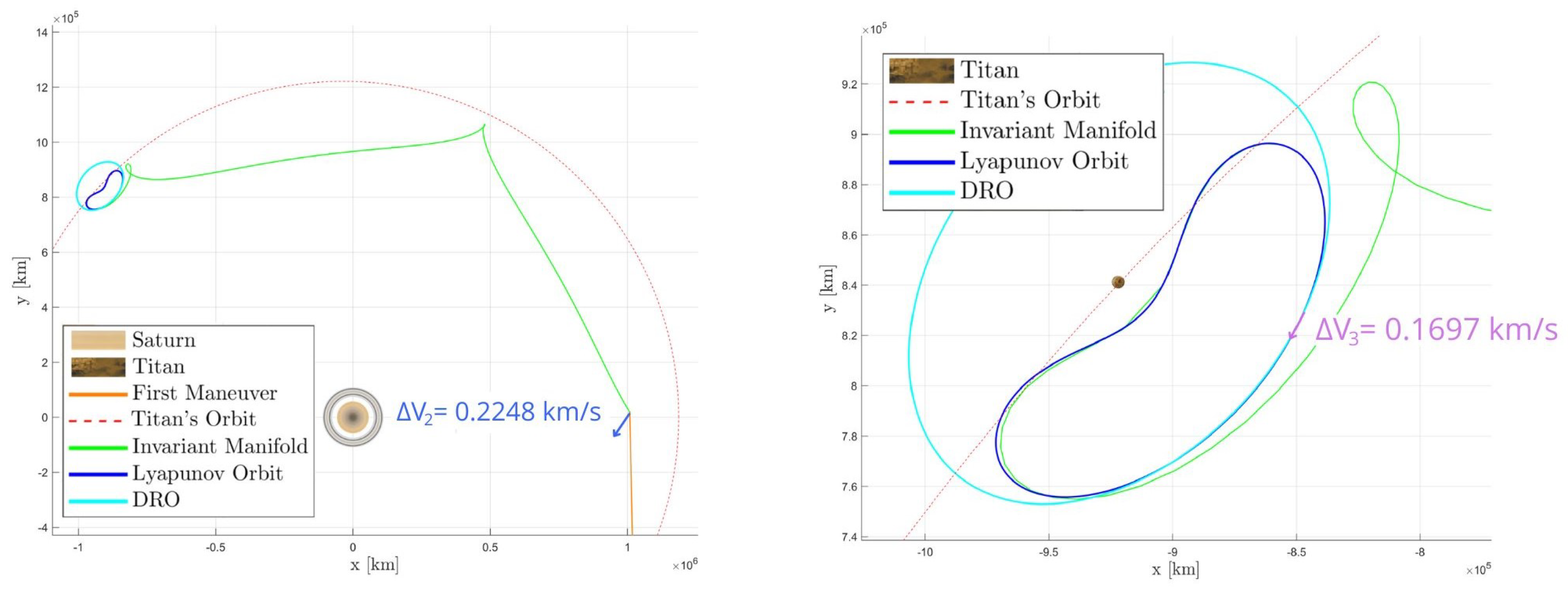
6. Trajectory Overview and Final Results
7. Conclusions and Future Work
- Refinement of optimization techniques: Continual refinement of optimization techniques could involve exploring machine learning or evolutionary algorithms to supplement or replace PSO. This exploration has the potential to yield even more optimized trajectories.
- Enhanced mission flexibility: Trajectories that enable exploration across various regions of Titan, particularly the polar areas, should be investigated while ensuring orbital stability.
- Multi−objective optimization: Optimization strategies should be extended to consider multiple objectives, such as reducing time of flight, maximizing scientific data collection, and minimizing propellant consumption simultaneously.
- Optimization of alternative trajectory selection: Alternative Lyapunov or other family orbits should be explored for insertion into DROs to potentially enhance efficiency and meet specific mission requirements while ensuring stability.
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| ASI | Agenzia Spaziale Italiana |
| CM | Center of Mass |
| CR3BP | Circular Restricted Three–Body Problem |
| DE | Differential Evolution |
| DRO | Distant Retrograde Orbit |
| DST | Dynamical Systems Theory |
| ESA | European Space Agency |
| EOMs | Equations Of Motion |
| GA | Genetic Algorithm |
| IRF | Inertial Reference Frame |
| JPL | Jet Propulsion Laboratory |
| NASA | National Aeronautics and Space Administration |
| ND | Non–Dimensional |
| NRHO | Near–Rectilinear Halo Orbit |
| ODE | Ordinary Differential Equation |
| PSO | Particle Swarm Optimization |
| RRF | Rotational Reference Frame |
| SOI | Sphere Of Influence |
| 1 | https://youtu.be/IGqLMqMeJS4, accessed on 27 November 2023. |
| 2 | NASA−Three-Body Periodic Orbits https://ssd.jpl.nasa.gov/tools/periodic_orbits.html, accessed on 6 October 2023. |
| 3 | JPL Horizons: https://ssd.jpl.nasa.gov/horizons, accessed on 21 October 2023. |
| 4 | ℏ denotes Saturn’s astronomical symbol. |
| 5 | https://youtu.be/KGaobWR8v1w, accessed on 3 November 2023. |
References
- Spilker, L.; Spilker, T. The future of Saturn system exploration: From the Cassini-Huygens legacy to a Horizon 2061 perspective. In Proceedings of the 43rd COSPAR Scientific Assembly, Sydney, Australia, 28 January–4 February 2021; Volume 43, p. 252. [Google Scholar]
- Stofan, E.R.; Elachi, C.; Lunine, J.I.; Lorenz, R.D.; Stiles, B.; Mitchell, K.L.; Ostro, S.; Soderblom, L.; Wood, C.; Zebker, H.; et al. The lakes of Titan. Nature 2007, 445, 61–64. [Google Scholar] [CrossRef] [PubMed]
- National, A. Origins, Worlds, and Life: A Decadal Strategy for Planetary Science and Astrobiology 2023–2032; National Academies of Sciences Engineering and Medicine: Washington, DC, USA, 2022. [Google Scholar]
- Barnes, J.W.; Turtle, E.P.; Trainer, M.G.; Lorenz, R.D.; MacKenzie, S.M.; Brinckerhoff, W.B.; Cable, M.L.; Ernst, C.M.; Freissinet, C.; Hand, K.P.; et al. Science Goals and Objectives for the Dragonfly Titan Rotorcraft Relocatable Lander. Planet. Sci. J. 2021, 2, 130. [Google Scholar] [CrossRef]
- Charles, A.; Wood, J.R. Morphologic Evidence for Volcanic Craters Near Titan’s North Polar Region. J. Geophys. Res. Planets 2020, 125, e2019JE006036. [Google Scholar] [CrossRef]
- Brown, R.; Lebreton, J.; Waite, J. Titan from Cassini-Huygens; Springer: Berlin, Germany, 2010. [Google Scholar]
- Baldwin, E. The Mysterious ‘Lakes’ on Saturn’s Moon Titan. 2015. Available online: https://solarsystem.nasa.gov/missions/cassini/mission/spacecraft/huygens-probe/ (accessed on 16 May 2023).
- Griffith, C.; Lora, J.; Turner, J.E.A. Possible tropical lakes on Titan from observations of dark terrain. Nature 2012, 486, 237–239. [Google Scholar] [CrossRef] [PubMed]
- NASA. First Global Geologic Map of Titan. 2007. Available online: https://www.nasa.gov/solar-system/the-first-global-geologic-map-of-titan-completed/ (accessed on 13 May 2023).
- NASA. In Depth—Voyager 1. 2021. Available online: https://solarsystem.nasa.gov/missions/voyager-1/in-depth/ (accessed on 14 May 2023).
- Martinez, C.; Brown, D. Cassini Spacecraft Images Seas on Saturn’s Moon Titan. NASA/JPL. 2007. Available online: https://solarsystem.nasa.gov/news/12381/cassini-spacecraft-images-seas-on-saturns-moon-titan/ (accessed on 16 May 2023).
- NASA/JHU-APL. NASA’s Dragonfly Will Fly Around Titan Looking for Origins, Signs of Life. 2019. Available online: https://www.nasa.gov/press-release/nasas-dragonfly-will-fly-around-titan-looking-for-origins-signs-of-life/ (accessed on 17 May 2023).
- Jacobi, C. Sur le movement d’un point et sur un cas particulier du problème des trois corps. Comptes Rendus L’AcadéMie Des Sci. Paris 1836, 3, 59–61. [Google Scholar]
- Poincaré, H. Les Méthodes Nouvelles de la Mécanique Céleste; Gauthier-Villars et fils: Paris, France, 1892. [Google Scholar]
- Howell, K.; Barden, B.; Lo, M. Application of Dynamical Systems Theory to Trajectory Design for a Libration Point Mission. J. Astronaut. Sci. 1997, 45, 161–178. [Google Scholar] [CrossRef]
- Burnett, D.S.; Barraclough, B.L.; Bennett, R.; Neugebauer, M.; Oldham, L.P.; Sasaki, C.N.; Sevilla, D.; Smith, N.; Stansbery, E.; Sweetnam, D.; et al. The Genesis Discovery Mission: Return of Solar Matter to Earth. Space Sci. Rev. 2003, 105, 509–534. [Google Scholar] [CrossRef]
- Johns, A.; Seaton, B.; Gal-Edd, J.; Jones, R.; Fatig, C.; Wasiak, F. James Webb Space Telescope: L2 communications for science data processing. In Observatory Operations: Strategies, Processes, and Systems II; Society of Photo-Optical Instrumentation Engineers (SPIE) Conference Series; Brissenden, R.J., Silva, D.R., Eds.; SPIE: Bellingham, WA, USA, 2008; Volume 7016, p. 70161D. [Google Scholar] [CrossRef]
- Spencer, D.; Conte, D. Interplanetary Astrodynamics, 1st ed.; Taylor & Francis Ltd.: Abingdon, UK, 2023. [Google Scholar]
- Kelly, P.; Junkins, J.; Majji, M. Orthogonal Approximation of Invariant Manifolds in the Circular Restricted Three-Body Problem. J. Guid. Control. Dyn. 2023, 46, 1536–1547. [Google Scholar] [CrossRef]
- Muralidharan, V.; Howell, K.C. Stretching directions in cislunar space: Applications for departures and transfer design. Astrodynamics 2022, 7, 153–178. [Google Scholar] [CrossRef]
- Pontani, M.; Conway, B. Particle Swarm Optimization Applied to Space Trajectories. J. Guid. Control Dyn. 2010, 33, 1429–1441. [Google Scholar] [CrossRef]
- Baraldi, V.; Conte, D. Trajectory Optimization and Control Applied to Landing Maneuvers on Phobos from Mars-Phobos Distant Retrograde Orbits. Universe 2023, 9, 348. [Google Scholar] [CrossRef]
- Lin, G.; Zhang, J.; Zhao-Hua, L. Hybrid Particle Swarm Optimization with Differential Evolution for Numerical and Engineering Optimization. Int. J. Autom. Comput. 2018, 15, 103–114. [Google Scholar] [CrossRef]
- Sentinella, M.; Casalino, L. Cooperative evolutionary algorithm for space trajectory optimization. Celest. Mech. Dyn. Astron. 2009, 105, 211–227. [Google Scholar] [CrossRef]
- Zhu, K.; Jiang, F.; Li, J.; Baoyin, H. Trajectory Optimization of Multi-Asteroids Exploration with Low Thrust. Jpn. Soc. Aeronaut. Space Sci. Trans. 2009, 52, 47–54. [Google Scholar] [CrossRef]
- NASA. Three-Body Periodic Orbits. Available online: https://ssd.jpl.nasa.gov/tools/periodic_orbits.html (accessed on 6 October 2023).
- Paluszek, M.; Price, A.; Koniaris, Z.; Galea, C.; Thomas, S.; Cohen, S.; Stutz, R. Nuclear fusion powered Titan aircraft. Acta Astronaut. 2023, 210, 82–94. [Google Scholar] [CrossRef]
- Li, Q.; Tao, Y.; Jiang, F. Orbital Stability and Invariant Manifolds on Distant Retrograde Orbits around Ganymede and Nearby Higher-Period Orbits. Aerospace 2022, 9, 454. [Google Scholar] [CrossRef]
- Hajdik, H.; Ramsey, S.; Wright, R. Titan Aerogravity Assist for Saturn Orbital Insertion and Study of Enceladus. Acta Astronaut. 2020, 176, 262–275. [Google Scholar]
- Gajeri, M. Trajectory Design for a Titan Mission Using the Direct Fusion Drive. Ph.D. Thesis, Politecnico di Torino, Torino, Italy, 2020. [Google Scholar]
- Mcquaide, M.; Ellison, D.; Englander, J.; Jesick, M.; Ozimek, M.; Roth, D. Dragonfly Phase B Mission Design, 2023. In Proceedings of the 2023 AAS/AIAA Astrodynamics Specialist Conference, Big Sky, Montana, USA, 13–17 August 2023. [Google Scholar]
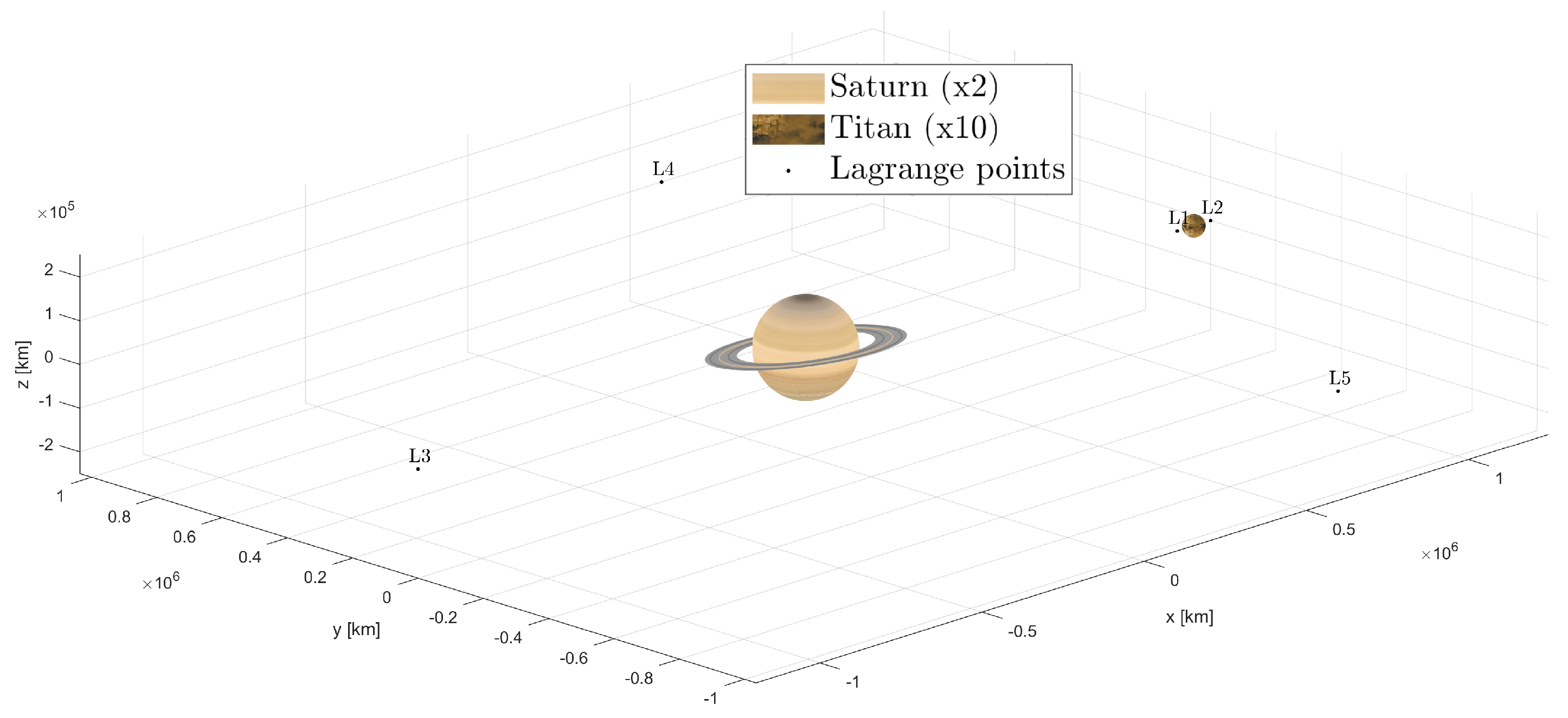

| Lagrange Point | (x, y) [ND] | (x, y) [km] |
|---|---|---|
| (0.9574961733, 0) | (1,144,856.15, 0) | |
| (1.0432564213, 0) | (1,247,397.71, 0) | |
| (−1.0000985997, 0) | (−1,195,794.89, 0) | |
| (0.4997633607, 0.8660254038) | (597,555.56, 1,035,486.66) | |
| (0.4997633607, −0.8660254038) | (597,555.56, −1,035,486.66) |
| Orbit | Period [Days] | Saturn Occultated [%] | Saturn Occultated [Days] | Titan’s Surface Visibility [%] |
|---|---|---|---|---|
| Lyapunov () | 8.377 | 0 | 0 | 76.20 |
| Assiale () | 10.259 | 9.417 | 0.9661 | 91.90 |
| Verticale () | 14.556 | 8.651 | 1.2591 | 88.27 |
| Halo () | 7.3308 | 0 | 0 | 64.79 |
| Halo () | 7.7367 | 0 | 0 | 64.35 |
| NRHO () | 4.6321 | 0 | 0 | 99.68 |
| Butterfly | 9.4883 | 0 | 0 | 100.00 |
| Dragonfly | 15.314 | 0 | 0 | 99.87 |
| DRO (≈9 days) | 9.2473 | 10.072 | 0.9314 | 87.10 |
| DRO (≈5 days) | 4.6768 | 13.889 | 0.6496 | 80.65 |
| Orbit | Stability Index2 |
|---|---|
| Lyapunov () | |
| Axial () | |
| Vertical () | |
| Halo () | |
| Halo () | |
| NRHO () | |
| Butterfly | |
| Dragonfly | |
| DRO (≈9 days) | |
| DRO (≈5 days) |
| Orbit | Period [Days] | Jacobi Constant | Stability Index |
|---|---|---|---|
| DRO | 9.5786 | 2.9922448517210601 | 1.0000000023234800 |
| Lyapunov | 10.2010 | 3.0034876561564201 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Papalia, G.; Conte, D. Leveraging the Interplanetary Superhighway for Propellant–Optimal Orbit Insertion into Saturn–Titan System. Universe 2024, 10, 405. https://doi.org/10.3390/universe10110405
Papalia G, Conte D. Leveraging the Interplanetary Superhighway for Propellant–Optimal Orbit Insertion into Saturn–Titan System. Universe. 2024; 10(11):405. https://doi.org/10.3390/universe10110405
Chicago/Turabian StylePapalia, Giuseppe, and Davide Conte. 2024. "Leveraging the Interplanetary Superhighway for Propellant–Optimal Orbit Insertion into Saturn–Titan System" Universe 10, no. 11: 405. https://doi.org/10.3390/universe10110405
APA StylePapalia, G., & Conte, D. (2024). Leveraging the Interplanetary Superhighway for Propellant–Optimal Orbit Insertion into Saturn–Titan System. Universe, 10(11), 405. https://doi.org/10.3390/universe10110405





