2D BAO vs. 3D BAO: Solving the Hubble Tension with Bimetric Cosmology
Abstract
1. Introduction
Notation
2. Bimetric Gravity
2.1. Historical Background
2.2. Theory
2.3. Cosmology
3. Methodology and Data
3.1. The SH0ES Estimate
3.2. Cosmic Microwave Background
3.3. Type Ia Supernovae
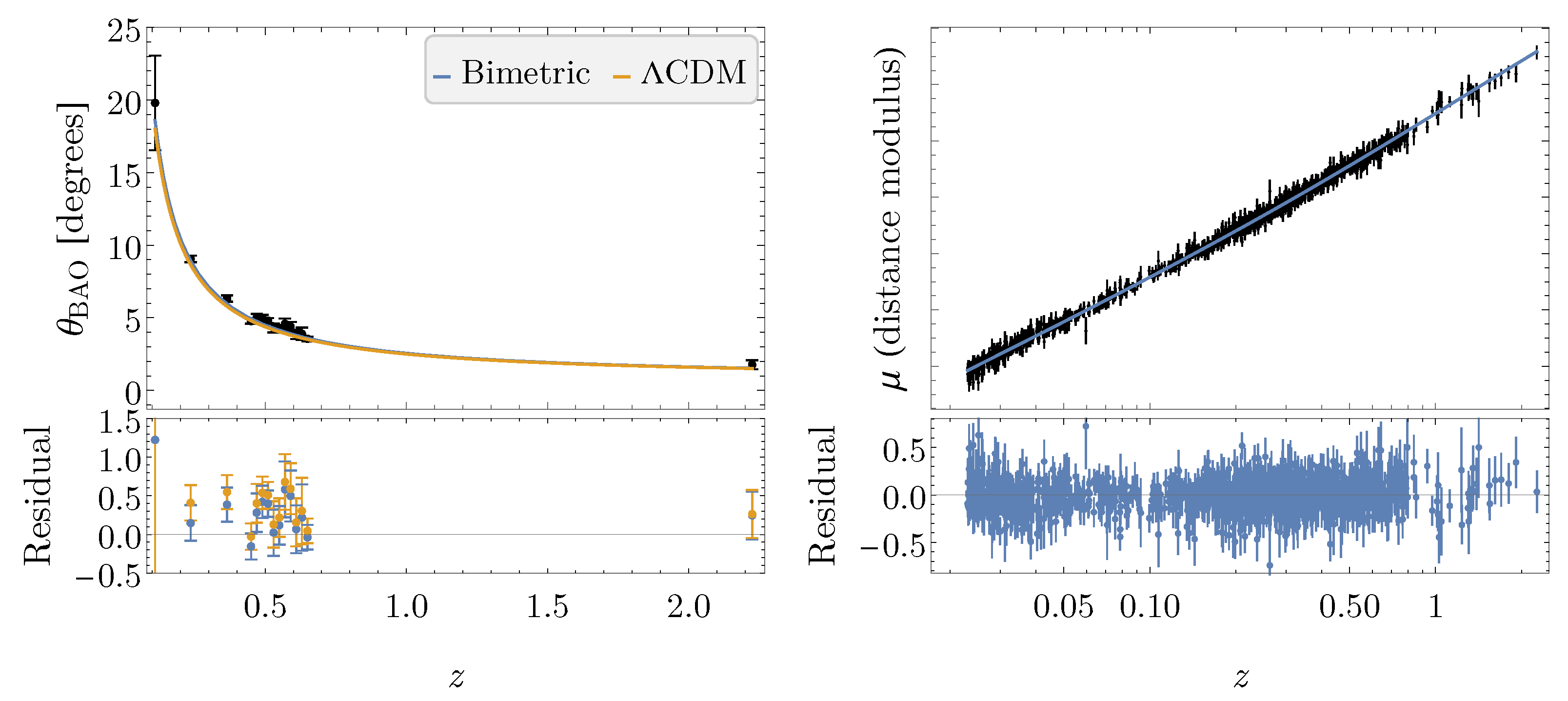
3.4. Baryon Acoustic Oscillations
3.5. Consistency Constraints
3.6. MCMC Sampling
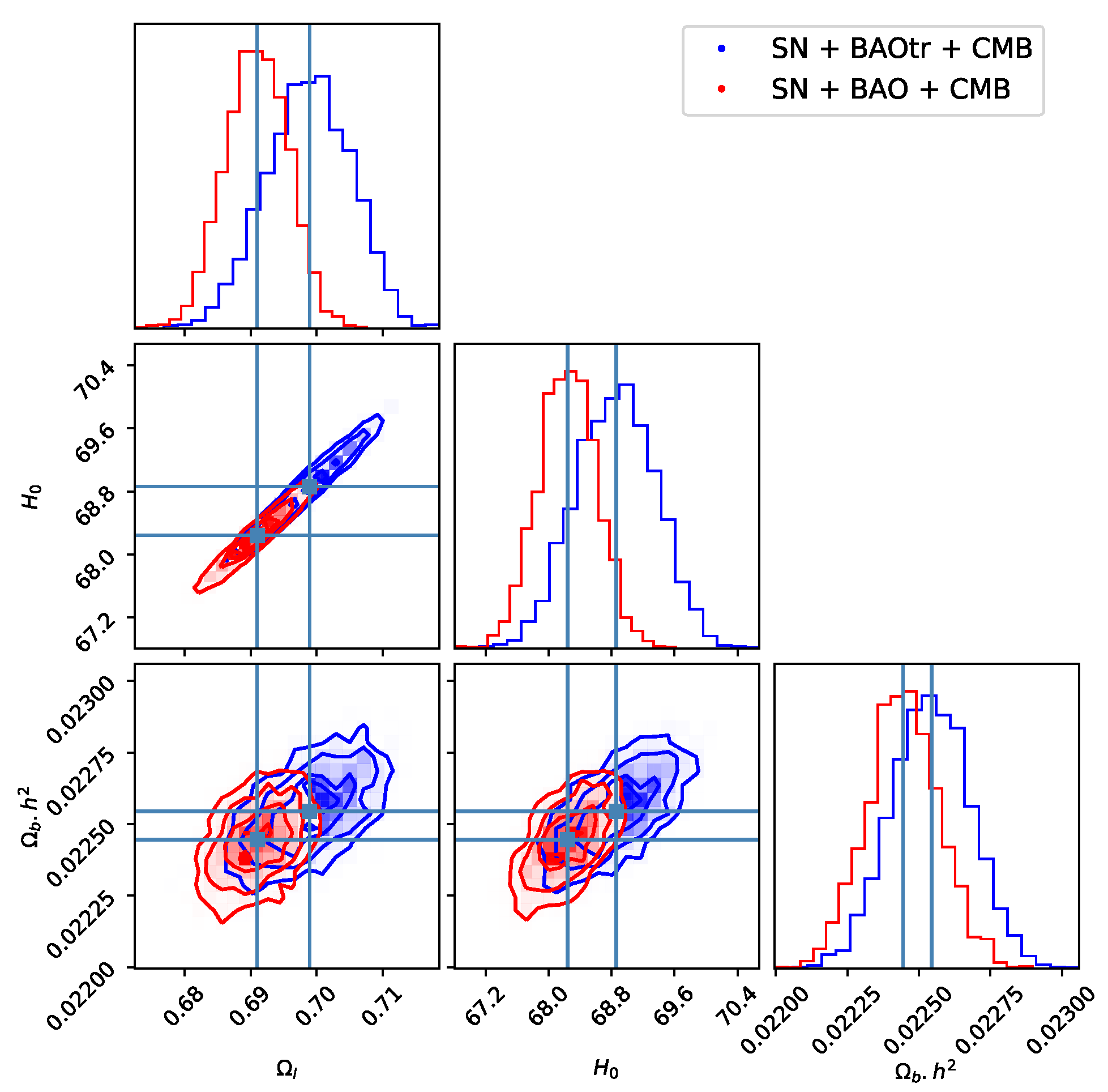
4. Results
5. Discussion
5.1. Minimal Theories of Bigravity (MTBG)
5.2. CDM
5.3. Quadratic Bimetric Gravity
5.4. Phenomenological Emergent Dark Energy
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Ratio of the Scale Factors: Equation of Motion
Appendix B. Complementary Results
| Model | CMB + SN + | (rad) | AIC | BIC | DIC | |||
|---|---|---|---|---|---|---|---|---|
| CDM | BAO | 68.3 ± 0.4 | 0 | 0.691 ± 0.005 | — | 0 | 0 | 0 |
| BAOtr | 68.9 ± 0.5 | 0 | 0.700 ± 0.006 | — | 0 | 0 | 0 | |
| BAO | 68.6 ± 0.5 | 0.078 ± 0.036 | 0.695 ± 0.006 | ≤1.9 | ||||
| BAOtr | 71.0 ± 0.9 | 0.163 ± 0.028 | 0.724 ± 0.010 | ≤1.7 | 1.1 | |||
| BAO | 68.5 ± 0.6 | 0.088 ± 0.040 | 0.695 ± 0.007 | ≤8.0 | ||||
| BAOtr | 70.9 ± 1.0 | 0.171 ± 0.059 | 0.726 ± 0.015 | ≤1.6 | 3.0 | |||
| BAO | 68.3 ± 0.4 | 0.015 ± 0.035 | 0.692 ± 0.005 | — | ||||
| BAOtr | 69.3 ± 0.8 | 0.1 ± 0.073 | 0.707 ± 0.013 | — | ||||
| BAO | 68.2 ± 0.4 | 0.691 ± 0.005 | — | |||||
| BAOtr | 68.9 ± 0.5 | 0.699 ± 0.006 | — |
| Model | CMB + SN + | (rad) | AIC | BIC | DIC | |||
|---|---|---|---|---|---|---|---|---|
| CDM | BAO + SH0ES | 68.9 ± 0.3 | 0 | 0.698 ± 0.004 | — | 0 | 0 | 0 |
| BAOtr + SH0ES | 69.7 ± 0.5 | 0 | 0.709 ± 0.006 | — | 0 | 0 | 0 | |
| BAO + SH0ES | 69.4 ± 0.5 | 0.119 ± 0.031 | 0.704 ± 0.006 | ≤ | ||||
| BAOtr + SH0ES | 71.9 ± 0.7 | 0.178 ± 0.023 | 0.732 ± 0.007 | ≤ | 13.2 | |||
| BAO + SH0ES | 69.2 ± 0.6 | 0.109 ± 0.038 | 0.704 ± 0.006 | ≤ | 0.2 | |||
| BAOtr + SH0ES | 71.8 ± 0.8 | 0.183 ± 0.022 | 0.733 ± 0.008 | ≤ | 15.0 | |||
| BAO + SH0ES | 69.0 ± 0.4 | 0.048 ± 0.057 | 0.701 ± 0.006 | — | ||||
| BAOtr + SH0ES | 70.6 ± 0.7 | 0.173 ± 0.067 | 0.723 ± 0.010 | — | 6.7 | |||
| BAO + SH0ES | 68.8 ± 0.4 | 0.698 ± 0.005 | — | |||||
| BAOtr + SH0ES | 69.7 ± 0.5 | 0.709 ± 0.006 | — |
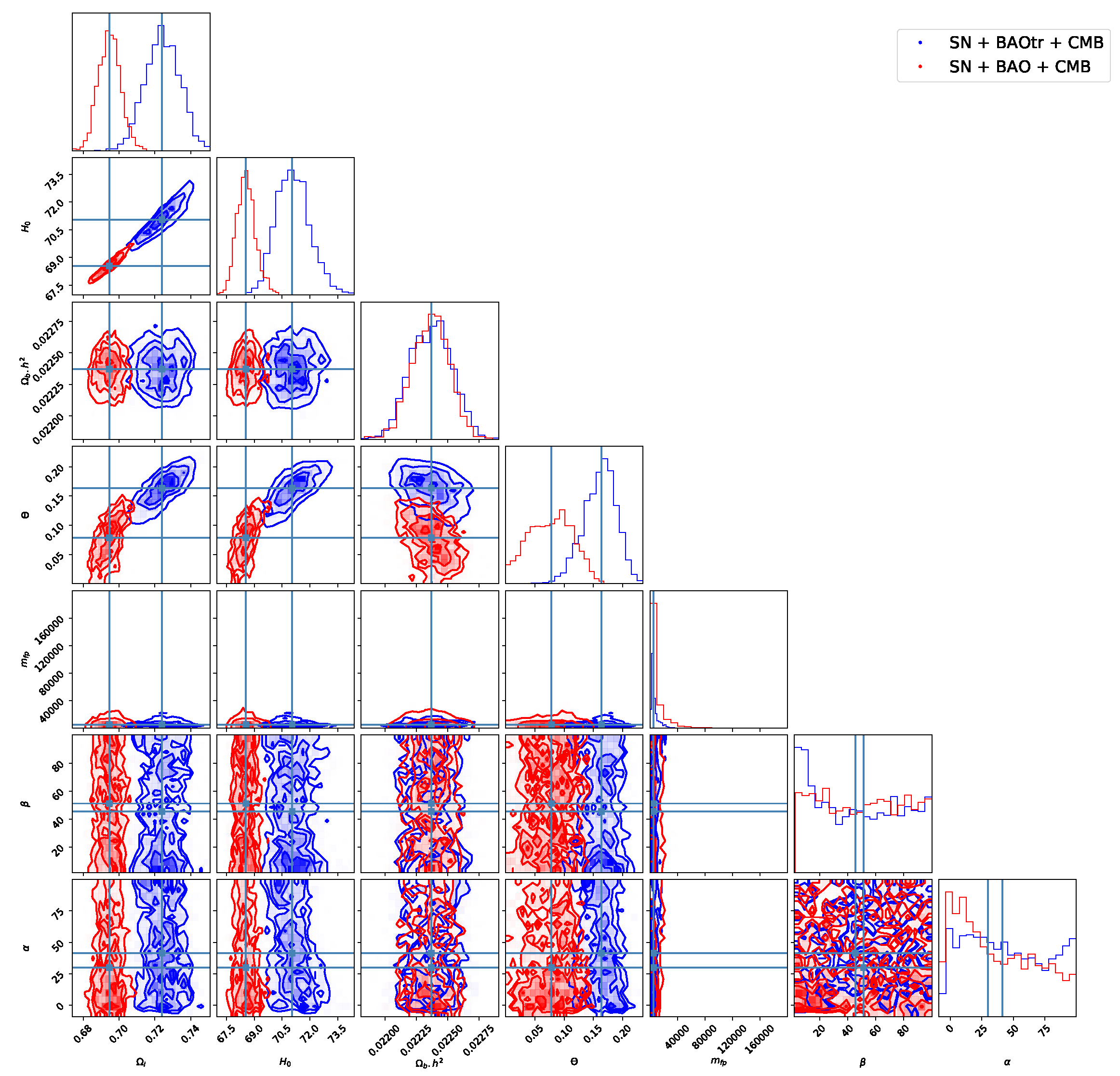
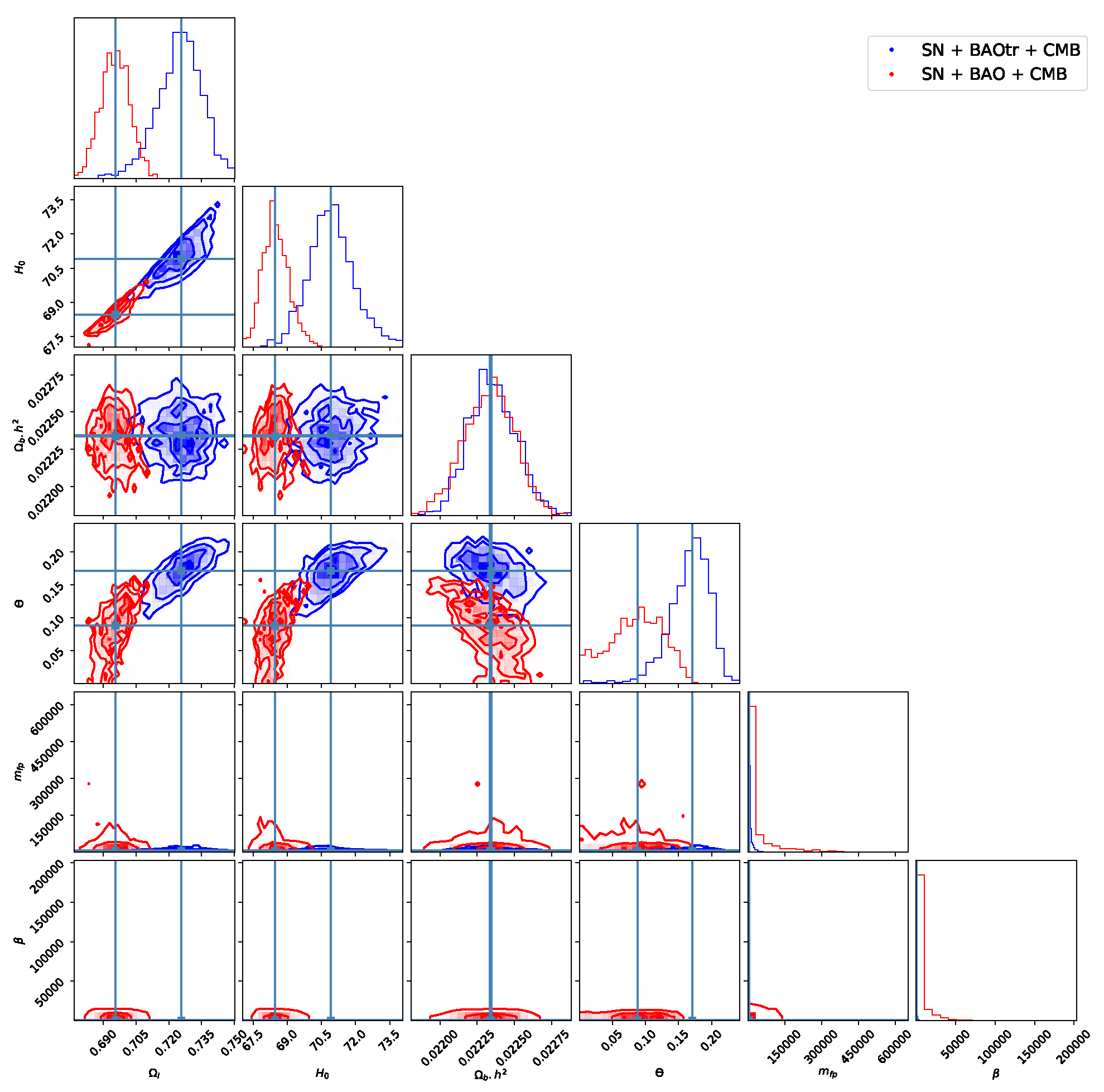
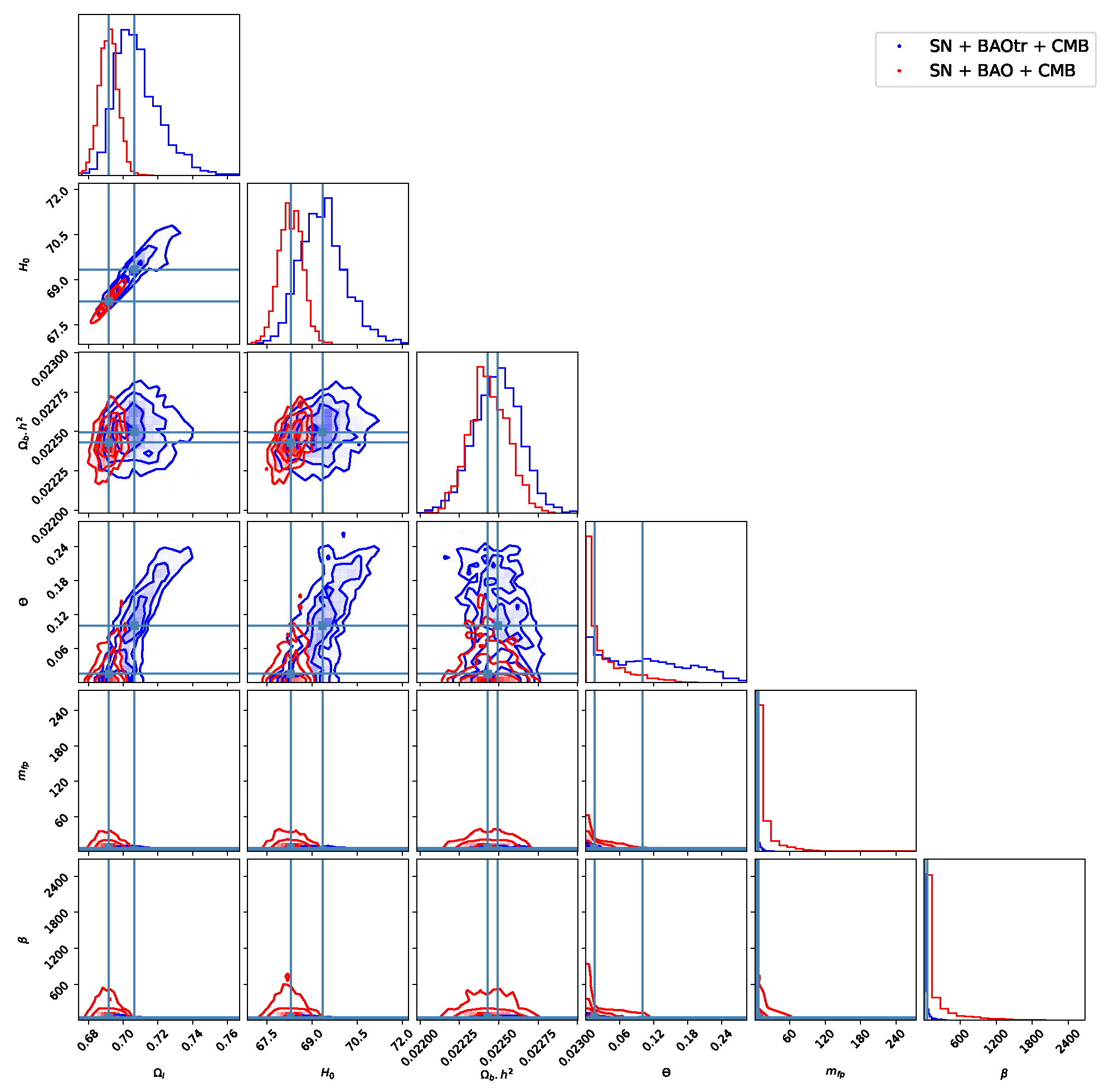
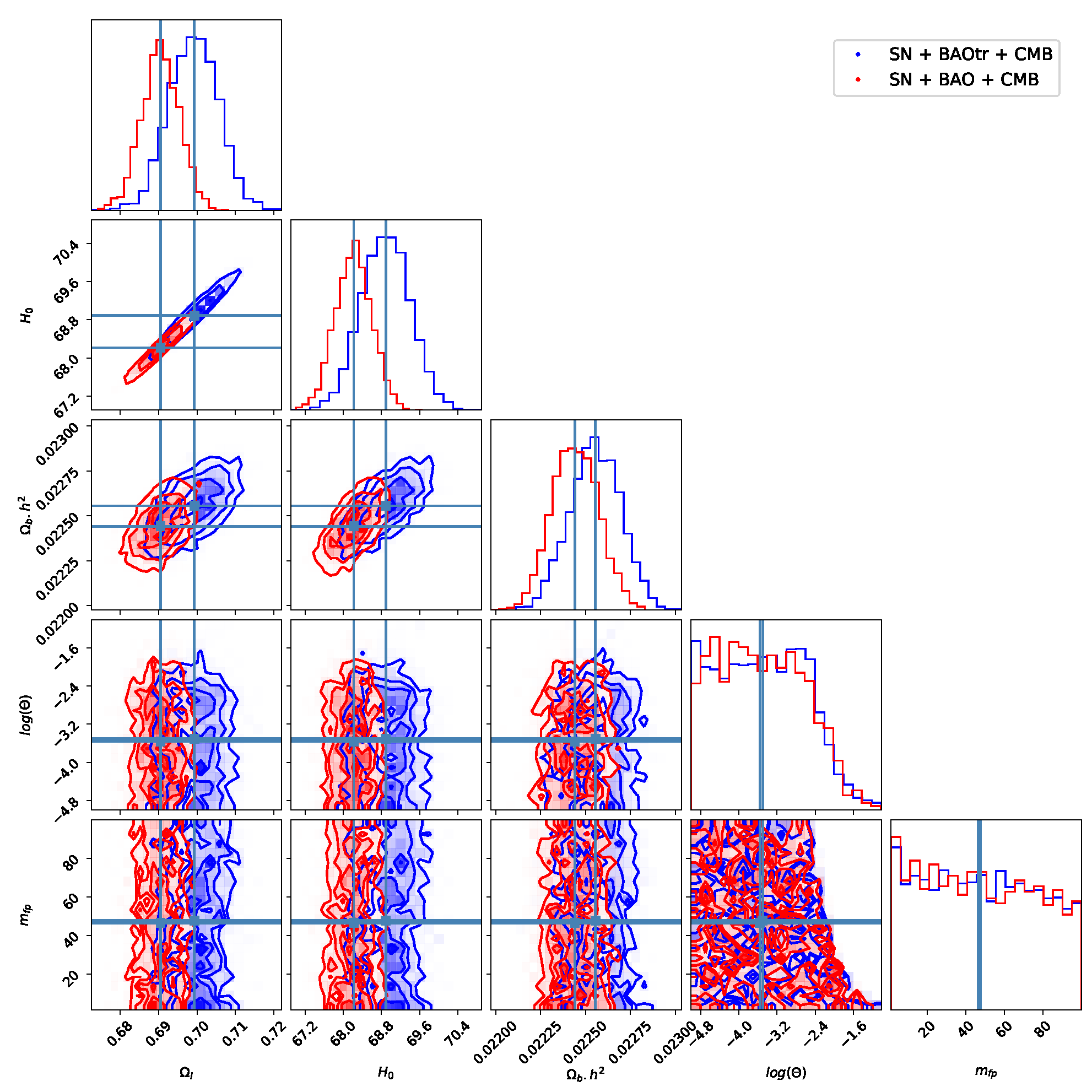
| 1 | A combination of the two is of course also an option. See, e.g., [4]. |
| 2 | Note that this equation has no unique solution generically. However, in Ref. [83] it was argued that the principal square root is the appropriate solution as it guarantees a sensible space-time interpretation of the theory. |
| 3 | For a more general discussion of a dark energy fluid with such properties, see Ref. [90]. |
| 4 | In Section 3.2, we show how is determined from the CMB temperature. |
| 5 | The dataset is available at https://github.com/PantheonPlusSH0ES/DataRelease/tree/main/Pantheon%2B_Data, last checked 2 July 2024. |
| 6 | |
| 7 | For the best-fit bimetric cosmology, shown in Figure 2, the sound horizons are and . |
| 8 | There are also windows of viable Fierz–Pauli masses in the ranges and . |
References
- Will, C.M. The Confrontation between General Relativity and Experiment. Living Rev. Rel. 2014, 17, 4. [Google Scholar] [CrossRef] [PubMed]
- Riess, A.G.; Yuan, W.; Macri, L.M.; Scolnic, D.; Brout, D.; Casertano, S.; Jones, D.O.; Murakami, Y.; Anand, G.S.; Breuval, L.; et al. A Comprehensive Measurement of the Local Value of the Hubble Constant with 1 km s−1 Mpc−1 Uncertainty from the Hubble Space Telescope and the SH0ES Team. Astrophys. J. Lett. 2022, 934, L7. [Google Scholar] [CrossRef]
- Aghanim, N.; Akrami, Y.; Ashdown, M.; Aumont, J.; Baccigalupi, C.; Ballardini, M.; Banday, A.J.; Barreiro, R.B.; Bartolo, N.; Basak, S.; et al. Planck 2018 results. VI. Cosmological parameters. Astron. Astrophys. 2020, 641, A6, Erratum in Astron. Astrophys. 2021, 652, C4. [Google Scholar] [CrossRef]
- Vagnozzi, S. Seven Hints That Early-Time New Physics Alone Is Not Sufficient to Solve the Hubble Tension. Universe 2023, 9, 393. [Google Scholar] [CrossRef]
- Desmond, H.; Jain, B.; Sakstein, J. Local resolution of the Hubble tension: The impact of screened fifth forces on the cosmic distance ladder. Phys. Rev. D 2019, 100, 043537, Erratum in Phys. Rev. D 2020, 101, 069904, 129901. [Google Scholar] [CrossRef]
- Högås, M.; Mörtsell, E. Hubble tension and fifth forces. Phys. Rev. D 2023, 108, 124050. [Google Scholar] [CrossRef]
- Högås, M.; Mörtsell, E. Impact of symmetron screening on the Hubble tension: New constraints using cosmic distance ladder data. Phys. Rev. D 2023, 108, 024007. [Google Scholar] [CrossRef]
- Knox, L.; Millea, M. Hubble constant hunter’s guide. Phys. Rev. D 2020, 101, 043533. [Google Scholar] [CrossRef]
- Vagnozzi, S. New physics in light of the H0 tension: An alternative view. Phys. Rev. D 2020, 102, 023518. [Google Scholar] [CrossRef]
- Di Valentino, E.; Mena, O.; Pan, S.; Visinelli, L.; Yang, W.; Melchiorri, A.; Mota, D.F.; Riess, A.G.; Silk, J. In the realm of the Hubble tension—A review of solutions. Class. Quant. Grav. 2021, 38, 153001. [Google Scholar] [CrossRef]
- Schöneberg, N.; Franco Abellán, G.; Pérez Sánchez, A.; Witte, S.J.; Poulin, V.; Lesgourgues, J. The H0 Olympics: A fair ranking of proposed models. Phys. Rept. 2022, 984, 1–55. [Google Scholar] [CrossRef]
- Abdalla, E.; Abellán, G.F.; Aboubrahim, A.; Agnello, A.; Akarsu, Ö.; Akrami, Y.; Alestas, G.; Aloni, D.; Amendola, L.; Anchordoqui, L.A.; et al. Cosmology intertwined: A review of the particle physics, astrophysics, and cosmology associated with the cosmological tensions and anomalies. J. High Energy Astrophys. 2022, 34, 49–211. [Google Scholar] [CrossRef]
- Carter, P.; Beutler, F.; Percival, W.J.; DeRose, J.; Wechsler, R.H.; Zhao, C. The impact of the fiducial cosmology assumption on BAO distance scale measurements. Mon. Not. Roy. Astron. Soc. 2020, 494, 2076–2089. [Google Scholar] [CrossRef]
- Sanz-Wuhl, S.; Gil-Marín, H.; Cuesta, A.J.; Verde, L. BAO cosmology in non-spatially flat background geometry from BOSS+eBOSS and lessons for future surveys. J. Cosmol. Astropart. Phys. 2024, 5, 116. [Google Scholar] [CrossRef]
- Pérez-Fernández, A. et al. [DESI Collaboration] Fiducial-Cosmology-dependent systematics for the DESI 2024 BAO Analysis. arXiv 2024, arXiv:2406.06085. [Google Scholar]
- Carvalho, G.C.; Bernui, A.; Benetti, M.; Carvalho, J.C.; Alcaniz, J.S. Baryon Acoustic Oscillations from the SDSS DR10 galaxies angular correlation function. Phys. Rev. D 2016, 93, 023530. [Google Scholar] [CrossRef]
- Anselmi, S.; Corasaniti, P.S.; Sanchez, A.G.; Starkman, G.D.; Sheth, R.K.; Zehavi, I. Cosmic distance inference from purely geometric BAO methods: Linear Point standard ruler and Correlation Function Model Fitting. Phys. Rev. D 2019, 99, 123515. [Google Scholar] [CrossRef]
- O’Dwyer, M.; Anselmi, S.; Starkman, G.D.; Corasaniti, P.S.; Sheth, R.K.; Zehavi, I. Linear Point and Sound Horizon as Purely Geometric standard rulers. Phys. Rev. D 2020, 101, 083517. [Google Scholar] [CrossRef]
- Di Valentino, E.; Melchiorri, A.; Mena, O.; Vagnozzi, S. Interacting dark energy in the early 2020s: A promising solution to the H0 and cosmic shear tensions. Phys. Dark Univ. 2020, 30, 100666. [Google Scholar] [CrossRef]
- Camarena, D.; Marra, V. A new method to build the (inverse) distance ladder. Mon. Not. Roy. Astron. Soc. 2020, 495, 2630–2644. [Google Scholar] [CrossRef]
- Nunes, R.C.; Yadav, S.K.; Jesus, J.F.; Bernui, A. Cosmological parameter analyses using transversal BAO data. Mon. Not. Roy. Astron. Soc. 2020, 497, 2133–2141. [Google Scholar] [CrossRef]
- Nunes, R.C.; Bernui, A. BAO signatures in the 2-point angular correlations and the Hubble tension. Eur. Phys. J. C 2020, 80, 1025. [Google Scholar] [CrossRef]
- Anselmi, S.; Starkman, G.D.; Renzi, A. Cosmological forecasts for future galaxy surveys with the linear point standard ruler: Toward consistent BAO analyses far from a fiducial cosmology. Phys. Rev. D 2023, 107, 123506. [Google Scholar] [CrossRef]
- Bernui, A.; Di Valentino, E.; Giarè, W.; Kumar, S.; Nunes, R.C. Exploring the H0 tension and the evidence for dark sector interactions from 2D BAO measurements. Phys. Rev. D 2023, 107, 103531. [Google Scholar] [CrossRef]
- Gómez-Valent, A.; Favale, A.; Migliaccio, M.; Sen, A.A. Late-time phenomenology required to solve the H0 tension in view of the cosmic ladders and the anisotropic and angular BAO datasets. Phys. Rev. D 2024, 109, 023525. [Google Scholar] [CrossRef]
- Favale, A.; Gómez-Valent, A.; Migliaccio, M. 2D vs. 3D BAO: Quantification of their tension and test of the Etherington relation. arXiv 2024, arXiv:2405.12142. [Google Scholar]
- Ruchika. 2D BAO vs 3D BAO: Hints for new physics? arXiv 2024, arXiv:2406.05453. [Google Scholar]
- Sanchez, E.; Carnero, A.; Garcia-Bellido, J.; Gaztanaga, E.; de Simoni, F.; Crocce, M.; Cabre, A.; Fosalba, P.; Alonso, D. Tracing The Sound Horizon Scale With Photometric Redshift Surveys. Mon. Not. Roy. Astron. Soc. 2011, 411, 277–288. [Google Scholar] [CrossRef]
- Alcaniz, J.S.; Carvalho, G.C.; Bernui, A.; Carvalho, J.C.; Benetti, M. Measuring baryon acoustic oscillations with angular two-point correlation function. Fundam. Theor. Phys. 2017, 187, 11–19. [Google Scholar] [CrossRef]
- de Carvalho, E.; Bernui, A.; Carvalho, G.C.; Novaes, C.P.; Xavier, H.S. Angular Baryon Acoustic Oscillation measure at z = 2.225 from the SDSS quasar survey. J. Cosmol. Astropart. Phys. 2018, 4, 064. [Google Scholar] [CrossRef]
- Carvalho, G.C.; Bernui, A.; Benetti, M.; Carvalho, J.C.; de Carvalho, E.; Alcaniz, J.S. The transverse baryonic acoustic scale from the SDSS DR11 galaxies. Astropart. Phys. 2020, 119, 102432. [Google Scholar] [CrossRef]
- de Carvalho, E.; Bernui, A.; Avila, F.; Novaes, C.P.; Nogueira-Cavalcante, J.P. BAO angular scale at zeff = 0.11 with the SDSS blue galaxies. Astron. Astrophys. 2021, 649, A20. [Google Scholar] [CrossRef]
- Li, X.; Shafieloo, A. Evidence for Emergent Dark Energy. Astrophys. J. 2020, 902, 58. [Google Scholar] [CrossRef]
- Yang, W.; Di Valentino, E.; Pan, S.; Shafieloo, A.; Li, X. Generalized emergent dark energy model and the Hubble constant tension. Phys. Rev. D 2021, 104, 063521. [Google Scholar] [CrossRef]
- Akarsu, O.; Kumar, S.; Özülker, E.; Vazquez, J.A. Relaxing cosmological tensions with a sign switching cosmological constant. Phys. Rev. D 2021, 104, 123512. [Google Scholar] [CrossRef]
- Akarsu, O.; Kumar, S.; Özülker, E.; Vazquez, J.A.; Yadav, A. Relaxing cosmological tensions with a sign switching cosmological constant: Improved results with Planck, BAO, and Pantheon data. Phys. Rev. D 2023, 108, 023513. [Google Scholar] [CrossRef]
- Akarsu, O.; Di Valentino, E.; Kumar, S.; Nunes, R.C.; Vazquez, J.A.; Yadav, A. ΛsCDM model: A promising scenario for alleviation of cosmological tensions. arXiv 2023, arXiv:2307.10899. [Google Scholar]
- Gomez-Valent, A.; Sola Peracaula, J. Phantom matter: A challenging solution to the cosmological tensions. arXiv 2024, arXiv:2404.18845. [Google Scholar] [CrossRef]
- Hernández-Almada, A.; Mendoza-Martínez, M.L.; García-Aspeitia, M.A.; Motta, V. Phenomenological emergent dark energy in the light of DESI Data Release 1. arXiv 2024, arXiv:2407.09430. [Google Scholar] [CrossRef]
- Li, X.; Shafieloo, A. A Simple Phenomenological Emergent Dark Energy Model can Resolve the Hubble Tension. Astrophys. J. Lett. 2019, 883, L3. [Google Scholar] [CrossRef]
- Hassan, S.F.; Rosen, R.A. Bimetric Gravity from Ghost-free Massive Gravity. J. High Energy Phys. 2012, 2, 126. [Google Scholar] [CrossRef]
- Hassan, S.F.; Schmidt-May, A.; von Strauss, M. On Consistent Theories of Massive Spin-2 Fields Coupled to Gravity. J. High Energy Phys. 2013, 5, 086. [Google Scholar] [CrossRef]
- von Strauss, M.; Schmidt-May, A.; Enander, J.; Mortsell, E.; Hassan, S.F. Cosmological Solutions in Bimetric Gravity and their Observational Tests. J. Cosmol. Astropart. Phys. 2012, 3, 042. [Google Scholar] [CrossRef]
- Sjors, S.; Mortsell, E. Spherically Symmetric Solutions in Massive Gravity and Constraints from Galaxies. J. High Energy Phys. 2013, 2, 080. [Google Scholar] [CrossRef]
- Akrami, Y.; Koivisto, T.S.; Sandstad, M. Accelerated expansion from ghost-free bigravity: A statistical analysis with improved generality. J. High Energy Phys. 2013, 3, 099. [Google Scholar] [CrossRef]
- Enander, J.; Mörtsell, E. Strong lensing constraints on bimetric massive gravity. J. High Energy Phys. 2013, 10, 031. [Google Scholar] [CrossRef]
- Babichev, E.; Crisostomi, M. Restoring general relativity in massive bigravity theory. Phys. Rev. D 2013, 88, 084002. [Google Scholar] [CrossRef]
- Koennig, F.; Patil, A.; Amendola, L. Viable cosmological solutions in massive bimetric gravity. J. Cosmol. Astropart. Phys. 2014, 3, 029. [Google Scholar] [CrossRef]
- Enander, J.; Mortsell, E. On stars, galaxies and black holes in massive bigravity. J. Cosmol. Astropart. Phys. 2015, 11, 023. [Google Scholar] [CrossRef]
- Max, K.; Platscher, M.; Smirnov, J. Gravitational Wave Oscillations in Bigravity. Phys. Rev. Lett. 2017, 119, 111101. [Google Scholar] [CrossRef]
- Dhawan, S.; Goobar, A.; Mörtsell, E.; Amanullah, R.; Feindt, U. Narrowing down the possible explanations of cosmic acceleration with geometric probes. J. Cosmol. Astropart. Phys. 2017, 7, 040. [Google Scholar] [CrossRef]
- Platscher, M.; Smirnov, J.; Meyer, S.; Bartelmann, M. Long Range Effects in Gravity Theories with Vainshtein Screening. J. Cosmol. Astropart. Phys. 2018, 12, 009. [Google Scholar] [CrossRef]
- Lüben, M.; Mörtsell, E.; Schmidt-May, A. Bimetric cosmology is compatible with local tests of gravity. Class. Quant. Grav. 2020, 37, 047001. [Google Scholar] [CrossRef]
- Högås, M.; Torsello, F.; Mörtsell, E. On the stability of bimetric structure formation. J. Cosmol. Astropart. Phys. 2020, 4, 046. [Google Scholar] [CrossRef]
- Lüben, M.; Schmidt-May, A.; Weller, J. Physical parameter space of bimetric theory and SN1a constraints. J. Cosmol. Astropart. Phys. 2020, 9, 024. [Google Scholar] [CrossRef]
- Lindner, M.; Max, K.; Platscher, M.; Rezacek, J. Probing alternative cosmologies through the inverse distance ladder. J. Cosmol. Astropart. Phys. 2020, 10, 040. [Google Scholar] [CrossRef]
- Caravano, A.; Lüben, M.; Weller, J. Combining cosmological and local bounds on bimetric theory. J. Cosmol. Astropart. Phys. 2021, 9, 035. [Google Scholar] [CrossRef]
- Högås, M.; Mörtsell, E. Constraints on bimetric gravity. Part I. Analytical constraints. J. Cosmol. Astropart. Phys. 2021, 5, 001. [Google Scholar] [CrossRef]
- Högås, M.; Mörtsell, E. Constraints on bimetric gravity. Part II. Observational constraints. J. Cosmol. Astropart. Phys. 2021, 5, 002. [Google Scholar] [CrossRef]
- Högås, M.; Mörtsell, E. Constraints on bimetric gravity from Big Bang nucleosynthesis. J. Cosmol. Astropart. Phys. 2021, 11, 001. [Google Scholar] [CrossRef]
- Högås, M. Was Einstein Wrong?: Theoretical and Observational Constraints on Massive Gravity. Ph.D. Thesis, Department of Physics, Faculty of Science, Stockholm University, Stockholm, Sweden, 2022. [Google Scholar]
- Volkov, M.S. Cosmological solutions with massive gravitons in the bigravity theory. J. High Energy Phys. 2012, 1, 035. [Google Scholar] [CrossRef]
- Comelli, D.; Crisostomi, M.; Nesti, F.; Pilo, L. FRW Cosmology in Ghost Free Massive Gravity. J. High Energy Phys. 2012, 3, 067, Erratum in J. High Energy Phys. 2012, 6, 020. [Google Scholar] [CrossRef]
- Volkov, M.S. Hairy black holes in the ghost-free bigravity theory. Phys. Rev. D 2012, 85, 124043. [Google Scholar] [CrossRef]
- Volkov, M.S. Exact self-accelerating cosmologies in the ghost-free massive gravity—The detailed derivation. Phys. Rev. D 2012, 86, 104022. [Google Scholar] [CrossRef]
- Volkov, M.S. Self-accelerating cosmologies and hairy black holes in ghost-free bigravity and massive gravity. Class. Quant. Grav. 2013, 30, 184009. [Google Scholar] [CrossRef]
- Aoki, K.; Mukohyama, S. Massive gravitons as dark matter and gravitational waves. Phys. Rev. D 2016, 94, 024001. [Google Scholar] [CrossRef]
- Babichev, E.; Marzola, L.; Raidal, M.; Schmidt-May, A.; Urban, F.; Veermäe, H.; von Strauss, M. Heavy spin-2 Dark Matter. J. Cosmol. Astropart. Phys. 2016, 9, 016. [Google Scholar] [CrossRef]
- Babichev, E.; Marzola, L.; Raidal, M.; Schmidt-May, A.; Urban, F.; Veermäe, H.; von Strauss, M. Bigravitational origin of dark matter. Phys. Rev. D 2016, 94, 084055. [Google Scholar] [CrossRef]
- Mörtsell, E.; Dhawan, S. Does the Hubble constant tension call for new physics? J. Cosmol. Astropart. Phys. 2018, 9, 025. [Google Scholar] [CrossRef]
- Fierz, M.; Pauli, W. On relativistic wave equations for particles of arbitrary spin in an electromagnetic field. Proc. Roy. Soc. Lond. A 1939, 173, 211–232. [Google Scholar] [CrossRef]
- Boulware, D.G.; Deser, S. Can gravitation have a finite range? Phys. Rev. D 1972, 6, 3368–3382. [Google Scholar] [CrossRef]
- Gabadadze, G. General Relativity With An Auxiliary Dimension. Phys. Lett. B 2009, 681, 89–95. [Google Scholar] [CrossRef]
- de Rham, C. Massive gravity from Dirichlet boundary conditions. Phys. Lett. B 2010, 688, 137–141. [Google Scholar] [CrossRef][Green Version]
- de Rham, C.; Gabadadze, G. Selftuned Massive Spin-2. Phys. Lett. B 2010, 693, 334–338. [Google Scholar] [CrossRef]
- de Rham, C.; Gabadadze, G. Generalization of the Fierz-Pauli Action. Phys. Rev. D 2010, 82, 044020. [Google Scholar] [CrossRef]
- de Rham, C.; Gabadadze, G.; Tolley, A.J. Resummation of Massive Gravity. Phys. Rev. Lett. 2011, 106, 231101. [Google Scholar] [CrossRef]
- Hassan, S.F.; Rosen, R.A. On Non-Linear Actions for Massive Gravity. J. High Energy Phys. 2011, 7, 009. [Google Scholar] [CrossRef]
- Hassan, S.F.; Rosen, R.A. Confirmation of the Secondary Constraint and Absence of Ghost in Massive Gravity and Bimetric Gravity. J. High Energy Phys. 2012, 4, 123. [Google Scholar] [CrossRef]
- Hassan, S.F.; Lundkvist, A. Analysis of constraints and their algebra in bimetric theory. J. High Energy Phys. 2018, 8, 182. [Google Scholar] [CrossRef]
- de Rham, C.; Heisenberg, L.; Ribeiro, R.H. On couplings to matter in massive (bi-)gravity. Class. Quant. Grav. 2015, 32, 035022. [Google Scholar] [CrossRef]
- de Rham, C.; Heisenberg, L.; Ribeiro, R.H. Ghosts and matter couplings in massive gravity, bigravity and multigravity. Phys. Rev. D 2014, 90, 124042. [Google Scholar] [CrossRef]
- Hassan, S.F.; Kocic, M. On the local structure of spacetime in ghost-free bimetric theory and massive gravity. J. High Energy Phys. 2018, 5, 099. [Google Scholar] [CrossRef]
- Higham, N. Functions of Matrices: Theory and Computation; Society for Industrial and Applied Mathematics (SIAM): Philadelphia, PA, USA, 2008. [Google Scholar]
- Horndeski, G.W. Second-order scalar-tensor field equations in a four-dimensional space. Int. J. Theor. Phys. 1974, 10, 363–384. [Google Scholar] [CrossRef]
- Higuchi, A. Forbidden Mass Range for Spin-2 Field Theory in De Sitter Space-time. Nucl. Phys. B 1987, 282, 397–436. [Google Scholar] [CrossRef]
- Fasiello, M.; Tolley, A.J. Cosmological Stability Bound in Massive Gravity and Bigravity. J. Cosmol. Astropart. Phys. 2013, 12, 002. [Google Scholar] [CrossRef]
- De Felice, A.; Gümrükçüoğlu, A.E.; Mukohyama, S.; Tanahashi, N.; Tanaka, T. Viable cosmology in bimetric theory. J. Cosmol. Astropart. Phys. 2014, 6, 037. [Google Scholar] [CrossRef]
- Könnig, F. Higuchi Ghosts and Gradient Instabilities in Bimetric Gravity. Phys. Rev. D 2015, 91, 104019. [Google Scholar] [CrossRef]
- Ozulker, E. Is the dark energy equation of state parameter singular? Phys. Rev. D 2022, 106, 063509. [Google Scholar] [CrossRef]
- Mortsell, E. Cosmological histories in bimetric gravity: A graphical approach. J. Cosmol. Astropart. Phys. 2017, 2, 051. [Google Scholar] [CrossRef]
- Leavitt, H.S.; Pickering, E.C. Periods of 25 Variable Stars in the Small Magellanic Cloud. Harv. Obs. Circ. 1912, 173, 1–3. [Google Scholar]
- Riess, A.G.; Casertano, S.; Yuan, W.; Macri, L.; Bucciarelli, B.; Lattanzi, M.G.; MacKenty, J.W.; Bowers, J.B.; Zheng, W.; Filippenko, A.V.; et al. Milky Way Cepheid Standards for Measuring Cosmic Distances and Application to Gaia DR2: Implications for the Hubble Constant. Astrophys. J. 2018, 861, 126. [Google Scholar] [CrossRef]
- Riess, A.G.; Casertano, S.; Yuan, W.; Bowers, J.B.; Macri, L.; Zinn, J.C.; Scolnic, D. Cosmic Distances Calibrated to 1% Precision with Gaia EDR3 Parallaxes and Hubble Space Telescope Photometry of 75 Milky Way Cepheids Confirm Tension with ΛCDM. Astrophys. J. Lett. 2021, 908, L6. [Google Scholar] [CrossRef]
- Reid, M.J.; Pesce, D.W.; Riess, A.G. An Improved Distance to NGC 4258 and its Implications for the Hubble Constant. Astrophys. J. Lett. 2019, 886, L27. [Google Scholar] [CrossRef]
- Pietrzyński, G.; Graczyk, D.; Gallenne, A.; Gieren, W.; Thompson, I.B.; Pilecki, B.; Karczmarek, P.; Górski, M.; Suchomska, K.; Taormina, M.; et al. A distance to the Large Magellanic Cloud that is precise to one per cent. Nature 2019, 567, 200–203. [Google Scholar] [CrossRef]
- Scolnic, D.; Brout, D.; Carr, A.; Riess, A.G.; Davis, T.M.; Dwomoh, A.; Jones, D.O.; Ali, N.; Charvu, P.; Chen, R.; et al. The Pantheon+ Analysis: The Full Data Set and Light-curve Release. Astrophys. J. 2022, 938, 113. [Google Scholar] [CrossRef]
- Efstathiou, G.; Bond, J.R. Cosmic confusion: Degeneracies among cosmological parameters derived from measurements of microwave background anisotropies. Mon. Not. Roy. Astron. Soc. 1999, 304, 75–97. [Google Scholar] [CrossRef]
- Hu, W.; Sugiyama, N. Small scale cosmological perturbations: An Analytic approach. Astrophys. J. 1996, 471, 542–570. [Google Scholar] [CrossRef]
- Chen, L.; Huang, Q.G.; Wang, K. Distance Priors from Planck Final Release. J. Cosmol. Astropart. Phys. 2019, 2, 028. [Google Scholar] [CrossRef]
- Goliath, M.; Amanullah, R.; Astier, P.; Goobar, A.; Pain, R. Supernovae and the nature of the dark energy. Astron. Astrophys. 2001, 380, 6–18. [Google Scholar] [CrossRef]
- Adame, A.G.; Aguilar, J.; Ahlen, S.; Alam, S.; Alexander, D.M.; Alvarez, M.; Alves, O.; Anand, A.; Andrade, U.; Armengaud, E.; et al. DESI 2024 VI: Cosmological Constraints from the Measurements of Baryon Acoustic Oscillations. arXiv 2024, arXiv:2404.03002. [Google Scholar]
- Foreman-Mackey, D.; Hogg, D.W.; Lang, D.; Goodman, J. emcee: The MCMC Hammer. Publ. Astron. Soc. Pac. 2013, 125, 306. [Google Scholar] [CrossRef]
- Goodman, J.; Weare, J. Ensemble samplers with affine invariance. Commun. Appl. Math. Comput. Sci. 2010, 5, 65–80. [Google Scholar] [CrossRef]
- Akaike, H. A new look at the statistical model identification. IEEE Trans. Autom. Control 1974, 19, 716–723. [Google Scholar] [CrossRef]
- Schwarz, G. Estimating the Dimension of a Model. Ann. Statist. 1978, 6, 461–464. [Google Scholar] [CrossRef]
- Raftery, A.E. Bayesian Model Selection in Social Research. Sociol. Methodol. 1995, 25, 111–163. [Google Scholar] [CrossRef]
- Guerrini, S.; Mörtsell, E. Probing a scale dependent gravitational slip with galaxy strong lensing systems. Phys. Rev. D 2024, 109, 023533. [Google Scholar] [CrossRef]
- Aoki, K.; Maeda, K.I.; Namba, R. Stability of the Early Universe in Bigravity Theory. Phys. Rev. D 2015, 92, 044054. [Google Scholar] [CrossRef]
- Mortsell, E.; Enander, J. Scalar instabilities in bimetric gravity: The Vainshtein mechanism and structure formation. J. Cosmol. Astropart. Phys. 2015, 10, 044. [Google Scholar] [CrossRef]
- Akrami, Y.; Hassan, S.F.; Könnig, F.; Schmidt-May, A.; Solomon, A.R. Bimetric gravity is cosmologically viable. Phys. Lett. B 2015, 748, 37–44. [Google Scholar] [CrossRef]
- Lüben, M.; Schmidt-May, A.; Smirnov, J. Vainshtein Screening in Bimetric Cosmology. Phys. Rev. D 2020, 102, 123529. [Google Scholar] [CrossRef]
- De Felice, A.; Larrouturou, F.; Mukohyama, S.; Oliosi, M. Minimal Theory of Bigravity: Construction and cosmology. J. Cosmol. Astropart. Phys. 2021, 4, 015. [Google Scholar] [CrossRef]
- Gialamas, I.D.; Tamvakis, K. Bimetric-affine quadratic gravity. Phys. Rev. D 2023, 107, 104012. [Google Scholar] [CrossRef]
- Gialamas, I.D.; Tamvakis, K. On the absence of ghosts in quadratic bigravity. J. Cosmol. Astropart. Phys. 2024, 3, 016. [Google Scholar] [CrossRef]
- Gialamas, I.D.; Tamvakis, K. Bimetric Starobinsky model. Phys. Rev. D 2023, 108, 104023. [Google Scholar] [CrossRef]
- Starobinsky, A.A. A New Type of Isotropic Cosmological Models Without Singularity. Phys. Lett. B 1980, 91, 99–102. [Google Scholar] [CrossRef]

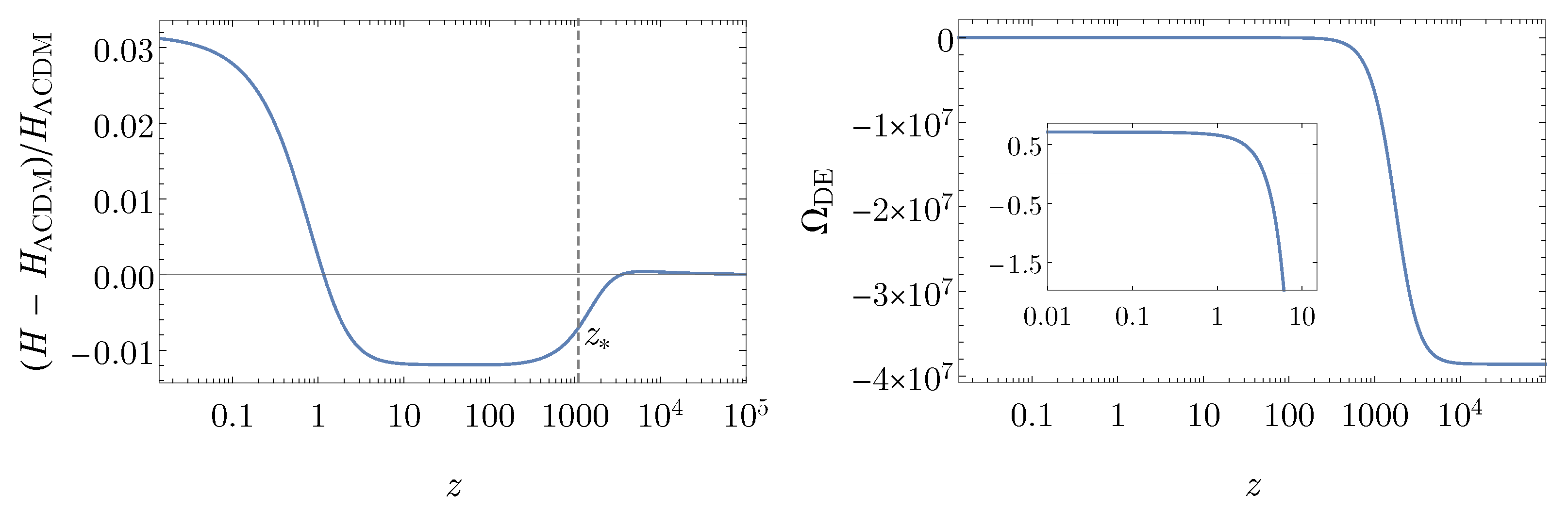
| Planck | ||||
|---|---|---|---|---|
| z | 0.11 | 0.236 | 0.365 | 0.45 | 0.47 | 0.49 | 0.51 | 0.53 |
|---|---|---|---|---|---|---|---|---|
| [deg] | 19.8 | 9.06 | 6.33 | 4.77 | 5.02 | 4.99 | 4.81 | 4.29 |
| [deg] | 3.26 | 0.23 | 0.22 | 0.17 | 0.25 | 0.21 | 0.17 | 0.30 |
| z | 0.55 | 0.57 | 0.59 | 0.61 | 0.63 | 0.65 | 2.225 | |
| [deg] | 4.25 | 4.59 | 4.39 | 3.85 | 3.90 | 3.55 | 1.77 | |
| [deg] | 0.25 | 0.36 | 0.33 | 0.31 | 0.43 | 0.16 | 0.31 |
| Model Parameter: | |||||
|---|---|---|---|---|---|
| Prior: |
| Model | CMB + SN + | (rad) | AIC | BIC | ||
|---|---|---|---|---|---|---|
| CDM | BAOtr | 68.9 ± 0.5 | 0 | 0.700 ± 0.006 | 0 | 0 |
| Bimetric | BAOtr | 71.0 ± 0.9 | 0.16 ± 0.03 | 0.724 ± 0.010 | 1.1 | |
| CDM | BAOtr + SH0ES | 69.7 ± 0.5 | 0 | 0.709 ± 0.006 | 0 | 0 |
| Bimetric | BAOtr + SH0ES | 71.9 ± 0.7 | 0.18 ± 0.02 | 0.732 ± 0.007 | 13.2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dwivedi, S.; Högås, M. 2D BAO vs. 3D BAO: Solving the Hubble Tension with Bimetric Cosmology. Universe 2024, 10, 406. https://doi.org/10.3390/universe10110406
Dwivedi S, Högås M. 2D BAO vs. 3D BAO: Solving the Hubble Tension with Bimetric Cosmology. Universe. 2024; 10(11):406. https://doi.org/10.3390/universe10110406
Chicago/Turabian StyleDwivedi, Sowmaydeep, and Marcus Högås. 2024. "2D BAO vs. 3D BAO: Solving the Hubble Tension with Bimetric Cosmology" Universe 10, no. 11: 406. https://doi.org/10.3390/universe10110406
APA StyleDwivedi, S., & Högås, M. (2024). 2D BAO vs. 3D BAO: Solving the Hubble Tension with Bimetric Cosmology. Universe, 10(11), 406. https://doi.org/10.3390/universe10110406








