A Hubble Constant Determination Through Quasar Time Delays and Type Ia Supernovae
Abstract
:1. Introduction
2. Materials and Methods
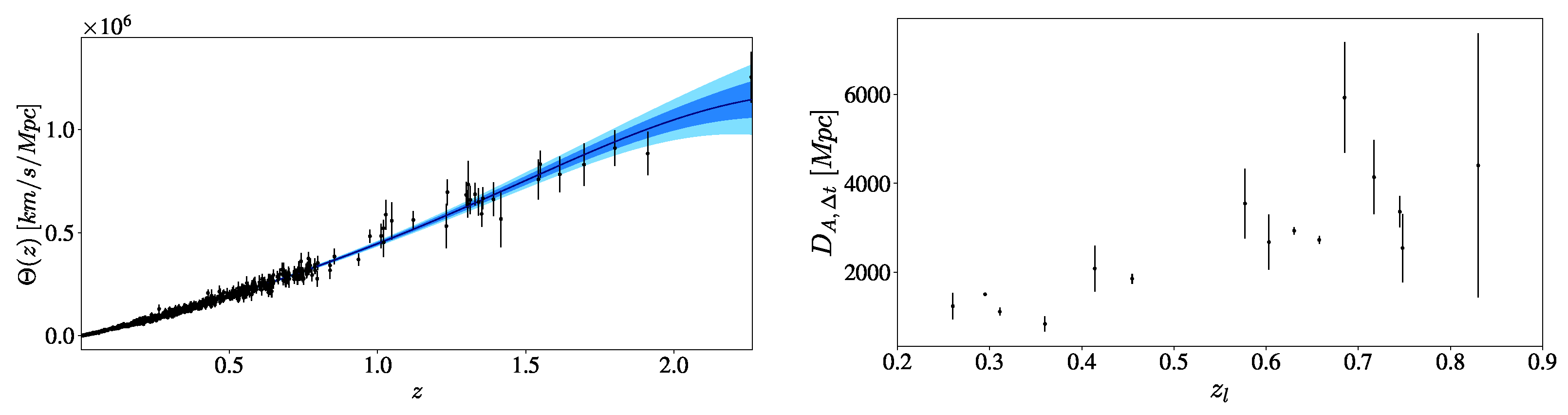
2.1. Time-Delay Angular Diameter Distance-
2.2. The Unanchored Luminosity Distances-
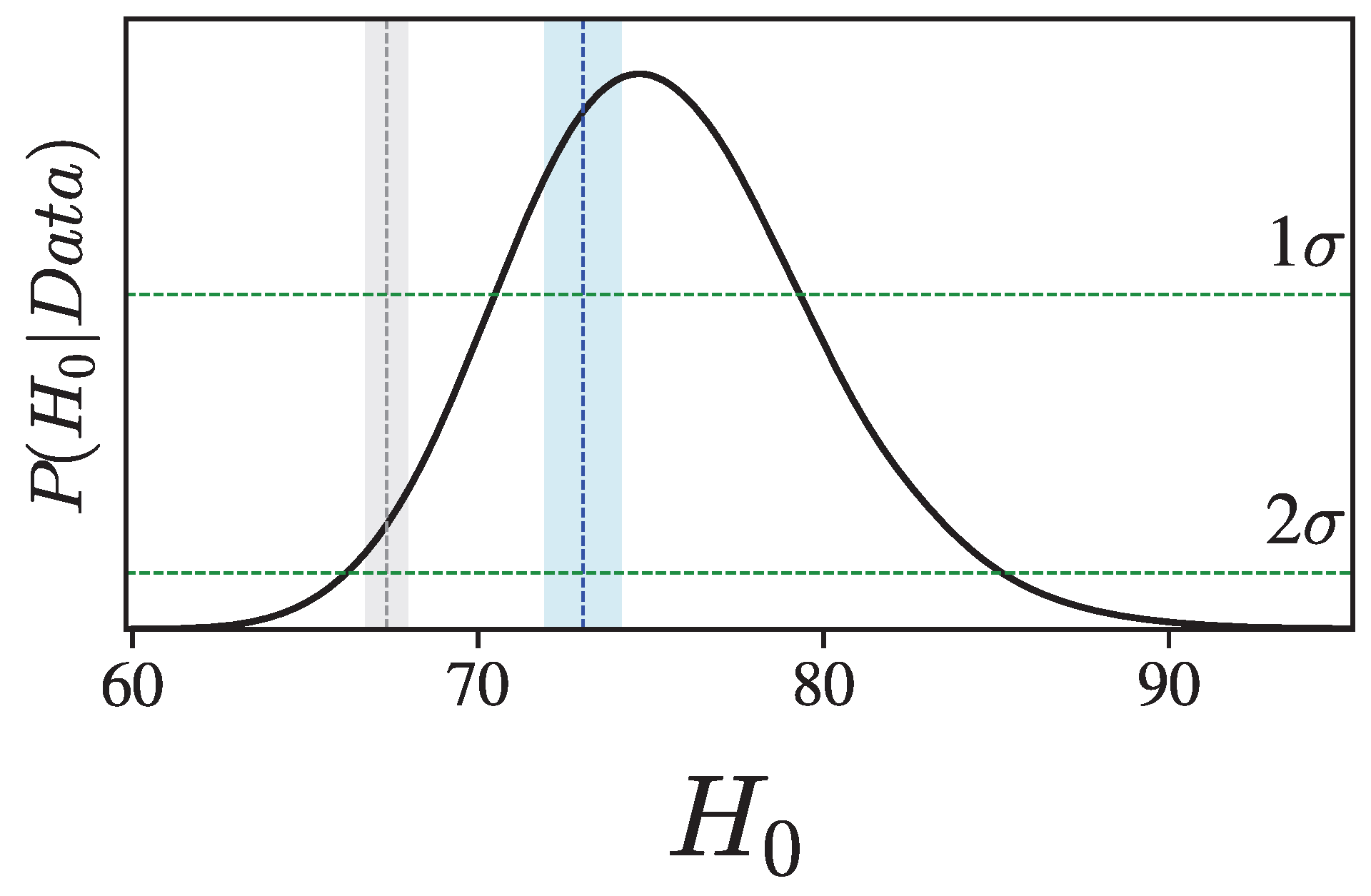
3. Results
4. Conclusions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
| 1 | This effect is relatively small. |
| 2 | Available online http://www.h0licow.org accessed on 1 December 2024. |
| 3 | |
| 4 | Such a sample has a significant increase compared with the original Pantheon sample, particularly at lower redshifts, and the full data releases are publicly available online https://pantheonplussh0es.github.io/, accessed on 1 January 2025. |
| 5 | If it is known that the covariance matrix is not diagonal, but we decide to set the off-diagonal elements to zero, it will provide the fitter inaccurate uncertainty estimates. It could alter the conclusions drawn from the fit. Ignoring correlations may lead to underestimating the analysis’s precision or affect the best-fit parameters’ central values. |
| 6 | Available online https://github.com/carlosandrepaes/GaPP, accessed on 1 December 2024. |
| 7 | The uncertainties are not correlated. |
References
- Perlmutter, S.; Aldering, G.; Goldhaber, G.; Knop, R.A.; Nugent, P.; Castro, P.G.; Deustua, S.; Fabbro, S.; Goobar, A.; Groom, D.E.; et al. Measurements of Ω and Λ from 42 High-Redshift Supernovae. Astrophys. J. 1999, 517, 565–586. [Google Scholar] [CrossRef]
- Riess, A.G.; Filippenko, A.V.; Challis, P.; Clocchiattia, A.; Diercks, A.; Garnavich, P.M.; Gilliland, R.L.; Hogan, C.J.; Jha, S.; Kirshner, R.P.; et al. Observational Evidence from Supernovae for an Accelerating Universe and a Cosmological Constant. Astron. J. 1998, 116, 1009–1038. [Google Scholar] [CrossRef]
- Riess, A.G.; Filippenko, A.V.; Challis, P.; Clocchiattia, A.; Diercks, A.; Garnavich, P.M.; Gilliland, R.L.; Hogan, C.J.; Jha, S.; Kirshner, R.P.; et al. A 2.4% Determination of the Local Value of the Hubble Constant. Astrophys. J. 2016, 826, 56. [Google Scholar] [CrossRef]
- Riess, A.G.; Yuan, W.; Macri, L.M.; Scolnic, D.; Brout, D.; Casertano, S.; Jones, D.O.; Murakami, Y.; Brueval, L.; Brink, T.G.; et al. A Comprehensive Measurement of the Local Value of the Hubble Constant with 1 km s−1 Mpc−1 Uncertainty from the Hubble Space Telescope and the SH0ES Team. Astrophys. J. Lett. 2022, 934, L7. [Google Scholar] [CrossRef]
- Reid, M.J.; Pesce, D.W.; Riess, A.G. An Improved Distance to NGC 4258 and Its Im-plications for the Hubble Constant. Astrophys. J. Lett. 2019, 886, L27. [Google Scholar] [CrossRef]
- Freedman, W.L. Measurements of the Hubble Constant: Tensions in Perspective. Astrophys. J. 2021, 919, 16. [Google Scholar] [CrossRef]
- Scolnic, D.; Riess, A.G.; Wu, J.; Li, S.; Anand, G.S.; Beaton, R.; Casertano, S.; Anderson, R.; Dhawan, S.; Ke, X. CATS: The Hubble Constant from Standardized TRGB and Type Ia Su-pernova Measurements. Astrophys. J. Lett. 2023, 954, L31. [Google Scholar] [CrossRef]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Abraham, S.; Acernese, F.; Ackley, K.; Adams, C.; Adhikari, R.X.; Adya, V.B.; Affeldt, C.; et al. A Gravitational-wave Measurement of the Hubble Constant Following the Second Observing Run of Advanced LIGO and Virgo. Astro-Phys. J. 2021, 909, 218. [Google Scholar] [CrossRef]
- Pogosian, L.; Zhao, G.-B.; Jedamzik, K. Recombination-independent Determina-tion of the Sound Horizon and the Hubble Constant from BAO. Astrophys. J. Lett. 2020, 904, L17. [Google Scholar] [CrossRef]
- eBOSS Collaboration; Alam, S.; Aubert, M.; Avila, S.; Balland, C.; Bautista, J.E.; Bershady, M.A.; Bizyaev, D.; Blanton, M.R.; Bolton, A.S.; et al. Completed SDSS-IV extended Baryon Oscillation Spectroscopic Survey: Cosmological implications from two decades of spectroscopic surveys at the Apache Point Observatory. Phys. Rev. D 2021, 103, 083533. [Google Scholar]
- Planck Collaboration; Aghanim, N.; Akrami, Y.; Ashdown, M.; Aumont, J.; Bac-cigalupi, C.; Ballardini, M.; Banday, A.J.; Barreiro, R.B.; Bartolo, N.; et al. Planck 2018 results. VI. Cosmological parameters. Astron. Astrophys. 2020, 641, A6. [Google Scholar]
- Perivolaropoulos, Leandros. Hubble tension or distance ladder crisis? Phys. Rev. D 2024, 110, 123518. [Google Scholar] [CrossRef]
- Abdalla, E.; Abellan, G.F.; Aboubrahim, A.; Agnello, A.; Akarsu, O.; Akrami, Y.; Alestas, G.; Aloni, D.; Amendola, L.; Anchordoqui, L.A.; et al. Cosmology intertwined: A review of the particle physics, astrophysics, and cosmology associated with the cosmological tensions and anomalies. J. High Energy Astrophys. 2022, 34, 49–211. [Google Scholar]
- Di Valentino, E.; Mena, O.; Pan, S.; Visinelli, L.; Yang, W.; Melchiorri, A.; Mota, D.F.; Riess, A.G.; Silk, J. In the realm of the Hubble tension—A review of solutions. Class. Quantum Gravity 2021, 38, 153001. [Google Scholar] [CrossRef]
- Hu, J.-P.; Wang, F.-Y. Hubble Tension: The Evidence of New Physics. Universe 2023, 9, 94. [Google Scholar] [CrossRef]
- McGaugh, S.S. Discord in Concordance Cosmology and Anomalously Massive Early Galaxies. Universe 2024, 10, 48. [Google Scholar] [CrossRef]
- Krishnan, C.; Mohayaee, R.; Colgáin, E.Ó.; Sheikh-Jabbari, M.M.; Yin, L. Does Hubble tension signal a breakdown in FLRW cosmology? Class. Quantum Gravity 2021, 38, 184001. [Google Scholar] [CrossRef]
- Beenakker, W.; Venhoek, D. A structured analysis of Hubble tension. arXiv 2021, arXiv:2101.01372. [Google Scholar]
- Benisty, D.; Mifsud, J.; Levi Said, J.; Staicova, D. On the robustness of the constancy of the Supernova absolute magnitude: Non-parametric reconstruction & Bayesian approaches. Phys. Dark Universe 2023, 39, 101160. [Google Scholar]
- Alestas, G.; Camarena, D.; Di Valentino, E.; Kazantzidis, L.; Marra, V.; Nesseris, S.; Perivolaropoulos, L. Late-transition versus smooth H(z)-deformation models for the resolution of the Hubble crisis. Phys. Rev. D 2022, 105, 063538. [Google Scholar] [CrossRef]
- Perivolaropoulos, L.; Skara, F. Hubble tension or a transition of the Cepheid SnIa calibrator parameters? Phys. Rev. D 2021, 104, 123511. [Google Scholar] [CrossRef]
- Mortsell, E.; Goobar, A.; Johansson, J.; Dhawan, S. Sensitivity of the Hubble Constant Determination to Cepheid Calibration. Astrophys. J. 2022, 933, 212. [Google Scholar] [CrossRef]
- Refsdal, S. On the possibility of determining Hubble’s parameter and the masses of galaxies from the gravitational lens effect. Mon. Not. R. Astron. Soc. 1964, 128, 307. [Google Scholar] [CrossRef]
- Birrer, S.; Millon, M.; Sluse, D.; Shajib, J.; Courbin, F.; Koopmans, L.V.E.; Suyu, S.H.; Treu, T. Time-Delay Cosmography: Measuring the Hubble Constant and Other Cosmological Param-eters with Strong Gravitational Lensing. Space Sci. Rev. 2024, 220, 48. [Google Scholar] [CrossRef] [PubMed]
- Saha, P.; Sluse, D.; Wagner, J.; Williams, L.L.R. Essentials of Strong Gravitational Lensing. Space Sci. Rev. 2024, 220, 12. [Google Scholar] [CrossRef]
- Treu, T.; Agnello, A.; Baumer, M.A.; Birrer, S.; Buckley-Geer, E.J.; Courbin, F.; Kim, Y.J.; Lim, H.; Marshall, P.J.; Nord, B.; et al. The STRong lensing Insights into the Dark Energy Survey (STRIDES) 2016 follow-up campaign-I. Overview and classification of candidates selected by two techniques. Mon. Not. R. Astron. Soc. 2018, 481, 1041–1054. [Google Scholar] [CrossRef]
- Lemon, C.; Anguita, T.; Auger-Williams, M.W.; Courbin, F.; Galan, A.; McMahon, R.; Neira, F.; Oguri, M.; Schechter, P.; Shajib, A.; et al. Gravitationally lensed quasars in Gaia-IV. 150 new lenses, quasar pairs, and projected quasars. Mon. Not. R. Astron. Soc. 2023, 520, 3305–3328. [Google Scholar] [CrossRef]
- Rodney, S.A.; Brammer, G.B.; Pierel, J.D.R.; Richard, J.; Toft, S.; O’Connor, K.F.; Akhshik, M.; Whitaker, K.E. A gravitationally lensed supernova with an observable two-decade time delay. Nat. Astron. 2021, 5, 1118–1125. [Google Scholar] [CrossRef]
- Millon, M.; Courbin, F.; Bonvin, V.; Buckley-Geer, E.; Fassnacht, C.D.; Frie-man, J.; Marshal, P.J.; Suyu, S.H.; Treu, T.; Anguita, T.; et al. TDCOSMO-II. Six new time delays in lensed quasars from high-cadence monitoring at the MPIA 2.2 m telescope. Astron. Astrophys. 2020, 642, A193. [Google Scholar] [CrossRef]
- Courbin, F.; Bonvin, V.; Buckley-Geer, E.; Fassnacht, C.D.; Frieman, J.; Lin, H.; Marshall, P.J.; Suyu, S.H.; Treu, T.; Anguita, T.; et al. COSMOGRAIL XVI: Time delays for the quadruply imaged quasar DES J0408-5354 with high-cadence photometric monitoring. Astron. Astrophys. 2018, 609, A71. [Google Scholar] [CrossRef]
- Wong, K.C.; Suyu, S.H.; Chen, G.C.-F.; Rusu, C.E.; Millon, M.; Sluse, D.; Bonvin, V.; Fassnacht, C.D.; Taubenberger, S.; Auger, M.W.; et al. H0LiCOW–XIII. A 2.4 per cent measurement of H0 from lensed quasars: 5.3σ tension between early- and late-Universe probes. Mon. Not. R. Astron. Soc. 2019, 498, 1420–1439. [Google Scholar] [CrossRef]
- Millon, M.; Galan, A.; Courbin, F.; Treu, T.; Suyu, S.H.; Birrer, S.; Chen, G.C.-F.; Shajib, A.J.; Sluse, D.; Wong, K.C.; et al. TDCOSMO. I. An exploration of systematic uncertainties in the inference of H0 from time-delay cosmography. Astron. Astrophys. 2020, 639, A101. [Google Scholar] [CrossRef]
- Birrer, S.; Shajib, A.J.; Galan, A.; Millom, M.; Treu, T.; Agnello, A.; Auger, M.; Chen, G.C.-F.; Christensen, L.; Collett, T.; et al. TDCOSMO-IV. Hierarchical time-delay cosmography–joint inference of the Hubble constant and galaxy density profiles. Astron. Astrophys. 2020, 643, A165. [Google Scholar] [CrossRef]
- Aubourg, É.; Bailey, S.; Bautista, J.E.; Beutler, F.; Bhardwaj, V.; Bizyaev, D.; Blanton, M.; Blomqvist, M.; Bolton, A.S.; Bovy, J.; et al. Cosmological implications of baryon acoustic oscillation measurements. Phys. Rev. D 2015, 92, 123516. [Google Scholar] [CrossRef]
- Cuesta, A.J.; Verde, L.; Riess, A.; Jimenez, R. Calibrating the cosmic distance scale ladder: The role of the sound-horizon scale and the local expansion rate as distance anchors. Mon. Not. R. Astron. Soc. 2015, 448, 3463–3471. [Google Scholar] [CrossRef]
- Liao, K.; Shafieloo, A.; Keeley, R.E.; Linder, E.V. Determining Mod-el-independent H 0 and Consistency Tests. Astrophys. J. Lett. 2020, 895, L29. [Google Scholar] [CrossRef]
- Liao, K.; Shafieloo, A.; Keeley, R.E.; Linder, E.V. A model-independent deter-mination of the Hubble constant from lensed quasars and supernovae using Gaussian process regression. Astrophys. J. Lett. 2019, 886, L23. [Google Scholar] [CrossRef]
- Li, X.; Liao, K. Determining Cosmological-model-independent H0 with Gravitationally Lensed Supernova Refsdal. Astrophys. J. 2024, 966, 121. [Google Scholar] [CrossRef]
- Li, X.; Keeley, R.E.; Shafieloo, A.; Liao, K. A Model-independent Method to De-termine H0 Using Time-delay Lensing, Quasars, and Type Ia Supernovae. Astrophys. J. 2024, 960, 103. [Google Scholar] [CrossRef]
- Gong, X.; Liu, T.; Wang, J. Inverse distance ladder method for determining H0 from angular diameter distances of time-delay lenses and supernova observations. Eu-Ropean Phys. J. C 2024, 84, 873. [Google Scholar] [CrossRef]
- Colaço, L.R.; Ferreira, M.; Holanda, R.F.L.; Gonzalez, J.E.; Nunes, R.C. A Hubble constant estimate from galaxy cluster and type Ia SNe observations. J. Cosmol. Astropart. Phys. 2024, 5, 098. [Google Scholar] [CrossRef]
- Gonzalez, J.E.; Ferreira, M.; Colaço, L.R.; Holanda, R.F.L. Unveiling the Hubble constant through galaxy cluster gas mass fractions. Phys. Lett. B 2024, 857, 138982. [Google Scholar] [CrossRef]
- Camarena, D.; Marra, V. A new method to build the (inverse) distance ladder. Mon. Not. R. Astron. Soc. 2020, 495, 2630–2644. [Google Scholar] [CrossRef]
- Scolnic, D.; Brout, D.; Carr, A.; Riess, A.G.; Davis, T.M.; Dwomoh, A.; Jones, D.O.; Ali, N.; Charvu, P.; Chen, R.; et al. The Pantheon+ Analysis: The Full Data Set and Light-curve Release. Astrophys. J. 2022, 938, 113. [Google Scholar] [CrossRef]
- Balmès, I.; Corasaniti, P.S. Bayesian approach to gravitational lens model selection: Constraining H0 with a selected sample of strong lenses. Mon. Not. R. Astron. Soc. 2013, 431, 1528–1540. [Google Scholar] [CrossRef]
- Wang, M.; Fu, X.; Xu, B.; Huang, Y.; Yang, Y.; Lu, Z. Testing the cosmic dis-tance duality relation with Type Ia supernova and transverse BAO measurements. Eur. Phys. J. C 2024, 84, 7. [Google Scholar] [CrossRef]
- Favale, A.; Gómez-Valent, A.; Migliaccio, M. 2D vs. 3D BAO: Quantification of their tension and test of the Etherington relation. Phys. Lett. B 2024, 858, 139027. [Google Scholar] [CrossRef]
- Kumar, D.; Rana, A.; Jain, D.; Mahajan, S.; Mukherjee, A.; Holanda, R.F.L. A non-parametric test of variability of Type Ia supernovae luminosity and CDDR. J. Cos-Mology Astropart. Phys. 2022, 1, 1. [Google Scholar] [CrossRef]
- Lima, F.S.; Holanda, R.F.L.; Pereira, S.H.; da Silva, W.J.C. On the cosmic distance duality relation and strong gravitational lens power-law density profile. J. Cosmol. Astropart. Phys. 2021, 8, 035. [Google Scholar] [CrossRef]
- Li, P. Distance Duality Test: The Evolution of Radio Sources Mimics a Non-expanding Universe. Astrophys. J. Lett. 2023, 950, L14. [Google Scholar] [CrossRef]
- Jesus, J.F.; Gomes, M.J.S.; Holanda, R.F.L.; Nunes, R.C. High-redshift cosmography with a possible cosmic distance duality relation violation. J. Cosmol. Astropart. Phys. 2025, 1, 88. [Google Scholar] [CrossRef]
- Ellis, G.F.R. On the definition of distance in general relativity: I. M. H. Etherington (Philosophical Magazine ser. 7, vol. 15, 761 (1933)). Gen. Relativ. Gravit. 2007, 39, 7. [Google Scholar] [CrossRef]
- Etherington, I.M.H. On the definition of distance in general relativity. Phil. Mag. Ser. 1933, 15, 761. [Google Scholar] [CrossRef]
- Renzi, F.; Silvestri, A. Hubble speed from first principles. Phys. Rev. D 2023, 107, 2. [Google Scholar] [CrossRef]
- Kochanek, C.S. Overconstrained gravitational lens models and the Hubble constant. Mon. Not. R. Astron. Soc. 2020, 493, 2. [Google Scholar] [CrossRef]
- Pandey, S.; Raveri, M.; Jain, B. Model independent comparison of supernova and strong lensing cosmography: Implications for the Hubble constant tension. Phys. Rev. D 2020, 102, 2. [Google Scholar] [CrossRef]
- Shapiro, I.I. Fourth Test of General Relativity. Phys. Rev. Lett. 1964, 13, 26. [Google Scholar] [CrossRef]
- Treu, T. Strong Lensing by Galaxies. Annu. Rev. Astron-Omy Astrophys. 2010, 48, 87–125. [Google Scholar] [CrossRef]
- Martel, H.; Premadi, P.; Matzner, R. Light Propagation in Inhomogeneous Universes. III. Distributions of Image Separations. Astrophys. J. 2002, 570, 17. [Google Scholar] [CrossRef]
- Christlein, D. The Dependence of the Galaxy Luminosity Function on Enviroment. Astrophys. J. 2000, 545, 145. [Google Scholar] [CrossRef]
- Keeton, C.R.; Christlein, D.; Zabludoff, A.I. What Fraction of Gravitational Lens Galaxies Lie in Groups? Astrophys. J. 2000, 545, 129. [Google Scholar] [CrossRef]
- Cao, S.; Pan, Y.; Biesiada, M.; Godlowski, W.; Zhu, Z.-H. Constraints on cosmological models from strong gravitational lensing systems. J. Cosmol. Astro-Part. Phys. 2012, 2012, 3. [Google Scholar] [CrossRef]
- Kelly, P.L.; Rodney, S.; Treu, T.; Oguri, M.; Chen, W.; Zitrin, A.; Birrer, S.; Bonvin, V.; Dessart, L.; Diego, J.M.; et al. Constraints on the Hubble constant from supernova Refsdal’s reappearance. Science 2023, 380, abh1322. [Google Scholar] [CrossRef] [PubMed]
- Riess, A.G.; Strolger, L.-G.; Casertano, S.; Ferguson, H.C.; Mobasher, B.; Gold, B.; Challis, P.J.; Filippenko, A.V.; Jha, S.; Li, W.; et al. New Hubble Space Telescope Discoveries of Type Ia Supernovae at z>=1: Narrowing Constraints on the Early Behavior of Dark Energy. Astrophys. J. 2007, 659, 98–121. [Google Scholar] [CrossRef]
- Betoule, M.; Kessler, R.; Guy, J.; Mosher, J.; Hardin, D.; Biswas, R.; Astier, P.; El-Hage, P.; Koing, M.; Kuhlmann, S.; et al. Improved cosmological constraints from a joint analysis of the SDSS-II and SNLS supernova samples. Astron. Astrophys. 2014, 568, A22. [Google Scholar] [CrossRef]
- Seikel, M.; Clarkson, C.; Smith, M. Reconstruction of dark energy and expan-sion dynamics using Gaussian processes. J. Cosmol. Astropart. Phys. 2012, 2012, 036. [Google Scholar] [CrossRef]
- Seikel, M.; Clarkson, C. Optimising Gaussian processes for reconstructing dark energy dynamics from supernovae. arXiv 2013, arXiv:1311.6678. [Google Scholar]
- Shafieloo, A.; Kim, A.G.; Linder, E.V. Gaussian process cosmography. Phys. Rev. D 2012, 85, 123530. [Google Scholar] [CrossRef]
- Jesus, J.F.; Valentim, R.; Escobal, A.A.; Pereira, S.H. Gaussian Process Estima-tion of Transition Redshift. J. Cosmol. Astropart. Phys. 2020, 4, 053. [Google Scholar] [CrossRef]
- Yang, T.; Guo, Z.-K.; Cai, R.-G. Reconstructing the interaction between dark en-ergy and dark matter using Gaussian Processes. Phys. Rev. D 2015, 91, 123533. [Google Scholar] [CrossRef]
- Li, X.; Keeley, R.E.; Shafieloo, A.; Zheng, X.; Cao, S.; Biesiada, M.; Zhu, Z.-H. Hubble diagram at higher redshifts: Model independent calibration of quasars. Mon. Not. R. Astron. Soc. 2021, 507, 919–926. [Google Scholar] [CrossRef]
- Jesus, J.F.; Valentim, R.; Escobal, A.A.; Pereira, S.H.; Benndorf, D. Gaussian processes reconstruction of the dark energy potential. J. Cosmol. Astropart. Phys. 2022, 11, 037. [Google Scholar] [CrossRef]
- Foreman-Mackey, D.; Hogg, D.W.; Lang, D.; Goodman, J. emcee: The MCMC Hammer. Publ. Astron. Soc. Pac. 2013, 125, 306. [Google Scholar] [CrossRef]
- Lewis, A. GetDist: A Python package for analysing Monte Carlo samples. arXiv 2019, arXiv:1910.13970. [Google Scholar]
- Treu, T.; Suyu, S.H.; Marshall, P.J. Strong lensing time-delay cosmography in the 2020s. Astron. Astrophys. Rev. 2022, 30, 8. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Colaço, L.R. A Hubble Constant Determination Through Quasar Time Delays and Type Ia Supernovae. Universe 2025, 11, 89. https://doi.org/10.3390/universe11030089
Colaço LR. A Hubble Constant Determination Through Quasar Time Delays and Type Ia Supernovae. Universe. 2025; 11(3):89. https://doi.org/10.3390/universe11030089
Chicago/Turabian StyleColaço, Leonardo R. 2025. "A Hubble Constant Determination Through Quasar Time Delays and Type Ia Supernovae" Universe 11, no. 3: 89. https://doi.org/10.3390/universe11030089
APA StyleColaço, L. R. (2025). A Hubble Constant Determination Through Quasar Time Delays and Type Ia Supernovae. Universe, 11(3), 89. https://doi.org/10.3390/universe11030089







