Abstract
Primordial black holes (PBHs) may have formed through the gravitational collapse of cosmological perturbations that were generated and stretched during the inflationary era, later entering the cosmological horizon during the decelerating phase, if their amplitudes were sufficiently large. In this review paper, we will briefly introduce the basic concept of PBHs and review the formation dynamics through this mechanism, the estimation of the initial spins of PBHs and the time evolution of type II fluctuations, with a focus on the radiation-dominated and (early) matter-dominated phases.
1. Introduction
Black holes may have formed in the early Universe. This possibility was first considered by Zel’dovich and Novikov (1966) [1] and Hawking (1971) [2]. These black holes have been termed primordial black holes (PBHs). The observational relevance of PBHs to cosmology has been established by the subsequent work of Carr and Hawking (1974) [3] and Carr (1975) [4]. See Refs. [5,6] for the recent brief reviews of the history and the future of PBHs.
Although our Universe can be well approximated by a homogeneous and isotropic cosmological model—the Friedmann–Lemaître–Robertson–Walker (FLRW) solution—on large scales, cosmological structures such as galaxy clusters, galaxies, planetary systems, and stars must still form. These structures arise from primordial fluctuations. Observations of anisotropies in the cosmic microwave background (CMB) radiation have revealed that the amplitude of these primordial fluctuations is generally very small. One of the most promising mechanisms to generate such fluctuations is inflation. In this scenario, quantum fluctuations provide the origin of the perturbations, strongly suggesting that the probability of generating large-amplitude perturbations would be small but finite. During inflation, these perturbations expand along with the inflationary expansion of the Universe. After inflation, when the Universe is reheated, sufficiently large-amplitude perturbations could eventually overcome cosmic expansion and collapse into black holes due to their self-gravity. Unlike the formation of typical astrophysical black holes, the formation of PBHs does not require stellar evolution.
The formation of PBHs through primordial fluctuations was initially proposed by Hawking (1971) [2] and Carr and Hawking (1974) [3] and further developed by Carr (1975) [4]. This formation mechanism has since been confirmed through numerical simulations based on numerical relativity, pioneered by Nadezhin, Novikov and Polnarev (1978) [7]. In this review paper, we will explore the recent developments in PBH formation studies and their implications for cosmology.
The motivation for PBH research is multi-faceted. Since PBHs can, in principle, be observed, they provide valuable information about the early Universe. In this sense, PBHs can be regarded as the fossils of the early Universe. Furthermore, they are also one of the most promising candidates for dark matter. Moreover, Hawking evaporation plays an important role in the study of PBHs. Hawking recognised PBHs as a unique laboratory for studying black hole evaporation when he discovered this phenomenon in 1974 [8,9]. Hawking evaporation is key to understanding quantum gravity, where the information loss problem has been extensively discussed. The details of this evaporation may depend on quantum gravity and high-energy physics. Recently, several gravitational wave observatories have become available as observational tools to study strongly gravitating but otherwise dark objects, following LIGO’s first direct detection of gravitational waves in 2015 [10]. It has been realized that gravitational waves provide a unique means of probing PBHs [11]. This suggests that PBHs lie at the intersection of various growing fields of modern physics, such as cosmology, general relativity, gravitational waves, quantum gravity and high-energy physics.
As observational data accumulate, gravitational waves are becoming an increasingly important means of observing our Universe. More than 100 events have been observed by the LIGO–Virgo–KAGRA (LVK) collaboration, and many of these have been identified as binary black holes. Several groups proposed the possibility that these binary black holes may be of cosmological origin, as many of them are approximately , which is more massive than was typically expected based on the standard theory of stellar evolution [12,13,14]. As more observational data accumulate, information about not only the masses but also the spins of binary black holes is obtained for some events [15], which may provide a new clue to the origin of these binary black holes. From the obtained mass function of binary black holes, a search for the population of PBHs was carried out [16]. It has also been argued that the existence of subsolar candidates in LIGO data would be a smoking gun for PBHs because no astrophysical scenario has yet been established to form subsolar-mass black holes [17]. Most recently, the NANOGrav collaboration reported evidence for nanohertz gravitational waves [18], which might be consistent with gravitational waves induced by scalar perturbations that could have produced the amount of PBHs responsible for the binary black holes observed by the LVK collaboration (e.g., [19]). The recent observations with the James Web Space Telescope have identified several very massive galaxies at high redshifts, which might indicate a tension with predictions in the standard CDM model but can be explained if we include PBH clusters in the formation scenario [20,21,22].
I would also comment on the possibility of PBHs constituting all or a considerable fraction of dark matter. We usually discuss this in terms of the fraction of PBHs to cold dark matter (CDM), , as a function of the mass of PBHs, M. This fraction is observationally constrained in some mass ranges but not in others. See Figure 10 of Carr, Kohri, Sendouda and Yokoyama (2021) [23] for an overview of the constraints. Recent observational constraints indicate two intriguing windows for dark matter. One is g, where is virtually unconstrained. This implies that PBHs could account for all the CDM for this mass range. The other mass range is , where , which is of interest in the context of terrestrial gravitational wave observations. Although there is currently a mass window in which all the CDM might be explained by PBHs, a stricter constraint could be placed on this mass window in the near future. Even if this turns out to be the case, it does not imply that studies of PBHs are without value. In this context, I would like to quote a profound statement by Bernard Carr: “Indeed their study may place interesting constraints on the physics relevant to these areas even if they never formed” [24].
The aim of this article is to briefly review the theoretical studies of PBH formation from primordial fluctuations, the recent estimation of the spins of PBHs and the formation of PBHs generated from the so-called type II configurations. In Section 2, we present the basic concept of PBHs. We discuss their masses, Hawking evaporation, the fraction of their contribution to the whole dark matter and the formation probability. In Section 3, we discuss the formation of PBHs. We focus on the formation mechanism from fluctuations generated by inflation and present the key ideas of this scenario. In Section 4, we discuss the spins of PBHs. The spins of PBHs have often been regarded just as negligible until recently. We quantitatively discuss the spins of PBHs formed not only in a radiation-dominated era but also in an (early) matter-dominated era. In Section 5 we discuss the initial configurations featured with their spatial geometry with throat structure, which is called type II, and the formation of PBHs from them based on the results of the recently conducted numerical simulations. In Section 6, we conclude the paper.
2. Basic Concept of Primordial Black Holes
2.1. Mass
The striking feature of PBHs is that they can have a large range of possible mass scales from g to g depending on the formation scenarios, at least in principle. Although the mass of the PBH may depend on the scenario, we usually assume that it can be approximately given by the mass enclosed within the cosmological horizon or Hubble horizon at the formation time from the big bang as
where c and G are the speed of light and the gravitational constant, respectively, for which the gravitational radius is given by
So, we can say “the smaller, the older”. Table 1 shows the relation between the formation time and the initial PBH mass. Nevertheless, we should keep a caveat in mind that the mass of PBHs could be much smaller than the horizon mass in certain formation scenarios.

Table 1.
The cosmological time from Big Bang and the initial mass of PBHs if they are formed then.
The mass of PBHs may have changed in time after they formed. As for the mass accretion, earlier works suggest that it does not so significantly affect the mass, at least in radiation domination [3]. This was confirmed by numerical simulations (e.g., [25]). On the other hand, Hawking evaporation is considered to decrease the mass of PBHs. The mass loss is considered to be virtually negligible if the mass of the PBH is much more massive than the critical mass ∼ g, which will be discussed below.
2.2. Evaporation
Based on quantum field theory in curved spacetimes, Hawking (1974) [8,9] found that black holes emit black body radiation. The temperature of the black body, which is called the Hawking temperature, is proportional to the surface gravity of the horizon and is given for the Schwarzschild black hole by
where ℏ and k are the reduced Planck constant and the Boltzmann constant, respectively. This is called the Hawking evaporation. If we assume that the black hole loses its mass due to this radiation of quantum fields according to the Stefan–Boltzmann law, which is the so-called semi-classical approximation, we obtain
where is the effective degrees of freedom and the grey-body factor is neglected. This implies that the evaporation timescale is given by
after which the black hole of mass M loses almost all of its mass. As the black hole decreases its mass, the temperature becomes higher and higher and the evaporation timescale becomes shorter and shorter. Although the black hole decreases its mass very slowly in most of its life, it rapidly loses its remaining mass at its final moment, which is called a black hole explosion. When it becomes as light as the Planck mass g, the semi-classical approximation necessarily breaks down and the subsequent evolution of the black hole should greatly depend on quantum gravity.
From Equation (5), the critical mass is approximately given by g for which is satisfied, where is the age of the Universe. So, if g, PBHs have dried up after the explosion until now, whether they leave Planck mass relics or not. If g, PBHs are currently emitting X-rays and rays and can be observed through those emissions. If g, the evaporation is mostly negligible and the mass of the PBH remains almost constant until now. It should also be noted that very recently there has been a debate on a specific hypothetical scenario that assumes that the Hawking evaporation is strongly affected due to the back reaction effect even if the black hole is macroscopic [26].
2.3. Probability
To discuss the formation, the fraction of the Universe which goes into PBHs when the mass contained within the cosmological horizon is M, is often used. This can also be regarded as the formation probability of PBHs. If we consider PBHs formed in the radiation-dominated phase, PBHs act as nonrelativistic particles surrounded by relativistic particles. Therefore, the energy density of PBHs, , decays as , while the energy density of relativistic particles, , decays as , where a is the scale factor of the Universe. This implies , that is, PBHs are condensed during the radiation-dominated era in proportion to the scale factor. Taking this concentration effect into account, is related to the the current fraction of PBHs of mass M to all the CDM
through
for g [4,23]. This formula can derived from the expansion law for the flat Friedmann–Lemaître–Robertson–Walker (FLRW) solution in radiation domination, the mass within the horizon at the matter-radiation equality g and Equation (1). This equation is important because it connects the theory and the observation of PBHs. Thus, for example, only a tiny probability is enough to explain all of the dark matter if g, while is necessary for that if .
For g, Equation (7) combined with the observational constraint on gives the observational constraint on . As for g, PBHs have evaporated away until now. However, the evaporation of PBHs may spoil big bang nucleosynthesis for g if is too large. Such a consideration gives the observational constraint on for g, where the lower limit is usually assumed to be the Planck mass. See Figure 18 of Ref. [23] for more details.
3. Formation
3.1. Overview
The serious study of PBH formation dates back to Carr (1975) [4]. One of its aims is to theoretically predict and, therefore, and other observables of PBHs for a given cosmological scenario. We can obtain the information of the early Universe from observational data on PBHs only through these studies. Apart from such an observational motivation, through the study of formation, we can understand physics in PBH formation and investigate new phenomena and/or new physics in highly nonlinear general relativistic dynamics and high-energy physics. There have been a lot of scenarios proposed for PBH formation. One of the most standard ones is the direct collapse of a large amplitude of primordial perturbations generated by inflation [27,28]. See also Ref. [11] for a recent review of this scenario. This can be considered as ‘inevitable’ as inflationary cosmology has been regarded as an essential part of standard cosmology. Among the other alternative scenarios, domain wall collapse, bubble nucleation, collapse of string networks and phase transitions have attracted more attention than others. Hereafter, we will focus on the formation scenario from fluctuations generated by inflation. Studies on this scenario have developed more than on other scenarios. The key ideas to this scenario are the following: fluctuations generated by inflation, long-wavelength solutions, formation threshold, black hole critical behavior, dependence on the equation of state (EOS) and statistics on the abundance estimate. We will briefly view these topics below. We will hereafter use the units in which over this paper unless they are explicitly given.
3.2. Fluctuations Generated by Inflation
The most striking feature of inflation is that it can not only solve the flatness problem and the horizon problem but also provide the mechanism to generate fluctuations through quantum effects. Those fluctuations seed structure formation of different scales in our Universe and provide anisotropies in CMB currently observed with high accuracy.
The evolution of fluctuations in the inflationary cosmology is schematically illustrated in Figure 1. The quantum fluctuations generated by inflation are stretched to length scales much larger than the Hubble horizon scale because the fluctuation scale, which is proportional to a, expands faster than the Hubble horizon scale, which is proportional to t, due to the accelerated expansion. This process is also considered to remove quantum coherence from the fluctuations. The generated classical fluctuations are further stretched away compared to the Hubble length as long as the inflationary phase continues. After the inflation ends, the expansion of the Universe begins to decelerate. There is a possibility that the Universe might experience the early matter-dominated phase due to the harmonic oscillation of an inflation field. In any case, the Universe eventually is dominated by the radiation field, tightly coupled relativistic particles in an almost complete thermal equilibrium state. This process is called reheating. If we consider the scale of the fluctuation to be much larger than the Hubble horizon in the decelerated Universe, the scale of the fluctuation, which is proportional to a, expands slower than the Hubble horizon scale, which is proportional to t. The time when the fluctuation scale is as large as the Hubble scale is called the horizon entry of the perturbation. Although inflationary cosmology has been becoming an essential part of standard cosmology, there has been no standard inflation model until now. There are lots of inflation models, each of which gives the power spectrum and the other statistics of the curvature perturbations . See Ref. [11] for details of different inflation models in the context of PBH formation.
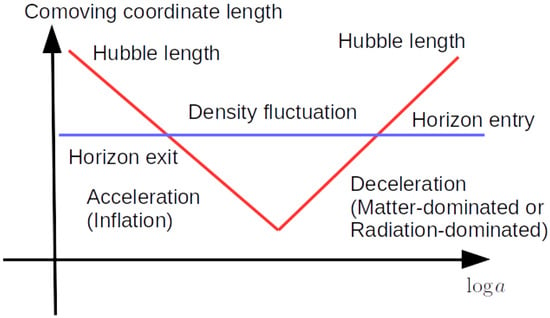
Figure 1.
The schematic figure for the evolution of the scales of fluctuations generated by inflation. The quantum fluctuations generated by inflation are stretched to length scales that are much larger than the Hubble horizon scale and are classical. In the decelerated phase after inflation, the scale of the fluctuation expands slower than the Hubble horizon scale. The time when the fluctuation scale becomes as large as the Hubble scale is called the horizon entry of the perturbation. After the horizon entry, the perturbation can collapse into a black hole leading to PBH formation if its amplitude is sufficiently large.
3.3. Large-Amplitude Long-Wavelength Solutions
As discussed above, fluctuations are generated and stretched to super-horizon scales by inflation. According to the standard cosmological scenario, the Universe must become radiation-dominated and decelerate after inflation. Then, the scale of the fluctuations become as large as the horizon scale, or in other words, the fluctuations re-enter the horizon. Then, if the amplitude of perturbation is nonlinearly large, the fluctuation can collapse into a black hole in the radiation-dominated era. This scenario has been conventionally studied for many years. In some scenarios, there can be an early matter-dominated era before the standard late one. In this case, we also need to think about the collapse of the fluctuation in the early matter-dominated era.
Based on the above scenarios, we discuss the fluctuations of super-horizon scales in the decelerated expansion after inflation. This situation is schematically illustrated in Figure 2. As we have already seen, in order to discuss PBH formation in radiation domination, it is necessary to deal with a nonlinearly large amplitude of perturbation of super-horizon scales. To obtain such perturbations, we solve the Einstein equation by a series expansion assuming that the spatial derivative is regarded as much smaller than the time derivative. This scheme is called gradient expansion and the solutions obtained by this scheme are called long-wavelength solutions.
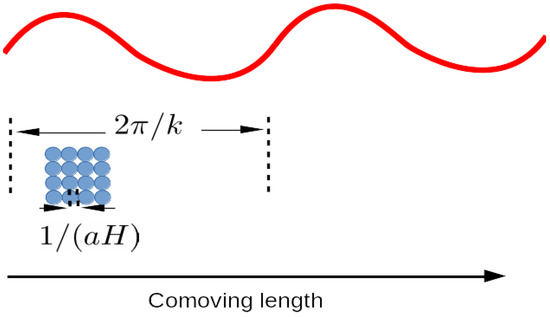
Figure 2.
Schematic figure of long-wavelength solutions. The long-wavelength solutions are obtained under the assumption that the comoving length scale of the perturbation in consideration is much longer than the Hubble horizon length , which gives the size of Hubble patches denoted with small blue disks.
First, we make the standard decomposition of the spacetime. We foliate four-dimensional spacetimes with constant t spacelike hypersurfaces . Let and be spatial coordinates on and the metric tensor on , respectively, where run over 1, 2 and 3. Then, the line element in four dimensions can be written by
where and are functions of t and and called the lapse function and the shift vector, respectively. The functions and specify the time slicing, i.e., how the spacetime is foliated with constant t spacelike hypersurfaces, and the coordinate threading, i.e., how the constant world lines cross the constant t hypersurfaces, respectively. We can choose the lapse and the shift according to the purposes so that we can fix four degrees of the gauge freedom in the Einstein equation. Using this decomposition, we can reformulate the Einstein equation in the form of the second-order time development, i.e., the Cauchy problem. See, e.g., Refs. [29,30] for more details.
In the next step towards the long-wavelength solutions, we take the following procedures [31,32,33,34,35]. In our situation, it is more useful to further decompose in the form
where and are both the functions of t and so that should hold, where is the time-independent metric of the flat 3-space, while is the scale factor of the reference flat FLRW spacetime. Thus, we have the line element in general spacetimes in four dimensions in the following form:
We call this the cosmological conformal decomposition.
Then, we assume that the scale of the perturbation is much larger than the Hubble horizon scale, i.e., that
is much smaller than unity, where k denotes the comoving wave number corresponding to the comoving scale of the perturbation. Applying the gradient expansion in powers of for the Einstein equation, we can obtain growing-mode solutions with an assumption that the zeroth-order solutions in powers of take the following form:
where is the zeroth-order part of , which is a function solely of and identified with primordial curvature perturbation. Note that this assumption is compatible with the comoving slice, the constant-mean-curvature (CMC) slice and the uniform-density slice but not with the conformal Newtonian gauge condition, which is often used in cosmology. This is because, as is well known, in the conformal Newtonian gauge, the density perturbation in the linear order approaches a time-independent function of in the super-horizon limit, while it approaches zero in the same limit in the cosmological long-wavelength solutions formulated in Refs. [32,33,34], although we do not exclude the existence of other formulations that are compatible with the conformal Newtonian gauge. The higher-order terms of the solutions are obtained in terms of the function if we impose the appropriate gauge conditions. In other words, , which is not suppressed due to the long-wavelength scheme, generates the long-wavelength solutions. For example, the density perturbation is and is given by
in the CMC slice.
If we apply this formulation to the spherically symmetric spacetime, where the zeroth order metric can be written in the following form
in the conformally flat coordinates, we can show that this is equivalent to the asymptotically quasihomogeneous solutions developed in Ref. [34] in the Misner–Sharp formulation, where the comoving slice and the comoving thread are adopted, and the explicit transformation between them is given in Ref. [35].
3.4. Formation Threshold in Radiation Domination
If the amplitude of the perturbation, which is generated by inflation and enters the horizon in the radiation-dominated era, is sufficiently large, it will directly collapse into a black hole. Since the linear perturbation in the radiation-dominated era does not significantly grow, such a perturbation must be nonlinearly large. This prevents us from accessing the full dynamics of PBH formation with analytical methods. Only full numerical relativity simulations can accurately describe the general relativistic dynamics of PBH formation, which has been pioneered by Nadezhin, Novikov and Polnarev (1978) [7]. In fact, it has been established by several analytical and numerical works such as Refs. [4,7] that PBHs really form in this scenario.
This scenario naturally implies that there exists a threshold for PBH formation. Carr (1975) derived the threshold for radiation domination according to the Jeans scale argument in terms of , the density perturbation at the horizon entry of the perturbation. In numerical relativity, the threshold value is obtained as in terms of the density perturbation averaged in the comoving slice over , where is the radius of the overdense region, at the horizon entry of the overdense region, where is regarded as that in the nontrivial lowest order of the long-wavelength expansion scheme [35,36,37,38]. Harada, Yoo and Kohri (2013) [39] refined Carr’s argument from a general relativistic point of view and analytically derived the threshold in the comoving slice. Although the averaged density perturbation might look straightforward to interpret, it has difficulty in its interpretation. This is because if we calculate the averaged density perturbation at the horizon entry using the nontrivial lowest order of the solutions, it cannot be a real physical value, as the latter can only be obtained after the full numerical simulation and is not necessarily useful.
Shibata and Sasaki (1999) [32] defined a compaction function in the CMC slice. Although it was intended to equal the ratio of the excess in the Misner–Sharp mass, or equivalently the Kodama mass, to the areal radius, it is not equal to that but
where the weak equality denotes the equality in the long-wavelength limit and we have omitted the subscript 0 in according to the convention [35,40]. This has been shown to have a geometrical origin as a compactness function in the static spacetime obtained by removing the scale factor in the long-wavelength limit [41]. It is proportional to the ratio of the Misner–Sharp mass excess to the areal radius in the comoving slice as
where
with being the Misner–Sharp mass excess in the comoving slice. Note the factor of 2 on the right-hand side of Equation (17). The threshold value is ∼ in terms of the maximum value of the Shibata–Sasaki compaction function in the long-wavelength limit [32,35,38]. This is more straightforward than the averaged density perturbation because, for the compaction function description, we only have to take the long-wavelength limit of the solutions, where all the higher-order contributions naturally disappear. This is probably why people have favored using the compaction function. On the other hand, this threshold can be transformed to ∼ in terms of the density perturbation in the comoving slice averaged over the ball at its horizon entry, where is the radius at which takes the maximum [42] again with a caveat that this value is only correct in the nontrivial lowest order of the long-wavelength expansion. The averaging over is more consistent and applicable than over the overdense ball as the definition of is problematic for density perturbations without an underdense region.
In the last decade, great effort has been paid to reveal the profile dependence of the threshold [42,43,44]. In particular, Escrivà, Sheth and Germani (2020) [44] found a universal threshold
in terms of , the spatial average of over , where takes a maximum at . This holds within accuracy over different profiles they surveyed. This gives a new threshold condition that uses the maximum and its second-order derivative . See Ref. [44] for details. More recently, Ianniccari, Iovino, Kehagias, Perrone and Riotto [45] reported some numerical coincidence between this threshold and that for the existence of a circular photon orbit.
There is a possibility that isocurvature perturbations may be produced depending on the cosmological scenario. Yoo, Harada, Hirano, Okawa and Sasaki (2021) [46], through numerical relativity simulations by introducing a massless scalar field perturbation into the radiation-dominated Universe, demonstrated that isocurvature perturbations can also produce PBHs in the radiation-dominated era. As isocurvature perturbations can play important roles in various intriguing inflationary scenarios, further studies are anticipated to achieve a comprehensive understanding of the formation threshold from isocurvature.
3.5. Softer Equation of State
There remain a lot of theoretical possibilities for the thermal history of the Universe. In addition to the standard phases of radiation dominance and subsequent matter dominance, there may be an early matter-dominated phase and/or phase transition or crossover phase in which the equation of the state of the dominant component of the Universe is significantly softer than the radiation fluid. Although PBH formation has been conventionally studied in the radiation-dominated phase, the scenarios in other phases with such significantly soft equations of state will also be important. This is because as we will see below, strongly depends on the threshold, which is smaller for the softer equation of state and, hence, PBH formation can be strongly enhanced so that PBHs formed in this phase may dominate those formed in the radiation-dominated era, provided that the power spectrum density perturbation is nearly scale-invariant.
This scenario was already suggested by Carr (1975) [4], where the threshold density perturbation was estimated to for the linear EOS using the simple application of the Jeans criterion in Newtonian gravity. Harada, Yoo and Kohri (2013) [39] refined it by comparing the free-fall time and the sound-crossing time in a simplified toy model of the fully general relativistic spacetime considering gauge difference to find the threshold value
in the comoving slice. This analytical expression showed a good agreement with the results of numerical relativity simulation [38,47] for as seen in Figure 3. These studies showed that the threshold for the EOS is an increasing function of w for and approaches 0 as . For example, for the QCD crossover, w drops to ∼ from [48], this suggests enhanced generation of PBHs. Although w is time-dependent in this case, the threshold has also been calculated based on the Jeans criterion [49]. Subsequently, full numerical relativity simulations have revealed that the PBH formation will be enhanced by a factor of the order of 1000 [50,51]. See Ref. [52] for a recent review on this subject.
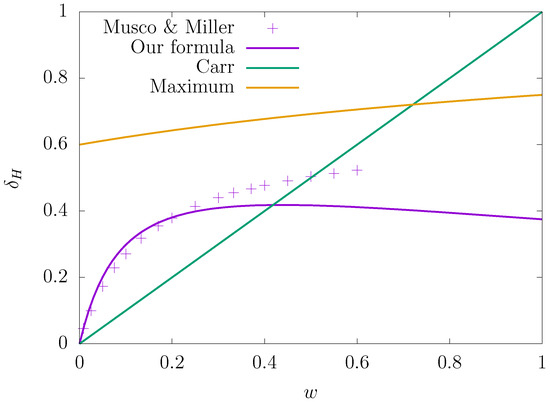
Figure 3.
EOS dependence of the PBH formation threshold. The horizontal axis is the parameter w for the EOS , while the vertical axis is the threshold value in terms of , the density perturbation over the overdense region, , at its horizon entry in the comoving slice. The crosses show the numerical result obtained in Ref. [38]. The purple curve is the plot of Equation (18), which shows an agreement with the numerical result within ∼, while the green curve shows Carr’s formula . See Ref. [39] for more details.
Musco and Papanikolaou (2022) [53] studied the effect of anisotropic stress, which is the deviation from the perfect fluid description, on PBH formation in radiation domination and found that if this is large enough, it could lead to a significant variation in the abundance of PBHs.
3.6. Matter Domination
If the argument in Section 3.5 for the EOS applied to for the matter-dominated phase, one might consider that PBHs could be overproduced. However, this cannot be correct because the realistic physical system is highly nonspherical and the deviation from spherical symmetry will grow during the collapse in matter domination. Not only after the standard matter-radiation equality time but also in a possible early matter-dominated phase, which may naturally occur in the preheating process or in the strong phase transition in the Universe, PBH formation will be enhanced. This is one of the interesting epochs to study in the context of PBH formation. Since the condition for PBH formation is not solely determined by the pressure gradient force, we would need a totally different treatment for this phase from that for the radiation-dominated phase.
The PBH formation in matter domination has been pioneered by Khlopov and Polnarev (1980) [54,55,56,57], where the effects of anisotropy and inhomogeneity are studied as an obstruction of the PBH formation process. Harada, Yoo, Kohri, Nakao and Jhingan (2016) [58] revisited the anisotropic effects by combining the picture of the pancake collapse of dark matter and the hoop conjecture by Thorne, which claims that black holes with horizons form when and only when a mass M gets compactified into a region whose circumference in every direction is [59,60]. This suppression due to the anisotropic effect is schematically shown in Figure 4. They not only qualitatively reproduced the result of Refs. [54,56] but also updated the coefficient as
where is the standard deviation of in the mass scale of M and the Gaussian distribution for density perturbation is assumed.
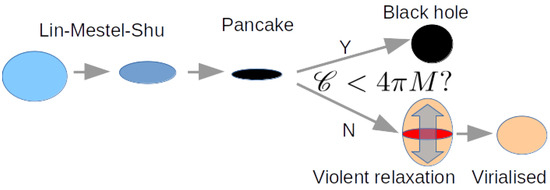
Figure 4.
Schematic illustration of the scenario on the anisotropic effect in the formation of PBHs in matter domination. denotes the hoop of the surface of the gravitating object of mass M. The scenario is the following. The collapse of a dust ball is unstable against nonspherical perturbations towards the pancake. Whether or not a horizon forms around the pancake is subject to the hoop conjecture. If the condition is satisfied, a black hole forms. Otherwise, the collapse leads to virialization by acquiring velocity dispersion through violent relaxation. See Ref. [58] for details.
Kopp, Hofmann and Weller (2010) [61] modeled the spherical formation of PBHs in matter domination with the Lemaître–Tolman–Bondi (LTB) solution and Harada and Jhingan (2015) [62] extended it to a nonspherical formation with the Szekeres quasispherical solutions. Kokubu, Kyutoku, Kohri and Harada (2018) [63] revisited the inhomogeneity effects by utilizing the LTB solution and not only qualitatively reproduced the result of Refs. [54,56] but also updated the coefficient so that the additional suppression factor is given by
with the caveat that its physical effect largely depends on the assumption that black hole formation is prevented by the appearance of an extremely high-density region before the black hole horizon formation surrounding it.
Harada, Kohri, Sasaki, Terada and Yoo (2022) [64] showed that the effects of velocity dispersion that may have been generated in the possible nonlinear growth of perturbation in the earlier phase can suppress PBH formation. The effects of the angular momentum can play important roles and suppress PBH formation for smaller [65]. We will later discuss the angular momentum in PBH formation in the matter-dominated era in the context of the initial spins of PBHs.
There is another intriguing approach to PBH formation during the early matter-dominated era. Such an era is thought to be naturally realized during the preheating phase following inflation when an oscillating massive scalar field dominates the Universe. It is possible to gain further insights into PBH formation during this phase by directly studying the perturbations in the Universe dominated by a massive scalar field. This approach was explicitly proposed by Padilla, Hidalgo and Malik (2022) [66,67,68], and numerical relativity simulations have been conducted based on this method, involving a mixture of a massive scalar field and a massless scalar field [69,70,71]. This approach may involve highly fruitful physics, and further studies will be necessary for a comprehensive understanding of this scenario.
3.7. Critical Behavior
One of the great achievements of numerical relativity is the discovery of critical behavior in gravitational collapse, which is also called black hole critical behavior. This was first discovered by Choptuik (1993) [72] in the spherically symmetric system of a massless scalar field and followed by Evans and Coleman (1994) [73] in the spherical system of a radiation fluid. The phenomena were theoretically understood in terms of the renormalization group analysis by Koike, Hara and Adachi (1995) [74]. These early studies were all on asymptotically flat spacetimes and whether they apply to PBH formation was not so trivial because of the different boundary conditions and the existence of the characteristic scale, the Hubble horizon length. The critical behavior in the PBH formation was discovered by Niemeyer and Jedamzik (1999) [75] but subsequently questioned [76]. Finally, Musco and Miller (2013) [38] beautifully confirmed the critical behavior in PBH formation. The essence of the critical behavior in the context of PBH formation is the following. Let us consider a one-parameter family of initial data of the Cauchy problem, for which we can choose the averaged density perturbation as the parameter of the family. The features of the critical behavior do not depend on the choice of the one-parameter family of the initial data. As we have already seen, there is a threshold value , beyond which a PBH forms. Then, the evolution of the initial data which has the critical value approaches a particular member of continuously self-similar solutions, which is called a critical solution. If is slightly above the critical value, we have PBH formation and the scaling law for the mass of the formed PBH, M, holds as follows:
where is called a critical exponent and K is a nondimensional positive constant that depends on the shape of the initial perturbation, varying between 3 and 30 with a typical value ∼5. In fact, the critical behavior, such as the critical solution and the critical exponent, does not depend on the choice of the one-parameter family of initial data, which is called universality. Note, however, that the critical solution and the critical exponent do depend on the matter field and the equation of state even if it is a perfect fluid [77].
In the context of PBH formation, if we assume that obeys some reasonable statistical distribution, the critical behavior implies that a tiny fraction of perturbations of mass scale can produce PBHs that are much smaller than , while a large fraction still produce those of the order of . This becomes important especially if we consider for g. This is because the PBHs of the critical mass ∼ g are severely constrained by observation through its X-ray or gamma-ray emission, while those of ∼ g are not. For example, the formation probability with the horizon mass g is severely constrained by such a tiny fraction of PBHs of the critical mass ∼ g considerably smaller than g [78,79].
3.8. Abundance Estimation and Statistics
Even if we can identify the threshold condition and the classical dynamics of PBH formation and subsequent evolution, it is not sufficient to determine . Clearly, we also need statistical properties of the perturbations. In inflationary cosmology, the statistical properties of fluctuations generated by inflation, such as the power spectrum and other statistical properties can be predicted, at least in principle, if we fix the inflation model.
Carr (1975) [4,39] simply assumed that obeys a Gaussian distribution and obtained the following formula
where and are the possible maximum value and the standard deviation of in the mass scale of M and in the last approximation is assumed. The factor of two in the above equation comes from the recommendation for structure formation by Press and Schechter (1975) [80,81], whereas whether or not this factor applies to PBH formation is highly nontrivial. Since we need at least for PBHs to contribute to a considerable fraction of dark matter, we can conclude that only the Gaussian tail beyond ∼ is responsible for PBHs. This implies that introducing small non-Gaussianities can significantly enhance the formation of PBHs [82]. See Ref. [83] for a recent review on non-Gaussianities in PBH formation and their link to induced gravitational waves. If we consider PBHs formed in the radiation-dominated era and assume or ∼, we need at least or . This is much larger than the observed value for the CMB anisotropies, although it does not immediately exclude the considerable formation of PBHs because the scales of the PBHs and the CMB anisotropies are usually very different from each other.
Although Carr’s formula (22), which is also called the Press–Schechter approximation, is very useful, this is considered as a very rough approximation. One of the reasons is that even if the curvature perturbation obeys a Gaussian distribution, the averaged density perturbation in the comoving slice cannot because it must be within a finite interval between the minimum and the maximum [61]. The other is that since PBHs will form only at very rare peaks of the perturbation, peak theory should apply, which is known to give a physically reasonable prediction for galaxy formation [84]. The prediction of peak theory may be significantly different from that of Carr’s formula for the estimation of PBH abundance. Currently, there are a few variations in the application of peak theory to the estimation of the PBH abundance, which comes from the theoretical ambiguity caused by an incomplete understanding of nonlinear, nonspherical and multi-scale general relativistic dynamics [85,86,87,88,89]. See also Ref. [90] for a recent review on this topic.
4. Initial Spins
If the black hole no hair conjecture holds in astrophysics, stationary black holes in vacuum should be well approximated by Kerr black holes which are characterized only by two parameters, the mass and the angular momentum. As we have already discussed, the mass of PBHs is approximately equal to that within the Hubble horizon at the time of formation. So, what determines the spin of PBHs? If black holes of masses from several to several tens of solar masses are observed, it would be very difficult to distinguish between PBHs and astrophysical black holes. Astrophysical black holes form in the final stage of the evolution of massive stars. If we observe an isolated black hole, the only information of its own other than its mass is its spin. So, if the spins of PBHs are expected to be very different from those of astrophysical black holes, the observation of spin can be potentially decisive information to distinguish between the two populations. Here, we focus on the initial spins of PBHs. However, it should be noted that the accretion and merger history after their formation could also greatly affect their spins depending on the scenarios [91] and, hence, the theoretically estimated values for the initial spins should be compared with the observation with great care.
4.1. Spins of Primordial Black Holes Formed in Radiation Domination
It was discussed that the formation process of PBHs in radiation domination is well approximated by spherically symmetric dynamics since Carr (1975) [4]. Recent studies have revealed that this early argument is basically correct. Chiba and Yokoyama (2017) [92] gave an upper bound ∼ on the root mean square of the nondimensional Kerr parameter , where a and M are the Kerr parameter and the mass of the black hole. He and Suyama (2019) [93] discussed the effect of angular momentum on the threshold.
Peak theory features more accurate quantitative analyses. For PBHs formed in radiation domination, the threshold density perturbation is of the order of the unity, which is considerably larger than its standard deviation. In other words, PBHs can form only at very rare peaks. Peak theory predicts that there is only a very small deviation from spherical symmetry for such rare peaks. This is very important to not only justify the spherical symmetry assumption but also estimate the angular momentum of PBHs formed in radiation domination. Based on the perturbative analysis based on peak theory, De Luca, Desjacques, Franciolini, Malhotra and Riotto (2019) [94] concluded that the root mean square of the nondimensional Kerr parameter is of the order of , while Harada, Yoo, Kohri, Koga and Monobe (2021) estimated the root mean square of to be in the order of and showed that a small fraction of PBHs of masses much smaller than the mass enclosed within the Hubble horizon, , as a result of critical phenomena, can have much larger spins [95].
Based on this analysis combined with peak theory, Koga, Harada, Tada, Yokoyama and Yoo (2022) [96] calculated the distribution of the effective spin parameter of binary black holes, which is a well-determined observable of the spins obtained from gravitational waveforms from inspiralling binaries. Figure 5 shows the distribution functions of the parameters and M of isolated PBHs on the top panel and of the mass ratio , the Chirp mass and of binary PBHs on the bottom panels, where , and () are individual masses, individual nondimensional Kerr parameters and the angles of individual spins with respect to the orbital angular momentum, respectively, with being assumed. Although there is a tendency for larger spins with smaller masses because of the critical phenomena, the probabilities for large values of the spin parameters are strongly suppressed. See Ref. [96] for details.
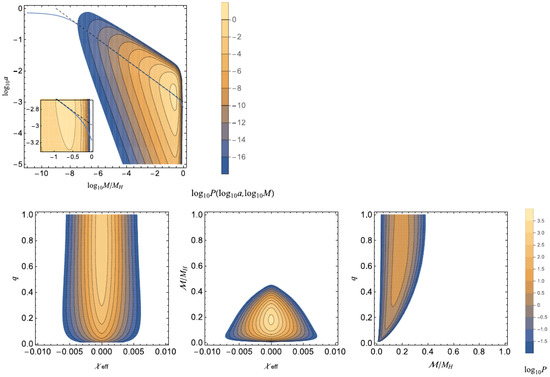
Figure 5.
Contour maps of the distribution functions of for isolated PBHs on the top panel, M and are the mass and the nondimensional Kerr parameter, respectively, and , and for binary PBHs from left to right on the bottom panels, where , and q are the effective spin parameter, the Chirp mass and the mass ratio of the binary PBHs, respectively. The definitions of q, and are , and , respectively, where , and () are individual masses, individual nondimensional Kerr parameters and the angles of individual spins with respect to the orbital angular momentum, respectively, with being assumed. Taken from Ref. [96].
In the above analyses, it was assumed that the power spectrum of curvature perturbation is nearly monochromatic. Recently, it has been revealed that if this assumption is relaxed, the root mean square of can be slightly larger for some set of broad power spectra but should still be bounded by the value of the order of [97].
4.2. Spins of Primordial Black Holes Formed with a Soft Equation of State
It is interesting to ask how much the results in Section 4.1 depend on the properties of the matter fields in the cosmological phase when the PBHs formed. In particular, it was shown that the PBH production is significantly enhanced in the QCD crossover, where the effective value of w drops from to ∼ [50,51]. Saito, Harada, Koga and Yoo (2023) [98] showed that for a soft EOS parameterized by , the root mean square of is a decreasing function of w and can be well fitted by the power law . However, since the dependence is weak for , the initial spins are only modestly enhanced for the QCD crossover such as to ∼ from ∼ for radiation. It also suggests that can be very large if , although the analysis in Ref. [98] is not well justified in the limit , where the treatment for matter domination should apply.
4.3. Spins of Primordial Black Holes Formed in (Early) Matter Domination
Since PBH formation will be enhanced in the (early) matter-dominated phase, it is very important to predict their spins. As we have seen before, nonspherical effects may become important. In fact, Harada, Yoo, Kohri and Nakao (2017) [65] investigated the effects of angular momentum for PBH formation in this phase. Both the first-order and second-order effects can potentially play important roles. The first-order effect generates angular momentum through the nonsphericity of the region to collapse into a black hole, which is generally misaligned with a mode wave number vector of the velocity perturbation. This is schematically illustrated in Figure 6, where the ellipsoidal region that will collapse is misaligned with the wave number of the velocity perturbation denoted by the red arrows and, hence, it carries nonvanishing angular momentum. The secondary effect also gives angular momentum through the coupling of two independent modes of linear perturbation, which is illustrated in Figure 1 of Ref. [65].
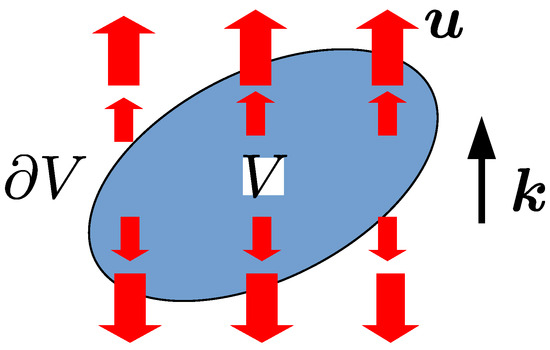
Figure 6.
Schematic illustration of the first-order effect to generate angular momentum. The blue region V denotes the region that will collapse, which is approximated by an ellipsoid. The red arrows denote the velocity perturbation with a wave number vector being parallel to the vertical direction. Since the ellipsoidal region V is misaligned with the wave number of the velocity perturbation, it carries nonvanishing angular momentum. The angular momentum can increase in time as the perturbation grows. This can also be understood through the effect of torque exerted on the boundary . See Ref. [65] for details.
Although the dynamics of PBH formation in matter domination are expected to be very complicated, a perturbative calculation under certain working assumptions gives
where is the nondimensional spin parameter of the region to collapse and is the standard deviation of at the horizon entry. Although the nondimensional numerical factor of the order of the unity on the right-hand side should be determined, this implies that most PBHs have spins if . The angular momentum effects will strongly suppress PBH formation if is even much smaller because of the Kerr bound . These results have recently been updated based on peak theory [99].
4.4. Nonspherical Simulation of PBH Formation
Although we have discussed the initial spins of PBHs, we have neglected nonspherical nonlinear general relativistic dynamics in the formation of black holes for simplicity. It is clearly important to numerically simulate the nonspherical formation of PBHs and investigate how much the initially nonspherical initial data will affect the formation threshold and the initial spins of the produced PBHs. This is complementary to the perturbative analysis as it can check the validity of assumptions made.
Yoo, Harada and Okawa (2020) [100] conducted a 3D numerical simulation of nonspherical PBH formation in radiation domination based on numerical relativity for the first time. They prepared the long-wavelength solutions as initial data, for which initial nonsphericity is expected to be typically very small according to peak theory. However, to make the numerical results clearer, they put ∼ nonsphericity in the initial data, which is much larger than the values expected from peak theory for PBH formation. They found that even such large nonsphericity changed the threshold of PBH formation only by ∼. See Figure 7 which is taken from Ref. [100] for the initial density perturbation on the left panel and the apparent horizon formation in the course of gravitational collapse on the right panel. We can see that in the simulation with the near-threshold value, a very small apparent horizon forms at the very central region. This implies that we need a very high resolution near the center. This problem was attacked with a rescaled radial coordinate [100].
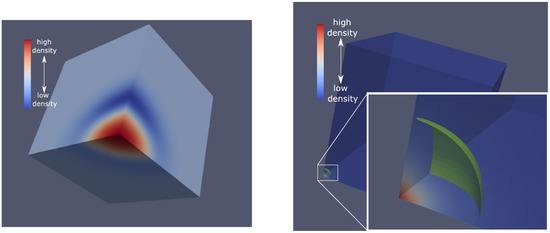
Figure 7.
The initial density perturbation is on the left panel and the apparent horizon formation in the course of gravitational collapse is on the right panel. We can see that an apparent horizon forms in the central region, which is very small compared to the size of the whole computational domain. It implies that to resolve the apparent horizon for the near-critical collapse requires very high resolution at least near the center. Both were taken from Ref. [100] with permission.
Yoo (2024) [101] conducted further numerical relativity simulations for the EOS with and with much higher resolution and accuracy. For this purpose, not only the rescaled radial coordinate but also the multi-level mesh refinement scheme was adopted. In such simulations, the estimation of the spin is not straightforward. In this work, it was implemented as follows: For the Kerr black hole, we can write the spin parameter using the event horizon configuration through the following relation
where d and A are the equatorial circumference and the area, respectively. Yoo (2024) [101] estimated the spin of the PBH as assuming Equation (24) for the numerically found apparent horizon. This is consistent with the perturbative estimates discussed in Section 4.1 and Section 4.2.
As far as I am aware, no 3D numerical relativity simulations for nonspherical PBH formation in the (early) matter-dominated phase have been carried out using a fluid or dust description of the matter fields. In the scalar field approach to the early matter-dominated phase, De Jong, Aurrekoetxea, Lim and França (2023) [70] studied nonspherical PBH formation through 3D numerical relativity simulations and reported that the spin in the final stage of formation would be negligible. Although this result is highly suggestive, further systematic studies are anticipated in the near future.
5. Type II Perturbation and Type B PBH
5.1. Introduction to Type II Perturbation
In the FLRW solution, the geometry of the constant cosmological time t spacelike hypersurface is given by a constant curvature space with a scale factor . The metric can be written in the following familiar form:
The spatial curvature K can be zero, positive, or negative. For , the geometry has a finite curvature radius up to the scale factor. The positive curvature solution generally has particular time evolution in , which begins to expand from the Big Bang, and reaches maximum expansion and collapses to a big crunch, while for the zero and negative cases it just continues expanding from the Big Bang to infinity. As is well known, for the positive-curvature FLRW spacetime, there is a coordinate singularity at in the line element (25). We can go beyond this singularity by introducing the radial coordinate in place of so that the line element can be written in the following form:
where K is normalized to 1 using the freedom in rescaling . We can see that the coordinate singularity which was at in the coordinates is now resolved at in the coordinates. Roughly speaking, a type II perturbation is the perturbation that covers the surface , while a type I does not.
In the perturbation theory in the flat FLRW solution, there are growing and decaying modes. We can usually neglect decaying modes in the early Universe if we are interested in subsequent structure formation including PBH formation. Then, we can expect that the regions with positive and negative density perturbations can be described by locally positive and negative curvature FLRW solutions, respectively. In fact, this is really true in the long-wavelength solutions because Equation (14), which is the metric in the long-wavelength limit, can be rewritten in the following form [34,35]:
in a new radial coordinate . Since type II perturbations need larger amplitudes of curvature perturbation, they are much rarer than type I in a standard probability distribution function of the curvature perturbation, whereas type II can be dominant in a particular inflationary scenario with large non-Gaussianities [102].
5.2. Positive Curvature Region, Type II Perturbation and Separate Universe Condition
As we have discussed, the region with a positive density perturbation can locally be well described by the positive-curvature FLRW solution at least in the long-wavelength limit. To understand the geometry and the dynamics of such a system, we introduce a toy model, which consists of a positive-curvature FLRW region surrounded by a flat FLRW region [39,61]. We call this model the three-zone model. Figure 8 gives its schematic figure. The line elements in regions I and III are written in the following forms, respectively,
for and
for , where and are the scale factors of the positive-curvature and flat FLRW solutions; in region II it cannot be written in a simple form. Although this toy model is not only unrealistic but also difficult to justify as the whole evolution of the spacetime unless we make strong assumptions about region II, it is still valid as the long-wavelength solution and useful to understand the concept of nonlinear perturbation. In this model, we have two independent physical length scales of region I, the curvature radius, which is normalized to 1 in the above metric, and the size of the region, which is given by . As is increased from 0 to , the comoving areal radius of region I, which is given by , monotonically increases from 0 to 1. However, as is further increased from to , the comoving areal radius turns to decrease from 1 to 0. This consideration implies the separate universe configuration for which , which is notified in Ref. [3]. Kopp, Hofmann and Weller (2010) [61] classified the configurations with and with into types I and II, respectively, while the marginal case is given by a three-hemisphere , where we neglect the contribution of region II.
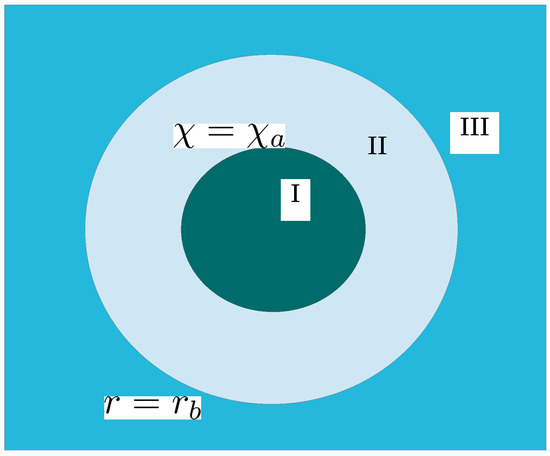
Figure 8.
The three-zone model of the positive density perturbation. Regions I and III are described by the closed and flat FLRW solutions, while region II is an underdense matching layer. The spheres of and give the outer edge of region I and the inner edge of region III, respectively. See Refs. [39,61] for more details.
Apart from this toy model, it is still true that there should be two independent physical length scales to characterize the spatial geometry, the curvature radius and the size of the curved region as schematically illustrated in Figure 9. It should be noted that this figure does not show the sequence of time evolution but each configuration gives a set of initial data for each time development of the perturbation. It is physically interesting to think of a nearly separate universe configuration, while a totally separate universe has nothing to do with our observable Universe.

Figure 9.
Classification of spatial configurations of overdense perturbations. The type II configuration is with the throat structure in the spatial geometry, while the type I is not. Note that the sequence does not correspond to the time evolution but to different initial curvature perturbations.
5.3. Type II Perturbation and Its Time Development
Here, we review the sets of initial data in terms of types I and II based on the recent work by Uehara, Escrivà, Harada, Saito and Yoo (2024) [103] for radiation domination. Here, the system is assumed to be spherically symmetric. They first constructed the long-wavelength solutions by choosing a function . One of the functional forms they tried for is given by
where the constant gives the amplitude of perturbation and is an appropriate window function chosen so that the Gaussian tail can be eliminated and can be smoothly matched to 0 at the outer boundary of the numerical domain. The areal radius R and the Shibata–Sasaki compaction function are plotted as functions of r in Figures 1b and 2a of [103], respectively, where we can see that for , R is no longer a monotonic function of the radial coordinate r, which implies that there is a throat and that has two peaks with the value of and a minimum in between. See Refs. [41,103] for the account for this peculiar behavior of the compaction function. These features are essentially the same in matter domination as discussed in Ref. [61] using the LTB solution.
Then, the time development of those initial data was constructed with a standard numerical relativity scheme based on the Baumgarte–Shapiro–Shibata–Nakamura formalism but adjusted for the spherical formation of PBHs. Figure 3 of [103] summarizes the evolution of the spacetime for the long-wavelength solutions generated by the curvature perturbation given by Equation (30). For , the amplitude of perturbation is so small that it cannot collapse but disperses away. For and , the amplitude of perturbation is so large that it can collapse into a black hole. This suggests that the critical value of for the black hole formation is between and .
5.4. Type B Horizon Structure
In the asymptotically flat spacetimes, black holes are conventionally defined by event horizons. However, in a cosmological setting, event horizons are not necessarily useful because the definition of an event horizon is teleological in the sense that it is only based on the infinite future and because the structure of infinities in cosmological spacetimes can be very different from asymptotically flat ones. Furthermore, in the expanding Universe, there may be another type of horizon, i.e., a cosmological horizon. As we will see below, we encounter the interplay between these two types of horizons for some classes of PBH formation from the type II configuration. This implies that we need to distinguish between these two types of horizons. For these reasons, we adopt the notion of trapping horizons, a quasilocal formulation of horizons [104,105]. This is akin to the notion of apparent horizons in the present setting. Here, we define horizons using the pair of null expansions and along outgoing and ingoing radial null coordinates and , respectively. Black hole horizons can be defined with one vanishing and one negative null expansion so that any radial light ray there cannot expand its cross-section. Similarly, cosmological horizons can be defined with one vanishing and one positive null expansion so that any radial light ray there cannot contract its cross-section. The black hole horizons and cosmological horizons are called future trapping horizons and past trapping horizons, respectively. In principle, we may also have a horizon with both null expansions vanishing, which is called a bifurcating trapping horizon [106]. In Appendix A, we will introduce trapping horizons in a more mathematical manner, whereas the intuitive understanding discussed above is still useful.
With the above terminology, we can now describe the structure of trapping horizons. We assign and as the null coordinates being the standard ones in the far region which is asymptotic to the flat FLRW solution, which we assume to exist. There is a big difference in the structure of trapping horizons and trapped regions between and . We schematically plot the horizon structures inferred by numerical simulations in Figure 10. For , as shown on the top panel, there is a past trapped region and a future-trapped region disconnected from each other, with the associated past and future trapping horizons being separate. We call this horizon structure type A. For , as shown on the bottom panel, the past and future trapped regions have contacts at two points. The two points of intersection, which are two spheres, correspond to bifurcating trapping horizons. There appears to be an untrapped region enclosed by the future and past trapping horizons and the two bifurcating trapping horizons, where and . We call this horizon structure type B.
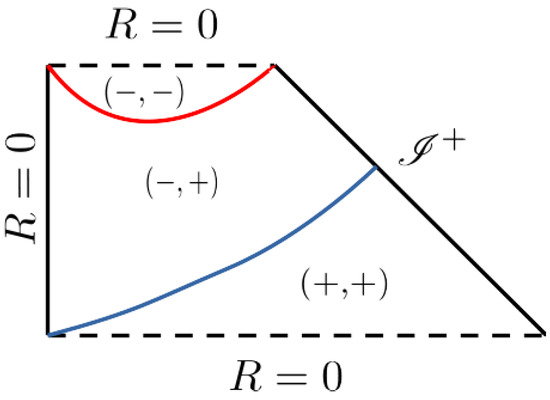
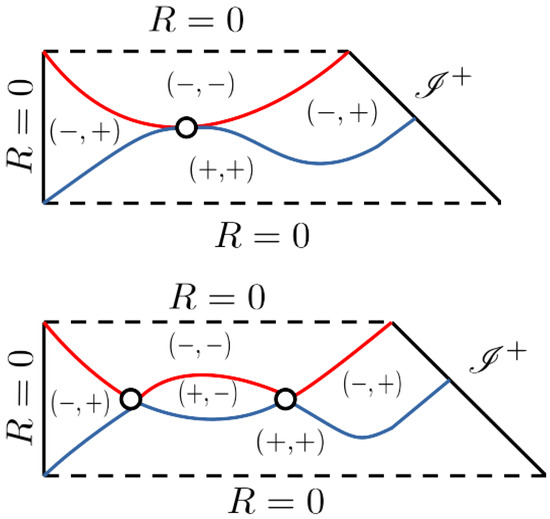
Figure 10.
Structures of trapping horizons and trapped regions inferred by numerical simulations. The structures indicated on the top, middle and bottom panels are called type A, marginal and type B, respectively. The signs of the radial null expansions are shown for each region. The regions are divided by trapping horizons, where . The future and past trapping horizons are denoted by the red and blue curves, respectively. The bifurcating trapping horizons are denoted by open circles. The black dashed lines denote spacetime singularities, while the black solid lines denote the regular centers and the null infinities. This figure is comparable to Figure 7 of Ref. [103]. See text for more details.
This numerical result for the perturbation indicates that there is a peculiar structure for trapping horizons and trapped regions, if is greater than some critical value. This was also true if we took another choice of , so the above features are at least general to some extent. So, we can regard this structure as common for a sufficiently large amplitude of curvature perturbation of type II. We infer the existence of the marginal horizon structure between types A and B, which is shown on the middle panel of Figure 10. We can say that a type II perturbation does not always result in a type B structure for radiation. This is due to the effect of pressure, because it is known that for the dust case a type II perturbation necessarily entails the horizon structure of type B. So, we can conclude that there are at least PBHs with structures of types I-A, II-A and II-B in radiation domination.
It should be noted that the type B horizon structure is not known in the gravitational collapse in asymptotically flat spacetimes and is, therefore, very unique to PBH formation as long as the author is aware. For this reason, the result of the type II-B PBH formation is very intriguing in the context of the variety of black hole formation in general relativity. On the other hand, their relevance to observational cosmology is yet unclear.
6. Conclusions
In the recent development of research on this subject, it has been revealed that PBHs lie at the intersection of various developing branches of modern physics. In this article, we review their basic concept, formation, spins and link to the type II configuration.
In Section 2, we present the basic concept of PBHs. The mass of PBHs is usually considered to be the mass scale within the cosmological horizon at the time of their formation. Mass accretion may significantly increase the PBH mass depending on the evolution scenario, whereas it has been shown to be negligible during the evolution in radiation domination. The mass of PBHs can be significantly reduced by Hawking evaporation, and they would have evaporated completely by now if they were lighter than the critical mass of approximately g, although the details of the evaporation process are still somewhat under debate. We can obtain constraints on the fraction of PBHs of mass M in relation to all dark matter through different observations. The fraction can be transformed into the formation probability depending on the cosmological evolutionary scenario. The standard cosmic history implies that a very small value of , as small as ∼ for g, can yield , i.e., can explain all dark matter, because the PBHs’ contribution to the energy of the Universe increases in proportion to the scale factor during the radiation-dominated phase.
In Section 3, we discuss PBH formation. A detailed and precise understanding of PBH formation physics has become increasingly important. The basic question in this study is how to predict and other observationally significant quantities from a given cosmological scenario. Focusing on PBH formation from fluctuations generated by inflation, the key terms are inflation models, long-wavelength solutions, thresholds, softer EOS, matter domination, critical behaviors and statistics.
In Section 4, we discuss the initial spins of PBHs. PBHs formed during radiation domination are unlikely to have large spins. Perturbative studies show that the nondimensional Kerr parameter of these PBHs is typically in the order of . In contrast, PBHs formed during matter domination can acquire large spins, at least initially. The effect of mass accretion after formation on the nondimensional Kerr parameter needs to be studied carefully. It is evident that numerical simulations based on numerical relativity should shed light on this problem.
In Section 5, we review the recently conducted numerical relativity simulations of the time evolution of type II perturbations during radiation domination. This is particularly relevant to a very rare perturbation peak or a specific inflationary scenario. The resulting structures of trapping horizons can be classified into two types: one is standard for PBHs, and the other is very unique, featured with the crossing of trapping horizons as bifurcating trapping horizons. We refer to these as types A and B, respectively, while we can also discuss the marginal structure. The numerical simulations suggest that the evolution of type II perturbations can be classified into type A and type B based on their horizon structure. Thus, we may call them types II-A and II-B.
Finally, I must acknowledge that there are many interesting issues concerning the formation of PBHs that cannot even be mentioned in this article. The study of PBH formation not only requires a deep understanding of physical phenomena within known standard physics but also offers the opportunity to explore unknown new physics through PBHs. Both of these aspects will play important roles in the future of PBH formation studies.
Funding
This research was funded by JSPS KAKENHI Grant Numbers JP20H05853 and JP24K07027.
Data Availability Statement
No data are associated with the manuscript.
Acknowledgments
The main part of this article is based on exciting collaborations with Bernard Carr, Albert Escrivà, Jaume Garriga, Shin-Ichi Hirano, Hayami Iizuka, Sanjay Jhingan, Yasutaka Koga, Kazunori Kohri, Takafumi Kokubu, Koutaro Kyutoku, Hideki Maeda, Takeru Monobe, Tomohiro Nakama, Ken-Ichi Nakao, Hirotada Okawa, A. G. Polnarev, Daiki Saito, Misao Sasaki, Yuichiro Tada, Takahiro Terada, Koichiro Uehara, Jun’ichi Yokoyama, Shuichiro Yokoyama and Chul-Moon Yoo. The author thanks Cristiano Germani, Mohammad Ali Gorji and the other participants of the conference “Barcelona Black Holes (BBH) I: Primordial Black Holes”, where this work was first presented, for helpful discussions and comments. The author is also very grateful to Ilia Musco and Theodoros Papanikolaou for their very helpful comments. The author is grateful to CENTRA, Departamento de F sica, Instituto Superior Técnico—IST at Universidade de Lisboa, and Niels Bohr International Academy at Niels Bohr Institute for their hospitality during the writing of this manuscript.
sica, Instituto Superior Técnico—IST at Universidade de Lisboa, and Niels Bohr International Academy at Niels Bohr Institute for their hospitality during the writing of this manuscript.
 sica, Instituto Superior Técnico—IST at Universidade de Lisboa, and Niels Bohr International Academy at Niels Bohr Institute for their hospitality during the writing of this manuscript.
sica, Instituto Superior Técnico—IST at Universidade de Lisboa, and Niels Bohr International Academy at Niels Bohr Institute for their hospitality during the writing of this manuscript.Conflicts of Interest
The author declares no conflicts of interest.
Appendix A. Trapping Horizons
For a spherically symmetric spacetime, we can generally introduce radial null coordinates such that the line element can be written in the following double-null form:
We introduce the future-directed radial null vectors such that , where . Then, we define as
We call a two-sphere specified with a future (past) trapped sphere if and . We call a two-sphere specified with a future (past) marginal sphere if and . We call a two-sphere specified with a bifurcating marginal sphere if . We call a two-sphere specified with an untrapped sphere if . We call a spacetime region a future (past) trapped region if any two-sphere given by in the region is a future (past) trapped sphere. We call a spacetime region an untrapped region if any two-sphere given by in the region is an untrapped sphere. We call a hypersurface foliated by future (past) marginal spheres a future (past) trapping horizon. We call a hypersurface foliated by bifurcating marginal spheres a bifurcating trapping horizon.
See Refs. [104,105,106] for more complete rigorous discussions and proofs of the basic properties of trapping horizons.
References
- Zel’dovich, Y.B.; Novikov, I.D. The Hypothesis of Cores Retarded during Expansion and the Hot Cosmological Model. Soviet Astron. AJ (Engl. Transl.) 1967, 10, 602. [Google Scholar]
- Hawking, S. Gravitationally Collapsed Objects of Very Low Mass. Mon. Not. R. Astron. Soc. 1971, 152, 75–78. [Google Scholar] [CrossRef]
- Carr, B.J.; Hawking, S.W. Black holes in the early Universe. Mon. Not. R. Astron. Soc. 1974, 168, 399–415. [Google Scholar] [CrossRef]
- Carr, B.J. The Primordial black hole mass spectrum. Astrophys. J. 1975, 201, 1–19. [Google Scholar] [CrossRef]
- Carr, B.J.; Green, A.M. The History of Primordial Black Holes. arXiv 2024, arXiv:2406.05736. [Google Scholar]
- Riotto, A.; Silk, J. The Future of Primordial Black Holes: Open Questions and Roadmap. arXiv 2024, arXiv:2403.02907. [Google Scholar]
- Nadezhin, D.K.; Novikov, I.D.; Polnarev, A.G. The hydrodynamics of primordial black hole formation. Sov. Astron. 1978, 22, 129–138. [Google Scholar]
- Hawking, S.W. Black hole explosions. Nature 1974, 248, 30–31. [Google Scholar] [CrossRef]
- Hawking, S.W. Particle Creation by Black Holes. Commun. Math. Phys. 1975, 43, 199–220, Erratum in Commun. Math. Phys. 1976, 46, 206. [Google Scholar] [CrossRef]
- Abbott, B.P.; Abbott, R.; Abbott, T.; Abernathy, M.R.; Acernese, F.; Ackley, K.; Aggarwal, N.; Aguiar, O.D.; Aiello, L.; Cavalieri, R.; et al. Observation of Gravitational Waves from a Binary Black Hole Merger. Phys. Rev. Lett. 2016, 116, 061102. [Google Scholar] [CrossRef]
- Sasaki, M.; Suyama, T.; Tanaka, T.; Yokoyama, S. Primordial black holes—Perspectives in gravitational wave astronomy. Class. Quant. Grav. 2018, 35, 063001. [Google Scholar] [CrossRef]
- Sasaki, M.; Suyama, T.; Tanaka, T.; Yokoyama, S. Primordial Black Hole Scenario for the Gravitational-Wave Event GW150914. Phys. Rev. Lett. 2016, 117, 061101, Erratum in Phys. Rev. Lett. 2018, 121, 059901. [Google Scholar] [CrossRef] [PubMed]
- Bird, S.; Cholis, I.; Muñoz, J.B.; Ali-Haïmoud, Y.; Kamionkowski, M.; Kovetz, E.D.; Raccanelli, A.; Riess, A.G. Did LIGO detect dark matter? Phys. Rev. Lett. 2016, 116, 201301. [Google Scholar] [CrossRef] [PubMed]
- Clesse, S.; García-Bellido, J. The clustering of massive Primordial Black Holes as Dark Matter: Measuring their mass distribution with Advanced LIGO. Phys. Dark Univ. 2017, 15, 142–147. [Google Scholar] [CrossRef]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; Cao, J.; et al. GW170104: Observation of a 50-Solar-Mass Binary Black Hole Coalescence at Redshift 0.2. Phys. Rev. Lett. 2017, 118, 221101, Erratum in Phys. Rev. Lett. 2018, 121, 129901. [Google Scholar] [CrossRef]
- Franciolini, G.; Baibhav, V.; De Luca, V.; Ng, K.K.Y.; Wong, K.W.K.; Berti, E.; Pani, P.; Riotto, A.; Vitale, S. Searching for a subpopulation of primordial black holes in LIGO-Virgo gravitational-wave data. Phys. Rev. D 2022, 105, 083526. [Google Scholar] [CrossRef]
- Carr, B.; Clesse, S.; Garcia-Bellido, J.; Hawkins, M.; Kuhnel, F. Observational evidence for primordial black holes: A positivist perspective. Phys. Rept. 2024, 1054, 1–68. [Google Scholar] [CrossRef]
- Agazie, G.; Anumarlapudi, A.; Archibald, A.M.; Arzoumanian, Z.; Baker, P.T.; Bécsy, B.; Blecha, L.; Brazier, A.; Brook, P.R.; NANOGrav Collaboration; et al. The NANOGrav 15 yr Data Set: Evidence for a Gravitational-wave Background. Astrophys. J. Lett. 2023, 951, L8. [Google Scholar] [CrossRef]
- Afzal, A.; Agazie, G.; Anumarlapudi, A.; Archibald, A.M.; Arzoumanian, Z.; Baker, P.T.; Bécsy, B.; Blanco-Pillado, J.J.; Blecha, L.; NANOGrav Collaboration; et al. The NANOGrav 15 yr Data Set: Search for Signals from New Physics. Astrophys. J. Lett. 2023, 951, L11, Erratum in Astrophys. J. Lett. 2024, 971, L27. [Google Scholar] [CrossRef]
- Liu, B.; Bromm, V. Accelerating Early Massive Galaxy Formation with Primordial Black Holes. Astrophys. J. Lett. 2022, 937, L30. [Google Scholar] [CrossRef]
- Hütsi, G.; Raidal, M.; Urrutia, J.; Vaskonen, V.; Veermäe, H. Did JWST observe imprints of axion miniclusters or primordial black holes? Phys. Rev. D 2023, 107, 043502. [Google Scholar] [CrossRef]
- Yuan, G.W.; Lei, L.; Wang, Y.Z.; Wang, B.; Wang, Y.Y.; Chen, C.; Shen, Z.Q.; Cai, Y.F.; Fan, Y.Z. Rapidly growing primordial black holes as seeds of the massive high-redshift JWST Galaxies. Sci. China Phys. Mech. Astron. 2024, 67, 109512. [Google Scholar] [CrossRef]
- Carr, B.; Kohri, K.; Sendouda, Y.; Yokoyama, J. Constraints on primordial black holes. Rept. Prog. Phys. 2021, 84, 116902. [Google Scholar] [CrossRef] [PubMed]
- Carr, B.J. Primordial black holes as a probe of cosmology and high energy physics. In Quantum Gravity; Lecture Notes in Physics; Springer: Berlin/Heidelberg, Germany, 2003; Volume 631, pp. 301–321. [Google Scholar] [CrossRef]
- Escrivà, A. Simulation of primordial black hole formation using pseudo-spectral methods. Phys. Dark Univ. 2020, 27, 100466. [Google Scholar] [CrossRef]
- Dvali, G.; Eisemann, L.; Michel, M.; Zell, S. Black hole metamorphosis and stabilization by memory burden. Phys. Rev. D 2020, 102, 103523. [Google Scholar] [CrossRef]
- Carr, B.J.; Lidsey, J.E. Primordial black holes and generalized constraints on chaotic inflation. Phys. Rev. D 1993, 48, 543–553. [Google Scholar] [CrossRef]
- Carr, B.J.; Gilbert, J.H.; Lidsey, J.E. Black hole relics and inflation: Limits on blue perturbation spectra. Phys. Rev. D 1994, 50, 4853–4867. [Google Scholar] [CrossRef]
- Wald, R.M. General Relativity; Chicago University Press: Chicago, IL, USA, 1984. [Google Scholar] [CrossRef]
- Poisson, E. A Relativist’s Toolkit: The Mathematics of Black-Hole Mechanics; Cambridge University Press: Cambridge, UK, 2009. [Google Scholar] [CrossRef]
- Tomita, K. Primordial Irregularities in the Early Universe. Prog. Theor. Phys. 1972, 48, 1503–1516. [Google Scholar] [CrossRef]
- Shibata, M.; Sasaki, M. Black hole formation in the Friedmann universe: Formulation and computation in numerical relativity. Phys. Rev. D 1999, 60, 084002. [Google Scholar] [CrossRef]
- Lyth, D.H.; Malik, K.A.; Sasaki, M. A General proof of the conservation of the curvature perturbation. J. Cosmol. Astropart. Phys. 2005, 5, 004. [Google Scholar] [CrossRef]
- Polnarev, A.G.; Musco, I. Curvature profiles as initial conditions for primordial black hole formation. Class. Quant. Grav. 2007, 24, 1405–1432. [Google Scholar] [CrossRef]
- Harada, T.; Yoo, C.M.; Nakama, T.; Koga, Y. Cosmological long-wavelength solutions and primordial black hole formation. Phys. Rev. D 2015, 91, 084057. [Google Scholar] [CrossRef]
- Musco, I.; Miller, J.C.; Rezzolla, L. Computations of primordial black hole formation. Class. Quant. Grav. 2005, 22, 1405–1424. [Google Scholar] [CrossRef]
- Musco, I.; Miller, J.C.; Polnarev, A.G. Primordial black hole formation in the radiative era: Investigation of the critical nature of the collapse. Class. Quant. Grav. 2009, 26, 235001. [Google Scholar] [CrossRef]
- Musco, I.; Miller, J.C. Primordial black hole formation in the early universe: Critical behavior and self-similarity. Class. Quant. Grav. 2013, 30, 145009. [Google Scholar] [CrossRef]
- Harada, T.; Yoo, C.M.; Kohri, K. Threshold of primordial black hole formation. Phys. Rev. D 2013, 88, 084051, Erratum in Phys. Rev. D 2014, 89, 029903. [Google Scholar] [CrossRef]
- Harada, T.; Yoo, C.M.; Koga, Y. Revisiting compaction functions for primordial black hole formation. Phys. Rev. D 2023, 108, 043515. [Google Scholar] [CrossRef]
- Harada, T.; Iizuka, H.; Koga, Y.; Yoo, C.M. Geometrical origin for the compaction function for primordial black hole formation. arXiv 2024, arXiv:2409.05544. [Google Scholar]
- Musco, I. Threshold for primordial black holes: Dependence on the shape of the cosmological perturbations. Phys. Rev. D 2019, 100, 123524. [Google Scholar] [CrossRef]
- Nakama, T.; Harada, T.; Polnarev, A.G.; Yokoyama, J. Identifying the most crucial parameters of the initial curvature profile for primordial black hole formation. J. Cosmol. Astropart. Phys. 2014, 1, 037. [Google Scholar] [CrossRef]
- Escrivà, A.; Germani, C.; Sheth, R.K. Universal threshold for primordial black hole formation. Phys. Rev. D 2020, 101, 044022. [Google Scholar] [CrossRef]
- Ianniccari, A.; Iovino, A.J.; Kehagias, A.; Perrone, D.; Riotto, A. The Black Hole Formation—Null Geodesic Correspondence. Phys. Rev. Lett. 2024, 133, 081401. [Google Scholar] [CrossRef] [PubMed]
- Yoo, C.M.; Harada, T.; Hirano, S.; Okawa, H.; Sasaki, M. Primordial black hole formation from massless scalar isocurvature. Phys. Rev. D 2022, 105, 103538. [Google Scholar] [CrossRef]
- Escrivà, A.; Germani, C.; Sheth, R.K. Analytical thresholds for black hole formation in general cosmological backgrounds. J. Cosmol. Astropart. Phys. 2021, 1, 030. [Google Scholar] [CrossRef]
- Byrnes, C.T.; Hindmarsh, M.; Young, S.; Hawkins, M.R.S. Primordial black holes with an accurate QCD equation of state. J. Cosmol. Astropart. Phys. 2018, 8, 041. [Google Scholar] [CrossRef]
- Papanikolaou, T. Toward the primordial black hole formation threshold in a time-dependent equation-of-state background. Phys. Rev. D 2022, 105, 124055. [Google Scholar] [CrossRef]
- Escrivà, A.; Bagui, E.; Clesse, S. Simulations of PBH formation at the QCD epoch and comparison with the GWTC-3 catalog. J. Cosmol. Astropart. Phys. 2023, 5, 004. [Google Scholar] [CrossRef]
- Musco, I.; Jedamzik, K.; Young, S. Primordial black hole formation during the QCD phase transition: Threshold, mass distribution, and abundance. Phys. Rev. D 2024, 109, 083506. [Google Scholar] [CrossRef]
- Jedamzik, K. Primordial black hole formation during cosmic phase transitions. arXiv 2024, arXiv:2406.11417. [Google Scholar]
- Musco, I.; Papanikolaou, T. Primordial black hole formation for an anisotropic perfect fluid: Initial conditions and estimation of the threshold. Phys. Rev. D 2022, 106, 083017. [Google Scholar] [CrossRef]
- Khlopov, M.Y.; Polnarev, A.G. Primordial black holes as a cosmological test of grand unification. Phys. Lett. B 1980, 97, 383–387. [Google Scholar] [CrossRef]
- Polnarev, A.G.; Khlopov, M.Y. Primordial Black Holes and the ERA of Superheavy Particle Dominance in the Early Universe. Sov. Astron. 1981, 25, 406. [Google Scholar]
- Polnarev, A.G.; Khlopov, M.Y. Dustlike Stages in the Early Universe and Constraints on the Primordial Black-Hole Spectrum. Sov. Astron. 1982, 26, 391–395. [Google Scholar]
- Polnarev, A.G.; Khlopov, M.Y. Cosmology, primordial black holes, and supermassive particles. Sov. Phys. Uspekhi 1985, 28, 213–232. [Google Scholar] [CrossRef]
- Harada, T.; Yoo, C.M.; Kohri, K.; Nakao, K.I.; Jhingan, S. Primordial black hole formation in the matter-dominated phase of the Universe. Astrophys. J. 2016, 833, 61. [Google Scholar] [CrossRef]
- Klauder, J.R. (Ed.) Magic Without Magic—John Archibald Wheeler. A Collection of Essays in Honor of His 60th Birthday; Freeman: San Francisco, CA, USA, 1972. [Google Scholar]
- Misner, C.W.; Thorne, K.S.; Wheeler, J.A. Gravitation; W. H. Freeman: San Francisco, CA, USA, 1973. [Google Scholar]
- Kopp, M.; Hofmann, S.; Weller, J. Separate Universes Do Not Constrain Primordial Black Hole Formation. Phys. Rev. D 2011, 83, 124025. [Google Scholar] [CrossRef]
- Harada, T.; Jhingan, S. Spherical and nonspherical models of primordial black hole formation: Exact solutions. Prog. Theor. Exp. Phys. 2016, 2016, 093E04. [Google Scholar] [CrossRef]
- Kokubu, T.; Kyutoku, K.; Kohri, K.; Harada, T. Effect of Inhomogeneity on Primordial Black Hole Formation in the Matter Dominated Era. Phys. Rev. D 2018, 98, 123024. [Google Scholar] [CrossRef]
- Harada, T.; Kohri, K.; Sasaki, M.; Terada, T.; Yoo, C.M. Threshold of primordial black hole formation against velocity dispersion in matter-dominated era. J. Cosmol. Astropart. Phys. 2023, 2, 038. [Google Scholar] [CrossRef]
- Harada, T.; Yoo, C.M.; Kohri, K.; Nakao, K.I. Spins of primordial black holes formed in the matter-dominated phase of the Universe. Phys. Rev. D 2017, 96, 083517, Erratum in Phys. Rev. D 2019, 99, 069904. [Google Scholar] [CrossRef]
- Padilla, L.E.; Hidalgo, J.C.; Malik, K.A. New mechanism for primordial black hole formation during reheating. Phys. Rev. D 2022, 106, 023519. [Google Scholar] [CrossRef]
- Padilla, L.E.; Hidalgo, J.C.; Núñez, D. Long-wavelength nonlinear perturbations of a complex scalar field. Phys. Rev. D 2021, 104, 083513. [Google Scholar] [CrossRef]
- Hidalgo, J.C.; Padilla, L.E.; German, G. Production of PBHs from inflaton structures. Phys. Rev. D 2023, 107, 063519. [Google Scholar] [CrossRef]
- de Jong, E.; Aurrekoetxea, J.C.; Lim, E.A. Primordial black hole formation with full numerical relativity. J. Cosmol. Astropart. Phys. 2022, 3, 029. [Google Scholar] [CrossRef]
- de Jong, E.; Aurrekoetxea, J.C.; Lim, E.A.; França, T. Spinning primordial black holes formed during a matter-dominated era. J. Cosmol. Astropart. Phys. 2023, 10, 067. [Google Scholar] [CrossRef]
- Aurrekoetxea, J.C.; Clough, K.; Muia, F. Oscillon formation during inflationary preheating with general relativity. Phys. Rev. D 2023, 108, 023501. [Google Scholar] [CrossRef]
- Choptuik, M.W. Universality and scaling in gravitational collapse of a massless scalar field. Phys. Rev. Lett. 1993, 70, 9–12. [Google Scholar] [CrossRef]
- Evans, C.R.; Coleman, J.S. Observation of critical phenomena and selfsimilarity in the gravitational collapse of radiation fluid. Phys. Rev. Lett. 1994, 72, 1782–1785. [Google Scholar] [CrossRef]
- Koike, T.; Hara, T.; Adachi, S. Critical behavior in gravitational collapse of radiation fluid: A Renormalization group (linear perturbation) analysis. Phys. Rev. Lett. 1995, 74, 5170–5173. [Google Scholar] [CrossRef]
- Niemeyer, J.C.; Jedamzik, K. Dynamics of primordial black hole formation. Phys. Rev. D 1999, 59, 124013. [Google Scholar] [CrossRef]
- Hawke, I.; Stewart, J.M. The dynamics of primordial black hole formation. Class. Quant. Grav. 2002, 19, 3687–3707. [Google Scholar] [CrossRef]
- Maison, D. Nonuniversality of critical behavior in spherically symmetric gravitational collapse. Phys. Lett. B 1996, 366, 82–84. [Google Scholar] [CrossRef]
- Niemeyer, J.C.; Jedamzik, K. Near-critical gravitational collapse and the initial mass function of primordial black holes. Phys. Rev. Lett. 1998, 80, 5481–5484. [Google Scholar] [CrossRef]
- Yokoyama, J. Cosmological constraints on primordial black holes produced in the near critical gravitational collapse. Phys. Rev. D 1998, 58, 107502. [Google Scholar] [CrossRef]
- Press, W.H.; Schechter, P. Formation of galaxies and clusters of galaxies by selfsimilar gravitational condensation. Astrophys. J. 1974, 187, 425–438. [Google Scholar] [CrossRef]
- Peebles, P.J.E. Principles of Physical Cosmology; Princeton University Press: Princeton, NJ, USA, 2020. [Google Scholar]
- Young, S.; Byrnes, C.T. Primordial black holes in non-Gaussian regimes. J. Cosmol. Astropart. Phys. 2013, 8, 052. [Google Scholar] [CrossRef]
- Pi, S. Non-Gaussianities in primordial black hole formation and induced gravitational waves. arXiv 2024, arXiv:2404.06151. [Google Scholar]
- Bardeen, J.M.; Bond, J.R.; Kaiser, N.; Szalay, A.S. The Statistics of Peaks of Gaussian Random Fields. Astrophys. J. 1986, 304, 15–61. [Google Scholar] [CrossRef]
- Yoo, C.M.; Harada, T.; Garriga, J.; Kohri, K. Primordial black hole abundance from random Gaussian curvature perturbations and a local density threshold. Prog. Theor. Exp. Phys. 2018, 2018, 123E01, Erratum in Prog. Theor. Exp. Phys. 2024, 2024, 049202. [Google Scholar] [CrossRef]
- Yoo, C.M.; Harada, T.; Hirano, S.; Kohri, K. Abundance of Primordial Black Holes in Peak Theory for an Arbitrary Power Spectrum. Prog. Theor. Exp. Phys. 2021, 2021, 013E02, Erratum in Prog. Theor. Exp. Phys. 2024, 2024, 049203. [Google Scholar] [CrossRef]
- Germani, C.; Sheth, R.K. Nonlinear statistics of primordial black holes from Gaussian curvature perturbations. Phys. Rev. D 2020, 101, 063520. [Google Scholar] [CrossRef]
- Kitajima, N.; Tada, Y.; Yokoyama, S.; Yoo, C.M. Primordial black holes in peak theory with a non-Gaussian tail. J. Cosmol. Astropart. Phys. 2021, 10, 053. [Google Scholar] [CrossRef]
- Germani, C.; Sheth, R.K. The Statistics of Primordial Black Holes in a Radiation-Dominated Universe: Recent and New Results. Universe 2023, 9, 421. [Google Scholar] [CrossRef]
- Young, S. Computing the abundance of primordial black holes. arXiv 2024, arXiv:2405.13259. [Google Scholar]
- De Luca, V.; Franciolini, G.; Pani, P.; Riotto, A. The evolution of primordial black holes and their final observable spins. J. Cosmol. Astropart. Phys. 2020, 4, 052. [Google Scholar] [CrossRef]
- Chiba, T.; Yokoyama, S. Spin Distribution of Primordial Black Holes. Prog. Theor. Exp. Phys. 2017, 2017, 083E01. [Google Scholar] [CrossRef]
- He, M.; Suyama, T. Formation threshold of rotating primordial black holes. Phys. Rev. D 2019, 100, 063520. [Google Scholar] [CrossRef]
- De Luca, V.; Desjacques, V.; Franciolini, G.; Malhotra, A.; Riotto, A. The initial spin probability distribution of primordial black holes. J. Cosmol. Astropart. Phys. 2019, 5, 018. [Google Scholar] [CrossRef]
- Harada, T.; Yoo, C.M.; Kohri, K.; Koga, Y.; Monobe, T. Spins of primordial black holes formed in the radiation-dominated phase of the universe: First-order effect. Astrophys. J. 2021, 908, 140. [Google Scholar] [CrossRef]
- Koga, Y.; Harada, T.; Tada, Y.; Yokoyama, S.; Yoo, C.M. Effective Inspiral Spin Distribution of Primordial Black Hole Binaries. Astrophys. J. 2022, 939, 65. [Google Scholar] [CrossRef]
- Banerjee, I.K.; Harada, T. Spin of Primordial Black Holes from Broad Power Spectrum: Radiation Dominated Universe. arXiv 2024, arXiv:2409.06494. [Google Scholar]
- Saito, D.; Harada, T.; Koga, Y.; Yoo, C.M. Spins of primordial black holes formed with a soft equation of state. J. Cosmol. Astropart. Phys. 2023, 7, 030. [Google Scholar] [CrossRef]
- Saito, D.; Harada, T.; Koga, Y.; Yoo, C.M. Revisiting spins of primordial black holes in a matter-dominated era based on peak theory. arXiv 2024, arXiv:2409.00435. [Google Scholar] [CrossRef]
- Yoo, C.M.; Harada, T.; Okawa, H. Threshold of Primordial Black Hole Formation in Nonspherical Collapse. Phys. Rev. D 2020, 102, 043526, Erratum in Phys. Rev. D 2023, 107, 049901. [Google Scholar] [CrossRef]
- Yoo, C.M. Primordial black hole formation from a nonspherical density profile with a misaligned deformation tensor. arXiv 2024, arXiv:2403.11147. [Google Scholar] [CrossRef]
- Escrivà, A.; Atal, V.; Garriga, J. Formation of trapped vacuum bubbles during inflation, and consequences for PBH scenarios. J. Cosmol. Astropart. Phys. 2023, 10, 035. [Google Scholar] [CrossRef]
- Uehara, K.; Escrivà, A.; Harada, T.; Saito, D.; Yoo, C.M. Numerical simulation of type II primordial black hole formation. arXiv 2024, arXiv:2401.06329. [Google Scholar]
- Hayward, S.A. General laws of black hole dynamics. Phys. Rev. D 1994, 49, 6467–6474. [Google Scholar] [CrossRef]
- Hayward, S.A. Gravitational energy in spherical symmetry. Phys. Rev. D 1996, 53, 1938–1949. [Google Scholar] [CrossRef]
- Maeda, H.; Harada, T.; Carr, B.J. Cosmological wormholes. Phys. Rev. D 2009, 79, 044034. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).