An Isotropic Cosmological Model with Aetherically Active Axionic Dark Matter

Abstract

Within the framework of the extended Einstein–aether–axion theory, we studied the model of a two-level aetheric control over the evolution of a spatially isotropic homogeneous Universe filled with axionic dark matter. Two guiding functions are introduced, which depend on the expansion scalar of the aether flow being equal to the tripled Hubble function. The guiding function of the first type enters the aetheric effective metric, which modifies the kinetic term of the axionic system; the guiding function of the second type predetermines the structure of the potential axion field. We obtained new exact solutions to the total set of master equations in the model (with and without cosmological constant), and studied four analytically solvable submodels in detail, for which both guiding functions are reconstructed and illustrations of their behavior are presented.

1. Introduction

A century ago Alexander Friedmann formulated the prediction that our Universe expands, and this event predetermined all further developments in cosmology and space sciences. While remaining within this general concept, modern cosmology focuses on describing the details of this expansion; in particular, the rate of expansion at different epochs. New sensational results obtained from observations made in the last decade have become the basis for restructuring our ideas about the history of the early Universe. The discovery of gravitational radiation was the first important event, which made theorists think about the validity of previous ideas. Indeed, in 2015, the first observation of gravitational waves from the black hole merger [1] presented researchers with a dilemma. In this event the masses of the colliding black holes were predicted to be of 36 and 29 $M_{\left(\mathrm{Sun}\right)}$, while mass values in the range 2.5–10 $M_{\left(\mathrm{Sun}\right)}$, predicted by the theory of stellar collapse, seemed to be reasonable. Then, the gravitational wave event indicated, as GW trigger S190521g (GW 190521) [2] has shown, that the black holes with the masses 85 and 66 $M_{\left(\mathrm{Sun}\right)}$ collided; the general consensus is that the mass of at least one of these black holes lies in a mass range that excludes its birth from being due to the collapse of a star. The discovery of black hole with so-called intermediate mass of 91.000 $M_{\left(\mathrm{Sun}\right)}$ [3], the existence of which can not be explained by the existing theories, completed the formulation of the dilemma: either it is necessary to abandon this interpretation, or admit that there is a new unknown mechanism for the formation of black holes. Fortunately, the second trend has triumphed and now theorists are actively involved in adequately extending the models for the birth of black holes. Another amazing theory is connected to observations from the newest James Webb Space Telescope (JWST). New observational data suggest the discovery of an extremely magnified monster star, estimations of the masses of warm dark matter particles and of the axion dark matter particles [4] and the abundance of carbon-containing molecules [5]. But the most important event, from our point of view, is the discovery of enormous distant galaxies that should not exist if one follows the standard model of the early Universe evolution. To be brief, the galaxies found in the JWST images [6] appeared to be shockingly big, and the stars in them too old, and these findings are in conflict with existing models. In other words, rapid development is predicted in the theory of the evolution of the early Universe over the next few years, and modifications to the current cosmological models are highly welcome.

At the moment, the most adequate picture of the Universe contains an early era of inflation, epochs of the domination of radiation and matter, and a late era of accelerated expansion. The theorists dream is to unify the entire history of the Universe within the framework of one cosmological model (see, e.g., [7,8,9,10,11,12,13]). The main obstacle to solving this problem is the difficulty in finding a unified equation of state for cosmic substrates that determines the rate of evolution of the Universe in the corresponding epoch. One of the attempts made was the search for the time-dependent parameters of the equation of state, and the introduction of a cosmological term depending on time. However, such attempts were considered unsuccessful because cosmological time is not an invariant, and therefore such equations of state are associated with the loss of covariance in the theory. A similar problem arises, when one tries to define the equation of state in terms of the redshift value Z, or equivalently, via the scale factor $a\left(t\right)$.

We follow another type of logic. We admit that the parameters of the equation of state depend on the set of scalars, which are formed on the basis of fundamental fields inherent to the cosmological model under consideration. To be more precise, we take the unit timelike vector field $U^j$ associated with the four-vector velocity of the dynamic aether [14,15,16,17] and consider the invariants obtained in the course of the decomposition of its covariant derivative ${\nabla }_k{U}^j$. In other words, we use four differential invariants (the expansion scalar of the aether flow, $\Theta ={\nabla }_k{U}^k$, the squares of the four-vector acceleration, and of the shear and vorticity tensors, $a^2$, ${\sigma }^2$, ${\omega }^2$, respectively), as the arguments of the parameters included in the equations of state. This means that we follow the paradigm of aetheric control over the evolution of physical systems (see, e.g., [18,19,20,21,22]). We must emphasize that, depending on the spacetime symmetry of the model, a part of the listed arguments can disappear. For instance, for the static spherically symmetrical model, we find that $\Theta =0$, ${\sigma }^2=0$, ${\omega }^2=0$, and we construct the guiding functions using $a^2$ only. For the Gödel spacetime, the only ${\omega }^2$ is non-vanishing. For the spacetime with planar gravitational waves we have to work with two non-vanishing scalars: $\Theta$ and ${\sigma }^2$. Spatially isotropic homogeneous cosmological models are unique in this sense, since for them, only the scalar $\Theta$ is non-vanishing, and this scalar coincides with the tripled Hubble function $\Theta =3H\left(t\right)$. In this context, the function $H\left(t\right)$ can be chosen as an appropriate argument of the guiding parameters of such cosmological models, unifying the paradigm of aetheric control over the evolution of physical systems on the one hand, and the physical interpretation of the theory predictions on the other hand. Since the function H has the dimensionality of inverse time (we consider the units with $c=1$), this quantity is often used to determine a specific time scale in a corresponding cosmological epoch.

In this paper we work within the Einstein–aether–axion model on the Friedmann–Lemaître–Robertson–Walker spacetime platform, and consider the interaction of the gravitational field, the pseudoscalar (axion) field $\varphi$, and the unit timelike vector field $U^j$. Two guiding functions depending on the scalar $\Theta$ are introduced into the Lagrangian. The guiding function of the first type, $\mathcal{A}(\Theta )$, enters the so-called aetheric effective metric $G^{mn}=g^{mn}+\mathcal{A}{U}^m{U}^n$ (see [23] for history, mathematical details, and motives); it modifies the kinetic term associated with the axion field, and thus it controls the evolution of the kinetic energy of the axionic dark matter in the Universe (see, e.g., [24,25,26,27,28,29], which present the history of axions, and [30,31,32,33,34], where various aspects of the problem of axions in cosmology are discussed). The guiding function of the second type, ${\Phi }_{*}(\Theta )$, enters the potential of the axion field, $V\left(\varphi ,{\Phi }_{*}\right)$, thus performing control over the evolution of the potential energy of the axionic dark matter. The set of master equations for the model is solved in quadratures and partially in the analytic form; the corresponding functions $\mathcal{A}(\Theta )$ and ${\Phi }_{*}(\Theta )$ are reconstructed.

The paper is organized as follows. Section 2 contains a description of the mathematical formalism. In Section 3 we analyze the key equations of the spatially isotropic homogeneous cosmological model and discuss the obtained solutions. Section 4 contains a discussion and conclusions.

2. The Formalism of the Extended Einstein–Aether–Axion Theory

2.1. The Extended Action Functional and Auxiliary Quantities

The extended Einstein–aether–axion theory is formulated on the basis of the following action functional:

$$-S_{\left(\mathrm{total}\right)}=\int d^{4}x\sqrt{-g}\left\{\frac{1}{2\kappa }\left[R+2\Lambda +\lambda \left(g_{mn}{U}^m{U}^n-1\right)+{\mathcal{K}}_{mn}^{ab}{\nabla }_a{U}^m{\nabla }_b{U}^n\right]+\right.$$

$$\left.+\frac{1}{2}{\Psi }_0^2\left[V(\varphi ,{\Phi }_{*})-G^{mn}{\nabla }_m\varphi {\nabla }_n\varphi \right]\right\}.$$

(1)

In this formula, the standard elements of this theory appear, such as the determinant of the spacetime metric g, the Ricci scalar R, the cosmological constant $\Lambda$, the Einstein constant $\kappa$, the Lagrange multiplier $\lambda$, the unit timelike vector field $U^i$, associated with the velocity four-vector of the aether flow, and the covariant derivative ${\nabla }_k$ with the connection consistent with spacetime metric $g_{mn}$, i.e., ${\nabla }_k{g}_{mn}=0$. Kinetic terms for the vector and axion fields contain the effective aetheric metric

$${\mathcal{K}}_{mn}^{ab}=C_1{G}^{ab}{G}_{mn}+C_2{\delta }_m^a{\delta }_n^b+C_3{\delta }_n^a{\delta }_m^b+C_4{U}^a{U}^b{G}_{mn},$$

(2)

$$G^{mn}=g^{mn}+\mathcal{A}{U}^m{U}^n,$$

(3)

where the scalar $\mathcal{A}\left(\theta \right)$ is the guiding function of the first type, and $C_1$, $C_2$, $C_3$, $C_4$ are the Jacobson coupling constants [14]. The potential of the axion field $V(\varphi ,{\Phi }_{*})$ is considered to have the periodic form

$$V(\varphi ,{\Phi }_{*})=\frac{m_A^2{\Phi }_{*}^2}{2{\pi }^2}\left[1-cos\left(\frac{2\pi \varphi }{{\Phi }_{*}}\right)\right],$$

(4)

where ${\Phi }_{*}(\Theta )$ is the guiding function of the second type, and the parameter ${\Psi }_0$ relates to the coupling constant of the axion–photon interaction $g_{A\gamma \gamma }$, $\frac{1}{{\Psi }_0}=g_{A\gamma \gamma }$. The potential (4) inherits the discrete symmetry $\frac{2\pi \varphi }{{\Phi }_{*}}\to \frac{2\pi \varphi }{{\Phi }_{*}}+2\pi n$. This periodic potential has its minima at $\varphi =n{\Phi }_{*}$. Near the minima, when $\varphi \to n{\Phi }_{*}+\psi$ and $|\frac{2\pi \psi }{{\Phi }_{*}}|$ is small, the potential takes the standard form $V\to m_A^2{\psi }^2$, where $m_A$ is the axion rest mass. When $\varphi =n{\Phi }_{*}$ (n is an integer), we deal with the axionic analog of the equilibrium state [19], since $V_{|\varphi =n{\Phi }_{*}}=0$, and ${\left(\frac{\partial V}{\partial \varphi }\right)}_{|\varphi =n{\Phi }_{*}}=0$.

The following decompositions are associated with the unit four-vector $U^j$:

$${\nabla }_k=U_{k}D+{\stackrel{\perp }{\nabla }}_k,D=U^s{\nabla }_s,{\stackrel{\perp }{\nabla }}_k={\Delta }_k^j{\nabla }_j,{\Delta }_k^j={\delta }_k^j-U^j{U}_k.$$

(5)

Here D is the convective derivative, and ${\Delta }_k^j$ is the projector. The covariant derivative ${\nabla }_k{U}_j$ can be decomposed as

$${\nabla }_k{U}_j=U_{k}D{U}_j+{\sigma }_{kj}+{\omega }_{kj}+\frac{1}{3}{\Delta }_{kj}\Theta ,$$

(6)

where the four-vector acceleration $D{U}_j\equiv a_j$, the symmetric traceless shear tensor ${\sigma }_{kj}$, the skew–symmetric vorticity tensor ${\omega }_{kj}$, and the expansion scalar $\Theta$ are presented by the well-known formulas

$$D{U}_j=U^s{\nabla }_s{U}_j,{\sigma }_{kj}=\frac{1}{2}\left({\stackrel{\perp }{\nabla }}_k{U}_j+{\stackrel{\perp }{\nabla }}_j{U}_k\right)-\frac{1}{3}{\Delta }_{kj}\Theta ,{\omega }_{kj}=\frac{1}{2}\left({\stackrel{\perp }{\nabla }}_k{U}_j-{\stackrel{\perp }{\nabla }}_j{U}_k\right),\Theta ={\nabla }_k{U}^k.$$

(7)

This decomposition (6) allows us to introduce one linear and three quadratic scalars

$$\Theta ={\nabla }_k{U}^k,a^2=D{U}_{k}D{U}^k,{\sigma }^2={\sigma }_{mn}{\sigma }^{mn},{\omega }^2={\omega }_{mn}{\omega }^{mn},$$

(8)

and thus the kinetic term of the vector field can be rewritten in the form

$${\mathcal{K}}_{mn}^{ab}\left({\nabla }_a{U}^m\right)\left({\nabla }_b{U}^n\right)=[C_1(1+\mathcal{A})+C_4]a^2+(C_1+C_3){\sigma }^2+(C_1-C_3){\omega }^2+\frac{1}{3}\left(C_1+3C_2+C_3\right){\Theta }^2.$$

(9)

Taking into account the constraints obtained after the detection of the event GRB170817 [35], we have to put $C_1+C_3=0$ into (9).

2.2. Master Equations of the Model

2.2.1. Master Equations for the Unit Vector Field

Variations of the extended action functional (1) with respect to the Lagrange multiplier $\lambda$ gives the normalization condition

$$g_{mn}{U}^m{U}^n=1.$$

(10)

Variation with respect to the four-vector $U^i$ gives the aetheric balance equations

$${\nabla }_a{\mathcal{J}}^{aj}=\lambda U^j-\mathcal{A}\kappa {\Psi }_0^{2}D\varphi {\nabla }^j\varphi -{\nabla }^j\left({\Omega }_1\frac{d{\Phi }_{*}}{d\Theta }+{\Omega }_2\frac{d\mathcal{A}}{d\Theta }\right),$$

(11)

where the following definitions are used:

$${\mathcal{J}}^{aj}={\mathcal{K}}^{abjn}{\nabla }_b{U}_n=C_1\left({\nabla }^a{U}^j-{\nabla }^j{U}^a\right)+C_2{g}^{aj}\Theta +\left(C_4+C_1\mathcal{A}\right)U^{a}D{U}^j,$$

(12)

$${\Omega }_1=\frac{\kappa {\Psi }_0^2{m}_A^2}{2{\pi }^2}\left\{{\Phi }_{*}\left[1-cos\left(\frac{2\pi \varphi }{{\Phi }_{*}}\right)\right]-\pi \varphi sin\left(\frac{2\pi \varphi }{{\Phi }_{*}}\right)\right\},$$

(13)

$${\Omega }_2=-\frac{1}{2}\kappa {\Psi }_0^2{\left(D\varphi \right)}^2.$$

(14)

Convolution of (11) with $U_j$ gives us the Lagrange multiplier $\lambda$:

$$\lambda =U_j{\nabla }_a{\mathcal{J}}^{aj}+\mathcal{A}\kappa {\Psi }_0^2{\left(D\varphi \right)}^2+D\left({\Omega }_1\frac{d{\Phi }_{*}}{d\Theta }+{\Omega }_2\frac{d\mathcal{A}}{d\Theta }\right).$$

(15)

2.2.2. Master Equation for the Axion Field

Variation in the extended action functional (1) with respect to the axion field yields means that

$${\nabla }_m\left[\left(g^{mn}+\mathcal{A}{U}^m{U}^n\right){\nabla }_n\varphi \right]+\frac{m_A^2{\Phi }_{*}}{2\pi }sin\left(\frac{2\pi \varphi }{{\Phi }_{*}}\right)=0,$$

(16)

or equivalently,

$$(1+\mathcal{A})D^2\varphi +[(1+\mathcal{A})\Theta +D\mathcal{A}]D\varphi -D{U}^m{\stackrel{\perp }{\nabla }}_m\varphi +{\stackrel{\perp }{\nabla }}_m\stackrel{\perp }{{\nabla }^m}\varphi +\frac{m_A^2{\Phi }_{*}}{2\pi }sin\left(\frac{2\pi \varphi }{{\Phi }_{*}}\right)=0.$$

(17)

Below, we use the ansatz that, when the axion field is in the equilibrium state, which corresponds to the basic minimum $\varphi ={\Phi }_{*}$, we obtain the master equation for the guiding function of the second type ${\Phi }_{*}(\Theta )$, i.e.,

$${\nabla }_m\left[\left(g^{mn}+\mathcal{A}{U}^m{U}^n\right){\nabla }_n{\Phi }_{*}\right]=0.$$

(18)

2.2.3. Master Equations for the Gravitational Field

Variation in the extended action functional (1) with respect to the metric gives the gravity field equation

$$R_{ik}-\frac{1}{2}R{g}_{ik}-\Lambda g_{ik}=T_{ik}^{\left(\mathrm{U}\right)}+\kappa T_{ik}^{\left(\mathrm{A}\right)}+T_{ik}^{\left(\mathrm{INT}\right)}.$$

(19)

The extended stress-energy tensor of the aether $T_{ik}^{\left(\mathrm{U}\right)}$ contains the following elements:

$$T_{ik}^{\left(\mathrm{U}\right)}=\frac{1}{2}{g}_{ik}{\mathcal{K}}_{mn}^{ab}{\nabla }_a{U}^m{\nabla }_b{U}^n+{\nabla }^m\left[U_{(i}{\mathcal{J}}_{k)m}-{\mathcal{J}}_{m(i}{U}_{k)}-{\mathcal{J}}_{\left(ik\right)}{U}_m\right]+U_i{U}_k{U}_j{\nabla }_a{\mathcal{J}}^{aj}+$$

(20)

$$+C_1\left[\left({\nabla }_m{U}_i\right)\left({\nabla }^m{U}_k\right)-\left({\nabla }_i{U}_m\right)\left({\nabla }_k{U}^m\right)\right]+(C_4+C_1\mathcal{A})\left(D{U}_{i}D{U}_k-U_i{U}_{k}D{U}_{m}D{U}^m\right).$$

As usual, the parentheses symbolize the symmetrization of indices. The extended stress-energy tensor of the axion field is of the form:

$$T_{ik}^{\left(\mathrm{A}\right)}={\Psi }_0^2\left[\left(1+\mathcal{A}\right){\dot{\varphi }}^2\left(U_i{U}_k-\frac{1}{2}{g}_{ik}\right)+\frac{1}{2}{g}_{ik}V\right].$$

(21)

The part of the total stress-energy tensor associated with the interaction terms contains the derivatives of the guiding functions $\mathcal{A}$ and ${\Phi }_{*}$ with respect to their argument $\Theta$:

$$T_{ik}^{\left(\mathrm{INT}\right)}=-g_{ik}\Theta \left({\Omega }_1\frac{d{\Phi }_{*}}{d\Theta }+{\Omega }_2\frac{d\mathcal{A}}{d\Theta }\right)-{\Delta }_{ik}\left[D\left({\Omega }_1\frac{d{\Phi }_{*}}{d\Theta }+{\Omega }_2\frac{d\mathcal{A}}{d\Theta }\right)\right].$$

(22)

The Bianchi identity

$${\nabla }^k\left[T_{ik}^{\left(\mathrm{U}\right)}+\kappa T_{ik}^{\left(\mathrm{A}\right)}+T_{ik}^{\left(\mathrm{INT}\right)}\right]=0$$

(23)

automatically holds for the solutions to the master equations for the vector and pseudoscalar fields.

3. Application to the Spatially Isotropic Homogeneous Cosmological Model

3.1. The Spacetime Platform, Reduced Master Equations, and Their Solutions

3.1.1. Geometric Aspects

Below, we work with the Friedmann–Lemaître–Robinson–Walker type spacetime, using the metric

$$d{s}^2=d{t}^2-a^2\left(t\right)\left(d{x}^2+d{y}^2+d{z}^2\right).$$

(24)

The four-vector velocity of the aether flow is known to be in the form $U^j={\delta }_0^j$, and the corresponding covariant derivative of the vector field has the following decomposition

$${\nabla }_k{U}_i=\frac{1}{2}{\dot{g}}_{ik}=\frac{\dot{a}}{a}{\Delta }_{ik}=H{\Delta }_{ik}=\frac{1}{3}\Theta {\Delta }_{ik}.$$

(25)

Clearly, in this case, $D{U}_j=0$, ${\sigma }_{mn}=0$, ${\omega }_{mn}=0$, $\Theta =3H=3\frac{\dot{a}}{a}$, and, standardly, the dot denote the derivative with respect to the cosmological time t.

3.1.2. Solution to the Equations for the Vector Field

Keeping in mind that $D{U}_j=0$, ${\sigma }_{mn}=0$, ${\omega }_{mn}=0$, we find that the extended Jacobson’s tensor (12) converts into

$$J^{aj}=C_2\Theta g^{aj},$$

(26)

and the equations for the unit vector field (11) take the form

$$C_2{\nabla }_j\Theta =\lambda U_j-\kappa {\Psi }_0^2\mathcal{A}{U}_j{\dot{\varphi }}^2-{\nabla }_j\left({\Omega }_1\frac{d{\Phi }_{*}}{d\Theta }+{\Omega }_2\frac{d\mathcal{A}}{d\Theta }\right).$$

(27)

Equation (27) contains only one non-trivial equation, which gives the solution for the Lagrange multiplier $\lambda$:

$$\lambda =C_2\dot{\Theta }+\kappa {\Psi }_0^2\mathcal{A}{\dot{\varphi }}^2+\frac{d}{dt}\left({\Omega }_1\frac{d{\Phi }_{*}}{d\Theta }+{\Omega }_2\frac{d\mathcal{A}}{d\Theta }\right).$$

(28)

Thus, the aetheric subset of the total system of master equations is solved.

3.1.3. First Integral of the Reduced Equation for the Axion Field

We suppose that the axion field $\varphi$ is frozen at the first minimum of the axion potential, i.e., $\varphi ={\Phi }_{*}\left(t\right)$. Then we put $\varphi ={\Phi }_{*}$ into (17) and obtain the key equation for ${\Phi }_{*}\left(t\right)$

$$(1+\mathcal{A}){\ddot{\Phi }}_{*}+\left[3(1+\mathcal{A})\frac{\dot{a}}{a}+\dot{\mathcal{A}}\right]{\dot{\Phi }}_{*}=0,$$

(29)

which admits the first integral with

$${\dot{\Phi }}_{*}\left(t\right)=\frac{\mathrm{const}}{a^3\left(t\right)[1+\mathcal{A}\left(t\right)]}={\dot{\Phi }}_{*}\left(t_0\right){\left[\frac{a\left(t_0\right)}{a\left(t\right)}\right]}^3\frac{\left[1+\mathcal{A}\left(t_0\right)\right]}{\left[1+\mathcal{A}\left(t\right)\right]}.$$

(30)

The parameter $t_0$ describes the initial time moment; $\mathcal{A}\left(t_0\right)$ is the initial value of the guiding function of the first type; and ${\dot{\Phi }}_{*}\left(t_0\right)$ indicates the initial value of the first derivative of the guiding function of the second type.

3.1.4. Key Equations for the Gravity Field

When $\varphi ={\Phi }_{*}$, the function ${\Omega }_1$ takes zero value, and the reduced extended equations of the gravitational field can be converted into one key equation

$$\frac{1}{3}{\Theta }^2\left(1+\frac{3}{2}{C}_2\right)-\Lambda =\frac{1}{2}\kappa {\Psi }_0^2{\dot{\Phi }}_{*}^2\left[1+\mathcal{A}+\Theta \frac{d\mathcal{A}}{d\Theta }\right].$$

(31)

Since ${\dot{\Phi }}_{*}$ has already been found and is of the form (30), we obtain the equation, which connects the scalar $\Theta$ with the reduced scale factor $x=\frac{a\left(t\right)}{a\left(t_0\right)}$ as follows:

$$\frac{1}{3}{\Theta }^2\left(1+\frac{3}{2}{C}_2\right)-\Lambda =\frac{1}{2x^6}\kappa {\Psi }_0^2{\dot{\Phi }}_{*}^2\left(t_0\right){\left[1+\mathcal{A}\left(t_0\right)\right]}^2\left[\frac{1}{1+\mathcal{A}}-\Theta \frac{d}{d\Theta }\left(\frac{1}{1+\mathcal{A}}\right)\right].$$

(32)

Then, we assume that $C_2>-\frac{2}{3}$, $\Lambda >0$, and introduce the auxiliary parameters

$$H_{\infty }=\sqrt{\frac{\Lambda }{3\left(\left(1+\frac{3}{2}{C}_2\right)\right)}},h^2=\frac{\kappa {\Psi }_0^2{\dot{\Phi }}^2\left(t_0\right){\left[1+\mathcal{A}\left(t_0\right)\right]}^2}{6\left(1+\frac{3}{2}{C}_2\right)}.$$

(33)

Now we are ready to analyze the main equation of the model for the function $H\left(x\right)$

$$x^6\left[H^2-H_{\infty }^2\right]=h^2\left[\frac{1}{1+\mathcal{A}}-H\frac{d}{dH}\left(\frac{1}{1+\mathcal{A}}\right)\right].$$

(34)

3.2. Modeling of the Guiding Function of the First Type

When we discuss the structure of the guiding function of the first type we use two assumptions. First, we assume that $\mathcal{A}=0$, if $\Theta =0$. Second, we assume that the right-hand side of the Equation (34) is a regular function of its argument H, and thus we can use the decomposition

$$\left[\frac{1}{1+\mathcal{A}}-H\frac{d}{dH}\left(\frac{1}{1+\mathcal{A}}\right)\right]=1-{\gamma }_{1}H-{\gamma }_2{H}^2-2{\gamma }_3{H}^3-3{\gamma }_4{H}^4-...$$

(35)

This decomposition allows us to reconstruct the function $\frac{1}{1+\mathcal{A}}$, which has the form

$$\frac{1}{1+\mathcal{A}}=1+{\gamma }_{1}H\left[1+log\frac{H}{H_{*}}\right]+{\gamma }_2{H}^2+{\gamma }_3{H}^3+{\gamma }_4{H}^4+...$$

(36)

Here, $H_{*}$ is some constant of integration. The key to our consideration is the analysis of the asymptotic regime ($x\to \infty$ ) of the equation

$$x^6\left[H^2-H_{\infty }^2\right]=h^2\left[1-{\gamma }_{1}H-{\gamma }_2{H}^2-2{\gamma }_3{H}^3-3{\gamma }_4{H}^4-...\right].$$

(37)

If we restrict ourselves with the term $H^m$ in the right-hand side of (37), we see that, first, $H^{m-2}\propto x^6$, second, $H\propto x^{\frac{6}{m-2}}$, and third, $a\left(t\right)\propto t^{-\frac{m-2}{6}}$. In other words, if $m>2$, the Universe collapses asymptotically, and this detail is in contradiction with the main idea of perpetual expansion. Of course, this point is disputable, but we follow this idea. Now we deal with the quadratic equation with respect to H

$$x^6\left[H^2-H_{\infty }^2\right]=h^2\left[1-{\gamma }_{1}H-{\gamma }_2{H}^2\right],$$

(38)

and its positive solution is

$$H\left(x\right)=\sqrt{\frac{{\gamma }_1^2{h}^4}{4{(x^6+{\gamma }_2{h}^2)}^2}+\frac{H_{\infty }^2{x}^6+h^2}{x^6+{\gamma }_2{h}^2}}-\frac{{\gamma }_1{h}^2}{2(x^6+{\gamma }_2{h}^2)}.$$

(39)

With the function $H\left(x\right)$, one can reconstruct the scale factor as the function of time if we use the formal quadrature

$$t-t_0={\int }_1^{\frac{a\left(t\right)}{a\left(t_0\right)}}\frac{dx}{xH\left(x\right)}.$$

(40)

Clearly, there are two asymptotic regimes.

(1) When $\Lambda \ne 0$, $H\to H_{\infty }$ and thus $a\left(t\right)\propto e^{H_{\infty }t}$.

(2) When $\Lambda =0$, $H\propto \frac{1}{x^3}$ and thus $a\left(t\right)\propto t^{\frac{1}{3}}$.

In order to have further progress in calculations, we consider four analytically solvable submodels.

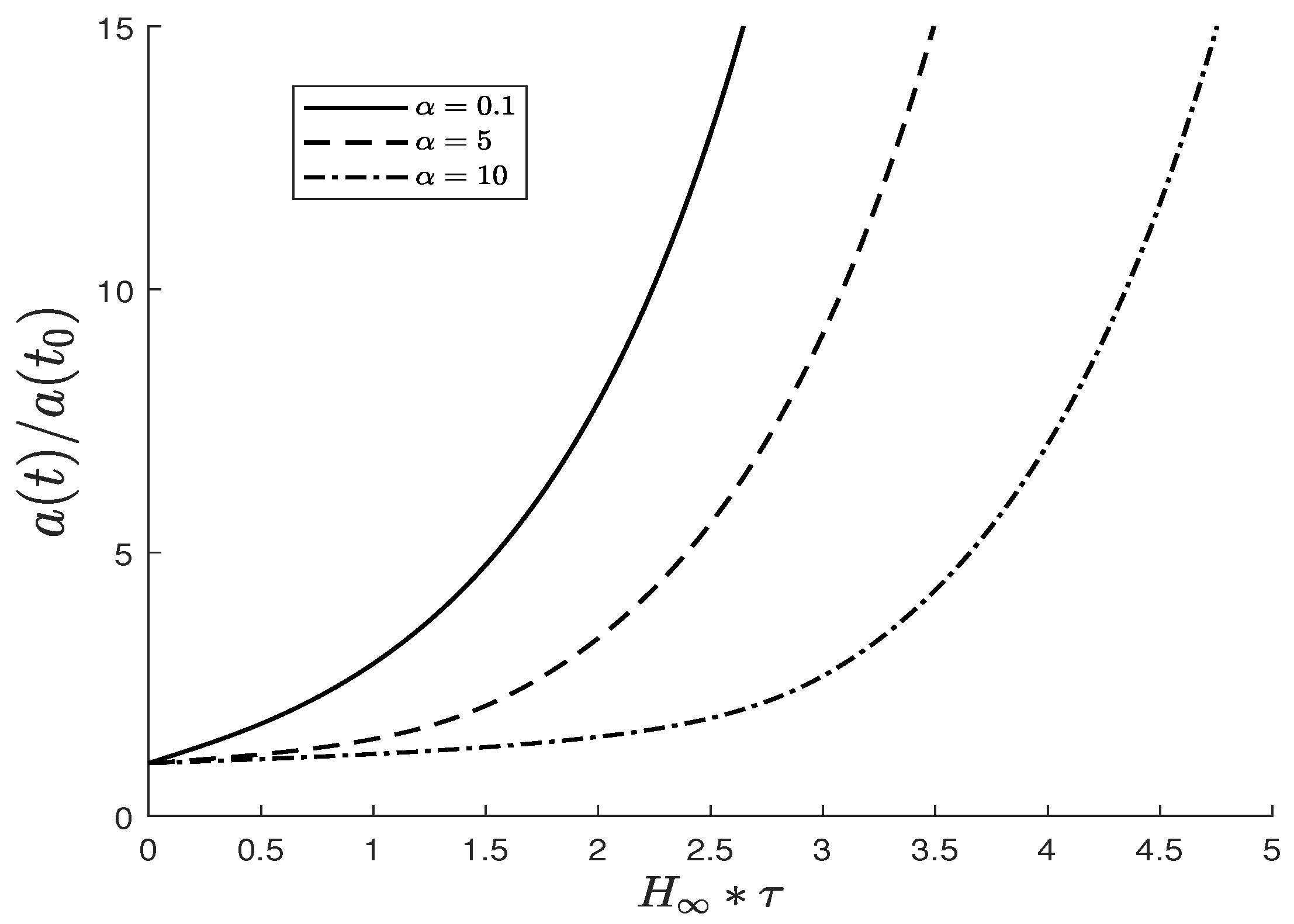
3.2.1. First Analytically Solvable Submodel

Let us consider the model with ${\gamma }_1=-\frac{1}{H_{\infty }}$ and ${\gamma }_2=0$. In this case the function $\mathcal{A}\left(H\right)$ satisfies the relationship

$$\frac{1}{1+\mathcal{A}}=1-\frac{H}{H_{\infty }}\left[1+log\frac{H}{H_{*}}\right].$$

(41)

In order to simplify the analysis, we assume that $H_{*}=H_{\infty }$ and obtain the following expression for the guiding function of the first type

$$\mathcal{A}=\frac{\frac{H}{H_{\infty }}\left(1+log\frac{H}{H_{\infty }}\right)}{1-\frac{H}{H_{\infty }}\left(1+log\frac{H}{H_{\infty }}\right)}.$$

(42)

Formally speaking, this function takes the infinite value, when the denominator is equal to zero. But this situation only appears at infinity $a=\infty$, when $H=H_{\infty }$. Now we deal with the key equation

$$H^2-H_{\infty }^2=\frac{h^2}{H_{\infty }{x}^6}\left(H_{\infty }+H\right),$$

(43)

we omit the negative root $H=-H_{\infty }$, and see that the positive solution is

$$H\left(x\right)=H_{\infty }+\frac{h^2}{H_{\infty }{x}^6}.$$

(44)

We should mention that this model is self-consistent when first, $H\left(t_0\right)>H_{\infty }$, and second, $h^2=H_{\infty }[H\left(t_0\right)-H_{\infty }]$. According to the definition in (33) the last requirement links the values $\mathcal{A}\left(t_0\right)$, $\dot{\Phi }\left(t_0\right)$, and $H\left(t_0\right)$.

The scale factor $a\left(t\right)$ and the Hubble function $H\left(t\right)$ can now be presented in the form

$$a\left(t\right)=a\left(t_0\right){\left[\left(1+\frac{h^2}{H_{\infty }^2}\right)e^{6H_{\infty }(t-t_0)}-\frac{h^2}{H_{\infty }^2}\right]}^{\frac{1}{6}},$$

(45)

$$H\left(t\right)=\frac{H_{\infty }}{\left\{1-\left[1-\frac{H_{\infty }}{H\left(t_0\right)}\right]e^{-6H_{\infty }(t-t_0)}\right\}}.$$

(46)

The acceleration parameter $-q\left(t\right)$ can be given by the formula

$$-q\left(t\right)=\frac{\ddot{a}}{a{H}^2}=1-\left(\frac{6h^2}{h^2+H_{\infty }^2}\right)e^{-6H_{\infty }(t-t_0)}$$

(47)

is the monotonic function of time, and it asymptotically tends towards one at $t\to \infty$.

Finally, we intend to reconstruct the guiding function of the second type ${\Phi }_{*}\left(H\right)$. The simplest way is the following. First, using the replacements $t\to x=\frac{a\left(t\right)}{a\left(t_0\right)}$ and $\frac{d}{dt}\to xH\left(x\right)\frac{d}{dx}$, we rewrite the relationship (30) as follows

$${\Phi }_{*}^{\prime }\left(x\right)=-\frac{{\dot{\Phi }}_{*}\left(t_0\right)\left[1+\mathcal{A}\left(t_0\right)\right]}{H_{\infty }{x}^4}\left[-\frac{H_{\infty }}{H}+1+log\left(\frac{H}{H_{\infty }}\right)\right].$$

(48)

Second, using (44), we integrate (48) and obtain

$${\Phi }_{*}\left(x\right)={\Phi }_{*}\left(t_0\right)+\frac{{\dot{\Phi }}_{*}\left(t_0\right)\left[1+\mathcal{A}\left(t_0\right)\right]}{3H_{\infty }}{\Re }_1\left(x\right),$$

(49)

$${\Re }_1\left(x\right)\equiv \left(1-\frac{1}{x^3}\right)+\frac{1}{x^3}log\left(1+\frac{h^2}{H_{\infty }^2{x}^6}\right)-log\left(1+\frac{h^2}{H_{\infty }^2}\right)+$$

(50)

$$+\frac{H_{\infty }}{\left|h\right|}\left(arctan\frac{\left|h\right|}{H_{\infty }{x}^3}-arctan\frac{\left|h\right|}{H_{\infty }}\right).$$

Third, using the replacement $\frac{1}{x^6}=\frac{H_{\infty }}{h^2}(H-H_{\infty })$, we recover the function ${\Phi }_{*}\left(H\right)$ based on the solution (49). The asymptotic value of the reconstructed guiding function is

$${\Phi }_{*}(\infty )={\Phi }_{*}\left(t_0\right)+\frac{{\dot{\Phi }}_{*}\left(t_0\right)\left[1+\mathcal{A}\left(t_0\right)\right]}{3H_{\infty }}{\Re }_1(\infty ),$$

(51)

$${\Re }_1(\infty )=1-log\left(1+\frac{h^2}{H_{\infty }^2}\right)-\frac{H_{\infty }}{\left|h\right|}arctan\frac{\left|h\right|}{H_{\infty }}.$$

Figure 1 illustrates the details of the function ${\Re }_1\left(x\right)$.

3.2.2. Second Analytically Solvable Submodel

The second submodel relates to the case when $\Lambda \ne 0$, ${\gamma }_1=0$, and ${\gamma }_2=\frac{{\alpha }^2}{H_{\infty }^2}>0$. With these assumptions, the guiding function of the first type

$$\mathcal{A}\left(H\right)=-\frac{{\gamma }_2{H}^2}{1+{\gamma }_2{H}^2}=-\frac{{\alpha }^2{H}^2}{H_{\infty }^2+{\alpha }^2{H}^2}$$

(52)

is the regular function of the Hubble function H. From the key equation for the gravity field (38) we obtain

$$H\left(x\right)=H_{\infty }\sqrt{\frac{x^6+\frac{h^2}{H_{\infty }^2}}{x^6+\frac{{\alpha }^2{h}^2}{H_{\infty }^2}}}.$$

(53)

The parameter ${\alpha }^2$ is connected to the initial value of the Hubble function as follows:

$$H\left(t_0\right)\equiv H(x=1)=H_{\infty }\sqrt{\frac{1+\frac{h^2}{H_{\infty }^2}}{1+\frac{{\alpha }^2{h}^2}{H_{\infty }^2}}}.$$

(54)

Clearly, we have to distinguish the cases ${\alpha }^2=1$ and ${\alpha }^2\ne 1$.

(1) When ${\alpha }^2=1$, we obtain that the Hubble function converts into the constant $H\left(x\right)=H\left(1\right)=H_{\infty }$, and we deal with the de Sitter type behavior of the Universe, for which $a\left(t\right)=a\left(t_0\right)e^{H_{\infty }(t-t_0)}$. The guiding function of the first type also is constant, as $\mathcal{A}=-\frac{1}{2}$, and the guiding function of the second type behaves as

$${\Phi }_{*}\left(t\right)={\Phi }_{*}\left(t_0\right)-\frac{{\dot{\Phi }}_{*}^2\left(t_0\right)a^3\left(t_0\right)}{3H_{\infty }}{e}^{-3H_{\infty }(t-t_0)}.$$

(55)

(2) When ${\alpha }^2\ne 1$, the direct integration of (40) yields

$$e^{6H_{\infty }(t-t_{*})}=\left|\frac{{(z-\alpha )}^{\alpha }(z+1)}{{(z+\alpha )}^{\alpha }(z-1)}\right|,$$

(56)

where we used the positive root $\alpha =+\sqrt{{\alpha }^2}$. The auxiliary function $z\left(t\right)$ and two new parameters, $z_{*}$ and $t_{*}$, are:

$$z=\sqrt{\frac{H_{\infty }^2{\left[\frac{a\left(t\right)}{a\left(t_0\right)}\right]}^6+{\alpha }^2{h}^2}{H_{\infty }^2{\left[\frac{a\left(t\right)}{a\left(t_0\right)}\right]}^6+h^2}},z_{*}=\sqrt{\frac{H_{\infty }^2+{\alpha }^2{h}^2}{H_{\infty }^2+h^2}},$$

(57)

$$t_{*}=t_0-\frac{1}{6H_{\infty }}log\left[\frac{(z_{*}+1){(z_{*}-\alpha )}^{\alpha }}{(z_{*}-1){(z_{*}+\alpha )}^{\alpha }}\right].$$

(58)

According to (57), $z\to 1$ when $a\to \infty$; the corresponding asymptotic behavior is characterized by the de Sitter-type law

$$a(t,\alpha )\to a\left(t_0\right){\left(\frac{h}{2H_{\infty }}\right)}^{\frac{1}{3}}{\left|\frac{1+\alpha }{1-\alpha }\right|}^{\frac{\alpha -1}{6}}{e}^{H_{\infty }(t-t_{*})}.$$

(59)

The formulas (56)–(58) give us the implicit representation. The function $a\left(t\right)$ has no extrema; we have illustrated the behavior of the scale factor in the early epoch in Figure 2.

The guiding function of the second type can be represented in terms of elliptic functions. For instance, if $0<\alpha <1$, the term

$${\Phi }_{*}\left(x\right)={\Phi }_{*}\left(t_0\right)-\frac{{\dot{\Phi }}_{*}\left(t_0\right)\left[1+\mathcal{A}\left(t_0\right)\right]}{3H_{\infty }}{\Re }_2\left(x\right)$$

(60)

contains the special function ${\Re }_2\left(x\right)$, which is equal to

$${\Re }_2\left(x\right)={\int }_1^{\frac{1}{x^3}}dz\left[\sqrt{\frac{1+{\alpha }^2\frac{h^2}{H_{\infty }^2}{z}^2}{1+\frac{h^2}{H_{\infty }^2}{z}^2}}+{\alpha }^2\sqrt{\frac{1+\frac{h^2}{H_{\infty }^2}{z}^2}{1+{\alpha }^2\frac{h^2}{H_{\infty }^2}{z}^2}}\right]=$$

(61)

$$=\frac{H_{\infty }}{h}\left\{(1+{\alpha }^2)\left[F(\phi ,k)-F\left({\phi }_{*},k\right)\right]-2\left[E(\phi ,k)-E\left({\phi }_{*},k\right)\right]\right\}+$$

$$+\frac{2}{x^3}\sqrt{\frac{H_{\infty }^2{x}^6+{\alpha }^2{h}^2}{H_{\infty }^2{x}^6+h^2}}-2\sqrt{\frac{H_{\infty }^2+{\alpha }^2{h}^2}{H_{\infty }^2+h^2}},$$

where the elliptic functions of the first and second types, respectively,

$$F(\phi ,k)\equiv {\int }_0^{\phi }\frac{d\psi }{\sqrt{1-k^2{sin}^2\psi }},E(\phi ,k)\equiv {\int }_0^{\phi }d\psi \sqrt{1-k^2{sin}^2\psi }$$

(62)

are characterized by the arguments

$$\phi =arctan\left(\frac{h}{H_{\infty }{x}^3}\right),{\phi }_{*}=arctan\left(\frac{h}{H_{\infty }}\right),k=\sqrt{1-{\alpha }^2}.$$

(63)

The asymptotic value of the guiding function of the second type is

$${\Phi }_{*}\left(x\right)={\Phi }_{*}\left(t_0\right)+\frac{{\dot{\Phi }}_{*}\left(t_0\right)\left[1+\mathcal{A}\left(t_0\right)\right]}{3H_{\infty }}\left\{\frac{H_{\infty }}{h}\left[(1+{\alpha }^2)F\left({\phi }_{*},k\right)-2E\left({\phi }_{*},k\right)\right]+2\sqrt{\frac{H_{\infty }^2+{\alpha }^2{h}^2}{H_{\infty }^2+h^2}}\right\}.$$

(64)

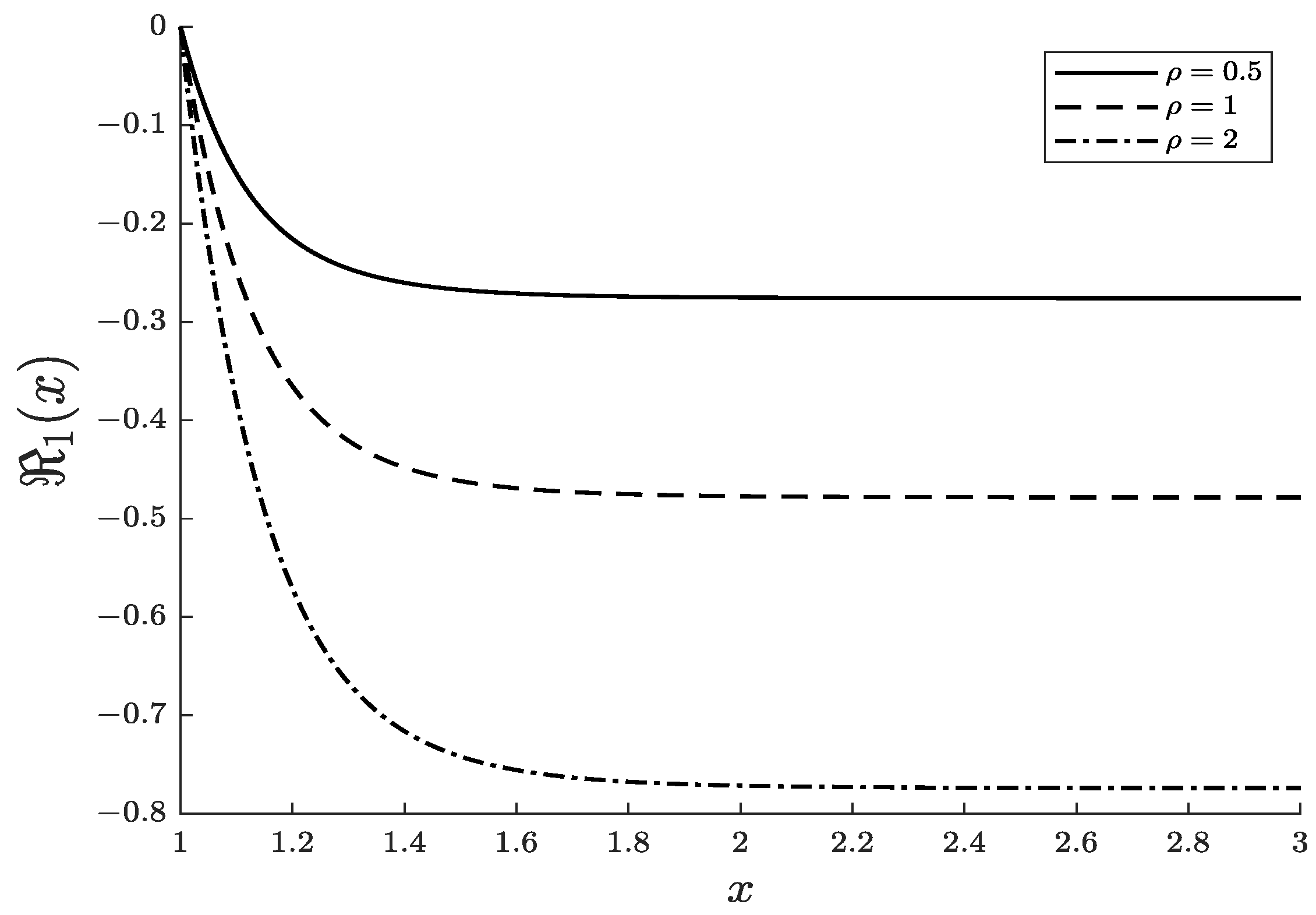
3.2.3. Third Analytically Solvable Submodel

Now we assume that the cosmological constant is equal to zero, $\Lambda =0$, i.e., $H_{\infty }=0$. Also, we assume that ${\gamma }_1=0$ and ${\gamma }_2=\frac{{\nu }^6}{h^2}>0$. Again, we find that $\mathcal{A}\left(H\right)$ is regular

$$\mathcal{A}\left(H\right)=-\frac{{\nu }^6{H}^2}{h^2+{\nu }^6{H}^2},$$

(65)

and the Hubble function is in the form

$$H\left(x\right)=\frac{\left|h\right|}{\sqrt{x^6+{\nu }^6}}.$$

(66)

Then, we obtain the reduced scale factor $x\left(t\right)$ in the implicit form

$$\frac{3\left|h\right|}{{\nu }^3}(t-t_{**})=\sqrt{1+\frac{x^6}{{\nu }^6}}-log\left[\sqrt{1+\frac{{\nu }^6}{x^6}}+\frac{{\nu }^3}{x^3}\right],$$

(67)

where we introduce, for simplicity, the formal parameter $t_{**}$

$$t_{**}=t_0-\frac{1}{3\left|h\right|}\sqrt{1+{\nu }^6}-\frac{{\nu }^3}{3\left|h\right|}log\left(\sqrt{1+{\nu }^6}-{\nu }^3\right).$$

(68)

Finally, we obtain the guiding function of the second type as the function of the reduced scale factor

$${\Phi }_{*}\left(x\right)={\Phi }_{*}\left(t_0\right)+\frac{1}{3\left|h\right|}{\dot{\Phi }}_{*}\left(t_0\right)\left[1+\mathcal{A}\left(t_0\right)\right]{\Re }_3\left(x\right).$$

(69)

$${\Re }_3\left(x\right)\equiv log\left[\frac{\left(x^3+\sqrt{{\nu }^6+x^6}\right)}{\left(1+\sqrt{1+{\nu }^6}\right)}\right]-2\sqrt{1+\frac{{\nu }^6}{x^6}}+2\sqrt{1+{\nu }^6}.$$

In the asymptotic limit $x\to \infty$, the function ${\Phi }_{*}\left(H\right)$ has the form

$${\Phi }_{*}\left(H\right)={\Phi }_{*}\left(t_0\right)-\frac{1}{3\left|h\right|}{\dot{\Phi }}_{*}\left(t_0\right)\left[1+\mathcal{A}\left(t_0\right)\right]log\left(\frac{{\nu }^{3}H}{2\left|h\right|}\right).$$

(70)

Figure 3 illustrates the behavior of the function ${\Re }_3\left(x\right)$.

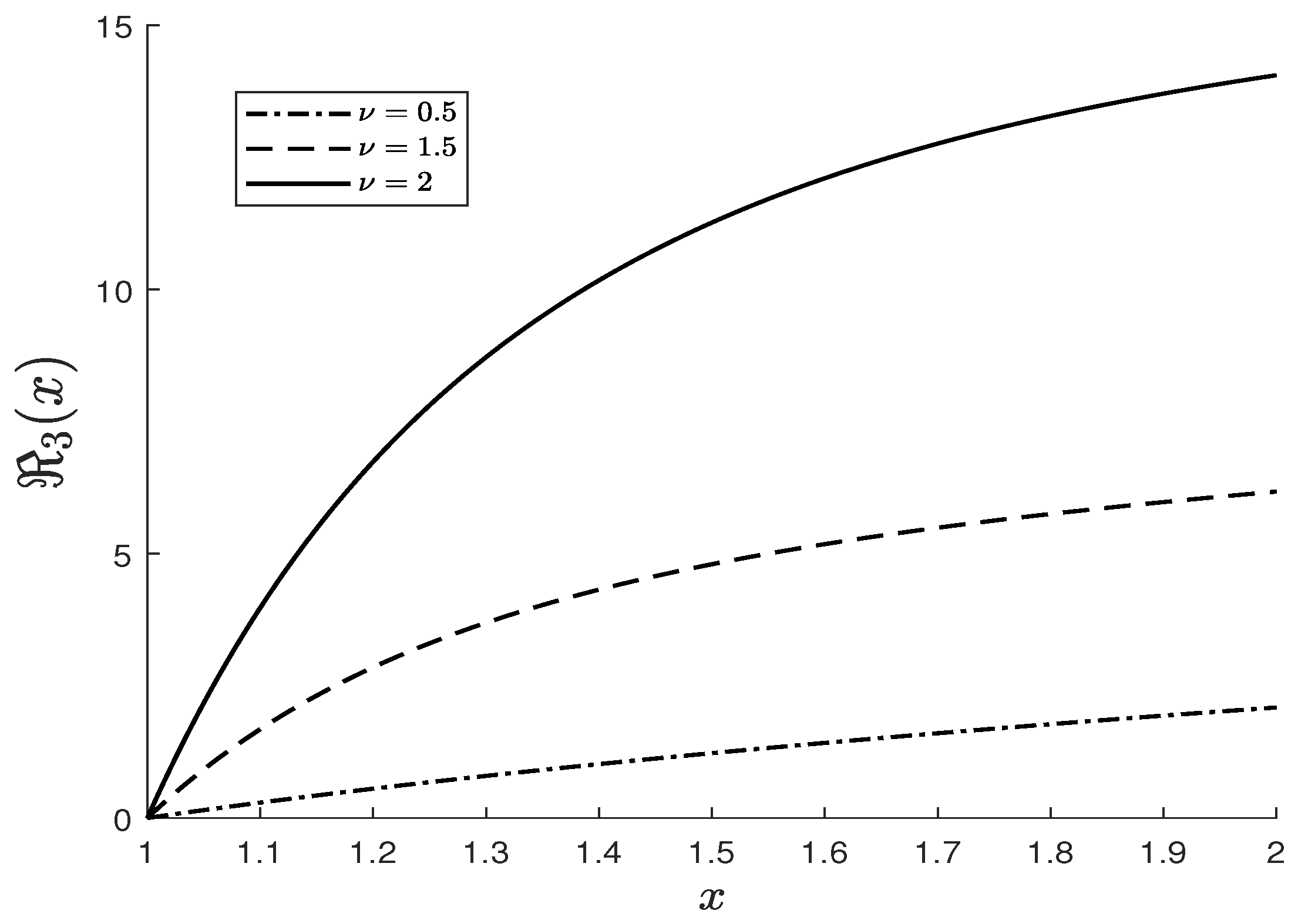
3.2.4. Special Case

The final interesting submodel relates to the case $\mathcal{A}=-1$, for which the aetheric effective metric converts into the projector $G^{mn}\to {\Delta }^{mn}=g^{mn}-U^m{U}^n$. For a guiding function like the first type, the axion field Equation (17) admits the solution depending on time if, and only if, $\varphi =n{\Phi }_{*}$, and thus $V=0$. The equation for the gravity field (31) gives the de Sitter-type solution $H=H_{\infty }$, and the Equation (29) turns into the identity $0=0$. In other words, the second type of guiding function happens to be arbitrarily constant ${\Phi }_{*}\left(t\right)={\Phi }_{*}\left(H_{\infty }\right)$.

4. Discussion and Conclusions

In the presented work we studied new exact solutions to the master equations for the extended version of the Einstein–aether–axion theory. The main idea of the theory’s extension is based on the introduction of two guiding functions $\mathcal{A}(\Theta )$ and ${\Phi }_{*}(\Theta )$, which depend on the expansion scalar of the aether flow, $\Theta ={\nabla }_k{U}^k$. This choice is dictated by the fact that, within the Friedmann–Lemaître–Robinson–Walker model, there is only one non-vanishing invariant reconstructed using the covariant derivative ${\nabla }_k{U}^j$ of the aether four-vector velocity $U^j$. The bonus of this approach is that, in the FLRW model, $\Theta =3H$, and thus the aetheric control over the axion system evolution happens to be described in terms of the Hubble function $H\left(t\right)$, which is intrinsic for this model and has a clear physical meaning. As for why we used namely two guiding functions, we kept in mind that, generally, the axion system is characterized by two state functions: kinetic and potential energy. The modification of the kinetic term in the Lagrangian of the extended theory is performed using the effective aetheric metric $G^{mn}=g^{mn}+\mathcal{A}{U}^m{U}^n$ (see (1)), where the scalar $\mathcal{A}(\Theta )$ has been indicated as the first type of guiding function. The modification of the axion field potential is carried out by the introduction of the guiding function of the second type ${\Phi }_{*}(\Theta )$, which predetermines the location and depth of the potential minima (see (4)).

The next question is how one can find $\mathcal{A}(\Theta )$ and ${\Phi }_{*}(\Theta )$. We have proposed the following idea. If the axion field is frozen in the first minimum of the potential, i.e., is in the first equilibrium state $\varphi ={\Phi }_{*}$, we see that the corresponding equation for the axion field (see (18) and (29)) can be indicated as the master equation for the guiding function of the second type. Fortunately, the Equation (29)) admits the first integral (30), which can be put into the equations for the gravity field, thus providing the key Equation (31) to be self-closed equation for the scalar function $\Theta \left(x\right)$, or equivalently, for the Hubble function $H\left(x\right)$. When H is found, the guiding function of the second type ${\Phi }_{*}$ can be reconstructed by the direct integration (see the results (49), (60), (61) and (69)).

Regarding the search for the guiding function of the first type $\mathcal{A}(\Theta )$, we follow the idea that, first, the right-hand side of the key equation of the gravity field (34) has to be a regular function, second, the model has to describe the perpetual Universe expansion without Big Rip and Big Crunch. From these two requirements, we restore the function $\mathcal{A}\left(H\right)$ up to three arbitrary parameters ${\gamma }_1$, ${\gamma }_2$ and $H_{*}$ using the formula

$$\frac{1}{1+\mathcal{A}}=1+{\gamma }_{1}H\left[1+log\frac{H}{H_{*}}\right]+{\gamma }_2{H}^2.$$

The Hubble function $H\left(x\right)$ is the solution to the quadratic equation and its positive root has the form (39) for arbitrary parameters ${\gamma }_1$, ${\gamma }_2$ and $H_{*}$; only the scale factor, as the function of cosmological time $a\left(t\right)$, can be presented in quadratures. In order to obtain the results presented in the analytical and special functions, we considered four particular submodels, selecting the listed parameters in a specific way. And our research objectives were achieved.

The last point of discussion is connected with an application of the extended model for the interpretation of observational data, in particular, for the estimation of the axion mass. In this context, we would like to draw attention to the equation of the axion field evolution (17). When the value of the axion field is close to one of the potential minima, i.e., $\varphi \to n{\Phi }_{*}+\psi$ with $\left|\frac{2\pi \psi }{{\Phi }_{*}}\right|<<1$, we deal with the linear differential equation, in which the quantity $M(\Theta )=\frac{m_{\mathrm{A}}}{\sqrt{1+\mathcal{A}}}$ plays the role of an effective axion mass depending on the scalar of expansion of the aether flow $\Theta$. Preliminary analysis shows that, for some choices of the guiding function $\mathcal{A}(\Theta )$, this equation admits unstable solutions, which are associated with the axionization of the early Universe in analogy with the results obtained in [20]. The growth of the number of axions in the early Universe leads to the formation of the axionic dark matter detected in our epoch; thus, the parameters of the presented extended model could be linked with the mass density of the relic axions. Clearly, this part of work should be more detailed;however, it is beyond the scope of this article and is planned to form the content of the next publication.