Nonrelativistic Quantum Mechanical Problem for the Cornell Potential in Lobachevsky Space
Abstract
1. Introduction
…the Russian mathematician A. Friedmann pointed out that the static nature of Einstein’s universe was the result of an algebraic mistake (essentially a division by zero) made in the process of its derivation. Friedmann then went on to show that the correct treatment of Einstein’s basic equations leads to a class of expanding and contracting universes…
2. Quark–Antiquark Bound States in Lobachevsky Space
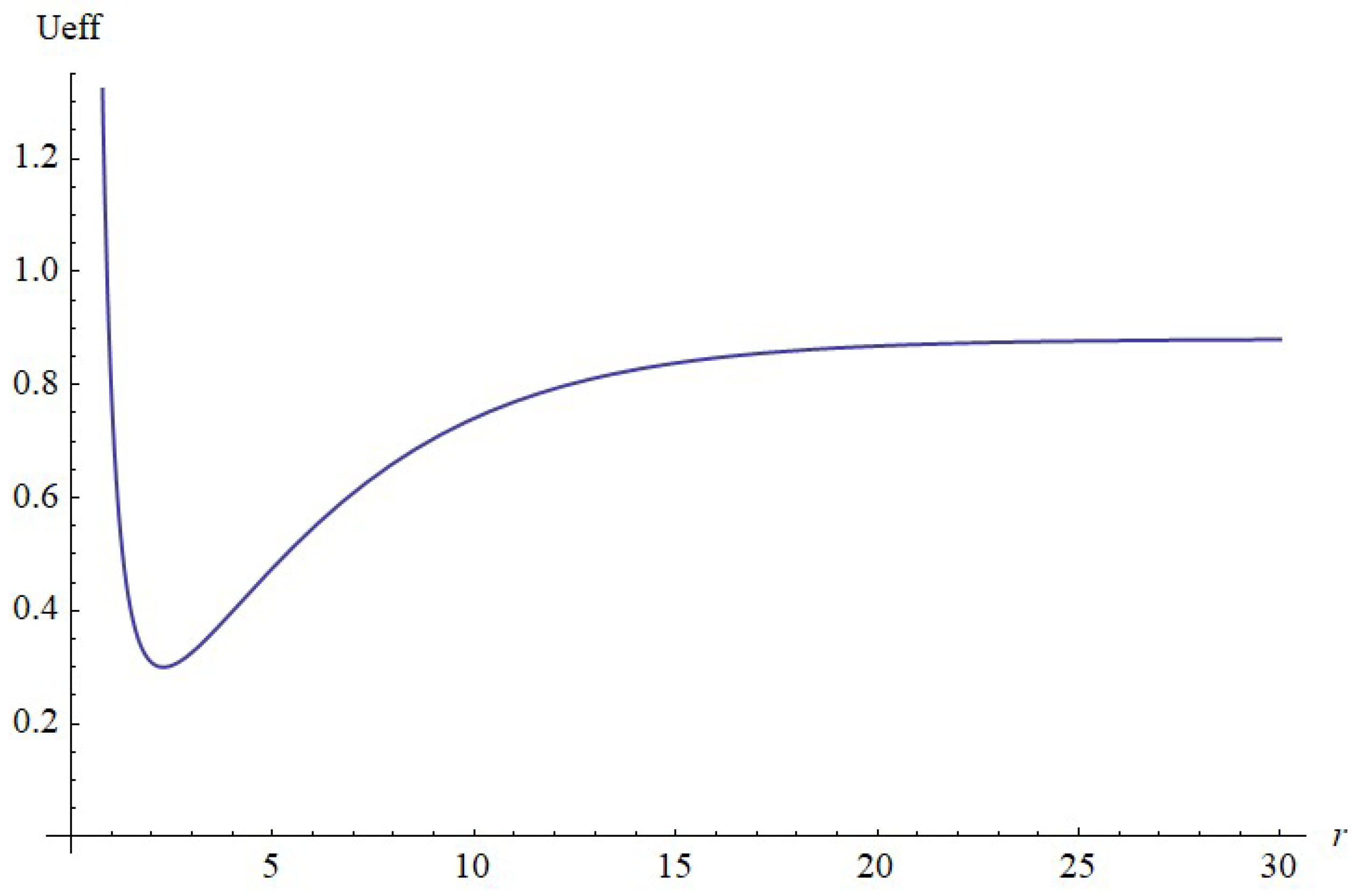
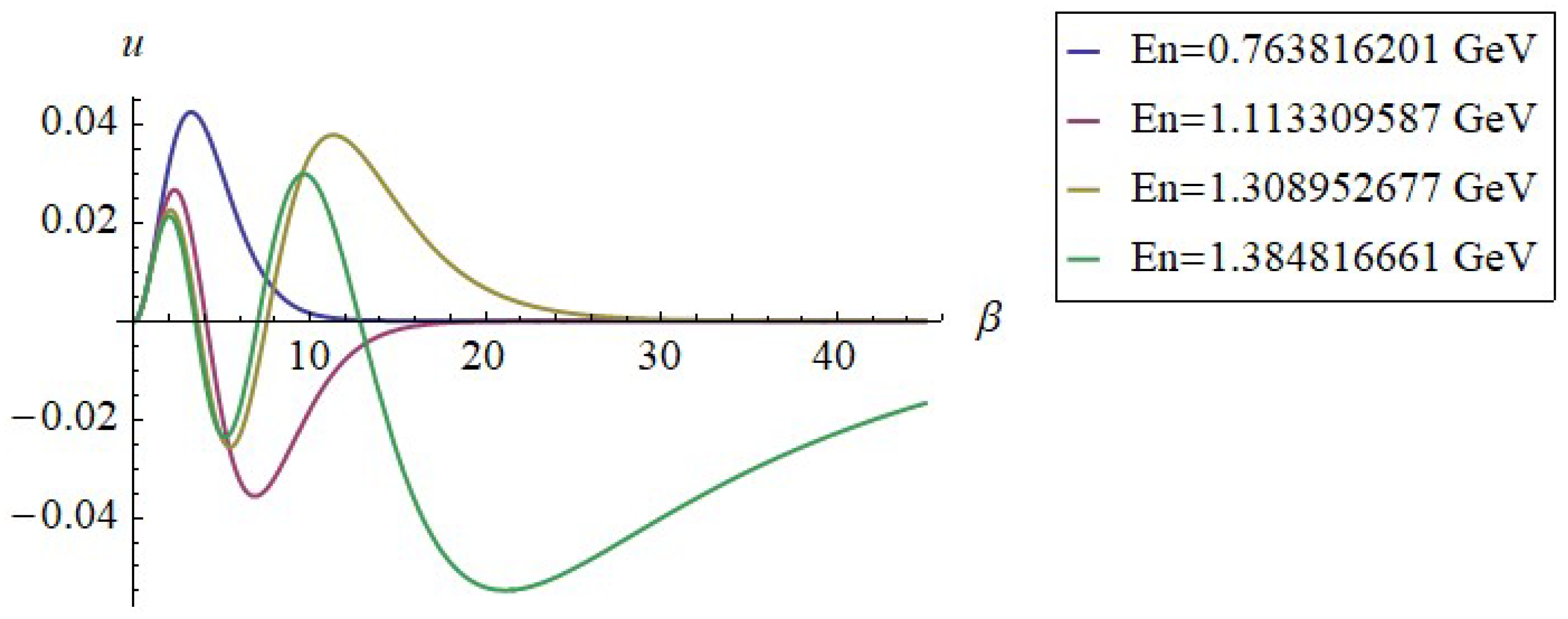
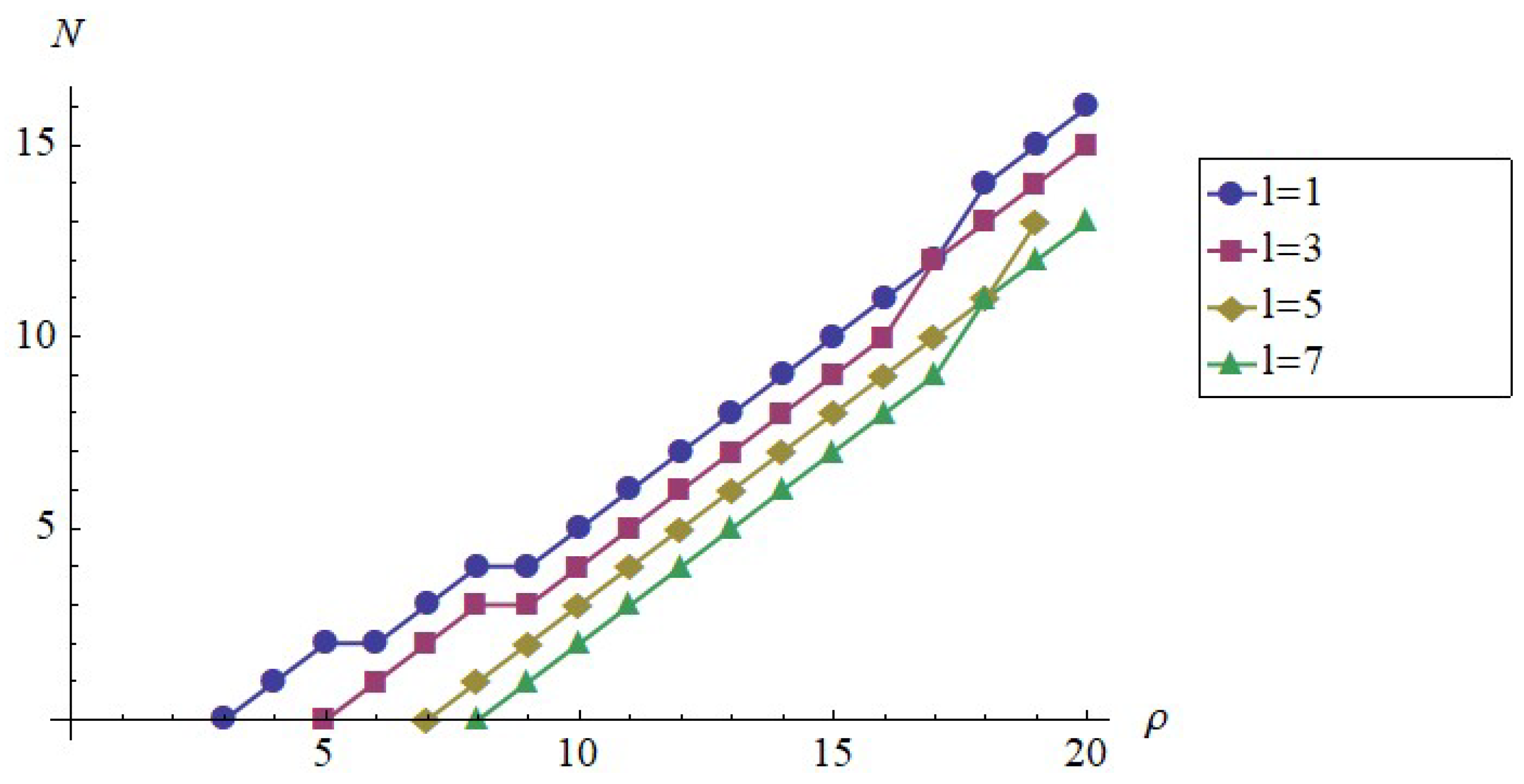
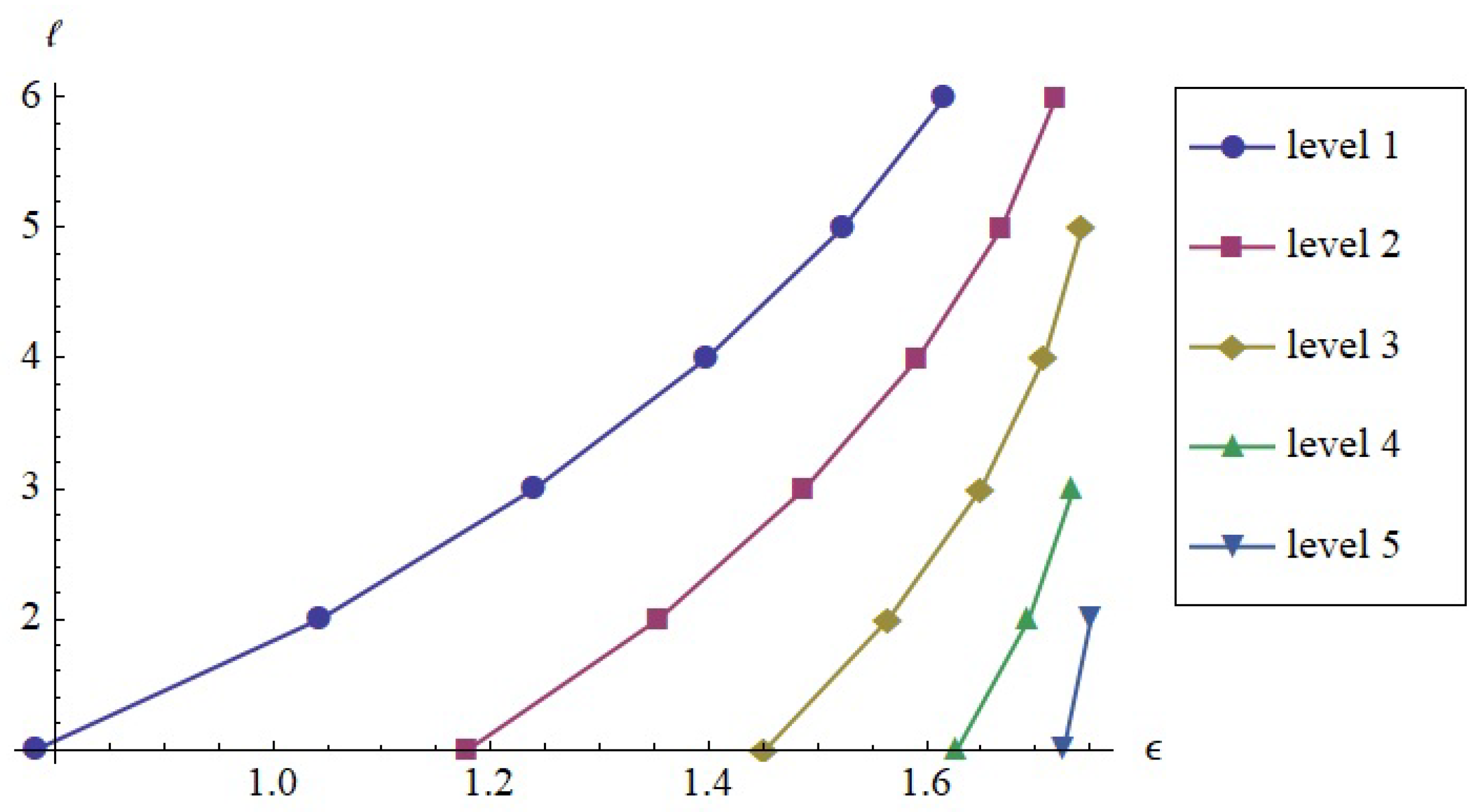
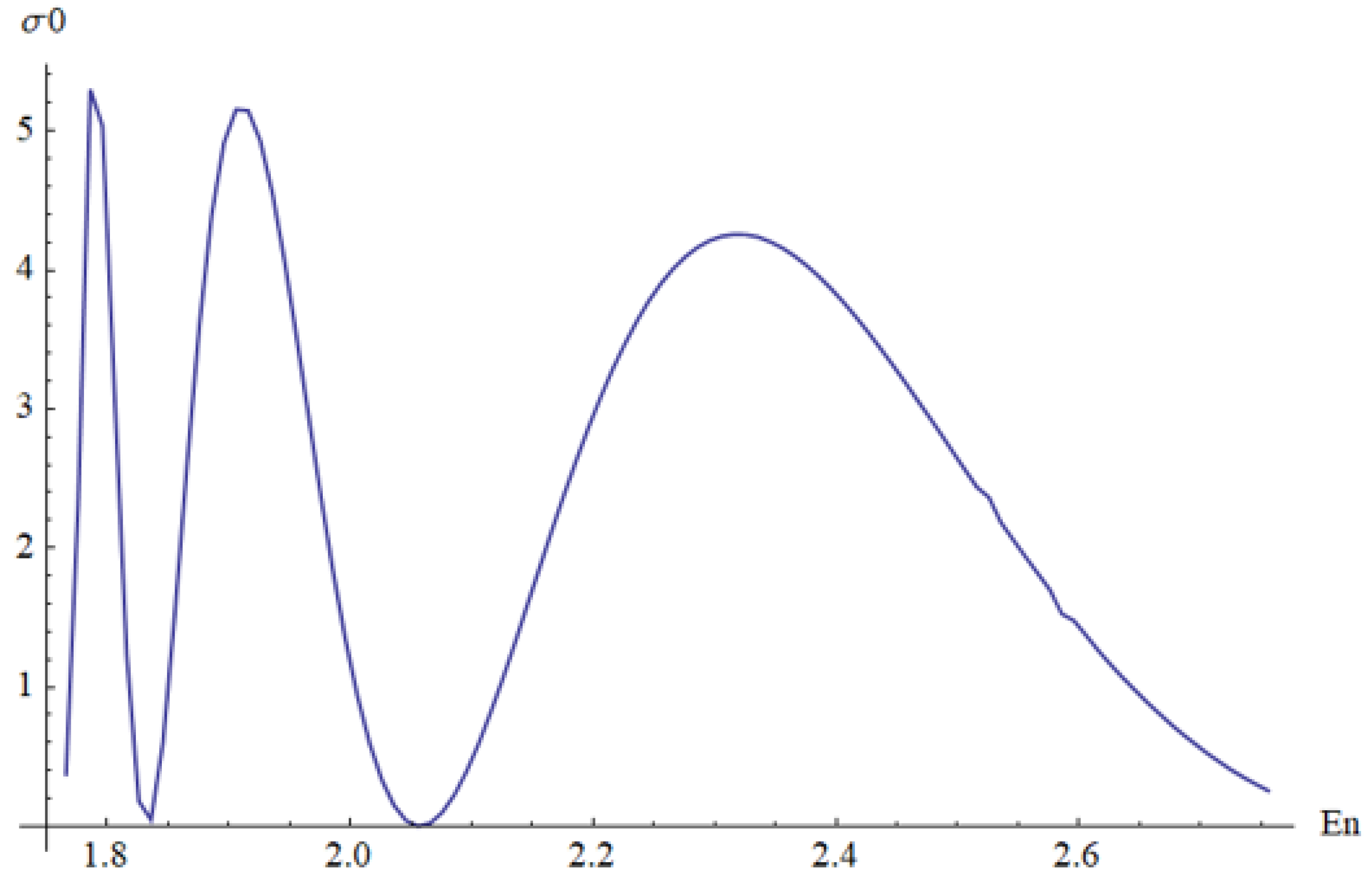
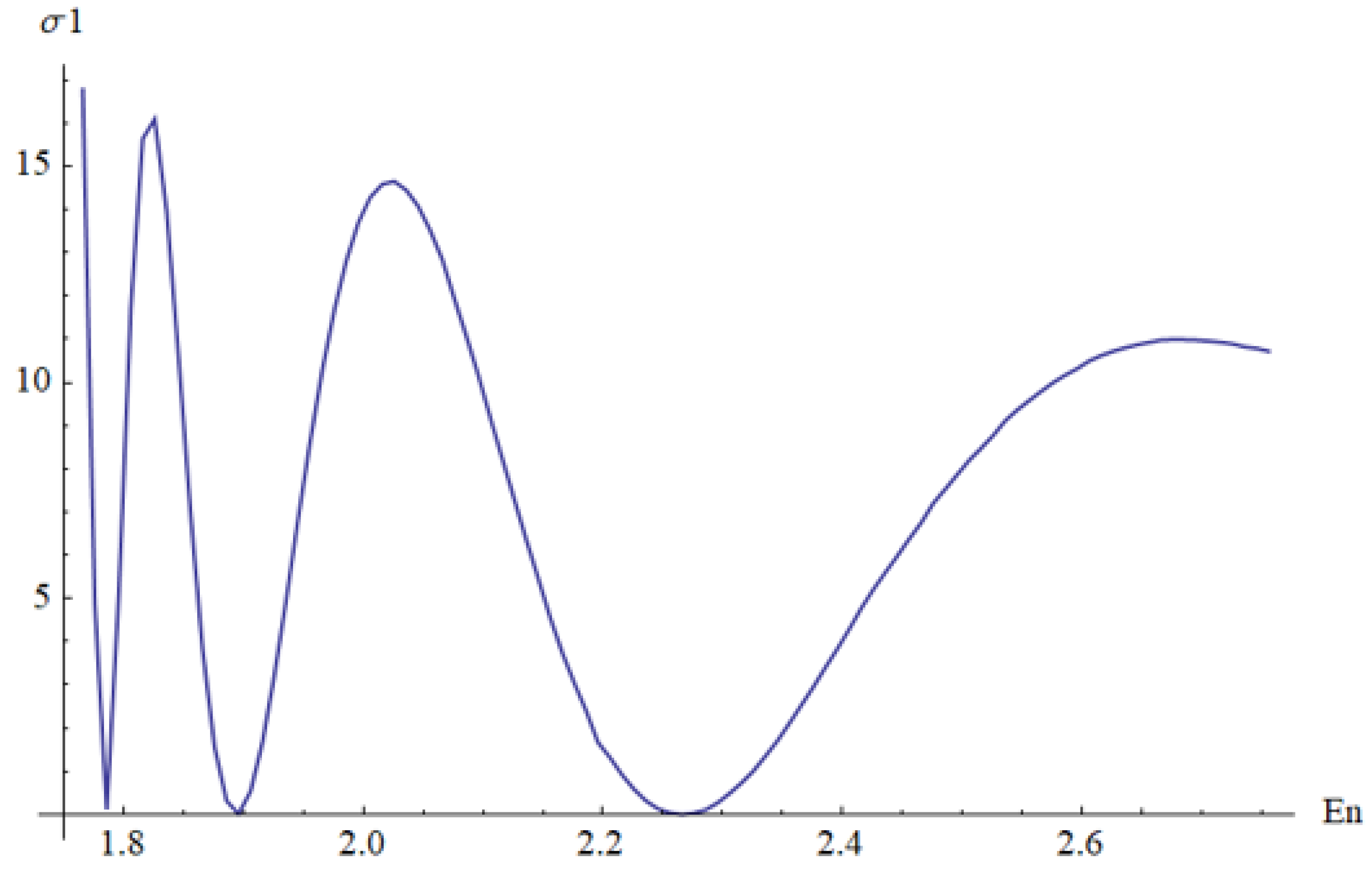
3. Scattering in the Cornell Potential
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Friedman, A. Über die Krümmung des Raumes. Z. Phys. 1922, 10, 377–386. [Google Scholar] [CrossRef]
- Friedmann, A. Über die Möglichkeit einer Welt mit konstanter negativer Krümmung des Raumes. Z. Phys. 1924, 21, 326–332. [Google Scholar] [CrossRef]
- Friedmann, A. On the Curvature of Space. Gen. Relativ. Gravit. 1999, 31, 1991–2000. [Google Scholar] [CrossRef]
- Friedmann, A. On the Possibility of a World with Constant Negative Curvature of Space. Gen. Relativ. Gravit. 1999, 31, 2001–2008. [Google Scholar] [CrossRef]
- Tropp, E.A.; Frenkel, V.Y.; Chernin, A.D. Alexander A. Friedmann. The Man Who Made the Universe Expand; Dron, A.; Burov, M., Translators; Cambridge University Press: Cambridge, MA, USA, 1993. [Google Scholar]
- Gliner, E.B. Algebraic properties of the energy-momentum tensor and vacuum-like states of matter. Sov. Phys. JETP 1966, 22, 378–382. [Google Scholar]
- Jenkovszky, L.L.; Trushevsky, A.A. Asymptotics of total cross-sections and ultimate temperature of hadronic systems. Nuovo C. A 1976, 34, 369–384. [Google Scholar]
- Bugrij, A.I.; Trushevsky, A.A. Some cosmological consequences of high-temperature phase transition in hadron matter. Astrofizika 1977, 13, 361–374. [Google Scholar]
- Kokkedee, J. Theory of Quarks; Mir: Moscow, Russia, 1971; 338p. [Google Scholar]
- Shelest, A.P.; Zinoviev, G.M.; Miranskij, V.A. Models of Strongly Interacting Particles; Atomizdat: Moscow, Russia, 1975; 232p. [Google Scholar]
- Bykov, A.A.; Dremin, I.M.; Leonidov, A.V. Potential models of quarkonium. Sov. Phys. Uspekhi 1984, 27, 321. [Google Scholar] [CrossRef]
- Sergeenko, M.N. Masses and widths of Resonances for the Cornell Potential. Adv. High Energy Phys. 2013, 2013, 325431. [Google Scholar] [CrossRef]
- Izmestiev, A.A. Exactly solvable potential model for quarkoniums. Nucl. Phys. 1990, 52, 1697–1710. [Google Scholar]
- Kudryashov, V.V.; Murzov, V.I.; Tomilchik, L.M. Triplet State of a Two-Fermion System with Homogeneous Relative Space; Preprint No. 568; B.I. Stepanov Institute of Physics, Academy of Sciences of the BSSR: Minsk, Russia, 1969; 19p. [Google Scholar]
- Gamow, G. The Creation of the Universe; Viking Press: New York, NY, USA, 1952. [Google Scholar]
- Gliner, E.B. Algebraic Properties of the Energy-momentum Tensor and Vacuum-like States o+ Matter. Sov. Phys. JETP 1965, 22, 378. [Google Scholar]
- Gliner, E.B. Vacuum-like state of a medium and Friedmann cosmology. Dokl. Akad. Nauk USSR 1970, 192, 771–774. [Google Scholar]
- Gliner, E.B.; Dymnikova, I.G. Nonsingular Friedmann cosmology. Sov. Astron. Lett. (Engl. Transl.) 1975, 1, 7. [Google Scholar]
- Bugrij, A.I.; Trushevsky, A.A. Some cosmological consequences of the high-temperature hadron phase transition. Astrophysics 1977, 13, 195–202. [Google Scholar] [CrossRef]
- Jenkovszky, L.L.; Kämpfer, B.; Sysoev, V.M. On the expansion of the universe during the confinement transition. Z. Phys. C 1990, 48, 147. [Google Scholar] [CrossRef]
- Jenkovszky, L.L.; Kaempfer, B.; Sysoev, V.M. Bubble-free energy during the confinement transition. Phys. Atomic Nuclei 1994, 57. [Google Scholar]
- Einstein, A. Kosmologiche Betrachtungen zur Allgemeinen Relativitätstheorie. Sitzungsberichte Königlich Preuss. Akad. Wiss. 1917, 1, 142. [Google Scholar]
- Schrödinger, E. A method of determining quantum mechanical eigenvalues and eigenfunctions. Proc. R. Irish. Acad. A 1940, 46, 9–16. [Google Scholar]
- Infeld, L. On a new treatment of some eigenvalue problems. Phys. Rev. 1941, 59, 737–747. [Google Scholar] [CrossRef]
- Infeld, L.; Schild, A. A note on the Kepler problem in a space of constant negative curvature. Phys. Rev. 1945, 67, 121–122. [Google Scholar] [CrossRef]
- Stevenson, A.F. A note on the Kepler problem in a spherical space, and the factorization method of solving eigenvalue problems. Phys. Rev. 1941, 59, 842–843. [Google Scholar] [CrossRef]
- Higgs, P. Dynamical symmetries in a spherical geometry. J. Phys. A Math. Gen. 1979, 12, 309–323. [Google Scholar] [CrossRef]
- Leemon, H. Dynamical symmetries in a spherical geometry. J. Phys. A Math. Gen. 1979, 12, 489–501. [Google Scholar] [CrossRef]
- Kurochkin, Y.A.; Otchik, V.S. Analog of the Runge—Lenz vector and energy spectrum in the Kepler problem on a three-dimensional sphere. Dokl. AN BSSR 1979, 987–990. [Google Scholar]
- Bogush, A.A.; Kurochkin, Y.A.; Otchik, V.S. On the quantum-mechanical Kepler problem in a three-dimensional Lobachevsky space. Dokl. AN BSSR. 1980, 19–22. [Google Scholar]
- Kurochkin, Y.A.; Otchik, V.S.; Tereshenkov, V.I. Electron in a magnetic charge field in three-dimensional Lobachevsky space. Proc. Acad. Sci. BSSR Phys. Math. Ser. 1984, 74–79. [Google Scholar]
- Kurochkin, Y.A.; Shoukavy, D.V. Regge trajectories of the Coulomb potential in the space of constant negative curvature 1S3. J. Math. Phys. 2006, 47, 022103. [Google Scholar] [CrossRef]
- Muradian, R. The Regge law for heavenly bodies. Phys. Part. Nucl. 1997, 28, 471. [Google Scholar]
- Trushevsky, A.A. Asymptotic Behavior of Boson Regge Trajectories. Ukr. J. Fiz. 2021, 97, 66. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jenkovszky, L.; Kurochkin, Y.A.; Shaikovskaya, N.D.; Soloviev, V.O. Nonrelativistic Quantum Mechanical Problem for the Cornell Potential in Lobachevsky Space. Universe 2024, 10, 76. https://doi.org/10.3390/universe10020076
Jenkovszky L, Kurochkin YA, Shaikovskaya ND, Soloviev VO. Nonrelativistic Quantum Mechanical Problem for the Cornell Potential in Lobachevsky Space. Universe. 2024; 10(2):76. https://doi.org/10.3390/universe10020076
Chicago/Turabian StyleJenkovszky, Laszlo, Yurii Andreevich Kurochkin, N. D. Shaikovskaya, and Vladimir Olegovich Soloviev. 2024. "Nonrelativistic Quantum Mechanical Problem for the Cornell Potential in Lobachevsky Space" Universe 10, no. 2: 76. https://doi.org/10.3390/universe10020076
APA StyleJenkovszky, L., Kurochkin, Y. A., Shaikovskaya, N. D., & Soloviev, V. O. (2024). Nonrelativistic Quantum Mechanical Problem for the Cornell Potential in Lobachevsky Space. Universe, 10(2), 76. https://doi.org/10.3390/universe10020076







