Falling into the Past: Geodesics in a Time Travel Metric

Abstract

We investigate timelike and null geodesics within the rotating “time machine” spacetime proposed by Ralph, T.C.; et al. Phys. Rev. D 2020, 102, 124013. This is a rotating analogue of Alcubierre’s warp drive spacetime. We obtain geodesics that begin and end in the surrounding flat space region, yet achieve time travel relative to static observers there. This is a global property, as the geodesics remain locally future-pointing, as well as timelike or null.

1. Introduction

Exotic spacetimes including wormholes, warp drives, and time machines have been used to probe frontier physics concepts, despite being of physically dubious construction themselves. An early example is Gödel’s [1] rotating universe which has a negative cosmological constant but motivated developments in relativistic causality [2]. More recently, the Kip Thorne group has studied billiard ball collisions in the context of wormhole spacetimes with closed timelike curves (CTCs) to see if a consistent mechanics may be determined from initial conditions [3,4]. Hawking argued that spacetimes of this type are unstable [5] as have others for different cases, including Krasnikov [6], but a more general argument has not emerged. Other authors have studied quantum particles in the presence of CTCs. Deutsch [7] described consistent evolutions using a quantum computation circuit model, which was clarified by Politzer [8] using a less abstract approach. An alternative approach to obtain consistent evolutions was described by Lloyd et al. [9] based on teleportation.

Closed timelike curves are spacetime trajectories that start and finish at the same spacetime event. Spacetimes that contain them may be referred to as time machine spacetimes, as they allow particles to travel into their own past. As well as in wormhole spacetimes, CTCs have have been found in rotating spacetimes, including rotating cylinders (studied by van Stockum), and the Kerr spacetime [10] that describes rotating black holes (albeit within an inner region that some consider unphysical). Tippett and Tsang [11] suggested a classification of time machine spacetimes into three classes. The first class is those that arise naturally in geometries with strong angular momentum. The Gödel and Kerr spacetimes previously mentioned are examples of this class. The second class is spacetimes designed specifically for time travel. These include metrics due to Ori and co-workers [12,13,14], the wormhole spacetimes discussed earlier, the spacetime of Mallary et al. [15], and Tippett and Tsang’s spacetime [11]. The third class is spacetimes that are designed to produce superluminal travel but allow time travel as a natural consequence. The spacetime we investigate here is of this third type.

Alcubierre [16] proposed a “warp drive” spacetime with a localized bubble region which travels faster than light as determined by a distant observer. Other warp drive spacetimes that have been proposed include those by Krasnikov [17], Olum [18], Natário [19] and Bobrick and Martire [20]. Everett [21] and Krasnikov [17] considered boosting between two different warp drive spacetimes and found that CTCs could be formed. Ralph and Chang [22] defined a “time machine” spacetime by incorporating an Alcubierre-like warp bubble, made to follow a circular loop, on a rotating platform. This allowed backwards-in-time travel for certain parameters and hence the explicit formation of CTCs by a relatively simple metric. The physical realizability of such a metric is uncertain due to the exotic matter required to produce it, which appears to be a generic feature of warp drive spacetimes [23]. However, its study may lead to useful advances in understanding.

In this paper, we study geodesics in the Ralph and Chang spacetime. Our main result is that, for a particular choice of parameters, we find timelike and null geodesics which transit the curved spacetime region and exit into flat space at an earlier time than when they enter, according to an observer in flat space. Timelike geodesics with this property have previously been identified by Fermi and Pizzocchero [24] for a different spacetime (belonging to class two), albeit one with a similar structure. Whilst the Ralph and Chang spacetime involves an Alcubierre “bubble” which travels around a circular path, here we will consider parameters for which the front of the bubble merges with the rear, forming a toric structure similar to [24]. Nevertheless, the metrics and their specific properties are distinct.

Our paper is arranged in the following way. In the next section, we describe the time machine metric, its derivation and how we parameterize it. In Section 3, we describe some properties of the time machine metric before outlining our method for finding certain classes of geodesics in Section 4. Section 5 describes our main results before we discuss and conclude in Section 6.

2. The Time Machine Spacetime

Conceptually, the Ralph and Chang time machine spacetime is a combination of Alcubierre spacetime, with a rotating disc in Minkowski spacetime.

2.1. Alcubierre Spacetime

Alcubierre [16] starts with coordinates $(t,x,y,z)$ on a manifold, and a path $x_s\left(t\right)$ along the x-axis, where the “s” stands for spaceship. The goal was to choose a metric such that this path is timelike and geodesic. Alcubierre defined a region around the worldline, since called the “bubble”, parametrized by a function f with value 1 on the worldline, and approximately 0 far from it. This f characterizes the amount of warp, and is discussed further in Section 2.4. $v_s\left(t\right):=d{x}_s/dt$ is the coordinate speed of the spaceship. Using the lapse–shift formalism (see [25], §21.4 for background), it suffices to use a shift 3-vector ${\overrightarrow{b}}^i=(-f{v}_s,0,0)$ and lapse $\alpha =1$. Then, the Eulerian observers, meaning those orthogonal to the hypersurfaces $t=\mathrm{const}$ but which we name “warp” observers, have 4-velocity $u_{\mathrm{warp}}^{\mu }=(1,f{v}_s,0,0)$. They are geodesic since their 4-acceleration is a function of the lapse gradient [26], §4.3.3. For $f=1$, they coincide with the spaceship worldline.

The coordinate speed $v_s$ has no limits. However, we stress there is never faster-than-light motion locally, that is, a massive test particle’s 4-velocity is never null nor spacelike. It has at most “‘effective’ superluminal travel” [27]. Furthermore, all valid 4-velocities are future-pointing, never past-pointing.

Alcubierre [16] briefly mentioned the case of an arbitrary lapse and shift. Here, the Eulerian observers are $u_{\mathrm{warp}}^{\mu }={\alpha }^{-1}(1,-b^1,-b^2,-b^3)$, with co-velocity ${}^{\mathrm{warp}}u_{\mu }=(-\alpha ,0,0,0)$. We generalize this construction in Appendix C to allow observers with vorticity, which are not orthogonal to any hypersurface. In our approach, Alcubierre spacetime is obtained by starting with Minkowski spacetime, including the metric. Take the static observers $\mathbf{u}:={\partial }_t$ as a starting point, which is the coordinate basis vector $(1,0,0,0)$ in some chosen inertial frame. Now, define a “warp shift” 4-vector field $\mathbf{b}:=-f{v}_s{\partial }_x$, and “warp lapse” scalar $\alpha =1$. These combine to add terms to the Minkowski metric, yielding the Alcubierre metric (Appendix C). Formally, our model is a single manifold with two Lorentzian metrics. But physically, we interpret this as two separate spacetimes, or two separate regions (“time” periods) within a single spacetime.

2.2. The Rotating Disc

Use cylindrical coordinates $(t,r,\varphi ,z)$ on Minkowski spacetime. A disc rotating at constant (coordinate) rate $d\varphi /dt=:\mathsf{\Omega }\in \mathbb{R}$ has a 4-velocity field:

$$u_{\mathrm{disc}}^{\mu }=\left(1,0,\mathsf{\Omega },0\right)/\sqrt{1-{\mathsf{\Omega }}^2{r}^2}.$$

(1)

This is valid within the region $r<1/\left|\mathsf{\Omega }\right|$ for subluminal motion. Intuitively, this field describes material elements making up the disc; however, our focus is on abstract reference frames not materials science. The motion is Born-rigid, meaning its expansion tensor vanishes: $\mathsf{\Theta }=\mathbf{0}$. At any given point, the Lorentz factor relative to a “lab” observer ${\partial }_t$ is $\gamma =-\langle {\mathbf{u}}_{\mathrm{disc}},{\partial }_t\rangle ={(1-{\mathsf{\Omega }}^2{r}^2)}^{-1/2}$, where the angle brackets refer to the metric scalar product. The following vector field points in the tangent direction:

$${\xi }^{\mu }=(\mathsf{\Omega }r,0,1/r,0)/\sqrt{1-{\mathsf{\Omega }}^2{r}^2}.$$

(2)

It has unit length $\langle \xi ,\xi \rangle =1$ and is purely spatial according to the disc observers, meaning $\langle {\mathbf{u}}_{\mathrm{disc}},\xi \rangle =0$. Intuitively, these model little rulers, but technically they are merely vectors in an orthonormal pair.

2.3. Ralph and Chang Spacetime

The time machine spacetime family we consider was introduced and analyzed in Ralph and Chang [22]. Here, we give a novel derivation starting with Minkowski spacetime with the disc 4-velocity field, also called the “platform”, $\mathbf{u}:={\mathbf{u}}_{\mathrm{disc}}$. Next, add an Alcubierre-like warp shift in the tangential direction for each observer $\mathbf{b}:=-f{v}_s\xi$. Warp lapse $\alpha :=1$. $v_s\in \mathbb{R}$ is taken as a constant, and our specific choices of bubble functions f are given in the following section. The resulting metric is (Appendix C):

$$\begin{array}{c}d{s}^2=\frac{{(f{v}_s+\mathsf{\Omega }r)}^2-1}{1-{\mathsf{\Omega }}^2{r}^2}d{t}^2-2\frac{f{v}_{s}r(1+{\mathsf{\Omega }}^2{r}^2+\mathsf{\Omega }rf{v}_s)}{1-{\mathsf{\Omega }}^2{r}^2}dtd\varphi \hfill \\ \hfill +d{r}^2+\frac{r^2({(1+\mathsf{\Omega }rf{v}_s)}^2-{\mathsf{\Omega }}^2{r}^2)}{1-{\mathsf{\Omega }}^2{r}^2}d{\varphi }^2+d{z}^2.\end{array}$$

(3)

This is Equation (5) in Ralph and Chang [22]. They call these the “lab” coordinates, because where $f=0$, the metric reduces to $d{s}^2=-d{t}^2+d{r}^2+r^{2}d{\varphi }^2+d{z}^2$, which is locally Minkowski spacetime, and ${\partial }_t$ reduces to the static “lab” observers. The value $r=1/\left|\mathsf{\Omega }\right|$ is not only a coordinate singularity but a curvature singularity for the spacetime parameters tested. This is the radius at which the spinning platform’s tangential velocity is the speed of light. Hence, we enforce $f=0$ in the region around $r=1/\left|\mathsf{\Omega }\right|$ throughout this paper, and as a result, Equation (3) reduces to the Minkowski metric there. Placing the point $r=1/\left|\mathsf{\Omega }\right|$ outside the region of curvature such that $f=0$ in its vicinity is a sufficient condition for removing the singularity. An interesting question for future investigation would be to find necessary conditions such that the singularity is removed.

Note that t is not necessarily timelike. (This is determined by the hypersurfaces $t=\mathrm{const}$, which have normal covector $dt$, satisfying $\langle dt,dt\rangle =g^{tt}$, which may have any sign.) Similarly, the coordinate basis vector ${\partial }_t$ is not necessarily timelike, and, likewise, $\varphi$ and ${\partial }_{\varphi }$ are not necessarily spacelike. On a partly related note, the standard lapse and shift quantities relative to the $t=\mathrm{const}$ hypersurfaces differ from our “warp lapse” and “warp shift”, even when t is timelike.

The metric of Equation (3) may be summarized as the following, for brevity:

$$g_{\mu \nu }=\left(\begin{array}{cccc}{g}_{tt}& 0& g_{t\varphi }& 0\\ 0& 1& 0& 0\\ g_{t\varphi }& 0& g_{\varphi \varphi }& 0\\ 0& 0& 0& 1\end{array}\right).$$

(4)

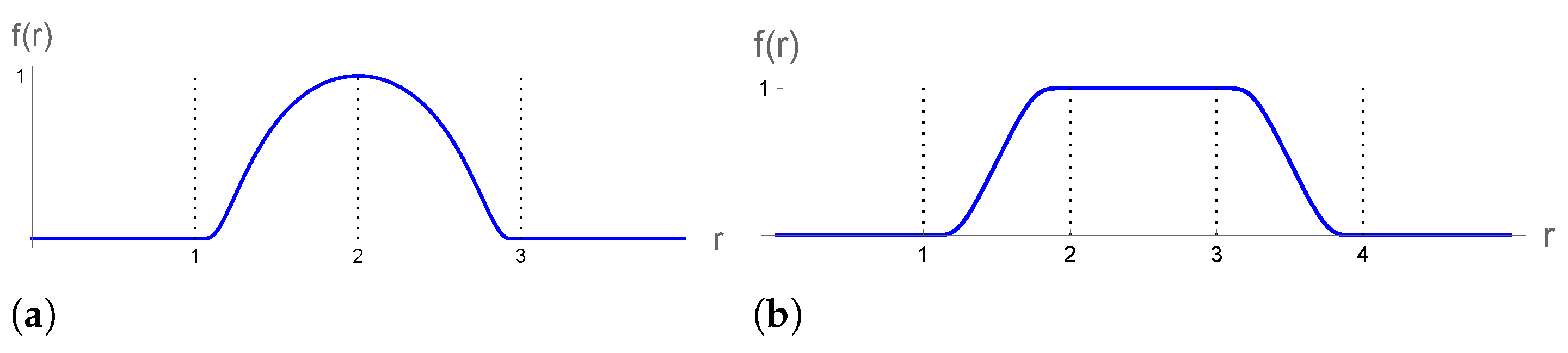
2.4. The Bubble Function f

The time machine spacetime was originally conceived as a warp bubble revolving about the origin [22]. If we write $\tilde{\mathsf{\Omega }}$ for the bubble’s (coordinate) rotation rate $d\varphi /dt$, a constant independent of the platform rate $\mathsf{\Omega }$, then we might expect f to have the form:

$$f=f_{\mathrm{rot}}(\varphi -\tilde{\mathsf{\Omega }}t)f_r\left(r\right)f_z\left(z\right),$$

(5)

where $f_z$ is symmetric. However, in this paper, we drop the angular dependence for simplicity, leaving f rotationally symmetric. This can be thought of as the bubble reaching around the entire cylinder. Also, we do not give our f an explicit time dependence. Hence, it is a function of r alone, and in principle also of z. This describes a torus rather than a bubble.1 Here, we use the bump functions in Figure 1, which vanish beyond a certain fixed r. The Gaussian-inspired function has the definition:

$$f\left(r\right)=\left\{\begin{array}{cc}exp\left(1-\frac{1}{1-{(r-2)}^2}\right)\hfill & 1<r<3\hfill \\ 0\hfill & \mathrm{otherwise},\hfill \end{array}\right.$$

(6)

whereas the plateau function is:

$$f\left(r\right)=\left\{\begin{array}{cc}\frac{1}{1+exp\left(\frac{1}{r-1}+\frac{1}{r-2}\right)}\hfill & 1<r<2\hfill \\ 1\hfill & 2\le r\le 3\hfill \\ \frac{1}{1+exp\left(-\frac{1}{r-3}-\frac{1}{r-4}\right)}\hfill & 3<r<4\hfill \\ 0\hfill & \mathrm{otherwise}.\hfill \end{array}\right.$$

(7)

These are smooth but not analytic. We define the time machine region of spacetime by $f\ne 0$, which coincides with the curved region.

We can think of the z-dependence of f as being a broad plateau function centered on $z=0$. However, we will start all our trajectories in the $z=0$ plane, where they will remain, so the exact details of the z dependence will not play a role in our calculations. Similarly, the t dependence of f can be thought of as a broad plateau function centered on (but much broader than) the time interval of interest for the trajectories. In other words, we might envisage that at some time in the past, the value of f was slowly increased from $0\to 1$. It then remained constant for an extended period, which includes the time of interest in this paper. At sometime in the future, it may be slowly decreased from $1\to 0$, returning the relevant spacetime to Minkowski. Hence, for the purposes of our calculations, f is taken to be constant in t and z.

3. Time Orientation and Warp Velocity

In Alcubierre spacetime, the Eulerian observers have co-velocity ${}^{\mathrm{warp}}u_{\mu }=(-1,0,0,0)$. We observe that these are the same components as static observers in Minkowski spacetime, with whom our construction started. It turns out this is not a coincidence as shown in Appendix C. To obtain the analogous field in the time machine spacetime, first lower the index on the disc 4-velocity (Equation (1)) using the Minkowski metric, so ${}^{\mathrm{disc}}u_{\mu }=(-1,0,\mathsf{\Omega }{r}^2,0)/\sqrt{1-{\mathsf{\Omega }}^2{r}^2}$ in cylindrical coordinates, which is also ${}^{\mathrm{warp}}u_{\mu }$. Now, raise the index using the time machine metric:

$$u_{\mathrm{warp}}^{\mu }:=\frac{1}{\sqrt{1-{\mathsf{\Omega }}^2{r}^2}}\left(1+\mathsf{\Omega }rf{v}_s,0,\mathsf{\Omega }+\frac{f{v}_s}{r},0\right).$$

(8)

We denote this as the warp velocity. Equivalently, ${\mathbf{u}}_{\mathrm{warp}}={\mathbf{u}}_{\mathrm{disc}}-\mathbf{b}$. It is unit timelike in the new metric: $\langle {\mathbf{u}}_{\mathrm{warp}},{\mathbf{u}}_{\mathrm{warp}}\rangle =-1$. Where $f=1$, it reduces to the bubble velocity defined in Ralph and Chang [22], though we have swapped the order of r and $\varphi$. Sharing the same co-velocity vector with the disc leads to interesting properties. For example, ${\mathbf{u}}_{\mathrm{warp}}$ has the same Killing energy and angular momentum (defined in the following section) as the rotating disc frames do in Minkowski spacetime. One downside is that Equation (8) is only valid for $r<1/\left|\mathsf{\Omega }\right|$.

Another possibility is a local Lorentz boost of the warp observers by speed $\beta :=\mathsf{\Omega }r$ “backwards”, which intuitively undoes the speed of the platform. Now, the vector $\xi$ points in the tangential direction; while this is formally just the disc ruler vector from Equation (2), it also satisfies $\langle \xi ,\xi \rangle =1$ and $\langle {\mathbf{u}}_{\mathrm{warp}},\xi \rangle =0$ in the new metric. The local boost in the negative $\xi$-direction is $\gamma ({\mathbf{u}}_{\mathrm{warp}}-\beta \xi )$, or:

$$u_{\mathrm{orient}}^{\mu }:=\left(1+\frac{\mathsf{\Omega }rf{v}_s}{1-{\mathsf{\Omega }}^2{r}^2},0,\frac{f{v}_s}{r(1-{\mathsf{\Omega }}^2{r}^2)},0\right),$$

(9)

where $\langle {\mathbf{u}}_{orient},{\mathbf{u}}_{orient}\rangle =-1$. This is an ideal time orientation, meaning a continuous timelike vector field. The expression remains valid for $r>1/\left|\mathsf{\Omega }\right|$, so we extend its range beyond the initial construction. In the flat space region $f\to 0$, it reduces to the lab observers ${\partial }_t$; hence, it agrees with the natural requirement that t increases towards the future in that region. It also agrees with the time orientation specified by the warp velocity on their region of overlap because they are related by a subluminal boost. A key point is that the time machine metric of Equation (3) is valid for $r<1/\left|\mathsf{\Omega }\right|$ and $r>1/\left|\mathsf{\Omega }\right|$, expanding the domain of applicability from what was considered in Ralph and Chang [22]. The metric retains a Lorentzian signature −+++ so it is a valid spacetime, despite not necessarily being constructed from a timelike platform. This is used in Section 5.2.

One may define the platform velocity as $u_{\mathrm{plat}}^{\mu }:=(1,0,\mathsf{\Omega },0)$ in the time machine spacetime (Appendix C). This may be timelike, null, or spacelike, and is not normalized as written. Similarly, for a revolving bubble, we may define the bubble velocity $u_{\mathrm{bubble}}^{\mu }:=(1,0,\tilde{\mathsf{\Omega }},0)$, which is also un-normalized.

4. Method for Finding the Geodesics

4.1. Killing Vector Fields

It is natural to classify geodesics and other curves using Killing vector fields to whatever extent this is possible. For the general f in Equation (5), the bubble velocity $(1,0,\tilde{\mathsf{\Omega }},0)$ is a Killing vector field. However, we drop the angular dependence, so the metric components are independent of t and $\varphi$. Hence, ${\partial }_t$ is a Killing vector, and gives rise to an “energy” which is conserved along the geodesics:

$$e:=-\langle \mathbf{u},{\partial }_t\rangle .$$

(10)

Here, $\mathbf{u}$ is the tangent to a curve parametrized by proper time or proper length if non-null. Since ${\partial }_t$ is not necessarily timelike, negative Killing energy is possible, but this is merely kinematics in contrast to the intrinsic negative energy of exotic matter. In addition, the Killing vector field ${\partial }_{\varphi }$ defines a natural angular momentum ℓ which is conserved along the geodesics:

$$\ell :=\langle \mathbf{u},{\partial }_{\varphi }\rangle .$$

(11)

Any trajectory with $z=0$ everywhere is classified by e and ℓ at each point, along with the sign of the r component. Its tangent is expressed most simply with a lowered index:

$$u_{\mu }=\left(-e,\pm \sqrt{ϵ+\frac{e^2{g}_{\varphi \varphi }+2e\ell g_{t\varphi }+{\ell }^2{g}_{tt}}{-g}},\ell ,0\right),$$

(12)

where $ϵ:=\langle \mathbf{u},\mathbf{u}\rangle$ is −1/0/1 for a timelike/null/spacelike vector respectively, and $g:=det\left(g_{\mu \nu }\right)$ evaluates to $-r^2$ for the time machine spacetime. However, this is only a “candidate” velocity, as it must satisfy several tests to be considered physical as follows.

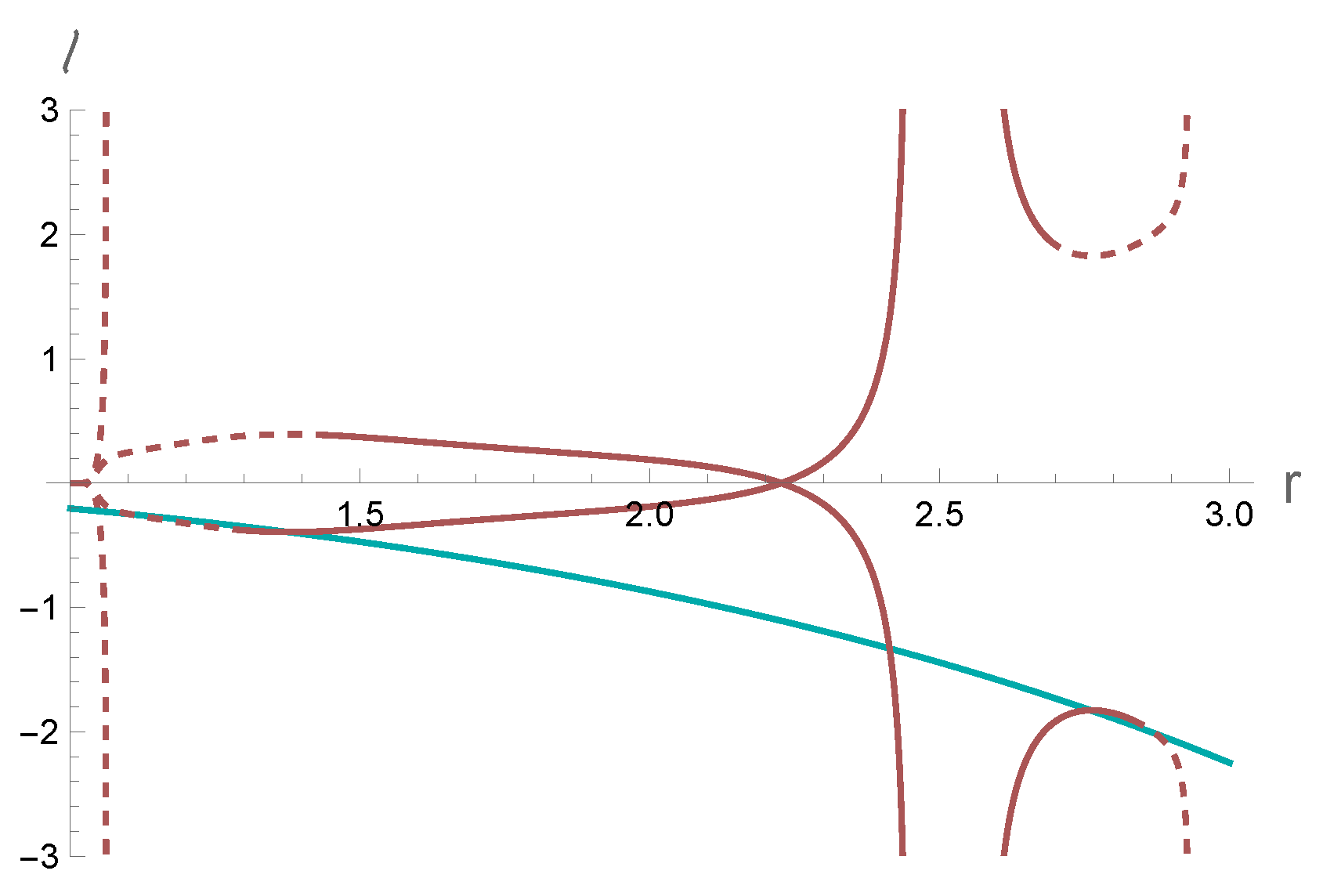
4.2. Inequalities

We consider three tests of the tangent to a curve, ranging from essential down to desirable.

(1)

Radicand test. Equation (12) involves a square root, so the radicand must be non-negative. Otherwise, one’s choice of e, ℓ and $ϵ$ does not define a valid trajectory at that particular spacetime point. With the time machine metric components, this is:

$$ϵ+e^2-\frac{{\ell }^2}{r^2}+f{v}_s(\ell -e\mathsf{\Omega }{r}^2)\frac{f{v}_s(\ell -e\mathsf{\Omega }{r}^2)-2r(e-\mathsf{\Omega }\ell )}{r^2(1-{\mathsf{\Omega }}^2{r}^2)}\ge 0.$$

(13)

(2)

Future-pointing test. Timelike and null tangents are required to be future-pointing if interpreted as physical particles. This is the local property: $\langle \mathbf{u},{\mathbf{u}}_{\mathrm{orient}}\rangle <0$, which utilizes Equation (9), giving:

$$f{v}_s\frac{\ell -e\mathsf{\Omega }{r}^2}{r(1-{\mathsf{\Omega }}^2{r}^2)}-e<0.$$

(14)

(3)

Backwards-in-t test. A desirable property of timelike and null tangents is to have $u^t<0$ for at least part of the curve. We seek paths with time travel, in the sense of returning to a lab observer worldline at an earlier lab time. For lab observers, t is the proper time, and t must increase in the flat region. Note that we make no insinuation of global simultaneity but have merely used the continuity of t on the manifold. Now, $u^t<0$ is:

$$e+f{v}_s\frac{\mathsf{\Omega }r(e-\mathsf{\Omega }\ell )+(e\mathsf{\Omega }{r}^2-\ell )(1+\mathsf{\Omega }rf{v}_s)/r}{1-{\mathsf{\Omega }}^2{r}^2}<0.$$

(15)

This trio of simultaneous inequalities is solvable as a large number of separate cases if we treat f as being independent of r as a first step. One may also show some simpler statements, for example, the restriction $r<1/\left|\mathsf{\Omega }\right|$ implies $\mathsf{\Omega }{v}_s<0$, so these parameters have opposite signs. In the flat region $f=0$, timelike and null test particles must have positive energy, an increasing t coordinate, and $ϵ+e^2-{\ell }^2/r^2\ge 0$.

4.3. Circular Paths

Circular trajectories are a simpler special case and aid in the discovery of other trajectories. With $r=\mathrm{const}$ and $z=0$, the candidate tangent is:

$$u_{\mu }=\left(\frac{\ell g_{t\varphi }-\pm \sqrt{-g({\ell }^2-ϵg_{\varphi \varphi })}}{g_{\varphi \varphi }},0,\ell ,0\right).$$

(16)

The ‘±’ indicates there are two possible solutions for the circular trajectories. It can be shown to correspond to the sign of $u^t$, at least when the latter is nonzero. Hence, it must be $-1$ to pass the backwards-in-t test. Note that e and ℓ are not independent because of the constraint of circular motion; rather, $e=-u_t$ may be read off from Equation (12).2 The radicand test is ${\ell }^2\ge ϵg_{\varphi \varphi }$, and the future-pointing test is $\langle \mathbf{u},{\mathbf{u}}_{\mathrm{orient}}\rangle <0$.

Again, these simultaneous inequalities are solvable, assuming that, at first, f is independent. For instance, in the case $ϵ=-1$ and $r<1/\left|\mathsf{\Omega }\right|$, we must have either $\mathsf{\Omega }rf{v}_s<-(1+|\mathsf{\Omega }\left|r\right)$; or else $-(r+1/\mathsf{\Omega })<rf{v}_s<(r-1/\mathsf{\Omega })$ together with:

$$\mathsf{\Omega }\ell \ge \left|\mathsf{\Omega }\right|r\sqrt{\frac{{\mathsf{\Omega }}^2{r}^2-{(1+\mathsf{\Omega }rf{v}_s)}^2}{1-{\mathsf{\Omega }}^2{r}^2}}.$$

(17)

Whilst for many cases now, requiring ℓ and e to be constant along a trajectory is necessary and sufficient to find the geodesics (such as the free-fall cases considered in the next section), this is not sufficient when circular motion is imposed. Given that ℓ and e are constant along a circular path, we further require that the particle feels no acceleration. The vector field $\mathbf{a}:={\nabla }_{\mathbf{u}}\mathbf{u}$, called the 4-acceleration for $ϵ=-1$, is directed radially:

$$a^{\mu }=\left(0,\frac{{\ell }^2(1-r{g}_{\varphi \varphi }^{\prime }/g_{\varphi \varphi })\pm \ell \sqrt{{\ell }^2+g_{\varphi \varphi }}(g_{t\varphi }^{\prime }-g_{t\varphi }{g}_{\varphi \varphi }^{\prime }/g_{\varphi \varphi })+g_{\varphi \varphi }-\frac{1}{2}r{g}_{\varphi \varphi }^{\prime }}{r{g}_{\varphi \varphi }},0,0\right).$$

(18)

A dash means derivative with respect to r. We used the determinant of the metric $g=-r^2$. It is computationally simpler to obtain the co-acceleration using ${\mathbf{a}}^{♭}=\mathbf{u}d{\mathbf{u}}^{♭}$ (Appendix B). Now, $\mathbf{a}=\mathbf{0}$ for an affinely parametrized geodesic. This does not typically have an exact solution for r. But conversely, if the spacetime parameters and a specific value of r are substituted, then this rearranges to a quadratic in ${\ell }^2$—that is, a quartic with terms in ${\ell }^4$, ${\ell }^2$, and 1. See Figure 2 for example solutions.

The abundance of circular geodesics suggests a strategy for time travel. Set up a test particle with ℓ and r chosen from the figure, and the corresponding e for circular motion, perhaps via a collision. It will accumulate negative t indefinitely, up to the time machine’s construction, or aside from any orbital instabilities. Then, arrange a collision to bump the particle out. From a lab frame, this may mean orchestrating the exit collision before the test particle is sent in. A different strategy is to pick a trajectory which is not circular but has similar parameters to a those of a circular geodesics. Most of our examples will be like this, starting from the flat region, making several roughly circular loops in the curved region and then exiting.

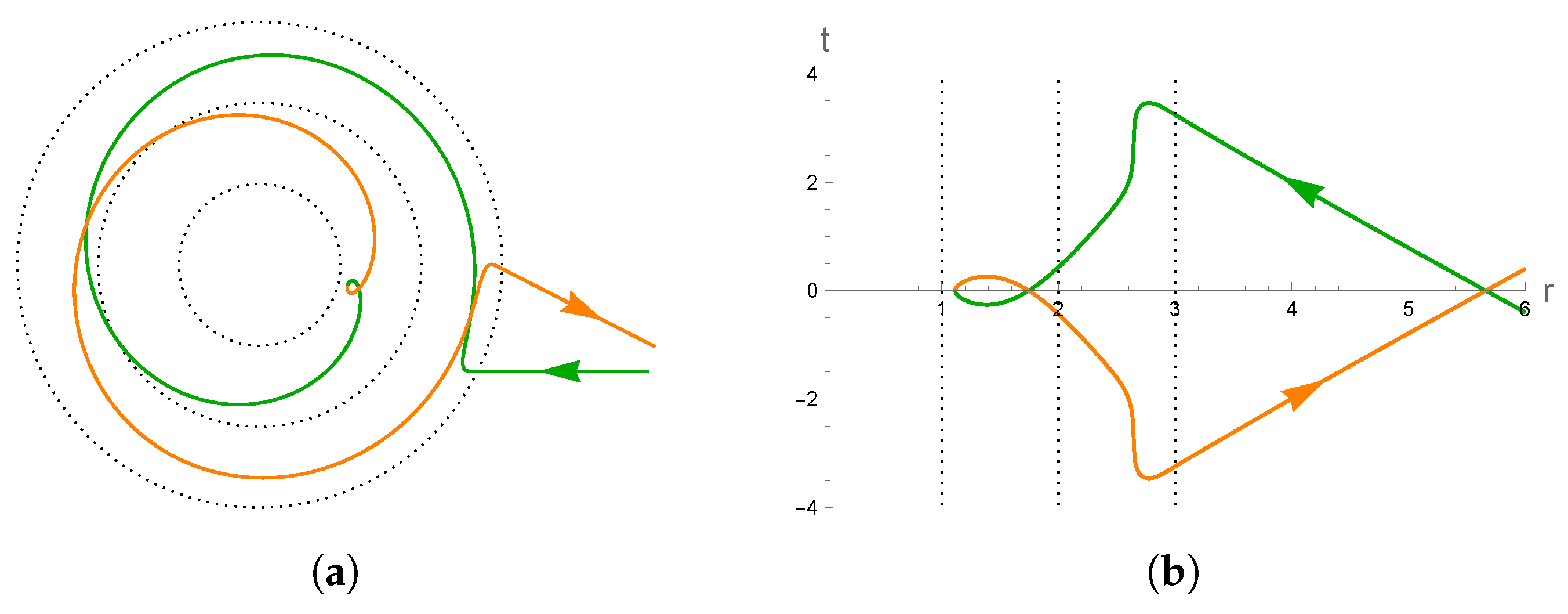
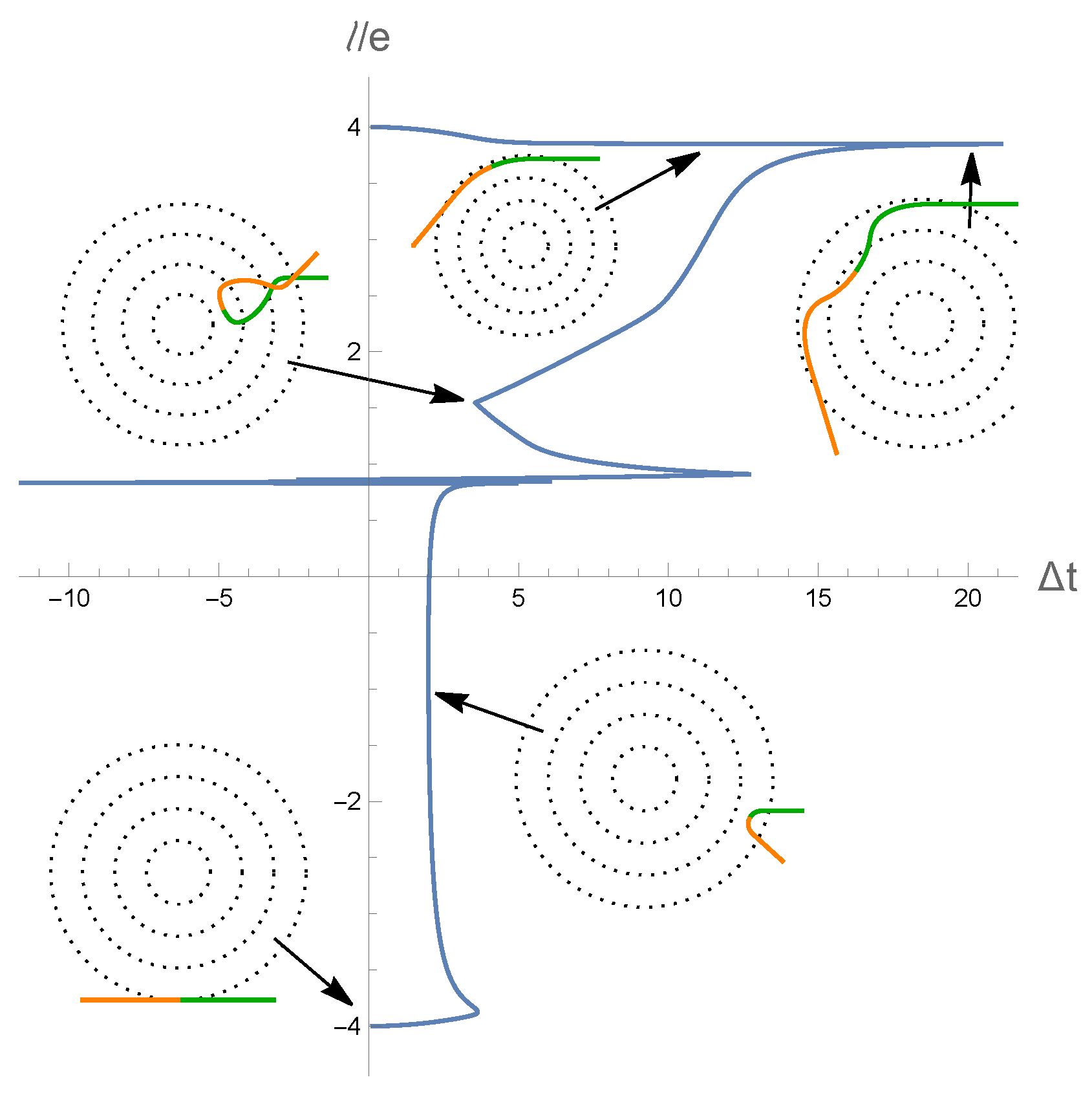
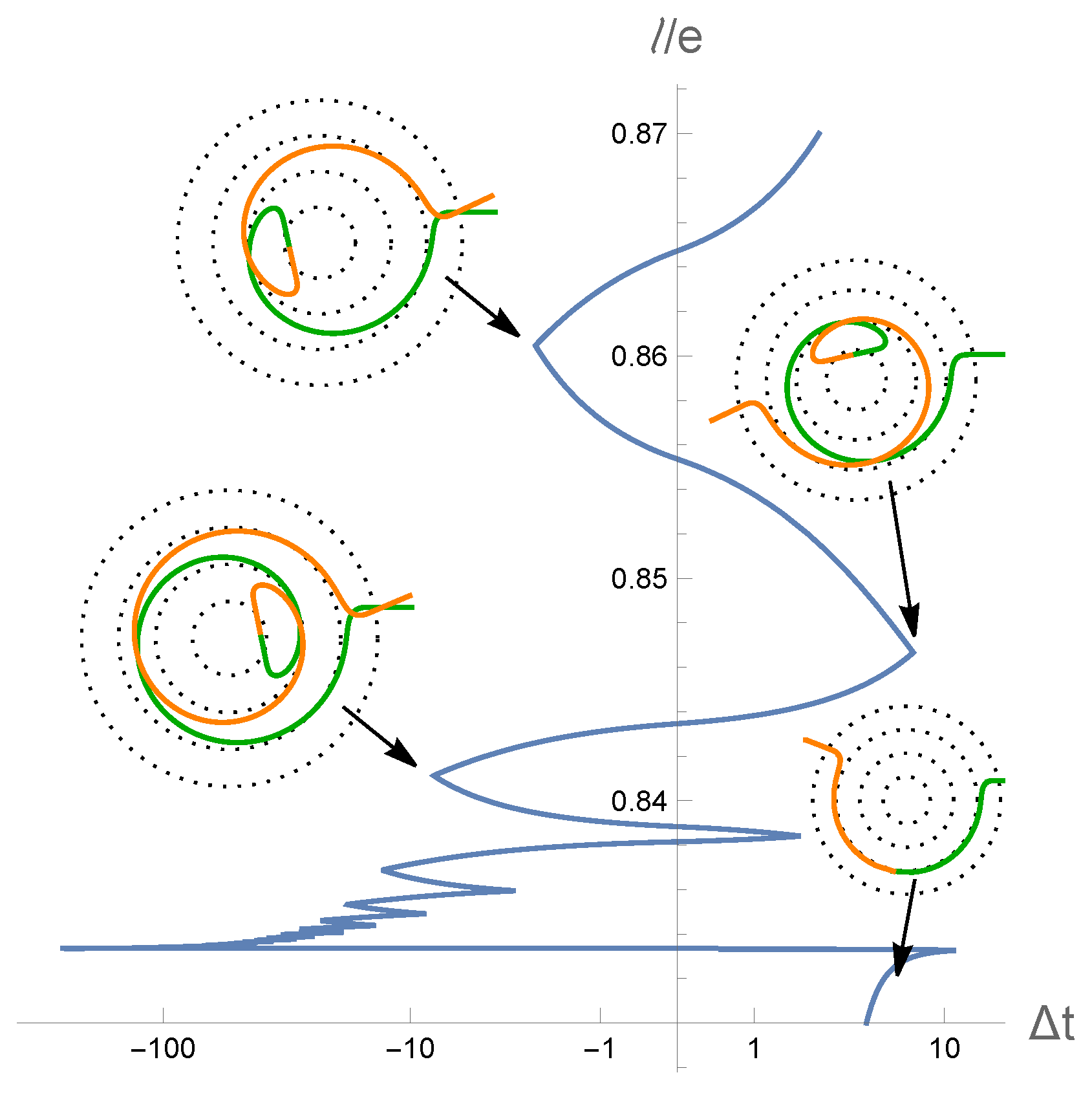
5. Free Fall to the Past

A very interesting situation is if particles can free fall from flat space into the time machine metric region and scatter back into flat space in such a way that they emerge in the past. We find such trajectories are possible given particular conditions for the metric and the initial trajectories. These trajectories do not form CTCs as such; indeed, closed loops are not what we desire for time travel. However, it is important to demonstrate in an operational way that there are events on the outward part of the trajectory that are indeed in the past of events on the inward part of the trajectory. We introduce a correction term that achieves this.

We start from the geodesic velocity field defined by Equation (12) for parameters where the physicality conditions, Equations (13) and (14), are satisfied. Then, for specific initial conditions (i.e., a particular incoming geodesic in flat space), the relevant geodesic in the region of curvature is calculated numerically from the velocity field. Timelike geodesics are found when $ϵ=-1$ and null geodesics when $ϵ=0$.

5.1. Timelike Geodesic Examples

In this section, we present timelike time-traveling geodesics in the spacetime with parameters $\mathsf{\Omega }=-1/5$, $v_s=7$, and the Gaussian-like f of Equation (6). The case of circular geodesics for the same parameters was already considered in Figure 2; however, these are stuck inside the time machine. Figure 3 exhibits a geodesic that achieves time travel, while starting and ending in the flat region.

In Figure 3b, the exit (orange) curve typically has a lesser t-value than the entry (green) curve, within the region shown. The t–r plot has striking steepness at $r\approx 2.64$, which corresponds to the outer loop in Figure 3a. Here, the trajectory parameters are close to those of a circular geodesic at that point, including the e; this appears as a point near the lower-right in Figure 2.

One way to unambiguously achieve time travel is if the particle returns to a given lab location at an earlier lab time. Now, a lab worldline appears vertical in the spacetime diagram; however, most apparent intersections actually have angular separation in $\varphi$. In the flat region, it is natural to use t as a simultaneity convention, as this is a proper time for the lab observers and is Poincaré–Einstein synchronized, meaning $t=\mathrm{const}$ is orthogonal to ${\partial }_t$. This justifies calling it an earlier lab time; however, this is largely just a convention. Physical or operational evidence would be the ability to send a causal signal from an outgoing event to an ingoing event. Suppose a lab observer is at some location along the ingoing curve. Time travel is achieved if there exists a timelike or null curve from the end (orange curve, later particle proper time) back to the start, arriving before the particle begins.

Suppose our causal signal is a null signal, sent along a circular arc at the time machine boundary, guided by an optical fiber, say. This curve segment takes lab time $\mathsf{\Delta }{t}_{\mathrm{arc}}=r\left|\mathsf{\Delta }\varphi \right|$, where the angular separation is at most $\pi$. Because we have not incorporated all possibilities, any conclusions that a given test particle trajectory achieves time travel should be understood as a sufficient condition but not necessary. Another approach is to compute the finite Minkowski interval between two points; this gives the length of a signal geodesic if the entire line passes through flat space. Another possibility is to send a geodesic signal though the curved region, but this calculation is more involved.

For the example trajectory, at $r=3$, the t-difference is ≈$-6.5$. Assuming our geometric units are meters, then 1 m of time is 1 m$/c\approx 3.3$ nanoseconds in SI units. The angular separation of ≈${25}^{\circ }$ (see Figure 3a) wastes $\approx 4.4$ ns, but in total the signal arrives with $\mathsf{\Delta }t\approx -17$ ns, which is before the particle leaves! For any readers creating their own plots, other time-traveling timelike geodesics with the Gaussian f include $\mathsf{\Omega }=-1/5$, $v_s=4.85$, $e=1.9$, and $\ell =-2.08$; or $\mathsf{\Omega }=-1/4$, $v_s=5.5$, $e=1.5$, and $\ell =-3.22$. These are adjusted so the $\varphi$-values roughly coincide at the boundary $r=3$.

To summarize the situation depicted in Figure 3a, the region of curvature is a cylinder of outer radius 3 m and inner radius 1 m. The particle moves in the $z=0$ plane. If the particle was to send a signal as it exits the region of curvature (orange curve, just outside the outer dotted radius), it would arrive at the entry point of the particle (green curve, just outside the outer dotted radius) approximately 17 nanoseconds before it enters.

5.2. Null Geodesic Examples

In this section, we consider null geodesics in the spacetime with parameters $\mathsf{\Omega }=1.2$, $v_s=1$, and the plateau f from Equation (7). Hence, in this section, the region of curvature is a cylinder of outer radius 4 m and inner radius 1 m. Note that this means our time machine spacetime ($f\ne 0$) is in the region $r>1/\left|\mathsf{\Omega }\right|$ for this section. Figure 4 shows an example trajectory chosen for its significant time travel. At the time machine boundary $r=4$, the difference between the t coordinates for the ingoing and outgoing path segments is $-46$ m to the nearest integer, or $-152$ ns. The angular difference here is ${74}^{\circ }$, which would take 17 ns for a causal signal to circumnavigate. The total time travel in our reckoning is still a respectable $\mathsf{\Delta }t=-135$ ns.

We focus on null geodesics, which start from the flat region, and hence have positive energy: $e>0$. Conveniently, their paths are classified by impact parameter $\ell /e$, up to rotational symmetry and the sign of $u^r$, and assuming constant $z=0$. A useful property is the “turning point”, where $u^r$ changes sign. This occurs at $u^r=0$, with solution:

$$\frac{\ell }{e}=\frac{-g_{t\varphi }\pm r}{g_{tt}}=r\frac{1+\mathsf{\Omega }rf{v}_s\mp \mathsf{\Omega }r}{\mathsf{\Omega }r+f{v}_s\mp 1}.$$

(19)

Figure 5 plots the turning points for the present spacetime parameters. In Minkowski spacetime or Newtonian physics, these would simply form a wedge $\ell /e=\pm r$, and correspond to the point of closest approach of a straight line to the origin. For the time machine with plateau f, this wedge graph does appear for $r\le 1$ and $r\ge 4$. Also, we see from inspection that none of the outside null geodesics can reach the origin. The closest is for $\ell /e$ just above $5/6$, which reach to just beyond $r=5/6$. There are two critical values of $\ell /e$ at $5/6$ and ≈$3.85$, where the minimum r attained by geodesics changes abruptly. This discontinuity is apparent in the diagram. Near the former value will turn out to be a rich parameter space for time travel. The latter corresponds to a turning point of Equation (19), which occurs at $r\approx 3.82$, with corresponding $\ell /e\approx 3.85$ as mentioned, which in turn has another intercept at $r\approx 2.70$.

Figure 6 shows the amount of time travel for null geodesics. Similarly to before, we define this as the difference in the t coordinate between the entry and exit points on the boundary $r=4$, plus a penalty of $r\left|\mathsf{\Delta }\varphi \right|$ for any angular offset, being the lab time (t) for a causal signal to return to the initial angle via a null circular arc. By definition, $\mathsf{\Delta }t=0$ for $\ell /e=\pm 4$ because these trajectories just graze the boundary.

Figure 7 exhibits the time travel to the past region by zooming in on Figure 6. From analytic and numerical investigation, it appears the number of loops increases without limit as $\ell /e\to 5/6$ from above, as does the time travel. In the figure, some points approach $1\mathsf{\mu }$s of time travel. As before, having $\mathsf{\Delta }t<0$, as we have defined $\mathsf{\Delta }t$, is a sufficient but not necessary condition for time travel because of our restricted choice of signal mechanism.

6. Discussion

We have discovered and analyzed certain classes of geodesic trajectories in the Ralph and Chang time machine spacetime, which result in time travel. The time travel is a large-scale property of a trajectory. As we have defined it, it occurs relative to static observers in the flat spacetime region.We emphasize again, that the trajectories are locally future-pointing everywhere, and remain timelike or null.

Most geodesics are not time-traveling. Those which are most successful, which complete many loops inside the time machine region, can be very sensitive to parameters. On the other hand, we found some very generic choices of bubble functions f were sufficient, without any fine-tuning. For the case of the massive particle geodesics, it would be interesting future work to look at the local environment (and tidal forces) of the particle as it traverses the trajectory. Another interesting future direction would be to try to engineer a collision between the ingoing and outgoing trajectories, thus forming an explicit geodesic CTC similar to the type discussed by Thorne et al. [3]. This would presumably require fine tuning of the parameters.

We also further analyzed the spacetime itself, obtaining a time orientation, and pointing out some Killing vector(s). We have also made a small contribution to the physical interpretation of spacetimes involving rotation, which has been a longstanding challenge in some cases. We also generalized Alcubierre’s construction based on hypersurface–orthogonal observers to allow vorticity.