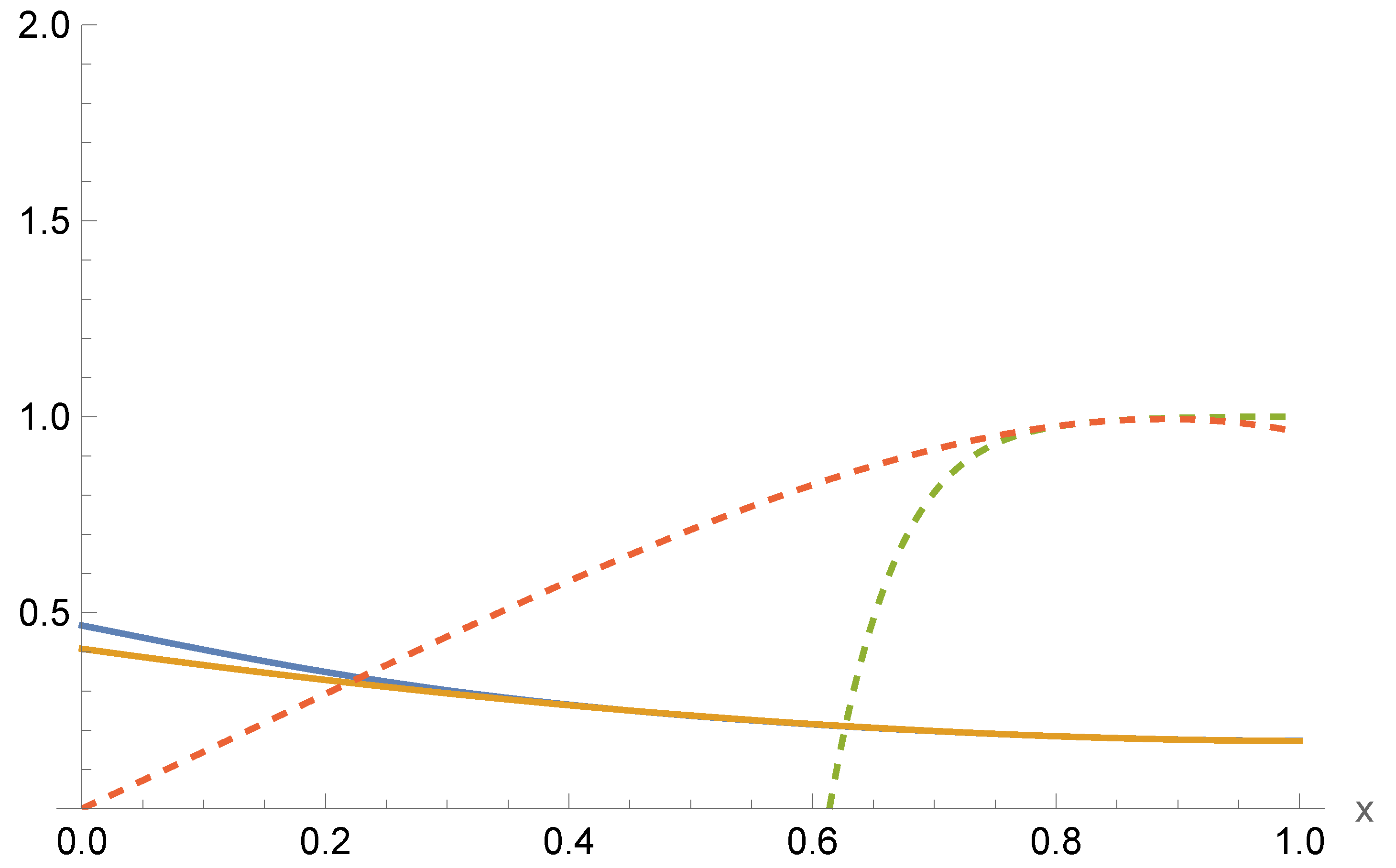Gravitational Wormholes

Abstract

Spacetime wormholes are evidently an essential component of the construction of a time machine. Within the context of general relativity, such objects require, for their formation, exotic matter—matter that violates at least one of the standard energy conditions. Here, we explore the possibility that higher-curvature gravity theories might permit the construction of a wormhole without any matter at all. In particular, we consider the simplest form of a generalized quasi topological theory in four spacetime dimensions, known as Einsteinian Cubic Gravity. This theory has a number of promising features that make it an interesting phenomenological competitor to general relativity, including having non-hairy generalizations of the Schwarzschild black hole and linearized equations of second order around maximally symmetric backgrounds. By matching series solutions near the horizon and at large distances, we find evidence that strong asymptotically AdS wormhole solutions can be constructed, with strong curvature effects ensuring that the wormhole throat can exist.

1. Introduction

It has long been known that if spacetime is to have closed timelike curves in some local regions [1], then wormholes are an essential part of this construction [2,3]. However, a key characteristic of such objects is that they require exotic matter that does not respect the energy conditions. Despite the challenges presented in constructing wormholes [4], the search nevertheless continues in the hopes of evading the constraints imposed by quantum physics in Einsteinian geometries [5].

Much effort has gone into exploring modified gravity to this end [6,7,8,9,10,11,12,13,14]. The higher-curvature Lovelock theories [15,16] have been of particular interest [17,18,19,20,21,22,23,24] since the field equations are of second order in the metric components. However, non-trivial solutions exist only in spacetime dimensions $D\ge 5$. Curiously, quasi-topological gravities [25,26,27,28,29,30] could also be considered for wormhole solutions, but none have been obtained to date. However, such objects would also exist only in $D\ge 5$ dimensions.

Both Lovelock and quasi-topological theories have been shown to be particular cases of a more general class called Generalized Quasi-Topological gravity (GQTG) [31,32,33,34,35]. These theories are characterized by second-order linearized equations around maximally symmetric backgrounds and admit single-function ($g_{tt}{g}_{rr}=-1$) non-hairy generalizations of the Schwarzschild black hole. These theories are ghost-free on constant-curvature backgrounds, but, on a generic background, will have ghosts. However, such ghosts cannot escape to infinity in spacetimes that are asymptotically of constant curvature. The effects of the additional degrees of freedom in GQTGs have not been fully explored, but it is known that they significantly modify the thermodynamics of black holes for small masses [34] and, in the cubic and quartic cases, exhibit an number of interesting features [34,36,37,38,39,40,41]. A comprehensive list of their properties has been given [35,42]. A key advantage of GQTGs is that they have non-trivial field equations (and solutions) in $D=4$ dimensions.

In this paper, we carry out the first investigations of wormhole solutions in $D=4$ Generalized Quasi-Topological gravity. For specificity, we shall consider the simplest GQTG, a theory known as Einsteinian Cubic Gravity (ECG) [31,43], whose action is of the form

$$\mathcal{I}={\displaystyle \frac{1}{16\pi }}\int d^{4}x\sqrt{-g}(-2{\mathsf{\Lambda }}_0+R+\alpha \mathcal{P}+\beta \mathcal{C}+\gamma {\mathcal{C}}^{\prime }),$$

(1)

with $\alpha$, $\beta$ and $\gamma$ being coupling constants, and three densities that are cubic in the Riemann curvature, given by

$$\mathcal{P}=12R_{ab}^{cd}{R}_{cd}^{ef}{R}_{ef}^{ab}+R_{ab}^{cd}{R}_{cd}^{ef}{R}_{ef}^{ab}-12R_{abcd}{R}^{ac}{R}^{bd}+8{R^b}_a{R^c}_b{R^a}_c,$$

(2)

$$\mathcal{C}={\displaystyle \frac{1}{2}}R{R_a}^b{R_b}^a-2R^{ac}{R}^{bd}{R}_{abcd}-{\displaystyle \frac{1}{4}}R{R}_{abcd}{R}^{abcd}+R^{de}{R}_{abcd}{R}_e^{abc},$$

(3)

$${\mathcal{C}}^{\prime }={R_a}^b{R_b}^c{R_c}^a-{\displaystyle \frac{3}{4}}R{R_a}^b{R_b}^a+{\displaystyle \frac{1}{8}}{R}^3.$$

(4)

For a general static spherically symmetric ansatz (GSSS)

$$d{s}^2=-f\left(r\right)d{t}^2+{\displaystyle \frac{1}{N\left(r\right)f\left(r\right)}}d{r}^2+r^2(d{\theta }^2+{sin}^2\theta d{\varphi }^2),$$

(5)

the densities $\mathcal{C}$ and ${\mathcal{C}}^{\prime }$ do not contribute in a linearly independent way to the field equations. Both of these terms become trivial when the metric function $N\left(r\right)$ is a constant. This situation is the one generally considered in ECG and clearly does not admit a vacuum wormhole. Note that, regardless of the values that the higher-curvature couplings take, the Einstein–AdS limit of the theory at large distances is preserved (albeit with a modified cosmological constant), since the contributions from the cubic terms fall off much more rapidly than the contributions from the Einstein–Hilbert part of the action if AdS asymptotic behaviour is imposed as a requirement.

We therefore consider the GSSS ansatz with $N^{\prime }\ne 0$. We find that this situation is possible if the spacetime has a spherical deficit/surfeit angle in the asymptotic large-r region. We shall specifically consider solutions whose metric functions have the asymptotic form

$$g_{tt}\sim -\left({\displaystyle \frac{r^2}{l^2}}+1+\delta \right)+\mathcal{O}\left(r^{-1}\right),g^{rr}\sim {\displaystyle \frac{r^2}{l^2}}+1+\delta +\mathcal{O}\left(r^{-1}\right)$$

(6)

where l is the AdS length scale and $\delta \ne 0$ parametrizes the deficit/surfeit angle.

We find that Einsteinian Cubic Gravity—and, by implication, higher-order GQTGs—admits wormhole solutions that are purely gravitational without any exotic matter. The solutions that we obtain are asymptotically anti-de Sitter, with a spherical deficit angle resembling that of a global monopole. Unlike other solutions with radial symmetry, these solutions have non-zero values for the coupling parameter $\beta$. We find that including $\beta$ provides a sufficiently large number of parameters to match the series solutions for the two metric functions over a broad range of radii at which the matching takes place.

2. The Non-Linear ODE System

For the ansatz (5), we find that the two independent field equations are

$$\begin{array}{cc}\hfill & -{\displaystyle \frac{1}{8r^5}}\{8r\left(r^2(-1+r^2{\mathsf{\Lambda }}_0)+6\alpha N^2{f}^{\prime 2}(-1+r^2{f}^{\prime }{N}^{\prime })+rN{f}^{\prime }(r^2+12\alpha f^{\prime }{N}^{\prime })\right)\hfill \\ \hfill & +2f[4r^2{N}^{\prime }(r^2+15\alpha f^{\prime }{N}^{\prime })+rN(3r^2(74\alpha +5\beta )f^{\prime 2}{N}^{\prime 2}+4r(r+48\alpha N^{\prime }{f}^{″})\hfill \\ \hfill & -24f^{\prime }\left((8\alpha -\beta )N^{\prime }-8r\alpha N^{″}\right))+24r\alpha N^3\left(4f^{\prime 2}+r^2{f}^{″2}+r{f}^{\prime }(-4f^{″}+r{f}^{‴})\right)\hfill \\ \hfill & +12N^2\left(f^{\prime }\left(8\alpha +r^3(22\alpha +\beta )N^{\prime }{f}^{″}\right)+8r^2\alpha f^{\prime 2}\left(-3N^{\prime }+r{N}^{″}\right)+4r\alpha \left(-2f^{″}+r{f}^{‴}\right)\right)]\hfill \\ \hfill & +6f^3[r^2{N}^{\prime 2}\left(-4\alpha N^{\prime }+r(8\alpha +\beta )N^{″}\right)+4N^2\left(2\beta N^{\prime }-r\left((-4\alpha +\beta )N^{″}+4r\alpha N^{‴}\right)\right)\hfill \\ \hfill & +rN\left((8\alpha -7\beta )N^{\prime 2}+2r^2(8\alpha +\beta )N^{″2}+2r{N}^{\prime }\left(-20\alpha N^{″}+r(8\alpha +\beta )N^{‴}\right)\right)]\hfill \\ \hfill & +3f^2[r{N}^{\prime }\left(6\beta N^{\prime }+r^2(28\alpha +3\beta )f^{\prime }{N}^{\prime 2}+16r\alpha N^{″}\right)-32\alpha N^3\left(2f^{\prime }+r(-2f^{″}+r{f}^{‴})\right)\hfill \\ \hfill & +2N(2r^2{N}^{\prime 2}\left(-52\alpha f^{\prime }+r(26\alpha +3\beta )f^{″}\right)+N^{\prime }\left(-8\beta +r^3(108\alpha +11\beta )f^{\prime }{N}^{″}\right)\hfill \\ \hfill & +4r\left((-4\alpha +\beta )N^{″}+4r\alpha N^{‴}\right))+4r{N}^2[r\left(r(12\alpha +\beta )f^{″}{N}^{″}+N^{\prime }\left(-48\alpha f^{″}+r(8\alpha +\beta )f^{‴}\right)\right)\hfill \\ \hfill & +f^{\prime }\left(6(8\alpha -\beta )N^{\prime }+4r\alpha (-12N^{″}+r{N}^{‴})\right)\left]\right]\}=0\hfill \end{array}$$

(7)

and

$$\begin{array}{cc}\hfill & {\displaystyle \frac{1}{8r^5}}\{-8r\left(r^2(-1+r^2{\mathsf{\Lambda }}_0)+6\alpha N^2{f}^{\prime 2}(-1+r^2{f}^{\prime }{N}^{\prime })+rN{f}^{\prime }(r^2+12\alpha f^{\prime }{N}^{\prime })\right)\hfill \\ \hfill & +6\beta f^{3}N\left(r{N}^{\prime 2}+N(-8N^{\prime }+4r{N}^{″})\right)-2f[-12r^2\alpha f^{\prime }{N}^{\prime 2}+rN(3r^2(26\alpha +3\beta )f^{\prime 2}{N}^{\prime 2}\hfill \\ \hfill & +4r\left(r+12\alpha N^{\prime }{f}^{″}\right)+24f^{\prime }\left((-2\alpha +\beta )N^{\prime }+2r\alpha N^{″}\right))+24r\alpha N^3(4f^{\prime 2}+r^2{f}^{″2}\hfill \\ \hfill & +r{f}^{\prime }(-4f^{″}+r{f}^{‴}))+12N^2(f^{\prime }\left(8\alpha +r^3(12\alpha +\beta )N^{\prime }{f}^{″}\right)+2r^2\alpha f^{\prime 2}(-8N^{\prime }+r{N}^{″})\hfill \\ \hfill & +4r\alpha (-2f^{″}+r{f}^{‴})\left)\right]+3f^2[r{N}^{\prime 2}\left(2\beta +r^2(8\alpha +\beta )f^{\prime }{N}^{\prime }\right)-2N(2r^2{N}^{\prime 2}(-4\alpha f^{\prime }\hfill \\ \hfill & +r(8\alpha +\beta )f^{″})+4r\beta N^{″}+N^{\prime }\left(-8\beta +3r^3(8\alpha +\beta )f^{\prime }{N}^{″}\right))+32\alpha N^3(2f^{\prime }+r\hfill \\ \hfill & \left(-2f^{″}+r{f}^{‴}\right))-4r{N}^2(2f^{\prime }\left((8\alpha -3\beta )N^{\prime }-8r\alpha N^{″}\right)+r(r(8\alpha +\beta )f^{″}{N}^{″}+N^{\prime }\hfill \\ \hfill & \left(-16\alpha f^{″}+r(8\alpha +\beta )f^{‴}\right)\left)\right)\left]\right\}=0\hfill \end{array}$$

(8)

where, without loss of generality, we can set $\gamma =0$ in (1), since its inclusion simply reproduces the preceding equations but with $\beta \to \beta +\gamma /2$.

If $N\left(r\right)$ is constant, then these equations become linearly dependent, and a wormhole solution is not possible since there will be a single metric function whose largest root corresponds to the horizon of a black hole.

We can see this by considering the series expansions

$$f_{\infty }=1-{\displaystyle \frac{\mathsf{\Lambda }}{3}}{r}^2+\sum _{i=1}{\displaystyle \frac{{\tilde{f}}_i}{r^i}},N_{\infty }=1+\sum _{i=1}{\displaystyle \frac{{\tilde{N}}_i}{r^i}}$$

(9)

in the asymptotically distant region at large r, where asymptotically flat solutions have $\mathsf{\Lambda }=0$. Inserting these into the field Equations (7) and (8) yields

$$\begin{array}{cc}\hfill h\left(\mathsf{\Lambda }\right)& =0\widetilde{N_i}=0\hfill \end{array}$$

(10)

$$\begin{array}{cc}\hfill f_{\infty }& =1-{\displaystyle \frac{\mathsf{\Lambda }}{3}}{r}^2-{\displaystyle \frac{r_h}{r}}+{\displaystyle \frac{(54-28\mathsf{\Lambda }{r}^2)\alpha r_h^2}{h^{\prime }\left(\mathsf{\Lambda }\right)r^6}}-{\displaystyle \frac{138\alpha r_h^3+20192{\mathsf{\Lambda }}^2{\alpha }^2{r}_h^3}{3h^{\prime 2}{r}^7}}+\mathcal{O}\left(r^{-9}\right)\hfill \end{array}$$

(11)

in the limit $r\to \infty$, where

$$h\left(x\right)\equiv \frac{8\alpha }{9}{x}^3+x-{\mathsf{\Lambda }}_0$$

(12)

and

$$\mathsf{\Lambda }=-{\displaystyle \frac{3}{l^2}}\equiv -3L,h^{\prime }\left(\mathsf{\Lambda }\right)={\displaystyle \frac{dh}{dx}}{|}_{\mathsf{\Lambda }}={\displaystyle \frac{8\alpha }{3}}{\mathsf{\Lambda }}^2+1=24\alpha L^2+1$$

(13)

and all $\beta$-dependent terms vanish.

From these formulae, we observe several aspects. First, a power-series solution in $1/r$ implies only a single independent function $f\left(r\right)$, which is the hallmark of GQTGs. Second, for asymptotically flat solutions $\mathsf{\Lambda }=0$, which in turn implies ${\mathsf{\Lambda }}_0=0$, we also have $h^{\prime }=1$, and so the asymptotically flat solution can be immediately obtained from (11) by setting $\mathsf{\Lambda }=0$. However, note that the converse is not true: even if ${\mathsf{\Lambda }}_0=0$, it is possible to have asymptotically de Sitter solutions with $\mathsf{\Lambda }=3/\sqrt{8\left|\alpha \right|}$ provided that $\alpha <0$.

We seek solutions that have the asymptotic form (6), where $N\left(r\right)$ is not constant so as to obtain wormhole solutions. The presence of the wormhole needs to be manifest at large-r in a way that differs from that of a spherically symmetric star or black hole. To this end, we consider the ansatz

$$f_{\infty }=K+L{r}^2+\sum _{i=1}{\displaystyle \frac{a_i}{r^i}},N_{\infty }=1+\sum _{i=1}{\displaystyle \frac{b_i}{r^i}}$$

(14)

where the quantity $K=1+\delta$ parameterizes a spherical deficit/surfeit angle produced by the wormhole. The effect is analogous to that produced by a global monopole [44,45]. Far from the wormhole, all light rays are deflected by the same angle regardless of their impact parameter.

Inserting the ansatz (14) into the field equations yields

$$\begin{array}{cc}\hfill & b_{1}L(24L^2\alpha +1)=0\hfill \end{array}$$

(15)

from both equations to leading order. This equation is satisfied by choosing either $b_1=0$ or $(24L^2\alpha +1)=0$. However, it is straightforward to show that the next order forces $b_1=0$ regardless of the value of $(24L^2\alpha +1)$. However, if this latter quantity is non-zero, then it is straightforward to show that there is no deficit angle, and all $b_i$ coefficients must vanish as per the discussion above.

Setting $(24L^2\alpha +1)=0$ then yields the non-trivial solution

$$\begin{array}{cc}{N}_{\infty }\hfill & =1-{\displaystyle \frac{5a_1}{2L{r}^3\left(9\beta L^2-2\right)}}+{\displaystyle \frac{135a_1^2\left(\beta L^2\left(99\beta L^2-49\right)+6\right)}{16(K-1)L{r}^4{\left(9\beta L^2-2\right)}^3}}\hfill \\ \hfill & +{\displaystyle \frac{a_1\left(192{(K-1)}^{2}K{\left(2-9\beta L^2\right)}^2-27a_1^{2}L\left(3\beta L^2\left(3972\beta L^2-2207\right)+919\right)\right)}{64{(K-1)}^2{L}^2{r}^5{\left(9\beta L^2-2\right)}^3}}+\cdots \hfill \end{array}$$

(16)

$$\begin{array}{cc}{f}_{\infty }\hfill & =K+L{r}^2+{\displaystyle \frac{a_1}{r}}-{\displaystyle \frac{9a_1^2\left(828{\beta }^2{L}^4-363\beta L^2+37\right)}{32(K-1)r^2{\left(9\beta L^2-2\right)}^2}}\hfill \\ \hfill & +{\displaystyle \frac{a_1\left(9a_1^{2}L\left(3\beta L^2\left(9\beta L^2\left(9932\beta L^2-6829\right)+13340\right)-2641\right)\right)}{224{(K-1)}^{2}L{r}^3{\left(9\beta L^2-2\right)}^3}}\hfill \\ \hfill & +{\displaystyle \frac{a_1\left(-32{(K-1)}^{2}K{\left(2-9\beta L^2\right)}^2\left(9\beta L^2-6\right)\right)}{224{(K-1)}^{2}L{r}^3{\left(9\beta L^2-2\right)}^3}}+\cdots \hfill \end{array}$$

(17)

where ${\mathsf{\Lambda }}_0=-2L$ from (10) and (12).

We now see that the condition $h^{\prime }\left(\mathsf{\Lambda }\right)=0$ from (13) allows for N to be a non-constant function, opening up the possibility of obtaining a wormhole solution. We pursue this in the next section.

3. Series Solutions

Anticipating the asymptotic behaviour (14), we rewrite the general static spherically symmetric (GSSS) ansatz (5) in the form

$$d{s}^2=-{\displaystyle \frac{r_0^{2}g\left(x\right)}{{(1-x)}^2}}d{\tilde{t}}^2+{\displaystyle \frac{r_0^{2}d{x}^2}{n\left(x\right)g\left(x\right){(1-x)}^2}}+{\displaystyle \frac{r_0^2}{{(1-x)}^2}}(d{\theta }^2+{sin}^2\theta d{\varphi }^2),$$

(18)

using the coordinate transformation

$$x=1-r_0/r\tilde{t}=t/r_0$$

where the metric functions $n\left(x\right)$ and $g\left(x\right)$, defined on $x\in [0,1]$, are

$$\begin{array}{c}\hfill n=Ng={\displaystyle \frac{f{r}_0^2}{r^2}}\end{array}$$

(19)

with $r_0$ a positive constant.

For wormhole solutions [1], these continuous functions must be everywhere positive in the interior of the domain, with n vanishing and g having a finite positive value at $x=0$, which locates the position of the wormhole throat. Under this map, $r\to \infty$ is compactified to $x=1$. With this new ansatz, the boundary condition (6) is equivalent to

$$g\sim {\displaystyle \frac{r_0^2}{l^2}}+{\displaystyle \frac{(1+\delta )r_0^2}{r^2}}+\mathcal{O}\left(r^{-3}\right),n\sim 1+\mathcal{O}\left(r^{-3}\right)$$

(20)

as x approaches 1. The effect of $\delta$ is analogous to that produced by a global monopole [44,45], which deflects light rays by the same angle regardless of their impact parameter.

The advantage of the ansatz (18) is clear—it compactifies the domain so that numerical and semi-analytic solutions become more easily attainable. We now employ this ansatz to obtain series solutions for the functions n and g. The field equations for $g\left(x\right)$ and $n\left(x\right)$ are given in Appendix A.

3.1. Large-r Solution

To obtain solutions asymptotic to (20), we substitute the formal series

$$g=a_0+\sum _{n=2}^{\infty }{a}_n{(1-x)}^n,n=1+\sum _{n=3}^{\infty }{b}_n{(1-x)}^n,a_0=r_0^2/l^2\equiv L{r}_0^2,a_2=1+\delta$$

(21)

into the equations and solve them order by order in $(1-x)$. Note that we have set $b_1=b_2=0$ due to the discussion following condition (15). The lowest two orders yield two constraints $h\left(a_0\right)=0$ and $(24\alpha L^2+1)(a_2-1)=0$. The first of these simply defines ${\mathsf{\Lambda }}_0$ in terms of the other parameters. Solutions with a vanishing deficit $a_2=1$ satisfy the second constraint but force $b_{n\ge 3}=0$ or, in other words, $n=1$. The only alternative non-trivial solution occurs when $a_2\ne 1$, yielding

$$\begin{array}{cc}g=\hfill & L{r}_0^2+a_2{(1-x)}^2-{\displaystyle \frac{2}{5}}{b}_{3}L{r}_0^2{(1-x)}^3\left(9\beta L^2-2\right)\hfill \\ \hfill & -{\displaystyle \frac{9b_3^2{L}^2{r}_0^4{(1-x)}^4\left(828{\beta }^2{L}^4-363\beta L^2+37\right)}{200(a_2-1)}}\hfill \\ \hfill & +{\displaystyle \frac{3b_3{(1-x)}^5}{3500{(a_2-1)}^2}}\{\left(200a_2^3\left(3\beta L^2-2\right)-400a_2^2\left(3\beta L^2-2\right)+200a_2\left(3\beta L^2-2\right)\right)\hfill \\ \hfill & +\left(3b_3^2{L}^3{r}_0^6\left(-268164{\beta }^3{L}^6+184383{\beta }^2{L}^4-40020\beta L^2+2641\right)\right)\}\hfill \\ \hfill & -{\displaystyle \frac{b_3^{2}L{r}_0^2{(1-x)}^6}{4480000{(a_2-1)}^3}}\{\left(-43200{(a_2-1)}^2(1803a_2+85){\beta }^2{L}^4\right.\hfill \\ \hfill & +13200{(a_2-1)}^2(3063a_2+545)\beta L^2-400{(a_2-1)}^2(13371a_2+3535)\hfill \\ \hfill & +72626980752{\beta }^4{b}_3^2{L}^{11}{r}_0^6-68916687624{\beta }^3{b}_3^2{L}^9{r}_0^6+23598134433{\beta }^2{b}_3^2{L}^7{r}_0^6\hfill \\ \hfill & -3385644966\beta b_3^2{L}^5{r}_0^6+164339937b_3^2{L}^3{r}_0^6)\}\hfill \\ \hfill & +{\displaystyle \frac{b_3{(1-x)}^7}{392000000{(a_2-1)}^{4}L{r}_0^2}}\{36000a_2{b}_3^2{L}^3{r}_0^6\left(5699484{\beta }^3{L}^6-3438357{\beta }^2{L}^4\right.\hfill \\ \hfill & \left.+659159\beta L^2-39732\right)+800a_2^3\left(295678404{\beta }^3{b}_3^2{L}^9{r}_0^6-211323051{\beta }^2{b}_3^2{L}^7{r}_0^6\right.\hfill \\ \hfill & \left.+49375923\beta b_3^2{L}^5{r}_0^6-3749468b_3^2{L}^3{r}_0^6+336000\beta L^2-448000\right)\hfill \\ \hfill & -800a_2^2\left(571755996{\beta }^3{b}_3^2{L}^9{r}_0^6-394347609{\beta }^2{b}_3^2{L}^7{r}_0^6+88894962\beta b_3^2{L}^5{r}_0^6\right.\hfill \\ \hfill & \left.-6518172b_3^2{L}^3{r}_0^6+84000\beta L^2-112000\right)-22400000a_2^6\left(3\beta L^2-4\right)\hfill \\ \hfill & +89600000a_2^5\left(3\beta L^2-4\right)-134400000a_2^4\left(3\beta L^2-4\right)\hfill \\ \hfill & +b_3^2{L}^3{r}_0^6\left(-170858662247952{\beta }^5{b}_3^2{L}^{13}{r}_0^6+207845496209160{\beta }^4{b}_3^2{L}^{11}{r}_0^6\right.\hfill \\ \hfill & -98339490752265{\beta }^3{b}_3^2{L}^9{r}_0^6+22351263412410{\beta }^2{b}_3^2{L}^7{r}_0^6-2386812017025\beta b_3^2{L}^5{r}_0^6\hfill \\ \hfill & +91235810916b_3^2{L}^3{r}_0^6+15680649600{\beta }^3{L}^6-22638794400{\beta }^2{L}^4+7885507200\beta L^2\hfill \\ \hfill & \left.-784611200\right)\}+\cdots \hfill \end{array}$$

(22)

$$\begin{array}{cc}n=\hfill & 1+b_3{(1-x)}^3+{\displaystyle \frac{27b_3^{2}L{r}_0^2{(1-x)}^4\left(11\beta L^2-3\right)}{20(a_2-1)}}\hfill \\ \hfill & +{\displaystyle \frac{3b_3{(1-x)}^5\left(-400a_2^3+800a_2^2-400a_2+9b_3^2{L}^3{r}_0^6\left(11916{\beta }^2{L}^4-6621\beta L^2+919\right)\right)}{1000{(a_2-1)}^{2}L{r}_0^2}}\hfill \\ \hfill & +{\displaystyle \frac{b_3^2{(1-x)}^6}{3500{(a_2-1)}^3}}\{\left(-750{(a_2-1)}^2(105a_2+16)\beta L^2+125{(a_2-1)}^2(175a_2+22)\right.\hfill \\ \hfill & +\left.28954908{\beta }^3{b}_3^2{L}^9{r}_0^6-24304212{\beta }^2{b}_3^2{L}^7{r}_0^6+6795981\beta b_3^2{L}^5{r}_0^6-633051b_3^2{L}^3{r}_0^6\right)\}\hfill \\ \hfill & +{\displaystyle \frac{9b_3{(1-x)}^7}{6272000{(a_2-1)}^4{L}^2{r}_0^4}}\{-160a_2^3\left(2795796{\beta }^2{b}_3^2{L}^7{r}_0^6-1577271\beta b_3^2{L}^5{r}_0^6\right.\hfill \\ \hfill & \left.+222099b_3^2{L}^3{r}_0^6+22400\right)+160a_2^2\left(5138172{\beta }^2{b}_3^2{L}^7{r}_0^6-2934417\beta b_3^2{L}^5{r}_0^6\right.\hfill \\ \hfill & \left.+417978b_3^2{L}^3{r}_0^6+5600\right)-480a_2{b}_3^2{L}^3{r}_0^6\left(629652{\beta }^2{L}^4-379007\beta L^2+56553\right)\hfill \\ \hfill & +896000a_2^6-3584000a_2^5+5376000a_2^4+3b_3^2{L}^3{r}_0^6\left(54758424816{\beta }^4{b}_3^2{L}^{11}{r}_0^6\right.\hfill \\ \hfill & -61487988408{\beta }^3{b}_3^2{L}^9{r}_0^6+25878434823{\beta }^2{b}_3^2{L}^7{r}_0^6-4838200650\beta b_3^2{L}^5{r}_0^6\hfill \\ \hfill & \left.+339035463b_3^2{L}^3{r}_0^6-24182400{\beta }^2{L}^4+11740000\beta L^2-1398400\right)\}+\cdots \hfill \end{array}$$

(23)

where

$$\begin{array}{c}\hfill 24\alpha L^2+1=0\end{array}$$

(24)

and ${\mathsf{\Lambda }}_0$ and $\alpha$ are replaced by expressions in terms of L via the two constraints $h\left(a_0\right)=0$ and (24).

The parameters $a_0=L{r}_0^2$, $a_2$ and $b_3$ are the only free variables in this solution; we also have $n\left(1\right)=n_0=1$. Furthermore $\beta$ is an independent coupling parameter. It can happen in a non-linear system that fewer constants of integration appear in a solution than the differential order of the equations. Due to the non-linearity, a spontaneous singularity could appear, which means that the radii of convergence for g and n depend on the initial conditions, namely the values of these parameters. We do not expect vanishing radii of convergence for all values of the parameters, since the series with $b_3=0$ converges to the AdS solution with a deficit.

3.2. Near-Throat Solution

There is likewise a near-throat solution for $(24L^2\alpha +1)=0$. Local solutions near $x=0$ compatible with (22) and (23) are necessarily Taylor series. In this case, the desired boundary conditions at the throat require the ansatz to be

$$n=\sum _{n=1}^{\infty }{A}_n{x}^{n}g=B_0+\sum _{n=1}^{\infty }{B}_n{x}^n,B_0\ne 0,$$

(25)

which yields two series whose coefficients are fully determined by $A_1$, $B_0$ and $a_0=L{r}_0^2$. We obtain

$$\begin{array}{cc}{n}_{th}\hfill & =A_{1}x+{\displaystyle \frac{1}{8A_1{B}_0^2{\left(A_1{B}_0\left(3\beta L^2-1\right)-1\right)}^2}}\hfill \\ \hfill & \{2A_1^2{B}_0^2\left(1-3\beta L^2\right)\left(A_1^2{B}_0^2\left(5-12\beta L^2\right)+9A_1{B}_0+4\right)\hfill \\ \hfill & -8L^2{r_0}^4\left(2A_1^2{B}_0^2\left(3\beta L^2-1\right)+A_1{B}_0\left(7-24\beta L^2\right)+12\right)\hfill \\ \hfill & +48L^3{r_0}^6\left(A_1{B}_0\left(8\beta L^2-3\right)-4\right)\}{x}^2+\cdots \hfill \end{array}$$

(26)

$$\begin{array}{cc}{g}_{th}\hfill & =B_0-{\displaystyle \frac{2L^2\left(3A_1^2{B}_0^2(A_1{B}_0+1)\left(\beta -{\displaystyle \frac{1}{3L^2}}\right)+8L{r_0}^6+4{r_0}^4\right)}{A_1^2{B}_0\left(A_1{B}_0\left(3\beta L^2-1\right)-1\right)}}x+\cdots \hfill \end{array}$$

(27)

Higher-order terms are very lengthy and cumbersome to write; we present some of them in Appendix B.

Note that in both series solutions (near $x=1$ and near $x=0$), the independent parameters $r_0$ and $\beta$ always appear as $L{r}_0^2$ and $L^2\beta$. Consequently, we can set $L=1$ and regard $r_0$ and $\beta$ as independent parameters without loss of generality.

4. Matching the Solutions

As a consequence of the uniqueness of Taylor series, we expect that the Taylor expansions of (22) and (23) at $x=0$ can be matched with (26) and (27) as long as a wormhole solution (analytic on $[0,1]$) exists for some values of $(\beta ,r_0,a_2,b_3,A_1,B_0)$. We achieve this matching by minimizing the quantity

$$\Delta \left(x_0\right)\equiv {\left({\displaystyle \frac{\Delta g}{0!}}\right)}^2+{\left({\displaystyle \frac{\Delta g^{\prime }}{1!}}\right)}^2+{\left({\displaystyle \frac{\Delta g^{″}}{2!}}\right)}^2+{\left({\displaystyle \frac{\Delta n}{0!}}\right)}^2+{\left({\displaystyle \frac{\Delta n^{\prime }}{1!}}\right)}^2+{\left({\displaystyle \frac{\Delta n^{″}}{2!}}\right)}^2$$

(28)

where $x_0$ is the matching point, as a function of the parameters $(\beta ,r_0,a_2,b_3,A_1,B_0)$, where $\Delta F\equiv F_{\infty }-F_{th}$. By matching the second derivatives, we ensure that there are no discontinuities in the Riemann curvature.

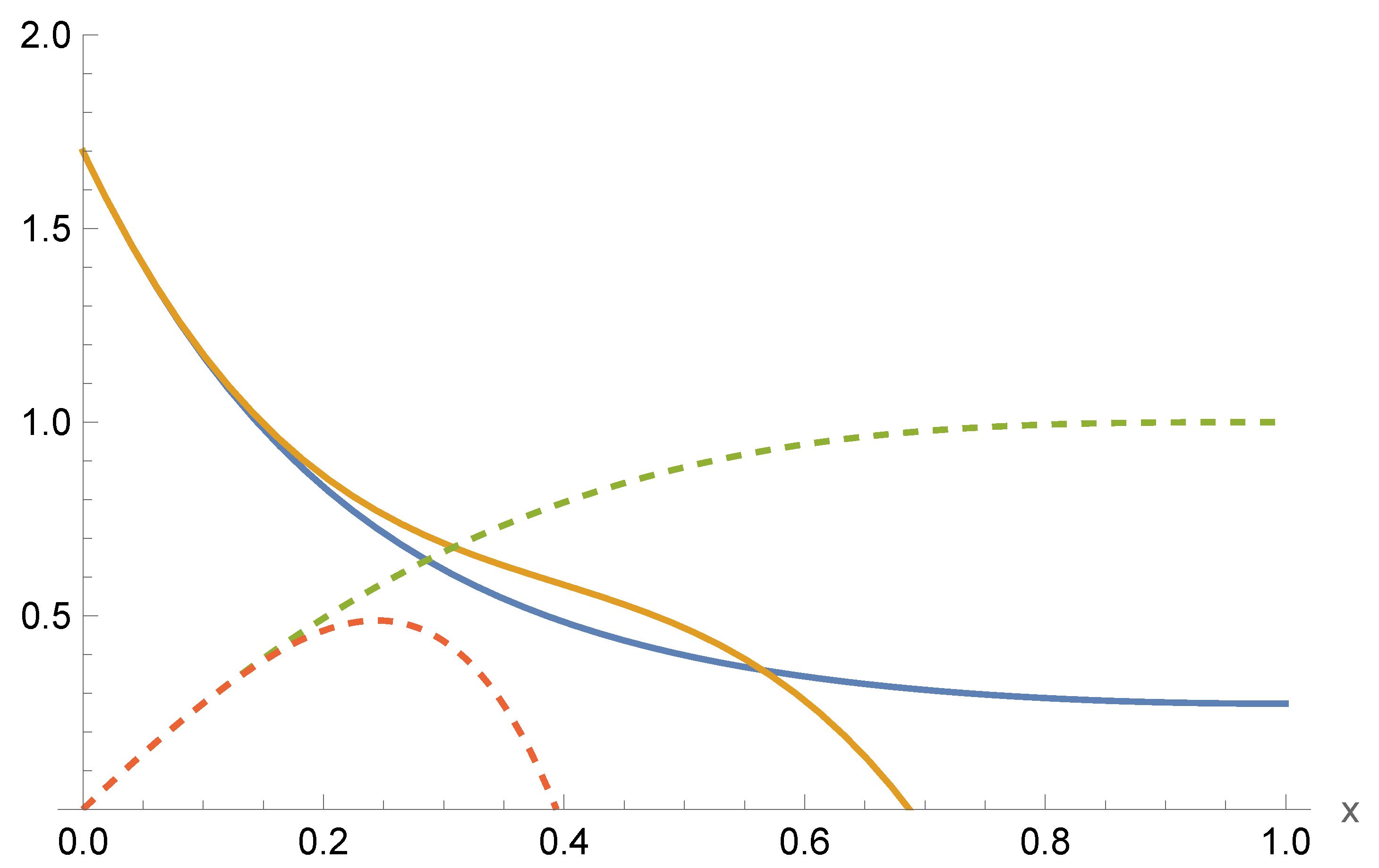
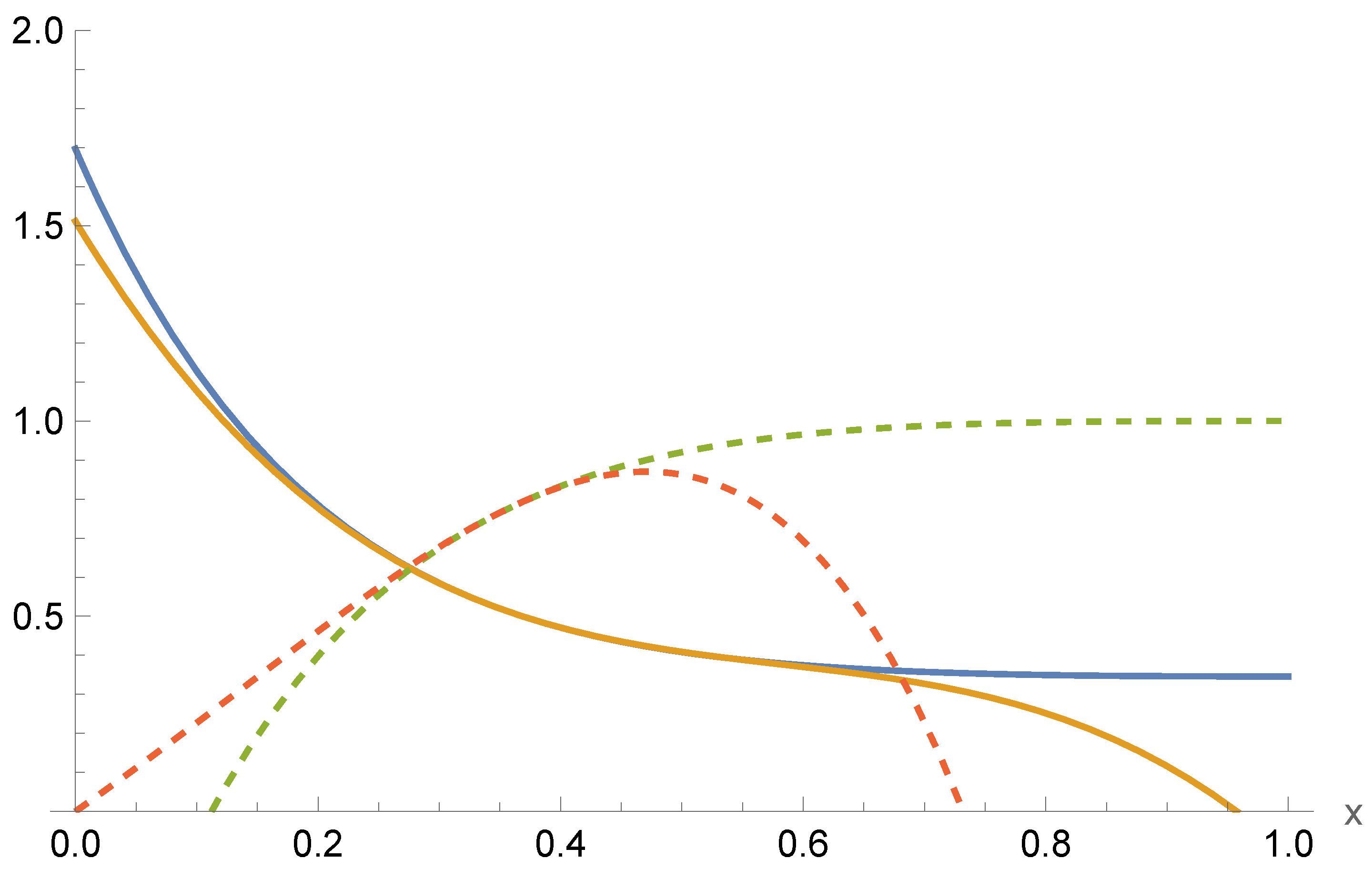
The presence of the coupling parameter $\beta$, irrelevant for asymptotically AdS solutions (with $K=1$), has a profound effect insofar as it yields a sufficient amount of freedom in the parameter space to minimize $\Delta$ to high precision. The precision of our matching is accurate to one part in ${10}^{15}$ at worst. Note from (24) that each solution appears for a specific choice of $\alpha$. We have found a broad range of wormhole solutions using this method. These are illustrated in Figure 1, Figure 2 and Figure 3 and, respectively, correspond to matching for small $x_0$, mid-range $x_0$, and large $x_0$.

Figure 1. Plots of the series solutions $\left[g\right(x),n(x\left)\right]$ for both large-r [(solid blue, dashed green)] and near-throat [(solid orange, dashed red)]. The solutions smoothly match with $\Delta =1.03924\times {10}^{-19}$ at $x=x_0=0.00505304$ for the parameters $\beta =0.505553,a_2=0.318022,b_3=-0.680002,$ $r_0=0.522375,A_1=3.03285,B_0=1.69888$.

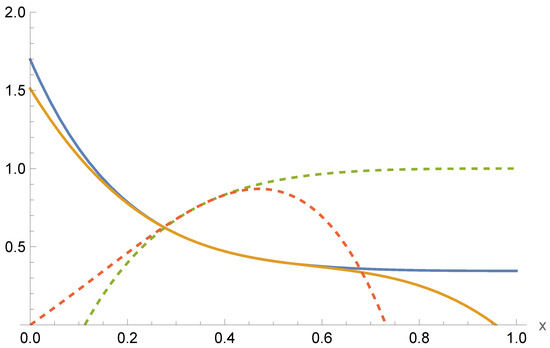
Figure 2. Plots of the series solutions $\left[g\right(x),n(x\left)\right]$ for both large-r [(solid blue, dashed green)] and near-throat [(solid orange, dashed red)]. The solutions smoothly match with $\Delta =3.22544\times {10}^{-15}$ at $x=x_0=0.35156$ for the parameters $\beta =0.792546, a_2=0.0368723, b_3=-0.327935,$$r_0=0.588074, A_1=2.1819, B_0=1.51153$.

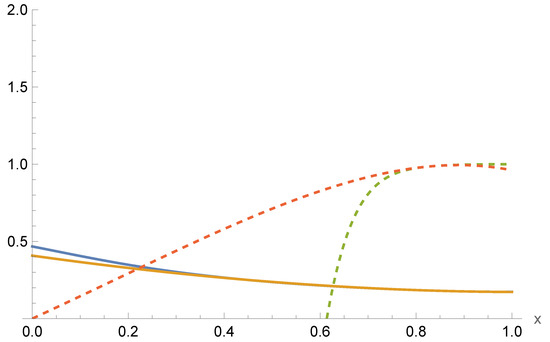
Figure 3. Plots of the series solutions $\left[g\right(x),n(x\left)\right]$ for both large-r [(solid blue, dashed green] and near-throat [(solid orange, dashed red]. The solutions smoothly match with $\Delta =3.2155\times {10}^{-16}$ at $x=x_0=0.83693$ for the parameters $\beta =0.0706116, a_2=0.34649, b_3=-3.53033, r_0=0.41619, A_1=1.43351, B_0=0.408057$.

5. Conclusions

We have shown that Einsteinian Cubic Gravity contains wormhole solutions that are purely gravitational. Unlike wormholes obtained in generic higher-curvature gravity theories, our solutions are in $(3+1)$-dimensions and require no exotic matter in their construction.

In contrast to previous solutions obtained in the theory, our wormhole solutions require three special characteristics. One is that their asymptotic behaviour is that of AdS spacetime with a global monopole deficit. The second is that the the coupling parameter $\alpha$ is related to the effective cosmological constant via (24). The third is that the coupling parameter $\beta \ne 0$. Our wormhole solutions have no horizons or singularities and so are traversable in principle. Imposing more stringent traversability requirements (such as requiring that the gravity at the throat not exceed Earth’s gravity) will reduce the range of allowed solutions; we have not imposed this constraint on the solutions that we have obtained.

Although our series-matching approach has yielded candidate gravitational wormholes, a full wormhole solution to the field Equations (A1) and (A2) remains to be obtained. This can be done numerically, but it presents a computational challenge. A solution in terms of Tchebyshev polyonomials requires many coefficients to obtain high accuracy. We were not able to achieve this using the computational resources available. While it is straightforward to apply the shooting method to an ODE system, here, we have a double shooting problem, which is considerably more challenging. The solution will necessarily depend on tuning the constants of integration appearing in the local series expansions of the metric functions near $x=1$ such that the integrated solution from $x=1$ satisfies the boundary condition at the other end (or vice versa, beginning at $x=0$). We did attempt such solutions but found that we typically encountered at least one spontaneous singularity for g between $x=0$ and $x=1$. Some of these cases might be indicative of a new class of black holes, which merit further investigation.