Elliptical Space with the McVittie Metrics
Abstract
:1. Introduction
2. Materials and Methods
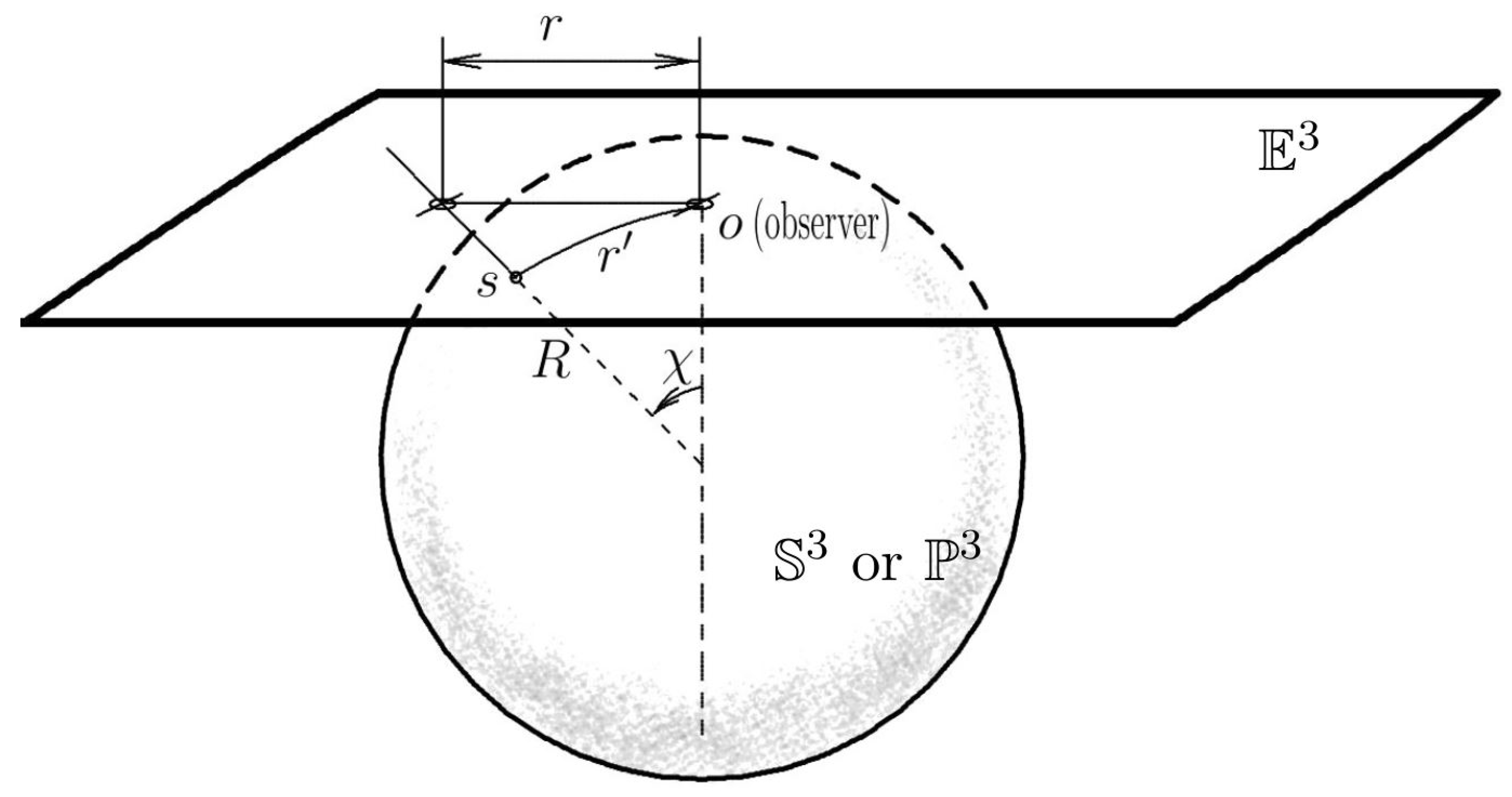
2.1. The Origin of Coordinates
2.2. Isotropy and Spherical Symmetry
2.3. Schwarzschild Metric
- —for the loss of luminosity due to the cosmological redshift z;
- —for the lower rate at which the photons reach the observer because of the cosmological time dilatation;
- —for the photon path distortion (the coefficient of the metric).
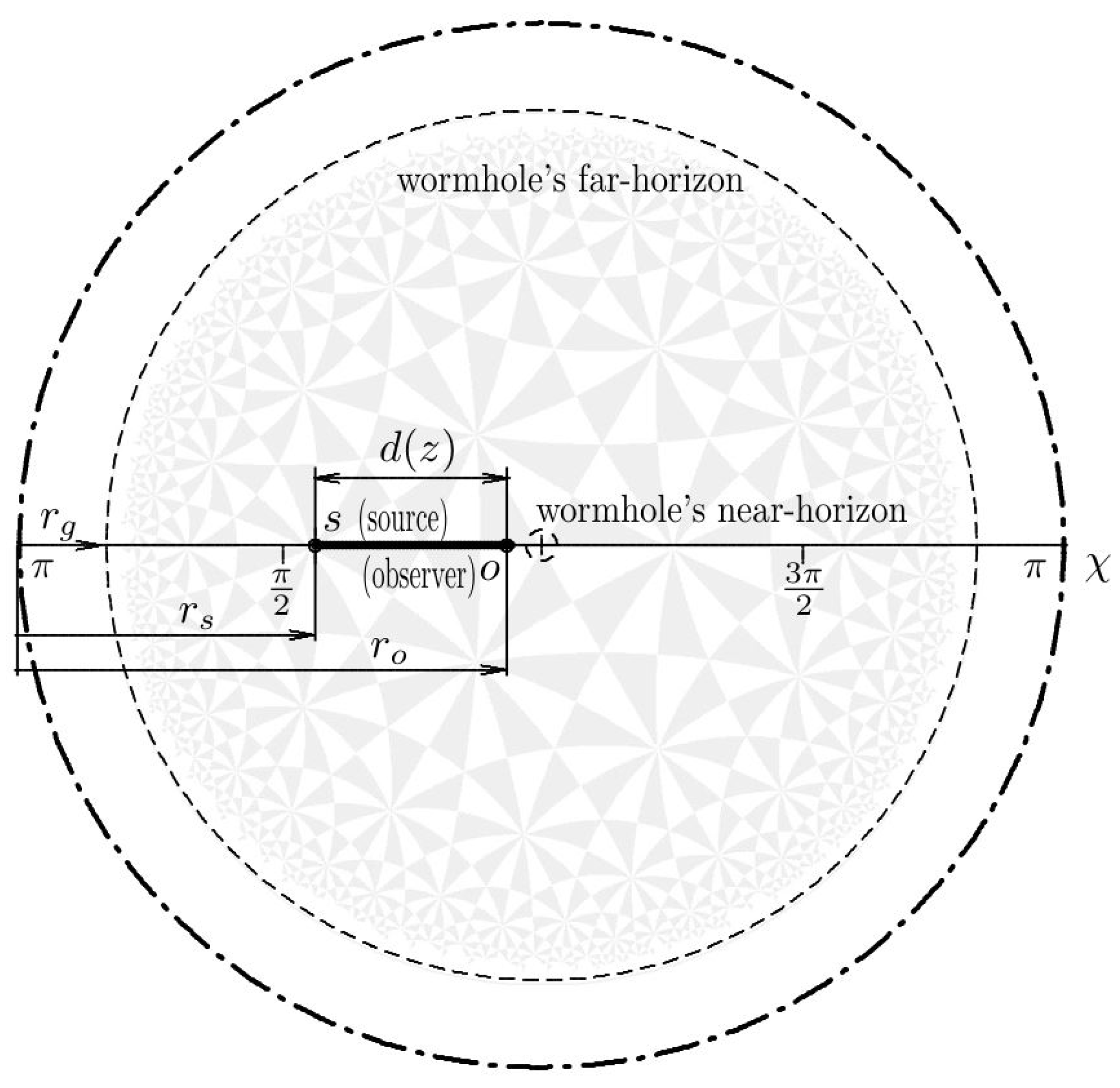
2.4. McVittie Metric
3. Results
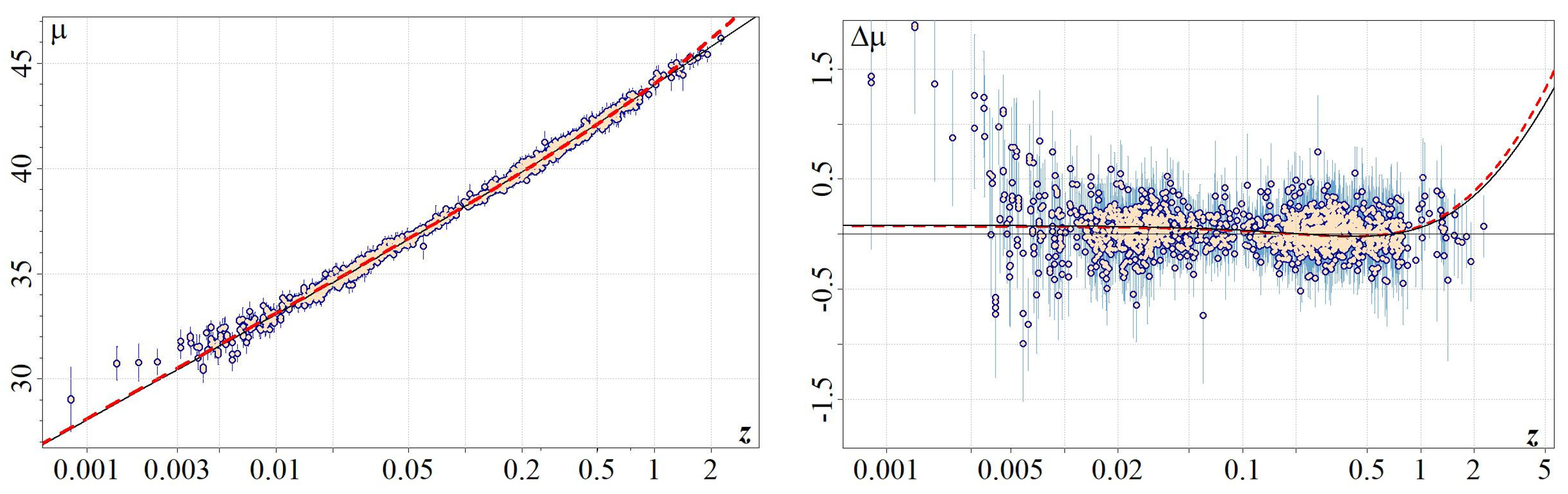
3.1. Parameter Estimation
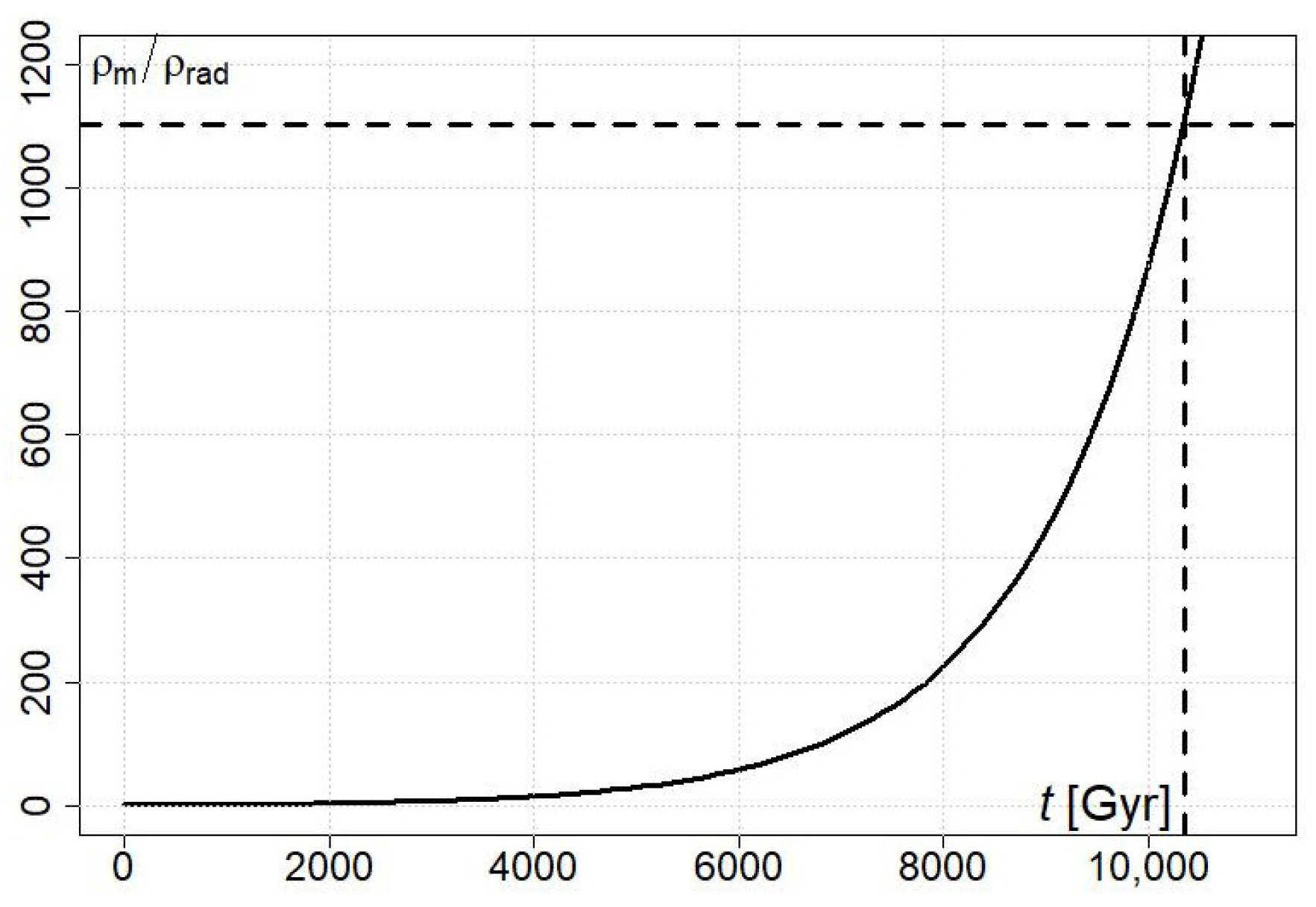
3.2. Age of the Universe
4. Discussion
4.1. Dark Energy
4.2. Dark Matter
4.3. Cosmological Redshift and the Cosmic Background
4.4. Abundances of Light Elements
4.5. Cosmic Structure
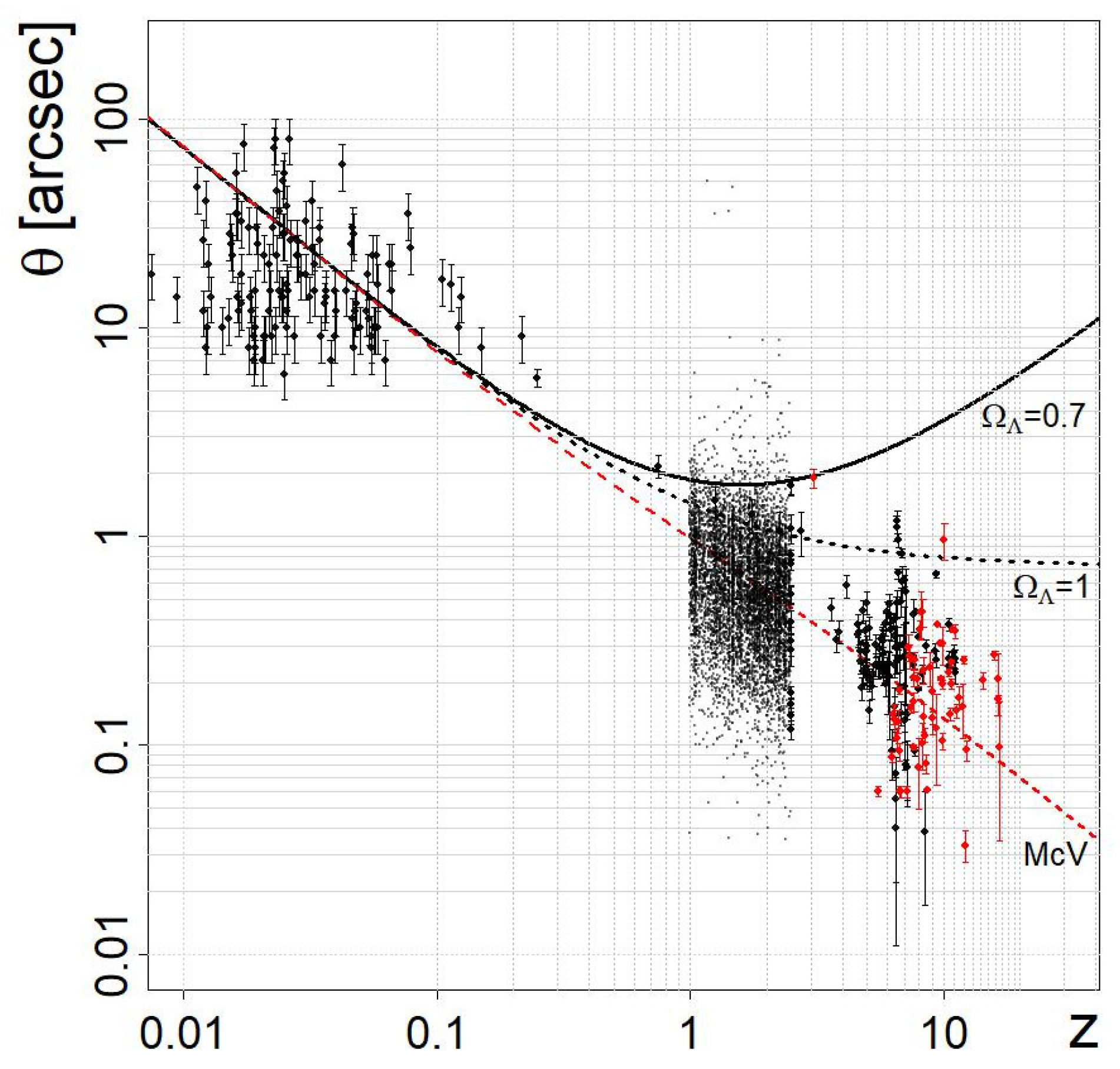
4.6. Angular Sizes
5. Conclusions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| CMBR | Cosmic Microwave Background Radiation |
| dS | de Sitter (metric) |
| FLRW | Friedmann-Lemaitre-Robertson-Walker (metric) |
| JWST | James Webb Space Telescope |
| CDM | Lambda-Cold-Dark-Matter (cosmological model) |
| McV | McVittie (metric) |
| MOND | Modified Newtonian Dynamics (theory) |
| SN | supernova |
| WMAP | Wilkinson Microwave Anisotropy Probe. |
| 1 | ; being the Hubble constant. |
References
- Hamilton, W.R. On quaternions; or on a new system of imaginaries in algebra. Philos. Ser. 1844, 10–13, 241–246. [Google Scholar] [CrossRef]
- De Sitter, W. On Einstein’s theory of gravitation, and its astronomical consequences. Third paper. Mon. Not. R. Astron. Soc. 1917, 78, 3–28. [Google Scholar] [CrossRef]
- Einstein, A. Kosmologische betrachtungen zur allgemeinen Relativitätstheorie. Sitz. Preuss. Akad. Wiss. Phys. 1917, VL, 142–152. [Google Scholar]
- Newcomb, S. Elementary theorems relating to the geometry of a space of three dimensions and of uniform positive curvature in the fourth dimension. J. Reine Angew. Math. 1877, LXXXIII, 293–299. [Google Scholar]
- Schwarzschild, K. Ueber das zulässige Krümmunsmass des Raumes. Vierteljahrssch. Astr. Ges. 1900, XXXV, 337–347. [Google Scholar]
- Lemaître, G. Un univers homogène de masse constante et de rayon croissant rendant compte de la vitesse radiale des nébuleuses extra-galactiques. Ann. Soc. Sci. Brux. A. 1927, 47, 49–59. [Google Scholar]
- Tolman, R.C. On the estimation of distances in a curved universe with a non-static line element. Proc. Natl. Acad. Sci. USA 1930, 16, 511–520. [Google Scholar] [CrossRef]
- Robertson, H.P. Kinematics and world structure I. Astrophys. J. 1935, 82, 284–301. [Google Scholar] [CrossRef]
- Robertson, H.P. Kinematics and World-Structure II. Astrophys. J. 1936, 83, 187–201. [Google Scholar] [CrossRef]
- Robertson, H.P. Kinematics and World-Structure III. Astrophys. J. 1936, 83, 257–271. [Google Scholar] [CrossRef]
- Hubble, E. A relation between distance and radial velocity among extragalactic nebulae. Proc. Natl. Acad. Sci. USA 1929, 15, 168–173. [Google Scholar] [CrossRef] [PubMed]
- Friedmann, A. Über die Krümmung des Raumes. Z. Phys. A 1922, 10, 377–386. [Google Scholar] [CrossRef]
- Walker, A.G. On Milne’s theory of world-structure. Proc. Lond. Math. Soc. Ser. 2 1937, 42, 90–127. [Google Scholar] [CrossRef]
- Brout, D.; Scolnic, D.; Popovic, B.; Riess, A.G.; Zuntz, J.; Kessler, R.; Carr, A.; Davis, T.M.; Hinton, S.; Jones, D.; et al. The Pantheon+ Analysis: Cosmological Constraints. Astrophys. J. 2022, 938, 110. [Google Scholar] [CrossRef]
- Scolnic, D.; Brout, D.; Carr, A.; Riess, A.G.; Davis, T.M.; Dwomoh, A.; Jones, D.O.; Ali, N.; Charvu, P.; Chen, R.; et al. The Pantheon+ Analysis: The Full Dataset and Light-Curve Release. Astrophys. J. 2022, 938, 113. [Google Scholar] [CrossRef]
- Kroupa, P.; Pawlowski, M.; Milgrom, V. The failures of the standard model of cosmology require a new paradigm. Int. J. Mod. Phys. D 2012, 21, 1230003. [Google Scholar] [CrossRef]
- Coleman, P.H.; Pietronero, L. The fractal structure of the universe. Phys. Rep. 1992, 213, 311–389. [Google Scholar] [CrossRef]
- Gaite, J. The fractal geometry of the cosmic web and its formation. Adv. Astron. 2019, 2019, 6587138. [Google Scholar] [CrossRef]
- Teles, S.; Lopes, A.R.; Ribeiro, M.B. Galaxy distributions as fractal systems. Eur. Phys. J. C 2021, 82, 896. [Google Scholar] [CrossRef]
- Mylläri, A.A.; Raikov, A.A.; Orlov, V.V.; Tarakanov, P.A.; Yershov, V.N.; Yezhkov, M.Y. Fractality of isotherms of the Cosmic Microwave Background based on data from the Planck Spacecraft. Astrophysics 2016, 59, 31–37. [Google Scholar] [CrossRef]
- Baryshev, Y. The hierarchical structure of metagalaxy a review of problems. Rep. Sp. Aph. Obs. Rus. Acad. Sci. 1981, 14, 24–43. [Google Scholar]
- Baryshev, Y.; Teerikorpi, P. The Discovery of Cosmic Fractals; World Scientific: Singapore, 2002; 408p. [Google Scholar]
- Lopez, A.L.; Clowes, R.G.; Williger, G.M. A giant arc on the sky. Mon. Not. R. Astron. Soc. 2022, 516, 1557–1572. [Google Scholar] [CrossRef]
- Yadav, J.K.; Bagla, J.S.; Khai, N. Fractal dimension as a measure of the scale of homogeneity. Mon. Not. R. Astron. Soc. 2010, 405, 2009–2015. [Google Scholar] [CrossRef]
- Sargent, W.L.W.; Searle, L. The interpretation of the helium weakness in halo stars. Astrophys. J. 1967, 150, L33–L37. [Google Scholar] [CrossRef]
- Terlevich, E.; Terlevich, R.; Skillman, E.; Stepanian, J.; Lipovetskii, V. The extremely low He abundance of SBS:0335-052. In Elements and the Cosmos; Edmunds, M.G., Terlevich, R., Eds.; Cambridge University Press: Cambridge, UK, 2010; pp. 21–27. [Google Scholar]
- Izotov, Y.I.; Thuan, T.X. The primordial abundance of 4He: Evidence for non-standard Big Bang nucleosynthesis. Astrophys. J. 2010, 710, L67–L71. [Google Scholar] [CrossRef]
- Di Valentino, E.; Melchiorri, A.; Silk, J. Planck evidence for a closed Universe and a possible crisis for cosmology. Nat. Astron. 2020, 4, 196–203. [Google Scholar] [CrossRef]
- Yang, W.; Giarè, W.; Pan, S.; Di Valentino, E.; Melchiorri, A.; Silk, J. Revealing the effects of curvature on the cosmological models. Phys. Rev. D 2023, 107, 063509. [Google Scholar] [CrossRef]
- Yershov, V.N.; Orlov, V.V.; Raikov, A.A. Correlation of supernova redshifts with temperature fluctuations of the cosmic microwave background. Mon. Not. R. Astron. Soc. 2012, 423, 2147–2152. [Google Scholar] [CrossRef]
- Yershov, V.N.; Orlov, V.V.; Raikov, A.A. Possible signature of distant foreground in the Planck Data. Mon. Not. R. Astron. Soc. 2014, 445, 2440–2445. [Google Scholar] [CrossRef]
- Yershov, V.N.; Raikov, A.A.; Lovyagin, N.Y.; Kuin, N.P.M.; Popova, E.A. Distant foreground and the Planck-derived Hubble constant. Mon. Not. Roy. Astron. Soc. 2020, 492, 5052–5056. [Google Scholar] [CrossRef]
- Granett, B.R.; Neyrinck, M.C.; Szapudi, I. An imprint of superstructures on the microwave background due to the integrated Sachs-Wolfe effect. Astrophys. J. 2008, 683, L99–L102. [Google Scholar] [CrossRef]
- Cai, Y.-C.; Neyrinck, M.C.; Szapudi, I.; Cole, S.; Frenk, C.S. A possible cold imprint of voids on the microwave background radiation. Astrophys. J. 2014, 786, 110. [Google Scholar] [CrossRef]
- Kovács, A.; García-Bellido, J. Cosmic troublemakers: The Cold Spot, the Eridanus supervoid, and the Great Walls. Mon. Not. Roy. Astron. Soc. 2016, 462, 1882–1893. [Google Scholar] [CrossRef]
- Kovács, A.; Jeffrey, N.; Gatti, M.; Chang, C.; Whiteway, L.; Hamaus, N.; Lahav, O.; Pollina, G.; Bacon, D.; Kacprzak, T.; et al. The DES view of the Eridanus supervoid and the CMB cold spot. Mon. Not. Roy. Astron. Soc. 2021, 510, 216–229. [Google Scholar] [CrossRef]
- Labbé, I.; van Dokkum, P.; Nelson, E.; Bezanson, R.; Suess, K.A.; Leja, J.; Brammer, G.; Whitaker, K.; Mathews, E.; Stefanon, M.; et al. A population of red candidate massive galaxies ∼600 Myr after the Big Bang. Nature 2023, 616, 266–269. [Google Scholar] [CrossRef] [PubMed]
- Yan, H.; Ma, Z.; Ling, C.; Cheng, C.; Huang, J.-S. First batch of z ≈ 11–20 candidate objects revealed by the James Webb Space Telescope early release observations on SMACS 0723–73. Astrophys. J. Lett. 2023, 942, L9. [Google Scholar] [CrossRef]
- Castellano, M.; Fontana, A.; Treu, T.; Merlin, E.; Santini, P.; Bergamini, P.; Grillo, C.; Rosati, P.; Acebron, A.; Leethochawalit, N.; et al. Early results from GLASS-JWST. XIX. A high density of bright galaxies at z ≈ 10 in the A2744 region. Astrophys. J. Lett. 2023, 948, L14. [Google Scholar] [CrossRef]
- Lovyagin, N.; Raikov, A.; Yershov, V.; Lovyagin, Y. Cosmological model tests with JWST. Galaxies 2022, 10, 108. [Google Scholar] [CrossRef]
- Gupta, R.P. JWST early Universe observations and ΛCDM cosmology. Mon. Not. R. Astron. Soc. 2023, 524, 3385–3395. [Google Scholar] [CrossRef]
- Melia, F. The cosmic timeline implied by the JWST high-redshift galaxies. Mon. Not. R. Astron. Soc. 2023, 521, L85–L89. [Google Scholar] [CrossRef]
- Yershov, V.N. Fitting type Ia supernova data to a cosmological model based on Einstein–Newcomb–De Sitter space. Universe 2023, 9, 24. [Google Scholar] [CrossRef]
- MvVittie, G.C. The mass-particle in an expanding Universe. Mon. Not. R. Astron. Soc. 1933, 93, 325–339. [Google Scholar] [CrossRef]
- Bondi, H. Spherically symmetrical models in general relativity. Mon. Not. R. Astron. Soc. 1947, 107, 410–425. [Google Scholar] [CrossRef]
- Einstein, A.; Rosen, N. The Particle Problem in the General Theory of Relativity. Phys. Rev. 1935, 48, 73–77. [Google Scholar] [CrossRef]
- Tamburini, F.; Licata, I. General relativistic wormhole connections from Planck-scales and the ER = EPR conjecture. Entropy 2020, 22, 3. [Google Scholar] [CrossRef] [PubMed]
- Morris, M.S.; Thorne, K.S. Wormholes in spacetime and their use for interstellar travel: A tool for teaching general relativity. Am. J. Phys. 1988, 56, 395–412. [Google Scholar] [CrossRef]
- Morris, M.S.; Thorne, K.S.; Yurtsever, U. Wormholes, time machines. and the weak energy condition. Phys. Rev. Lett. 1988, 61, 1446–1449. [Google Scholar] [CrossRef] [PubMed]
- Fuller, R.W.; Thorne, K.S. Causality and multiply connected space-time. Phys. Rev. 1962, 128, 919–929. [Google Scholar] [CrossRef]
- Markov, M.A. Limiting density of matter as a universal law of nature. JETP Lett. 1982, 36, 214–216. [Google Scholar]
- Bronnikov, K.; Lipatova, L.; Novikov, I.; Shatskiy, A. Example of a stable wormhole in general relativity. Grav. Cosmol. 2013, 19, 269–274. [Google Scholar] [CrossRef]
- Blázquez-Salcedo, J.-L.; Knoll, C.; Radu, E. Traversable wormholes in Einstein-Dirac-Maxwell theory. Phys. Rev. Lett. 2021, 126, 101102. [Google Scholar] [CrossRef]
- Koiran, P. Infall time in the Eddington–Finkelstein metric, with application to Einstein–Rosen bridges. Int. J. Mod. Phys. 2021, 30, 2150106. [Google Scholar] [CrossRef]
- Rosa, J.L. Double gravitational layer traversable wormholes in hybrid metric-Palatini gravity. Phys. Rev. D 2022, 104, 064002. [Google Scholar] [CrossRef]
- Cox, P.H.; Harms, B.C.; Hou, S. Stability of Einstein-Maxwell-Kalb-Ramond wormholes. Phys. Rev. D 2016, 93, 044014. [Google Scholar] [CrossRef]
- Battista, E.; Esposito, G. What is a reduced boundary in general relativity? Int. J. Mod. Phys. 2021, 30, 2150050. [Google Scholar] [CrossRef]
- Battista, E.; Esposito, G. Discontinuous normals in non-euclidean geometries and two-dimensional gravity. Symmetry 2022, 14, 1979. [Google Scholar] [CrossRef]
- Schwarzschild, K. Über das Gravitationsfeld eines Massenpunktes nach der Einsteinschen Theorie. Sitz. Preuss. Akad. Wiss. 1916, 3, 189–196. [Google Scholar]
- Eddington, A.S. The Mathematical Theory of Relativity; Cambridge University Press: Cambridge, UK, 1923; p. 161. [Google Scholar]
- Eddington, A.S. Internal Constitution of the Stars; Cambridge University Press: Cambridge, UK, 1926; p. 407. [Google Scholar]
- Nernst, W. Weitere prüfung der annahme lines stationären zustandes im weltall. Zeit. Phys. 1937, 106, 633–661. [Google Scholar] [CrossRef]
- Gamow, G. The expanding universe and the origin of galaxies. Kgl. Dan. Vidensk. Selsk. Mat. Fys. Medd. 1953, 27, 3–15. [Google Scholar]
- Baryshev, Y.V.; Raikov, A.A.; Tron, A.A. Microwave background radiation and cosmological large numbers. Astron. Astroph. Trans. 1996, 10, 135–138. [Google Scholar] [CrossRef]
- Cirkovic, M.M.; Perovic, S. Alternative explanations of the Cosmic Microwave Background: A historical and an epistemological perspective. Stud. Hist. Philos. Mod. Phys. 2018, 62, 1–18. [Google Scholar] [CrossRef]
- Muller, S.; Beelen, A.; Black, J.H.; Curran, S.J.; Horellou, C.; Aalto, S.; Combes, F.; Guélin, M.; Henkel, C. A precise and accurate determination of the cosmic microwave background temperature at z = 0.89. Astron. Astrophys. 2013, 551, A109. [Google Scholar] [CrossRef]
- Luzzi, G.; Shimon, M.; Lamagna, L.; Rephaeli, Y.; De Petris, M.; Conte, A.; De Gregori, S.; Battistelli, E.S. Redshift dependence of the cosmic microwave background temperature from Sunyaev-Zeldovich measurements. Astron. J. 2009, 705, 1122–1128. [Google Scholar] [CrossRef]
- Burbidge, G.R. Was there really a Big Bang? Nature 1971, 233, 36–40. [Google Scholar] [CrossRef] [PubMed]
- Burbidge, G.R.; Hoyle, F. The origin of helium and the other light elements. Astrophys. J. 1998, 509, L1–L3. [Google Scholar] [CrossRef]
- Salvaterra, R.; Ferrara, A. Is primordial 4He truly from the Big Bang? Mon. Not. R. Astron. Soc. 2003, 340, L17–L20. [Google Scholar] [CrossRef]
- Pagel, B.E.J. Abundances of elements of cosmological interest. Phil. Trans. R. Soc. Lond. A 1982, 307, 19–35. [Google Scholar] [CrossRef]
- Spite, F.; Spite, M. Abundances of Lithium in unevolved halo stars and old disk stars: Interpretations and consequences. Astron. Astrophys. 1982, 115, 357–366. [Google Scholar]
- Reeves, H.; Fpwler, W.A.; Hoyle, F. Galactic cosmic ray origin of Li, Be and B in stars. Nature 1970, 226, 727–729. [Google Scholar] [CrossRef]
- Austin, S.M. The creation of the light elements—Cosmic rays and cosmology. Progr. Part. Nucl. Phys. 1981, 7, 1–46. [Google Scholar] [CrossRef]
- Silverberg, R.; Tsao, C.H. Spallation processes and nuclear interaction products of cosmic rays. Phys. Rep. 1990, 191, 351–408. [Google Scholar] [CrossRef]
- Olive, K.A.; Schramm, D.N. Astrophysical 7Li as a product of Big Bang nucleosynthesis and galactic cosmic-ray spallation. Nature 1992, 360, 439–442. [Google Scholar] [CrossRef]
- Yamanaka, M.; Jittoh, T.; Kazunori Kohri, K.; Koike, M.; Sato, J.; Sugai, K.; Yazaki, K. Big-bang nucleosynthesis with a long-lived CHAMP including He4 spallation process. J. Phys. Conf. Ser. 2014, 485, 012020. [Google Scholar] [CrossRef]
- Meyer, B.S.; Woosley, S.E.; Hoffman, R.D.; Mathews, G.J.; Wilson, J.R. Neutrino spallation reactions on 4He and the r-process. AIP Conf. Proc. 1995, 327, 441–445. [Google Scholar] [CrossRef]
- Oliver, B.M.; James, M.R.; Garner, F.A.; Maloy, S.A. Helium and hydrogen generation in pure metals irradiated with high-energy protons and spallation neutrons in LANSCE. J. Nucl. Mat. 2002, 307–311, 1471–1477. [Google Scholar] [CrossRef]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; Adya, V.B.; et al. [LIGO, Virgo and Other Collaborations]. Multi-messenger Observations of a Binary Neutron Star Merger. Astrophys. J. 2017, 848, L12. [Google Scholar] [CrossRef]
- Gompertz, B.P.; Ravasio, M.E.; Nicholl, M.; Levan, A.J.; Metzger, B.D.; Oates, S.R.; Lamb, G.P.; Fong, W.-F.; Malesani, D.B.; Rastinejad, J.C.; et al. The case for a minute-long merger-driven gamma-ray burst from fast-cooling synchrotron emission. Nat. Astron. 2022, 7, 67–79. [Google Scholar] [CrossRef]
- Jeans, J. Astronomy and Cosmogony; Cambridge University Press: Cambridge, UK, 1928; 428p. [Google Scholar] [CrossRef]
- Hoyle, F. On the fragmentation of gas clouds into galaxies and stars. Astrophys. J. 1953, 118, 513–528. [Google Scholar] [CrossRef]
- Eddington, A.S. On the instability of Einstein’s spherical world. Mon. Not. R. Astron. Soc. 1930, 90, 668–678. [Google Scholar] [CrossRef]
- Rosen, N. Static universe and cosmic field. Ann. Math. Pure Appl. 1970, 14, 305–308. [Google Scholar] [CrossRef]
- Yang, L.; Morishita, T.; Leethochawalit, N.; Castellano, M.; Calabro, A.; Treu, T.; Bonchi, A.; Fontana, A.; Mason, C.; Merlin, E.; et al. Early results from GLASS-JWST. V: The first rest-frame optical size-luminosity relation of galaxies at z > 7. Astrophys. J. Lett. 2022, 938, L17. [Google Scholar] [CrossRef]
- Finkelstein, S.L.; Bagley, M.B.; Haro, P.A.; Dickinson, M.; Ferguson, H.F.; Kartaltepe, J.S.; Papovich, C.; Burgarella, D.; Kocevski, D.D.; Iyer, K.G.; et al. A long time ago in a galaxy rar, far away: A candidate z ∼ 14 galaxy in early JWST CEERS imaging. Astrophys. J. Lett. 2022, 940, L55. [Google Scholar] [CrossRef]
- Chen, Z.; Stark, D.P.; Endsley, R.; Topping, M.; Whitler, L.; Charlot, S. JWST/NIRCam observations o stars and HII regions in z ∼ 6–8 galaxies: Properties of star forming complexes on 150 pc scales. Mon. Not. R. Astron. Soc. 2023, 518, 5607–5619. [Google Scholar] [CrossRef]
- Ono, Y.; Harikane1, Y.; Ouchi, M.; Yajima, H.; Abe, M.; Isobe, Y.; Shibuya, T.; Wise, J.H.; Zhang, Y.; Nakajima, K.; et al. Morphologies of galaxies at z = 9–12 uncovered by JWST/NIRCam imaging: Cosmic size evolution and an identification of an extremely compact bright galaxy at z ∼ 12. Astrophys. J. 2023, 951, 72. [Google Scholar] [CrossRef]
- Wu, Y.; Cai, Z.; Sun, F.; Bian, F.; Lin, X.; Li, Z.; Li, M.; Bauer, F.E.; Egami, E.; Fan, X.; et al. The identification of a dusty grand design spiral galaxy at z=3.06 with JWST and ALMA. Astrophys. J. Lett. 2023, 942, L1. [Google Scholar] [CrossRef]
- Atek, H.; Shuntov, M.; Furtak, L.J.; Richard, J.; Kneib, J.-P.; Mahler, G.; Zitrin, A.; McCracken, H.J.; Charlot, S.; Chevallard, J.; et al. Revealing Galaxy Candidates out to ∼16 with JWST Observations of the Lensing Cluster SMACS0723. Mon. Not. R. Astron. Soc. 2023, 519, 1201–1220. [Google Scholar] [CrossRef]
- Tacchella, S.; Johnson, B.D.; Robertson, B.E.; Carniani, S.; D’Eugenio, F.; Kumari, N.; Maiolino, R.; Nelson, E.J.; Suess, K.A.; Übler, H.; et al. JWST NIRCam+NIRSpec: Interstellar medium and stellar populations of young galaxies with rising star formation and evolving gas reservoirs. Mon. Not. R. Astron. Soc. 2023, 522, 6236–6249. [Google Scholar] [CrossRef]
- Naidu, R.P.; Oesch, P.A.; Setton, D.J.; Matthee, J.; Conroy, C.; Johnson, B.D.; Weaver, J.R.; Bouwens, R.J.; Brammer, G.B.; Dayal, P.; et al. Schrodinger’s galaxy candidate: Puzzlingly luminous at z ≈ 17, or dusty/quenched at z ≈ 5? arXiv 2022, arXiv:2208.02794. [Google Scholar]
- Naidu, R.P.; Oesch, P.A.; van Dokkum, P.; Nelson, E.J.; Suess, K.A.; Brammer, G.; Whitaker, K.E.; Illingworth, G.; Bouwens, R.; Tacchella, S.; et al. Two remarkably luminous galaxy candidates at z ≈ 11–13 revealed by JWST. Astrophys. J. Lett. 2022, 940, L14. [Google Scholar] [CrossRef]
- Adams, N.J.; Conselice, C.J.; Ferreira, L.; Austin, D.; Trussler, J.; Juodzbalis, I.; Wilkins, S.M.; Caruana, J.; Dayal, P.; Verma, A.; et al. Discovery and properties of ultra-high redshift galaxies (9 < z < 12) in the JWST ERO SMACS 0723 Field. Mon. Not. R. Astron. Soc. 2023, 518, 4755–4766. [Google Scholar] [CrossRef]
- Salzer, J.J.; MacAlpine, G.M.; Boroson, T.A. Oservations of a complete sample of emission-line galaxies: I. Astrophys. J. Suppl. 1989, 70, 447–477. [Google Scholar] [CrossRef]
- Koo, D.C.; Bershady, M.A.; Wirth, G.D.; Stanford, S.A.; Majewski, S.R. HST images of very compact blue galaxies at z ∼ 0.2. Astrophys. J. 1994, 427, L9–L12. [Google Scholar] [CrossRef]
- Guzman, R.; Gallego, J.; Koo, D.C.; Phillips, A.C.; Lowenthal, J.D.; Faber, S.M.; Illingworth, G.D.; Vogt, N.P. The nature of compact galaxies in the Hubble Deep Field. I. Global properties. Astrophys. J. 1997, 489, 543–558. [Google Scholar] [CrossRef]
- Zirm, A.W.; van der Wel, A.; Franx, M.; Zirm, A.W.; van der Wel, A.; Franx, M.; Labbe, I.; Trujillo, I.; van Dokkum, P.; Toft, S.; et al. NICMOS imaging of DRGs in the HDF-S: A relation between star-formation and size at z ∼ 2.5. Astrophys. J. 2007, 656, 66–72. [Google Scholar] [CrossRef]
- Hathi, N.P.; Malhotra, S.; Rhoads, J.E. Starburst intensity limit of galaxies at z ∼ 5–6. Astrophys. J. 2008, 678, 686–693. [Google Scholar] [CrossRef]
- Van der Wel, A.; Franx, M.; van Dokkum, P.G.; Skelton, R.E.; Momcheva, I.G.; Whitaker, K.E.; Brammer, G.B.; Bell, E.F.; Rix, H.-W.; Wuyts, S.; et al. 3D-HST+CANDELS: The evolution of the galaxy size-mass distribution since z = 3. Astrophys. J. 2014, 788, 28. [Google Scholar] [CrossRef]
- Bowler, R.A.A.; Dunlop, J.S.; McLure, R.J.; McLeod, D.J. Unveiling the nature of bright z ≈ 7 galaxies with the Hubble Space Telescope. Mon. Not. R. Astron. Soc. 2017, 466, 3612–3635. [Google Scholar] [CrossRef]
- Bridge, J.S.; Holwerda, B.W.; Stefanon, M.; Bouwens, R.J.; Oesch, P.A.; Trenti, M.; Bernard, S.R.; Bradley, L.D.; Illingworth, G.D.; Kusmic, S.; et al. The super eight galaxies: Properties of a sample of very bright galaxies at 7 < z < 8. Astrophys. J. 2019, 882, 42. [Google Scholar] [CrossRef]
- Bagley, M.B.; Finkelstein, S.L.; Rojas-Ruiz, S.; Diekmann, J.; Finkelstein, K.D.; Song, M.; Papovich, C.; Somerville, R.S.; Baronchelli, I.; Dai, Y.S.; et al. Bright z ∼ 9 galaxies in parallel: The bright end of the rest-UV luminosity function from HST parallel programs. arXiv 2022, arXiv:2205.12980. [Google Scholar] [CrossRef]
- Zavala, J.A.; Casey, C.M.; Spilker, J.; Tadaki, K.-I.; Tsujita, A.; Champagne, J.; Iono, D.; Kohno, K.; Manning, S.; Montana, A.; et al. Probing cold gas in a massive, compact star-forming galaxy at z = 6. Astrophys. J. 2022, 933, 242. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yershov, V.N. Elliptical Space with the McVittie Metrics. Universe 2024, 10, 165. https://doi.org/10.3390/universe10040165
Yershov VN. Elliptical Space with the McVittie Metrics. Universe. 2024; 10(4):165. https://doi.org/10.3390/universe10040165
Chicago/Turabian StyleYershov, Vladimir N. 2024. "Elliptical Space with the McVittie Metrics" Universe 10, no. 4: 165. https://doi.org/10.3390/universe10040165
APA StyleYershov, V. N. (2024). Elliptical Space with the McVittie Metrics. Universe, 10(4), 165. https://doi.org/10.3390/universe10040165






