Abstract
K-essence theories are usually studied in the framework of a single scalar field . Namely, the Lagrangian of K-essence is the function of the single scalar field and its covariant derivative. However, in this paper, we explore a double-field pure K-essence, i.e., the corresponding Lagrangian is the function of covariant derivatives of double scalar fields without a dependency on scalar fields themselves. This is why we call it double-field pure K-essence. The novelty of this K-essence is that its Lagrangian contains the quotient term of the kinetic energies from the two scalar fields. This results in the presence of many interesting features; for example, the equation of state can be arbitrarily small and arbitrarily large. In comparison, the range of the equation of state for quintessence is to . Interestingly, this novel K-essence can play the role of an inflation field, dark matter, or dark energy by appropriately selecting the expressions of Lagrangian.
1. Introduction
K-essence is a certain class of scalar field with non-standard kinetic terms. The name was first coined in a paradigm for inflation by Armendariz-Picon et al. [1,2]. One of the motivations for taking this kind of Lagrangian seriously stems from the action of a low-energy approximation for string theory. Subsequently, it was shown that K-essence can present interesting models for dark energy [3,4,5,6,7,8,9]. Right after these studies, Scherrer shows that K-essence can also serve in the unified model as dark matter and dark energy [10]. Afterwards, the literature on K-essence theories rapidly grew.
Specifically, Chimonto and Lazkoz made an analysis of atypical K-essence cosmologies [11]. Abramo et al. conducted research on the stability problem of phantom k-essence theories [12]. Bonvin et al. [13] demonstrated that if one uses K-essence to solve the coincidence problem and play the role of dark energy in the universe, the fluctuations of the field have to propagate superluminally at some stage. This implies that successful K-essence models violate causality. Therefore, K-essence cannot arise as a low energy effective field theory of a causal, consistent high-energy theory. On the other hand, K-essence can yield a complete picture of the evolution of the universe, starting from the early inflation, the subsequent dark matter domination, and to the late-time cosmic acceleration [14,15]. Interestingly, Tian and Zhu’s research [16] reveal that the K-essence framework is also conducive to the Hubble tension problem [17,18].1 However, Adi et al. found that if the cosmic acceleration is sourced by baryonic and K-essence dark matter, observations support phantom dark energy and help in resolving the Hubble tension problem [20].
Very recently, Kehayias and Scherrer found a new generic evolution for K-essence dark energy with the equation of state of a roughly cosmological constant [21]. Chen et al. made a study on the stability problem and geometrical diagnostic for the power-law K-essence dark energy [22]. Chen et al. also made the phase space analysis of interacting K-essence dark energy in loop quantum cosmology [23]. Jawad et al. studied the inflationary scenario in the realm of the K-essence model and swampland conjectures [24]. Socorro et al. presented an analysis of a chiral cosmological scenario from the perspective of K-essence formalism [25]. Huang [26] constructed thawing K-essence models by generating the Taylor expansion coefficients of Lagrangian functions from random matrices. Finally, the K-essence model in which K-essence can be responsible for both primordial inflation and the present observed acceleration, while also admitting a non-singular de Sitter beginning of the universe was achieved by Ferreira et al. [27].
Up to this point, what we need to emphasize is that all of the above research on K-essence is actually focused on single-field K-essence. Specifically, the Lagrangian of K-essence is the function of a single field and its derivatives . However, in this paper, we shall consider double-field K-essence, where there are two scalar fields and together with their derivatives. The novelty of this research is that the Lagrangian functions are significantly different from the previous ones. To be exact, they are constructed by the quotient form , with x and y being the kinetic terms of the fields.
What is the motivation for this quotient form “potential”, ? We state it as follows. As is known, the Einstein cosmological constant is perhaps the best candidate for dark energy. It is consistent with nearly all astronomical and cosmological observations. However, there are two fundamental problems, i.e., the cosmological constant problem and the coincidence problem. The two problems are so difficult that one resorts to the quintessence field model. When quintessence rolls very slowly, it behaves as a cosmological constant, but quintessence has the well-known fine-tuning problem. Then, are there any other alternatives for the cosmological constant except for quintessence? We find that in double-field pure K-essence theory, a quotient form of the Lagrangian can exactly play the role of the cosmological constant, although the scalar fields are dynamic. This motivates us to make an analysis on the cosmic evolution of even more general Lagrangians except for the quotient form.
To our knowledge, no investigation has been conducted on this type of K-essence. On the other hand, we consider this as a pure K-essence, making the calculations considerably simpler. In fact, we can obtain the energy density, the pressure, and the equation of state in a straightforward manner because the equations of motion of K-essence can be solved exactly without the help of dynamical analysis.
The paper is organized as follows. In Section 2, we derive the Einstein equations and the equations of motion for the double-field pure K-essence. In Section 3, we study the cosmic evolution of the K-essence in the background of the Friedmann–Robertson–Walker universe. First, we revise the Lagrangian functions of the K-essence for some conventional EOSs (equations of state). Then, inspired by the Lagrangian expressions of the K-essence for several conventional EOSs, we explore the so-called novel K-essence Lagrangian, which has quotient “potentials”. In this manner, we meet several unconventional EOSs (equations of state) of K-essence. In Section 4, we study the stability of the novel K-essence in the background of Minkowski spacetime. We find that there always exist stable solutions. Finally, Section 5 gives the conclusion and discussion. Throughout this paper, we adopt a system of units in which and the metric signature is .
2. Equations of Motion
We consider the action
where
is the Lagrangian of the double-field pure K-essence. Following Ref. [10], we call it pure K-essence because it does not depend explicitly on the two scalar fields, and . The Lagrangian is only the function of the terms x and y. Here, x and y are the kinetic energy of the scalar fields and , respectively. They are defined by
and they are positive with the signature of in the Friedmann–Robertson–Walker universe. The dimensions of x and y are the inverse of the area. R is the Ricci scalar and is the Lagrangian for matters. Making a variation in the action with respect to the metric tensor, we obtain the Einstein equations
where and represent the energy-momentum of matter and K-essence, respectively. The expression of is found to be
where the comma denotes the derivative with respect to x and y. When , we obtain the energy-momentum tensor for the Einstein cosmological constant. When or , we obtain the energy-momentum tensor for stiff matter. Finally, variation in the action with respect to and results in their equations of motion as follows
3. Cosmic Evolution
In this section, we explore the cosmic evolution of the double-field pure K-essence in the background of the Friedmann–Robertson–Walker universe. To this end, we should first derive the cosmological equations of motion.
3.1. Cosmological Equations of Motion
In the background of Friedmann–Robertson–Walker universe with the line element
where is the scale factor of the universe, the Einstein equations appear as the Friedmann equation and the acceleration equation
Here, the energy density and pressure of K-essence are
H is the Hubble parameter, and the dot denotes the derivative with respect to the cosmic time t. and are the present-day energy density values for dark matter and radiation. The equations of motion for the two scalar fields are
Equations (8)–(11) constitute the cosmological equations of motion. Observing the expressions of density and pressure, we find they are the functions of Lagrangian F. So, once the equation of state for K-essence is given, we can obtain the expression of F by solving the partial differential equations. In the next subsection, we shall investigate three conventional EOSs in this way.
3.2. Motivation: The Power of Double-Field Pure K-Essence
In this subsection, we consider three conventional EOSs, namely, that for the Einstein cosmological constant, the constant EOS, and the generalized Chaplygin gas in order to show that the double-field pure K-essence is so powerful that it can play the role of many types of matter.
3.2.1. Dynamical Cosmological Constant
If we assume the EOS for the K-essence is that for the cosmological constant, i.e.,
and take into account Equation (10), we obtain
This is a differential equation for . We then obtain the solution
Here and thereafter, represents the arbitrary function . It is apparent that is dimensionless. We note that the unnecessary integration constant is dropped. Once the Lagrangian function F is given by in the form of Equation (14), energy density and the pressure are derived from Equation (10)
with the scalar fields and found to be dynamic from Equation (11)
Considering the definition of x and y, we find that the Lagrangian function Equation (14) gives the cosmological constant exactly. We emphasize that, in general, for example in the background of anisotropic and inhomogeneous spacetime, the Lagrangian of Equation (14) would be significantly different from the Einstein cosmological constant because their energy-momentum tensors are obviously different.
It is interesting that the Lagrangian has the quotient form for two scalar fields. We find the quotient form of Lagrangian is inevitably encountered, even in multi-scalar field theories with , etc., and the kinetic terms of scalar fields , etc. It can be verified that the Lagrangian
behaves as a cosmological constant in the background of the Friedmann–Robertson–Walker universe although those scalar fields are dynamic.
In all, in the background of Friedmann–Robertson–Walker universe, the double-field pure K-essence can play the role of Einstein cosmological constant.
3.2.2. Constant Equation of State
If we assume the equation of state for K-essence is a constant , i.e.,
and take into account Equation (10), we find
This is a differential equation for . We then obtain the solution
Once again, the Lagrangian contains the function of the quotient form of kinetic energies. After the Lagrangian is fixed, the energy density and pressure of K-essence are found to be
It seems the Lagrangian Equation (21) is divergent in the limit of (for dark matter). This is an illusion; if we choose
such that the Lagrangian emerges as below
then there is no divergence in the expression when . We remind that is dimensionless, and has a dimension of , (L stands for the length.). When , it is included by Equation (14). One can make an examination that the scalar fields evolve in the following form
Now we see that the double-field pure K-essence can play the role of dark matter (), relativistic matter (), stiff matter (), and so on.
3.2.3. Generalized Chaplygin Gas
If we assume the equation of state for K-essence is the same as that for the generalized Chaplygin gas [28], i.e.,
and take into account Equation (10), we obtain
Solving this differential equation, we obtain
where A and n are positive constants. The resulting energy density is
with as two positive constants. When the term dominates, it behaves as a cosmological constant, while when the term dominates, it behaves as dark matter. This form of dark matter and dark energy model has been studied in great detail in [29].
Up to this point, we conclude that the double-field pure K-essence is very powerful since it can play the role of the Einstein cosmological constant, a fluid with a constant EOS, and the generalized Chaplygin gas in the background of Friedmann–Robertson–Walker universe. Of course, in the background of other spacetimes, the behavior of the double-field pure K-essence is certainly different from the others because they have different energy-momentum tensors. Observing the Lagrangian Equations (14), (21) and (28), we find they are all the functions of quotient . This motivates us, in the next section, to perform a study on the cosmic evolution of this novel K-essence by starting from even more general expressions of the Lagrangian and several unconventional EOSs are found.
3.3. Some Unconventional EOSs
In this section, we shall first assume the expression of a Lagrangian function F and then explore its cosmic evolution. In this way, some novel EOSs are found.
3.3.1. The Case of
First, we consider the Lagrangian function
where s and n are constants. n is dimensionless, and s has the dimension of . The first term is the normal canonical kinetic term and the second term denotes the “potential ”. The potential is constructed by the quotient form of kinetic terms. We note that the sign before the kinetic term is positive. This indicates that is a phantom scalar field. Then, the cosmological equations of motion, Equations (10) and (11), give the density and pressure of K-essence as follows
where and are positive integration constants. The equation of state is
It is interesting that for large n, we have the energy density
which is the sum of dark matter and the cosmological constant. Thus, when n is sufficiently large, the K-essence unifies cold dark matter and the Einstein cosmological constant. When , we have
It consists of two terms: one is the Einstein cosmological constant, and the other is a phantom. In this case, the K-essence can play the role of dark energy for present-day cosmic acceleration.
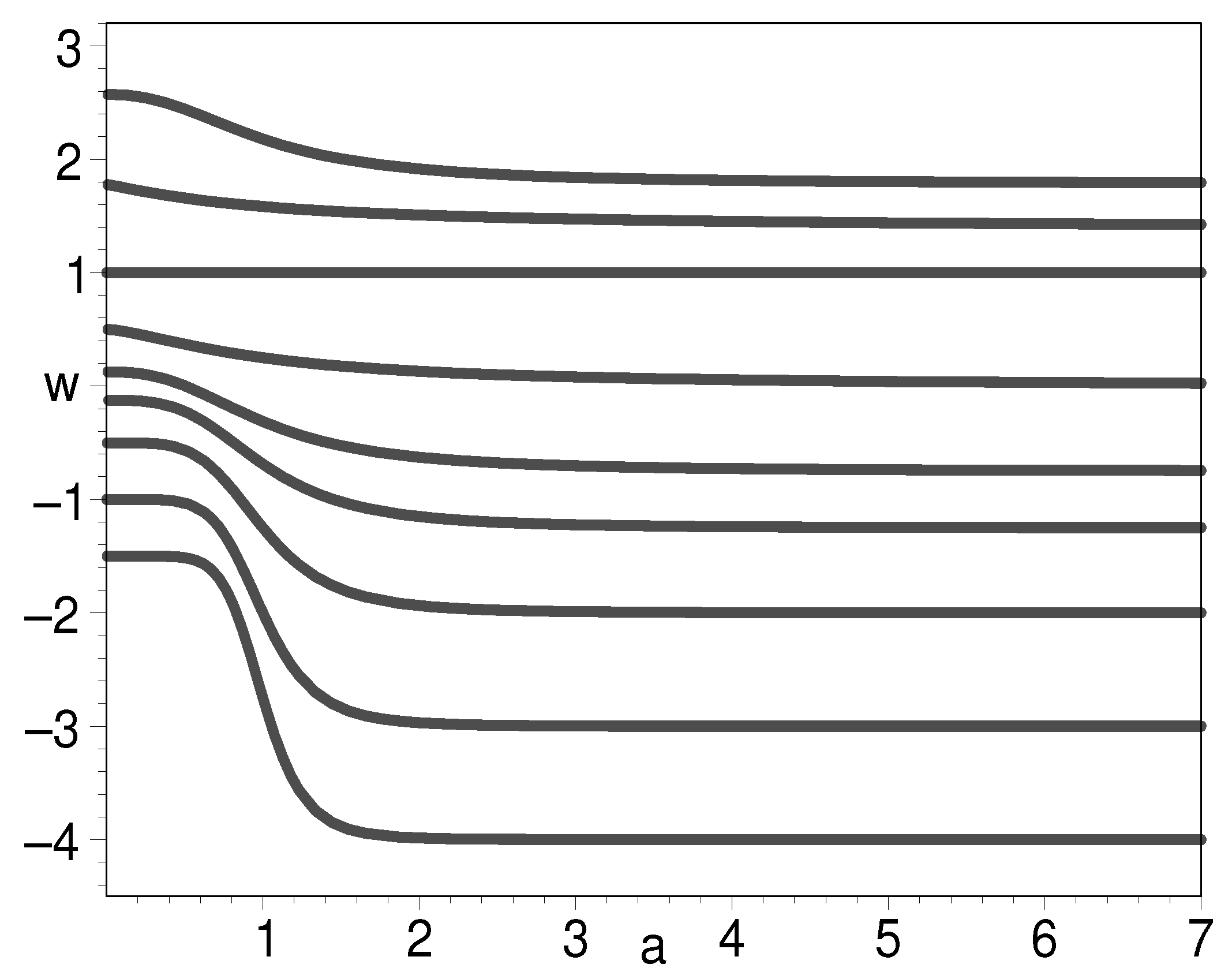
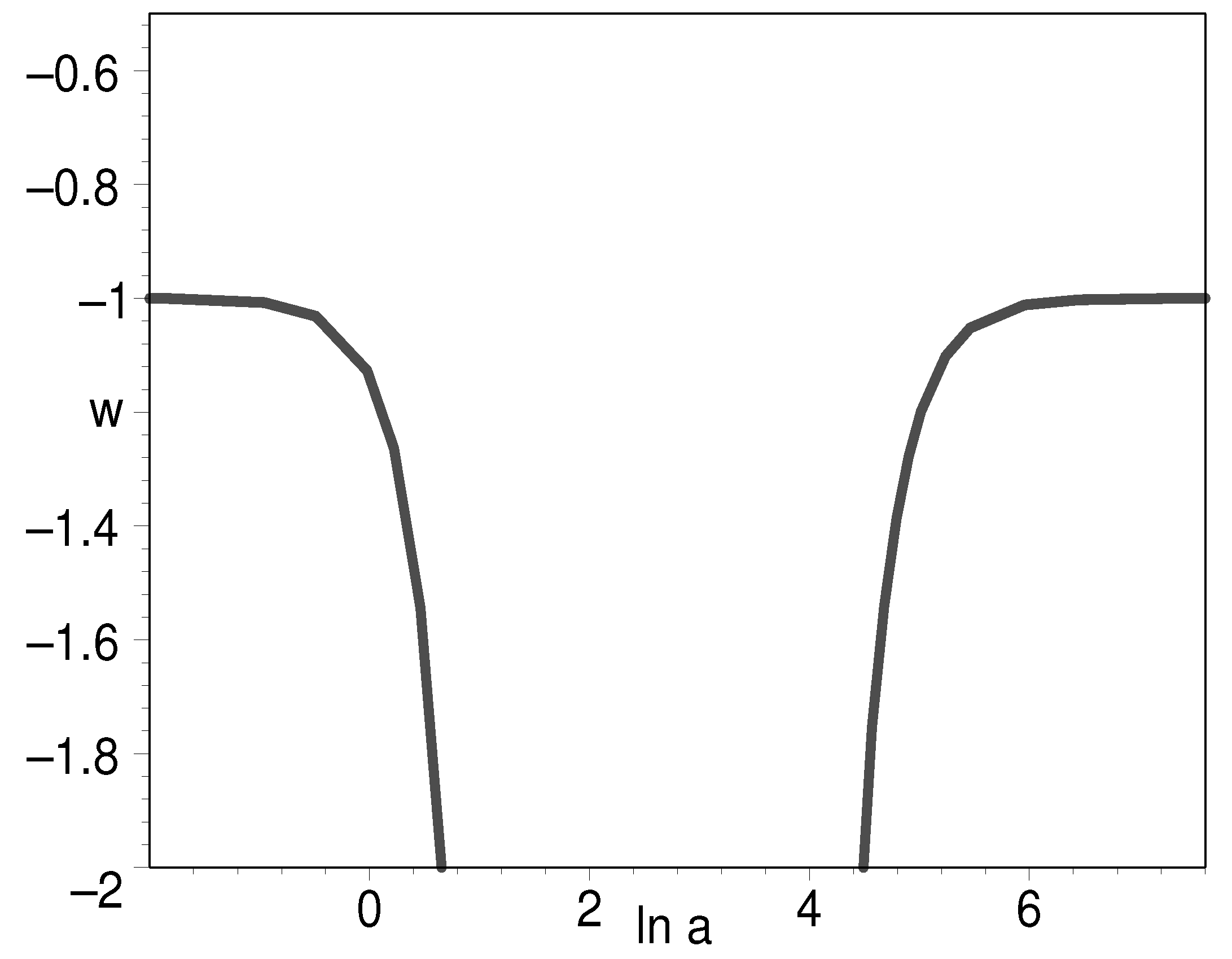
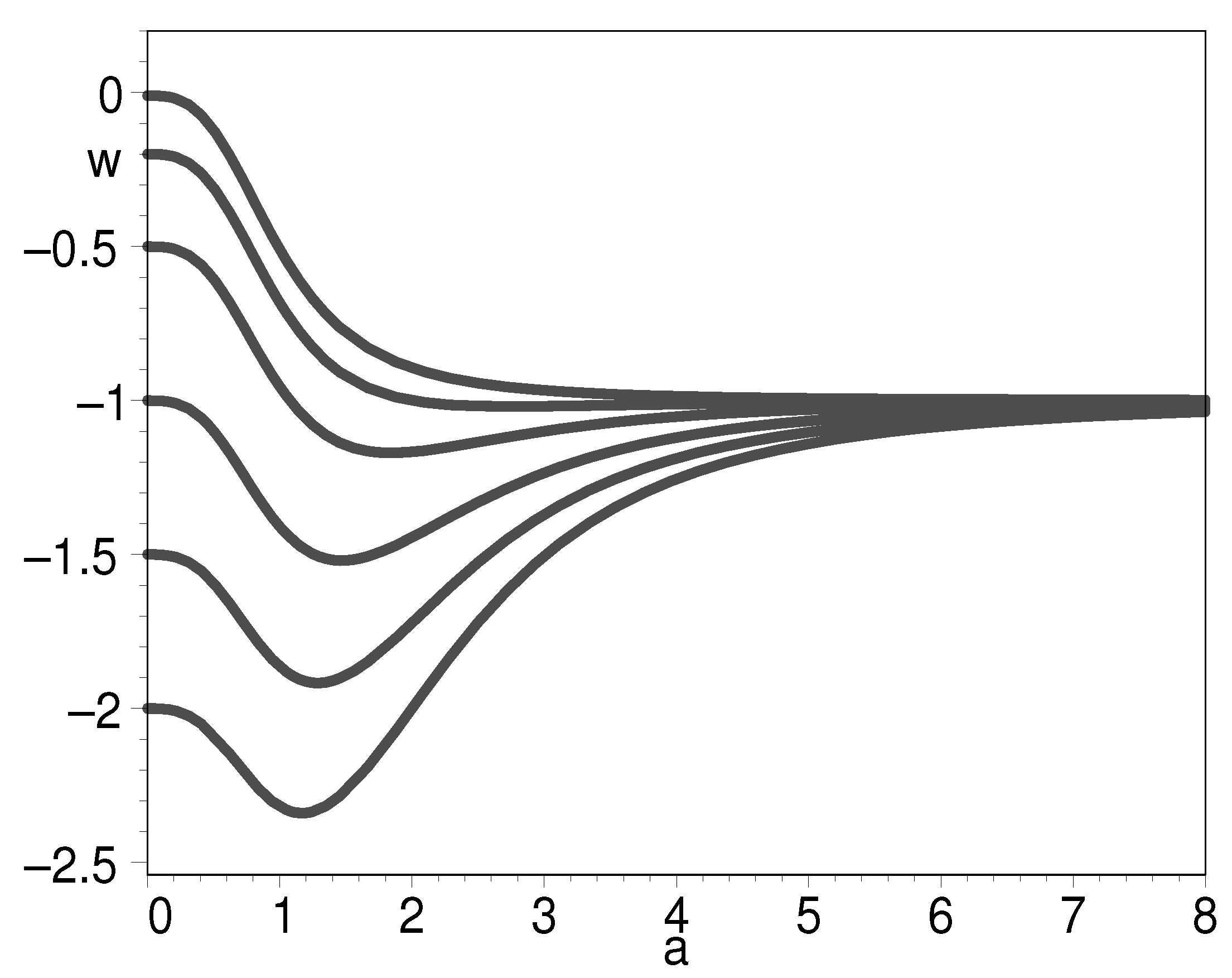
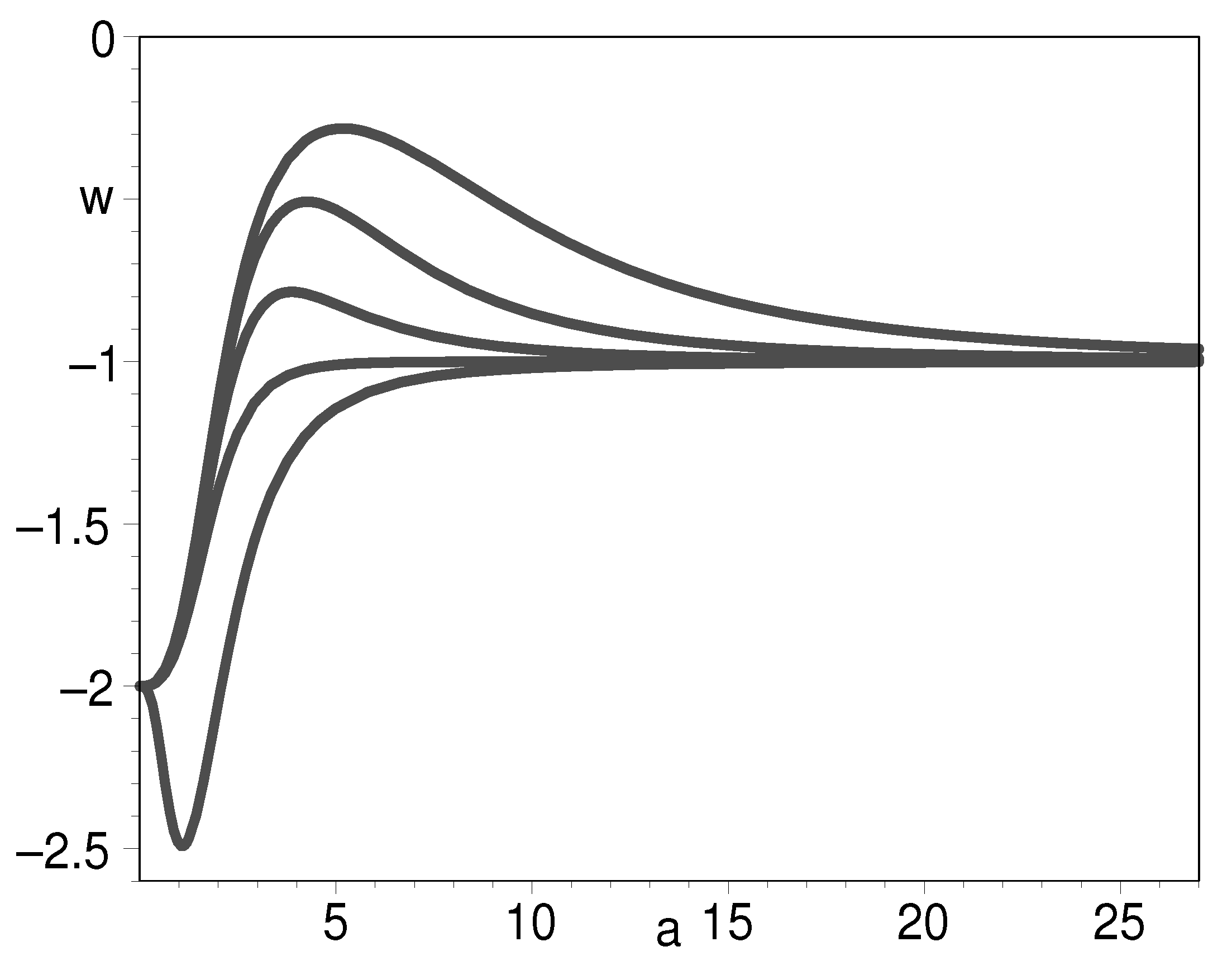
In Figure 1, we plot the equation of state with respect to the scale factor. In cosmology, the scale factor is related to redshift as , meaning is today, is the beginning of universe, and is the distant future of universe. Therefore, the domain of scale factor is . In order to ensure that the energy density is always positive, we assume the two integration constants and . The figure shows that when , the K-essence behaves as stiff matter that has the equation of state . However, it is amazing that its Lagrangian function is obviously different from that for conventional stiff matter . If , the K-essence can play the role of cosmic dark energy as mentioned above. On the other hand, if , the K-essence unifies the Einstein cosmological constant and the cold dark matter model. Finally, when , the equation of state can be very large such that . Now, the K-essence becomes the stiffest matter in nature.
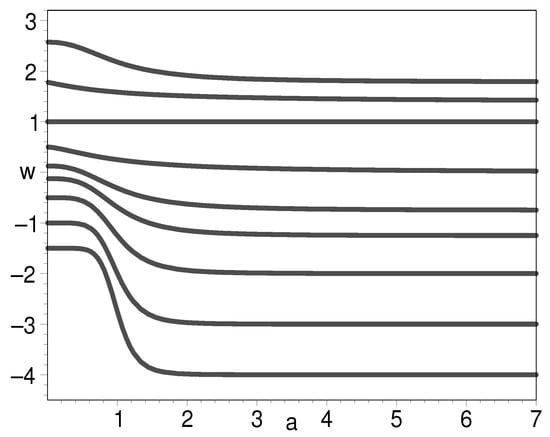
Figure 1.
The evolution of EOS for K-essence with respect to the scale factor when from down to top, respectively, for the lower half of the graph. For the upper half of the graph, we put from up to down. We assume .
3.3.2. The Case of
Secondly, we consider the Lagrangian function
where , and n are constants. n is dimensionless, and s has the dimension of while have the same dimension of . We recognize that and terms are actually the kinetic terms of Cuscuton action [30]. It is amazing that the and terms of the Lagrangian also appear in the Lagrangian of two interacting particles in the low-velocity limit [31]. The third term denotes the novel potential. The reason we call it “potential” is that it behaves exactly as the Einstein cosmological constant in the background of the Friedmann–Robertson–Walker universe in the absence of the and terms. The cosmological equations of motion, Equations (10) and (11), give the energy density
where and are integration constants. It is straightforward to obtain the pressure and equation of state for K-essence by substituting the energy density into the energy conservation equation
In order to ensure that the energy density is always positive, we let
Of course, there are other options available, depending on the values of n.
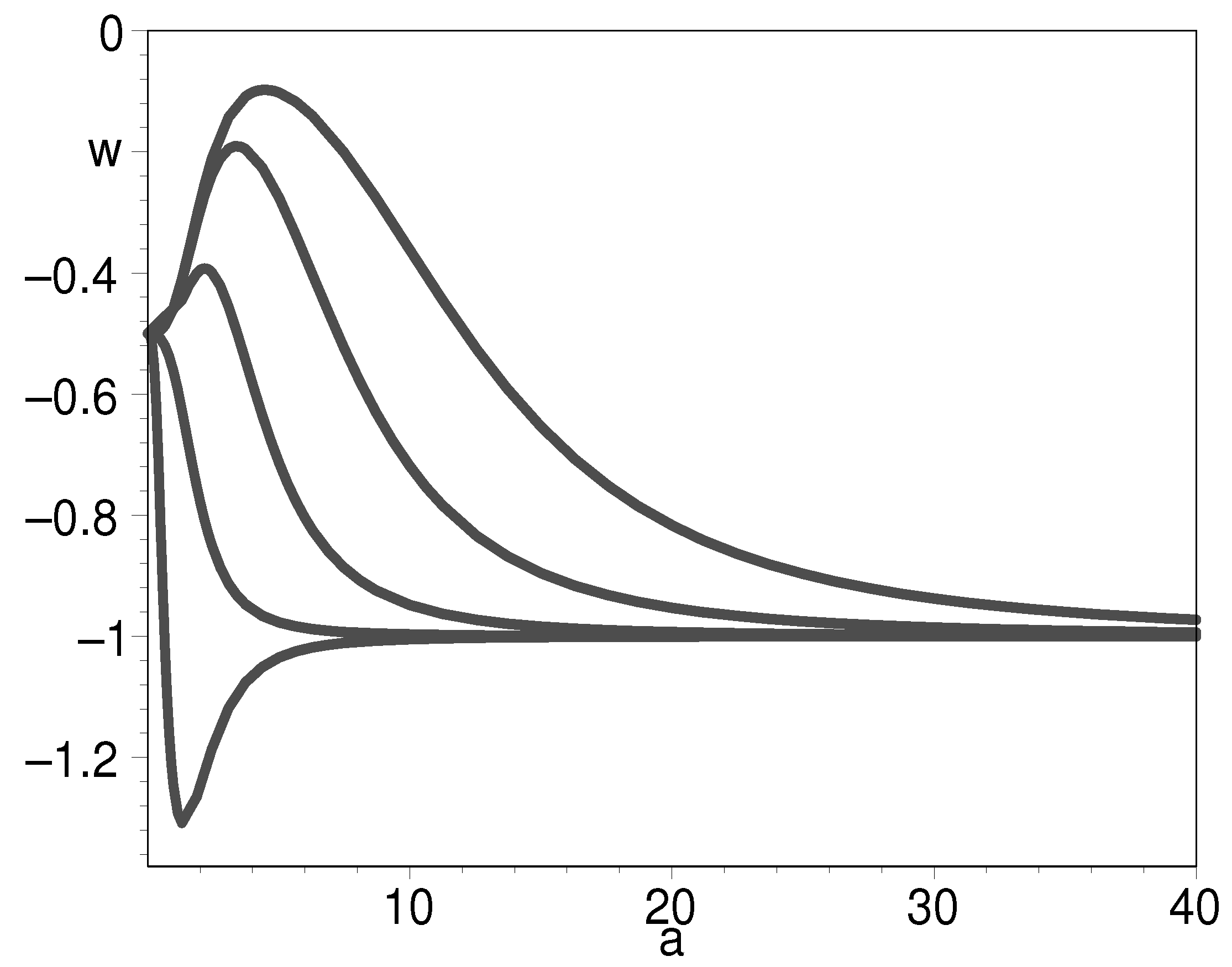
In Figure 2, we plot the EOS with respect to the scale factor. It shows that the EOS starts from at the very early universe and then decreases to negative. Subsequently it approaches in the distant future. This shows that the energy density emerges as nearly a constant in the very early universe. Then, it experiences a remarkable growth. Eventually, the energy density climbs to a very huge constant again. To show this point, we plot the evolution for the log-ratio.
of K-essence density to its present-day value in Figure 3. Thus, we conclude that the fate of our universe is to undergo an inflation a third time.
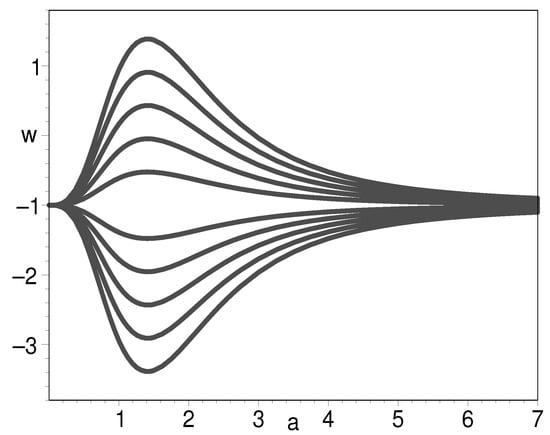
Figure 2.
The evolution of EOS for K-essence with respect to the scale factor when from down to top, respectively. We have put .
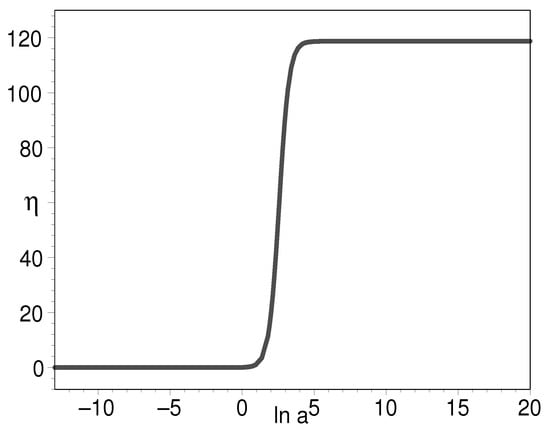
Figure 3.
The evolution of for the log-ratio of K-essence density to its present-day value with respect to the scale factor. We have put .
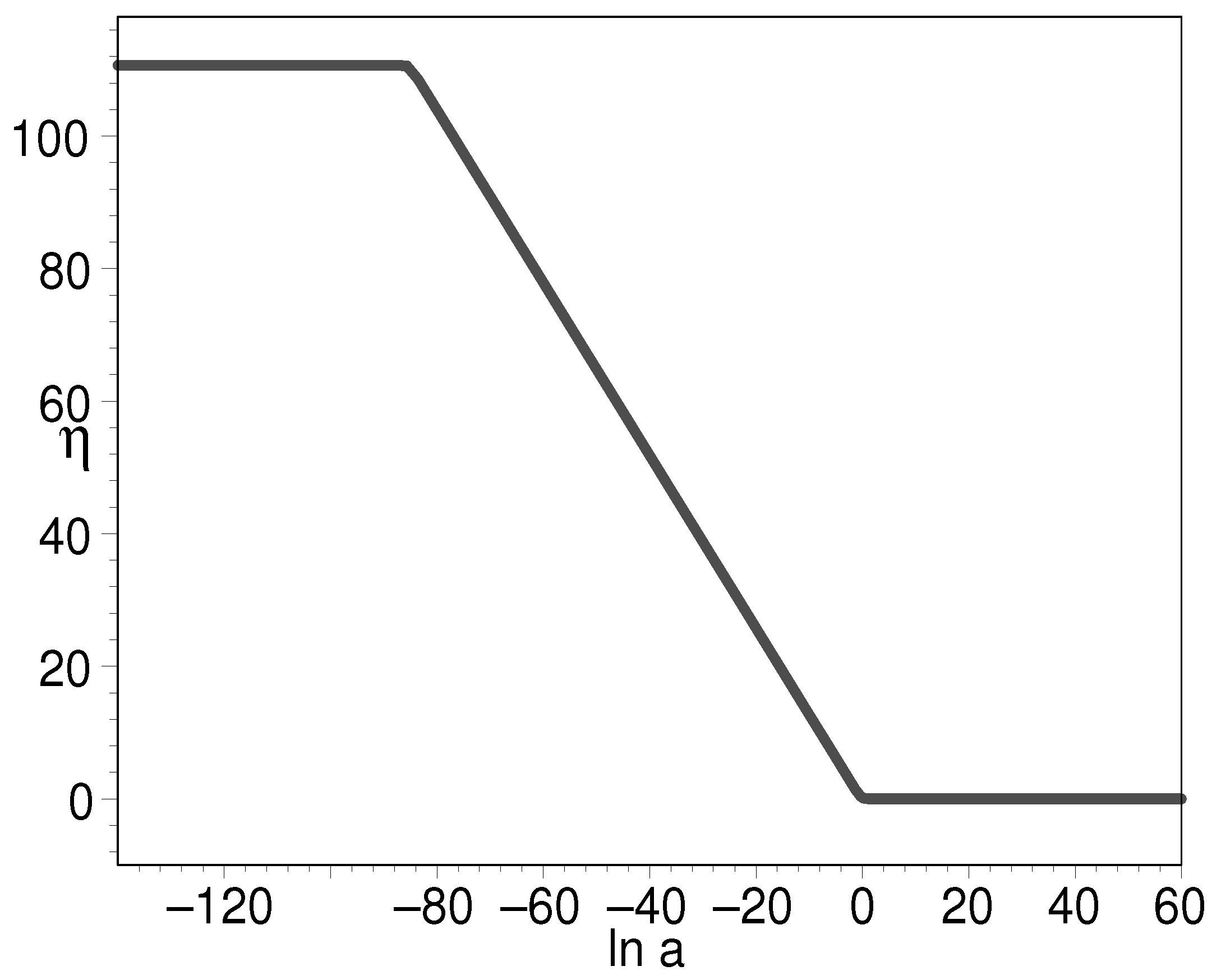
In Figure 4 and Figure 5, we plot the evolution of EOS for K-essence with respect to the natural logarithm of the scale factor. The present-day EOS is slightly less than , which is consistent with the astronomical observations [32,33].
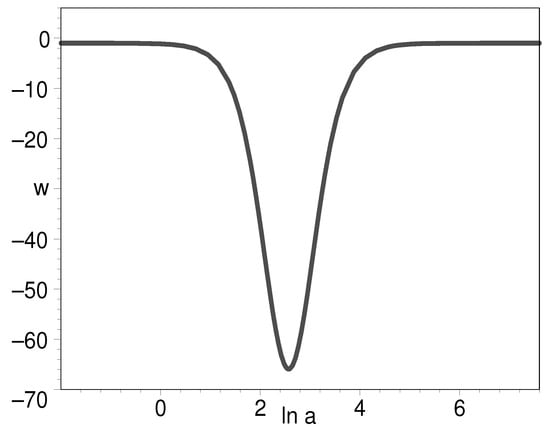
Figure 4.
The evolution of EOS for K-essence with respect to the natural logarithm of scale factor. We have put .
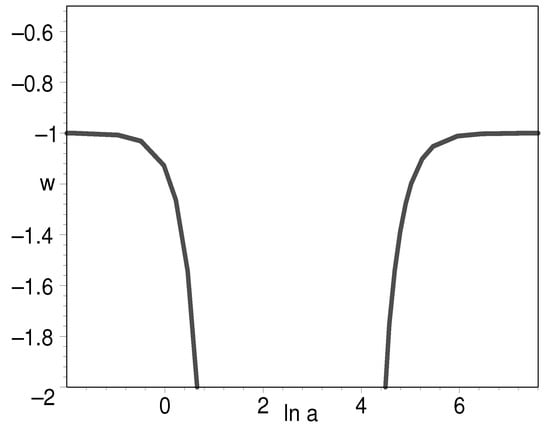
Figure 5.
The evolution of EOS for K-essence being a part of Figure 4 with respect to the natural logarithm of scale factor.
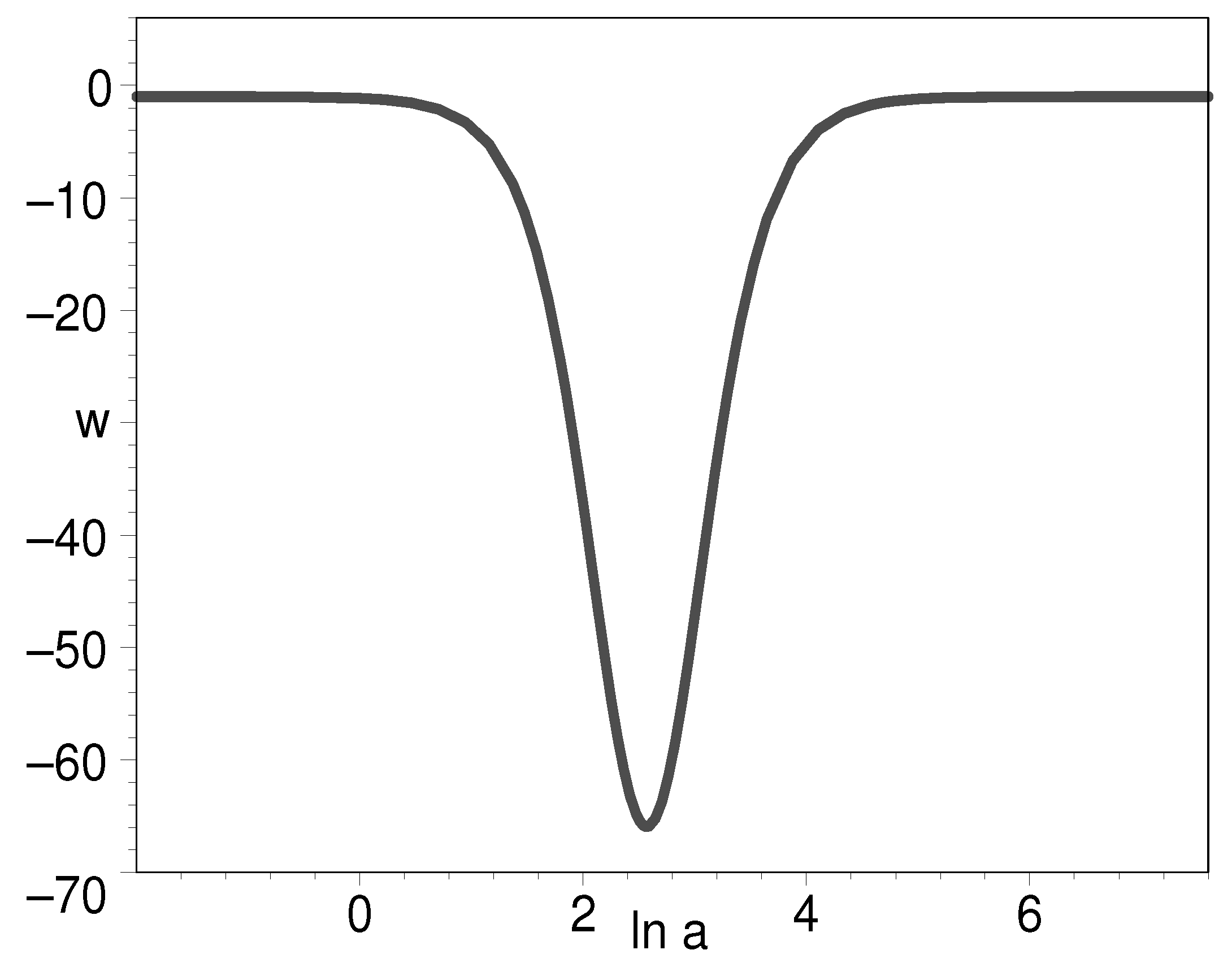
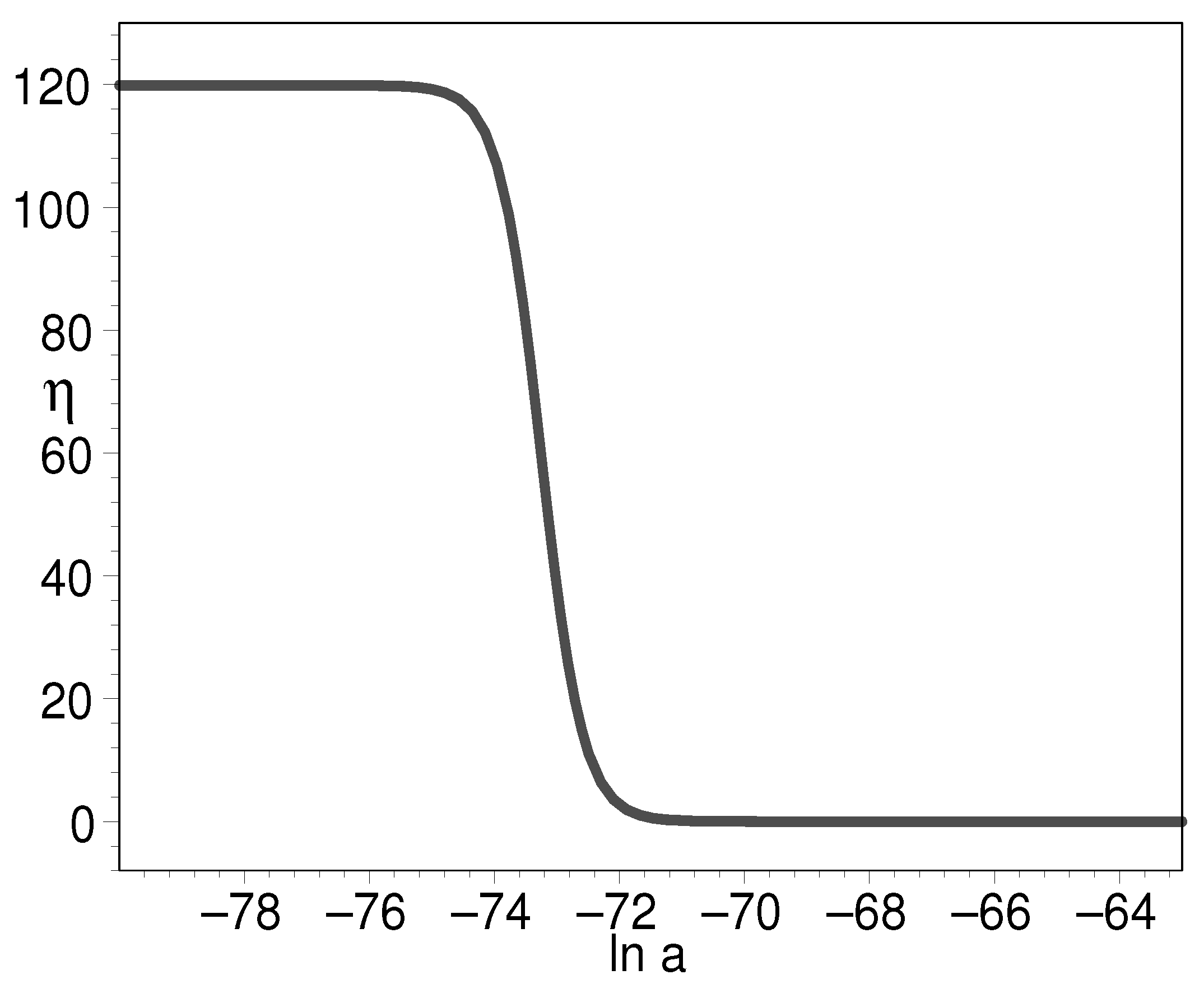
On the other hand, Figure 2 also shows that the EOS might start from in the very early universe and then increases to positive, its curves bulging and distended. In the end, it arrives at . This shows that the energy density is nearly a constant in the very early universe and then it decreases significantly. Finally, the energy density dwells on a very small constant. This indicates that the K-essence can unify the early inflation field and the later dark energy. In order to make this clear, we plot the evolution for the log-ratio of K-essence density to its present-day value, the equation of state of K-essence with respect to the natural logarithm of scale factor in Figure 6, Figure 7 and Figure 8.
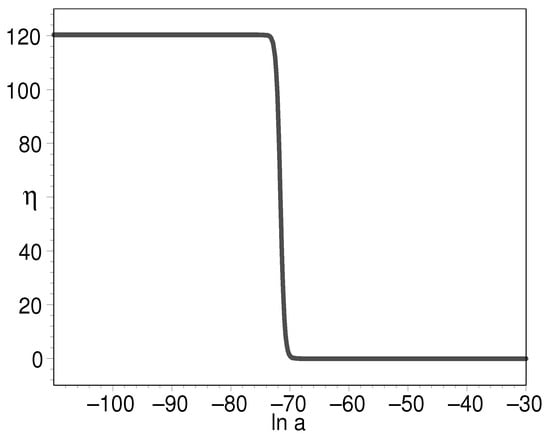
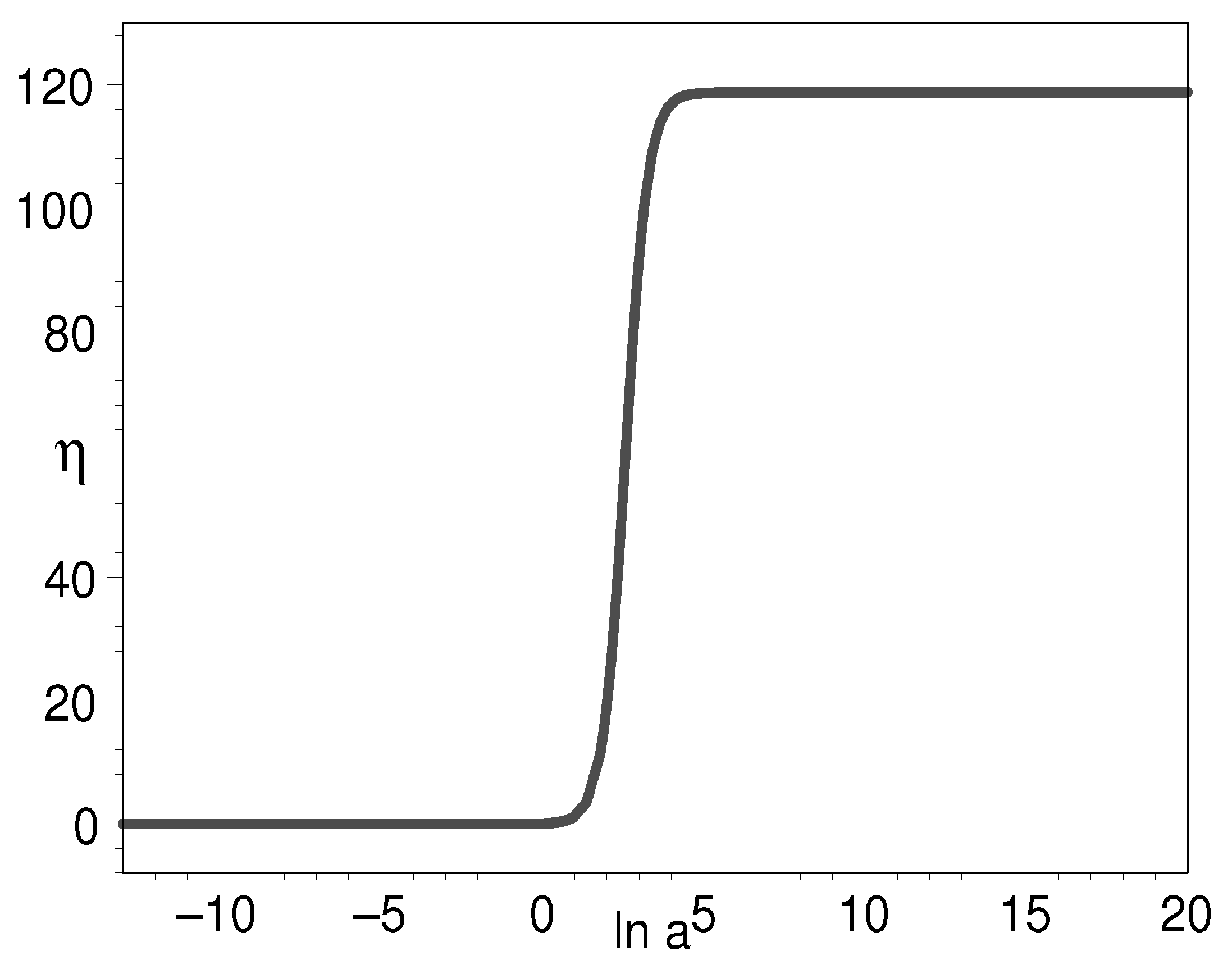
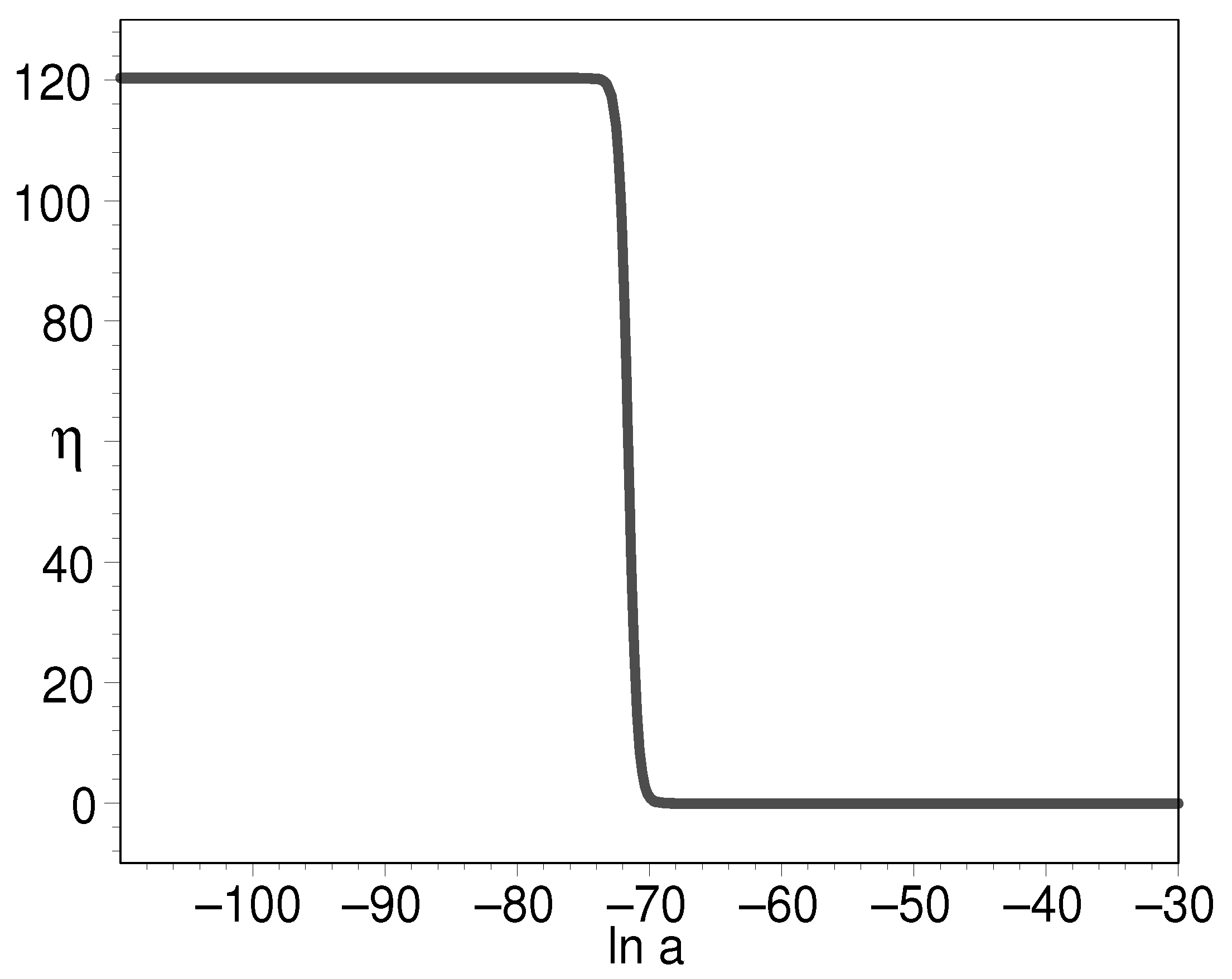
Figure 6.
The evolution of for the log-ratio of K-essence density to its present-day value with respect to the natural logarithm of scale factor. We have put .
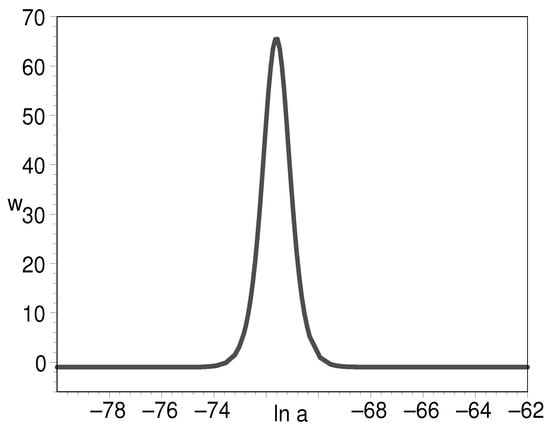
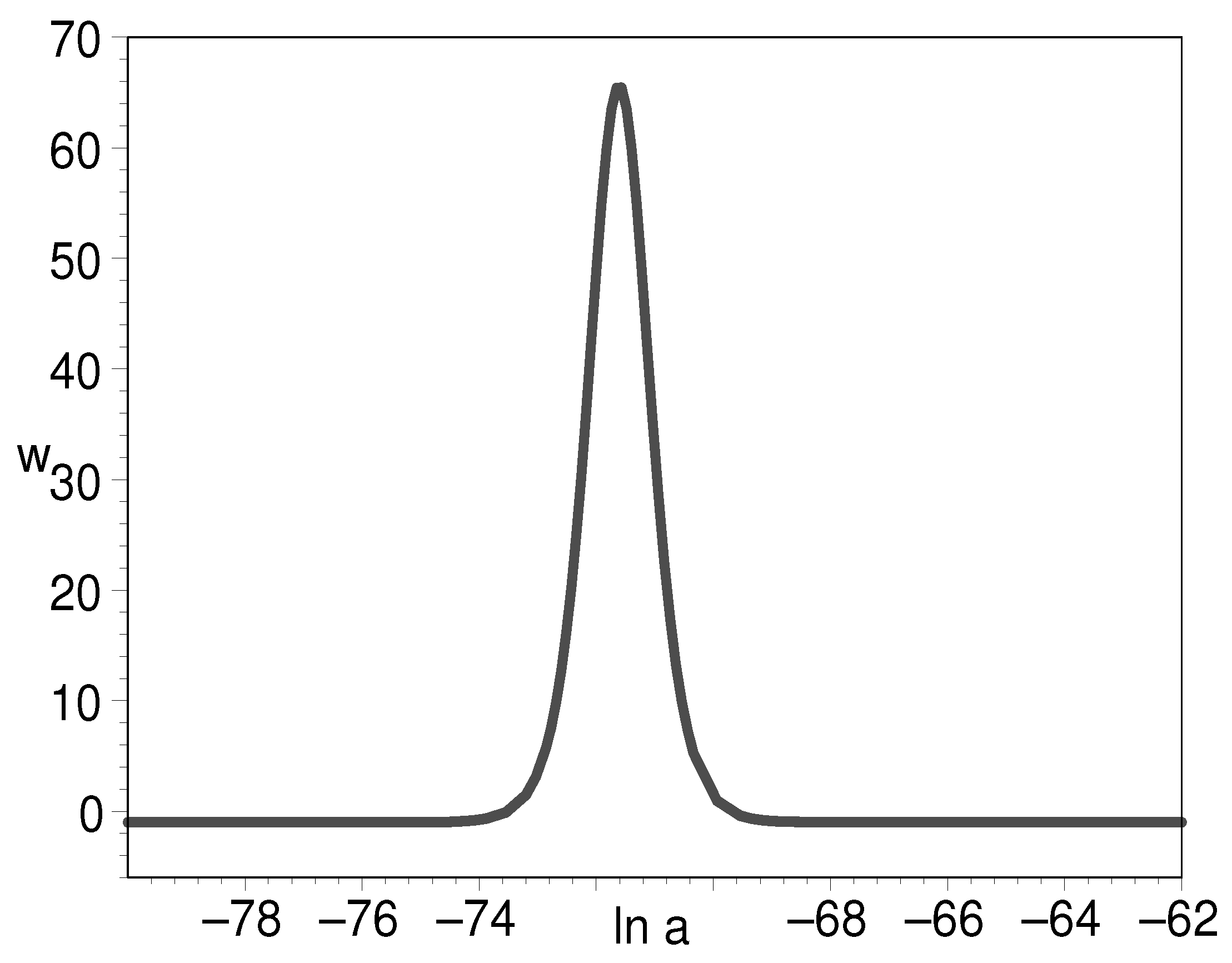
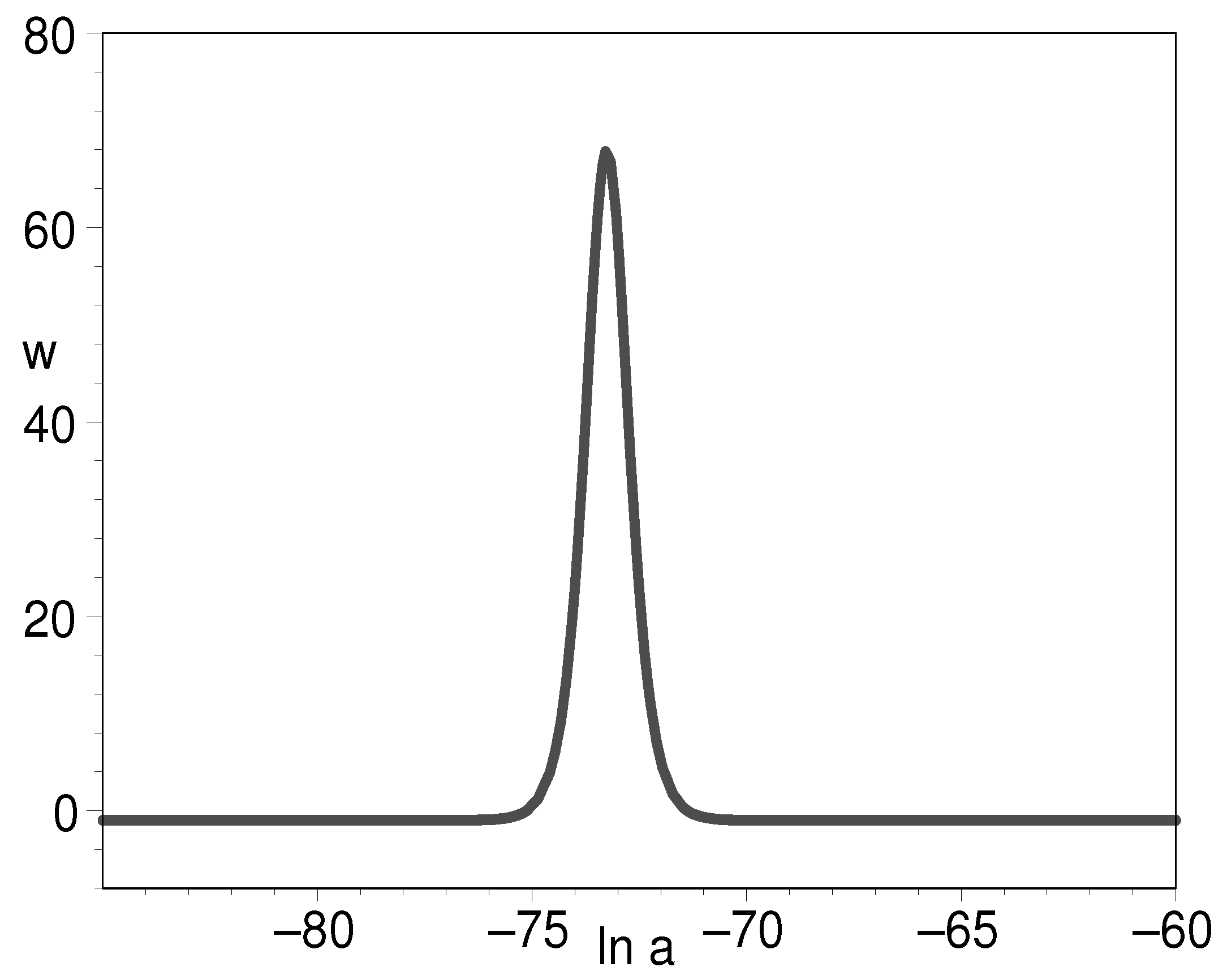
Figure 7.
The evolution of EOS for K-essence with respect to the natural logarithm of scale factor. We have put .
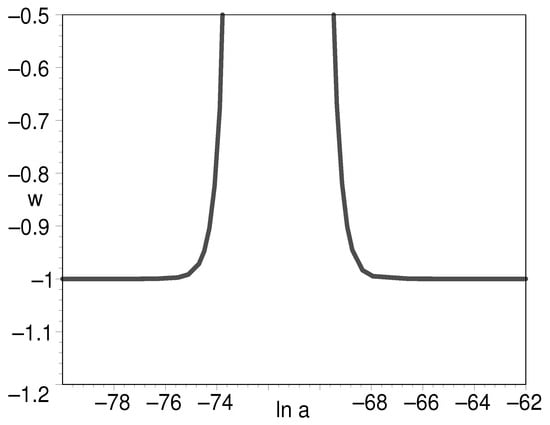
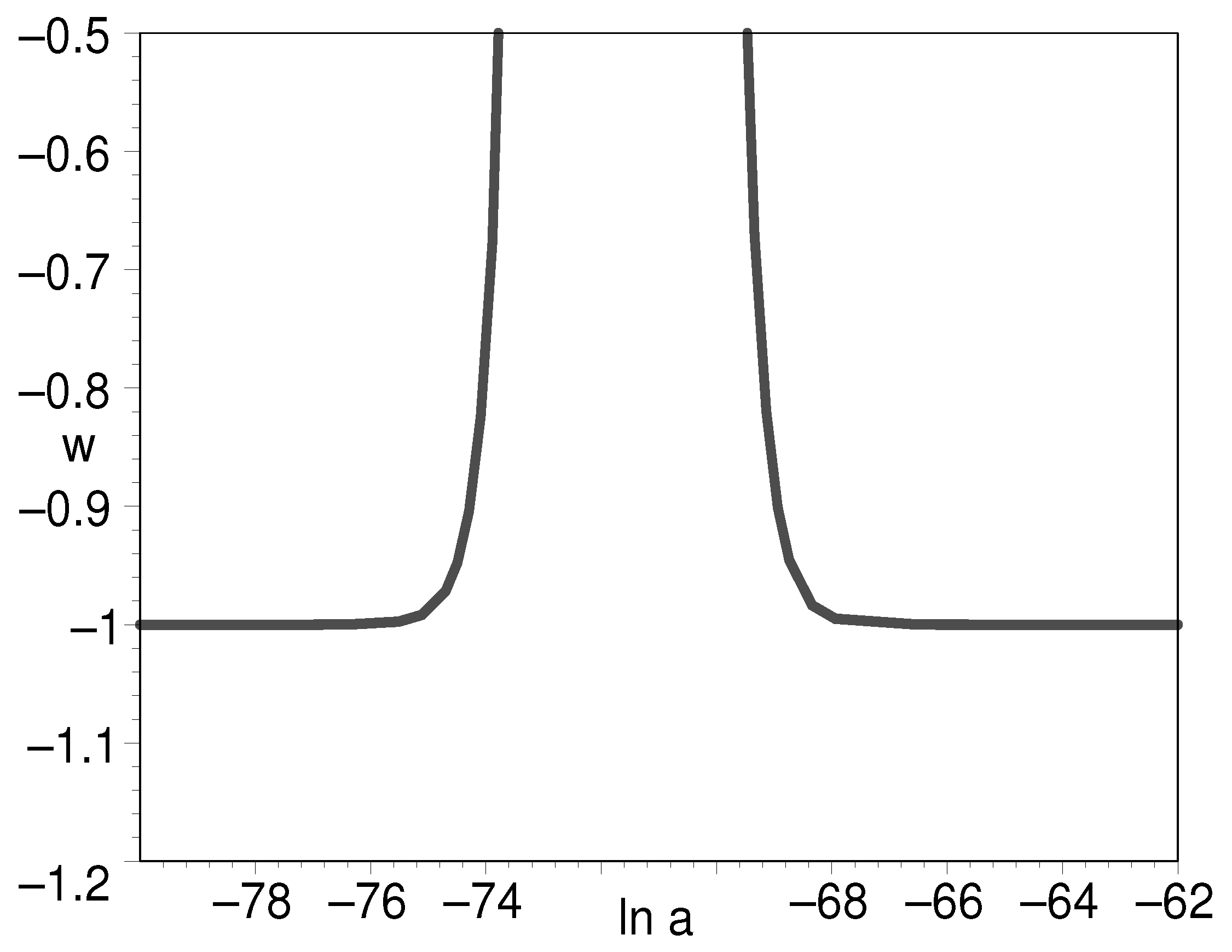
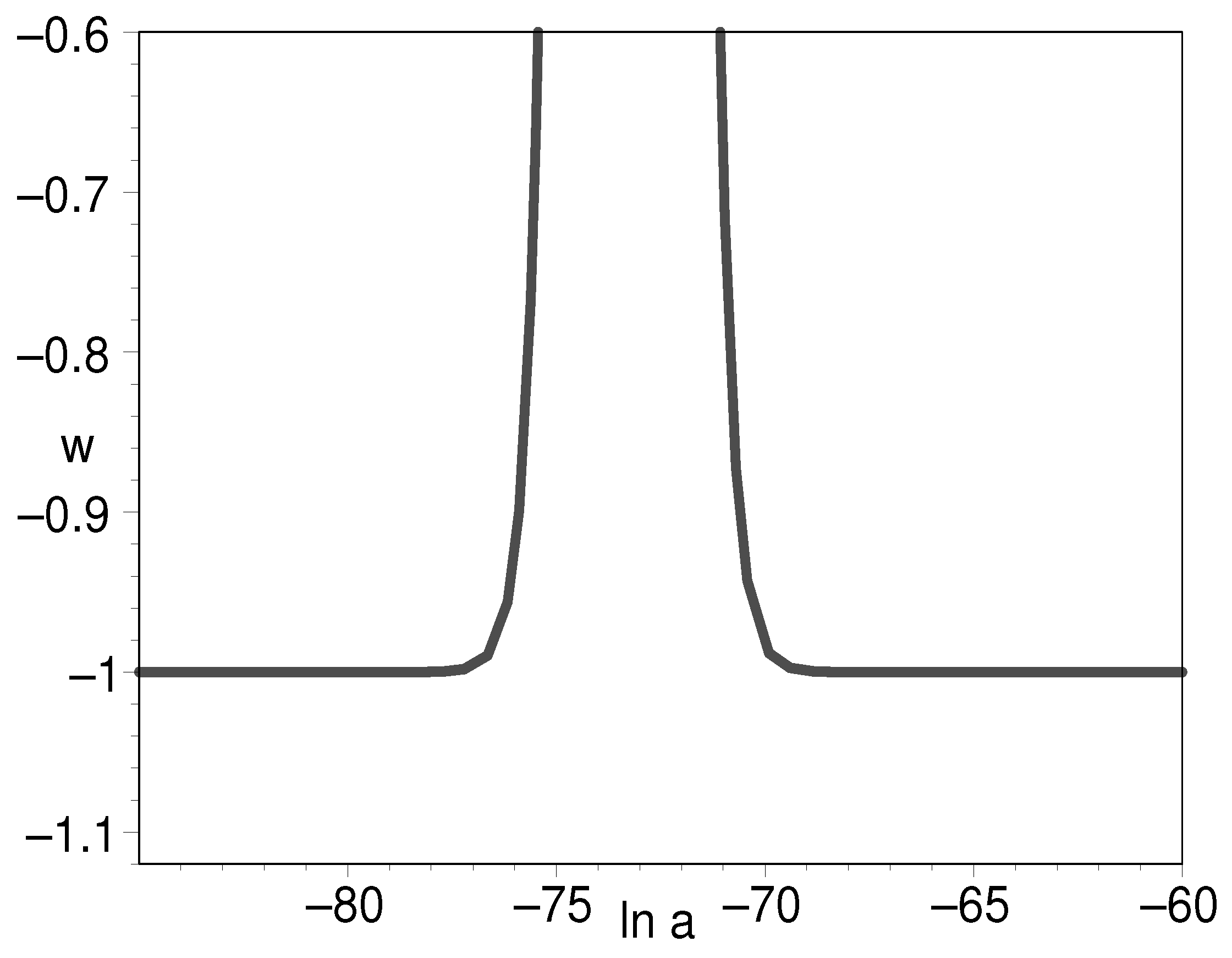
Figure 8.
The evolution of EOS for K-essence being a part of Figure 7, with respect to the natural logarithm of scale factor.
The Hubble radius of the present-day universe is in the order of m. Inflation is generally assumed as starting from the Planck length, m. On the whole, the scale factor expands by an order of or 140 e-folds. In order to solve the horizon problem, 60 e-folds from inflation are needed, more or less. Without a loss of generality, we assume inflation produces 70 e-folds. Therefore, inflation starts from to . Then, from to , the universe goes through three stages, namely, the radiation-dominated, matter-dominated, and matter plus dark-energy dominated stages, respectively.
Figure 6 tells us that the early density of double-field K-essence can be to the order of 120 as compared to the present-day cosmic density. This is commonly assumed in the inflation paradigm. Figure 7 shows that the EOS can be very large, which indicates the K-essence energy density undergoes a precipitous decline at this instant. Figure 8 clearly shows that the EOS has as its starting point and final result. This is a desirable feature for it to play the role of the early inflation field and the later cosmic dark energy.
In the next subsection, we shall present the other example which can unify the early inflation field and the later cosmic dark energy.
3.3.3. The Case of
Thirdly, we consider the Lagrangian
where and m are constants. Here, both n and m are dimensionless. The and terms are the kinetic terms of Cuscuton action [30]. The exponential term is the potential and it behaves exactly as the Einstein cosmological constant in the background of the Friedmann–Robertson–Walker universe in the absence of the and terms. The cosmological equations of motion, Equations (10) and (11), give the energy density
where and are two integration constants. When the scale factor a is sufficiently small, i.e., , we obtain a constant energy density
On the other hand, when the scale factor is sufficient large, we also have a constant energy density
The log-ratio of above constant densities is
If we require
we would find
Namely, the constant energy density for inflation is 120 orders of magnitude larger than the present dark energy density. To make this clear and for simplicity, we consider the parameter
Then, we obtain the energy density
Given the energy conservation equation (Equation (38)), the EOS can be obtained. In Figure 9, Figure 10 and Figure 11, we plot the evolution for the log-ratio of the K-essence density to its present-day value, the EOS of K-essence with respect to the natural logarithm of scale factor. To conclude, we find the Lagrangian function Equation (41) can be used as a model of unification of early inflation field and later cosmic dark energy.
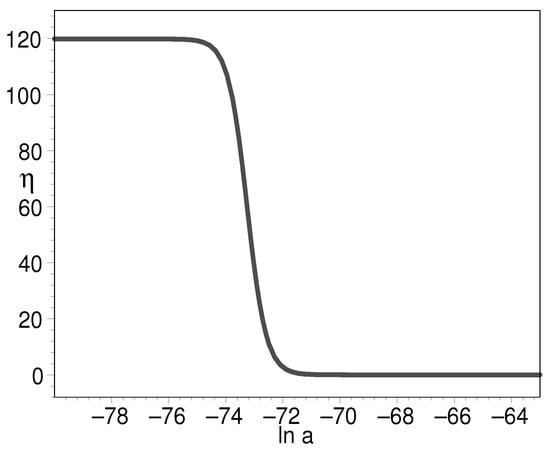
Figure 9.
The evolution of for the Log-ratio of K-essence density to its present-day value with respect to the natural logarithm of scale factor. We have put .
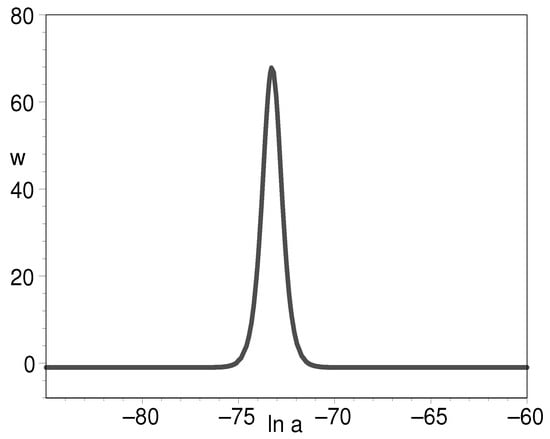
Figure 10.
The evolution of EOS for K-essence with respect to the natural logarithm of scale factor. We have put .
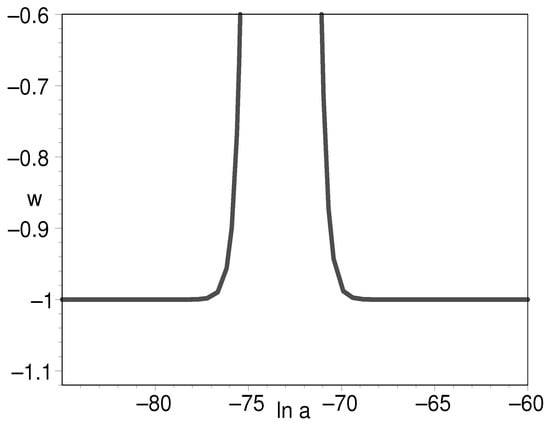
Figure 11.
The evolution of EOS for K-essence being a part of Figure 10 with respect to the natural logarithm of scale factor.
3.3.4. The Case of
Finally, we consider the Lagrangian
where , and n are constants. Now, s has a dimension of . The cosmological equations of motion, Equations (10) and (11), give the energy density
where and are integration constants. In order to ensure that the energy density is always positive, we require
It is straightforward to obtain the pressure and thus equation of state
for K-essence by substituting the energy density into the energy conservation equation. In Figure 12, Figure 13 and Figure 14, we plot the EOS with respect to the scale factor. Figure 12 shows that the absolute value of EOS can be very large at the early universe. The large number of the EOS means that the energy density decreases or increases remarkably fast. When , we have the EOS.
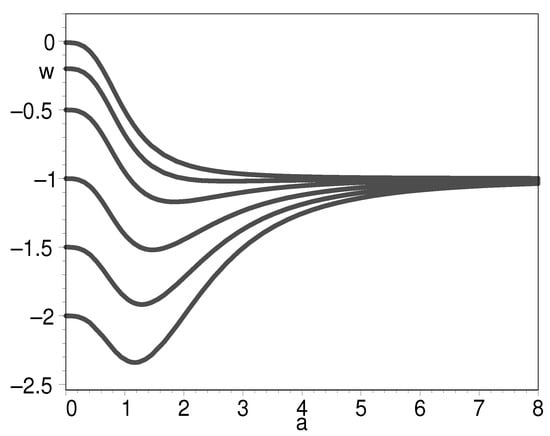
Figure 12.
The evolution of EOS for K-essence with respect to the scale factor when from bottom to top. We set .
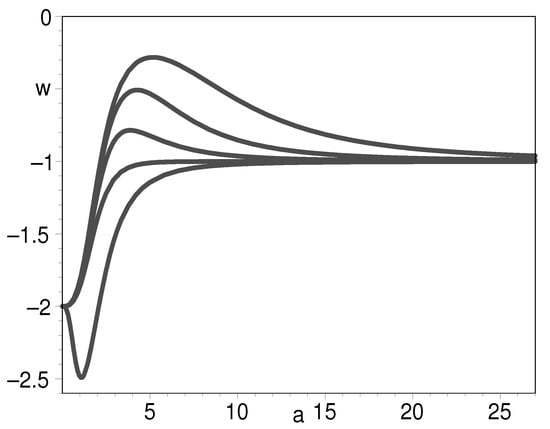
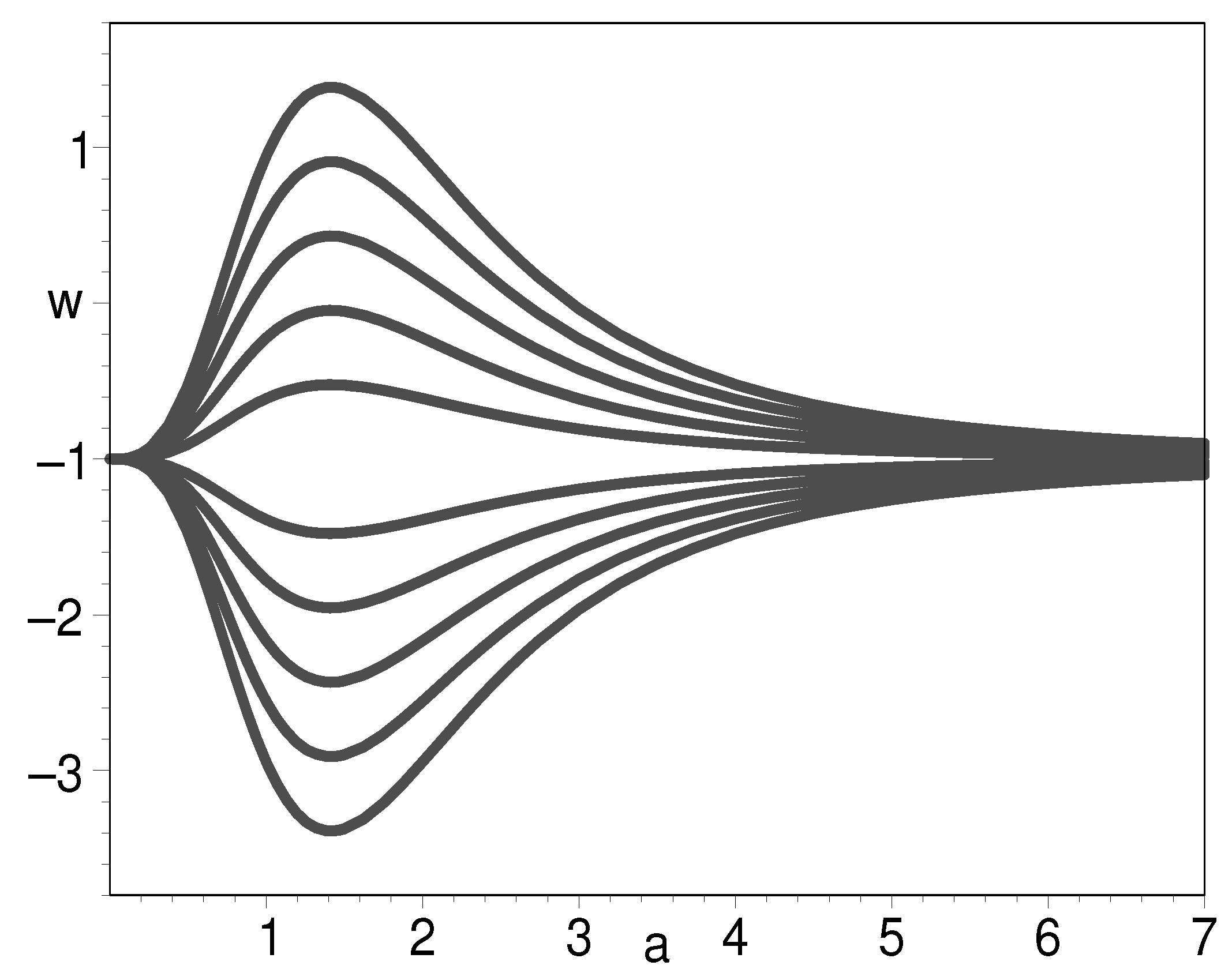
Figure 13.
The evolution of EOS for K-essence with respect to the scale factor when from bottom to top. We set .
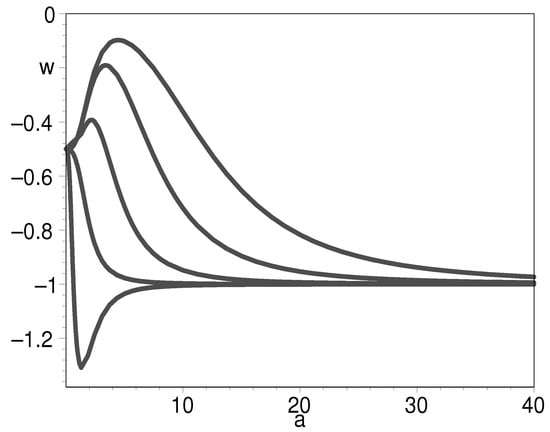
Figure 14.
The evolution of EOS for K-essence with respect to the scale factor when from bottom to top. We set .
Then, when , we have , as shown in Figure 12. On the other hand, when , we have
Figure 13 and Figure 14 reveal that the EOS can cross the phantom divide either from large to small as shown in Figure 14 or from small to large as shown in Figure 13. They have one thing in common: namely, they all approach in the distant future.
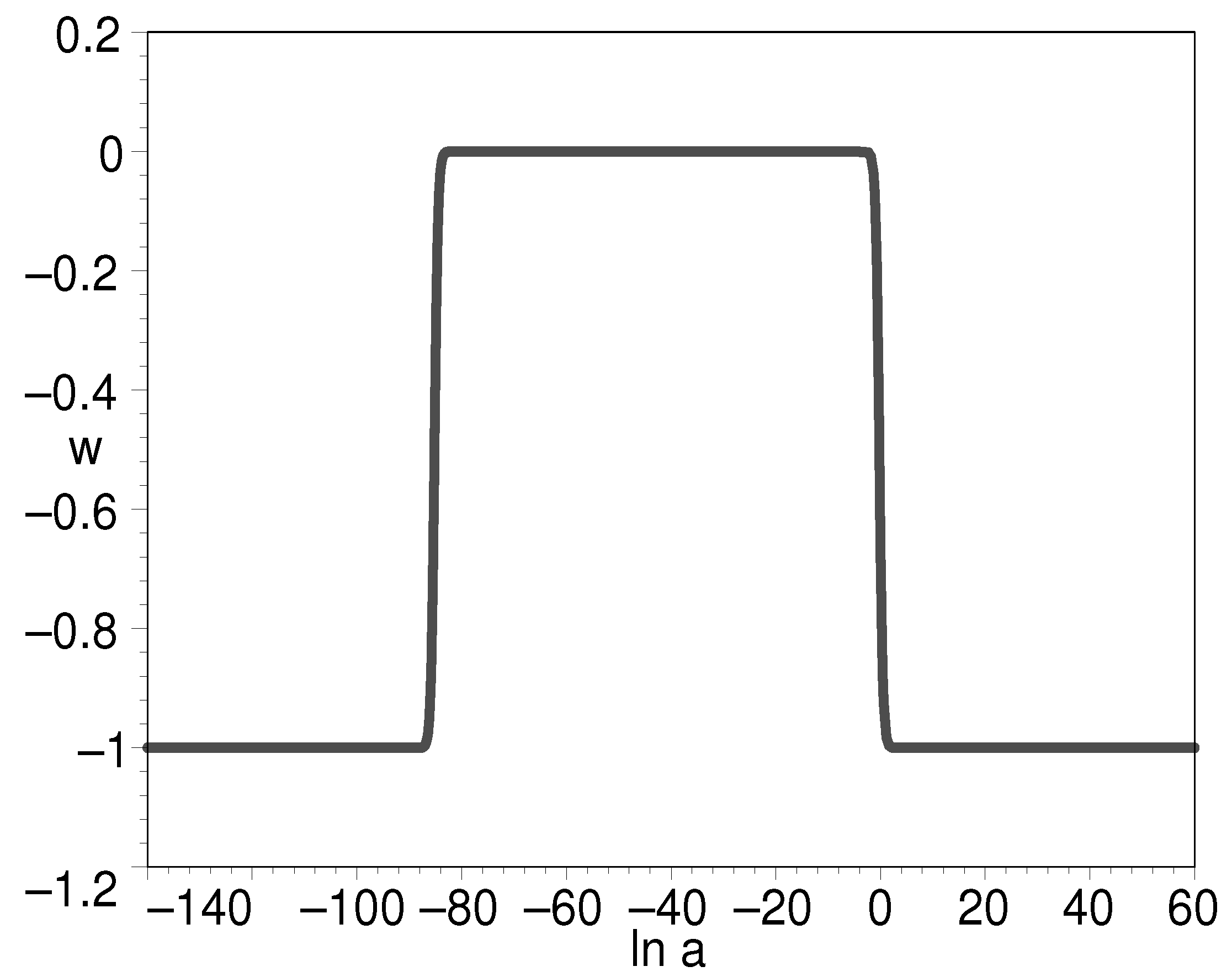
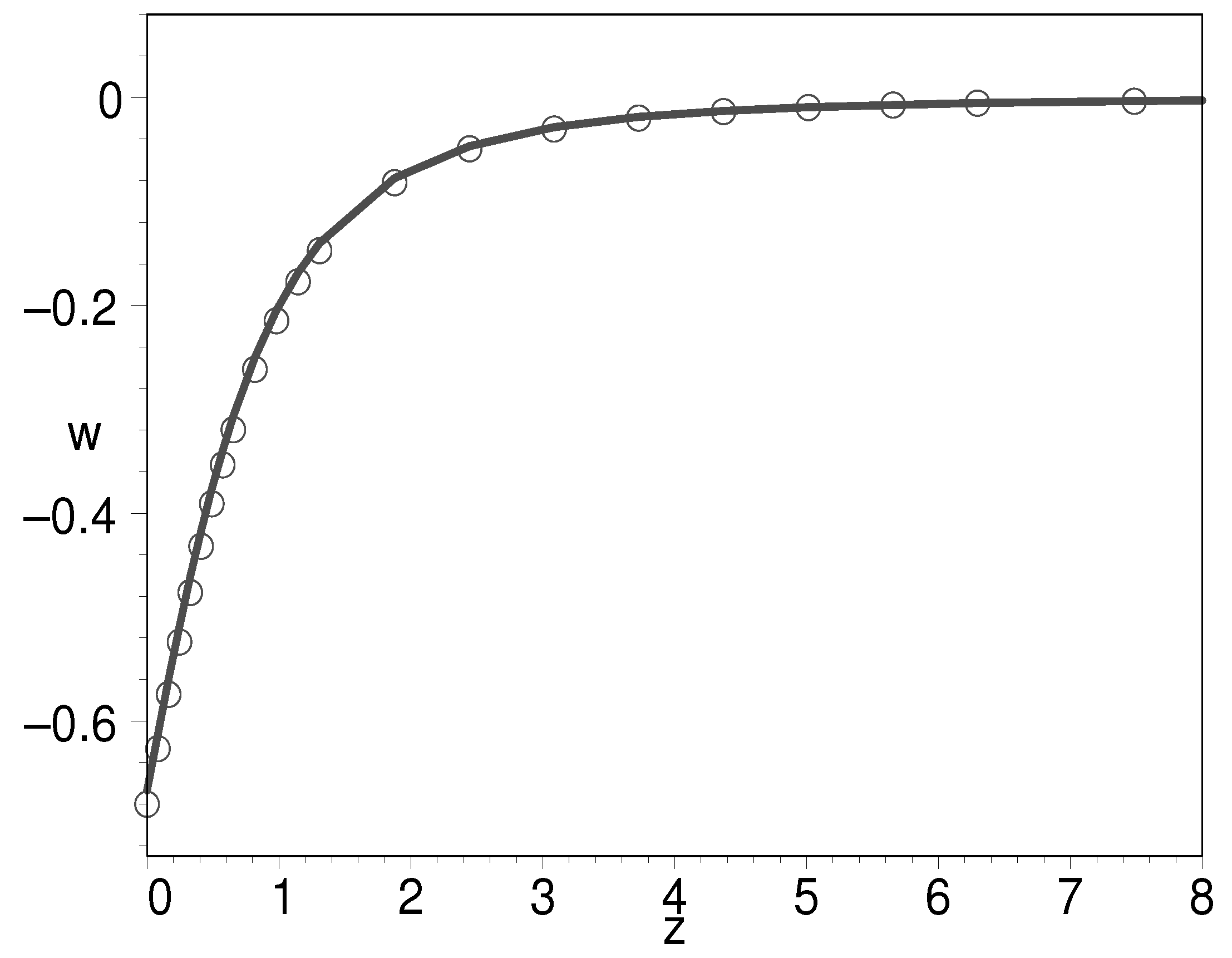
It is of particular interest when . We find that in this case, the K-essence can unify the inflation field, dark matter, and dark energy. Equations (54) and (55) tell us that the EOS is both in the very early universe and the later universe, which is a desired feature for the candidates of inflation field and dark energy. In Figure 15, we plot the EOS of the K-essence with respect to the natural logarithm of scale factor when . The figure shows that inflation starts from to , i.e., 60 e-folds are generated by inflation. Then, from to , K-essence plays the role of dark matter with an EOS of 0. Finally, in the vicinity of , namely, the present-day universe, the K-essence plays the role of both dark matter and dark energy. To illustrate this point, we plot the evolution of the EOS with respect to cosmic redshift in Figure 16. The circled line is for the paradigm. As we can see, the two curves are almost overlap with each other, suggesting that the unification model holds here. In Figure 17, we plot the evolution for the log-ratio of the K-essence density to its present-day value with respect to the natural logarithm of scale factor. There is a slope between the two platforms. The slope denotes the decrease in dark matter with the expansion of the universe.
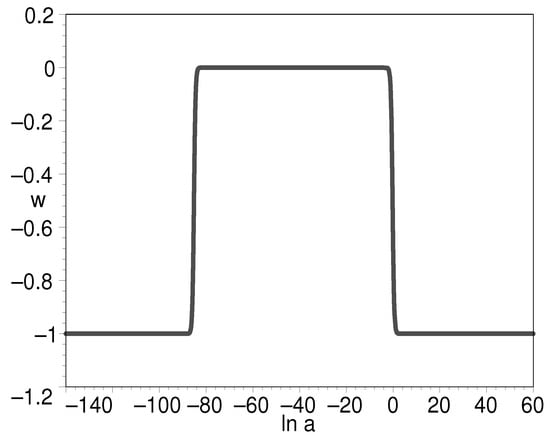
Figure 15.
The evolution of EOS for K-essence with respect to the natural logarithm of scale factor when .
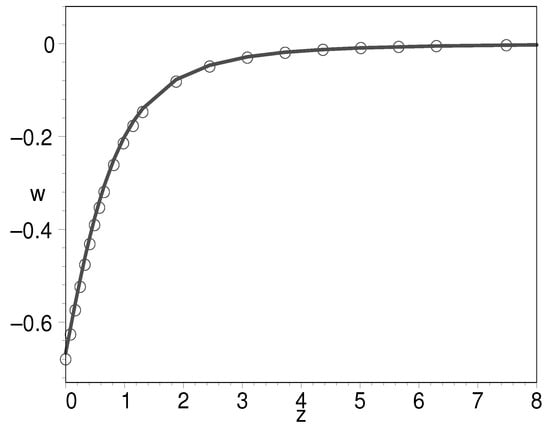
Figure 16.
The evolution of EOS for K-essence with respect to the cosmological redshift when . The circled line is for the paradigm.
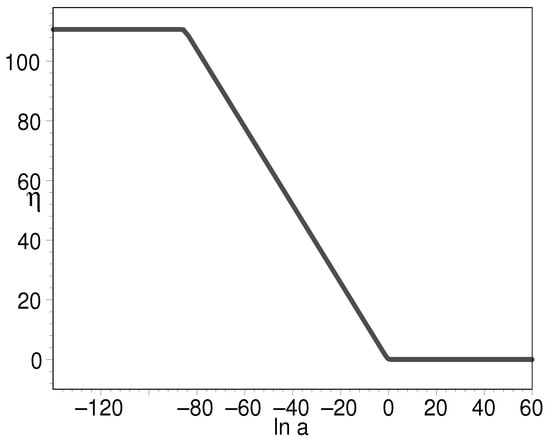
Figure 17.
The evolution of EOS for the log-ratio of K-essence density to its present-day value with respect to the natural logarithm of scale factor when .
To summarize at this stage, the double-field pure K-essence is a potential candidate to unify the inflation field, dark matter, and dark energy. In this scenario, the coincidence problem no longer exists because dark matter and dark energy are the same field. This is different from the conventional method in order to solve the coincidence problem where it assumes an interaction between dark matter and dark energy (see for example the review [34]). Other models that attempt to unify inflation, dark energy, and dark matter are mainly developed in framework of one scalar field theory, for example [35,36].
4. Stability Analysis
The stability conditions for K-essence with a single field were obtained by Kase and Tsujikawa in [37]. In this section, we carry out the stability analysis of double-field pure K-essence theories in the background of Minkowski spacetime. The search for gauge-ready formulation of scalar perturbations in in-homogeneous universe as performed in [37] is a large and complex subject and thus beyond the scope of this paper.
It is easily found that in the background of Minkowski spacetime, the evolution of two scalars for a general Lagrangian function is always
with and as two constants. This means that the two scalars are always varying uniformly over time. So, we expand them in the form
where the delta terms are the perturbations. Substituting them into the Lagrangian Equation (30) and collecting the second order terms for perturbations, we obtain the final Lagrangian,
where represents the three-dimensional Laplace operator in Euclidean space. Then, the equation of motion for linear perturbations are obtained
They have the stable solutions
with
The square of frequencies, Equation (61), shows that there exists a decaying mode (for imaginary w) or oscillating mode (for real w) dependent on the sign of , and n. Therefore, it is physically reasonable. Similarly, we obtain the square of frequencies for other three models. They are given by
and
respectively. In all, the double-field pure K-essence models are physically allowable at the level of perturbations in the background of Minkowski spacetime.
5. Conclusions and Discussion
In conclusion, we have studied a class of novel double-field pure K-essence whose Lagrangians are the functions of the kinetic terms of two scalar fields while independent of the scalar fields and . The absence of the scalar field variables in the Lagrangians makes the equations of motion for scalar fields considerably simpler and their analytic solutions can be found. The novelty of this K-essence lies in the “potential”, which is made up of the quotient of kinetic terms x/y of the scalar fields.
Why do we study this quotient form “potential”, ? Actually, we find in the double-field pure K-essence theory, that a quotient form of the Lagrangian can exactly play the role of the cosmological constant in the background of a homogeneous and isotropic universe. However, the scalar fields are dynamic, although the energy density is a constant. Of course, in an inhomogeneous and anisotropic universe, the quotient form of the K-essence would be different from the Einstein cosmological constant because they have different energy-momentum tensor. On the other hand, in the process of looking for the double-field K-essence description of constant EOM matter and generalized Chaplygin gas matter, the quotient terms inevitably occur in the Lagrangians. These facts motivate us to make an analysis of the cosmic evolution of the double-field K-essence with the quotient-form potentials. To our knowledge, this is the first time that this type of K-essence has been explored. As for the kinetic terms in the Lagrangians, we emphasize that they are actually the Cuscuton terms [30]. It is surprising that the Cuscuton terms of the Lagrangian also appear in the Lagrangian of two interacting particles in the low-velocity limit [31].
We find that the equation of state for this novel K-essence has many interesting features. They are outlined as follows.
First, the EOS can cover a very large parameter space, , which is remarkably different from that of quintessence, . The large magnitude of means that the energy density of K-essence can increase, , or decrease, , extremely dramatically.
Secondly, the EOS can start from in the very early universe. Then, it increases or decreases dramatically, and finally equals in the distant future. Accordingly, two fates of the universe are laid before us. One is a de Sitter-like universe governed by a very small nearly constant energy density (with the order of dark energy density in the present universe) and the other is an inflationary universe governed by a very large nearly constant energy density (with the order of Planck energy density). In the former case, the universe will expand forever exponentially while in the later case, it starts a new inflation again.
Thirdly, the EOS also begins from , goes through 0, and ends in . Therefore, the novel K-essence has the potential to unify the early inflation field, the later dark energy, and the dark matter in between. In this scenario, the coincidence problem no longer exists because of the sameness of dark matter and dark energy in nature.
Fourthly, we find that the novel double-field pure K-essence can incorporate the scenario of sign-switching dark energy like the ones investigated in [38,39,40] by appropriately selecting the values of parameters and in the energy density, Equation (51), for example. It is found that the sign-switching dark energy is asymptotically positive and vanishing, but negative at the Big Bang. As a consequence, the Hubble tension is alleviated.
Finally, we must acknowledge that while our studies have revealed above interesting features, it is not enough. In brief, we only studied the cosmic evolution of the novel K-essence in a homogeneous universe. The research on the behavior of this novel K-essence in an inhomogeneous universe should be carried out in the following work.
Funding
The work is supported by the National Key R&D Program of China grants No. 2022YFF0503404 and No. 2022SKA0110100.
Data Availability Statement
The data is included in the paper.
Acknowledgments
We thank the referees for insightful comments leading to improvements in the original manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
Note
| 1 | But Lee et al. [19] proved that the EOS (equation of state) of dark energy and the present-day Hubble parameter are anti-correlated in K-essence theories. So, K-essence acting as late-time dark energy may make the Hubble tension even worse. The reason for this is that if the K-essence scalar does not rest at the minimum of the potential, the present-day Hubble parameter would be decreased. |
References
- Armendariz-Picon, C.; Damour, T.; Mukhanov, V. k-Inflation. Phys. Lett. B 1999, 458, 209–218. [Google Scholar] [CrossRef]
- Garriga, J.; Mukhanov, V.F. Perturbations in k-inflation. Phys. Lett. B 1999, 458, 219–225. [Google Scholar] [CrossRef]
- Chiba, T.; Okabe, T.; Yamaguchi, M. Kinetically driven quintessence. Phys. Rev. D 2000, 62, 023511. [Google Scholar] [CrossRef]
- Armendariz-Picon, C.; Mukhanov, V.; Steinhardt, P.J. Dynamical solution to the problem of a small cosmological constant and late-time cosmic acceleration. Phys. Rev. Lett. 2000, 85, 4438. [Google Scholar] [CrossRef]
- Armendariz-Picon, C.; Mukhanov, V.; Steinhardt, P.J. Essentials of k-essence. Phys. Rev. D 2001, 63, 103510. [Google Scholar] [CrossRef]
- Chiba, T. Tracking k-essence. Phys. Rev. D 2002, 66, 063514. [Google Scholar] [CrossRef]
- Chimento, L.P.; Feinstein, A. Power-low expansion in k-essence cosmology. Mod. Phys. Lett. A 2004, 19, 761–768. [Google Scholar] [CrossRef]
- Chimento, L.P. Extended tachyon field, Chaplygin gas, and solvable k-essence cosmologies. Phys. Rev. D 2004, 69, 123517. [Google Scholar] [CrossRef]
- Malquarti, M.; Copeland, E.J.; Liddle, A.R. K-essence and the coincidence problem. Phys. Rev. D 2003, 68, 023512. [Google Scholar] [CrossRef]
- Scherrer, R.J. Purely kinetic k essence as unified dark matter. Phys. Rev. Lett. 2004, 93, 011301. [Google Scholar] [CrossRef]
- Chimento, L.P.; Lazkoz, R. Atypical k-essence cosmologies. Phys. Rev. D 2005, 71, 023505. [Google Scholar] [CrossRef]
- Abramo, L.R.; Pinto-Neto, N. Stability of phantom k-essence theories. Phys. Rev. D 2006, 73, 063522. [Google Scholar] [CrossRef]
- Bonvin, C.; Caprini, C.; Durrer, R. No-go theorem for k-essence dark energy. Phys. Rev. Lett. 2006, 97, 081303. [Google Scholar] [CrossRef]
- Bose, N.; Majumdar, A.S. K-essence model of inflation, dark matter, and dark energy. Phys. Rev. D 2009, 79, 103517. [Google Scholar] [CrossRef]
- Bose, N.; Majumdar, A.S. Unified model of k-inflation, dark matter, and dark energy. Phys. Rev. D 2009, 80, 103508. [Google Scholar] [CrossRef]
- Tian, S.X.; Zhu, Z.-H. Early dark energy in k-essence. Phys. Rev. D 2021, 103, 043518. [Google Scholar] [CrossRef]
- Riess, A.G.; Casertano, S.; Yuan, W.; Bowers, J.B.; Macri, L.; Zinn, J.C.; Scolnic, D. Cosmic distances calibrated to 1% precision with Gaia EDR3 parallaxes and Hubble Space Telescope photometry of 75 Milky Way Cepheids confirm tension with ΛCDM. Astrophys. J. Lett. 2021, 908, 6. [Google Scholar] [CrossRef]
- Freedman, W.L. Measurements of the Hubble constant: Tensions in perspective. Astrophys. J. 2021, 919, 16. [Google Scholar] [CrossRef]
- Lee, B.-H.; Lee, W.; Colgáin, E.Ó.; Sheikh-Jabbari, M.M.; Thakur, S. Is local H 0 at odds with dark energy EFT? J. Cosmol. Astropart. Phys. 2022, 4, 004. [Google Scholar] [CrossRef]
- Adi, S.A.; Gangopadhyay, M.R.; Sami, M.; Sharma, M.K. Late-time acceleration due to a generic modification of gravity and the Hubble tension. Phys. Rev. D 2021, 104, 103534. [Google Scholar]
- Kehayias, J.; Scherrer, R.J. New generic evolution for k-essence dark energy with w ≈-1. Phys. Rev. D 2019, 100, 023525. [Google Scholar] [CrossRef]
- Chen, B.H.; Wu, Y.B.; Xu, D.F.; Dong, W.; Zhang, N. Dynamical Stability and Geometrical Diagnostic of the Power Law K-Essence Dark Energy Model with Interaction. Universe 2020, 6, 244. [Google Scholar] [CrossRef]
- Chen, B.H.; Wu, Y.B.; Chi, J.; Liu, W.; Hu, Y. The Phase Space Analysis of Interacting K-Essence Dark Energy Models in Loop Quantum Cosmology. Universe 2022, 8, 520. [Google Scholar] [CrossRef]
- Jawad, A.; Rani, S.; Sultan, A.M.; Embreen, K. k-Essence Inflation Evading Swampland Conjectures and Inflationary Parameters. Universe 2022, 8, 532. [Google Scholar] [CrossRef]
- Socorro, J.; Pérez-Payán, S.; Hernández-Jiménez, R.; Espinoza-García, A.; Díaz-Barrón, L.R. Quintom fields from chiral K-essence cosmology. Universe 2022, 8, 548. [Google Scholar] [CrossRef]
- Huang, Z. Statistics of thawing k-essence dark energy models. Phys. Rev. D 2021, 104, 103533. [Google Scholar] [CrossRef]
- Ferreira, A.L.; Pinto-Neto, J.N.; Zanelli, J. Inflation and late-time accelerated expansion driven by k-essence degenerate dynamics. Phys. Rev. D 2024, 109, 023515. [Google Scholar] [CrossRef]
- Padmanabhan, T. Cosmological constant—The weight of the vacuum. Phys. Rep. 2003, 380, 235. [Google Scholar] [CrossRef]
- Bento, M.C.; Bertolami, O.; Sen, A.A. Generalized Chaplygin gas, accelerated expansion, and dark-energy-matter unification. Phys. Rev. D 2002, 66, 043507. [Google Scholar] [CrossRef]
- Afshordi, N.; Chung, D.J.H.; Geshnizjani, G. Causal field theory with an infinite speed of sound. Phys. Rev. D 2007, 75, 083513. [Google Scholar] [CrossRef]
- Riehle, F.; Ulbricht, S. Einstein’s basement—A model for dark matter and an expanding universe? arXiv 2024, arXiv:2402.13679. [Google Scholar]
- Zhao, G.; Raveri, M.; Pogosian, L.; Wang, Y.; Crittenden, R.G.; Handley, W.J.; Percival, W.J.; Beutler, F.; Brinkmann, J.; Chuang, C.; et al. 2017NatAs. 1. 627Z: Dynamical dark energy in light of the latest observations. arXiv 2017, arXiv:1701.08165v2. [Google Scholar]
- Dai, J.; Yang, Y.; Xia, J. Reconstruction of the dark energy equation of state from the latest observations. Astrophys. J. 2018, 857, 9. [Google Scholar] [CrossRef]
- Wang, B.; Abdalla, E.; Atrio-Barandela, F.; Pavon, D. Dark matter and dark energy interactions: Theoretical challenges, cosmological implications and observational signatures. Rep. Prog. Phys. 2016, 79, 096901. [Google Scholar] [CrossRef]
- Capozziello, S.; Nojiri, S.; Odintsov, S.D. Unified phantom cosmology: Inflation, dark energy and dark matter under the same standard. Phys. Lett. B 2006, 632, 597–604. [Google Scholar] [CrossRef]
- Gao, C.; Kunz, M.; Liddle, A.R.; Parkinson, D. Unified dark energy and dark matter from a scalar field different from quintessence. Phys. Rev. D 2010, 81, 043520. [Google Scholar] [CrossRef]
- Kase, R.; Tsujikawa, S. Dark energy in Horndeski theories after GW170817: A review. Int. J. Mod. Phys. D 2019, 28, 1942005. [Google Scholar] [CrossRef]
- Akarsu, O.; Barrow, J.D.; Escamilla, L.A.; Vazquez, J.A. Graduated dark energy: Observational hints of a spontaneous sign switch in the cosmological constant. Phys. Rev. D 2020, 101, 063528. [Google Scholar] [CrossRef]
- Akarsu, O.; Kumar, S.; Ozulker, E.; Vazquez, J.A. Relaxing cosmological tensions with a sign switching cosmological constant. Phys. Rev. D 2021, 104, 123512. [Google Scholar] [CrossRef]
- Gennaro, S.D.; Ong, Y.C. Sign switching dark energy from a running barrow entropy. Universe 2022, 8, 541. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).