Abstract
In this work we discuss the correlation between luminosity L and velocity dispersion observed in different astrophysical contexts, in particular that of early-type galaxies (ETGs; Faber–Jackson (FJ) law) and that of active galactic nuclei (AGN). Our data for the ETGs confirm the bending of the FJ at high masses and the existence of similar curvatures in the projections of the Fundamental Plane (FP) approximately at the mass scale of ∼. We provide an explanation for such curvatures and for the presence of the Zone of Exclusion (ZoE) in these diagrams. The new prospected theory for the FJ law introduces a new framework to understand galaxy evolution in line with the hierarchical structure of the Universe. The classic analysis carried out for a class of type 1 AGN accreting gas at very high rates, confirms that a FJ law of the form is roughly consistent with the observations, with a slope quite similar to that of ETGs. We discuss the physics behind the FJ law for the AGN in different contexts and also examine the biases affecting both the luminosity and the velocity dispersion, paying particular attention to the effects induced by the spherical symmetry of the emitting sources on the accuracy of the luminosity estimates.
1. Introduction
The correlation between luminosity L and absorption/emission line broadening (closely linked to the rotational velocity V or the velocity dispersion of gas and stars) is observed in different astrophysical contexts.
The most well-known is the Faber–Jackson (FJ) relation, which is the correlation observed between the luminosity L of galaxies and the velocity dispersion (of stars). The history of this correlation is very long and cannot be reported here. In brief, the first papers were by Minkowski [1] (who used a sample of 13 ETGs), and Morton and Chevalier [2] a decade later. The relation took the power law form , that we all know only with the work of Faber and Jackson [3] (who used a sample of 25 ETGs), and since then it is commonly known as the FJ relation, customarily expressed as , where and take suitable values that depend on the available observational data. It is worth recalling here that the usual FJ relation refers to galaxies (ETGs) of the Local Universe, therefore, old objects at redshift zero, unless otherwise specified. In other words, it is a picture of the present day situation. No temporal effects due to the ever-changing physical content of a galaxy are included. Finally, the FJ relation is a projection of the Fundamental Plane in the multidimensional space of the luminosity L, the mass M (usually the stellar mass), the radius R (usually the half-light or half-mass radius ), the specific intensity , and the velocity dispersion (see a recent discussion by [4]).
The possibility of a direct physical connection between L and in a galaxy has been hastily rejected since the discovery of the correlation: why in a galaxy should the total light emitted by its stars be aware of their mean velocity? Despite this, the correlation has been observed in different astrophysical contexts and was eventually accepted as one of the most important relationships, followed by galaxies, and it is a basic tool of analysis in many astrophysical circumstances. It suffices to mention its use of distance indicator for galaxies, because it links the distance-independent quantity to an intrinsic property such as the total luminosity L of the stars (see, e.g., [5,6,7,8,9]). In recent times the classical FJ relation [3] in its modern declinations was extended by D’Onofrio et al. [10] to include evolutionary effects in the galaxy population. They adopted the same formalism of the FJ relation but supposed that and are time and galaxy dependent. The new relation is . This simple idea, combined with the virial theorem expressing the dynamical equilibrium of a galaxy, was very rewarding because it led to a description of the FP (inclination, thickness, and distribution of galaxies on it), together with its projection planes, as functions of the variables and .
Passing to active galactic nuclei (AGN), the luminosity- relation is also present in these systems. The consensus that the broadening of emission lines in quasar and Seyfert nuclei results from the Doppler effect, attributed to the rapid motion of the line-emitting gas, emerged early on; already Carl Seyfert, in his initial systematic study of galaxies named after him [11], attributed the large widths of lines to Doppler shifts, with velocities reaching up to approximately 8500 km/s for the hydrogen lines of NGC 3516 and 7469 [12]. The nature of the motions has been debated ever since (see, e.g., and references therein, [13,14,15,16]). The realization that two systems of emission lines—one dominated by virial broadening and one affected by strong outflow motions—are coexisting in AGN came slowly [17,18,19,20,21]. Since then, the broadening of the low-ionization emission lines (LILs, especially H and Mgii2800) has been used in numerous attempts to estimate the black hole mass assuming virial motions (and references therein [22,23,24,25,26]).
In this study we will focus on the formulation of updated scaling laws based on recipes to correct for viewing angle and accretion rate effects, whose importance has only very recently been appreciated in full [27,28].
So, it is perhaps not surprising that the formulation of a FJ-like law in the context of AGN has a relatively recent history. Regarding the use of a FJ law as a luminosity indicator, one has to first consider that quasars are the opposite of standard candles, since their luminosity is spread over more than five orders of magnitude (see the interviews on the exploitation of quasars as distance indicators in [29]). Attempts to define correlation between spectral parameters and luminosity have been systematically frustrated by the increasing dispersion that arose when samples of increasing size have become available. A case in point is the Baldwin effect [30,31,32], a luminosity trend that becomes shallower and statistically weaker with an increasing sample size. A connection between quasars observational and accretion parameters has become possible only after the systematic organization of the diverse spectral properties along an easily identified sequence (the so-called Eigenvector-1 sequence or quasar main sequence [14,33,34,35]). Since then, two main populations and several spectral types along the sequence have provided contextualization for most type-1 AGN [36,37], in both low and high luminosity samples [38,39]. The distinction between the two populations—conventionally named A and B—is rooted in systematic differences in terms of Eddington ratio, which in turn translates into the possibility of two different accretion modes [40,41]. Of special interest is a spectral type at one end of the quasar main sequence (MS), characterized by the most intense optical singly-ionized iron emission [9,42]. Even if the strong Feii emitters have been studied systematically since the 1990s [43,44,45], the association of Feii emissions with a high Eddington ratio is a more recent result [35,42,46,47,48]. At very high accretion rates, a geometrically thick, optically thick disk is expected to develop, with the accretion flow becoming advection-dominated [49,50]. As a consequence, the Eddington ratio tends asymptotically to values of order unity [51] for a dimensionless accretion rate , where is the mass accretion rate and L is the quasar luminosity. This important result is at the basis of the exploitation of a quasar FJ-like relation for cosmology (as will be amply discussed below), and confirms that the luminosity follows a dependence on line broadening consistent with the virial theorem, at least for Population A sources. Finally, a luminosity versus velocity relationship is also possible for type-A AGN.
Given these introductory premises, the chief aim of this review is to report in some detail on the past history and most recent results concerning the luminosity–velocity relation in galaxies (ETGs) and AGN.
The plan of the paper is as follows. In Section 2 we briefly review the state of the art of the relation both for ETGs and AGN. In Section 3 we deal with ETGs in some detail, present the observational data and the Illustris galaxy models we have adopted, discuss the classical FJ relation, examine the four possible projections of the FP and the distribution of galaxies in these projection planes, and report on the results obtained with the time-dependent FJ relationship. In Section 5 we address the subject of AGN, describe the two populations of AGN, the current estimates of the masses of central Black Holes, different estimates of the velocity dispersion and corrections of this by different effects, and finally derive luminosity versus velocity dispersion relationships for two groups of so-called population-A AGN. In Section 5, we apply the formalism developed by D’Onofrio et al. [10] to derive the variables and to our group of AGN, pointing out the remarkable similarity in the scaling laws for AGN and ETGs. Lastly, in Section 6 we summarize the results and present some conclusions. Finally, in Appendix A we present some details on measuring the velocity dispersion in xA sources.
All the calculations and figure are obtained using the -CDM cosmological parameters [52]: km s−1 Mpc−1.
2. State of the Art of the ETGs and AGN Space
2.1. The ETGs
Several works have addressed the correlation looking at different aspects of the observed distribution of ETGs in this parameter space, taking advantage of the even larger samples of galaxies with available measurements of provided by the big surveys (e.g., ATLAS, SDSS, BOSS, etc.). Many such works are concerned with the slope of the relation, the observed scatter, the evolution of the relation with redshift, and its power as a distance indicator.
Very soon it became clear that the slope of the relation depends on the range in luminosity of the ETGs under analysis. Values larger than 4 were measured for luminous ETGs (e.g., [53,54,55,56,57]) and ∼2 for faint systems (e.g., [58,59,60,61,62,63], Lauer et al. [64]) for example, using a compilation of HST observations for ∼200 ETGs, measured a slope of ∼7. Similarly the team of the ATLAS3D [65] survey, working with 260 local ETGs, measured a high-mass slope of ∼ for the stellar mass relation above ∼ [55]. The analysis of Focardi and Malavasi [66] instead reported a value of ∼, using a sample of a few hundred objects extracted from HYPERLEDA [67].
The measured slopes of the FJ therefore vary among different works, from ∼ to ∼8 for luminous ETGs and ∼ for faint objects. Such curvature at high luminosity has been confirmed with high statistical significance with the SDSS and BOSS CMAS data [63,68,69,70,71,72]).1
Bernardi et al. [73] correctly pointed out that the slope of the correlation depends on the fitting strategy and that selection effects play a different role according to the correlation chosen. The fit of the luminosity at each velocity dispersion () does not give the same result of the fit of the velocity dispersion as a function of luminosity (), nor of the joint distribution of L and . The first allows for the use of to predict L, whereas the second allows the opposite.
For what concerns the intrinsic scatter, the conclusions are a bit contradictory: Nigoche-Netro et al. [74] measured a decrease (with mass), whereas Shu et al. [75] seems to indicate the opposite. Montero-Dorta et al. [63] measured an intrinsic scatter in log units at a fixed L using the big BOSS CMAS database and found no significant evolution of the scatter up to z∼0.5. Hyde and Bernardi [70] observed instead a scatter decreasing towards high luminosities. They estimated a value of ∼0.05 dex at . At the high-mass end, Kormendy and Bender [56] derived an intrinsic scatter of 0.06 in for “core” galaxies and 0.10 for “core-less” ellipticals at a given magnitude. A mass (or luminosity) dependence of the intrinsic scatter of the relation has been also been reported in other papers [66,69,74,76]. Nigoche-Netro et al. [71,77,78,79] also claimed that the intrinsic dispersion is affected by geometrical effects and that its value does not diminish with the magnitude range.
Being that the FJ relation is a projection of the Fundamental Plane (FP) [80,81], in this case of the space where the effective radius and the central velocity dispersion are correlated with the luminosity L, the redshift evolution of the FJ relation is closely linked to the evolution of the ETG distribution in the FP. It is known that the zero-point of the FP evolves from z∼1 in a way consistent with the passive evolution of stellar populations [73,82]. Montero-Dorta et al. [63] found that the evolution of the zero-point of the FJ relation is consistent with such passive evolutions since the redshift of , which is in good agreement with the FP results, and that the high-mass end of the relation does not change in the range and is consistent with that at z∼0.
The data of the hydro-dynamical numerical simulations, e.g., that of Illustris [83], analyzed by D’Onofrio et al. [10], also seem to indicate that the slope of the FJ relation was much steeper at redshift and that the curvature observed at high luminosity appeared only at redshifts lower than 1.5 in all projections of the FP.
In general, the indications coming from different studies suggest that several scaling relations obtained with the structural parameters of the FP change with redshift. Some works claim that only the zero-point vary with redshift (e.g., [84,85,86,87]), while others find that both zero-point and slope are variables (e.g., [82,88,89]). In this context, dwarf and bright ETGs seem to have different behaviors, possibly originating from different paths of evolution [69,90,91,92,93,94,95].
Recently D’Onofrio et al. [10] introduced a new idea concerning the origin of the FJ relation, proposing that this relation comes out of the combination of two different scaling laws, the virial theorem (VT) on one side and a new empirical relation, the law, that accounts for the variation in mass and luminosity due to mergers and stripping phenomena typical of the hierarchical scenario of galaxy formation and evolution. In the formulation the main role is played by the terms and . The idea is that the total luminosity of galaxies is the result of star assemblies, star formation history, and stellar evolution. In this view, and are variables parameters that change significantly from galaxy to galaxy. The advantage of this approach is that, when the law is coupled with the VT, one can reproduce the whole distribution of ETGs in all the projections of the FP, the trends observed for the high mass tail of ETGs, and explain the origin of the Zone of Exclusion (ZoE) [4]. The parameter can assume both large positive and negative values (and consequently can spread over quite a big interval). This is not a problem for the scatter observed in the FJ, because the maximum possible variation in L is of the order of ∼ in log units (a factor of ∼2) when two equal mass objects merge. This is a very rare phenomenon, in particular at z = 0. In practice the whole scatter of the FJ is preserved at almost all redshifts.
The extended FJ law might imply that the luminosity of galaxies L depends, although in a mild way, on the velocity dispersion . Such ideas can be draw back to Brosche [96], who first suggested a failing of the simple law of star formation Schmidt [97], based only on the gas density , favoring a scenario in which star formation is a function ∼, where v is the velocity of stars and is a variable parameter. The stars born in large gas aggregates have a characteristic velocity that depends on the physical condition of the galaxies during the star forming event (collapse, shock, merging, etc.). For this reason the global star formation and consequently the total luminosity of galaxies might keep a memory of the velocity of this gas, and later on, of the velocity dispersion of its stars. This opens the possibility of a “physical” connection between L and , leaving to the classical FJ relation the meaning of a “translation” of the relation, obtained substituting the mass M (difficult to measure) with the luminosity L (easy to measure).
When we leave the domain of ETGs we discover that L and correlate also in other physical contexts. It is well known that in young massive star clusters, where giant extra-galactic HII regions exist, a correlation between luminosity and width of the emission lines is observed; this is the L() − relation [98] between the luminosity of the Hβ line and the velocity dispersion of the HII gas. The scatter in this relation is small enough that it has been used as a distance indicator [99,100,101,102,103,104]. One key property is that, when the mass of the young cluster increases, both the number of ionizing photons and the motion of the ionized gas increase. The HII feature in the optical spectrum is visible out to z∼3.5 and, according to Koo et al. [105] and Guzman et al. [106], a large fraction of compact star-forming galaxies at an intermediate redshift have a similar L() − of local galaxies. Bordalo and Telles [102] explored the correlation and its systematic errors in the redshift range (), concluding that something close to a power law () is observed when objects with Gaussian emission line profiles are considered. The root mean square (rms) scatter they measured is ∼0.30.
It is important to emphasize that the L() − relation observed at high redshift is that of a young burst of star formations and not of the whole parent galaxy. The size of the star-forming region enters, in fact, as a second parameter in the relation, as well as the emission-line equivalent width, the continuum colour, and the metallicity, which also contribute to produce a small rms scatter (). The coefficients derived from the best fit of the relation are very close to the expectation of the virial theorem, as in the case of the relation observed for ETGs. At the same time the total amount of stellar and ionized gas mass2 is similar to the dynamical mass, suggesting that gravity is the main mechanism behind the broadening of the emission lines in these young clusters.
2.2. The AGN
In the context of AGN research, a similar relation is observed when the intensity of the Hβ line, emitted in the broad line region (BLR) around the central black hole, is correlated with the full width, half maximum, or with the velocity dispersion of the gas). This correlation is observed for a particular class of quasars, the xA, that radiate at extreme along the quasar main sequence [9]. Accretion disk theory predicts for these objects a low radiative efficiency at a high accretion rate and a ratio converging toward a limiting value [49,107,108]. The inner part of the disk is puffed up by radiation pressure, while the outermost one remains geometrically thin. This change from the standard thin disk provides two key elements for the BLR structure: the existence of a collimated cone-like region, where the high ionization outflows might be produced, and the shadowing of the outer disk where low-ionization emission lines form [109]. The low-ionization emitting region may therefore remain shadowed from the intense radiation field that is associated with the continuum observed if the line of sight is not too far from the polar axis, and the velocity field stays unperturbed.
The self similarity of the xA spectra permits an easy identification of these sources up to z∼, making the relation of quasars a powerful cosmological probe [110,111,112]. xA quasars satisfy three conditions: (1) a constant Eddington ratio , close to the Eddington limit; (2) the assumption of virial motions for the low-ionization BLR, so that the black hole mass can be expressed by a virial relation; and (3) the spectral invariance. For xA the ionization parameter U can be written as [15], where is the number of hydrogen ionizing photons. U has to be approximately constant, otherwise we should observe a significant change in the spectral appearance. The three constraints make it possible to derive a relation between the line width (the FWHM of the H broad component is expressed in units of 1000 km s−1) and luminosity:
where depends on the square of , the ionizing range of the spectral energy distribution, and a parameter directly derived from the UV spectra, the product density times ionization parameter that has been scaled to the typical value cm−3 [113,114,115]. Until now, the FWHM of the H broad component and of Aliii1860 have been adopted as virial broadening estimators [116,117,118]. Equation (1) implies that a simple measurement of the FWHM of a low-ionization line yields a z-independent estimate of the accretion luminosity (c.f. [8,9]). The virial equation has been applied to xA quasars only (∼ 1), although in principle it could be useful for all quasars with known , provided a suitable emission line broadened by virial motions is used for the luminosity computation. Potentially, the virial equation can be considered for all xA quasars distributed over a wide range of luminosity and redshift, where conventional cosmological distance indicators are not available [117,118,119].
The virial luminosity equation of AGN is therefore very similar to the FJ law of ETGs and HII regions. Why does L correlate with approximately in the same way in so different a context? The aim of this work is to try to find a possible answer to such a question. In particular, we will analyze the relation in galaxies and AGN, discussing the properties of the observed relations in both contexts and providing a uniform view of the FJ correlation. In particular, we will discuss the origin of the slope/scatter of the relation and the presence of a curvature in the observed trend. Finally, we will argue why a similar slope is observed in systems that are so different.
3. The Relation of ETGs
In this section we thoroughly discuss the case of ETGs, first presenting the observational data in use, the relation, and the revised presenting the so - theory and discussing the great advantages offered by it in the interpretation of the Fundamental Plane and all its projections on 2D planes such as , , , etc.
3.1. The ETGs Data Sample in Use
The observational data for the ETGs are those extracted from the WINGS and Omega-WINGS databases [120,121,122,123,124,125,126,127,128,129]. The WINGS and Omega-WINGS datasets are two optical surveys of nearby clusters (). The databases include a large amount of information: galaxy magnitudes, morphological types, effective radii, effective surface brightness, stellar velocity dispersions, star formation rates, etc.
The data used here are: 1. The velocity dispersion of ∼1700 ETGs, already used by [130] to infer the properties of the FP; 2. A new set of derived by [131] for the dwarf ETGs (∼20 objects); 3. The luminosities, the effective radii, and the effective surface brightness in the V-band of several thousand ETGs derived by [131] with the software GASPHOT [132]; 4. The distance of the galaxies derived from the redshifts measured by [122,127].
The errors on the photometric parameters are always . The values of were measured within a fixed aperture of three arcsecs and come from the SDSS and NOAO databases. One might question if the results we obtain depend on such an aperture, and change using a velocity dispersion averaged within the effective radius (temporarily indicated as ) instead of (measured in the central region). The values of and are known to be related to each other by the relation (see for details Busarello et al. [133], Busarello et al. [134]), so the net effect of such a change is a systematic variation of the slope and the proportionality factor of the FJ, while the scatter of the relation remains nearly the same. In other words, such a systematic effect does not alter our conclusion about the curvature of the FJ slope between bright and faint ETGs.
In this work we have chosen to represent with different colors three different samples of objects: the black color marks the dataset of brightest (BCGs) and second brightest ETGs (2ndBCGs), both brighter than ; the red color marks the sub-sample of the WINGS ETGs for which both stellar mass and velocity dispersion are available. These are generally objects fainter than . The sample also includes the dwarf ETGs analyzed by [131]; the gray color marks the data-set of ETGs used by D’Onofrio et al. [130] for the analysis of the FP properties. They span a large range of luminosities.
In addition to real data, we have used the artificial data of the Illustris simulation (see, e.g., [83,135,136]). This dataset contains ∼2400 galaxies and is marked in all plots by yellow dots. A full description of these data is given in [128,137]. We used the run with full-physics (with both baryonic and dark matter) having the highest degree of resolution, i.e., Illustris-1 (see Table 1 in [83]), extracting the -band luminosities of the galaxies, their mass, velocity dispersion, half-mass radii of the stellar particles, morphological types, etc. The projected light and mass profiles of ETGs have been studied in the paper of [137], who computed the effective radius (Re) the effective surface brightness , the best-fit Sérsic index, and the line-of-sight velocity dispersion .
The Illustris-1 models are known to be in conflict with the real data in the case of the effective radius [10]. However, a careful comparison with the WINGS data showed that they nicely reproduce the tail of the plane and the tail of the − relation of the bright ETGs. They fail instead to reproduce the location of dwarf galaxies (masses in the interval to ) on both planes. The relatively larger radii of these latter galaxies can be easily explained as an indirect effect of recent mergers and galactic winds (see for more details [138]). The velocity dispersion of the Illustris models, on the other hand, are in good agreement with the observed ones, as well as the FJ based on them (see below). For all these reasons we feel safe in using the Illustris-1 models for the purposes of the present study.
3.2. The FJ Relation for ETGs
Figure 1 shows the relation of ETGs and simulated objects. Both samples span the same magnitude range from to , although real data and artificial models have a different richness. This is due to observational (WINGS) and computational reasons (Illustris). At low luminosity, WINGS suffers a deficit due to the difficulty of measuring , whereas at high luminosity Illustris has a deficit of high mass galaxies, being that the data were extracted from a limited number of clusters. The figure clearly confirms that the slope of the FJ relation for bright objects deviates from that of faint objects.
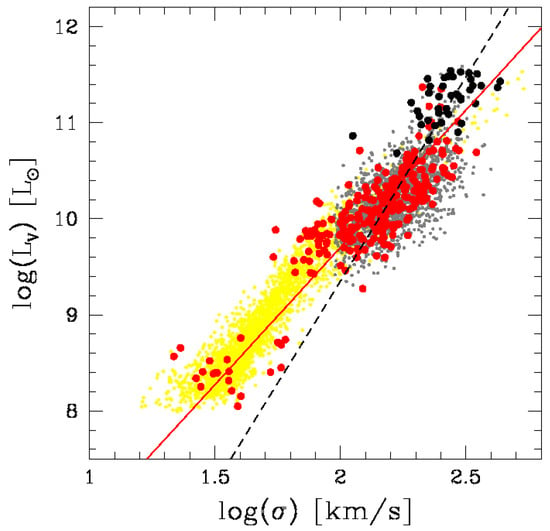
Figure 1.
The relation for ETGs. Black dots mark BCGs and 2ndBCGs. Red dots are normal ETGs with available stellar mass and velocity dispersion. The gray dots are the ETGs used by [130] to analyze the FP. The yellow dots are the parameters derived by [4] from the Illustris dataset. The red solid line is the fit obtained for the sample of ETGs less luminous than . The dashed black line is the fit obtained for the brightest cluster galaxies ().
The orthogonal fits marked by the red solid line and the black dashed line, obtained with the SLOPES software (Slope 3 Version 1) [139]), for the ETGs fainter and brighter than are reported in Table 1. The slope varies from to when we consider these two datasets. The whole rms scatter instead appears ∼ for both samples. Considering the contribution of the measurement errors we get an intrinsic rms of ∼0.07, in agreement with the previous literature.

Table 1.
The fits of the FJ relation for the bright and faint ETGs obtained using the WINGS data. The luminosity L is in solar units and the velocity dispersion in km/s.
Notably, the data of the Illustris simulation follow the same trend of real ETGs (although with a bit smaller scatter), with the exception of the bright objects that appears to follow the same trend of fainter galaxies.
As remarked in our Introduction, the correct interpretation of such a change of slope in the FJ relation should be searched for by looking at the whole trends observed in all projections of the FP. Figure 2 shows some of these projections3.
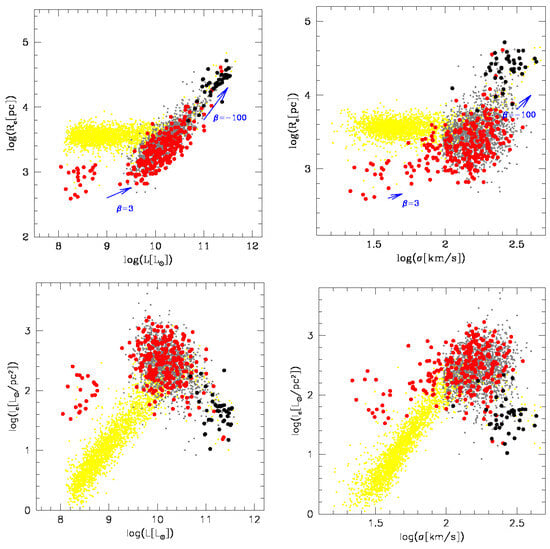
Figure 2.
Four different projections of the FP. (Upper left panel): the diagram. (Upper right panel): the diagram. (Lower left panel): the diagram. (Lower right panel): the diagram. Symbols and colors as in Figure 1.
The feature in common in all these diagrams is that all the relations are curved. The curvature occurs approximately at in all diagrams. Such bending implies that the distribution of galaxies in the FP is far from uniform or that we are seeing a curvature of the FP itself. Clearly the more luminous ETGs follow a different trend with respect to the faint objects. We will try a possible explanation of this behavior in Section 3.3.
It is important to note here that the simulated data fail to reproduce correctly the effective radius of many galaxies and consequently the effective surface brightness. This was already noted and discussed by D’Onofrio et al. [10]. The most probable reason for such a discrepancy is the difficulty of taking into account the correct amount of feedback from SNe events. The strong winds of gas from these explosions can determine a puffing-up of the galaxies.
The curvature appears more pronounced in the diagrams that involve the and parameters. Indeed, when we plot both such parameters we obtain the plane (Figure 3). Here the two populations of bright and faint ETGs form an acute angle. In this figure we used the whole database of ETGs measured for the WINGS sample. They are shown here by the small gray dots.
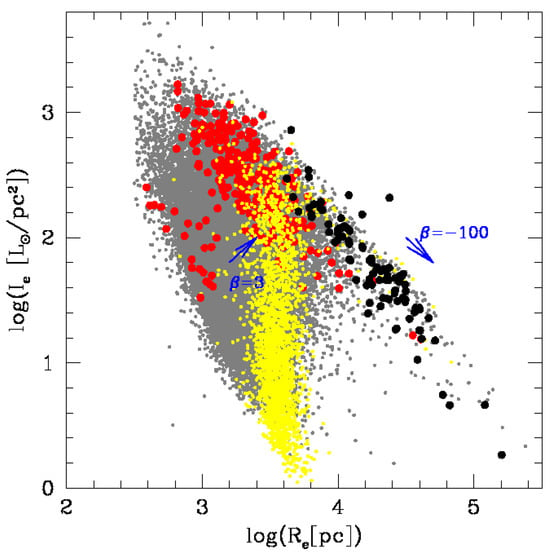
Figure 3.
The relation for ETGs. Black dots mark BCGs and 2ndBCGs. Red dots are normal ETGs with available stellar mass and velocity dispersion. The gray dots are the ETGs of the WINGS database measured with the software GASPHOT (∼20,000 ETGs) [125]. The yellow dots are the data of the Illustris dataset.
The peculiar distribution of Figure 3 was first shown by Capaccioli et al. [93], who suggested the existence of two different populations of ETGs, the ‘ordinary’ and the ‘bright’. This is a long debated question concerning the existence of two distinct channels of formation for dwarf and giant ETGs (see e.g., [140,141,142,143,144,145,146,147,148,149,150]).
Of great importance in this diagram is the presence of a Zone of Exclusion (ZoE), i.e., a region completely avoided by any object. In this plane, the existence of the ZoE was first noted by [92,151] using the k-space version of the FP. The distribution of ETGs appears indeed limited in the maximum surface brightness at each . The slope of this line of avoidance is close to (when is units), i.e., the slope predicted by the Virial Theorem (VT) [10].
This feature is present in every diagram involving and . It is in fact easy to observe that in the and planes galaxies appear limited in the maximum luminosity that can be achieved at each radius or surface brightness. The slope of such ZoE in these cases is again the value predicted by the VT, i.e., that of the dynamical equilibrium of the stellar system.
3.3. Discussion of the Stellar FJ
There is a large consensus today that the steeper slope of the FJ relation at high masses is due to the different evolution of ETGs at different mass ranges. An attempted explanation invoked the evidence that high-mass galaxies are preferentially “core” ellipticals, whereas intermediate and lower mass objects are generally “core-less” [55,152,153]. The transition occurs at ∼. Core ellipticals have boxy isophotes and are slow rotators, while core-less ellipticals have disky isophotes and rotate faster [55,56,152,153,154,155]. This picture is consistent with the systematic variation of the total mass profiles in the central region of ETGs [156], with more massive galaxies having shallower mass profiles. In this framework the change of slope is the result of the relative efficiency of gas cooling and feedback in ETGs at different mass scales. The cooling of gas allows the condensation of baryons in the central regions, and consequently an increase in the central concentration of mass [157,158,159,160]). Dynamical friction and SNe/AGN feedback, in contrast, are a source of heating, decreasing the central density concentration [160,161,162,163,164,165,166]).
The explanation that we propose here is instead totally different. The starting point is the law proposed by [4]. The interesting fact in this relation is that it is completely independent from the VT, i.e., it is not a replica of the classical FJ relation. As a consequence, one can put in a system the scalar virial law and the law. After some algebra, it is quite easy to get the following equations:
where is a factor that depends on , , , and (see for details [4]. This equation give the slope in the plane as a function of .
Another combination gives:
which gives the slope in the − plane as a function of .
In addition, we have:
which gives the slope of the relation, and finally
which gives the slope of the relation.
Table 2 list the observed slopes in these diagrams for different values of . You can also appreciate the predicted slopes, marked by blue arrows in the above plots. They represent the direction of motion of a galaxy in the FP projections, when is equal to 3 and , two extreme cases that correspond, respectively, to an object with active star formation and an object in a passive quenched state, in which the luminosity decreases at a nearly constant .

Table 2.
The slopes in the log form of the , , , and planes for different values of .
Having demonstrated that the combination of the VT and law is the key to interpret the different aspects of the FP projection, we can also easily show that such behavior is necessarily present in the FJ plane. Starting from the VT:
when the luminosity is substituted to and , one obtains two different trends:
This occurs because scale as over the whole mass range, while follows two different trends at the low and high mass ranges. In particular, we derive that at the low masses and at the high masses. The slopes in log units are therefore very close to that observed. Clearly a small difference in the relation can fit exactly the trends derived from the fits. The curvature of the FJ is, in conclusion, due to the role played by luminosity and the mechanism producing such curvature is the same in all the projections of the FP.
We can summarize arguing that the different condition of evolution in galaxies of different masses are the main aspect responsible for the observed distribution in all the projections of the FP. Passive and quenched objects are very close to the virial equilibrium and therefore follow a path close to the ZoE consistent with the slope predicted by the VT. In addition, the converging values of the slopes obtained in each plane, when diverges to extremely negative values (pure passive objects), naturally determines the existence of the ZoE, easily visible in many of these diagrams. No object can overcome the ZoE, because the coupling of the VT and the law constrains all passive virialized systems to move along the same direction (parallel to the ZoE).
4. The of AGN
4.1. Populations of AGN
The Eigenvector-1 correlation technique permitted the definition of two populations of luminous type-1 AGN. Population A sources have been identified as the type-1 AGN encompassing sources above a threshold value ∼ up to super-Eddington candidates with the maximum (e.g., [9,167,168,169,170]), i.e., in the range . The observational selection criterion for low-z samples is FWHM H km s−1, although one has to consider that the limit ≈ 4000 km s−1 is luminosity dependent if it is intended to mark a fixed [171]. The low-ionization emission lines (LILs) such as the Hi Balmer lines, Mgii are thought to be emitted by gas, mainly following a virial velocity field (and references therein [15,24,172,173]). This is not to say that the BLR of Population B—characterized by —is not virialized. There is strong evidence that the line broadening is predominantly virial [172], with increasing width and ionization for lines whose emission is weighted closer to the central black hole. In addition, Pop. B’s high-ionization lines are less affected by outflow motion, instead giving an overwhelming contribution to high-ionization lines such as Civ1549 especially in extreme Population A sources (e.g., [20,174,175,176,177]). The presence of an extended red wing in the H and other line profiles, even if due to gravitational redshift [178,179,180,181,182,183], is also ultimately consistent with a virial velocity field. We focus on Pop. A because these sources are believed to be more representative of high-z quasars [14]: Pop. B sources are more prone to selection effects at high-z because of the lower Eddington ratio [184]. The exploration of a FJ-like for Pop. B is deferred to future studies.
4.2. Virial Estimates
The following subsections discuss at first H and subsequently Aliii1860 scaling laws that are (1) relying on measurements of the H line dispersion (Section 4.3), and (2) relaxing the assumption of strict equivalence with Vestergaard and Peterson [22] (Section 4.4). Both relations entail assumptions that make them more speculative than the ones presented in Marziani et al. [185], although they attempt to include corrections for the likely important effects of Eddington ratio and viewing angle that are not considered in the empirical relation entirely based on the FWHM.
The virial mass equation can be written in the following form:
where the virial factor is now a function of the viewing angle (the angle between the line of sight and the accretion disk axis) and is a function of both luminosity and [27,186]. Awareness of the dependence by and viewing angle has been growing in the latter years, and it is now imperative that some alternative strategies are devised to improve estimates to make them free of systematic effects as well as reduce the statistical noise down to the one expected from measurement errors of the observational parameters employed for the estimates.
4.3. Scaling Laws Based on H
Recently, Dalla Bontà et al. [187] pointed out that the dispersion from single-epoch observations could be the best estimator of the of the rms spectrum for sources studied with reverberation mapping. The could be used in place of the FWHM, as recommended by Peterson and Dalla Bontà [188]. This approach is made more difficult in the context of Population A sources, where line profiles are Lorentzian-like (e.g., [36,167,189,190,191]). However, accurate measurements are possible, especially for spectra recorded with high S/N or high-quality parameter . Appendix A.1 and Appendix A.2 summarize the measurements and introduce the parameter as a more proper uncertainty predictor than S/N evaluated on the continuum.
We considered a sample of Population A sources covering a wide range of redshift and luminosity (, [erg s−1] for which H, Aliii1860, and [Ciii]1909 emission lines were observed (Marziani et al. [185], hereafter [185]). For the H of this sample, we derive the following relation between the velocity dispersion and FWHM (left panel of Figure 4):
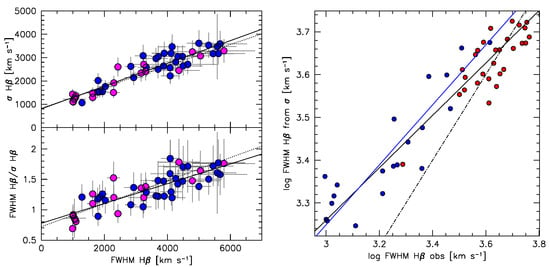
Figure 4.
(Left) vs. FWHM H (top) and FWHM/ vs. FWHM H (bottom) for the [185] sample. Magenta circles represent xA sources, while blue circles are Population A not xA (also indicated as à in the text). (Right) correlation between the observed FWHM H and FWHM H derived from the FWHMσ for our sample sources. The blue and black line corresponds to the data points within the same luminosity limits of Dalla Bontà et al. [187] (blue circles) and the full sample, respectively. Red circles are data points for sources whole luminosity is equal or above the luminosity limit of Dalla Bontà et al. [187]. The dot-dashed line is the equality line.
The measurements were carried out on the Hβ profiles of our sample spectra (corresponding to in Dalla Bontà et al. [187]).
In addition, a FWHM predicted on the basis of the measured , FWHMσ was obtained by isolating the Population A sources from Table 3 of Dalla Bontà et al. [187] to construct a relation yielding the FWHMM from . The procedure was similar to the one of Dalla Bontà et al. [187] and involved the exclusion of outlying points with a 2.6 clipping criterion4. The resulting relation applied to our data is (Figure 4, right panel):
A word of caution is that the highest luminosity covered by Dalla Bontà et al. [187] is [erg s−1]. The majority of our sources (red circles in Figure 4) are above this limit. The FWHM predicted from the is larger than the observed one, especially for the narrowest H profiles: the constant term ensures that FWHMσ ≳ FWHM for all reasonable FWHM values; the largest mass estimates would be unaffected since FWHMσ ≈ FWHM if FWHM ≈ 7000 km s−1, an extremely large value considering the luminosity-dependent maximum FWHM for Pop. A sources [38]. This result is potentially interesting as it is likely that the narrowest profiles are the ones most affected by an almost pole-on orientation. The simplest use of Equation (12) would be to substitute it in the H relation of Vestergaard and Peterson [22]. The scaling law would then become:
where the luminosity at 5100 Å is in units of erg s−1, and the FWHM is in km s−1.
We now attempt to account for orientation and effects. The dependence of on the viewing angle has been parameterized by Mejía-Restrepo et al. [192] as (FWHM/4550)−1.17, and the dependence on the Eddington ratio by applying a correction to the standard scaling between and optical luminosity at 5100 Å [27,193], yielding
The main empirical correlate with the Eddington ratio is the prominence parameter [14,33,35,48,194]. A tight relation between and luminosity can be derived once is corrected using in place of . The following relation applies [27]:
yielding:
Equation (14) implies a significant increase in the values for the sources with the narrowest profile with respect to the scaling law of Vestergaard and Peterson [22]. One of the best-studied sources in the low domain M⊙ is I Zw 1. A recent estimate is M⊙ [195] assuming . The estimates using the Vestergaard and Peterson [22] H and the Aliii1860 and Civ1549 scaling laws are consistent with . They would imply a value for , as suggested by Collin et al. [196] for Population A, to be in agreement with Huang et al. [195]. Spectropolarimetric measurements are expected to provide estimates less biased from the viewing angle [197,198]. The estimate from the H polarization profile is log [197], in turn implying . In the case of Equation (14) there are two competing effects: on the one hand, the narrow H requires ; on the other hand, the high (log ) implies a significant reduction in the measurement, by 0.64. The value derived from Equation (14) for I Zw 1, log [M⊙], is consistent with the value derived from the spectropolarimetry.
The relation FWHM−1 may introduce a bias if applied to a broad range of FWHM: it neglects an intrinsic dependence on luminosity (or mass) of the line width. However, the FWHM-dependent correction on becomes negligible at high L, where FWHM ∼ 5000 km s−1, not unlike in the case of Equation (13). At high L, the dominating effect in our sample is the correction because of the Eddington ratio that implies . The largest estimates a decrease from log to 9.2 [M⊙] (Figure 5).
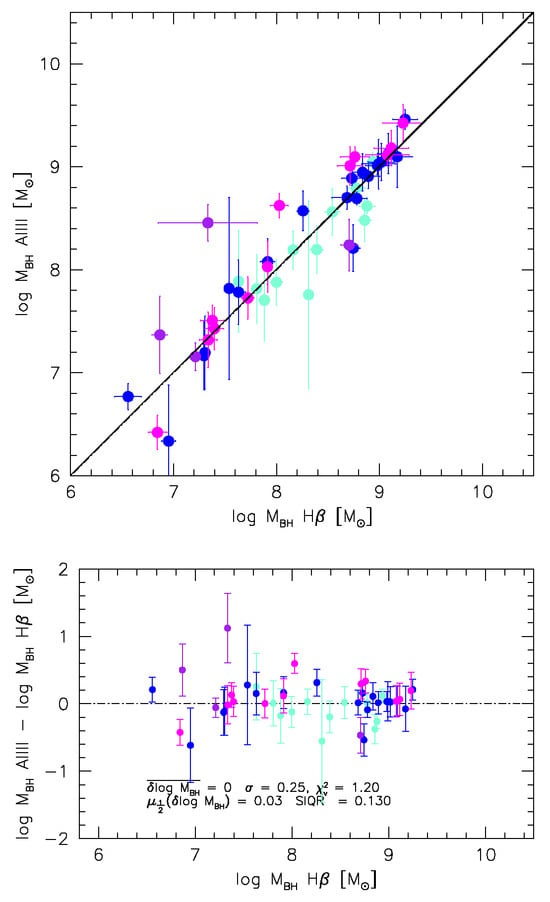
Figure 5.
Decimal logarithm of black hole mass in units of solar masses computed from the relation of Equation (14) based on FWHM H vs. the one computed from the Aliii1860 FWHM following Equation (20). The bottom panel shows the parameters related to the differences. Different colors identify sources belonging to difference spectral types in Population A, in order of increasing : A1 (cyan, ); A2 (blue, ); A3 (magenta, ); A4 (purple, ).
4.4. Two Aliii1860 Relations
4.4.1. -Derived Relation
Contingent to the data in Ref. [185], the Aliii1860 is observed at a lower S/N with respect to H. This implies that the Aliii1860 will be measured on a line whose wings are lost in noise, creating a bias in the relation between the velocity dispersion of the two lines. On the other hand, there is an empirical consistency between the FWHM of H and the one of Aliii1860. Presently, there is evidence that H might be predominantly emitted in the same flattened and virialized region (e.g., [199,200]), and that Aliii1860 might be emitted in a region largely co-spatial with H [201]. These lines of evidence suggest that orientation effects might be similarly affecting the two lines.
Even if an accurate measure of Aliii1860 is not viable, Equation (12) may still provide a way to correct for inclination effects if a correction is applied to both H and Aliii1860 FWHM and H and [Ciii]1909. The use of FWHMσ in place of the measured FWHM yields scaling laws that are formally very similar to the ones obtained for Aliii1860 and [Ciii]1909 FWHM (Equations (17) and (18) below), with a significant change in the low-end estimates by one order of magnitude:
Uncertainties have been estimated as described in [185], and the subscript means that the Aliii1860 and [Ciii]1909 FWHM have been “corrected” according to Equation (12). Note that for [Ciii]1909 the correction has to be computed first before multiplying the FWHMσ by . The application of the scaling laws to our data is shown in Figure 6.
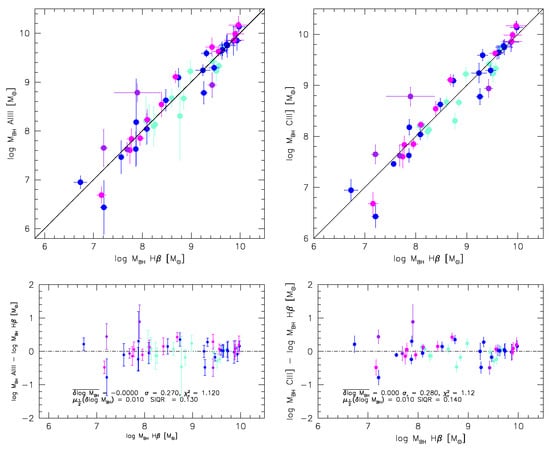
Figure 6.
Decimal logarithm of black hole mass in units of solar masses computed from the relation of Vestergaard and Peterson [22] based on FWHMσH vs. the one computed from the Aliii1860 FWHM following Equation (17) (left) and from the [Ciii]1909 following Equation (18) (right) with sub-samples identified by color according to their spectral types. The filled lines trace the scaling laws, while the dot-dashed line is the equality line. The bottom panel shows the residuals as a function of the derived from H. Average values of the log differences, standard deviation, and normalized are reported for the joint sample (top row). The bottom row yields the median and the SIQR.
The resulting scaling laws are qualitatively consistent with the one obtained in Section 4.3 for H, in the sense that both scaling laws predict an increase in at the low end of the range (Figure 5 and Figure 6), but differ little at the high end. The -based relation relies on the application of a highly uncertain correction, i.e., the relation shown in Figure 4 to the Aliii1860 and [Ciii]1909 widths. This cautions us to the use of Equations (17) and (18). A test against samples with fully independent estimates of the mass from the Vestergaard and Peterson [22] relation at low z is beyond the scope of the present work.
4.4.2. An Aliii1860 Scaling Law Equivalent to Equation (14)
Enforcing the equality condition (Figure 5):
between the estimated with Aliii1860 and with the H scaling law with orientation and corrections (Equation (14)) implies an Aliii1860-based provided by:
with an rms scatter . In principle, Equation (20) takes into account two effects that are likely to affect the dispersion and bias the results of the Vestergaard and Peterson [22] relation: the increased likelihood for the narrowest profiles to be affected by an almost pole-on view [200], and the dependence on the spectral type of the − L relation [27].
4.5. A FJ Law for Extreme Population A Type-1 AGN
We focus on a special sub-population involving the most extreme Eddington ratio () that may involve super-Eddington accretion [9,41,110,112]. Extreme Population A is defined by the strongest Feii emission with an optical and are at one end of the quasar Eigenvector 1/main sequence ([33,40], see [37,168] for reviews).
The xA quasars offer a potential luminosity indicator (as do spiral galaxies, following the Tully–Fisher law): the luminosity should be proportional to the 4th power of the virial FWHM: . A difficulty here is more to relate the accretion luminosity to a distance indicator free from anisotropic effects and uncertain corrections, starting from observed fluxes. The xA quasars, however, may provide a class of luminosity indicators (also dubbed as “Eddington standard candles) covering cosmic epochs from almost present day up to less than 1 Gyr from the Big Bang, well beyond the limits of optical cosmological distance indicators such as supernovæ [9,116,118]. The H observations might be difficult in correspondence of , due to strong sky emission emission in the red and near IR. At higher redshift, round based observations are possible only within the J, H, K, …bands, where atmosphere is not opaque to the frequency of the incoming radiation. Apart from these limitations, the redshift distribution could be extended up to 3–4. The importance of covering the redshift rests in the fact that, above this limit, the effects of the energy density of matter are dominant. In addition, data in the broad range have the potential to assess the equation of state of dark energy as a function of redshift [109,110,117,202]. Preliminary applications were carried of the “virial luminosity’’ equation to the Hubble diagram have been promising [9,116,118]. The coverage of the redshift range between 1 and 3 allows for a good precision in the estimate of higher than optical surveys of supernovæ [9]. Intermediate redshift quasars and supernovæ could be said to provide “ortogonal” information: tight constraints on and loose constraints on , and the converse for quasars [118].
The virial luminosity equation derived by Marziani and Sulentic [9] can be written in the form:
where the energy value has been normalized to 100 eV ( Hz), is the fraction of bolometric luminosity belonging to the ionizing continuum scaled to 0.5, the product () has been scaled to the typical value cm−3 [113,114,115], and the FWHM of the H BC is expressed in units of 1000 km s−1. The is scaled to the value 2 following the determination of Collin et al. [196]. The FWHM of H broad component and of Aliii1860 are hereafter adopted as a virial broadening estimator. Equation (21) implies that, by a simple measurement of the FWHM of a LIL, we can derive a z-independent estimate of the accretion luminosity ([9], c.f. Teerikorpi [8]). The constant can be determined from the best fit of the Hubble diagram. It is sample dependent, in the sense that different samples as considered in the following (Section 4.7) might be affected not only by slightly different intrinsic properties (right hand of Equation (21)) but also instrumental factor such as different light losses or aperture effects (for example, SDSS aperture spectroscopy vs. narrow long slit spectroscopy). The has been found in the range erg s−1.
To achieve a calibration of Equation (21) suitable for precision cosmology, however, several issues related to the factors entering in its right end should be resolved: the foremost is the non-virial broadening of the emission lines. Continuum emission of quasars is also not isotropic, although model predicts that the dependence on the viewing angle should be very modest till ([109], and references therein). The constant of proportionality between L and FWHM depends on SED parameters [9], and it is not as yet clear if the SEDs are all consistent, and X-ray spectral slopes have a small scatter [203,204,205]. By the same token, the product Hydrogen density times ionization parameter is not expected to be exactly the same for every xA source. It would not be a surprise to find a dependence on or chemical abundances [113,206]. Nonetheless, a large sample of inter-calibrated rest frame optical and UV ranges would make it possible to estimate the virial broadening, and hence the distance modulus over a wide range of redshift. In turn, an estimate of independent from all other methods as yet employed would become possible.
In the following, the focus is on the possibility of using the velocity dispersion as an alternative virial broadening indicator, that would be less affected than the FWHM from orientation effects [187,207,208].
4.6. Velocity Dispersion Measurements for Extreme Population-A AGN
To this aim, we measured the velocity dispersion on a sample of 133 AGN largely overlapping with the one of Negrete et al. [200]. Measurements were carried out as described in Appendix A.1. Figure 7 shows the relation between the and the FWHM for the xA sources of Negrete et al. [200], computed as for the [185] sample of generic Population A quasars (Figure 4). The relation resulting from an unweighted least square fit are:
roughly consistent with the ones of Population-A as a whole (Figure 4).
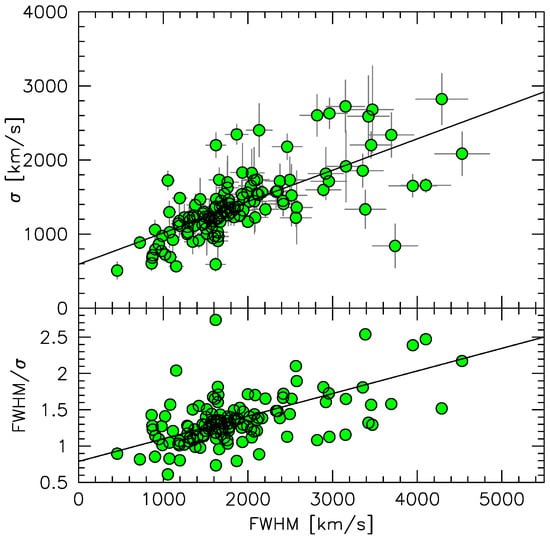
Figure 7.
Relation between FWHM and for the xA sample of Negrete et al. [200], as for the [185] sample of Figure 4.
4.7. The Hubble Diagram
xA
We applied the measurements of the to the derivation of the redshift-independent luminosity (Equation (21)). The comparison is between estimates of distance modulus from FWHM and (Figure 8), taking as a reference the distance moduli computed for “concordance cosmology.” The middle panel of Figure 8 overlays the residual in distance modulus with respect to concordance, and shows that the FWHM-based measurements provide a significant bias in the estimate, with the best fitting line significantly different from 0. This is due to a luminosity dependence on the FWHM that is much shallower than the one expected for the virial relation (FWHM ). The limited scope in luminosity of the Negrete et al. [200] sample, along with large scatter and a statistical bias (fewer data points are available in correspondence of the lowest and highest line widths; inset in the top panel of Figure 8) might be at the origin of the problem. The unbiased range in FWHM shows a trend consistent with a slope 4 in the vs. logFWHM (steeper line in the inset). The bias visible in the middle panel is due to the H line profiles at higher redshift being significantly narrower than the expected values, resulting in lower luminosity estimates, and hence in lower values. The trend is not improved if measurements are restricted to (bottom panel). The bias is intrinsic to the data, as it is present for both FWHM and and, like the large scatter, might be associated with orientation effects: Negrete et al. [200] explained all discrepancies between the virial luminosity and the one expected from the concordance model to orientation effects due to virial factor in the form of Equation (26). The effect of orientation will be discussed in Section 4.8.
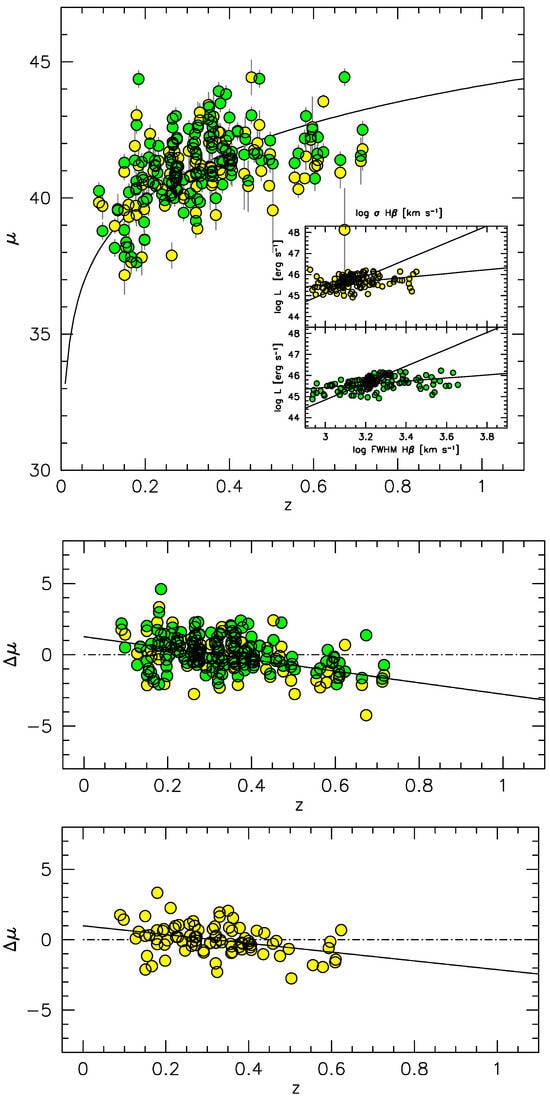
Figure 8.
Top panel: Hubble diagram vs. z using velocity dispersion measurements (yellow) and FWHM (green) for data in the sample of Negrete et al. [200]. The inset shows the relation between luminosity and , and luminosity and FWHM for the same sample. Middle: residuals vs. z. Bottom: measurement residuals, with restriction to .
Generally speaking, the luminosity values predicted from FWHM in samples of modest size are within the scatter expected from larger samples. Indeed, a sample including 200 xA objects for which H FWHM measurements are available, covering redshifts from 0 to provides results in agreement with the concordance cosmology (Figure 9). A linear fit to the residuals yields
consistent with slope 0. If the objects from [185] discussed in this paper were removed, the slope would be , perfectly consistent with no bias with respect to concordance cosmology. The deviation introduced by the new sample is within the statistical uncertainties. Less clear if the large deviation observed from the measurements can be referred to statistical fluctuations or rather to an intrinsic phenomenon, due also to the increase of the FWHM/ ratio as a function of FWHM. Figure 10 emphasizes the consistency between the average (z) computed from the H line broadening (the data are the ones of Figure 9): it provides a sound proof that the H lines is emitted by a predominantly virialized system (within the framework of the assumption made in the formulation of Equation (21)). Some of the deviations from the (z) predicted by standard cosmology are appreciable also in the averages of Figure 10. It is imperative to populate the Hubble diagram with high quality H observations allowing for accurate deblending of the line profiles and estimates of both FWHM and to better study the evolution of the FWHM/ ratio as a function of luminosity, at least for xA and the non-xA Population A independently.
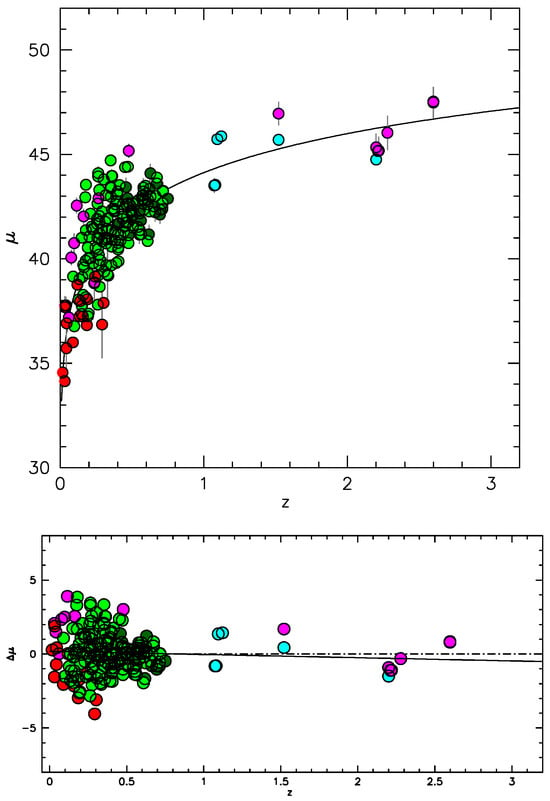
Figure 9.
The Hubble diagram using velocity FWHM H only. Various samples presented in Dultzin et al. [116] are included: red Du et al. [170], green Negrete et al. [200], dark green Marziani et al. [209]. Cyan data points represents the xA quasars of the HEMS survey [38], magenta the sample analyzed in this paper [185].
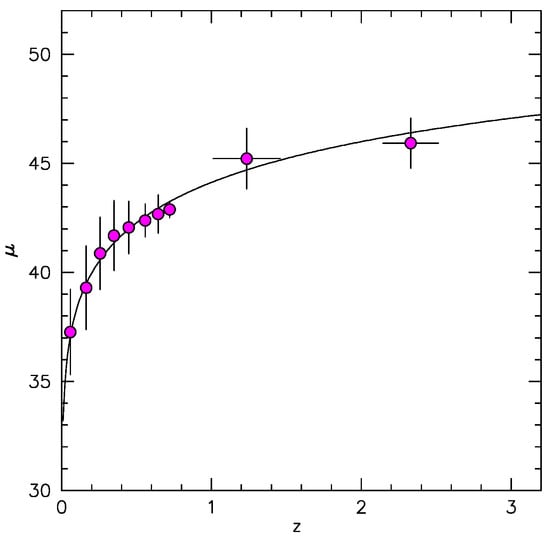
Figure 10.
The Hubble diagram using all the H FWHM measurements of xA quasars (magenta), averaged over 10 bins in redshift (c.f. [117]).
4.8. Orientation Dependent Luminosity-Line Broadening Relation
The effect of orientation can be quantified by assuming that the line broadening is due to an isotropic component + a flattened component whose velocity field projection along the line of sight is :
The structure factor in the Equation (9) is set to since Collin et al. [196] derived values for 2.1 for Pop. A, with a substantial scatter. If we considered a flattened distribution of clouds with an isotropic and a velocity component associated with a rotating flat disk , the structure factor appearing in Equation (9) can be written as
which can reach values if , and if is also small ( deg). The assumption implies that we are seeing a highly flattened system (if all parameters in Equation (9) are set to their appropriate values); an isotropic velocity field would yield .
The virial luminosity equation may be rewritten in the form:
where is the true virial luminosity (which implies ) with , since was scaled to .
An immediate application of the relation is the ability to recover the distribution of a sample of xA sources, assuming a particular cosmology (in practice a “standard" cosmology with km s−1 Mpc−1). The values that are obtained cannot be used for cosmology, since a given cosmology has been assumed. However, the distribution is by itself only slightly dependent on cosmology, with a modest change of the estimated viewing angles (Figure 11). This paves the road to the inclusion of correction for viewing angle by using the distribution of as a prior, or by applying a random correction to the FWHM value.
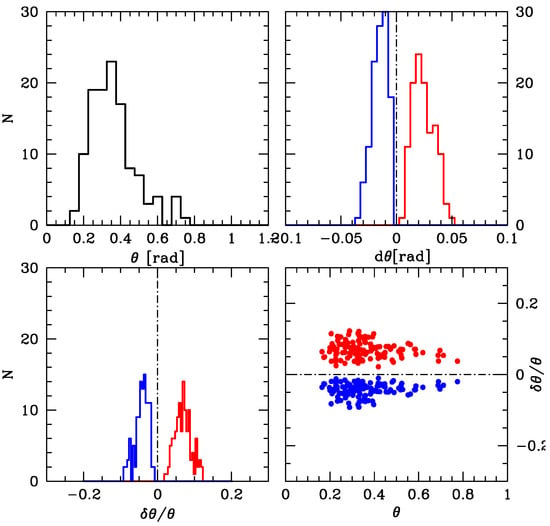
Figure 11.
Top left: Distribution of viewing angle for concordance cosmology from the sample of Negrete et al. [200]. Top right: differences in values for two extreme cosmologies, = 1.0, = 0.0 (red) and = 0.0, = 1.0 (blue). Bottom left: same as top right, for relative difference . Bottom right: vs. .
The resulting distribution of (Figure 11) is reasonable considering the constraints imposed by unification models for type-1 AGN [210,211], with 40, and maximum likelihood at . R. If the distribution is assumed isotropic, we expect . A trend like this seems to be followed up to , meaning . For larger , the detection of the sources – and their inclusion in color-based surveys—might be disfavored by the anisotropic emission of the geometrically thick torus that is expected in sources accreting at super-Eddington rates [112], and by the presence of a dusty obscuring torus that would suppress the view of the BLR at angles , according to the unification schemes [210].
Assuming the “standard” cosmology, Equation (26) can be computed for individual objects. The missing parameter in the computation of the virial mass (Equation (9)) is then that can be computed from a scaling law (most notably, the one of Martínez-Aldama et al. [193] that includes a correction because of the dependence in the relation ). Alternatively, via a photoionization method, if the UV rest frame spectrum is available [115,212]. To check the reliability of the method, a comparison with reverberation mapping results should be carried out [213,214]. This comparison goes beyond the scope of the present paper and is in preparation.
Population A
The xA sources are relatively rare in optically selected samples, with a prevalence [173]. In view of a possible exploitation of the line width as a luminosity indicator, it is worth exploring the possibility of an Hubble diagram based on H for the full Population A. The Population A sample of [185] covers a much wider range in luminosity than the one of Negrete et al. [200], and the relation between L and FWHM is dominating over the large scatter of individual measurements. Figure 12 shows the relation between luminosity and (top panel) and between luminosity and FWHM (bottom) for the generic Population A (less the xA, blue circles, and labeled as ) and for a subsample of 16 xAs.
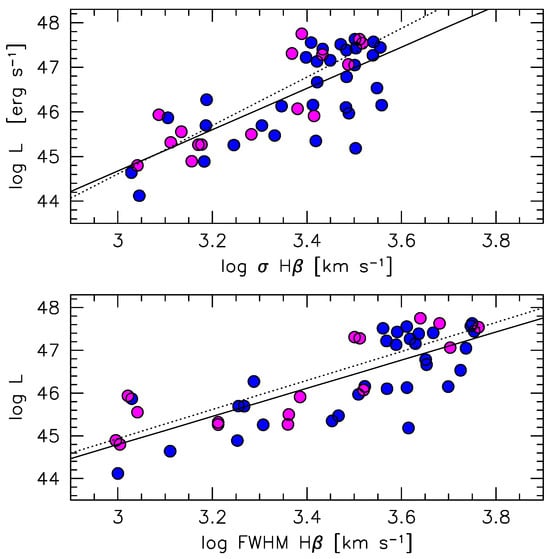
Figure 12.
Relation between bolometric luminosity and (top) and FWHM H (bottom) for the sample of Population A sources of [185]. The line is the result of an unweighted least square fit. The line is the result of an unweighted least square fit: filled for xA, and dotted for the generic Population A (less the xA, blue circles, and labeled as ).
The resulting trends
are all consistent with within confidence level. The scatter is larger for Pop. Ã (32 sources, excluding xA), and for the -based luminosity estimates. Figure 13 shows the Hubble diagram based on the virial luminosity from and FWHM. Pop. Ã data are affected by more severe biases; and the estimates deviate strongly from the prediction of concordance cosmology. It is as if the line fails to grow with luminosity: in this case, a lower implies a lower luminosity and hence a smaller distance modulus: the source being fainter, for the same optical flux it has to be closer. The effect depends on , and is present also for the FWHM-derived values. However, the result is more severely biased if is used to estimate the luminosity: vs. for vs. FWHM (lower panels of Figure 13). The slope of the residuals is not changing if is adjusted to reproduce the high-z range. The origin of this behavior may be residing in the line broadening mechanism: if the line wings are significantly affected by electron scattering [215], the width should be set by the electron temperature of the scattering plasma, not by the velocity field of the emitting gas. On the converse, the broadening of the core of the line might be more closely associated with the velocity and better sampled by the FWHM.
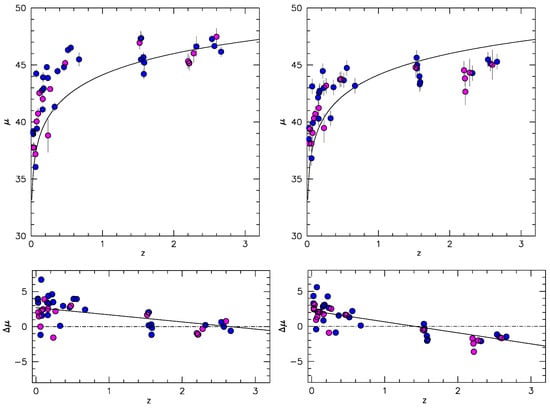
Figure 13.
Hubble diagram for the sample of [185]. (Left): distance modulus estimated from FWHM; (right), from . , for both FWHM and .
5. The Law for AGN
At this point an interesting issue to examine is whether the vision developed for ETGs by means of the theory (proportionality constant and exponent varying with time for any object and from object to object) can be extended to AGN, despite the completely different astrophysical context. To do this, we derived an estimate of the main astrophysical parameters involved in the scaling relations typical of ETGs (e.g., L, M, , , , etc.) also for AGN. We used the radius of the BLRs, their luminosity, their gas mass, and the measured velocities of the gas derived from the FWHM of the emission lines. With these values, the equations of the virial theorem and the variable were solved to derive and and . The four panels of Figure 14 show the key scaling relations among the main parameters, that is the plane (left upper panel), the plane (right upper panel), the plane (lower left panel), and finally the plane (lower right panel) both for AGN (red dots) and ETGs (black dots). The inspection of the various panels reveals that ETGs and AGN behave in similar way but differ in some important details. While ETGs and AGN have comparable luminosity (the latter ones are indeed as luminous as the brightest ETGs or even brighter) their surface brightness is much higher than that of ETGs (by more that twelve orders of magnitude). This can be easily explained by the much smaller dimensions of the emitting regions in AGN ( pc). Furthermore, both AGN and ETGs follow a relation, the slope of which gets steeper at increasing luminosity. In addition, the plane (right upper panel), the plane (lower left panel) show similar trends, but for the large difference in the of the two groups. Finally, some comments on the values of in the two groups are mandatory. In ETGs the velocity dispersion measures the random motions along the three coordinate directions of stars in virial equilibrium within the galaxy gravitational potential well. In AGN there are two components, namely random motions in the overall gravitational potential well combined with circular motion of gas in the central region of the disc spiraling in around the central black hole. Looking at the mean values of of ETGs and AGN brighter than about we estimate in between 1/3 to 1/6. For the sake of consistency, when plotting some variable (e.g., L or ) as function of (bottom and top left panels of Figure 14) one should apply this correction to the data for AGN to compare them with ETGs. Finally, the bottom right panel of Figure 14 displays versus plane for ETGs (black dots) and AGN (red dots). Apart from the effect of large difference in , AGN yield βs spanning very large both positive and negative values. Small values of seem to be absent in AGN. The large values of seem to suggest that also AGN are in state of virial equilibrium. It is beyond the aims of this study to investigate further the physical implications of the parameter in the case of AGN. We limit ourselves to call attention on this important issue and leave it to future investigation.
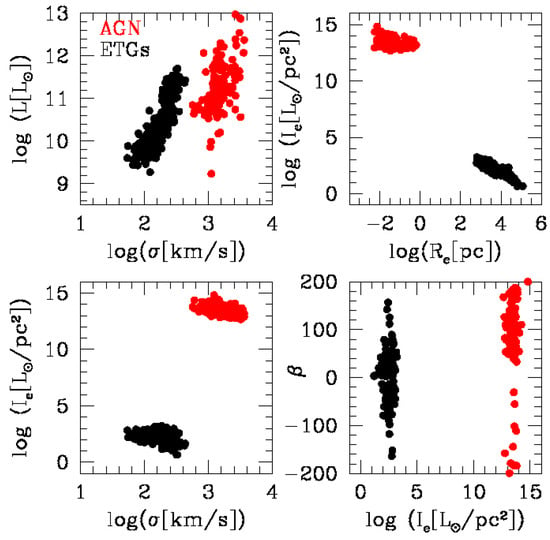
Figure 14.
Comparison between the scaling laws of ETGs and AGN. (Upper left panel): the plane. Red dots mark AGN, black dots ETGs. (Upper right panel): the plane. (Lower right panel): the plane. (Lower right panel): the plane.
The remarkable similarity of the scaling laws of AGN and ETGs spurred us to analyze the distribution in the plane of different astrophysical systems. Figure 15 shows the relation for five different kinds of objects: Galaxy Clusters, AGN, ETGs, Dwarf galaxies and Globular Clusters. The data have been extracted from our previous studies on this subject see e.g., [4,10,216]. In the figure the velocity of the AGN has been scaled to of measured value to correct it for the effect of the ordered circular motion around the central black hole. It is impressive to see that over an enormous range of luminosity the distribution of all systems is very similar. Apart from small deviations, that anyhow demand an explanation, a linear trend in log units between luminosity and velocity dispersion is found.
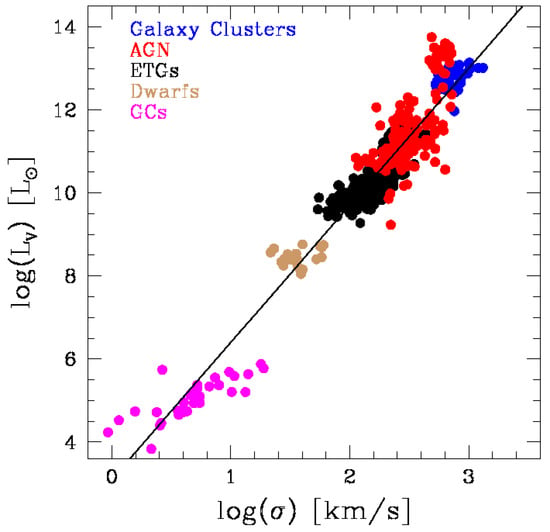
Figure 15.
The relation for different systems. In this plot the velocity of the AGN systems has been scaled down, considering that only of the measured velocity can be attributed to random motions.
Such similarity of behavior finds its basic explanation in the virial theorem. At all scales the virialized systems vary in the same way with the mass. Since the light L is a proxy of the mass, this is not a surprise. The real interesting physics is hidden in the peculiar deviations from such a linear trend. When L varies for other causes (e.g., scattering, quenching, induced star formation, merging, etc.) that are mass independent, the variations reflect peculiar physical phenomena that are not taken into account. The framework is a first step toward this wider context by providing additional degrees of freedom with respect to the simple luminosity-mass dependence. It is indeed an important tool to understand the evolution of objects in the hierarchical scenario.
6. Summary and Conclusions
In this critical review, we have reported on the scaling relation between the luminosity and velocity dispersion in two groups of objects with very different properties such as ETGs and AGN. For both groups we surveyed several basic aspects of scaling relations with particular attention to recent developments, calling attention on the many point of similarity. In the case of ETGs, we have also reported on the recent revision by [10] of the classical FJ relation (), in which the proportionality factor and exponent are let vary with time and from object to object thus taking explicitly into account the temporal evolution of the correlation between luminosity and velocity dispersion caused by many physical processes during the life of each individual galaxy (e.g., natural evolution of the stellar populations changing their luminosity, different efficiencies of star formation, both spontaneous and induced by mergers, causing sudden variation of the total luminosity, mass, radius, and velocity dispersion in turn, and so forth). The relation is replaced by where and vary from galaxy to galaxy and as function of time. The classical FJ relation is the mean of many different relations (one for each galaxy) at a fixed time, that is the present age (redshift z = 0). The combination of the Virial Theorem and allows us to determine the quantities relation and at any given time; the present for the galaxies in the local Universe and back in past for those at redshift . In this context the FJ relation has to vary with time.
Similar analysis has been made for AGN showing that also these objects follow a FJ-like relationship that is fully consistent with the classical FJ for galaxies (ETGs), the slopes are nearly the same. We have extended the concept of time dependent individual relation to the case of AGN and found results that are fully consistent with those of classical ETGs. Since in the case of AGN the velocity contains also a component due to rotation around the central black hole, we have estimated the rotational component and corrected the observational velocity to get the component relative to motions different from rotation, therefore fully consistent with dispersion velocity of ETGs. In such a case, the position of AGN in various diagnostic planes, e.g., L − , − , − − closely mimics that of ETGs. Finally, objects going from Globular Clusters, to Dwarf Galaxies, ETGs, and finally AGN seem to obey the same relation with minor deviations from it. Considering these objects span a luminosity range extending across about ten orders of magnitude, the result is very intriguing and demands further investigation.
The conclusions we derive from this analysis are as follows:
- Galaxies of all types share the FJ relation. The classical interpretation is that light L makes the role of mass M and that the correlation is generated by the virialization of the stellar systems. The different slope followed by bright and faint galaxies is likely an indication that the use of the light parameter L introduces a systematic difference for the two types of objects or that the degree of virialization is different. The scatter of the relation seems almost equivalent at all masses.
- In addition to the classical interpretation of the FJ relation, we have shown that it is possible to think at L and as variable mutually connected with the evolution experienced by every galaxy. Using indeed the relation with two free time-dependent parameters and , one can verify that the parameter enters in all the projections of the FP, providing the direction of motion of any objects forced by the evolutionary effects (e.g., mergers, accretion, star formation, etc.). Many characteristics features of the scaling relations can be understood adopting this “temporal” view of the FJ: the best example is the "zone of exclusion" (ZoE), the region empty of galaxies in the plane, that clearly have its origin in the fact that at large ’s galaxies can only move in a direction with slope .
- Regarding AGN, we have proposed several alternative scaling laws to estimate the black hole mass taking into account, at least tentatively, the effect of orientation and on the line broadening and on the BLR radius, respectively. The validity of these scaling law should be tested against derived from reverberation mapping and estimates of the obtained with photoionization method. In the near future, spectro-astrometry from GRAVITY holds the promise of estimate the BLR radius for hundreds of intermediate redshift AGN [217], much beyond the first (and already extremely valuable) estimates of the virial factor for low z AGN [218]. Simple scaling laws applicable to the huge influx of data coming from DESI, Euclid, etc. [219] will retain of course a value to permit straightforward mass estimates for samples that will be tenfold and more in size with respect to the ones available to-date. This might prove useful for cosmological applications [220], too. Figure 10 wants to emphasize the overall consistency of H distance moduli estimates by averaging over redshift bins.
- The virial luminosity equation for AGN is a reinstatement of a law that appears universal in the form , holding from stars to clusters of galaxies. In the case of AGN, the dominance of Keplerian motions and the restriction to a very limited range of for the xA sources imply a well-defined scaling between luminosity and FWHM or with exponent 4, analogous to the 21 cm line broadening that is due to (mainly) Keplerian motion in galaxy disks [221,222]. The agreement between the magnitudes estimates is not the results of a circular argument, but rather, an indication of the fundamental correctness of the compact central object scenario and of the dominance of virial motions in at least a substantial part of the BLR. Yet, the fact that the agreement with the prediction of the virial luminosity for quasars is somewhat sample dependent means that we are not understanding in full the line broadening phenomenology of type 1 AGN.
Author Contributions
Conceptualization, M.D., P.M., C.C. and C.A.N.; methodology, M.D., P.M. and C.C.; software, M.D., P.M., C.C. and C.A.N.; validation, M.D., P.M. and C.C.; writing—original draft preparation, M.D., P.M. and C.C.; writing—review and editing, M.D., P.M. and C.C. All authors have read and agreed to the published version of the manuscript.
Funding
C.A.N. is thankful for the support from the CONAHCyT project Paradigmas y Controversias de la Ciencia 2022-320020 and DGAPA-UNAM grant IN111422.
Data Availability Statement
Data are contained within the article.
Conflicts of Interest
The authors declare no conflicts of interest.
Appendix A. Measurement of Velocity Dispersion for xA Sources
Appendix A.1. Empirical Model of the Spectrum and σ Measurements
Measurements were carried out over two samples:
- A total of 52 Population A AGNs covering a wide range in redshift and luminosity ( erg/s), for which H and intermediate ionization line observations were available [185].
- A total of 133 extreme Population As from the SDSS [200]. All these sources satisfy the condition , reputed sufficient to identify high—possibly super-Eddington—accretors [9,170].
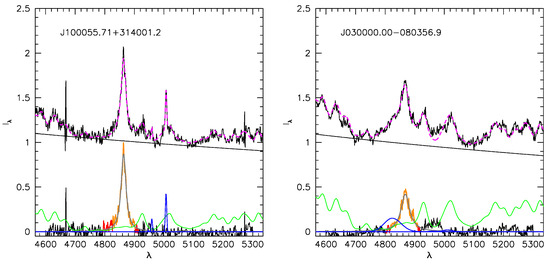
Figure A1.
Example of velocity dispersion measurement. (Top) normalized spectrum with continuum placement and full empirical model (magenta dashed line). (Bottom) the same spectrum after continuum subtraction, with emphasis on the H model and integration range: the Lorentzian function is traced in grey, while the orange and red lines cover the observed H profile down to the noise rms and 0 flux, respectively. Blue lines: [Oiii]5007, green: model Feii emission. (Left) and (right) panels refer to a lesser extreme and to one of the strongest Feii emitters in the sample.
These sources are characterized by Lorentzian-like low-ionization line profiles. Often, especially for extreme Population A (xA) sources, the blue wing of the symmetric unshifted Lorentzian is affected by the presence of a blueshifted excess emission, ultimately associated with a BLR outflow that can be the dominant contribution to high ionization lines [177,223,224]. In addition, Pop. A sources and even more so xA are contaminated by strong Feii emissions, and by the [Oiii]5007 doublet, often highly blueshifted and semi-broad (e.g., [177,225,226,227,228]). We have applied a non-linear, multicomponent fitting technique [229] implemented in the data analysis package IRAF [230] to adequately subtract the AGN continuum emission and deconvolve the H profile from its contaminants. The same technique has been successfully applied in a number of earlier papers [39,115,200,231,232].
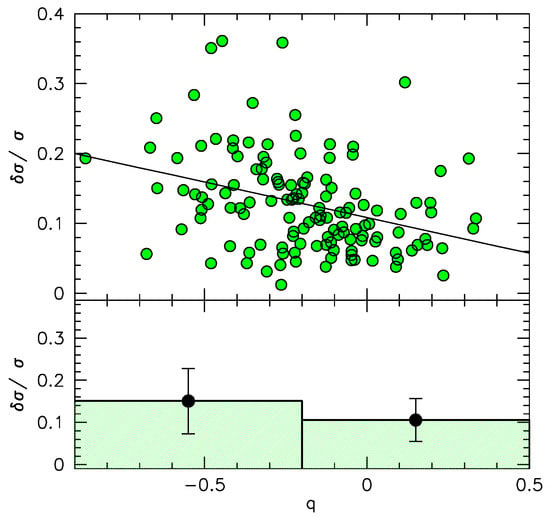
Figure A2.
Relation between relative uncertainty and the parameter—a good predictor of uncertainty. The lower panel shows a significant reduction in the average uncertainty above .
Figure A1 shows the original spectrum of two sources. Both are xA; however, the left one is less extreme in terms of . The fitting function was assumed to be Lorentzian leaving the possibility of the additional blueshifted emission modeled by an asymmetric Gaussian [233]. The measurement has been carried out on the observed profile down to 0 flux, from the relations:
where the summation has been extended to the region where the line profiles has detectable flux (the orange + red line in Figure A1). Uncertainties were estimated by computing the rms between the measurement as described above, the Lorentzian fit on the same wavelength range, and the same measurements with observed profile and fit restricted to noise level. The measurement of the has been carried out without the blueshifted component that is most likely not due to virial motions.
Appendix A.2. The Quality Parameter Q
Uncertainty in Full Width at Half Maximum (FWHM) has been linked to a quality parameter , which could prove useful when analyzing very large samples of quasars [185]. The quality parameter is defined as:
Here, W represents the line equivalent width, denotes the Full Width at Half Maximum, and signifies the signal-to-noise ratio. increases with the signal-to-noise ratio and line prominence over the continuum and decreases with the increasing line widths. The signal in each resolution element is proportional to the ratio , which measures the sharpness of the line. Consequently, . The parameter addresses the inadequacy of the signal-to-noise measurement carried out on the continuum. By multiplying it by the ratio , we compute a more suitable average signal-to-noise ratio for a line based on its strength and width. The parameter is higher for sharp lines in spectra with a high signal-to-noise ratio in the continuum. In the context of measurements, for to be practically applicable, it needs to be associated with estimates of uncertainties. This will, in turn, establish a threshold beyond which measurements of can be reliably conducted with acceptable uncertainties at a given confidence level.
Notes
| 1 | The size of the z∼0.1 sample of Bernardi et al. [72] contains more than 15,000 ETGs with . |
| 2 | The derived masses span the range to and the radii range from few tens to few hundred pc. |
| 3 | We consider here equal representations of the FP both the and parameter spaces, being . |
| 4 | We could not use the relations of Dalla Bontà et al. [187] reported in their Table 3 since their sample contains a large fraction of Population B sources. |
References
- Minkowski, R. Internal Dispersion of Velocities in Other Galaxies. Probl.-Extra-Galact. Res. 1962, 15, 112. [Google Scholar]
- Morton, D.C.; Chevalier, R.A. Velocity dispersions in galaxies. II. The ellipticals NGC 1889, 3115, 4473, 4494. Astrophys. J. 1973, 179, 55–68. [Google Scholar] [CrossRef]
- Faber, S.M.; Jackson, R.E. Velocity dispersions and mass-to-light ratios for elliptical galaxies. Astrophys. J. 1976, 204, 668–683. [Google Scholar] [CrossRef]
- D’Onofrio, M.; Cariddi, S.; Chiosi, C.; Chiosi, E.; Marziani, P. On the Origin of the Fundamental Plane and Faber-Jackson Relations: Implications for the Star Formation Problem. Astrophys. J. 2017, 838, 163. [Google Scholar] [CrossRef]
- de Vaucouleurs, G. The extragalactic distance scale and the Hubble constant. Observatory 1982, 102, 178–194. [Google Scholar]
- de Vaucouleurs, G. Five crucial tests of the cosmic distance scale using the Galaxy as fundamental standard. Nature 1982, 299, 303–307. [Google Scholar] [CrossRef]
- Paturel, G.; Garnier, R. The use of velocity dispersion in globular clusters as a distance indicator. Astron. Astrophys. 1992, 254, 93–95. [Google Scholar]
- Teerikorpi, P. On Öpik’s distance evaluation method in a cosmological context. Astron. Astrophys. 2011, 531, A10. [Google Scholar] [CrossRef]
- Marziani, P.; Sulentic, J.W. Highly accreting quasars: Sample definition and possible cosmological implications. Mon. Not. R. Astron. Soc. 2014, 442, 1211–1229. [Google Scholar] [CrossRef]
- D’Onofrio, M.; Chiosi, C.; Sciarratta, M.; Marziani, P. The parallelism between galaxy clusters and early-type galaxies. II. Clues on the origin of the scaling relations. Astron. Astrophys. 2020, 641, A94. [Google Scholar] [CrossRef]
- Seyfert, C.K. Nuclear Emission in Spiral Nebulae. Astrophys. J. 1943, 97, 28. [Google Scholar] [CrossRef]
- Shields, G.A. A Brief History of Active Galactic Nuclei. Publ. Astron. Soc. Pac. 1999, 111, 661–678. [Google Scholar] [CrossRef]
- Mathews, W.G.; Capriotti, E.R. Structure and dynamics of the broad line region. In Astrophysics of Active Galaxies and Quasi-Stellar Objects; Miller, J.S., Ed.; Oxford University Press: Oxford, UK, 1985; pp. 185–233. [Google Scholar]
- Sulentic, J.W.; Marziani, P.; Dultzin-Hacyan, D. Phenomenology of Broad Emission Lines in Active Galactic Nuclei. Annu. Rev. Astron. Astrophys. 2000, 38, 521–571. [Google Scholar] [CrossRef]
- Netzer, H. The Physics and Evolution of Active Galactic Nuclei; Cambridge University Press: Cambridge, UK, 2013. [Google Scholar]
- D’Onofrio, M.; Marziani, P.; Sulentic, J.W. (Eds.) Fifty Years of Quasars from Early Observations and Ideas to Future Research; Astrophysics and Space Science Library; Springer: Berlin/Heidelberg, Germany, 2012; Volume 386. [Google Scholar]
- Gaskell, C.M. A redshift difference between high and low ionization emission-line regions in QSOs—Evidence for radial motions. Astrophys. J. 1982, 263, 79–86. [Google Scholar] [CrossRef]
- Tytler, D.; Fan, X.M. Systematic QSO emission-line velocity shifts and new unbiased redshifts. Astrophys. J. Suppl. Ser. 1992, 79, 1–36. [Google Scholar] [CrossRef]
- Sulentic, J.W.; Marziani, P.; Dultzin-Hacyan, D.; Calvani, M.; Moles, M. First direct comparison of high and low ionization line kinematics in active galactic nuclei. Astrophys. J. 1995, 445, L85–L89. [Google Scholar] [CrossRef]
- Leighly, K.M.; Moore, J.R. Hubble Space Telescope STIS Ultraviolet Spectral Evidence of Outflow in Extreme Narrow-Line Seyfert 1 Galaxies. I. Data and Analysis. Astrophys. J. 2004, 611, 107–124. [Google Scholar] [CrossRef]
- Wang, H.; Wang, T.; Zhou, H.; Liu, B.; Wang, J.; Yuan, W.; Dong, X. Coexistence of Gravitationally-bound and Radiation-driven C IV Emission Line Regions in Active Galactic Nuclei. Astrophys. J. 2011, 738, 85. [Google Scholar] [CrossRef]
- Vestergaard, M.; Peterson, B.M. Determining Central Black Hole Masses in Distant Active Galaxies and Quasars. II. Improved Optical and UV Scaling Relationships. Astrophys. J. 2006, 641, 689–709. [Google Scholar] [CrossRef]
- Marziani, P.; Dultzin-Hacyan, D.; Sulentic, J.W. Accretion onto Supermassive Black Holes in Quasars: Learning from Optical/UV Observations. In New Developments in Black Hole Research; Kreitler, P.V., Ed.; Nova Press: New York, NY, USA, 2006; p. 123. [Google Scholar]
- Marziani, P.; Sulentic, J.W. Estimating black hole masses in quasars using broad optical and UV emission lines. NARev 2012, 56, 49–63. [Google Scholar] [CrossRef]
- Shen, Y.; Liu, X. Comparing Single-epoch Virial Black Hole Mass Estimators for Luminous Quasars. Astrophys. J. 2012, 753, 125. [Google Scholar] [CrossRef]
- Shen, Y. The mass of quasars. Bull. Astron. Soc. India 2013, 41, 61–115. [Google Scholar]
- Du, P.; Wang, J.M. The Radius-Luminosity Relationship Depends on Optical Spectra in Active Galactic Nuclei. Astrophys. J. 2019, 886, 42. [Google Scholar] [CrossRef]
- Martínez-Aldama, M.L.; Czerny, B.; Kawka, D.; Karas, V.; Panda, S.; Zajaček, M.; Życki, P.T. Can Reverberation-measured Quasars Be Used for Cosmology? Astrophys. J. 2019, 883, 170. [Google Scholar] [CrossRef]
- D’Onofrio, M.; Burigana, C. Questions of Modern Cosmology: Galileo’s Legacy; Springer: Berlin/Heidelberg, Germany, 2009. [Google Scholar] [CrossRef]
- Baldwin, J.A. Luminosity Indicators in the Spectra of Quasi-Stellar Objects. Astrophys. J. 1977, 214, 679–684. [Google Scholar] [CrossRef]
- Baldwin, J.A.; Burke, W.L.; Gaskell, C.M.; Wampler, E.J. Relative quasar luminosities determined from emission line strengths. Nature 1978, 273, 431–435. [Google Scholar] [CrossRef]
- Bian, W.H.; Fang, L.L.; Huang, K.L.; Wang, J.M. The C IV Baldwin effect in quasi-stellar objects from Seventh Data Release of the Sloan Digital Sky Survey. Mon. Not. R. Astron. Soc. 2012, 427, 2881–2888. [Google Scholar] [CrossRef]
- Boroson, T.A.; Green, R.F. The emission-line properties of low-redshift quasi-stellar objects. Astrophys. J. Suppl. Ser. 1992, 80, 109–135. [Google Scholar] [CrossRef]
- Sulentic, J.W.; Marziani, P.; Zwitter, T.; Dultzin-Hacyan, D.; Calvani, M. The Demise of the Classical Broad-Line Region in the Luminous Quasar PG 1416-129. Astrophys. J. 2000, 545, L15–L18. [Google Scholar] [CrossRef]
- Marziani, P.; Sulentic, J.W.; Zwitter, T.; Dultzin-Hacyan, D.; Calvani, M. Searching for the Physical Drivers of the Eigenvector 1 Correlation Space. Astrophys. J. 2001, 558, 553–560. [Google Scholar] [CrossRef]
- Sulentic, J.W.; Marziani, P.; Zamanov, R.; Bachev, R.; Calvani, M.; Dultzin-Hacyan, D. Average Quasar Spectra in the Context of Eigenvector 1. Astrophys. J. 2002, 566, L71–L75. [Google Scholar] [CrossRef]
- Marziani, P.; Bon, E.; Bon, N.; D’Onofrio, M.; Punsly, B.; Śniegowska, M.; Czerny, B.; Panda, S.; Martnez Aldama, M.L.; del Olmo, A.; et al. The main sequence of quasars: The taming of the extremes. Astron. Nachrichten 2022, 343, e210082. [Google Scholar] [CrossRef]
- Marziani, P.; Sulentic, J.W.; Stirpe, G.M.; Zamfir, S.; Calvani, M. VLT/ISAAC spectra of the Hβ region in intermediate-redshift quasars. III. Hβ broad-line profile analysis and inferences about BLR structure. Astron. Astrophys. 2009, 495, 83–112. [Google Scholar] [CrossRef]
- Deconto-Machado, A.; del Olmo Orozco, A.; Marziani, P.; Perea, J.; Stirpe, G.M. High-redshift quasars along the main sequence. Astron. Astrophys. 2023, 669, A83. [Google Scholar] [CrossRef]
- Marziani, P.; Dultzin, D.; Sulentic, J.W.; Del Olmo, A.; Negrete, C.A.; Martinez-Aldama, M.L.; D’Onofrio, M.; Bon, E.; Bon, N.; Stirpe, G.M. A main sequence for quasars. Front. Astron. Space Sci. 2018, 5, 6. [Google Scholar] [CrossRef]
- Giustini, M.; Proga, D. A global view of the inner accretion and ejection flow around super massive black holes. Radiation-driven accretion disk winds in a physical context. Astron. Astrophys. 2019, 630, A94. [Google Scholar] [CrossRef]
- Du, P.; Lu, K.X.; Hu, C.; Qiu, J.; Li, Y.R.; Huang, Y.K.; Wang, F.; Bai, J.M.; Bian, W.H.; Yuan, Y.F.; et al. Supermassive Black Holes with High Accretion Rates in Active Galactic Nuclei. VI. Velocity-resolved Reverberation Mapping of the Hβ Line. Astrophys. J. 2016, 820, 27. [Google Scholar] [CrossRef]
- Sulentic, J.W.; Zheng, W.; Arp, H.C. N2841-UB3: A QSO with Unusually Strong Optical Fe II Emission. Publ. Astron. Soc. Pac. 1990, 102, 1275. [Google Scholar] [CrossRef]
- Lipari, S.; Terlevich, R.; Macchetto, F. Extreme optical Fe II emission in luminous IRAS active galactic nuclei. Astrophys. J. 1993, 406, 451–456. [Google Scholar] [CrossRef]
- Graham, M.J.; Clowes, R.G.; Campusano, L.E. A quasar with ultrastrong, ultraviolet Fe II emission. Mon. Not. R. Astron. Soc. 1996, 279, 1349–1356. [Google Scholar] [CrossRef]
- Boroson, T.A. Black Hole Mass and Eddington Ratio as Drivers for the Observable Properties of Radio-loud and Radio-quiet QSOs. Astrophys. J. 2002, 565, 78–85. [Google Scholar] [CrossRef]
- Sun, J.; Shen, Y. Dissecting the Quasar Main Sequence: Insight from Host Galaxy Properties. Astrophys. J. 2015, 804, L15. [Google Scholar] [CrossRef]
- Panda, S.; Marziani, P.; Czerny, B. The Quasar Main Sequence Explained by the Combination of Eddington Ratio, Metallicity, and Orientation. Astrophys. J. 2019, 882, 79. [Google Scholar] [CrossRef]
- Abramowicz, M.A.; Czerny, B.; Lasota, J.P.; Szuszkiewicz, E. Slim accretion disks. Astrophys. J. 1988, 332, 646–658. [Google Scholar] [CrossRef]
- Abramowicz, M.A.; Straub, O. Accretion discs. Scholarpedia 2014, 9, 2408. [Google Scholar] [CrossRef]
- Sądowski, A. Slim Disks Around Kerr Black Holes Revisited. Astrophys. J. 2009, 183, 171–178. [Google Scholar] [CrossRef]
- Hinshaw, G.; Larson, D.; Komatsu, E.; Spergel, D.N.; Bennett, C.L.; Dunkley, J.; Nolta, M.R.; Halpern, M.; Hill, R.S.; Odegard, N.; et al. Nine-year Wilkinson Microwave Anisotropy Probe (WMAP) Observations: Cosmological Parameter Results. Astrophys. J. 2013, 208, 19. [Google Scholar] [CrossRef]
- Schechter, P.L. Mass-to-light ratios for elliptical galaxies. Astron. J. 1980, 85, 801–811. [Google Scholar] [CrossRef]
- Malumuth, E.M.; Kirshner, R.P. Dynamics of luminous galaxies. Astrophys. J. 1981, 251, 508–517. [Google Scholar] [CrossRef]
- Cappellari, M. Effect of Environment on Galaxies’ Mass-Size Distribution: Unveiling the Transition from outside-in to inside-out Evolution. Astrophys. J. Lett. 2013, 778, L2. [Google Scholar] [CrossRef]
- Kormendy, J.; Bender, R. The Lvpropσ8 Correlation for Elliptical Galaxies with Cores: Relation with Black Hole Mass. Astrophys. J. 2013, 769, L5. [Google Scholar] [CrossRef]
- Quenneville, M.E.; Blakeslee, J.P.; Ma, C.P.; Greene, J.E.; Gwyn, S.D.J.; Ciccone, S.; Nyiri, B. The MASSIVE survey—XVIII. Deep wide-field K-band photometry and local scaling relations for massive early-type galaxies. Mon. Not. R. Astron. Soc. 2024, 527, 249–264. [Google Scholar] [CrossRef]
- Tonry, J.L. Velocity dispersions of low luminosity ellipticals—L approximately equal to sigma-cubed. Astrophys. J. 1981, 251, L1–L5. [Google Scholar] [CrossRef]
- Davies, R.L.; Efstathiou, G.; Fall, S.M.; Illingworth, G.; Schechter, P.L. The kinematic properties of faint elliptical galaxies. Astrophys. J. 1983, 266, 41–57. [Google Scholar] [CrossRef]
- Held, E.V.; de Zeeuw, T.; Mould, J.; Picard, A. NGC 185 and the Extended Faber-Jackson Relation. In The Stellar Populations of Galaxies; Barbuy, B., Renzini, A., Eds.; Springer: Dordrecht, The Netherlands, 1992; Volume 149, p. 429. [Google Scholar]
- de Rijcke, S.; Michielsen, D.; Dejonghe, H.; Zeilinger, W.W.; Hau, G.K.T. Formation and evolution of dwarf elliptical galaxies. I. Structural and kinematical properties. Astron. Astrophys. 2005, 438, 491–505. [Google Scholar] [CrossRef]
- Matković, A.; Guzmán, R.; Sánchez-Blázquez, P.; Gorgas, J.; Cardiel, N.; Gruel, N. Kinematic Properties and Stellar Populations of Faint Early-Type Galaxies. II. Line-Strength Measurements of Central Coma Galaxies. Astrophys. J. 2009, 691, 1862–1878. [Google Scholar] [CrossRef]
- Montero-Dorta, A.D.; Shu, Y.; Bolton, A.S.; Brownstein, J.R.; Weiner, B.J. A steep slope and small scatter for the high-mass end of the L-σ relation at z ∼ 0.55. Mon. Not. R. Astron. Soc. 2016, 456, 3265–3281. [Google Scholar] [CrossRef]
- Lauer, T.R.; Tremaine, S.; Richstone, D.; Faber, S.M. Selection Bias in Observing the Cosmological Evolution of the M•-σ and M•-L Relationships. Astrophys. J. 2007, 670, 249–260. [Google Scholar] [CrossRef]
- Cappellari, M.; Emsellem, E.; Krajnović, D.; McDermid, R.M.; Scott, N.; Verdoes Kleijn, G.A.; Young, L.M.; Alatalo, K.; Bacon, R.; Blitz, L.; et al. The ATLAS3D project—I. A volume-limited sample of 260 nearby early-type galaxies: Science goals and selection criteria. Mon. Not. R. Astron. Soc. 2011, 413, 813–836. [Google Scholar] [CrossRef]
- Focardi, P.; Malavasi, N. The Effect of the Environment on the Faber-Jackson Relation. Astrophys. J. 2012, 756, 117. [Google Scholar] [CrossRef]
- Paturel, G.; Petit, C.; Prugniel, P.; Theureau, G.; Rousseau, J.; Brouty, M.; Dubois, P.; Cambrésy, L. HYPERLEDA. I. Identification and designation of galaxies. Astron. Astrophys. 2003, 412, 45–55. [Google Scholar] [CrossRef]
- Choi, Y.Y.; Park, C.; Vogeley, M.S. Internal and Collective Properties of Galaxies in the Sloan Digital Sky Survey. Astrophys. J. 2007, 658, 884–897. [Google Scholar] [CrossRef]
- Desroches, L.B.; Quataert, E.; Ma, C.P.; West, A.A. Luminosity dependence in the Fundamental Plane projections of elliptical galaxies. Mon. Not. R. Astron. Soc. 2007, 377, 402–414. [Google Scholar] [CrossRef]
- Hyde, J.B.; Bernardi, M. Curvature in the scaling relations of early-type galaxies. Mon. Not. R. Astron. Soc. 2009, 394, 1978–1990. [Google Scholar] [CrossRef]
- Nigoche-Netro, A.; Aguerri, J.A.L.; Lagos, P.; Ruelas-Mayorga, A.; Sánchez, L.J.; Machado, A. The Faber-Jackson relation for early-type galaxies: Dependence on the magnitude range. Astron. Astrophys. 2010, 516, A96. [Google Scholar] [CrossRef]
- Bernardi, M.; Roche, N.; Shankar, F.; Sheth, R.K. Evidence of major dry mergers at M* > 2 × 1011M⊙ from curvature in early-type galaxy scaling relations? Mon. Not. R. Astron. Soc. 2011, 412, L6–L10. [Google Scholar] [CrossRef]
- Bernardi, M.; Sheth, R.K.; Annis, J.; Burles, S.; Eisenstein, D.J.; Finkbeiner, D.P.; Hogg, D.W.; Lupton, R.H.; Schlegel, D.J.; SubbaRao, M.; et al. Early-Type Galaxies in the Sloan Digital Sky Survey. III. The Fundamental Plane. Astron. J. 2003, 125, 1866–1881. [Google Scholar] [CrossRef]
- Nigoche-Netro, A.; Ruelas, A.; Sánchez, L.J. The Dependence of the Faber-Jackson relation on the magnitude range. Rev. Mex. De Astron. Y Astrofis. Ser. De Conf. 2011, 40, 126. [Google Scholar]
- Shu, Y.; Bolton, A.S.; Schlegel, D.J.; Dawson, K.S.; Wake, D.A.; Brownstein, J.R.; Brinkmann, J.; Weaver, B.A. Evolution of the Velocity-dispersion Function of Luminous Red Galaxies: A Hierarchical Bayesian Measurement. Astron. J. 2012, 143, 90. [Google Scholar] [CrossRef]
- Sheth, R.K.; Bernardi, M.; Schechter, P.L.; Burles, S.; Eisenstein, D.J.; Finkbeiner, D.P.; Frieman, J.; Lupton, R.H.; Schlegel, D.J.; Subbarao, M.; et al. The Velocity Dispersion Function of Early-Type Galaxies. Astrophys. J. 2003, 594, 225–231. [Google Scholar] [CrossRef]
- Nigoche-Netro, A.; Moles, M.; Ruelas-Mayorga, A.; Franco-Balderas, A.; Kjørgaard, P. Structural properties of isolated early-type galaxies. The dependence of scaling relations on environment. Astron. Astrophys. 2007, 472, 773–784. [Google Scholar] [CrossRef]
- Nigoche-Netro, A.; Ruelas-Mayorga, A.; Franco-Balderas, A. The Kormendy relation for early-type galaxies. Dependence on the magnitude range. Astron. Astrophys. 2008, 491, 731–738. [Google Scholar] [CrossRef]
- Nigoche-Netro, A.; Ruelas-Mayorga, A.; Franco-Balderas, A. The Fundamental Plane for early-type galaxies: Dependence on the magnitude range. Mon. Not. R. Astron. Soc. 2009, 392, 1060–1069. [Google Scholar] [CrossRef]
- Djorgovski, S.; Davis, M. Fundamental Properties of Elliptical Galaxies. Astrophys. J. 1987, 313, 59. [Google Scholar] [CrossRef]
- Dressler, A.; Lynden-Bell, D.; Burstein, D.; Davies, R.L.; Faber, S.M.; Terlevich, R.; Wegner, G. Spectroscopy and Photometry of Elliptical Galaxies. I. New Distance Estimator. Astrophys. J. 1987, 313, 42. [Google Scholar] [CrossRef]
- Jorgensen, I.; Chiboucas, K.; Flint, K.; Bergmann, M.; Barr, J.; Davies, R. The Fundamental Plane for z = 0.8–0.9 Cluster Galaxies. Astrophys. J. 2006, 639, L9–L12. [Google Scholar] [CrossRef]
- Vogelsberger, M.; Genel, S.; Springel, V.; Torrey, P.; Sijacki, D.; Xu, D.; Snyder, G.; Bird, S.; Nelson, D.; Hernquist, L. Properties of galaxies reproduced by a hydrodynamic simulation. Nature 2014, 509, 177–182. [Google Scholar] [CrossRef] [PubMed]
- Barger, A.J.; Aragón-Salamanca, A.; Smail, I.; Ellis, R.S.; Couch, W.J.; Dressler, A.; Oemler, A.; Poggianti, B.M.; Sharples, R.M. New Constraints on the Luminosity Evolution of Spheroidal Galaxies in Distant Clusters. Astrophys. J. 1998, 501, 522–532. [Google Scholar] [CrossRef]
- Ziegler, B.L.; Saglia, R.P.; Bender, R.; Belloni, P.; Greggio, L.; Seitz, S. Probing early-type galaxy evolution with the Kormendy relation. Astron. Astrophys. 1999, 346, 13–32. [Google Scholar]
- La Barbera, F.; Busarello, G.; Merluzzi, P.; Massarotti, M.; Capaccioli, M. On the Invariant Distribution of Galaxies in the re-<μ>e Plane out to z = 0.64. Astrophys. J. 2003, 595, 127–136. [Google Scholar] [CrossRef]
- Barr, J.; Jørgensen, I.; Chiboucas, K.; Davies, R.; Bergmann, M. The Fundamental Plane in RX J0142.0+2131: A Galaxy Cluster Merger at z = 0.28. Astrophys. J. 2006, 649, L1–L4. [Google Scholar] [CrossRef]
- Treu, T.; Ellis, R.S.; Liao, T.X.; van Dokkum, P.G.; Tozzi, P.; Coil, A.; Newman, J.; Cooper, M.C.; Davis, M. The Assembly History of Field Spheroidals: Evolution of Mass-to-Light Ratios and Signatures of Recent Star Formation. Astrophys. J. 2005, 633, 174–197. [Google Scholar] [CrossRef]
- Fritz, A.; Jorgensen, I.; Schiavon, R.P.; Chiboucas, K. The evolution of cluster early-type galaxies over the past 8 Gyr. Astron. Nachrichten 2009, 330, 931. [Google Scholar] [CrossRef]
- Kormendy, J. Families of ellipsoidal stellar systems and the formation of dwarf elliptical galaxies. Astrophys. J. 1985, 295, 73–79. [Google Scholar] [CrossRef]
- Hamabe, M.; Kormendy, J. Correlations Between R/1/4—Law Parameters for Bulges and Elliptical Galaxies. In Structure and Dynamics of Elliptical Galaxies; de Zeeuw, P.T., Ed.; Cambridge University Press: Cambridge, UK, 1987; Volume 127, p. 379. [Google Scholar] [CrossRef]
- Bender, R.; Burstein, D.; Faber, S.M. Dynamically Hot Galaxies. I. Structural Properties. Astrophys. J. 1992, 399, 462. [Google Scholar] [CrossRef]
- Capaccioli, M.; Caon, N.; D’Onofrio, M. Families of galaxies in the mu.e-R.e plane. Mon. Not. R. Astron. Soc. 1992, 259, 323–327. [Google Scholar] [CrossRef]
- Caon, N.; Capaccioli, M.; D’Onofrio, M. On the shape of the light profiles of early-type galaxies. Mon. Not. R. Astron. Soc. 1993, 265, 1013–1021. [Google Scholar] [CrossRef]
- Aguerri, J.A.L.; González-García, A.C. On the origin of dwarf elliptical galaxies: The fundamental plane. Astron. Astrophys. 2009, 494, 891–904. [Google Scholar] [CrossRef]
- Brosche, P. The Manifold of Galaxies. Galaxies with known Dynamical Parameters. Astron. Astrophys. 1973, 23, 259–268. [Google Scholar]
- Schmidt, M. The Rate of Star Formation. Astrophys. J. 1959, 129, 243. [Google Scholar] [CrossRef]
- Terlevich, R.; Melnick, J. The dynamics and chemical composition of giant extragalactic H II regions. Mon. Not. R. Astron. Soc. 1981, 195, 839–851. [Google Scholar] [CrossRef]
- Melnick, J.; Moles, M.; Terlevich, R.; Garcia-Pelayo, J.M. Giant H II regions as distance indicators—I. Relations between global parameters for the local calibrators. Mon. Not. R. Astron. Soc. 1987, 226, 849–866. [Google Scholar] [CrossRef]
- Melnick, J.; Terlevich, R.; Moles, M. Giant H II regions as distance indicators- II. Application to H II galaxies and the value of the Hubble constant. Mon. Not. R. Astron. Soc. 1988, 235, 297–313. [Google Scholar] [CrossRef]
- Siegel, E.R.; Guzmán, R.; Gallego, J.P.; Orduña López, M.; Rodríguez Hidalgo, P. Towards a precision cosmology from starburst galaxies at z > 2. Mon. Not. R. Astron. Soc. 2005, 356, 1117–1122. [Google Scholar] [CrossRef]
- Bordalo, V.; Telles, E. The L-σ Relation of Local H II Galaxies. Astrophys. J. 2011, 735, 52. [Google Scholar] [CrossRef]
- Plionis, M.; Terlevich, R.; Basilakos, S.; Bresolin, F.; Terlevich, E.; Melnick, J.; Chavez, R. A strategy to measure the dark energy equation of state using the H II galaxy Hubble function and X-ray active galactic nuclei clustering: Preliminary results. Mon. Not. R. Astron. Soc. 2011, 416, 2981–2996. [Google Scholar] [CrossRef]
- Chávez, R.; Terlevich, E.; Terlevich, R.; Plionis, M.; Bresolin, F.; Basilakos, S.; Melnick, J. Determining the Hubble constant using giant extragalactic H II regions and H II galaxies. Mon. Not. R. Astron. Soc. 2012, 425, L56–L60. [Google Scholar] [CrossRef]
- Koo, D.C.; Guzman, R.; Faber, S.M.; Illingworth, G.D.; Bershady, M.A.; Kron, R.G.; Takamiya, M. High-Resolution Spectra of Distant Compact Narrow Emission Line Galaxies: Progenitors of Spheroidal Galaxies? Astrophys. J. 1995, 440, L49. [Google Scholar] [CrossRef]
- Guzman, R.; Koo, D.C.; Faber, S.M.; Illingworth, G.D.; Takamiya, M.; Kron, R.G.; Bershady, M.A. On the Nature of the Faint Compact Narrow Emission-Line Galaxies: The Half-Light Radius–Velocity Width Diagram. Astrophys. J. 1996, 460, L5. [Google Scholar] [CrossRef]
- Mineshige, S.; Kawaguchi, T.; Takeuchi, M.; Hayashida, K. Slim-Disk Model for Soft X-ray Excess and Variability of Narrow-Line Seyfert 1 Galaxies. Publ. Astron. Soc. Jpn. 2000, 52, 499–508. [Google Scholar] [CrossRef]
- Sa̧dowski, A.; Narayan, R.; McKinney, J.C.; Tchekhovskoy, A. Numerical simulations of super-critical black hole accretion flows in general relativity. Mon. Not. R. Astron. Soc. 2014, 439, 503–520. [Google Scholar] [CrossRef]
- Wang, J.M.; Qiu, J.; Du, P.; Ho, L.C. Self-shadowing Effects of Slim Accretion Disks in Active Galactic Nuclei: The Diverse Appearance of the Broad-line Region. Astrophys. J. 2014, 797, 65. [Google Scholar] [CrossRef]
- Wang, J.M.; Du, P.; Valls-Gabaud, D.; Hu, C.; Netzer, H. Super-Eddington Accreting Massive Black Holes as Long-Lived Cosmological Standards. Phys. Rev. Lett. 2013, 110, 081301. [Google Scholar] [CrossRef] [PubMed]
- La Franca, F.; Bianchi, S.; Ponti, G.; Branchini, E.; Matt, G. A New Cosmological Distance Measure Using Active Galactic Nucleus X-ray Variability. Astrophys. J. 2014, 787, L12. [Google Scholar] [CrossRef]
- Wang, J.M.; Du, P.; Hu, C.; Netzer, H.; Bai, J.M.; Lu, K.X.; Kaspi, S.; Qiu, J.; Li, Y.R.; Wang, F.; et al. Supermassive Black Holes with High Accretion Rates in Active Galactic Nuclei. II. The Most Luminous Standard Candles in the Universe. Astrophys. J. 2014, 793, 108. [Google Scholar] [CrossRef]
- Padovani, P.; Rafanelli, P. Mass-luminosity relationships and accretion rates for Seyfert 1 galaxies and quasars. Astron. Astrophys. 1988, 205, 53–70. [Google Scholar]
- Matsuoka, Y.; Kawara, K.; Oyabu, S. Low-Ionization Emission Regions in Quasars: Gas Properties Probed with Broad O I and Ca II Lines. Astrophys. J. 2008, 673, 62–68. [Google Scholar] [CrossRef]
- Negrete, A.; Dultzin, D.; Marziani, P.; Sulentic, J. BLR Physical Conditions in Extreme Population A Quasars: A Method to Estimate Central Black Hole Mass at High Redshift. Astrophys. J. 2012, 757, 62. [Google Scholar] [CrossRef]
- Dultzin, D.; Marziani, P.; de Diego, J.A.; Negrete, C.A.; Del Olmo, A.; Martínez-Aldama, M.L.; D’Onofrio, M.; Bon, E.; Bon, N.; Stirpe, G.M. Extreme quasars as distance indicators in cosmology. Front. Astron. Space Sci. 2020, 6, 80. [Google Scholar] [CrossRef]
- Marziani, P.; Dultzin, D.; Del Olmo, A.; D’Onofrio, M.; de Diego, J.A.; Stirpe, G.M.; Bon, E.; Bon, N.; Czerny, B.; Perea, J.; et al. The quasar main sequence and its potential for cosmology. arXiv 2020, arXiv:2002.07219. [Google Scholar] [CrossRef]
- Czerny, B.; Martínez-Aldama, M.L.; Wojtkowska, G.; Zajaček, M.; Marziani, P.; Dultzin, D.; Naddaf, M.H.; Panda, S.; Prince, R.; Przyluski, R.; et al. Dark Energy Constraints from Quasar Observations. Acta Phys. Pol. A 2021, 139, 389–393. [Google Scholar] [CrossRef]
- Czerny, B.; Beaton, R.; Bejger, M.; Cackett, E.; Dall’Ora, M.; Holanda, R.F.L.; Jensen, J.B.; Jha, S.W.; Lusso, E.; Minezaki, T.; et al. Astronomical Distance Determination in the Space Age. Secondary Distance Indicators. Space Sci. Rev. 2018, 214, 32. [Google Scholar] [CrossRef]
- Fasano, G.; Marmo, C.; Varela, J.; D’Onofrio, M.; Poggianti, B.M.; Moles, M.; Pignatelli, E.; Bettoni, D.; Kjærgaard, P.; Rizzi, L.; et al. WINGS: A WIde-field Nearby Galaxy-cluster Survey. I. Optical imaging. Astron. Astrophys. 2006, 445, 805–817. [Google Scholar] [CrossRef]
- Varela, J.; D’Onofrio, M.; Marmo, C.; Fasano, G.; Bettoni, D.; Cava, A.; Couch, W.J.; Dressler, A.; Kjærgaard, P.; Moles, M.; et al. WINGS: A WIde-field Nearby Galaxy-cluster Survey. II. Deep optical photometry of 77 nearby clusters. Astron. Astrophys. 2009, 497, 667–676. [Google Scholar] [CrossRef]
- Cava, A.; Bettoni, D.; Poggianti, B.M.; Couch, W.J.; Moles, M.; Varela, J.; Biviano, A.; D’Onofrio, M.; Dressler, A.; Fasano, G.; et al. WINGS-SPE Spectroscopy in the WIde-field Nearby Galaxy-cluster Survey. Astron. Astrophys. 2009, 495, 707–719. [Google Scholar] [CrossRef]
- Valentinuzzi, T.; Woods, D.; Fasano, G.; Riello, M.; D’Onofrio, M.; Varela, J.; Bettoni, D.; Cava, A.; Couch, W.J.; Dressler, A.; et al. WINGS: A WIde-field nearby Galaxy-cluster survey. III. Deep near-infrared photometry of 28 nearby clusters. Astron. Astrophys. 2009, 501, 851–864. [Google Scholar] [CrossRef]
- Moretti, A.; Poggianti, B.M.; Fasano, G.; Bettoni, D.; D’Onofrio, M.; Fritz, J.; Cava, A.; Varela, J.; Vulcani, B.; Gullieuszik, M.; et al. WINGS Data Release: A database of galaxies in nearby clusters. Astron. Astrophys. 2014, 564, A138. [Google Scholar] [CrossRef]
- D’Onofrio, M.; Bindoni, D.; Fasano, G.; Bettoni, D.; Cava, A.; Fritz, J.; Gullieuszik, M.; Kjærgaard, P.; Moretti, A.; Moles, M.; et al. Surface photometry of WINGS galaxies with GASPHOT. Astron. Astrophys. 2014, 572, A87. [Google Scholar] [CrossRef]
- Gullieuszik, M.; Poggianti, B.; Fasano, G.; Zaggia, S.; Paccagnella, A.; Moretti, A.; Bettoni, D.; D’Onofrio, M.; Couch, W.J.; Vulcani, B.; et al. OmegaWINGS: OmegaCAM-VST observations of WINGS galaxy clusters. Astron. Astrophys. 2015, 581, A41. [Google Scholar] [CrossRef]
- Moretti, A.; Gullieuszik, M.; Poggianti, B.; Paccagnella, A.; Couch, W.J.; Vulcani, B.; Bettoni, D.; Fritz, J.; Cava, A.; Fasano, G.; et al. OmegaWINGS: Spectroscopy in the outskirts of local clusters of galaxies. Astron. Astrophys. 2017, 599, A81. [Google Scholar] [CrossRef]
- Cariddi, S.; D’Onofrio, M.; Fasano, G.; Poggianti, B.M.; Moretti, A.; Gullieuszik, M.; Bettoni, D.; Sciarratta, M. Characterization of Omega-WINGS galaxy clusters. I. Stellar light and mass profiles. Astron. Astrophys. 2018, 609, A133. [Google Scholar] [CrossRef]
- Biviano, A.; Moretti, A.; Paccagnella, A.; Poggianti, B.M.; Bettoni, D.; Gullieuszik, M.; Vulcani, B.; Fasano, G.; D’Onofrio, M.; Fritz, J.; et al. The concentration-mass relation of clusters of galaxies from the OmegaWINGS survey. Astron. Astrophys. 2017, 607, A81. [Google Scholar] [CrossRef]
- D’Onofrio, M.; Fasano, G.; Varela, J.; Bettoni, D.; Moles, M.; Kjærgaard, P.; Pignatelli, E.; Poggianti, B.; Dressler, A.; Cava, A.; et al. The Fundamental Plane of Early-Type Galaxies in Nearby Clusters from the WINGS Database. Astrophys. J. 2008, 685, 875–896. [Google Scholar] [CrossRef]
- Bettoni, D.; Kjærgaard, P.; Milvan-Jensen, B.; D’Onofrio, M.; Moretti, A.; Poggianti, B.M.; Fasano, G.; Cava, A.; Couch, W.; Fritz, J.; et al. The Properties of Faint Galaxies in Nearby Clusters of the WINGS Sample. In The Universe of Digital Sky Surveys; Napolitano, N.R., Longo, G., Marconi, M., Paolillo, M., Iodice, E., Eds.; Springer: Berlin/Heidelberg, Germany, 2016; Volume 42, p. 183. [Google Scholar] [CrossRef]
- Pignatelli, E.; Fasano, G.; Cassata, P. GASPHOT: A tool for Galaxy Automatic Surface PHOTometry. Astron. Astrophys. 2006, 446, 373–388. [Google Scholar] [CrossRef]
- Busarello, G.; Capaccioli, M.; Capozziello, S.; Longo, G.; Puddu, E. The relation between the virial theorem and the fundamental plane of elliptical galaxies. Astron. Astrophys. 1997, 320, 415–420. [Google Scholar]
- Busarello, G.; Capaccioli, M.; Longo, G.; Puddu, E. Dynamical Non-Homology and the Tilt of the Fundamental Plane. In The Nature of Elliptical Galaxies, Proceedings of the 2nd Stromlo Symposium, Canberra, Australia, 26–30 August 1996; Arnaboldi, M., Da Costa, G.S., Saha, P., Eds.; Astronomical Society of the Pacific Conference Seriesm; Astronomical Society of the Pacific: San Francisco, CA, USA, 1997; Volume 116, p. 184. [Google Scholar]
- Genel, S.; Vogelsberger, M.; Springel, V.; Sijacki, D.; Nelson, D.; Snyder, G.; Rodriguez-Gomez, V.; Torrey, P.; Hernquist, L. Introducing the Illustris project: The evolution of galaxy populations across cosmic time. Mon. Not. R. Astron. Soc. 2014, 445, 175–200. [Google Scholar] [CrossRef]
- Nelson, D.; Pillepich, A.; Genel, S.; Vogelsberger, M.; Springel, V.; Torrey, P.; Rodriguez-Gomez, V.; Sijacki, D.; Snyder, G.F.; Griffen, B.; et al. The illustris simulation: Public data release. Astron. Comput. 2015, 13, 12–37. [Google Scholar] [CrossRef]
- D’Onofrio, M.; Sciarratta, M.; Cariddi, S.; Marziani, P.; Chiosi, C. The Parallelism between Galaxy Clusters and Early-type Galaxies. I. The Light and Mass Profiles. Astrophys. J. 2019, 875, 103. [Google Scholar] [CrossRef]
- Chiosi, C.; D’Onofrio, M.; Merlin, E.; Piovan, L.; Marziani, P. The parallelism between galaxy clusters and early-type galaxies. III. The mass-radius relationship. Astron. Astrophys. 2020, 643, A136. [Google Scholar] [CrossRef]
- Feigelson, E.D.; Babu, G.J. Linear Regression in Astronomy. II. Astrophys. J. 1992, 397, 55. [Google Scholar] [CrossRef]
- Binggeli, B.; Sandage, A.; Tarenghi, M. Studies of the Virgo Cluster. I. Photometry of 109 galaxies near the cluster center to serve as standards. Astron. J. 1984, 89, 64–82. [Google Scholar] [CrossRef]
- Bothun, G.D.; Mould, J.R.; Caldwell, N.; MacGillivray, H.T. Comparative photometric parameters of dwarf irregular and elliptical galaxies in the Virgo cluster: Two different classes of dwarf galaxies? Astron. J. 1986, 92, 1007–1019. [Google Scholar] [CrossRef]
- Caldwell, N.; Bothun, G.D. Dwarf Elliptical Galaxies in the Fornax Cluster. II. Their Structure and Stellar Populations. Astron. J. 1987, 94, 1126. [Google Scholar] [CrossRef]
- Capaccioli, M.; Caon, N.; D’Onofrio, M. The (log re,μe) Plane of Hot Stellar Systems. In Proceedings of the European Southern Observatory Conference and Workshop 1993, Garching, Germany, 26–27 April 1993; Volume 45, p. 43. [Google Scholar]
- Caldwell, N. Structure and stellar content of dwarf elliptical galaxies. Astron. J. 1983, 88, 804–812. [Google Scholar] [CrossRef]
- Kormendy, J.; Fisher, D.B.; Cornell, M.E.; Bender, R. Structure and Formation of Elliptical and Spheroidal Galaxies. Astrophys. J. Suppl. 2009, 182, 216–309. [Google Scholar] [CrossRef]
- Kormendy, J.; Bender, R. A Revised Parallel-sequence Morphological Classification of Galaxies: Structure and Formation of S0 and Spheroidal Galaxies. Astrophys. J. Suppl. 2012, 198, 2. [Google Scholar] [CrossRef]
- Tolstoy, E.; Hill, V.; Tosi, M. Star-Formation Histories, Abundances, and Kinematics of Dwarf Galaxies in the Local Group. Ann. Rev. Astron. Astrophys. 2009, 47, 371–425. [Google Scholar] [CrossRef]
- Somerville, R.S.; Davé, R. Physical Models of Galaxy Formation in a Cosmological Framework. Ann. Rev. Astron. Astrophys. 2015, 53, 51–113. [Google Scholar] [CrossRef]
- Kormendy, J. Elliptical Galaxies and Bulges of Disc Galaxies: Summary of Progress and Outstanding Issues. In Galactic Bulges; Laurikainen, E., Peletier, R., Gadotti, D., Eds.; Astrophysics and Space Science Library; Springer: Cham, Switzerland, 2016; Volume 418, p. 431. [Google Scholar] [CrossRef]
- Graham, A.W. Re. I. Understanding galaxy sizes, associated luminosity densities, and the artificial division of the early-type galaxy population. Pub. Astron. Soc. Aust. 2019, 36, e035. [Google Scholar] [CrossRef]
- Burstein, D.; Bender, R.; Faber, S.; Nolthenius, R. Global Relationships Among the Physical Properties of Stellar Systems. Astron. J. 1997, 114, 1365. [Google Scholar] [CrossRef]
- Lauer, T.R.; Gebhardt, K.; Faber, S.M.; Richstone, D.; Tremaine, S.; Kormendy, J.; Aller, M.C.; Bender, R.; Dressler, A.; Filippenko, A.V.; et al. The Centers of Early-Type Galaxies with Hubble Space Telescope. VI. Bimodal Central Surface Brightness Profiles. Astrophys. J. 2007, 664, 226–256. [Google Scholar] [CrossRef]
- Hyde, J.B.; Bernardi, M.; Sheth, R.K.; Nichol, R.C. A search for the most massive galaxies—III. Global and central structure. Mon. Not. R. Astron. Soc. 2008, 391, 1559–1576. [Google Scholar] [CrossRef]
- Kormendy, J.; Bender, R. A Proposed Revision of the Hubble Sequence for Elliptical Galaxies. Astrophys. J. 1996, 464, L119. [Google Scholar] [CrossRef]
- Faber, S.M.; Tremaine, S.; Ajhar, E.A.; Byun, Y.I.; Dressler, A.; Gebhardt, K.; Grillmair, C.; Kormendy, J.; Lauer, T.R.; Richstone, D. The Centers of Early-Type Galaxies with HST. IV. Central Parameter Relations. Astron. J. 1997, 114, 1771. [Google Scholar] [CrossRef]
- Shu, Y.; Bolton, A.S.; Brownstein, J.R.; Montero-Dorta, A.D.; Koopmans, L.V.E.; Treu, T.; Gavazzi, R.; Auger, M.W.; Czoske, O.; Marshall, P.J.; et al. The Sloan Lens ACS Survey. XII. Extending Strong Lensing to Lower Masses. Astrophys. J. 2015, 803, 71. [Google Scholar] [CrossRef]
- Gnedin, O.Y.; Kravtsov, A.V.; Klypin, A.A.; Nagai, D. Response of Dark Matter Halos to Condensation of Baryons: Cosmological Simulations and Improved Adiabatic Contraction Model. Astrophys. J. 2004, 616, 16–26. [Google Scholar] [CrossRef]
- Gustafsson, M.; Fairbairn, M.; Sommer-Larsen, J. Baryonic pinching of galactic dark matter halos. Phys. Rev. D 2006, 74, 123522. [Google Scholar] [CrossRef]
- Abadi, M.G.; Navarro, J.F.; Fardal, M.; Babul, A.; Steinmetz, M. Galaxy-induced transformation of dark matter haloes. Mon. Not. R. Astron. Soc. 2010, 407, 435–446. [Google Scholar] [CrossRef]
- Velliscig, M.; van Daalen, M.P.; Schaye, J.; McCarthy, I.G.; Cacciato, M.; Le Brun, A.M.C.; Dalla Vecchia, C. The impact of galaxy formation on the total mass, mass profile and abundance of haloes. Mon. Not. R. Astron. Soc. 2014, 442, 2641–2658. [Google Scholar] [CrossRef]
- Nipoti, C.; Treu, T.; Ciotti, L.; Stiavelli, M. Galactic cannibalism and cold dark matter density profiles. Mon. Not. R. Astron. Soc. 2004, 355, 1119–1124. [Google Scholar] [CrossRef]
- Romano-Díaz, E.; Shlosman, I.; Hoffman, Y.; Heller, C. Erasing Dark Matter Cusps in Cosmological Galactic Halos with Baryons. Astrophys. J. 2008, 685, L105. [Google Scholar] [CrossRef]
- Duffy, A.R.; Schaye, J.; Kay, S.T.; Dalla Vecchia, C.; Battye, R.A.; Booth, C.M. Impact of baryon physics on dark matter structures: A detailed simulation study of halo density profiles. Mon. Not. R. Astron. Soc. 2010, 405, 2161–2178. [Google Scholar] [CrossRef]
- Governato, F.; Brook, C.; Mayer, L.; Brooks, A.; Rhee, G.; Wadsley, J.; Jonsson, P.; Willman, B.; Stinson, G.; Quinn, T.; et al. Bulgeless dwarf galaxies and dark matter cores from supernova-driven outflows. Nature 2010, 463, 203–206. [Google Scholar] [CrossRef] [PubMed]
- Martizzi, D.; Teyssier, R.; Moore, B. The formation of the brightest cluster galaxies in cosmological simulations: The case for active galactic nucleus feedback. Mon. Not. R. Astron. Soc. 2012, 420, 2859–2873. [Google Scholar] [CrossRef]
- Dubois, Y.; Pichon, C.; Devriendt, J.; Silk, J.; Haehnelt, M.; Kimm, T.; Slyz, A. Blowing cold flows away: The impact of early AGN activity on the formation of a brightest cluster galaxy progenitor. Mon. Not. R. Astron. Soc. 2013, 428, 2885–2900. [Google Scholar] [CrossRef]
- Marziani, P.; Zamanov, R.K.; Sulentic, J.W.; Calvani, M. Searching for the physical drivers of eigenvector 1: Influence of black hole mass and Eddington ratio. Mon. Not. R. Astron. Soc. 2003, 345, 1133–1144. [Google Scholar] [CrossRef]
- Marziani, P.; Sulentic, J.W.; Negrete, C.A.; Dultzin, D.; D’Onofrio, M.; Del Olmo, A.; Martinez-Aldama, M.L. Low- and high-z highly accreting quasars in the 4D Eigenvector 1 context. Astron. Rev. 2014, 9, 6–25. [Google Scholar] [CrossRef]
- Śniegowska, M.; Czerny, B.; You, B.; Panda, S.; Wang, J.M.; Hryniewicz, K.; Wildy, C. Properties of active galaxies at the extreme of Eigenvector 1. Astron. Astrophys. 2018, 613, A38. [Google Scholar] [CrossRef]
- Du, P.; Zhang, Z.X.; Wang, K.; Huang, Y.K.; Zhang, Y.; Lu, K.X.; Hu, C.; Li, Y.R.; Bai, J.M.; Bian, W.H.; et al. Supermassive Black Holes with High Accretion Rates in Active Galactic Nuclei. IX. 10 New Observations of Reverberation Mapping and Shortened Hβ Lags. Astrophys. J. 2018, 856, 6. [Google Scholar] [CrossRef]
- Marziani, P.; del Olmo, A.; D’ Onofrio, M.; Dultzin, D.; Negrete, C.A.; Martiinez-Aldama, M.L.; Bon, E.; Bon, N.; Stirpe, G.M. Narrow-line Seyfert 1s: What is wrong in a name? arXiv 2018, arXiv:1807.03003. [Google Scholar]
- Peterson, B.M.; Wandel, A. Keplerian Motion of Broad-Line Region Gas as Evidence for Supermassive Black Holes in Active Galactic Nuclei. Astrophys. J. 1999, 521, L95–L98. [Google Scholar] [CrossRef]
- Marziani, P.; Sulentic, J.W.; Plauchu-Frayn, I.; del Olmo, A. Is Mg II 2800 a Reliable Virial Broadening Estimator for Quasars? Astron. Astrophys. 2013, 555, 89. [Google Scholar] [CrossRef]
- Mejía-Restrepo, J.E.; Trakhtenbrot, B.; Lira, P.; Netzer, H.; Capellupo, D.M. Active galactic nuclei at z∼1.5: II. Black Hole Mass estimation by means of broad emission lines. Mon. Not. R. Astron. Soc. 2016, 460, 187. [Google Scholar] [CrossRef]
- Sulentic, J.W.; del Olmo, A.; Marziani, P.; Martínez-Carballo, M.A.; D’Onofrio, M.; Dultzin, D.; Perea, J.; Martínez-Aldama, M.L.; Negrete, C.A.; Stirpe, G.M.; et al. What does CIVλ1549 tell us about the physical driver of the Eigenvector quasar sequence? Astron. Astrophys. 2017, 608, A122. [Google Scholar] [CrossRef]
- Bisogni, S.; di Serego Alighieri, S.; Goldoni, P.; Ho, L.C.; Marconi, A.; Ponti, G.; Risaliti, G. Simultaneous detection and analysis of optical and ultraviolet broad emission lines in quasars at z 2.2. Astron. Astrophys. 2017, 603, A1. [Google Scholar] [CrossRef]
- Vietri, G.; Piconcelli, E.; Bischetti, M.; Duras, F.; Martocchia, S.; Bongiorno, A.; Marconi, A.; Zappacosta, L.; Bisogni, S.; Bruni, G.; et al. The WISSH quasars project. IV. Broad line region versus kiloparsec-scale winds. Astron. Astrophys. 2018, 617, A81. [Google Scholar] [CrossRef]
- Netzer, H. On the profiles of the broad lines in the spectra of QSOs and Seyfert galaxies. Mon. Not. R. Astron. Soc. 1977, 181, 89–92. [Google Scholar] [CrossRef]
- Corbin, M.R. QSO Broad Emission Line Asymmetries: Evidence of Gravitational Redshift? Astrophys. J. 1995, 447, 496. [Google Scholar] [CrossRef]
- Punsly, B. The Redshifted Excess in Quasar C IV Broad Emission Lines. Astrophys. J. 2010, 713, 232–238. [Google Scholar] [CrossRef]
- Bon, N.; Bon, E.; Marziani, P.; Jovanović, P. Gravitational redshift of emission lines in the AGN spectra. Astrophys. Space Sci. 2015, 360, 7. [Google Scholar] [CrossRef]
- Mediavilla, E.; Jiménez-Vicente, J.; Fian, C.; Muñoz, J.A.; Falco, E.; Motta, V.; Guerras, E. Systematic Redshift of the Fe III UV Lines in Quasars: Measuring Supermassive Black Hole Masses under the Gravitational Redshift Hypothesis. Astrophys. J. 2018, 862, 104. [Google Scholar] [CrossRef]
- Mediavilla, E.; Jiménez-vicente, J.; Mejía-restrepo, J.; Motta, V.; Falco, E.; Muñoz, J.A.; Fian, C.; Guerras, E. Measuring Supermassive Black Hole Masses: Correlation between the Redshifts of the Fe III UV Lines and the Widths of Broad Emission Lines. Astrophys. J. 2019, 880, 96. [Google Scholar] [CrossRef]
- Sulentic, J.W.; Marziani, P.; del Olmo, A.; Dultzin, D.; Perea, J.; Alenka Negrete, C. GTC spectra of z ≈ 2.3 quasars: Comparison with local luminosity analogs. Astron. Astrophys. 2014, 570, A96. [Google Scholar] [CrossRef]
- Marziani, P.; Olmo, A.d.; Negrete, C.A.; Dultzin, D.; Piconcelli, E.; Vietri, G.; Martínez-Aldama, M.L.; D’Onofrio, M.; Bon, E.; Bon, N.; et al. The Intermediate-ionization Lines as Virial Broadening Estimators for Population A Quasars. Astrophys. J. 2022, 261, 30. [Google Scholar] [CrossRef]
- Panda, S. Parameterizing the AGN Radius–Luminosity Relation from the Eigenvector 1 Viewpoint. Front. Astron. Space Sci. 2022, 9, 850409. [Google Scholar] [CrossRef]
- Dalla Bontà, E.; Peterson, B.M.; Bentz, M.C.; Brandt, W.N.; Ciroi, S.; De Rosa, G.; Fonseca Alvarez, G.; Grier, C.J.; Hall, P.B.; Hernández Santisteban, J.V.; et al. The Sloan Digital Sky Survey Reverberation Mapping Project: Estimating Masses of Black Holes in Quasars with Single-epoch Spectroscopy. Astrophys. J. 2020, 903, 112. [Google Scholar] [CrossRef]
- Peterson, B.; Dalla Bontà, E. Reverberation Mapping and Implications for Narrow-Line Seyfert 1 Galaxies. In Revisiting Narrow-Line Seyfert 1 Galaxies and their Place in the Universe; Proceedings of Science (PoS, Trieste, Italy) 2018; Padova Botanical Garden: Padua, Italy, 2018; p. 8. [Google Scholar] [CrossRef]
- Véron-Cetty, M.P.; Véron, P.; Gonçalves, A.C. A spectrophotometric atlas of Narrow-Line Seyfert 1 galaxies. Astron. Astrophys. 2001, 372, 730–754. [Google Scholar] [CrossRef]
- Kollatschny, W.; Zetzl, M. Broad-line active galactic nuclei rotate faster than narrow-line ones. Nature 2011, 470, 366–368. [Google Scholar] [CrossRef]
- Kollatschny, W.; Zetzl, M. The shape of broad-line profiles in active galactic nuclei. Astron. Astrophys. 2013, 549, A100. [Google Scholar] [CrossRef]
- Mejía-Restrepo, J.E.; Lira, P.; Netzer, H.; Trakhtenbrot, B.; Capellupo, D.M. The effect of nuclear gas distribution on the mass determination of supermassive black holes. Nat. Astron. 2018, 2, 63–68. [Google Scholar] [CrossRef]
- Martínez-Aldama, M.L.; Zajaček, M.; Czerny, B.; Panda, S. Scatter Analysis along the Multidimensional Radius-Luminosity Relations for Reverberation-mapped Mg II Sources. Astrophys. J. 2020, 903, 86. [Google Scholar] [CrossRef]
- Du, P.; Wang, J.M.; Hu, C.; Ho, L.C.; Li, Y.R.; Bai, J.M. The Fundamental Plane of the Broad-line Region in Active Galactic Nuclei. Astrophys. J. 2016, 818, L14. [Google Scholar] [CrossRef]
- Huang, Y.K.; Hu, C.; Zhao, Y.L.; Zhang, Z.X.; Lu, K.X.; Wang, K.; Zhang, Y.; Du, P.; Li, Y.R.; Bai, J.M.; et al. Reverberation Mapping of the Narrow-line Seyfert 1 Galaxy I Zwicky 1: Black Hole Mass. Astrophys. J. 2019, 876, 102. [Google Scholar] [CrossRef]
- Collin, S.; Kawaguchi, T.; Peterson, B.M.; Vestergaard, M. Systematic effects in measurement of black hole masses by emission-line reverberation of active galactic nuclei: Eddington ratio and inclination. Astron. Astrophys. 2006, 456, 75–90. [Google Scholar] [CrossRef]
- Afanasiev, V.L.; Popović, L.Č.; Shapovalova, A.I. Spectropolarimetry of Seyfert 1 galaxies with equatorial scattering: Black hole masses and broad-line region characteristics. Mon. Not. R. Astron. Soc. 2019, 482, 4985–4999. [Google Scholar] [CrossRef]
- Capetti, A.; Laor, A.; Baldi, R.D.; Robinson, A.; Marconi, A. Spectropolarimetry of low redshift quasars: Origin of the polarization and implications for black hole mass estimates. Mon. Not. R. Astron. Soc. 2021, 502, 5086–5103. [Google Scholar] [CrossRef]
- Martinez-Aldama, M.L.; Del Olmo, A.; Marziani, P.; Sulentic, J.W.; Negrete, C.A.; Dultzin, D.; Perea, J.; D’Onofrio, M. Highly Accreting Quasars at High Redshift. Front. Astron. Space Sci. 2018, 4, 65. [Google Scholar] [CrossRef]
- Negrete, C.A.; Dultzin, D.; Marziani, P.; Esparza, D.; Sulentic, J.W.; del Olmo, A.; Martínez-Aldama, M.L.; García López, A.; D’Onofrio, M.; Bon, N.; et al. Highly accreting quasars: The SDSS low-redshift catalog. Astron. Astrophys. 2018, 620, A118. [Google Scholar] [CrossRef]
- Marziani, P.; Olmo, A.; Martínez-Aldama, M.; Dultzin, D.; Negrete, A.; Bon, E.; Bon, N.; D’Onofrio, M. Quasar Black Hole Mass Estimates from High-Ionization Lines: Breaking a Taboo? Atoms 2017, 5, 33. [Google Scholar] [CrossRef]
- Marziani, P. Highly Accreting Supermassive Black Holes as Eddington Standard Candles. Phys. Sci. Forum 2023, 7, 39. [Google Scholar] [CrossRef]
- Krawczyk, C.M.; Richards, G.T.; Mehta, S.S.; Vogeley, M.S.; Gallagher, S.C.; Leighly, K.M.; Ross, N.P.; Schneider, D.P. Mean Spectral Energy Distributions and Bolometric Corrections for Luminous Quasars. Astrophys. J. Suppl. 2013, 206, 4. [Google Scholar] [CrossRef]
- Duras, F.; Bongiorno, A.; Ricci, F.; Piconcelli, E.; Shankar, F.; Lusso, E.; Bianchi, S.; Fiore, F.; Maiolino, R.; Marconi, A.; et al. Universal bolometric corrections for active galactic nuclei over seven luminosity decades. A&A 2020, 636, A73. [Google Scholar] [CrossRef]
- Laurenti, M.; Piconcelli, E.; Zappacosta, L.; Tombesi, F.; Vignali, C.; Bianchi, S.; Marziani, P.; Vagnetti, F.; Bongiorno, A.; Bischetti, M.; et al. X-ray spectroscopic survey of highly accreting AGN. Astron. Astrophys. 2022, 657, A57. [Google Scholar] [CrossRef]
- Marziani, P.; Floris, A.; Deconto-Machado, A.; Panda, S.; Sniegowska, M.; Garnica, K.; Dultzin, D.; D’Onofrio, M.; Del Olmo, A.; Bon, E.; et al. From Sub-Solar to Super-Solar Chemical Abundances along the Quasar Main Sequence. Physics 2024, 6, 216. [Google Scholar] [CrossRef]
- Yu, L.M.; Bian, W.H.; Wang, C.; Zhao, B.X.; Ge, X. Calibration of the virial factor f in supermassive black hole masses of reverberation-mapped AGNs. Mon. Not. R. Astron. Soc. 2019, 488, 1519–1534. [Google Scholar] [CrossRef]
- Yu, L.M.; Bian, W.H.; Zhang, X.G.; Zhao, B.X.; Wang, C.; Ge, X.; Zhu, B.Q.; Chen, Y.Q. The Supermassive Black Hole Masses of Reverberation-mapped Active Galactic Nuclei. Astrophys. J. 2020, 901, 133. [Google Scholar] [CrossRef]
- Marziani, P.; Sulentic, J.W.; Plauchu-Frayn, I.; del Olmo, A. Low-Ionization Outflows in High Eddington Ratio Quasars. Astrophys. J. 2013, 764, 150. [Google Scholar] [CrossRef]
- Urry, C.M.; Padovani, P. Unified Schemes for Radio-Loud Active Galactic Nuclei. Publ. Astron. Soc. Pac. 1995, 107, 803. [Google Scholar] [CrossRef]
- Antonucci, R. Unified models for active galactic nuclei and quasars. Annu. Rev. Astron. Astrophys. 1993, 31, 473–521. [Google Scholar] [CrossRef]
- Negrete, C.A.; Dultzin, D.; Marziani, P.; Sulentic, J.W. Reverberation and Photoionization Estimates of the Broad-line Region Radius in Low-z Quasars. Astrophys. J. 2013, 771, 31. [Google Scholar] [CrossRef]
- Kaspi, S.; Brandt, W.N.; Maoz, D.; Netzer, H.; Schneider, D.P.; Shemmer, O.; Grier, C.J. Taking a Long Look: A Two-decade Reverberation Mapping Study of High-luminosity Quasars. Astrophys. J. 2021, 915, 129. [Google Scholar] [CrossRef]
- Shen, Y.; Grier, C.J.; Horne, K.; Stone, Z.; Li, J.I.; Yang, Q.; Homayouni, Y.; Trump, J.R.; Anderson, S.F.; Brandt, W.N.; et al. The Sloan Digital Sky Survey Reverberation Mapping Project: Key Results. arXiv 2023, arXiv:2305.01014. [Google Scholar] [CrossRef]
- Laor, A. Evidence for Line Broadening by Electron Scattering in the Broad-Line Region of NGC 4395. Astrophys. J. 2006, 643, 112–119. [Google Scholar] [CrossRef]
- D’Onofrio, M.; Chiosi, C. A tomography of the log(⟨I⟩e) − log(Re) plane. arXiv 2020, arXiv:2011.07315. [Google Scholar]
- Drescher, A.; Fabricius, M.; Shimizu, T.; Woillez, J.; Bourget, P.; Widmann, F.; Shangguan, J.; Straubmeier, C.; Horrobin, M.; Schuhler, N.; et al. GRAVITY+ Wide: Towards hundreds of z 2 AGN. In Optical and Infrared Interferometry and Imaging VIII, Proceedings of the Society of Photo-Optical Instrumentation Engineers (SPIE) Conference; Mérand, A., Sallum, S., Sanchez-Bermudez, J., Eds.; SPIE: Bellingham, WA, USA, 2022; Volume 12183, p. 121830T. [Google Scholar] [CrossRef]
- GRAVITY Collaboration; Amorim, A.; Bourdarot, G.; Brandner, W.; Cao, Y.; Clénet, Y.; Davies, R.; de Zeeuw, P.T.; Dexter, J.; Drescher, A.; et al. The size-luminosity relation of local active galactic nuclei from interferometric observations of the broad-line region. arXiv 2024, arXiv:2401.07676. [Google Scholar] [CrossRef]
- D’Onofrio, M.; Marziani, P. A multimessenger view of galaxies and quasars from now to mid-century. Front. Astron. Space Sci. 2018, 5, 31. [Google Scholar] [CrossRef]
- Marziani, P.; Sulentic, J.W. Quasars and their emission lines as cosmological probes. Adv. Space Res. 2014, 54, 1331–1340. [Google Scholar] [CrossRef]
- Tully, R.B.; Fisher, J.R. Reprint of 1977A&A...54..661T. A new method of determining distance to galaxies. Astron. Astrophys. 1977, 500, 105–117. [Google Scholar]
- McGaugh, S.S.; Schombert, J.M.; Bothun, G.D.; de Blok, W.J.G. The Baryonic Tully-Fisher Relation. Astrophys. J. 2000, 533, L99–L102. [Google Scholar] [CrossRef]
- Sulentic, J.W.; Bachev, R.; Marziani, P.; Negrete, C.A.; Dultzin, D. C IV λ1549 as an Eigenvector 1 Parameter for Active Galactic Nuclei. Astrophys. J. 2007, 666, 757–777. [Google Scholar] [CrossRef]
- Richards, G.T.; Kruczek, N.E.; Gallagher, S.C.; Hall, P.B.; Hewett, P.C.; Leighly, K.M.; Deo, R.P.; Kratzer, R.M.; Shen, Y. Unification of Luminous Type 1 Quasars through C IV Emission. Astron. J. 2011, 141, 167. [Google Scholar] [CrossRef]
- Zamanov, R.; Marziani, P.; Sulentic, J.W.; Calvani, M.; Dultzin-Hacyan, D.; Bachev, R. Kinematic Linkage between the Broad- and Narrow-Line-emitting Gas in Active Galactic Nuclei. Astrophys. J. 2002, 576, L9–L13. [Google Scholar] [CrossRef]
- Zhang, K.; Dong, X.B.; Wang, T.G.; Gaskell, C.M. The Blueshifting and Baldwin Effects for the [O III] λ5007 Emission Line in Type 1 Active Galactic Nuclei. Astrophys. J. 2011, 737, 71. [Google Scholar] [CrossRef]
- Concas, A.; Popesso, P.; Brusa, M.; Mainieri, V.; Erfanianfar, G.; Morselli, L. Light breeze in the local Universe. Astron. Astrophys. 2017, 606, A36. [Google Scholar] [CrossRef]
- Zhang, X.G. Evidence for obscured broad [O III] components in Type-2 AGN. Mon. Not. R. Astron. Soc. 2021, 502, 2508–2512. [Google Scholar] [CrossRef]
- Kriss, G. Fitting Models to UV and Optical Spectral Data. Astron. Data Anal. Softw. Syst. III A.S.P. Conf. Ser. 1994, 61, 437. [Google Scholar]
- Tody, D. IRAF in the Nineties. In Astronomical Data Analysis Software and Systems II, Proceedings of the Astronomical Society of the Pacific Conference, San Diego, CA, USA, 13–15 July 1993; Hanisch, R.J., Brissenden, R.J.V., Barnes, J., Eds.; Astronomical Society of the Pacific: San Francisco, CA, USA, 1993; Volume 52, p. 173. [Google Scholar]
- Marziani, P.; Sulentic, J.W.; Negrete, C.A.; Dultzin, D.; Zamfir, S.; Bachev, R. Broad-line region physical conditions along the quasar eigenvector 1 sequence. Mon. Not. R. Astron. Soc. 2010, 409, 1033–1048. [Google Scholar] [CrossRef]
- Sulentic, J.W.; Marziani, P.; Zamfir, S.; Meadows, Z.A. No Evidence for a Systematic Fe II Emission Line Redshift in Type 1 Active Galactic Nuclei. Astrophys. J. 2012, 752, L7. [Google Scholar] [CrossRef]
- Azzalini, A.; Regoli, G. Some properties of skew-symmetric distributions. Ann. Inst. Statist. Math. 2012, 64, 857–879. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).